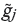PAPERS OF GENERAL INTEREST

 

A stochastic mathematical model for determination of transition time in the non-simultaneous case of surface and underground mining

 

 

E. Bakhtavar^I; J. Abdollahisharif^II; A. Aminzadeh^II

^IDepartment of Mining and Materials Engineering, Urmia University of Technology, Iran
^IIFaculty of Engineering, Urmia University, Iran

 

 

---

SYNOPSIS

This research introduces a stochastic mathematical model that uses open pit long-term production planning on an integrated open pit and underground block model to determine the optimal time for transition from open pit to underground mining. In the model, ore grade is considered a random parameter in objective function and ore grade blending constraints. The objective function is modelled as the maximization of net present value in the mode of non-simultaneous combined open pit and underground mining. Moreover, the most important and conventional constraints in open pit long-term production planning are developed for non-simultaneous combined mining. Finally, information on an iron ore deposit is used to evaluate the results of the model.

Keywords: stochastic programming, transition time, non-simultaneous, combined mining.

---

 

 

Introduction

The problems of non-simultaneous combined mining by open pit and underground methods and transition from open pit to underground mining are among the most important challenges in mining engineering, and have been recently considered in many research investigations. Different researchers have attempted to solve these problems and presented solutions based on empirical, heuristic, and mathematical programming methods. In these works, the transition problem has been examined in three modes: (1) optimizing transition from open pit to underground mining, (2) determining the point, depth, or limit of transition from open pit to underground operation, and (3) determining the time of transition.

Bakhtavar, Shahriar, and Mirhasani (2012) reviewed the solutions proposed for the transition problem, a summary of which is given in Table I, together with the most recent solutions. It can be seen from Table I that few of the solutions have an empirical basis, ultimately leading to only an estimated response. The main weaknesses of the empirical solutions are ignoring the time value of money, production planning, and uncertainties.

Most of the solutions for the transition problem have a heuristic basis and follow a similar process by use of the cash flow solution introduced by Nilsson (1982). They make an economic comparison among different options, including open pit and underground mining. Some other heuristic solutions, such as the algorithms proposed by Bakhtavar and Shahriar (2007) and Shahriar (2007) and Bakhtavar, Shahriar, and Oraee (2008a, 2008b) are based on an economic comparison of open pit and underground mining methods at different levels of an ore deposit. The main drawback of the heuristic solutions is their complete dependence on the optimization algorithms of surface and underground mining. For this reason, they cannot solve the transition problem independently. Another deficiency of the heuristic solutions, excluding the research presented by Opoku and Musingwini (2013), is failure to consider uncertainty. This deficiency leads to the small difference between their responses and the reality. The working steps of the solution presented by Opoku and Musingwini (2013) are mostly similar to the solution by Visser and Ding (2007), except that Opoku and Musingwini emphasized uncertainties during geological simulation (in kriging) and prepared production planning and economic models employing conventional mining software.

Among the solutions for the transition problem, studies by Bakhtavar, Shahriar, and Mirhasani (2012), Newman, Yano, and Rubio (2013), Chung, Topal, and Ghosh (2016), and MacNeil and Dimitrakopoulos (2017) have a mathematical basis and are more stable than others. These methods can be considered a foundation and then developed or modified to achieve an optimum solution to the transition problem, similar to the development of the optimization models of final pit limits and production planning.

The model by Bakhtavar, Shahriar, and Mirhasani (2012) started to apply mathematical programming in combined mining by open pit and underground methods and in solving the transition problem. It has some deficiencies, such as failure to consider production planning and net present value (NPV), presentation on a two-dimensional block model, limitation in the number of decision variables, and ignoring uncertainties such as ore grade. Among the important advantages of this model are its detail-oriented trend (on blocks with economic value) and its independence from other pit limits and production planning optimization algorithms. This model uses binary integer programming to maximize the profit from combined open pit and underground mining. A computerized tool was developed based on the model established by Bakhtavar, Shahriar, and Mirhasani (2012) for simple applications (Bakhtavar, 2015).

The model introduced by Newman, Yano, and Rubio (2013) follows a holistic trend based on investigating various strata of an ore deposit at different levels using network programming. In this model, which is stated by schematic networks, the method of determining deposit boundaries in each stratum was not specified. Using strata instead of blocks in a block model can reduce the number of decision variables and investigations; however, this may not lead to an accurate response compared to blocks. The strata were considered due to the large size of the deposits with combined open pit and underground mining potential. In these cases, using conventional ore blocks would limit problem-solving using the available solvers and personal computers. Since each stratum is mined during two or more scheduling periods, mining sequence and production planning cannot determine which part of the stratum must be mined in the first place. To solve this problem, the strata must include ore blocks with a grade or economic net value. The main weakness of the network model by Newman, Yano, and Rubio (2013) is failure to consider uncertainty. This model is primarily based on maximizing NPV and decision-making based on production planning, which is a benefit of this model.

An integer programming-based model was developed by Chung, Topal, and Ghosh (2016) to determine the transition point from open pit to underground mining in three-dimensional space. Some strategies for shortening the solution time were attempted in order to deal with the problem of a large number of variables. This research focused on the optimal mining strategy, in addition to the optimal determination of the transition point from open pit to underground mining.

MacNeil and Dimitrakopoulos (2017) developed a two-stage stochastic integer programming model by use of geological uncertainty and managing technical risk to determine the transition from open pit to underground mining. The discounted cash flow values of different transition depth alternatives are calculated after optimizing the production schedules of each depth for open pit and underground operations. The most profitable transition depth alternative is determined by comparing the sum of both open pit and underground mining values. This base concept of making a comparison among a set of transition depth alternatives is similar to the work by Bakhtavar, Shahriar, and Oraee (2008a, 2009). The only deficiency of the model is holistically investigating and solving the transition problem by use of a two-stage process of open pit and underground production scheduling.

In the present study, attempts are made to introduce a stochastic binary integer programming model, which not only eliminates the deficiencies of other methods but also incorporates their benefits as far as is possible. Therefore, the model follows the following objectives:

► Determining the optimal time for transition from open pit to underground mining based on maximizing NPV

► Searching three-dimensional block models based on a detail-oriented trend

► Independence from the software and algorithms of production planning and pit limit and underground layout optimization (i.e., independent working)

► Considering ore grade uncertainty in mathematical planning of the model

► Considering technical and economic criteria (constraints).

For these purposes, the stochastic model presented by Gholamnejad, Osanloo, and Khorram (2008) for optimal long-term production planning for open pits, which was originally introduced by Rao (1996), is the basis for the present research.

 

Stochastic mathematical modelling

Objective function and the basis of the model

This research aims to maximize the overall NPV obtained from combined open pit and underground mining. Thus, in mathematical modelling, the objective function is defined as the maximization of the combined NPV resulted from both open pit and underground operations. To this end, the following requirements are taken into account.

First, the economic net values of combined open pit and underground blocks are determined. In the transition problem, the main objective is to identify levels, and consequently blocks, extractable by open pit or underground methods so that an economic comparison is made for each block and level between open pit and underground methods. Then, the mining method with a higher NPV is selected as the superior option. This research uses the concept of the priority of open pit to underground mining. In this case, the combined economic value for each block is calculated by subtracting open pit and underground block net values. This concept has been used in some solutions for the transition problem, such as the work by Camus (1992) and Tulp (1998). Open pit and underground economic net values for each block are calculated by use of Equations [1] and [2], respectively. Moreover, according to Equation [3] and by subtraction of open pit and underground block net values, combined (subtracted) block net value can be calculated using Equation [4]. It should be noted that block caving is the most practicable underground method in the case of non-simultaneous open-pit and underground mining. In block caving, ore recovery can usually be close to the open pit recovery, approaching 100%. Therefore, in Equation [4], ore recovery (r) is considered to be 100% for both open pit and underground methods (rop = r_Ug = 1).

where

BEV_op: Open pit economic net value for each block

P: Unit selling price of metal

C&. Unit selling cost of metal

r₀p: Total metal recovery in open pit mining

g: Block grade

To: Total amount of ore in each block C₀p. Unit open pit cost of ore extraction

C_WUnit open pit cost of waste removal

T_WTotal amount of waste in each block

BEV_Ug: Underground economic net value for each block

r_ug: Total metal recovery in underground mining

C_ug: Unit underground cost of ore extraction

B: Open pit and underground combined economic net value for each block.

In Equations [1] to [4], the economic net value of a waste block is negative, since a waste block imcurs removal cost without any profit. The NPV resulting from combined open pit and underground mining is obtained by Equation [5].

In certainty mode, based on Equations [1] to [5], the objective function can be defined as Equation [6] in the form of a programming model using (0-1) integer decision variables.

All the model variables, parameters, indices, counters, and indicators are defined in Appendix 1.

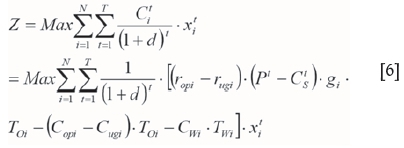
The most important uncertainties should be involved to minimize the errors of the optimization process and to achieve the optimal response, especially in specific mining situations that are greatly influenced by uncertainties. Simulating a deposit and preparing a geological block model with block grade estimation are the basis for the optimization of production planning and mining layout. These simulations and grade block models, which are constructed using exploration data, particularly from exploration boreholes, contain estimation errors. As a result, these errors are incorporated directly into all the processes based on using data on grade (geological) block models in optimizing production planning. Therefore, block grade is randomly considered with uncertainty in the optimization of production planning to minimize the impact of grade error resulting from exploration phase and block model simulation. In this case, the objective of maximizing NPV is accompanied by minimizing risks arising from the uncertainty in block grade.

The random grade parameter is imported to the objective function and the related constraints of the model. Accordingly, the objective function of maximizing NPV as given in Equation [6] is randomly formulated in the following stages.

After applying changes associated with the random variable to the objective function and constraints, they are non-linearized. They can be converted into linear mode using linear approximation methods, or the model can be solved in the same nonlinear mode. When a parameter is randomly considered in stochastic programming, some changes are made to the objective function and constraints. Assuming that a random variable has a normal distribution, a specific probability is considered for a constraint, and then the expected values and the variance are calculated. Given that the random variable has a normal distribution, the objective function would also have a normal distribution, and the expected value and variance would be calculated in the objective function. In such a case, a new objective function is defined in two stages: the first stage consists of maximizing the average of NPV, and the second is minimizing deviation from the main objective, which is the maximization of NPV.

Now that ore grade is considered as a random variable, a confidence level is first assumed based on Equation [7] for the constraint related to the average grade as given in Equations [8] and [9].

Then, the expected value and variance of a random variable are calculated. The calculation results for expected value (average) and variance on the constraint with ore grade random variable are applied as given in Equations [10] to [14].

Given that the random variable of ore grade exists in the objective function, the expected value and variance of the objective function by the random variable of the ore grade are calculated by Equations [15] and [16].

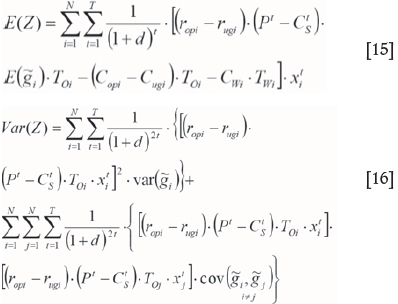
According to Equation [17], the new objective function maximizes the average NPV resulting from combined mining and minimizes the deviation from grade distribution where optimal production planning is applied only to open pit mining in the combined block model.

Equation [18] indicates that values for the expected value and variance of the objective function are imported to Equation [17].

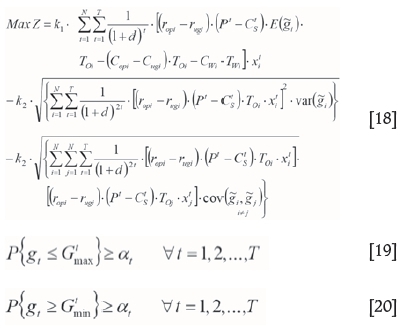
Constraints

Consistent with the long-term production planning model presented by Gholamnejad, Osanloo, and Khorram (2008), the following constraints are considered for the problem of transition from open pit to underground mining.

Constraints of ore grade blending

The average ore grade of materials that are sent to the processing plant in each period is different, and has upper and lower bounds, as given in Equations [21] and [22] by Gholamnejad, Osanloo, and Khorram (2008).

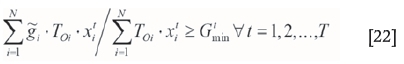
The normal distribution function of the ore grade random variable is converted into a standard normal distribution by use of Equations [23] and [24].

where '·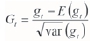 is a standard normal random variable associated with ore grade which has an expected value (average) of zero and variance of unity. In this case, S_t is the value of a random variable that is true in Equation [25].

Equation [26] can be derived from Equations [23] and

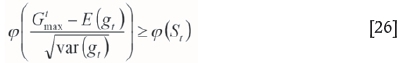
According to Equation [26], the following certain and nonlinear inequality (Equation [27]) can be fixed. Thus, the constraint of the problem changes from random and uncertain mode to certain but nonlinear.

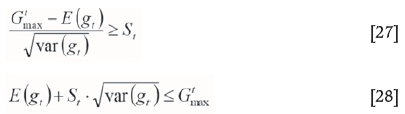
Now, the values for the expected value and variance of a random variable are substituted into Equation [28], and the grade-related constraints are given by Equations [29] and [30].

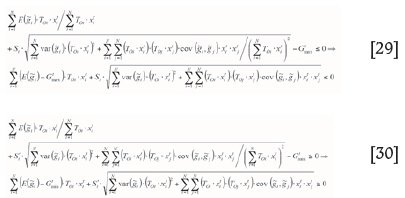
Equation [33] shows the constraint related to the lower bound of the grade blending constraint. The values of S_tand S' are calculated by taking the integral of standard normal distribution function as given in Equations [31] and [32].

Constraints ofmining capacity and available equipment

The tonnage of ore and waste materials mined in one period cannot exceed the maximum capacity or be less than a minimum capacity of equipment available in that period. Accordingly, the constraints of the maximum and minimum capacity of equipment can be formulated as Equations [33] and [34].

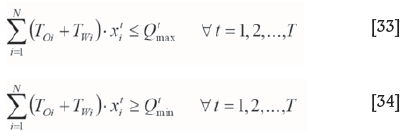
Constraints related to slope stability

All blocks above the desired block must be extracted so that, for the stability of the pit wall, a cone with at least three blocks would comprise the desired block. This constraint also indicates that all rows of the pit limit should be assumed continuous in mining. This constraint is mathematically defined by Equation [35].

Constraints related to reserve extraction

According to the constraints of reserve extraction, any block in the block model can be extracted only once, in one period and using only one method (open pit or underground mining). This constraint is mathematically modelled using Equation [36].

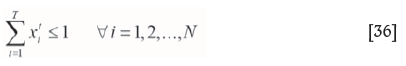
Linearizing the nonlinear model of the transition problem

The objective function of the model (Equation [18]) and the constraints of the upper and lower bounds of grade (Equations [29] and [30]) are certain but nonlinear. They are linearized by use of a linear approximation method.

If x_iand x_jare assumed as two interdependent random variables, a parameter can be defined as a correlation coefficient between these two variables as given in Equation [37].

Since the correlation coefficient is between 1 and -1, Equation [38] can be applied.

Therefore, the maximum amount of covariance can be equal to the product of the variance of two variables. In Equations [18], [29], and [30], instead of covariance, the product of the variance of two variables is imported, yielding Equation [39].

Now, the certain and nonlinear equations are linearized and rewritten as in Equations [40] and [41].

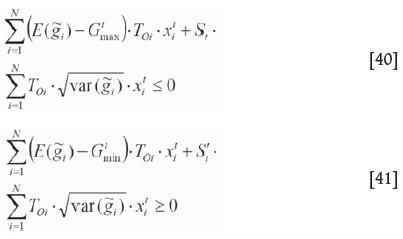
In Equation [29], changes are applied as Equation [42].

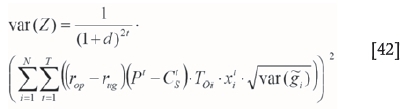
According to Equation [18], this can be written as:

These values are substituted in the objective function, which is written as Equation [45].

Using the linear approximation method, the objective function and the constraints for grade blending become linear. Finally, the model for determining the transition time in non-simultaneous combined mining is formulated employing ore grade uncertainty based on binary (zero and unity) integer programming as follows:

 

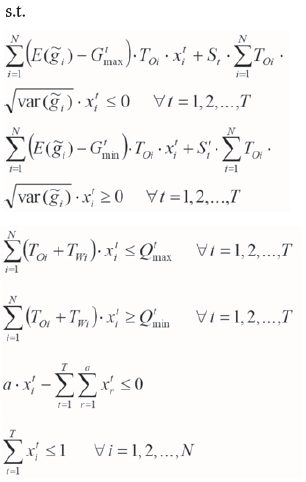
Results and discussion

An iron ore deposit with potential for mining by a combination of open pit and block caving is used to apply the introduced stochastic programming model. The size of the ore deposit was estimated at approximately 160 Mt at an average grade of 51%. According to the mine design parameters, the height of the benches in the open pit part was to be 15 m. It should be noted that in addition to block caving, sublevel caving can also be used as an alternative the case of non-simultaneous underground and open pit mining.

A geological model of the iron ore deposit that includes blocks with Fe grades is first created. The model consisted of 11 023 blocks with an average grade of 51%. The block size is 15x15x15 m. Table II summarizes some essential technical and economic parameters for applying the presented stochastic model in the non-simultaneous case of open pit and block caving mining. The grade value of each block that resulted from the kriging-based geostatistical process is imported to the stochastic model. A normal distribution function is assumed by the mean (kriging estimate) and variance (estimation variance) values of the grade parameter taken from the kriging process. The normal distribution function of the ore grade random variable was also considered by Gholamnejad, Osanloo, and Khorram (2008) and Halatchev and Lever (2005) for simplifying the calculation procedures.

 

 

Then, the stochastic mathematical model of the studied case with 22046 decision variables is solved in approximately 55 minutes, and the optimal solution obtained. As shown in Figure 1, the results indicated that the optimal transition time is when the pit depth reaches the 1765 m level in the case of non-simultaneous combined open pit and block caving mining. According to the optimal transition time, a total NPV of $5159.7 million is determined. In the optimal case, the iron ore deposit should be mined by open pit to the 1765 m level, and the rest of the ore deposit between levels 1765 m and 1630 m by block caving.

 

 

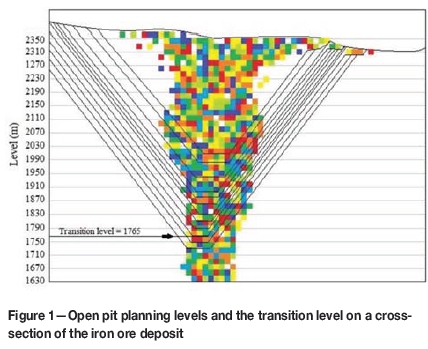
It is noteworthy that the determination of the transition time from open pit to underground mining is a very complex multi-attribute decision-making (MADM) process. Mathematical modelling of the transition problem based on the MADM concepts is very complicated, especially in the case of a detail-oriented trend as was considered in this research by searching for blocks on a block model with combinational economic values. The current research focused only on the technical and economic parameters (attributes) to avoid the complexity of modelling the transition problem as a multi-attribute system.

The transition problem is similar to other mining problems based on strategic planning and asset management, which are long-term processes. Komljenovic, Abdul-Nour, and Popovic (2015) explained that the strategic planning and asset management models in mining projects should incorporate all related economic, operational, technical, engineering, organizational, natural, and other important factors in a systematic manner. The impacts of uncertainties and operational complexities should also be considered.

Accordingly, mining problems and challenges are quite complex with a multidimensional space because of major uncertainties arising through the complexity of the system. The traditional models in strategic planning, asset management, and decision-making in the case of mining problems have some limitations which make it difficult to deal with the complexities adequately. For this reason, many mining organizations have employed the strategic planning and management models that decrease uncertainties to increase the overall efficiency of the system. In this case, the new approaches are required to model and analyse mining problems as complex adaptive systems (Komljenovic, Abdul-Nour, and Popovic, 2015).

 

Conclusion

A mathematical model was presented utilizing open pit long-term production planning and the stochastic effect of ore grade to determine the optimal transition time from open pit to underground mining. The objective function of the model is based on the maximization of NPV in the case of non-simultaneous combined open pit and underground mining. The most important constraints are developed for the non-simultaneous combined mining based on open pit long-term production planning. A database from an iron ore deposit of about 160 Mt was used to implement the model in detail. The deposit is suitable for mining by a combination of open pit and block caving. The proposed model was developed and solved considering the essential technical and economic data for the mining system. The results indicate that a total NPV of $ 5159.7 million is obtained based on the 1765 m level being selected as the optimal level for the transition from open pit to block caving.

 

References

Bakhtavar, E. 2013. Transition from open-pit to underground in the case of Chah-Gaz iron ore combined mining. Journal of Mining Science, vol. 49, no. 6. pp. 955-966.         [ Links ]

Bakhtavar, E. 2015. OP-UG TD optimizer tool based on Matlab code to find transition depth from open pit to block caving. Archives of Mining Science, vol. 60, no. 2. pp. 487-495.         [ Links ]

Bakhtavar, E. and Shahriar, K. 2007. Optimal ultimate pit depth considering an underground alternative. Proceeding of the Fourth Aachen International Mining Symposium - High Performance Mine Production, Aachen, Germany. RWTH Aachen. pp. 213-221.         [ Links ]

Bakhtavar, E., Shahriar, K., and Mirhasani, A. 2012. Optimization of the transition from open pit to underground operation in combined mining using (0-1) integer programming. Journal of the Southern African Institute of Mining and Metallurgy, vol. 112. pp. 1059-1064.         [ Links ]

Bakhtavar, E., Shahriar, K., and Oraee, K. 2008a, A model for determining optimal transition depth over from open pit to underground mining. MassMin 2008: Proceedings of the 5th International Conference and Exhibition on Mass Mining, Luleá, Sweden, 9-11 June 2008. Schunnesson, H. and Nordlund, E. (eds.). Luleá University of Technolog. pp. 393-400.         [ Links ]

Bakhtavar, E., Shahriar, K., and Oraee, K. 2008b. An approach towards ascertaining open-pit to underground transition depth. Journal of Applied Sciences, vol. 8, no. 23. pp. 4445-4449.         [ Links ]

Bakhtavar, E., Shahriar, K., and Oraee, K. 2009. Transition from open-pit to underground as a new optimization challenge in mining engineering. Journal of Mining Science, vol. 45. pp. 485-494.         [ Links ]

Camus, J.P. 1992. Open pit optimization considering an underground alternative. Proceedings of 23th International Symposium on the Application of Computers and Operations Research in the Mineral Industry (APCOM), Tucson, AZ, 7-11 April 1992. Kim, Y.C. (ed.). Society of Mining Engineers of AiME. pp. 435-441.         [ Links ]

Chen, J., Guo, D., and Li, J. 2003. Optimization principle of combined surface and underground mining and its applications. Journal of Central South University of Technology, vol. 10, no. 3. pp. 222-225.         [ Links ]

Chen, J., Li, J., Luo, Z., and Guo, D. 2001. Development and application of optimum open-pit limits software for the combined mining of surface and underground. Proceedings of CAMI Symposium. Sweets & Zeitlinger, Lisse, The Netherlands. pp. 303-306.         [ Links ]

Chung, J., Topal, E., and Ghosh, A.K. 2016. Where to make the transition from open-pit to underground? Using integer programming. Journal of the Southern African Institute of Mining and Metallurgy, vol. 116, no. 8. pp. 801-808.         [ Links ]

Gholamnejad, J., Osanloo, M., anD Khorram, E. 2008. A chance constrained integer programming model for open pit long-term production planning. Scientific Information Database, vol. 21. pp. 407-418.         [ Links ]

Halatchev, R. and Lever, P. 2005. Risk model of long-term production scheduling in open pit gold mining. Proceedings of the CRC Mining Technology Conference, Fremantle, WA, 27-28 September 2005.         [ Links ]

Komljenovic, D., Abdul-Nour, G., and Popovic, N. 2015. An approach for strategic planning and asset management in the mining industry in the context of business and operational complexity. International Journal of Mining and Mineral Engineering, vol. 6, no. 4. pp. 338-360.         [ Links ]

MacNeil, J.A.L. and Dimitrakopoulos, R.G. 2017. A stochastic optimization formulation for the transition from open pit to underground mining. Optimization and Engineering. https://doi.org/10.1007/s11081-017-9361-6        [ Links ]

Newman, A., Yano, C.A., and Rubio, E. 2013. Mining above and below ground: timing the transition. IIE Transactions. pp. 865-882.         [ Links ]

Nilsson, D. 1982. Open pit or underground mining, Underground Mining Methods Handbook. AIME, New York. pp. 70-87.         [ Links ]

Nilsson, D. 1992. Surface vs. underground methods. SME Mining Engineering Handbook.Hartman, H.L. (ed.). Society for Mining, Metallurgy and Exploration, Littleton, Co. pp. 2058-2068.         [ Links ]

Nilsson, D. 1997. Optimal final pit depth once again. International Journal of Mining Engineering. pp. 71-72.         [ Links ]

Opoku, S. and Musingwini, C. 2013. Stochastic modelling of the open pit tounderground transition interface for gold mines. International Journal of Mining, Reclamation and the Environment, vol. 27, no. 6. pp. 407-424.         [ Links ]

Rao, S.S. 1996. Engineering Optimization (Theory and Practice). Wiley, New York. p. 903.         [ Links ]

Soderberg, A. and Rausch, D.O. 1968. Pit planning and layout. Surface Mining. Pfleider, E.P. (ed.). American Institute of Mining, Metallurgical, and Petroleum Engineers, New York. pp. 142-143.         [ Links ]

Tulp, T. 1998. Open pit to underground mining. Proceeding of Mine Planning and Equipment Selection (MPES) 1998. Balkema, Rotterdam. pp. 9-12.         [ Links ]

Visser, W. and Ding, B. 2007. Optimization of the transition from open pit to underground mining. Proceeding of the Fourth Aachen International Mining Symposium - High Performance Mine Production, Aachen, Germany. RWTH Aachen. pp. 131-148.         [ Links ]

 

 

Paper received Feb. 2017
Revised paper received Aug. 2017

 

 

Appendix

i: Index for blocks (i=1,2.....N)

N: Total number of blocks

t: Index for planning period (t=1,2,...,T)

T: Total number of planning periods

d: Discount rate

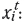A binary integer variable; 1, if block i to be planned for extraction, and 0, otherwise

T_oi: Total amount of ore in block i to be extracted in period t

T_wi: Total amount of waste in block i to be removed in period t

C_opi: Unit open pit cost of ore extraction for block i

Cwc Unit open pit cost of waste removal for block i

Cugi: Unit underground cost of ore extraction for block i

P^t: Unit selling price of metal in period t

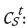Unit selling cost of metal in period t

ropi: Total metal recovery of block i using open pit

r_ug_i: Total metal recovery of block i using underground mining

Q^t_max: Maximum capacity of the available equipment in period

Q^t_min: Minimum capacity of the available equipment in period

a: The total number of blocks overlaying block i in period

: NPV resulting from combined openpit and underground mining of block i in period t

at: A confidence level in the form of the least probability of fulfilling the demand in period t

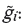Grade of block i, which is a random variable

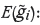Expected value of the random variable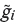

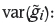Variance estimation of the random variable

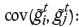Covariance betweenand