PAPERS OF GENERAL INTEREST

 

Where to make the transition from open-pit to underground? Using integer programming

 

 

J. Chung^I; E. Topal^I; A.K. Ghosh^II

^IDepartment of Mining Engineering and Metallurgical Engineering, Western Australian School of Mines, Curtin University, Bentley Campus, WA, Australia
^IIDepartment of Mining Engineering and Metallurgical Engineering, Western Australian School of Mines, Curtin University, Kalgoorlie Campus, WA, Australia

 

 

---

SYNOPSIS

The transition from open pit (OP) to underground (UG) operation is one of the challenging mining engineering issues. Mines that have the potential to transition from OP mining to UG mining will eventually come to a 'transition point' where the decision needs to be taken whether to extend the pit or switch to UG mining. In this paper we present a new integer programming (IP) formulation to obtain the optimal transition point from OP to UG mining. The proposed model is implemented on a three-dimensional (3D) gold deposit and a two-dimensional (2D) case study is used to demonstrate the validity of the model. Due to the large number of variables, strategies are proposed to shorten the solution time. The proposed model has successfully determined the optimal transition point and generated a significantly better undiscounted profit than that of the traditional approach.

Keywords: open pit, underground, transition point, mine optimization, integer programming.

---

 

 

Introduction

A mining project starts with an exploration stage that defines the location of the orebody and its properties that help to develop the geological block model. The geological block model can then be converted into an economic block model by including economic parameters such as mineral price and mining and processing cost. Later, the determination of the best possible mining strategy is emphasized.

The strategy for mining method selection plays an important role as it will directly affect the profit of the operation. Therefore, at this stage, the question is often 'Is the optimal mining method by open pit (OP), underground (UG) or combination of both?' (Topal, 2008). Globally, shallow deposits are generally mined by the OP method as it is economically superior to most UG mining methods with respect to production rate, dilution, safety, and other technical issues. However, OP mining is fairly sensitive to the mining depth because of haulage cost; thus, UG mining is usually applied for deep deposits.

Some shallow deposits extend vertically to considerable depth and thus have the potential to make the transition from OP to UG mining. Combining the OP and UG mining methods is referred to as combination mining. Worldwide, there are a few mines that have the potential to make the transition, or the transition has already been made, such as Kanowna Bell Western Australia, Chuquicamata in Chile, Grasberg in Indonesia, and Sunrise Dam in Western Australia.

The deposits that have the potential to make the transition from OP to UG will usually confront the 'transition problem'. In the combination mining method, 'transition point' refers to the point at which the decision has to be taken whether to (1) extend the pit or (2) switch from OP to UG. The determination of the optimum transition point is the 'transition problem'. The general view of the transition problem is illustrated in Figure 1.

 

 

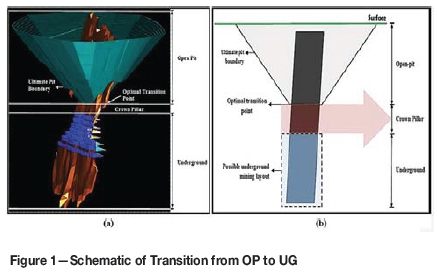
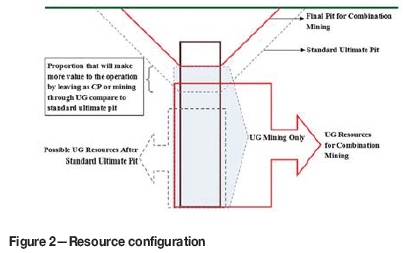
In the current traditional approach to combined mining, the ultimate pit boundary will be determined and pit design will be accomplished as the first step. At this stage, the ultimate pit limit can be determined optimally by using algorithms such as the Lerchs-Grossman (LG) algorithm (Lerchs and Grossman, 1964) or maximum flow-based algorithms e.g., pseudoflow algorithm (Hochbaum and Chen, 2000). The UG mine optimization and design will be started after the standard ultimate pit limit. However, according to Fuentes (2004), if the economic potential associated with the UG resources is taken into account, the final pit can be significantly diminished as shown in Figure 2. Therefore, it is essential to consider both OP and UG mining potential simultaneously, in order to maximize the project profit. In this paper we propose a new mathematical model in order to not only determine optimal transition point in three-dimensional space, but also the optimal mining strategy.

 

 

We firstly review the relevant literature to provide the context for the transition problem. The methodology used to formulate the transition problem and the formulation of the proposed integer programming (IP) model which optimizes the transition problem is then presented. The application of the proposed model in a two-dimensional (2D) case study is then illustrated, followed by a three-dimensional (3D) implementation along with strategies to reduce the computational size of the model. The paper concludes with a summary of the research findings and recommendations for future work.

 

Literature review and problem definition

Several research studies have been carried out previously to solve the transition problem. The first method was introduced by Soderberg and Rausch (1968), and involves the breakeven cost differential between two mining methods as shown in the following formula:

This method emphasizes the relationship between the mining costs of 1 t of ore in both OP and UG compared to the waste removal cost. For instance, if the stripping ratio for any part of the deposit is less than the indicated stripping ratio; mining should be by OP. The shortcoming of this method is that it does not consider the cost of leaving a crown pillar and UG development work.

A methodology based upon cash flow was introduced by Nilsson (1982). This method takes the variations in the economic situation into consideration, including the impact of stripping ratio, interest rate, mining cost, and other components (Nilsson 1992, 1997). This is a trial-and-error method which is mainly based on the experience of the mine planner, and does not include any optimization strategy. Furthermore, the location of the crown pillar and the timing of transition are unknown.

Camus (1992) presented an innovative way to estimate block economic value (BEV) for block i which includes the profit on OP, UG, and stripping ratio as shown in the formula:

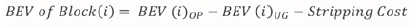
By using the traditional ultimate pit optimization methods, the pit boundary for a combined mining method can be determined. This approach is advantageous in large-scale case studies as it uses only a single block economic model, which reduces the size of the problem by 50%. However, this method has difficulty in crown pillar location and also takes no consideration of the UG mining process.

A heuristic approach has been used to solve the transition problem (Bakhtavar and Shahriar, 2007). In this method, the optimal pit limit is solved by using the Korabov algorithm and the blocks in the final pit level are divided into small sub-blocks and compared with the UG block values. These steps can help to define the transition depth. In addition, Abdollahisharif et al. (2008) also introduced a heuristic approach that outlines all the possible mining layout options and compares the profit generated by each option. A case study that employed this method was presented by Bakhtavar et al. (2010). The disadvantage of the heuristic approach is that the result is not optimal due to the nature of the methodology.

Mathematical modelling techniques are also used to solve the transition problem. For example, Bakhtavar et al. (2012) developed the binary integer programming model to define the optimal transition depth. The objective of the model is to maximize the overall profit by taking into account both the technical and the economic aspects of OP and UG mining methods. However, there are flaws in this mathematical model such as: (1) there is no consideration of an OP and crown pillar contiguous row of blocks, which will result in the location of the crown pillar away from bottom of the pit, and (2) the model is difficult to apply in real case studies due to its scale problem and computational intensity. Lastly, the model is formulated in 2D.

Opoku and Musingwini (2013) presented a structured approach to address the indicators to guide the decision-making process for the transition problem. The method chooses the most significant qualitative factors for the transition problem and incorporates them. Case scenarios are considered in the study for evaluation purposes. In the evaluation process, a comparison technique is utilized to overcome the transition problem. The authors introduced the term 'transition indicator' to guide the decision-making process. However, this approach depends heavily on the predetermined transition indicators and is not a true optimization process.

Newman et al. (2013) evaluated the transition problem via a series of small longest-path problems with the objective of maximizing the profit, which is the discounted gross margin from the mined level minus the discounted UG development cost. The main objectives of this method are which level to mine by OP or UG and when to make the transition, as well as when to start UG mine development. The drawback of this approach is the scheduling that is developed per level/stratum is not practical.

Carli and Peroni (2014) proposed a preliminary analysis for the transition problem. The approach firstly generates the optimum ultimate pit by using the cut-off grade for OP mining and then estimates the UG resources (after pit exhaustion) considering the cut-off grade for UG mining. This approach considers OP and UG separately, which is not appropriate; as mentioned above, OP, UG, and crown pillar designs need to be considered simultaneously.

Dagdelen and Traore (2014) presented an iterative approach to determine the transition depth through an analysis of production scheduling for both OP and UG. The method starts the iteration process using the Whittle software to generate an ultimate pit boundary. Studio 5 and EPS software from CAE are then used to generate the stope layouts for UG mining, and OptiMine scheduler for the life-of-mine production schedule. Even though, the method aims to answer the questions 'where' and 'when' to transit from OP to UG, the methodology has some drawbacks. For example, it is based on an iterative process that does not generate an optimal solution; it assumes that transition will occur only after the ultimate pit boundary, which is not the case in most applications; and the crown pillar is unlikely to be at the optimum location.

Morales et al. (2015) assessed the optimal economic envelope for the combination mining method by creating a mathematical model. In order to solve the model, an algorithm that parameterizes the problem with regard to the location of the crown pillar and production level is developed. The framework of the algorithm uses the ultimate pit computations to search both the OP and UG mine plans. The iterative calculations are used to compute the different combinations of the OP mining level, UG mining level, and crown pillar location by placing the crown pillar at different locations. Evaluation of the results generated by different combinations will indicate the optimal transition envelope. The only criticisms of this method are that it is an iterative process, and also it does not consider the UG mine design, which leads to the impracticality of the transition envelope.

As many OP operations are approaching the final pit limit and/or have the potential to make the transition to UG mining, a competent method to handle the transition problem is required to maximize the project value and the resource utilization. This paper presents a new mathematical model that defines and resolves the transition problem for the combination mining method. Furthermore, the proposed model also helps to determine the best possible mining option for the deposit. The objective of the proposed model is to maximize the project's undiscounted profit among the options of (a) OP mining only, (b) UG mining only, or (c) a combination of OP and UG mining. Furthermore, if the model suggests combination mining as the preferred method, it will further define the mining layouts for OP and UG, including the position of the crown pillar.

 

Proposed model for the transition problem

The aim of a mathematical model is to represent a real-world problem through mathematical formulations. As the demand for mine planning optimization techniques increases in line with the number of shallow deposits approaching the designed final pit, the establishment of a mathematical model for the transition problem becomes more and more significant. IP, which is a well-recognized optimization technique in operation research, has the ability to find the optimal solution for the complex problem. Therefore, a special version of IP, namely the binary integer programming technique, is utilized in this paper to solve the transition problem optimally.

The IP technique is a branch of linear programming (LP). Generally, a LP problem is built with an objective function, a set of linear constraints, and a set of non-negativity restrictions which are shown as follows:

where z represents the objective function, which aims to maximize the profits or minimize the costs, x_i represents the decision variable for which values are to be determined by the model, a_ij and Cj are the constant coefficients representing the nature of the problem, and b_iis the right-hand side constant representing the availability of the resource for a constraint. Generally, an IP problem is a subcategory of an LP problem in which all the decision variables must be integer values as they represent entities that cannot be divided, such as people or machinery. A binary IP model is formed to capture the binary decisions 'yes' (0) and 'no' (1) such as if the block needs to be mined or not. Therefore, it is formed as a decision-making process, and 0 and 1 will be attributed to a decision of not extracting and extracting, respectively.

Notation and variables

Subscript notations

i, i' Block reference name for OP mining

j, j' Stope reference name for UG mining

k, k' Mining level

m Mining method; = 1 for OP mining and 2 for UG mining

Sets

M_i Set of all blocks i in block model for OP mining

N_j Set of all possible stopes j in block model for UG mining

O_i Set of overlying blocks should be removed in order to mine block i

B_j Set of the all stopes that share common blocks with stope j

LO_k Set of all OP blocks on level k LU_kSet of all UG stopes on level k

Parameters

C_i The undiscounted profit to be generated by mining i

S_j The undiscounted profit to be generated by mining j

A Number of overlying blocks that need to be removed in order to mine ore block i

ℓ Number of rows that should successively remain as crown pillar

Decision variables

Formulation

Objective function:

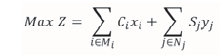
Subject to:

OP slope constraints

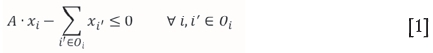
UG stope design constraints

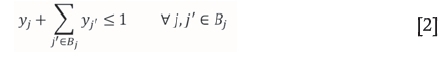
Reserve restriction and 'one mining methodfor each level' constraints

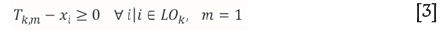
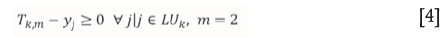
Crown pillar location constraints

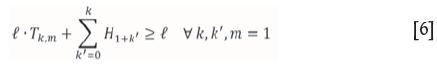
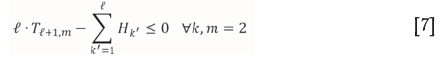
Non-negativity and integer constraints

 

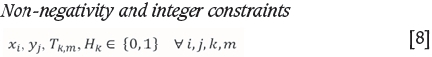
The objective function is formulated to maximize the profit gained through OP and UG mining operations. and S are the constants that represent the undiscounted profit of OP and UG mining, respectively. These values will associate with one decision variable from either OP (x_ior UG y_ito form the equation representing the objective function.

The constraint [1] is established to hold the OP slope restriction. It forces all the overlying blocks to be mined in order to extract a given block. Conventionally, a 45-degree slope angle is considered. Therefore, in a three-dimensional case, it can be 1 to 5 or 1 to 9, which means that in order to mine an ore block, 5 or 9 overlying blocks will need to be removed.

Constraint [2] ensures that there is no overlapping stope is the final stope layout - only one stope can be removed from all possible stopes which share at least one common block. For further explanation, if the stope j which is formed by blocks 1-8 is selected to be mined, none of these blocks can be part of another mineable stope to avoid overlapping in the final stope layout.

Constraints [3], [4], and [5] are formed for the purpose of reserve restriction and to ensure that only one mining method (OP or UG) is employed for each row. Constraints [3] and [4] enforce that if a block or a stope is selected to be mined, the entire row will be mined through the same mining method. As an example, if block i located at level k is removed with OP mining, the entire k level will be mined through OP mining, and if one of the blocks within the mineable stope j located at level k is mined with UG mining, the entire k level will be mined through UG only. Constraint [5] is used to ensure that each row can be mined either through OP or UG or left as crown pillar.

The crown pillar plays an important role in the transition problem as it is used for strata control and to prevent inrush of water. Therefore, a good crown pillar design will reduce or even eliminate most of the geotechnical issues, particularly in the combination mining method. Constraint [6] is used to make sure that an appropriate number of rows remain as crown pillar, as dictated by the geotechnical requirements of the deposit. It also ensures that the crown pillar is located between the UG layout and final pit limit.

Furthermore, constraint [7] is structured to guarantee that if the whole deposit is mined through the UG method, an adequate thickness of roof remains.

Constraint [8] ensures non-negativity and integer nature of the variables, as required.

 

Validation of the proposed model

In order to demonstrate the validation of the proposed IP formulation, a 2D hypothetical block model has been developed and utilized. This section discusses the results generated by the model and compares the results of the combination mining method and single mining method, as well as the traditional transition approach. The IP model and its data file were written using Microsoft Excel VBA (2010) programming code. IBM CPLEX ILOG Corp. (2013) was used to solve the optimization model on a standard office computer (Dell OPTIPLEX 9020 with Intel Core i7 3.40 GHz CPU and 8 GB installed RAM).

The 2D hypothetical deposit containing 204 blocks with a size of 20 x 20 m and a stope size of 2 x 2 was used. The BEVs of both OP and UG have been calculated and are shown in Figure 3 and Figure 4 respectively.

 

 

 

 

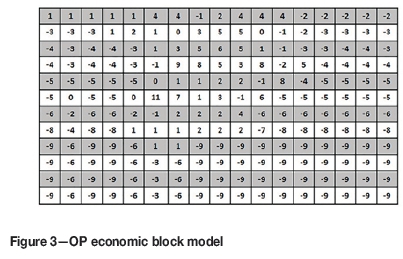
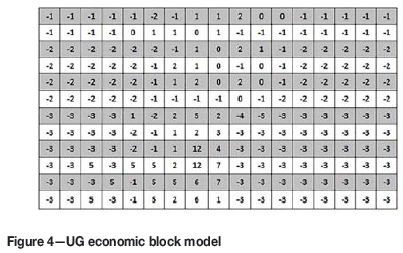
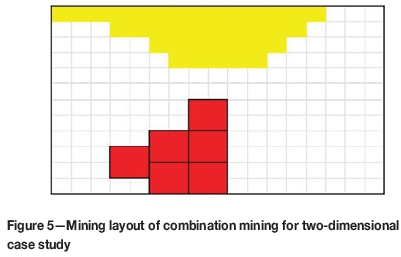
For the 2D case study, the number of decision variables and constraints required to solve the proposed model is 444 and 841 respectively. The solution time for this case is less than a minute with 0% gap. As can be seen from Figure 5, the model recommends that levels 1 to 5 should be mined through OP, two levels below the pit will be reserved as a crown pillar, and the remaining levels will employ UG mining. Therefore, the optimal transition depth is 80 m. According to Figure 6, all the constraints included in the model are satisfied. Thus, the validity of the model has successfully been verified through the 2D hypothetical case.

 

 

 

 

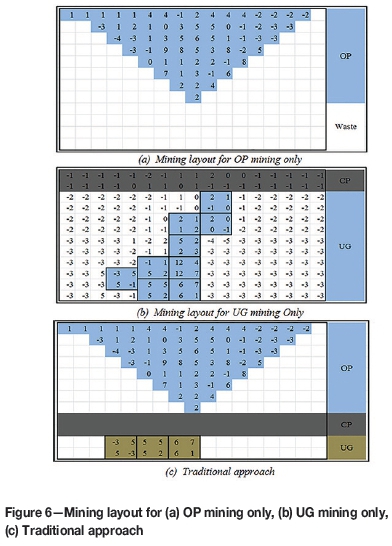
Furthermore, three other mining strategies have been considered: (1) OP mining only, (2) UG mining only, and (3) the traditional approach which utilizes OP mining until the ultimate pit boundary is determined via LG, then switches to UG mining. The results generated by these mining strategies are shown in Figure 6.

The result generated by each mining strategy is shown in Table I. It demonstrates that by using the proposed IP model, the profit generated by the 2D hypothetical case study can maximize the undiscounted profit up to 186 units. The proposed method has successfully improved the undiscounted profit by more than 30% for the traditional approach, and more than 75% and 84% for UG mining and OP mining respectively.

 

 

Implementation of proposed model in a 3D case study

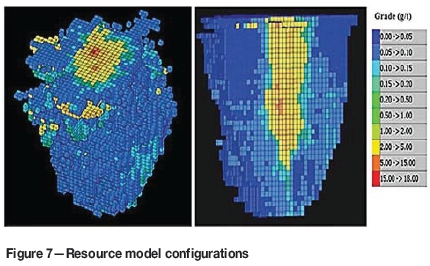
The proposed IP model is applied to a gold deposit in 3D consisting of 83 025 blocks with average grade of 1 g/t. The block size is 20 x 20 x 20 m and each stope size consists of 2 x 2 x 2 blocks totalling 8 blocks. Figure 7 presents the grade distribution of the resource model.

 

 

The computational time required to obtain an optimized solution depends heavily on the decision variables; as the number of variables increases, the solution time increases exponentially. Therefore, in order to keep the solution time reasonable, reduction of the problem size is crucial.

For the 3D case study, 166 173 decision variables and 332 183 constraints are required to formulate the problem to obtain the optimal solution, which requires approximately 34.5 hours. Therefore, some strategies are suggested in the next section to reduce the solution time while maintaining optimality of the results.

Strategies to handle a large-scale IP problem

The IP technique has been recognized as the method that has the potential to optimally solve real case problems; however, it requires a large number of variables and constraints to formulate the large-scale models. Furthermore, the magnitude of the variables can increase substantially when the stochastic models are considered (Groeneveld and Topal, 2011). It may, in some instances, preclude obtaining an optimal solution considering today's computing power. In order to overcome the deficiencies of the IP model, some tactics have been employed to keep the number of variables at the minimum level. With the assistance of these tactics, the efficiency of the proposed model can be maintained and it will be able to generate the optimal solution that satisfies the model integrity. The main techniques applied in the proposed model are focused on UG mine design and optimization as follows.

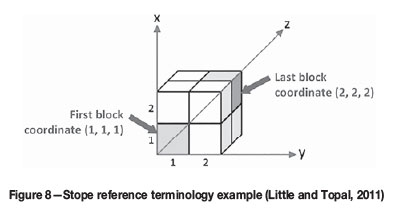
► Stope-based modelling is introduced instead of block-based modelling, as shown in Figure 8. The idea, which was proposed by Little and Topal (2011), is an innovative way to reduce the number of variables in the optimization model. For instance, instead of considering eight decision variables in 2 x 2 x 2 stope design, only one variable is considered for each stope, which represents eight blocks. The naming of the stope is X (first block coordinate) / (last block coordinate); using Figure 8 as an example, the stope is referenced as X (1,1,1)/(2,2,2)

► The predetermination of the positive value stope strategy is also utilized. This determines all the positive stopes in the prior stage of the mathematical model for UG mining. This strategy successfully reduces the variables in the proposed model by taking only the positive stopes into consideration and removing all the unprofitable stopes, which shortens the solution time (Little et al., 2013). This strategy provides the optimality of the proposed model by considering all the positive stopes and discarding the stopes formed by waste (meaningless variables) in the model.

 

 

Gap is often represented as x% which means that the feasible solution is to be within x% optimality. To solve large-scale models, it is usually thought that a proved optimum is unlikely to be obtained within a reasonable amount of computational time. Thus, a gap can be chosen to reduce the solution times.

Model implementation and discussion ofresults

As many hours are required for obtaining an optimal solution of a larger model, the strategies discussed in the previous section have been adopted for the purpose of reduction the scale of the problem and solution time.

1. A stope-based mathematical model is used for UG mine planning and optimization. This approach has reduced the number of constraints drastically by one-eighth

2. A pre-processing step to determine the qualified stope has been included. This has successfully excluded all the non-profitable stopes and reduced the variables in the mathematical model. In the 3D case study, the mathematical model for UG mine optimization has 86 562 blocks. The process of obtaining the positive stopes takes approximately 1 hour, with 2910 positive stopes obtained. This strategy helps to reduce the 86 562 UG variables to 2910 variables in the proposed IP model. The profitable stopes thus determined will be substituted into the proposed IP model.

3. Often, an improvement of 1% gap will take quite a lot of time but may not improve the optimal result. Therefore, a 5% gap is used in this paper.

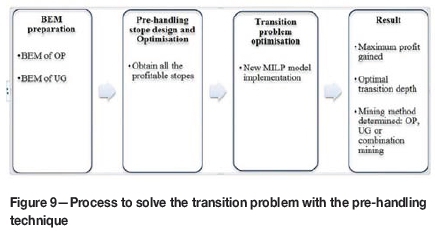
The whole process for solving the transition problem and associated size reduction strategies is demonstrated in Figure 9. Firstly, the block economic model (BEM) of both OP and UG mining is established. Then, the size reduction strategies are implemented:

1. Find all the possible stopes in the UG BEV

2. Obtain all the profitable stopes out of all possible stopes.

 

 

Then, by substituting the outcome from the pre-handling stope design and optimization step, and the OP's BEM into the proposed model, the IP model for the transition problem is formulated. The model is solved by using one of the commercially available solvers, in this case CPLEX. CPLEX is used to solve the IP model to find optimal transition depth that creates the maximum profit for the project.

By employing all the suggested strategies, the decision variables required to solve the 3D case study have successfully been reduced from 166 173 to 86 058. The optimal result with less than 5% gap is obtained in approximately 2.5 hours with an $8.813 million undiscounted profit. The result obtained by the proposed model is compared with the result from other mining strategies in Table II. The result generated by the proposed model provides a much higher undiscounted profit compared to any other options.

 

 

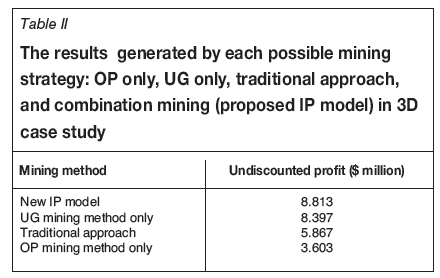
Currently, mines that have the potential to make the transition mostly exercise the traditional approach - obtain the optimal pit limit first and observe the transition later. However, the traditional approach may not generate the maximum profit for the operation. This can be observed from the result presented in Table II; the proposed model generated approximately 5% more undiscounted profit than the UG mining method only, and 50% and 144% better than the traditional approach and OP mining method, respectively. Therefore, in order to maximize the value of the operation, it is essential to consider OP and UG mining methods simultaneously.

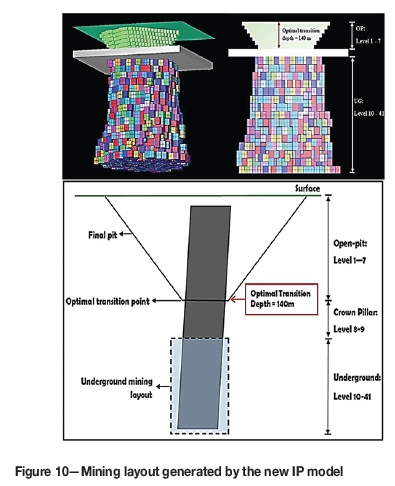
Furthermore, as indicated previously, the proposed model gives guidance for mining strategy selection by means of the maximized profit generated by the deposit through OP, UG, or combination mining strategy. Table II shows that UG mining results in a better undiscounted profit than OP mining, while the traditional approach also does not achieve as much as UG mining. Figure 2 illustrates the resource split for different mining strategies. It shows that there is a proportion of the resource to be left as the crown pillar or mined by UG methods in order to generate the maximized profit.

Figure 10 presents the result generated by the model for different mining strategies. It recommends that the first seven levels should be mined by OP, and then two levels left for the crown pillar followed by UG mining starting from level 10 and ceasing at level 41. The optimal transition point is at level 7 and the transition depth is 140 m - 7 (levels) x 20 m.

 

 

For the 3D case study, to obtain the optimal solution for the transition problem, the process presented in Figure 9 was followed. The whole process took approximately 3.5 hours (1 hour for UG optimization plus 2.5 hours to solve the new IP model) to generate the optimal solution for the transition problem, which is a significant improvement as it is a reduction of approximately 90% on the initial computation time (34.5 hours). Consequently, these strategies help to reduce the variables handling in the proposed IP model and improve the solution time drastically for a large-scale implementation.

 

Conclusion and recommendations

Over the years, the optimization of the transition from OP to UG operation has become a significant issue and created a new challenge for the mine design process. A new IP model is proposed to provide a tool to solve the transition problem, which is able to maximize the profit gained from the operation within a reasonable solution time. The framework of the proposed model is on a 3D basis. It uses the block economic values as the coefficients in the objective function associated with a set of constraints for OP mining, UG stope mining, mining method, and reserve restriction.

A hypothetical 2D model was generated and utilized as the inputs to the proposed model to demonstrate the validity of the model. The result generated by the proposed model -combination mining method ($186) was compared with the results from other considered mining methods, which included the traditional transition approach ($146), UG mining method only ($106), and OP mining method only ($101). This showed that in the hypothetical case study, the combination mining method would generate the maximum profit for the operation. It also proved that it is essential to consider both OP and UG simultaneously.

The 3D case study, which had 83 025 blocks, required roughly 27.5 hours to solve. It was shown that an increase in the number of decision variables will increase the solution time exponentially. Therefore, stope reference and pre-handling stope design and optimization strategies are employed to reduce the number of decision variables required for the proposed model. The solution time for the IP model, which employed the proposed strategies, was reduced to 3.5 hours. The 3D case study generated approximately $8.813 million undiscounted profit with a 5% gap, with an optimal transition depth of 140 m. This is approximately 50% higher than the undiscounted profit generated by the traditional approach to the transition problem. Furthermore, the approach proposed in this paper is equally effective in both greenfield and brownfield projects.

Although this research has demonstrated that IP modelling is an effective technique for solving the transition problem, there is a need to improve the practicality and performance of the current model. Further research is underway that focuses on the timing of the transition to maximize the NPV of the project, as well as methodologies to reduce the solution time further. Future research will also study the effect of the uncertainties involved in mining projects that affects the transition points. Changes in uncertain variables such as commodity price, operating cost, and geological uncertainty will influence the transition point directly. For instance, grade uncertainty has a great impact on the determination of the transition point (Chung et al., 2015).

 

References

Abdollahisharif, J., Bakhtavar, E., Shahriar, K., Sobczyk, J., and Kicki, J. 2008. Open-pit to underground mining - where is the optimum transition depth. Proceedings of the 21st World Mining Congress & Expo 2008. pp. 189-196.         [ Links ]

Bakhtavar, E., Namin, F.S., and Oraee, K. 2010. Practical final pit depth considering the future underground mining - a case study. SME Annual Meeting and Exhibit. Society for Mining, Metallurgy and Exploration, Littleton, Colorado.         [ Links ]

Bakhtavar, E. and Shahriar, K. 2007. Optimal ultimate pit depth considering an underground alternative. Proceedings of the Fourth Aachen International Mining Symposium on High Performance Mine Production, Germany. pp. 213-221.         [ Links ]

Bakhtavar, E., Shahriar, K., and Mirhassani, A. 2012. Optimization of the transition from open-pit to underground operation in combined mining using (0-1) integer programming. Journal of the Southern African Institute of Mining and Metallurgy, vol. 112, no. 12. pp. 1059-1064.         [ Links ]

Camus, J.P. 1992. Open pit optimization considering an underground alternative. Proceedings of the 23th International APCOM Symposium, Tucson, Az. Society for Mining, Metallurgy and Exploration, Littleton, Colorado. pp. 435-441.         [ Links ]

Carli, C.D. and Peroni, R.L. 2014. An approach to define the optimal transition point from open pit to underground mining. Proceedings of the 36th APCOM Symposium, Porto Alegre, Brazil. pp. 367-377.         [ Links ]

Chung, J., Topal, E. and Erten, O. 2015. Transition from open-pit to underground - using Integer Programming considering grade uncertainty. Proceedings of the 17th Annual Conference of the International Association/or Mathematical Geosciences, Freiberg, Germany. Schaeben, H., Delgado, R.T., Boogart, K. G., and Boogart, R. (eds.). pp. 268-277.         [ Links ]

Dagdelen, K. and Traore, I. 2014. Open pit transition depth determination through global analysis of open pit and underground mine scheduling. Proceedings of Orebody Modelling and Strategic Mine Planning, Perth, Australia, Dimitrakopoulus, R. (ed.). Australasian Institute of Mining and Metallurgy, Melbourne. pp. 195-200.         [ Links ]

Fuentes, S.S. 2004. Going to an underground (UG) mining method. Proceedings of MassMin 2004, Santiago, Chile. pp. 633-636.         [ Links ]

Groeneveld, B. and Topal, E. 2011. Flexible open-pit mine design under uncertainty. Journal of Mining Science, vol. 47, no. 2. pp. 212-226.         [ Links ]

Hochbaum, D.S. and Chen, A. 2000. Performance analysis and best implementations of old and new algorithms for the open-pit mining problem. Operations Research, vol. 48, no. 6. pp. 894-914.         [ Links ]

Ibm Cplex Ilog Corp. 2013. Version 12.6.

Lerchs, H. and Grossmann, F.I. 1964. Optimum design of open-pit mines. CIM Bulletin, vol. 58. pp. 47-54.         [ Links ]

Little, J., Knights, P., and Topal, E. 2013. Integrated optimization of underground mine design and scheduling. Journal of the Southern African Institute of Mining and Metallurgy, vol. 113, no. 10. pp. 775-785.         [ Links ]

Little, J. and Topal, E. 2011. Strategies to assist in obtaining an optimal solution for an underground mine planning problem using Mixed Integer Programming. International Journal of Mining and Mineral Engineering, vol. 3, no. 2. pp. 152-172.         [ Links ]

Morales, N., Julio, C., Amaya, J., and Lamghari, A. 2015. Optimal economic envelope of joint open pit and underground mines. Proceedings of the 37th APCOM Symposium, Fairbanks, Alaska. Society for Mining, Metallurgy and Exploration, Littleton, Colorado. pp. 343-351.         [ Links ]

Newman, A.M., Yano, C.A., and Rubio, E. 2013. Mining above and below ground: timing the transition. IIE Transactions, vol. 45, no. 8. pp. 865-882.         [ Links ]

Nilsson, D. 1982. Open-pit or underground mining. Underground Mining Methods Handbook. Hustrulid, W.A. (ed.). American Institute of Mining, Metallurgical, and Petroleum Engineers, New York. pp. 70-87.         [ Links ]

Nilsson, D. 1992. Surface vs. underground methods. SME Mining Engineering Handbook. Hartman, H.L. (ed.). Society for Mining, Metallurgy, and Exploration, Littleton, Colorado. vol. 2. pp. 2058-2069.         [ Links ]

Nilsson, D. 1997. Technical note: Optimal final pit depth: once again. Mining Engineering, vol. 49, no. 1. pp. 71-72.         [ Links ]

Opoku, S. and Musingwini, C. 2013. Stochastic modelling of the open pit to underground transition interface for gold mines. International Journal of Mining Reclamation and Environment, vol. 27, no. 6. pp. 407-424.         [ Links ]

Soderberg, A. and Rausch, D.O. 1968. Pit planning and layout. Surface Mining. Pfleider, E.P. (ed.). American Institute of Mining, Metallurgical, and Petroleum Engineers, New York. pp. 142-143.         [ Links ]

Topal, E. 2008. Early start and late start algorithms to improve the solution time for long-term underground mine production scheduling. Journal of the Southern African Institute of Mining and Metallurgy, vol. 108, no. 2. pp. 99-107.         [ Links ]

 

 

Paper received Jan. 2016
Revised paper received Feb. 2016