Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
SAIEE Africa Research Journal
On-line version ISSN 1991-1696
Print version ISSN 0038-2221
SAIEE ARJ vol.113 n.4 Observatory, Johannesburg Dec. 2022
Controlling a Low Cost Bang Bang Pneumatic Monopod
Callen FisherI; Jacques MeyerII
IMember, IEEE; Department of Electrical and Electronic Engineering,University of Stellenbosch, 7599 Stellenbosch, South Africa cfisher@sun.ac.za
IIStudent Member, IEEE; Department of Electrical and Electronic Engineering, University of Stellenbosch, 7599 Stellenbosch, South Africa 19171072@sun.ac.za
ABSTRACT
To date there have been great advances in the legged robotics community. However, these platforms are extremely costly to develop and require complex controllers to perform agile motion, limiting their research to well funded institutions, or purely simulation based studies. This research focuses on an extremely low cost robotic monopod platform that consists of a high powered servo motor as well as a pneumatic actuator. Due to the on/off (bang bang) nature of pneumatics, the platform is challenging to mathematically model. Using a reduced order model of the pneumatic actuator, trajectory optimization methods were implemented to generate acceleration, steady-state and deceleration trajectories. These were then analyzed and a simple state machine controller was developed to implement these trajectories on the robotic platform, with comparisons to the simulation results. In order to test the capabilities of the monopod robot, the above method was further extended with the robot running on multiple different surfaces (hard surface as well as two different gravel surfaces). Results are promising and reveal that simple models and controllers are sufficient to generate stable transient motions for a legged robot running on nonuniform terrain.
Index Terms: legged robot, rough terrain, trajectory optimization
I. Introduction
Recently, there has been great advancements in using trajectory optimization to study complex motion such as turning [1], acceleration [2] and deceleration [2]. New novel methods to implement an accurate friction model in simulation have also been investigated [3], along with improved through contact methods [4] (allow any contact order) and integrator accuracy [4] (resulting in more accurate trajectories). The problem with these more accurate and advanced methods, is that they drastically increase the complexity of problem, which increases the time taken to solve the problem, placing a strain on computational resources [2], making these methods somewhat infeasible for real time optimization.
A common trend amongst the robotic literature is to use model predictive control (MPC) methods to control the robot, such as on the Mini Cheetah [5] and MIT Cheetah 3 [6]. These methods generally rely on complex whole body models, in a hierarchical control structure [7]. This typically results in a number of simplifications, such as a fixed contact order [8], [9] or the assumption of no slipping (infinite friction) [10]. Even with these assumptions, these controllers are fairly complex to implement.
Some advantages of MPC includes the ability to embed additional complex controllers, such as balance and locomotion into the modular control architecture, as done on the MIT Cheetah 3 [6]. Results showed that the robot was capable of handling terrain disturbances, by utilizing reactive gait modifications.
It is in our opinion that advanced locomotion in the presence of rough terrain, can be achieved using simplified models and simple controllers. Raibert [11] has shown that simplicity in controlling these platforms is key. This is backed up with research done on the simplified SLIP template used as an assumption to mathematically model the CoM trajectory of legged animals and robots.
Additionally, a common trend in the literature is to perform purely simulation based studies. These studies are crucial in developing the theoretical framework, however, many of these research groups cannot test their results due to the lack of funds to develop a robotic platform. Simulation based studies have been vital in studying animal locomotion in order to gain insight for controller design [12]. They have also been used to investigate non-periodic, complex transient locomotion, such as rapid acceleration [2], deceleration [2], turning [1] and other a-periodic motions [13].
Our approach is to leverage off trajectory optimization methods to aid in controller design and tuning. These controllers will be tested and validated on a low cost free-body hybrid pneumatic-electric monopod robot, as seen in Fig. 1. As the robot makes use of pneumatics, it is infeasible to create an accurate complex model of the robot, as the fluid dynamic equations of motion for the cylinder will certainly not solve in the trajectory optimization problem in a reasonable time span. However, the commonly used simplified SLIP model will not be implemented, instead a full kinematic model of the robot will be utilized, which includes leg mass and inertia. To further complicate the matter, the robot will also be expected to perform non-periodic motions such as acceleration and deceleration and traverse non-smooth terrain (gravel).

The methods followed throughout this research are detailed in Section II, which also covers the hardware, mathematical modelling as well as the trajectory optimization method utilized. These methods resulted in a number of trajectories generated in simulation, which were analyzed and aided in the controller design detailed in Section III. This is followed by a description of the experiments performed on the physical robot as well as the results in Section IV. The paper ends with the discussion and conclusion in Section V and VI respectfully.
II. Method
Firstly, a low cost hybrid pneumatic-electric monopod robot was developed, as seen in Fig. 1. The purpose of the platform was to validate all methods and results detailed in this paper. The platform is further described in Section II-A. Once the robot was developed, a simplified mathematical model of the system was developed and is detailed in Section II-B. Following this, the trajectory optimization problem was formulated (Section II-C) and the results were analyzed to aid in the controller design, detailed in Section III.
A. Mechanical Robot
A low cost platform in the form of a hybrid pneumatic-electric monopod was developed and shown in Fig. 1. The motivation for the use of pneumatics was two fold. Firstly they are extremely explosive low cost actuators that are suited for dynamic agile manoeuvres, secondly they add a level of complexity to the problem (fluid dynamics) that will validate our approach of using simplified mathematical models.
The robot consisted of a Festo DSNU-16-125-P-A pneumatic cylinder that lengthened and shortened the length of the leg. The cylinder operated at 8 bar from a 100 litre compressor and was controlled using two Festo CPE10-M1BH-5L-QS-6 solenoid valves. A Feetech DS5160 servo motor was utilized to rotate the leg (hip actuator). The body of the robot was free to rotate and the robot was attached to a support rig that kept the robot in the sagittal plane.
The support rig provided real time state information such as X and Z position (and velocity) as well as body angle (and velocity) through the use of encoders (1000 PPR encoders were used to measure the body angle, angle of the support arm and the distance the support arm had moved). All on board control and data logging was performed on a Teensy 4.0 micro controller at 200Hz.
A gravel pit was also constructed with two different types of gravel, namely fine and coarse. The gravel pit was sufficiently deep so that the hard bottom would not influence the results. The relevant parameters for the robot can be seen in Table I.

B. Mathematical Modelling
Once the robot had been developed, measurements (mass, size, inertia etc) could be performed to create a moderately accurate mathematical model of the robot. A number of simplifications were implemented such as:
1) The mass was assumed to be uniformly distributed
2) The pneumatic cylinder was modelled as a bang-bang force with damping [14] and hard-stops to limit the extension and contraction
3) Only planar motion was allowed, with the support rig modelled as an added mass to the body
4) The leg (pneumatic cylinder) and support rig were assumed to attach directly to the CoM of the body
Euler-Lagrange methods, in the form of the manipulator equation, were utilized to generate the EoM of the system. These equations were in the form:

where q are the generalized coordinates (with q being their velocities) of the robot, as seen in Fig. 1. M(q) is the mass matrix, C(q, q) is the Coriolis matrix and G(q) the gravitational potential matrix. The applied forces and torques due to the actuators are represented by t, and are mapped to the generalized coordinates due to the matrix B. The external ground reaction forces, A, are mapped to the generalized coordinates through the matrix A.
C. Trajectory Optimization
Once the EoM of the system had been defined, the trajectory optimization problem could be formulated. This involved specifying the problem in terms of constraints, variable bounds and specifying how the problem would be optimized and solved.
As the long-time-horizon trajectory consists of multiple distinct phases of motion (acceleration, steady-state and deceleration), the trajectory was split into three smaller trajectories [2]. This reduces the burden on the solver and allows for quicker solve times. The required constraints to ensure a smooth trajectory are listed below.
Additional constraints are also added to accurately model the robot and the environment. These constraints ensure the problem results in a kinematically feasible result that can be implemented on the robotic platform. These are discussed in further detail below.
D. Constraints
A number of constraints were applied to the optimization problem to accurately model the robot, support rig and the environment (contact events etc). As trajectory optimization works on discrete problems, methods were implemented to generate an accurate representation of the continuous system. The constraints are listed below:
• 3 Point Collocation: Each state variable was divided by the specified number of node points, denoted N. Polynomials were used to link each node point. For this research, 70 nodes were used for the steady-state trajectories, 120 for the acceleration trajectories and 50 for the deceleration trajectories. These polynomials were in the form of a Runge-Kutta basis, with 3 collocation points (3 point Radau) [4]. These polynomials were used to solve the differential equations in (1), at specified points in time. However, as contacts are extremely hard to solve, a variable time-step integrator was required, with the time between node points governed by the following equation:

where hm is the time constant defined as hm = T/N, where T is the expected duration of the trajectory (ranging from 0.2 to 1.5 seconds) and N is the number of nodes. h(i) is the duration of the ith node. • Contact Implicit Methods: These methods allowed the optimizer to pick the contact order and type (slipping or sticking), as well as the duration and time of the contact. This was made possible with the above mentioned variable integrator. This method does require a large number of complex complimentary constraints, which are detailed in [15], equation (8) to (16). Slipping was modelled using coulomb friction, with an inelastic collision [15]. As complimentary constraints are inherently difficult for trajectory optimization methods to solve, epsilon relaxation methods were implemented [4] as follows:

where a(i,j) and β(i, j) are the two parts of the complimentary constraint for the ith node and jth collocation point. e is the relaxation parameter that starts off large and tends towards zero. These variables are summed across the collocation points (positive variables) and evaluated at the node points, reducing the overall complexity of the problem.
• Actuator Models: The robotic model consisted of a servo motor at the hip, with a pneumatic actuator acting as the leg (lengthening and shortening). These were modelled as follows:
- Servo motor: A standard linear torque motor model was utilized using the parameters of the servo motor (max RPM and stall torque). This ensured that the generated trajectories would work on the physical system. The motor model took the following form:
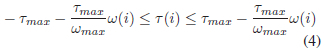
where Tmax and wmax are the maximum torque and angular rate of the actuator. t(i) and w(i) are the applied torque and angular rate at node i.
- Pneumatic cylinder: The pneumatic cylinder was modelled as a bang-bang actuator (on/off actuator) due to the dynamics of the solenoids controlling the air flow into the cylinder. The velocity of the cylinder was determined by the applied force (due to the pressurized air) and the damping present in the cylinder. Solenoids were used to either extend the cylinder, contract the cylinder, or leave the cylinder un-pressurized. End stops were also modelled to ensure the cylinder did not over extend or contract. As the solenoid had a mechanical delay (of approximately 20 ms), the rate of solenoid toggling was limited to every 10 nodes. This was implemented by breaking the N nodes into K buckets of 10 nodes each, as follows:

where Fextension(i) and Fcontraction(i) are the applied forces to extend and contract the cylinder due to the pressurized air at the ith node.
Fbucket extension(k) and Fbucket contraction(k) limit the rate at which the force can vary, with k e (1,N/10)
A number of complimentary constraints were implemented to model the actuator. The bang-bang force was implemented as follows:

where the applied force on the leg is split into two components, Fextension(i) and Fcontraction(i). The top two equations makes sure each component of the force is a positive number between zero and the maximum force. The next two equations ensures that each component is either zero or Fmax. The final constrain ensures that only one force has a value greater than zero. The applied force on the leg is then F(i) Fextension(i) Fcontraction(i).
The end stops were similarly modelled as follows:

where r is the leg length with rmax and rmin the bounds on the leg length. The two forces, Fextend reaction(i) and Fcontract reaction(i), are forces at the end stops to stop the cylinder from over/under extending/contracting.
• Stitching Methods and Initial/Terminal Conditions: As the trajectory was divided into a number of smaller trajectories, constraints were included to ensure these trajectories could be joined to form a smooth trajectory (the end state of the accelerating trajectory must match the start point of the steady-state trajectory, etc). Initially steady-state trajectories were generated with the following initial and terminal conditions:

where the first equation ensures the robot starts at the zero position, the second equation ensures the configuration (angles) of the robot at the end of the trajectory match the start configuration (periodic). This equation does not apply for the X coordinate (which is detailed in the first equation).
The third equation ensures the trajectory starts at the apex of the steady-state trajectory, with the fourth equation enforcing periodicity in terms of start and end velocities. This does not apply to the Z coordinate (which is detailed in the third equation).
The acceleration trajectories had the following initial (start at rest) and terminal (end at the apex of the steady-state trajectory) conditions:

where the first equation forces the robot to start from the rest position with zero velocity (second equation). The third and fourth equation ensure the robot ends in the apex position and velocity of the steady-state step. The deceleration trajectories swap the start and terminal conditions of the acceleration trajectory.
Soft Contact Model: Drop tests were first performed on the two gravel surfaces, to estimate the average penetration depth. The gravel was then modelled as a combination of a spring and damper system (during initial penetration) and a rigid contact (once the gravel had been penetrated). In order the estimate the spring and damper parameters, the rigid contact trajectories were analyzed to determine the average velocity of the foot before contact. This was used, along with the estimated force to stop the contact (from the GRF) to estimate the parameters as follows:

where c and k are the damping and spring constants. Fa is the estimated force required to stop the foot, zfoot contact is the velocity of the foot before it hits the ground and d is the penetration depth of the foot, measured from the drop tests.
In order to model this in the trajectory optimization problem, a prescribed contact order was enforced, where the contact node was determined from the rigid terrain trajectories. The contact was also split into the soft contact, and hard contact (once fully deformed) by analyzing the rigid terrain trajectories. For the soft contact portion, the spring damper model was implemented to generate a force on the foot, once fully compressed, the complimentarity constraints for the rigid contact was then enforced until the foot left the ground.
E. Bounds
In order to implement these trajectories on the physical robot, a number of variable bounds were implemented. These bounds also narrowed the search space of the trajectory optimization problem, enabling a solution to be found quicker. Table II shows the variable bounds for the generalized coordinates and their velocities.

Bounds were placed on the remainder of the variables. These bounds were sufficiently high as to not rule out any feasible solutions, but to sufficiently narrow the search space. For example, all slack variables were bounded as positive variables, with GRF variables bound to 10 times the mass of the robot. This ensures the external forces lie within a reasonable range that will not cause damage to the robot.
F. Solve Method
In order to start the solving process, a starting point, known as the seed, is required for the optimization problem. In order to thoroughly search the solution space, and to not bias the optimizer into a known solution, multiple random seeds were generated. The optimal trajectory was considered as the best result in terms of the cost function of all the feasible results generated. All trajectories were generated using the minimum time cost function:

where N is the total number of nodes, and h(i) is the time duration of the ith node.
To generate the random seed, a number of methods from the literature were implemented, which improved the convergence rate and time. This involved randomizing the generalized coordinates between their bounds [16], while initializing all other variables to a constant value [17] (0.01).
The seed was solved iteratively, implementing e relaxation methods [18]. Initially e started at 1000, being divided by 10 each solve loop for a total of 8 solves. This aids in solving the complex complimentary constraints. All optimizations were performed in Jupyter notebooks using Pyomo, with the IPOPT solver [19].
III. Controller Design
First trajectories were generated for the steady-state motion. Acceleration trajectories were then generated from rest to the apex of the steady-state trajectory (and vice versa for the deceleration trajectory). These were stitched together to form the long-time-horizon trajectory (start and end at rest while travelling a fixed distance).
Initially, the trajectories were implemented directly on the robot, in open loop control. However, with the free body, the robot could not successfully achieve the trajectory. The simulation results were analyzed and a state-machine was developed to control the servo motor and pneumatic cylinder. This enabled the robot to successfully traverse rigid terrain, however it failed on the rough gravel, as seen in Fig. 2.

The above method was repeated for two additional trajectories for the two different soft contacts (fine and rough gravel). These trajectories were then analyzed and aided in the controller design. In order to generate these, the average penetration depth was determined by doing drop tests (from the apex height of the steady-state trajectories on the hard contact). For each of the three terrain types, an actuation height was identified. For the rigid terrain, a height of 34.6 cm, for the rough gravel, 34.9 cm and 36.2 cm for the fine gravel.
When the robot is above this height, it contracts the cylinder, when it is below, it extends the cylinder. Touchdown and lift off angles were also identified from the simulation results (different angles for the three different terrain types). The state-machine also sent these angles (relative to the X axis, requiring a measurement of 0body) to the servo.
IV. Experiments and Results
The above controllers were implemented on the hybrid pneumatic-electric monopod robotic platform to achieve the long-time-horizon trajectory. This involved starting in the rest configuration, accelerating to a steady-state velocity, and then decelerating back to the rest configuration, while travelling a fixed distance.
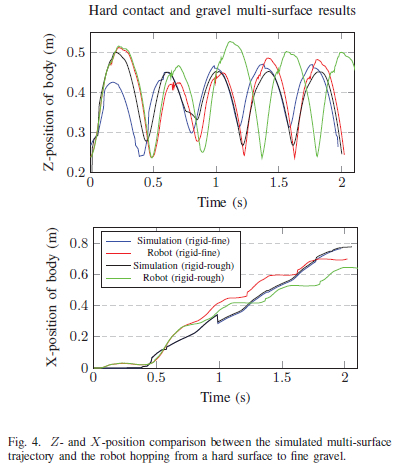
Initially, only the rigid terrain controller was tested on the robot. It successfully ran on rigid terrain, however, it failed on the gravel surface and was not able to travel the required distance, as seen in Fig. 2. The above relevant gravel controllers were then tested on the two gravel surfaces, and were shown to track the desired trajectories and achieve the correct distance. The results can be seen in Fig. 3. Further investigation into running on multiple terrains was also investigated, taking a gait library approach. The state-machine parameters were initially set for a rigid terrain, after an X position of 40 cm, the terrain either changed to the rough gravel, or fine gravel, along with the relevant state-machine parameters. These results can be seen in Fig. 4, and indicate that the robot can successfully transition between gaits stored in the gait library in real time, without having to re-optimize or implement new controllers.

V. Discussion
In order to leave the confines of the laboratory, it is crucial that our legged robots can transition on multiple different terrain types, and remain stable even on non-uniform terrain such as gravel. Novel trajectory optimization techniques were utilized to implement the bang-bang nature of the pneumatic actuator, while taking into account the solenoid mechanical delays. These simplified models enabled the solver to find optimal trajectories in a feasible amount of time. The results were then studied for trends to design a state-machine controller around. These controllers were of the same form, however had unique parameters for each terrain type, forming a gait library of different controllers.
These simple controllers showed that the robot can reliably perform long-time-horizon trajectories on a number of different terrains, as well as transitioning from one terrain to another. Similar observations were made about simple controllers by Raibert [11]. These results show that complex, detailed models of the system and terrain are not required, as well as simple controllers can perform dynamic and complex motions, such as acceleration and deceleration.
VI. Conclusion and Future Work
From the above results it is clear that simplified models and controllers for a relatively complex hybrid dynamic robot is suitable to perform agile transient manoeuvres. These results also show how a gait library can be utilized to transition between multiple different terrain types while still remaining stable. Future work involves extending the above methods to a hybrid pneumatic-electric bipedal robot, on more complex and dynamic terrain.
References
[1] P. M. Wensing and D. E. Orin, "3d-slip steering for high-speed humanoid turns," IEEE/RSJ International Conference on Intelligent Robots and Systems, 2014.
[2] C. Fisher, C. Hubicki, and A. Patel, "Do intermediate gaits matter when rapidly accelerating?" IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 3418-3424, 2019. [ Links ]
[3] D. Pretorius and C. Fisher, "A novel method for computing the 3d friction cone using complimentary constraints," IEEE International Conference on Robotics and Automation, 2021.
[4] A. Patel, S. L. Shield, S. Kazi, A. M. Johnson, and L. T. Biegler, "Contact-implicit trajectory optimization using orthogonal collocation," IEEE Robotics and Automation Letters, vol. 4, no. 2, pp. 2242-2249, 2019. [ Links ]
[5] D. Kim, J. D. Carlo, B. Katz, G. Bledt, and S. Kim, "Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control," arXiv preprint,arXiv:1909.06586, 2019.
[6] G. Bledt, M. Powell, B. Katz, J. Carlo, P. Wensing, and S. Kim, "Mit cheetah 3: Design and control of a robust, dynamic quadruped robot," IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2245-2251, 2018.
[7] J. Luo, Y. Su, L. Ruan, Y. Zhao, D. Kim, L. Sentis, and C. Fu, "Robust bipedal locomotion based on a hierarchical control structure," Robotica, vol. 37, no. 10, 2019. [ Links ]
[8] W. Xi, Y. Yesilevskiy, and C. Remy, "Selecting gaits for economical locomotion of legged robots," Int. J. Robot. Res., vol. 35, no. 9, pp. 1140-1154, 2016. [ Links ]
[9] T. Kamimura, S. Aoi, K. Tsuchiya, and F. Matsuno, "Body flexibility effects on foot loading in quadruped bounding based on a simple analytical model," IEEE Robot. Autom. Lett., vol. 3, no. 4, pp. 28302837, 2018. [ Links ]
[10] K. T. T. Kamimura, S. Aoi, and F. Matsuno, "Body flexibility effects on foot loading in quadruped bounding based on a simple analytical model," IEEE Robotics and Automation Letters, 2018.
[11] M. Raibert, B. B. Jr, M. Chepponis, J. Koechling, J. K. Hodgins, D. Dustman, and W. K. Brennan, "Dynamically stable legged locomotion," Massachusetts Institute ofTechnology, 1989.
[12] T. Nath, A. Mathis, A. C. Chen, A. Patel, M. Bethge, and M. W. Mathis, "Using deeplabcut for 3d markerless pose estimation across species and behaviors," Nature protocols, vol. 14, no. 7, pp. 2152-2176, 2019. [ Links ]
[13] P. M. Wensing and D. E. Orin, "Generation of dynamic humanoid behaviors through task-space control with conic optimization," 2013 IEEE International Conference on Robotics and Automation, pp. 31033109, 2013.
[14] C. Fisher, J. V. Zyl, R. Govender, and A. Patel, "Optimization-inspired controller design for transient legged locomotion," IEEE International Conference on Robotics and Automation, 2021.
[15] C. C. M. Posa and R. Tedrake, "A direct method for trajectory optimization of rigid bodies through contact," The International Journal of Robotics Research, vol. 33, no. 1, pp. 69-81, 2014. [ Links ]
[16] S. Safdarnejad, J. Hedengren, N. Lewis, and E. Haseltine, "Initialization strategies for optimization of dynamic systems," Journal ofComputers and Chemical Engineering, vol. 78, 2015. [ Links ]
[17] C. Hubicki, M. Jones, M. Daley, and J. Hurst, "Do limit cycles matter in the long run? stable orbits and sliding-mass dynamics emerge in task-optimal locomotion," IEEE International Conference on Robotics and Automation (ICRA), 2015.
[18] D. Ralph and S. Wright, "Some properties of regularization and penalization schemes for mpecs," Optimization Methods and Software, vol. 19, no. 5, p. 527-556, 2004. [ Links ]
[19] A. Wachter and L. T. Biegler, "On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming," Mathematical programming, vol. 106, no. 1, pp. 25-57, 2006. [ Links ]
The authors would like to thank the NRF (grant number 129830) and Sub Comm B for funding this research.

Callen Fisher received his PhD in the department of Electrical Engineering at the University of Cape Town in 2021. Dr. Fisher is now a senior lecturer at Stellenbosch University and is currently focused on legged robotics in extreme environments.

Jacques Meyer received his MEng in Electrical and Electronic Engineering at Stellenbosch University, South Africa in 2022. He is currently the co-founder and director of Simplifi Engineering, an IOT consulting startup.














