Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.52 n.2 Midrand Oct. 2010
TECHNICAL PAPER
Spherical void formers in concrete slabs
C C Marais; J M Robberts; B W J van Rensburg
ABSTRACT
Large span concrete flat-slab systems with internal spherical void formers (SVF) have been used in Europe for over a decade. They are bi-axially reinforced concrete flat-slab systems with a grid of internal spherical void formers.
This paper addresses three issues associated with SVF slab systems: their shear resistance, their short-term elastic deflections and their economical value in a South African context.
Due to the "loss" (or reduction) of aggregate interlock required for shear resistance in SVF slabs, the design requirements of the reinforced concrete design code are affected. Research at the Technical University of Darmstadt (TUD) in Germany proved a shear resistance reduction factor of 0,55 to be conservative, while research at the University of Pretoria suggests a greater factor of 0,85 when taking into account the shear capacity of the permanent steel cages that hold the spheres in position in some SVF slab systems.
Laboratory tests at the TUD, supported by theoretical calculations, further showed reduced deflections for SVF slabs compared to solid slabs. Stiffness is not reduced as much as the selfweight, resulting in smaller overall deflections for SVF slabs compared to those of solid slabs with the same thickness.
In this paper the economical value of SVF slabs in South Africa will be investigated by comparing the direct construction cost to that of two other large span slab systems, namely coffer and post-tensioned slabs.
Keywords: spherical void formers, flat slab, shear, economy
INTRODUCTION
Large span concrete flat-slab systems with internal spherical void formers (SVF) have been used in Europe for over a decade. They are bi-axially reinforced concrete flat-slab systems with a grid of internal spherical void formers.
The applicability of such a slab system in South Africa was investigated. South Africa has (at the stage of this study) its own loading and concrete design code. The cost framework for concrete construction is obviously different to that of European countries.
Because of the "loss" of aggregate interlock required for shear resistance in SVF slabs due to the voided zones along potential 45º shear cracks, the design requirements of the South African reinforced concrete design code SANS 10100-1 (SABS 2000) are affected. Research at the Technical University of Darmstadt (TUD) in Germany proved a shear resistance reduction factor of 0,55 (Schellenbach-Held & Pfeffer 1999) to be conservative, while research at the University of Pretoria suggests a greater factor of 0,85 when taking into account the shear capacity of the permanent steel cages that hold the spheres in position in some SVF slabs.
Laboratory tests at the TUD (Schellenbach-Held & Pfeffer 1999), supported by theoretical calculations, further showed reduced deflections for SVF slabs. Stiffness is not reduced as much as the self-weight, resulting in smaller overall shortterm deflections for SVF slabs than for solid slabs with the same thickness.
In this paper the economical value of SVF slabs in South Africa will be investigated by comparing the direct construction costs to those of two other large span slab systems, namely coffer and post-tensioned slabs.
Before this comparison can be made, the structural integrity of SVF slabs has to be investigated in accordance with SANS 10100-1 (SABS 2000) to establish whether SVF slabs adhere to South African design standards.
SHEAR RESISTANCE OF SVF SLABS
Introduction to shear behaviour of SVF slabs
Shear behaviour of SVF slabs will be different from that of solid concrete flat slabs due to the presence of internal spherical voids in SVF slabs. Two main criteria that need to be considered are the loss of aggregate interlock due to the fact that a diagonal shear crack will encounter voids in the central part of the beam, and the presence of steel reinforcement cages that hold the spheres in position and that act as partial shear reinforcement. It is therefore necessary first to briefly investigate the general shear behaviour of concrete slabs before discussing the unique behaviour of SVF slabs.
General shear behaviour of concrete beams without shear reinforcement
Equilibrium in the shear span of a beam is described by Park and Paulay (1975) as follows:
Figure 1 shows one side of a simply supported beam with a constant shear force over the length of the beam under consideration. The top region of the beam is in compression (C) and the bottom region in tension (T). The equilibrium is maintained by internal and external forces, bounded on one side by a diagonal crack. In a reinforced concrete beam without web reinforcement, the external transverse force is resisted mainly by combining three components:
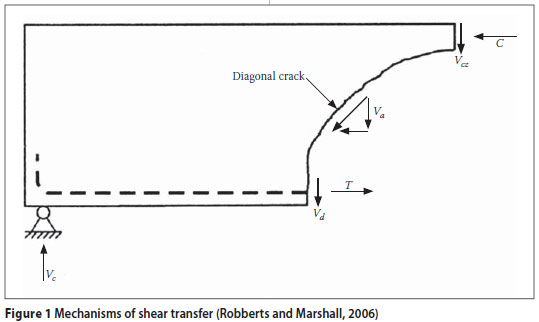
Shear force across the uncracked compression zone Vcz (20 to 40%).
A dowel shear force transmitted across the crack by flexural (tension) reinforcement Vd (15 to 20%).
The sum of the vertical components of inclined shear stresses Va transmitted across the inclined crack by means of interlocking of the aggregate particles. Va is referred to as aggregate interlocking (35 to 50%).
The approximate contribution of each component is given in parentheses (Kong & Evans 1987). The largest contribution results from aggregate interlock.
The equilibrium condition can be stated by the formula:

which is the total shear capacity resulting from the three main shear-carrying components Vcz, Va and Vd described above.
Three different 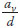 ratio sectors of mechanisms causing shear failure of simply supported beams loaded with point loads can be established, where:
ratio sectors of mechanisms causing shear failure of simply supported beams loaded with point loads can be established, where:
av = distance of a single point load to the face of the support
d = effective depth of the tension reinforcement
This was discovered by Leonhardt and Walther (Leonhardt 1965) who tested ten beams. The beams had no shear reinforcement (stirrups), and the material properties of all the specimens were almost exactly the same.
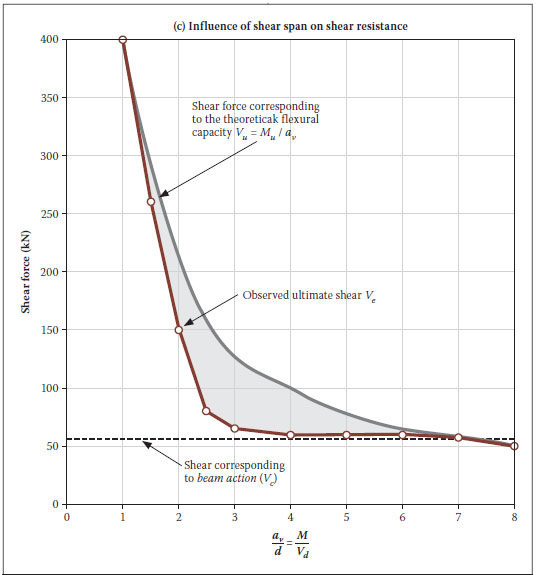
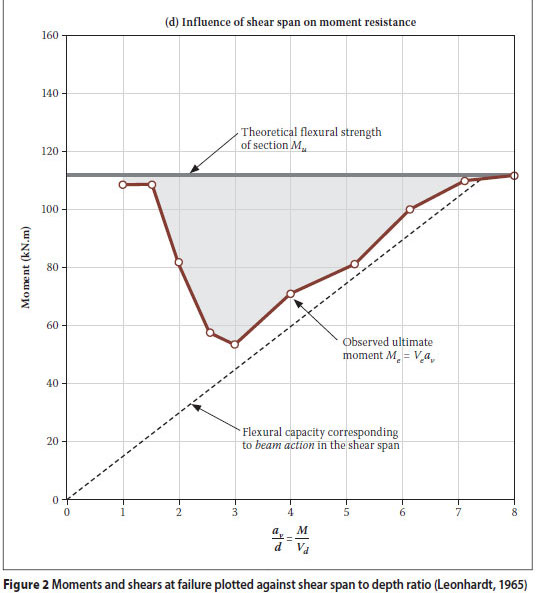
Figures 2.c and 2.d show the observed shear forces (Ve) and failure moments (Me) respectively for these ten beams plotted in terms of shear span versus depth ratio. Vu and Mu are the theoretical ultimate shear forces and moments represented by the solid lines without dots in Figures 2.c and 2.d respectively.
From Figure 2 the three types of 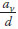 ratios can be described as follows:
ratios can be described as follows:
Type 1: For 3 <
< 7 the failure of the beam mechanisms is precisely at, or shortly after the application of the load resulting in diagonal cracking. This means that the arch mechanism is incapable of sustaining the load.
Type 2: For 2 <
< 3 a shear compression or flexural tension failure of the compression zone occurs above the diagonal cracking load. This is in most cases an arch action failure.
Type 3: For
< 2 failure occurs by crushing or splitting of the concrete (i.e. arch action failure).
In Figure 2 it can clearly be seen that for 1,5 < 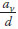 < 7 the flexural capacity of the beams is not attained and thus the design is governed by shear capacity. The shaded area of the right-hand side of the figure displays the difference between the predicted flexural capacity and actual strength, with the largest difference in the 2,5 <
< 7 the flexural capacity of the beams is not attained and thus the design is governed by shear capacity. The shaded area of the right-hand side of the figure displays the difference between the predicted flexural capacity and actual strength, with the largest difference in the 2,5 < 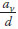 < 3 range. This is the critical range where failure is least likely to be in bending, but without the benefits of the arch action.
< 3 range. This is the critical range where failure is least likely to be in bending, but without the benefits of the arch action.
From the left-hand side of Figure 2 it is clear that an 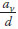 ratio of approximately 3 will result in both the lowest observed shear resistance (ranging from
ratio of approximately 3 will result in both the lowest observed shear resistance (ranging from 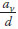 = 3 to 7), as well as the greatest difference between the observed ultimate shear and the shear force corresponding to the theoretical flexural capacity. A beam with an
= 3 to 7), as well as the greatest difference between the observed ultimate shear and the shear force corresponding to the theoretical flexural capacity. A beam with an 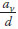 ratio of 3 will for this reason be the critical case to investigate for shear failure.
ratio of 3 will for this reason be the critical case to investigate for shear failure.
Apart from the 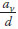 ratio, the area of tension reinforcement, the concrete strength and the beam depth will also influence the shear capacity of beams without shear reinforcement (Park & Paulay 1975).
ratio, the area of tension reinforcement, the concrete strength and the beam depth will also influence the shear capacity of beams without shear reinforcement (Park & Paulay 1975).
Construction sequence of SVF slabs
Figure 3 illustrates the contents of the SVF slab system. The bottom light brown flat is the flat-slab formwork. The light purple grid represents the bottom tension reinforcement bars placed on top of the black spacer strips. The red lines represent the steel cages holding the blue spheres in place, which are fabricated from polypropylene or polyethylene. The cages are fixed to bottom reinforcement with wire. The dark grey bottom layer of concrete indicates the first concrete pour, extending above the horizontal red line of the cages, followed by the light grey top layer of concrete, extending to the top of the slab.
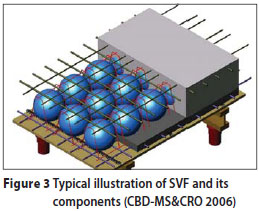
When the first pour hardens, it will keep the spheres in place and avoid uplift due to buoyancy during the second pour, which usually follows a few hours after the first pour. The green grid on top indicates the top reinforcement of the slab. All steel and the spheres are installed before any pouring of concrete commences. The result is a slab with a flat soffit, allowing the use of conventional flat-slab formwork as for any regular solid slab.
Experimental work on shear in SVF slabs
Theoretical calculations for the shear strength of SVF slabs were compared with force-controlled shear tests performed on SVF specimens in the concrete laboratory of the University of Pretoria (Marais 2008) in 2007. This comparison had to be conducted to establish the shear strength reduction factor for SVF slabs compared to a solid slab with the same thickness, tension reinforcement and concrete properties.
Earlier research at the TUD indicated that a lower-bound SVF shear strength reduction factor of 0,55 times the shear strength of a solid concrete slab with the same thickness, and without shear reinforcement, approximated the shear strength of SVF slabs (Schellenbach-Held & Pfeffer 1999). The shear strength of the solid slabs was calculated in accordance with Eurocode 2 (1992) specifications.
The SVF steel cages were omitted in the TUD tests. These steel cages, which hold the SVF spheres in position during construction, act as shear reinforcement inside the slab, resulting in a higher shear strength reduction factor.
The experimental work at UP (Marais 2008) comprised the testing of 12 beam specimens of equal length and width, but having varying thicknesses and quantities of tension reinforcement, some with SVF spheres, and some solid. All the beams, simulating strips of flat slabs 600 mm wide, were set up to fail in shear before failing in flexure in accordance with the work of Park and Paulay (1975) discussed above, to allow conclusions to be drawn regarding their shear capacities.
Figure 4 displays the cross-section through Sample 1, an SVF specimen, containing high-yield tension reinforcement bars 16 mm in diameter (Y16), represented by the red dots and lines at the bottom of the slab. The purple circles are the internal hollow spheres forming the voids, and the green lines indicate the 5 mm diameter steel cages holding the spheres in position (these were omitted in the TUD tests). The blue edges simulate the concrete boundaries of the sample. The spheres on the sides of each SVF specimen were cut in half to demonstrate crack formation during testing.
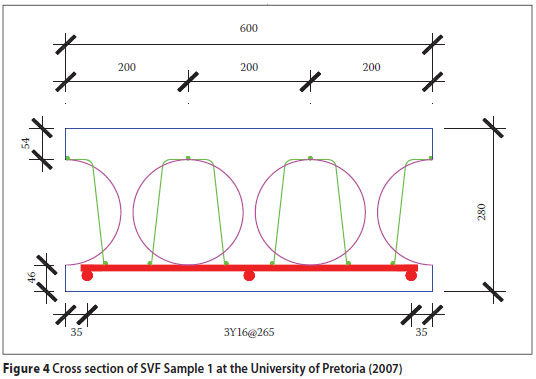
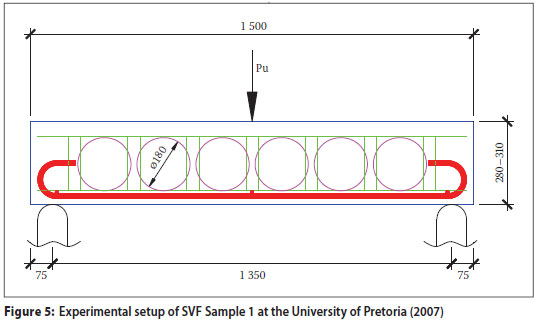
The sample beams were simply supported with a span of 1 350 mm as shown in Photo 1 and Figure 5, where Figure 5 simulates a long-section through the same sample displayed in Figure 4. The knife-edge load (Pu) was applied at the midspan of the sample. All the samples were tested in force control at a rate of 40 kN/min. Throughout the tests the applied loads at midspan, as well as the displacements, were measured at 25 readings per second (25 Hz).

The flexural and shear capacity of each sample were calculated in accordance with SANS 10100-1 (SABS 2000) to ensure that shear failure would precede flexural failure. The results are presented in Table 1. Material factors were set to unity to calculate the actual strength rather than the design strength.
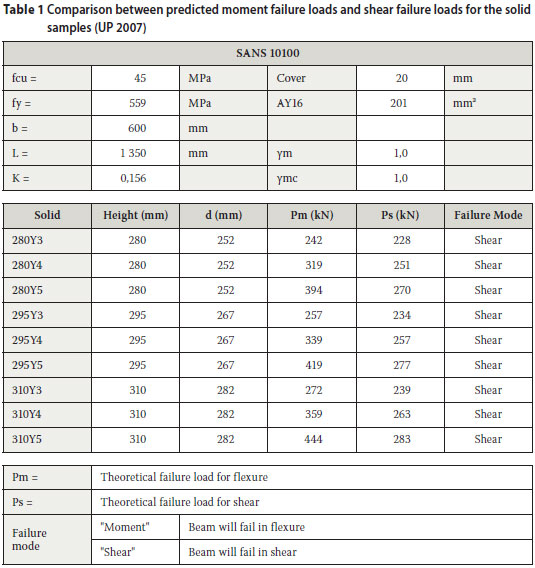
In Table 1 the definitions of the symbols are:
| Pm | = theoretical failure load for flexure |
| Ps | = theoretical failure load for shear |
| fcu | = characteristic concrete cube compression strength |
| fy | = steel reinforcement yield strength |
| b | = width of the specimen |
| L | = span of the specimen |
| K | = factor |
| γm and γmc | = material factors |
| AY16 | = area of a 16 mm diameter steel reinforcement bar |
| d | = centroid depth of the tension steel, measured from the top of the beam |
The legends, for example 280Y3, are understood as follows:
| 280 | = total thickness of the beam |
| Y | = high yield steel |
| 3 | = number of Y16 steel reinforcement bars spread over the 600 mm beam width |
Theoretical calculations at UP (Marais 2008) indicated that Eurocode 2 (1992) predicted shear capacities of up to 45% higher than SANS 10100-1 (SABS 2000) for slabs with minimum tension reinforcement, and over 20% higher for the UP samples with the highest amount of tension reinforcement. Shear capacities predicted by Eurocode 2 (1992) are in fact so high that they exceed the actual failure values of the samples in shear for low and medium amount of tension reinforcement, making it an unconservative code for calculation of shear in concrete slabs. However, the material factors were set to unity as for the SANS 10100-1 (SABS 2000) calculations.
The SVF beams were expected to have a lower shear capacity than the solid beams. All the calculations for the solid beams showed that shear failure would precede flexural failure, and it was therefore concluded that the SVF beams would display a similar behaviour.
The depth of a stress block in flexure for any of the SVF beams will never exceed the minimum depth of the top flange based on the dimensions of these research samples (Schellenbach-Held & Pfeffer 1999). The method used to design SVF slabs for flexure is for this reason the same as for solid slabs, where the presence of the voids only reduces the self-weight and slightly reduces the slab stiffness as well as the shear capacity.
As can be seen in Photo 2, the shear cracks started from bending cracks in the case of the solid specimens. This is common for 2,5 < 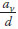 < 6,0. However, in the case of the SVF specimens, the crack sometimes started at the web, and then further developed down and back to the support along the tension reinforcement and also upwards to the top of the beam towards the line of load application as seen in Photo 3. These observations are well justified by the predictions of Park and Paulay (1975).
< 6,0. However, in the case of the SVF specimens, the crack sometimes started at the web, and then further developed down and back to the support along the tension reinforcement and also upwards to the top of the beam towards the line of load application as seen in Photo 3. These observations are well justified by the predictions of Park and Paulay (1975).


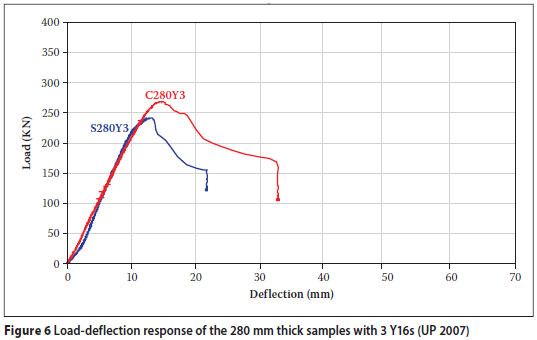
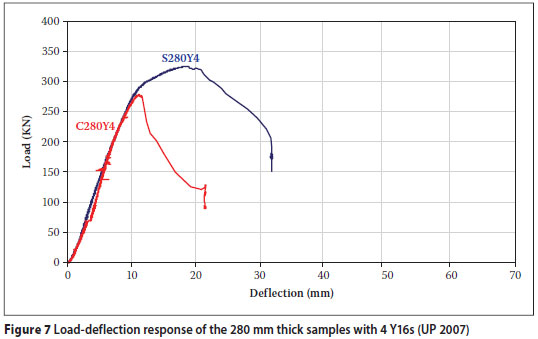
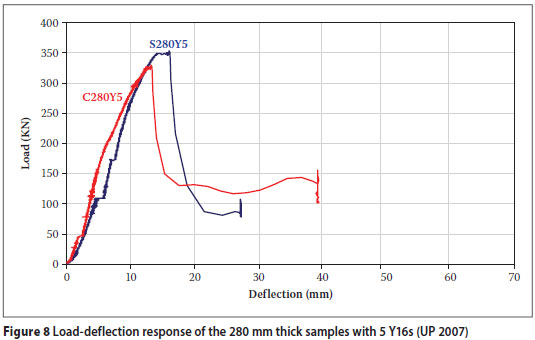
Figures 6 to 8 compare the load-deflection responses of 280 mm thick solid samples to those of the SVF samples. The peak loads achieved by the solid samples were higher than those of the SVF samples with the exception of sample S280Y3,
where
| S | = solid sample |
| C | = SVF sample |
| 280 | = 280 mm thick slab |
| Y | = high-yield steel |
| 3 | = number of Y16 steel reinforcement bars spread over the 600 mm beam width |
The minimum SVF slab-to-solid slab shear capacity ratio obtained was 0,857. This is the first indication that the vertical steel cages partially act as shear reinforcement in SVF slabs. This observation can be made since, as previously mentioned, ratio results of 0,55 were observed during tests at the TUD (Schellenbach-Held & Pfeffer 1999), where cages had been omitted. The presence of the cages therefore tends to add additional shear strength to the SVF samples.
It is interesting to note in Figures 6 to 8 that the SVF samples resist the applied loads up to certain peak values, yet then in two out of three cases tend to display more ductile behaviour than solid samples without shear reinforcement as the load decreases. This behaviour could also be observed during the sample tests. The solid samples began to show shear cracks and then suddenly collapsed, compared to the SVF samples which started to show shear cracks that opened much wider, allowing more deflection to occur before failure. This occurs when no further deflection takes place and the load drops to zero.
The observed ductility is not characteristic of a shear failure in beams without shear reinforcement, and can only be attributed to the presence of the vertical legs of the SVF steel cages acting partially as shear reinforcement. Where the 45º angle crack crosses the path of these vertical bars, they tend to hold the concrete on both sides of the crack together for much longer until they are torn out of the concrete or sheared off.
The TUD tests are applicable only to SVF slabs with no steel cages holding the spheres in position. However, one could conservatively apply the TUD suggestion of 55% of the shear capacity of a solid slab with the same thickness and material properties to any SVF slab. Since the UP samples did include the 5 mm diameter high-yield steel cages, it can be argued that the 85% value UP prediction is more applicable to SVF slabs with steel cages.
Assuming that the cages do serve as shear reinforcement, the area of shear reinforcement provided in the samples was greater than that which was required by SANS 10100-1 (SABS 2000). The only requirement not met was that the shear reinforcement had to be anchored in the tension zone of the sample.
Should one wish to establish the shear resistance of the vertical cage bars, one approach could be to subtract the theoretical SANS 10100-1 (SABS 2000) shear resistance provided by the bars from the experimental results to obtain the capacity provided by the voided concrete. However, the remaining shear capacity can be shown to end up being unrealistically low when compared to earlier research at the TUD, indicating 55% of the shear capacity of a solid slab with the same thickness and material properties to be a lower limit for SVF slab capacities without cages.
It can therefore be accepted that the cages increase the shear capacity but not to the full possible value that can be achieved by properly anchored shear links. This comment is confirmed by studying the load deflection results in Figures 6 to 8. The results indicate a failure pattern tending more towards that of a brittle failure than a ductile failure, which would have been expected in the presence of fully anchored shear reinforcement.
An important comment on the subject of shear in SVF slabs is that 85% of the theoretically calculated shear capacity of a solid slab can be adopted as the shear capacity of SVF slabs with steel cages having the same thickness and material properties as that of the solid slab. The TUD's 55% value is nevertheless recommended, since it was established through numerous tests results. It will always yield more conservative results as it ignores the beneficial effect of the steel cages on the shear capacity of SVF slabs.
A theoretical investigation at UP further indicated that a detailed sensitivity analysis for 85% versus 55%, as discussed above, is likely to result in negligible cost savings for SVF slabs. This assumption is based on the fact that the zone that needs to remain solid in the column region will shrink only marginally due to the steep increase in shear force close to a support. The designer may be able to introduce one extra row of spheres surrounding the column for the 85% case, but the cost of additional SVF spheres may outweigh the very small saving in concrete. Reducing the self-weight of a flat slab close to a support will also have negligible deflection benefits, and the 85% case will therefore not result in a thinner SVF slab, which would have been the preferred result.
PUNCHING SHEAR RESISTANCE OF SVF SLABS
Figure 9 illustrates the plan view layout of a simple continuous three span by three span SVF slab system without any column heads. Typical solid zones are illustrated by the pink areas surrounding the black columns in this figure. The blue areas are filled with hollow spherical void formers. The pink areas are usually left solid in SVF slabs, which make up approximately 25% of the total slab area. These solid areas start where the applied shear in the flat slab exceeds 55% of the total shear capacity of the solid slab. The voided areas, being approximately 75% of the total slab area, can resist shear stresses below 55% of the solid slab's shear capacity as previously discussed.
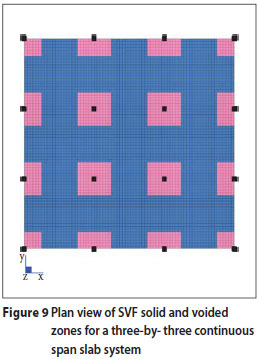
The fact that the slab zones around the columns are solid simplifies the punching shear design, since all critical parameters for punching shear usually fall within these solid zones (Schellenbach-Held & Pfeffer 1999). Normal punching shear reinforcement can therefore be calculated for the solid slab surrounding the columns in accordance with SANS 10100-1 (SABS 2000), with the benefit of the reduced self-weight of the slab, which reduces the axial forces in the columns.
HORIZONTAL SHEAR RESISTANCE OF SVF SLABS
The cold joint in SVF slabs formed due to the two-pour system also required some investigation. Laboratory tests done at the TUD confirmed that SVF slabs constructed with two pours will behave in the same way as a slab with no horizontal cold joint. This is probably the best way to confirm the effective horizontal shear capacity, which is obtained by friction at the surface of the horizontal cold joint as well as at the vertical cage bars passing through the cold joint.
Practical experience indicates that a concrete slump ranging from 120 mm to 140 mm will generally result in easier workability of the first concrete layer of SVF slabs, and is therefore strongly recommended.
TMH7 Part 3 (1989), as well as SANS 10100-1 (SABS 2000), stipulates that the minimum reinforcement crossing a shear plane shall be 0,0015 times the area of contact between the top and bottom parts of any composite concrete section for high-yield steel shear reinforcement. Usually this requirement results in a greater area of horizontal shear reinforcement than that calculated from the formulae provided by TMH7 Part 3 (1989) for composite concrete sections.
The SVF high-yield steel cages shall therefore be designed to have diameters resulting in steel areas which adhere to the TMH7 Part 3 (1989) code requirements.
It may be argued that almost no horizontal shear reinforcement will be required passing through the cold joint (as shown by the TUD test results), since the code requirements are based on precast members that may be a couple of days old before receiving a topping, while the second pour of SVF slabs generally follows within four hours of the first pour. This will allow much less creep and shrinkage to take place in SVF slabs.
FLAT SLAB DEFLECTION BEHAVIOUR OF SVF SLABS
The discussion below follows the research summary in the Cobiax Technology Handbook (CBD-MS&CRO 2006).
The values in this handbook are based on calculations done in deflection state I (uncracked), assuming a vertically centred position of the spheres in SVF slabs, as well as a fixed position of the spheres at a distance of 50 mm from the bottom of the slab.
The presence of the spheres in deflection state II (cracked) has been researched with laboratory bending tests at the TUD. The results have revealed that the stiffness reduction factor in state I is the determining factor. The stiffness reduction factors were derived from calculations done on the second moment of area ICB (for SVF slabs) and ISS (for solid flat slabs).
With these factors in mind, and taking into account the reduced self-weight of SVF slabs, the deflection for SVF slabs can be calculated. The following are to be observed:
Despite its reduced stiffness, the SVF slab's total short-term deflection is smaller than that of a solid slab with the same thickness for identical loads, except where the imposed load exceeds 1,5 times the amount of dead load.
In common buildings the ratio of imposed load to dead load is generally significantly less than 1,5. In practice this means that the total deflection of SVF slabs is usually smaller than it is in solid slabs with the same thickness. Hence in most cases a smaller depth can be prescribed for SVF slabs to bridge the same span length as solid slabs.
Long-term deflections for the cracked state of SVF slabs can be calculated in accordance with SANS 10100-1 (SABS 2000) or estimated by multiplying the short-term deflection for the uncracked state of SVF slabs with an applicable factor. Many engineers in South Africa will recommend a factor between 2,5 and 4. Otherwise creep and shrinkage deflections can be calculated in accordance with Appendix A of SANS 10100-1 (SABS 2000). Here the concrete type and properties, area of uncracked concrete, area of reinforcement, loads and age of concrete at loading will play a major role.
The factor between 2,5 and 4 however, as well as how great a percentage of the live load is to be taken as permanent (SABS 0160 (1989) 1994), remains the engineer's decision. It is suggested that the designer approach the long-term deflection calculation of SVF slabs in exactly the same way as he would have done for a solid flat slab with the same thickness, but taking into account the reduced self-weight and second moment of area due to the voids of the SVF slab.
A stiffness reduction factor had to be calculated for all types of SVF slabs. The formula for elastic deflection calculation due to a load spread evenly over the whole surface of the slab is:

where
k = a factor depending on the support conditions of the specific span
w = serviceability limit state load
L = span length
E = elasticity of concrete
I = second moment of area of the slab
It will make no difference whether a stiffness reduction factor is applied to the E or I value in Equation 2. Figure 9 shows a Strand7 (2006) eight-noded finite element plate model for an SVF slab. After modelling the plate elements of the voided zones (pink areas) to have the same thickness as the plates of the solid zones, the "correct" calculated elastic deflection values could be obtained by simply reducing the E-value by the applicable stiffness reduction factor, and adding an additional upward force to simulate the loss in self-weight due to the voids.
The reduction in dead load was simply the displaced concrete weight (25 kN/m3) as a result of the hollow spheres in the voided areas. However, the calculation of the stiffness reduction factors for SVF slabs is more complicated.
Figure 10 shows a section through an SVF slab on the left-hand side, displaying only two spheres cut exactly where the diameter is greatest. This section will be exactly the same for the perpendicular direction. If half a sphere is used for performing calculations, an x distance can be calculated from the centroid of the sphere to the centroid of the hemisphere, where

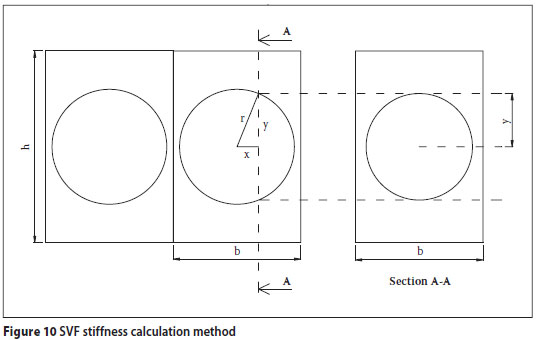
and r is the radius of the sphere.
Using the formula for a circle (Pythagoras)

one can easily obtain the y distance, which is the distance perpendicular to the x distance, measured from the hemisphere's centroid to the closest outer surface of the sphere.
Section AA in Figure 10 was taken at the x position, displaying a new cross-section on the right-hand side. This cross-section represents the average void of the voided part of SVF slabs when calculating the second moment of area. The second moment of area for the solid region (Is), ignoring the void, can thus be calculated with:

where
b = width of the section surrounding a single sphere
h = total thickness of the slab

Equation 6 represents the second moment of area of a circle (the average voided area) with radius y. Ic can then be subtracted from Is and the answer can then be divided by Is to provide a ratio of the stiffness of a voided slab to a solid slab.
Along the length of an SVF slab, 90% of the slab will be voided and 10% will be completely solid (small distance inbetween voids) when following general grid placement practice of SVF spheres. Due to the gradual change in void size along the length of the slab, one can assume that the stiffness ratio of SVF slabs will change gradually enough to be given by adding 90% of the ratio of the voided zone to 10% of the ratio of the solid zone.
The stiffness reduction factors obtained by this method of calculation complements those obtained by the TUD very well, where both empirical tests were done and theoretical calculations performed. For various thicknesses of SVF slabs, calculations showed that the average reduction in stiffness due to the spheres was only 10%. Simply put, an SVF slab has on average 90% of the stiffness of a solid slab with the same thickness and material properties. This statement will only be true as long as the correct sphere sizes are used in the slab in accordance with general products descriptions. The stiffness reduction may also vary for different SVF systems.
ECONOMICAL VALUE OF SVF SLABS IN SOUTH AFRICA
Introduction
Two slab systems that can be compared with SVF slabs are coffer slabs and unbonded post-tensioned slabs. The reason for comparing them with the relatively new SVF slab system is that they serve the same function and are well known as cost-effective systems for large span slabs in South Africa. The material for the construction of these three large span slab systems is also readily available in the country.
Similar to many other cost-comparative studies on slab systems (Goodchild 1997), these slabs were all modelled as shown in Figure 9. These three-by-three equal continuous spans provide the researcher with a relatively conservative, yet practical system, displaying the behaviour of both an internal span and external span.
Research done at the University of Pretoria (Marais 2008) consisted of Strand7 (2006) eight-noded finite element plate models for the three large span slab systems. The arrangement in Figure 9 was used to model various combinations of equal three-by-three span lengths, subdivided further for various intensities of applied load.
All the designs were performed in accordance with SANS 10100-01 (SABS 2000) requirements and adhered to the code's suggestions for minimum reinforcement, deflection and punching shear resistance. The total cost described the direct cost of a slab only, which included all the slab material, form-work, labour, site delivery and contractor's mark-ups, but excluding VAT.
All columns were assumed to be pinned to the slab soffit. Buildings with four storeys or fewer were assumed, since this will result in very small differences in column and foundation costs for the different slab systems analysed.
The concrete strength for all models was taken to be 30 MPa. The elasticity of concrete was taken as 26 GPa. The reinforcement yield strength was set as being equal to 450 MPa.
Load application
The loading of the finite element models was kept simple. Pattern loading was ignored and only one ultimate limit state load combination applied to the various slab types was compared, namely the 1,2 factor for dead load and the 1,6 factor for live load. Sixty per cent of the live load was taken as permanent loading for calculation of serviceability limit state long-term deflection. This 60% is a good estimate, supported by the SABS 0160 (1989) design code.
Reinforcement
The reinforcement provided was always kept to a minimum, but never allowed to be less than the SANS 10100-1 (SABS 2000) minimum reinforcement specifications. Curtailment and lap lengths were provided for by multiplying the total reinforcement per m2 of slab area by a factor of 1,1, therefore allowing for 10% extra reinforcement. In practice this 10% would normally complement the correct amount of reinforcement reasonably well. The Strand7 (2006) software models were set up in accordance with SANS 10100-1 (SABS 2000) criteria for the direct calculation of reinforcement using Wood-Armer moments (Park & Gamble 2000).
Punching shear reinforcement was also included in the cost analyses for the various models where applicable in accordance with SANS 10100-1 (SABS 2000). In Europe SVF slabs can be thinner, saving costs due to the use of Eurocode 2 (1992), which is not as conservative as SANS 10100-1 (SABS 2000) for shear calculations, and also due to the use of the Halfen shear stud system, which is a more efficient shear reinforcement system than the conventional shear links used in South Africa.
Coffer slabs
The stiffness of coffer slabs was established in a manner similar to that for SVF slabs discussed earlier in this report under deflection of SVF slabs. The deflection requirements of SANS 10100-1 (SABS 2000) were the dominant factor for calculating slab thicknesses of coffer slabs.
Solid zones near columns in coffer slabs were also taken to be 25% of the total slab area in Figure 9. This assumption was based on the investigation of Strand7 (2006) shear contour output for various coffer models. Coffers were omitted where the shear capacity of the coffer zones had been exceeded.
Unbonded post-tensioned slabs
The cables inside the post-tensioned slab models were introduced to the applicable Strand7 (2006) models using distributed loads calculated in accordance with suggestions made by Marshall and Robberts (2000). For the post-tensioned Strand7 finite element analysis models, the cables were designed to balance 70% of the dead load, which should result in an economical solution for commercial structures. The dominant factor for establishing post-tensioned slab thicknesses was vibration, accounted for by suggestions made by Marshall and Robberts (2000).
Formwork
A formwork cost analysis was done by Jan Kotze (2007) at Wiehahn Formwork (Pty) Ltd for both SVF flat slabs and coffer slabs. No column heads were used for the purposes of this research. All formwork material, delivery on site and labour were included in this analysis, but VAT was excluded. The analysis was based on large slab areas with 3 m floor heights, where repetition of formwork usage resulted in 5-day cycle periods for both flat-slab (SVF and post-tensioned slabs) and coffer formwork. Coffer formwork worked out to be approximately R50/m2 more than flat-slab formwork for large slab areas in 2007.
Direct construction cost comparison
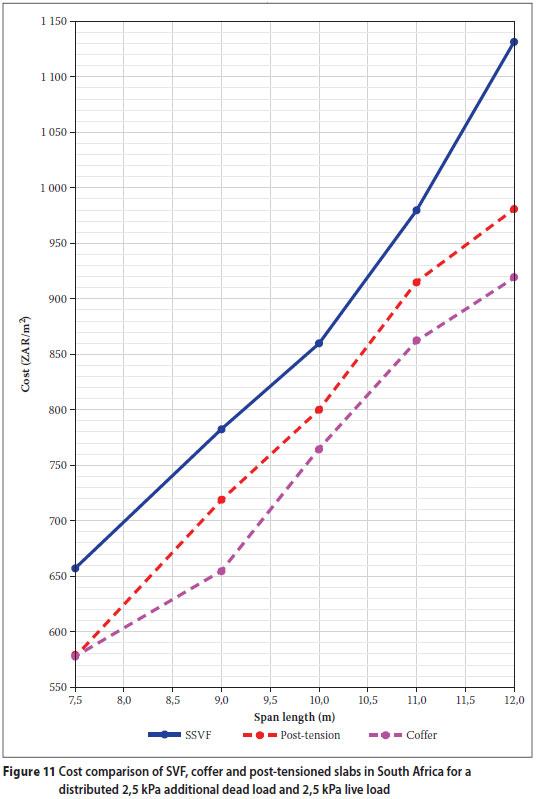
Using the criteria set out above for finite element model preparations and analysis results, an estimate could be made for the direct construction costs of SVF slabs, coffer slabs and unbonded post-tensioned slabs. The cost comparison was based on average material prices across South Africa in 2007. Figure 11 displays the cost comparison for the three slab systems, where SVF (blue line) was the most expensive system, post-tensioned slabs (red line) a less expensive system, and the coffer system (pink line) the least expensive system.
CONCLUSION
Large span concrete flat-slab systems with internal spherical void formers (SVF) can be successfully designed in accordance with SANS 10100-1 (SABS 2000) by applying some additional simplified design factors. Various design requirements were scrutinised.
The shear resistance of the voided areas can be taken as 55% of that of a solid slab with the same thickness (Schellenbach-Held & Pfeffer 1999). Shear test results on SVF slabs with steel cages at the University of Pretoria (Marais 2008) suggests that this percentage may be increased to 85%. Further tests are required to validate this factor.
Punching shear calculations were performed for the solid areas of SVF slabs around the columns. In an SVF slab the solid areas usually cover approximately 25% of the total slab area.
Tests at the Technical University of Darmstadt proved that the cold joint formed in SVF slabs due to the two-pour system will not influence the performance of the slabs in terms of serviceability and strength requirements (Schellenbach-Held & Pfeffer 1999).
Calculations at UP have indicated that the stiffness of SVF slab areas should be reduced by approximately 10% compared to that of a solid slab with same thickness. The slab can be designed in the same way as one would design a solid concrete flat slab, subtracting the concrete weight displaced by the spheres.
Based on the cost structure in South Africa in 2007 and the applicable South African codes at the time, the direct construction cost of SVF slabs was determined to be higher than that of coffer and unbonded post-tensioned slab systems. The main reason for the higher cost is the price of the SVF slab components (spheres and steel cages).
Another reason for the higher cost is the conservative shear requirements of SANS 10100-1 (SABS 2000) compared to that of Eurocode 2 (1992), and the use of conventional punching shear reinforcement instead of the Halfen shear stud system as used in Europe. Shear is not the restricting factor when calculating coffer and post-tensioned slab thicknesses, and therefore improvements in shear capacity will not reduce the costs of these two systems, but only that of SVF slab systems.
REFERENCES
CBD-MS&CRO 2006. Cobiax Technology Handbook. Switzerland: Cobiax Technologies AG Zug. [ Links ]
Eurocode 2. 1992. Design of concrete structures. UK: CEN. [ Links ]
Goodchild, C H 1997. Economic concrete frame elements. Berkshire: British Cement Association. [ Links ]
Kong, F K & Evans, R H 1987. Reinforced and prestressed concrete, 3rd ed. London: Chapman & Hall, London. [ Links ]
Leonhardt, F 1965. Reducing shear reinforcement in concrete beams and slabs. Magazine of Concrete Research, 17(53): 187-198. (This is a brief summary of the original work done by Leonhardt and Walther in Stuttgart from 1961 to 1963. [ Links ])
Marais, C C 2008. Design adjustment factors and the economical application of concrete flat-slabs with internal spherical voids in South Africa. MEng Dissertation, University of Pretoria. [ Links ]
Marshall, V & Robberts, J M 2000. Prestressed concrete design and practice, Concrete Society of Southern Africa. [ Links ]
Park, R & Gamble, W L 2000. Reinforced concrete slabs, 2nd ed. Canada: Wiley. [ Links ]
Park, R & Paulay, T 1975. Reinforced concrete structure, New York: Wiley. [ Links ]
South African Bureau of Standards (SABS) 1994. SABS 0160 (1989). Code of practice for the general procedures and loadings to be adopted in the design of buildings (as amended 1990, 1991 and 1993). Pretoria: SABS. [ Links ]
South African Bureau of Standards (SABS) 2000. SANS 10100-1 2000. South African National Standards 200. Code of practice for the structural use of concrete. Part 1. Pretoria: SABS. [ Links ]
Schellenbach-Held, M & Pfeffer, K 1999. Transverse force capability of the BubbleDeck, Technical University Darmstadt's Institute for Solid Construction (in German), Germany. [ Links ]
Strand7 2006. Strand7 finite element analysis software. Strand7 Pty Ltd, Australia. [ Links ]
Committee of State Road Authorities (CSRA) 1989. Code of practice for the design of highway bridges and culverts in South Africa. Pretoria: National Department of Transport. [ Links ]
 Contact details:
Contact details:
34 Barnsbury Road
Warwick, 6024, Western Australia
Tel: 61 8 92469285; Mobile: 61 400440304
e-Mail: ccmarais@bigpond.com
Contact details:
Nuclear Structural Engineering (Pty) Ltd
Balblair Building, Kildrummy Office Park, Cnr Witkoppen Road & Umhlanga Road
Paulshof, Johannesburg, South Africa
Mobile: 27 82 784 8743, Fax: 27 86 601 4522
e-Mail: john.robberts@nucse.com
Contact details:
Department of Civil Engineering, University of Pretoria
Pretoria, 0002
South Africa
Tel: 27 12 420 2439
e-Mail: ben.vanrensburg@up.ac.za
 | CORNEILLE MARAIS (CPEng, Visitor SAICE) was associated with the Department of Civil Engineering at the University of Pretoria when the research for this paper was done. Corneille Marais is a chartered professional engineer in Australia in the fields of structural and civil engineering. He graduated from the University of Pretoria in 1999 and completed his honours degree in transportation engineering in 2001 and honours degree in structural engineering in 2003 at the same university. His career involves commercial, industrial, nuclear, mining and bridge structural designs. |
 | JOHN ROBBERTS (PrEng, Member SAICE) was associated with the Department of Civil Engineering at the University of Pretoria when supervising the background research for this paper. John Robberts obtained his BEng (Civil) in 1986 from the University of Pretoria and then joined this institution as a lecturer in structural engineering. He obtained his MEng (Structural Engineering) from the University of Pretoria, and his PhD from Imperial College London. During his stay in the UK, he also worked at the Atkins bridge office in Epsom, Surrey, at the Pebble Bed Modular Reactor (Pty) Ltd and is at present a Director of Nuclear Structural Engineering (Pty) Ltd. He remains involved with the University of Pretoria, in a part-time capacity, supervising research students and presenting postgraduate courses in reinforced and prestressed concrete. |
 | BEN VAN RENSBURG (PrEng, Fellow SAICE) is Professor in the Department of Civil Engineering at the University of Pretoria where he teaches and does research in structural engineering. He started his career in consulting engineering, worked in a research organisation and then joined the University of Pretoria. He obtained BSc and MSc degrees in civil engineering at the University of Pretoria, an MSc (Structural Eng) from the University of Southampton and a PhD (Civil Eng) from the University of Pretoria. |