Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.51 n.2 Midrand Oct. 2009
TECHNICAL PAPER
Dynamic behaviour of damaged reinforced concrete beams and application of white noise analysis to crack detection
MA Lotfollahi-Yaghin; R Shahinpar; H Ahmadi
ABSTRACT
Vibration monitoring is a useful and precise method for non-destructive evaluation of defective members. The fundamental concept underlying this method is that the dynamic properties and responses of the structure will change if any defect occurs. The aim of this paper is to investigate the responses of damaged reinforced concrete members to dynamic excitation and to identify the location of probable defects. A powerful multi-purpose finite element (FE) package, COSMOS/M, is used for the analysis of the damaged concrete cantilever beams studied in this paper. The mechanical and geometrical properties of all beams are the same, but the location and the depth of the cracks are changed in these members. The analysis process is performed in the frequency domain. Initially, a modal analysis is performed to determine and compare the natural frequencies and mode shapes of the various defective members. Each member is then excited by an individual vertical force, with the specifications of white noise located at the end of the member, and the responses are monitored at different locations along the member. These responses are used to investigate the dynamic properties of the defective members and to identify the crack location.
Keywords: white noise, reinforced concrete, crack detection, finite element method, dynamic response
INTRODUCTION
The development of cracks in a concrete structural element during its lifetime is always a probability. In this situation, rehabilitation of the damaged element is necessary, otherwise the structural functions of the member will be in jeopardy. Identifying the location and the dimensions of the cracks is the first stage of recovery. This process may be performed through either direct observation or structural tests (ACI Manual of Concrete Practice 1996). These tests are divided into two main categories: destructive tests and non-destructive tests. There are various types of non-destructive test, such as ultrasonic, radiography and dynamic identification tests (Liew & Wang 1998).
In this paper, a dynamic identification technique is used to investigate the responses of damaged reinforced concrete (RC) members to dynamic excitation and to identify the location of probable defects. A powerful finite element method (FEM) software package, COSMOS/M, is used to analyse the samples studied here. These samples are cracked RC cantilever beams with the same mechanical and geometrical properties, but with different locations and depth of the cracks. The analysis process is performed in the frequency domain. Since the study of natural frequencies and mode shapes of damaged concrete beams can be useful in understanding their dynamic behaviour, initially a modal analysis is performed to determine and compare the natural frequencies and mode shapes of the different defective members. A random vibration analysis is then performed to identify the crack location. In this process each member is excited by an individual vertical force, with the specifications of white noise located at the end of the member, and the responses are monitored at different locations along the member. A study of the changes in these responses can be useful not only for determining the dynamic properties of the defective members, but also for identifying the crack locations.
LITERATURE REVIEW
Reinforced concrete (RC) structures are often exploited as partly cracked. Typical examples are RC bridges in which the cracks develop gradually from the moment they are erected as a result of sudden overloading, seismic effects (Zembaty 1997), corrosion, excessive temperature effects, etc. There is also an opposite phenomenon as concrete strength increases over many years after casting (Castellani 1992). Consequently, the actual, overall elastic properties of RC structures are difficult to predict. Since some of the RC structures will crumble suddenly or have to be put out of operation without an early warning, the problems of Non-destructive Damage Evaluation (NDE) of these structures become ever more important.
During the last 20 years, methods of system identification and modal analysis have developed into quite a large interdisciplinary field. Ewins (1986) and Maia et al (1997) have also studied the problems involved in NDE. For example, it is now routine to use rotating machines to detect damage even without taking the elements out of service (Wauer 1990). However, the practical application of these methods for large engineering structures has met with some difficulties (see the Los Alamos state-of-the-art reports by Doebling et al (1996) and Sohn et al (2003)). Nevertheless, the search for effective ways of implementing these methods continues (see, e.g., the state-of-the-art review by Salawu (1997)). For RC structures such research started as early as the 1950s (Penzien & Hansen 1954), but even more experimental research took place from the early 1980s. For example, Wang et al (1998) experimented with impact tests on small beams (61 cm) with various boundary conditions. They noted a 25% drop in the natural frequencies and a substantial increase in structural damping. Maeck & De Roeck (1999) investigated 6-m-long RC beams after damage had been imposed statically at several levels. They included an analysis of the curvature of the beams, as well as investigations into the bending and reduction of torsional stiffness resulting from the damage that occurred. They noted a drop in stiffness reaching 50 and 40% for bending and torsional stiffness respectively. Recently, Ndambi et al (2002) also carried out an analysis of 6-m-long RC beams, but with the general aim of localising the statically inflicted damage.
Litorowicz (2006) reported a method for identifying and quantifying crack patterns in concrete by means of optical fluorescence microscopy and image analysis using impregnated reground polished sections. Observation of the concrete surface under ultraviolet light using an optical microscope at a 10x magnification is sufficient to detect fine cracks. This technique generates images with good contrast, which are convenient for automatic quantitative analysis.
The data obtained by means of image analysis methods are not obtainable from conventional test procedures. Litorowicz's (2006) proposed method provides a quantitative determination of the crack system using parameters such as dendritic length, area, average width, density, area fraction, degree of orientation and distribution of crack widths. This researcher obtained evidence of concrete damage due to freezing during the hydration and hardening period.
Torigoe et al (2005) proposed and investigated a signal-processing method which has the ability to distinguish automatically a vibration signal output by an LDV-based detector used to observe the surface of a concrete structure that has been excited by a shock tube. It was confirmed that the system detects exponentially decaying sinusoids corresponding to the flexural vibrations generated when an internal crack is present in the concrete, and is capable of calculating the frequencies of the exponentially decaying sinusoid. Also, it was predicted that the system could be applied in a scanning-type detector for observing large concrete structures. Although this method has been discussed only in the context of crack-inspection procedures, it could also be extended to other uses of the impact-echo method where the conditions are, in terms of signal theory, the same as the above conditions (Torigoe et al 2005).
NUMERICAL MODELLING OF RC BEAMS
FE modelling procedure
A multi-purpose FE package, COSMOS/M, was used for the modelling and analysis of RC beams. COSMOS/M presents 29 different types of element for structural modelling for the purpose of dynamic analysis (COSMOS/M Advanced Modules 1995). In this study, TRUSS 2D and PLANE 2D were selected to create the model. PLANE 2D is a two-dimensional quadrilateral element which can have either four or eight nodes. This element is applicable to plane stress, plane strain and axially symmetrical structural problems. In this research, four-noded PLANE 2D elements were used for modelling of the concrete. TRUSS 2D is an axial element which has two nodes. It was used here for modelling of the reinforcing bars (COSMOS/M Advanced Modules 1995). Since the modelling is two-dimensional, the material properties and the equivalent area of the reinforcing bars are assigned to TRUSS 2D elements.
Initially, the surface of the concrete and the reinforcing bars must be meshed. Then the bar elements must be merged into the adjacent concrete elements using the NMERGE command. It must be noted that before the bar and the concrete elements are merged, the elements located on the face of the crack must be displaced adequately to avoid merging these elements together. Once the bar and the concrete elements have been merged, the crack face elements are returned to their initial location. Since the aim of this research was to investigate the macroscopic behaviour of RC beams and the study was restricted to the elastic zone, the interface between the concrete and reinforcing bars was not modelled.
Specifications of samples
All the samples are cantilever beams having the same geometric shape, dimensions and materials. Selected beam height and width are the common values in typical framed reinforced concrete buildings and the value of the beam length is the maximum length of the cantilever beams used in the balconies and stairs of typical buildings. The number and size of the bars are selected to be proportional to the beam dimensions. The distance between the centre of the tensile/compressive reinforcing bars and the top/bottom of the beam section is 5 cm. General specifications of the beams are presented in Table 1.
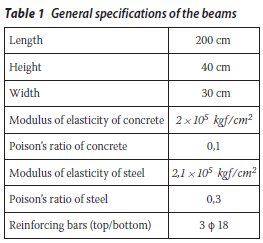
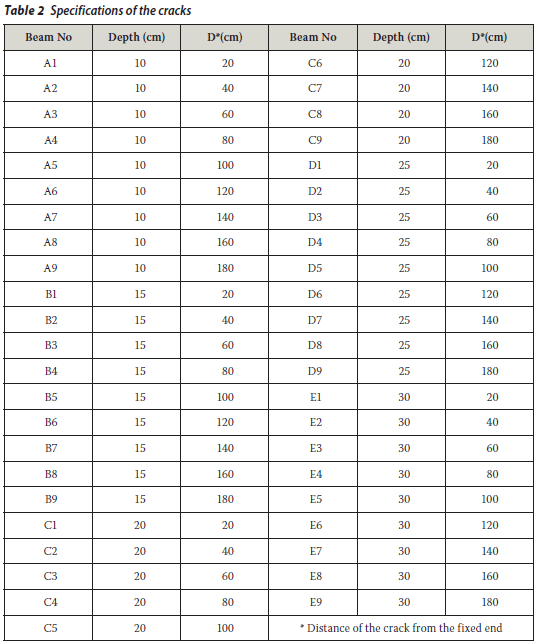
In this study 45 beams were analysed. Each beam has a single transverse crack. Five different crack depths are chosen such that they range from a relatively important crack depth (e.g. 10 cm) to a significantly critical one (e.g. 30 cm) for the beam height considered (40 cm). As the width of the crack is very small, it can only be considered as a discontinuity. The crack is placed at nine different distances from the fixed end so that its effect can be investigated at any location along the beam. The crack direction is chosen to be perpendicular to the beam axis because the flexural cracks will develop in this direction. Specifications of the cracks are listed in Table 2.
An intact beam (N1) was also modelled in order to compare its dynamic response with that of the damaged beam.
Mesh size optimisation
The size, shape and number of elements used in the model directly affect the convergence and the accuracy of the results. Obviously, when smaller elements are used, the number of elements is increased and the results will be more accurate. But it must be remembered that the use of smaller elements will lead to increased calculation time. For each problem, there is a specific element size below which the accuracy of the results will not be increased significantly.
Since the most important factor affecting the accuracy of the results in a modal-based problem is the natural frequency, the criterion for optimisation of the size of the elements is the accuracy of natural frequencies obtained. To investigate this factor, four different sizes are selected for elements and a modal analysis performed by using each of them. The results of the first natural frequency are presented in Figure 1 and the results of first ten natural frequencies are shown in Table 3.
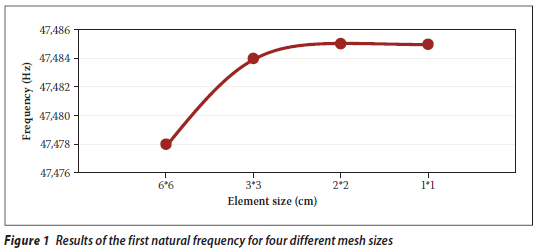
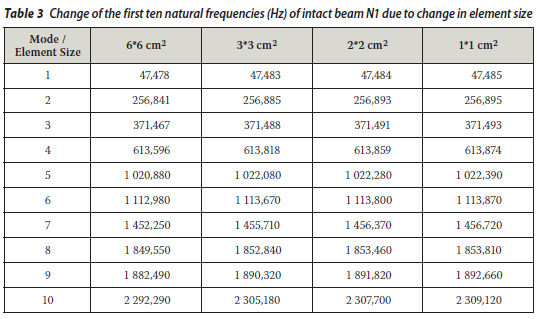
It can be seen that although the 1 x 1 element leads to the most accurate results, the difference between the results obtained from the 1 x 1 element and the 2 x 2 element is negligible. Consequently, the selected sizes are 2 cm x 2 cm for plane elements and 2 cm for truss elements.
MODAL ANALYSIS
Consideration of the natural frequencies and mode shapes of damaged concrete beams can be useful for understanding their dynamic behaviour. By using the subspace iteration numerical method and assuming that the masses are concentrated, a modal analysis is performed. The maximum number of iterations is 16 (Theoretical Manual for COSMOS/M 1993). The natural frequencies, periods and the type of mode shapes for beam N1 are listed in Table 4.
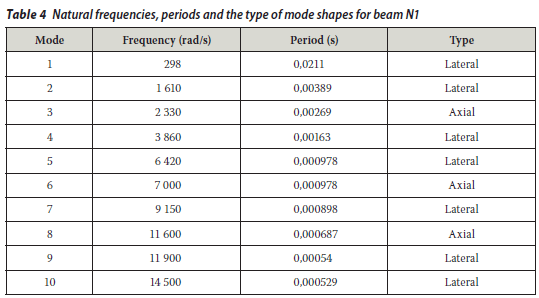
It can be seen that the majority of mode shapes are flexural and three of them (the 3rd, 6th and 8th) are axial. Since the problem is two-dimensional, torsional mode shapes do not exist.
The mode shapes of oscillation for beam A1 are shown in Figures 2 to 11. The left end in these figures is the fixed end of the beam.

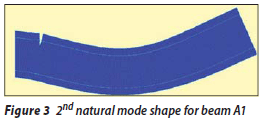
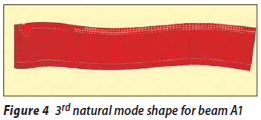
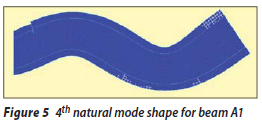
It can be seen that the first to fifth mode shapes are similar to those obtained in the case of beam N1, but the sixth and eighth modes, which were axial oscillation modes in beam N1, are transformed into a combination of axial and lateral oscillation modes. Also the seventh, ninth and tenth mode shapes are lateral oscillation modes, the same as they were in beam N1. It is also obvious that the creation of a crack can lead to some changes in the higher mode shapes of oscillation. The type of mode shape may be changed or two types may be combined. Investigating the pattern of these changes can be useful for identifying the damage to the structures.
The types of mode shape for beams A1 to A9 are presented in Table 5. It can be seen that the majority of the changes occur in the higher mode shapes. Thus the higher modes are more sensitive to damage and suitable for the study of damage effects in structures.
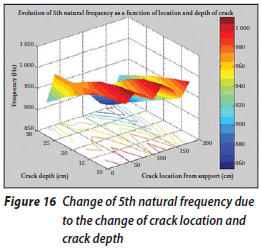
Once the results have been arranged according to the location and depth of the crack and then plotted in three-dimensional diagrams, some remarkable results are obtained. These diagrams are presented in Figures 12 to 21.
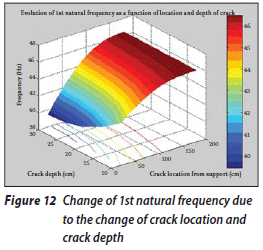
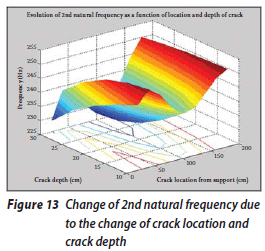
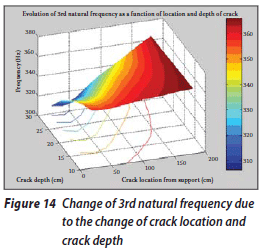
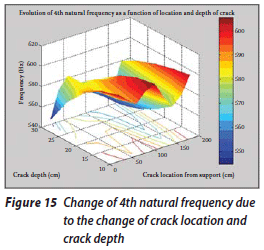
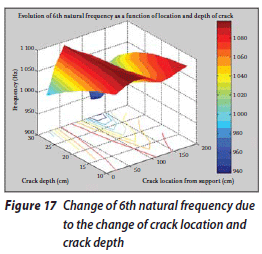
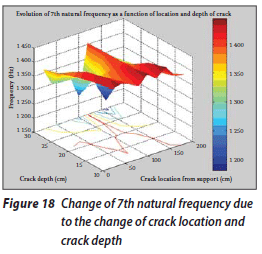
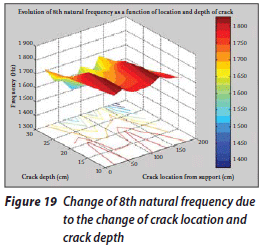
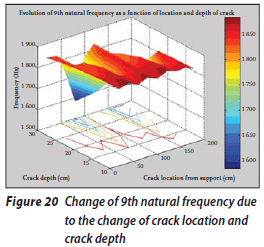
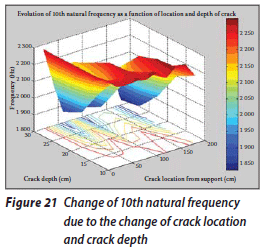
The change of the first natural frequency due to the change in the depth and location of the crack is shown in Figure 12. It can be seen that when the depth of the crack is increased, the rate of decrease in natural frequencies increases, and when the location of the crack comes closer to the free end of the beam, the rate of the frequency decrease is reduced. However, the change in the first natural frequency due to the increase in the crack depth and the change in the crack location occur at an approximately uniform rate. Figure 13 shows the change in the second natural frequency due to the change in these factors. It can be seen that this change does not occur at a uniform rate. The change in the third natural frequency (the first axial oscillation mode) is shown in Figure 14. In this case the changes in frequency occur at a uniform rate too. The frequency values vary from 310 to 370 Hz. Figure 15 shows the change in the fourth natural frequency due to these factors. It can be seen that when the crack location is far from the fixed end, the rate of the changes is increased, although it generally decreases due to the increase in crack depth.
A study of these figures shows that the pattern of frequency changes due to the change in the crack location depends on their corresponding mode shapes. When the crack location approaches those points of the system for which the deformation amplitude is higher in a specific mode shape, the rate of reduction of the corresponding specific natural frequency will increase.
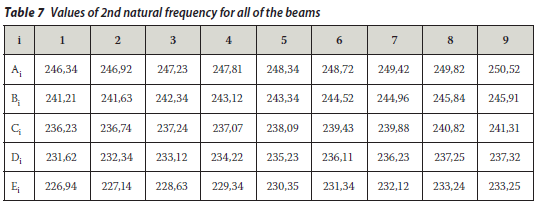
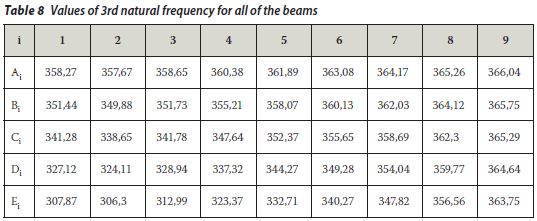
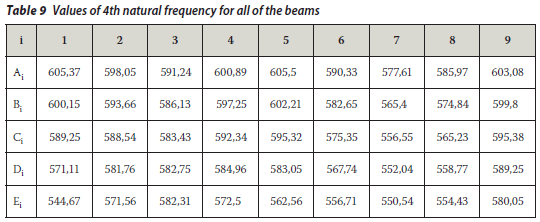
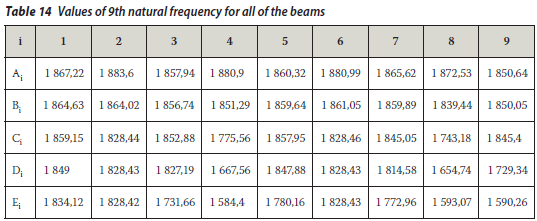
The values of the natural frequencies are listed in Tables 6 to 15 for whole beams.

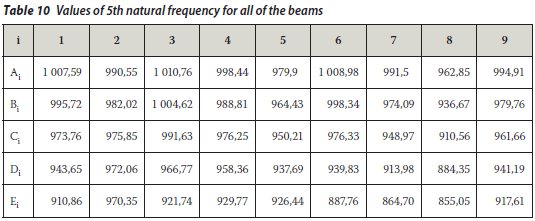
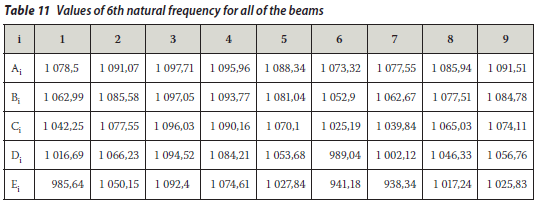
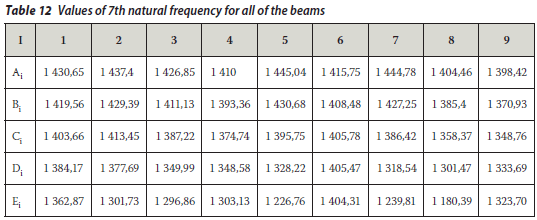
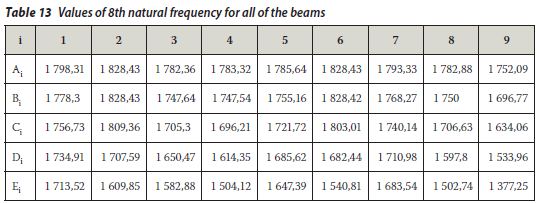

RANDOM VIBRATION ANALYSIS
General considerations
Study of the frequency response of an oscillatory system and dynamic identification can be useful for determining the existence and location of probable defects such as cracks in a structural member. For this purpose, the structure must be excited by a force source. Then its response must be monitored at various points and transferred to a frequency domain to study the changes. Specific fast Fourier transform (FFT) techniques are used to transfer the responses.
Since the exciting force in both the laboratory and in situ works is usually an impact hammer, the excitation frequency will be broad-banded. An individual vertical force, with the specifications of the white noise located at the free end of the beam, is used to excite the member and to investigate its response by random vibrational analysis. In this case, the amplitude of the force will be constant throughout the frequency band. Random vibrational analysis is performed in the frequency domain. Input and output data are in the form of power spectral density (PSD), whose function is defined as follows:
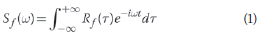
where Sƒ (ω) is the PSD of random variable ƒ(t), and Rƒ (τ) is the autocorrelation function of this random variable, which is expressed as:
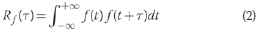
It is noted that the units of "PSD of displacement", "PSD of velocity" and "PSD of acceleration" will be "[displacement unit]2/[frequency unit]", "[velocity unit]2/[frequency unit]" and "[acceleration unit]2/[frequency unit]" respectively. In such problems, in order to increase the accuracy of the analysis, the range of the white noise is determined in such a way that the frequency of the last mode shape becomes at least 80% of the upper limits of the excitation frequency band (Bensalem et al 1996). In this paper the maximum frequency considered, which is the frequency of tenth mode shape, is approximately 2 000 Hz. Although the upper limit of the excitation frequency is 3 000 Hz for all the beams analysed, the responses at frequencies higher than 2 000 Hz are not studied here. The white noise input signal is shown in Figure 22.

The aim of this study was to investigate the changes in the responses of damaged members, such as accelerations, displacements and velocities, and to compare them with the responses of an intact member.
Adequate care must be taken in choosing the location of the applied force and the response recorders because this significantly affects the success of the work. Numerical methods such as FEM can be useful for determining suitable locations. These locations must be sufficiently far from the nodal points. In this investigation the free end of the beam was selected as the location for the applied force. Since the force is vertical, it is obvious that the axial mode shapes either will not be excited at all or their response amplitude will be very small.
Results of the random vibrational analysis
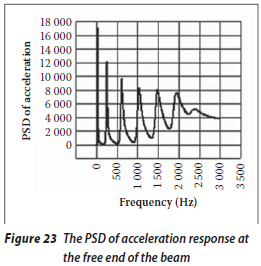
If the displacement, velocity and vertical acceleration responses are studied at the different points along the beams, it can be seen that when the distance of the point from the fixed end is increased, the amplitude of the responses is increased too. Also, it can be shown that the displacement and velocity responses are very small (approximately zero) at high frequencies in comparison with the responses at low frequencies. However, the acceleration response is more illustrative, having a high amplitude at high frequencies. Investigating the acceleration PSD diagrams is therefore a suitable way to study the change in the frequency response.
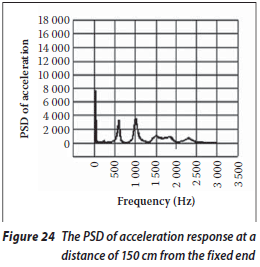
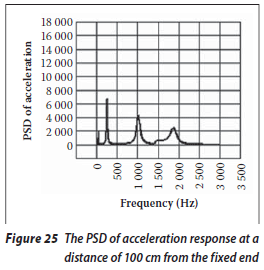
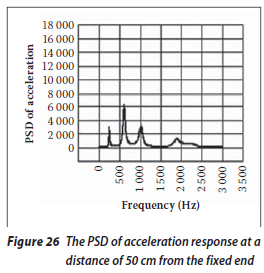
The acceleration responses at different points along the beam A1 are presented in Figures 23 to 26. The acceleration response at the free end of the beam is shown in Figure 23 and the responses at the distances of 150, 100 and 50 cm from the fixed end are shown in Figures 24, 25 and 26 respectively. It can be seen that the peak responses are considerably smaller than they were in the intact beam. The reason is the reduction in beam stiffness due to the existence of a crack.
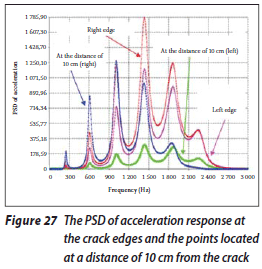
The acceleration responses at the crack edges and at the points located at a distance of 10 cm from the crack are presented in Figure 27. It can be seen that the amplitude of the responses at the points located to the right of the crack is higher than at the points to the left of the crack. The reason is that these points to the right are closer to the free end of the beam.
For investigation of the response to the white noise along the beam, 58 three-dimensional diagrams are provided by the program. As an example, the PSD of the acceleration response along the beam N1 is presented in Figures 28 and 29.
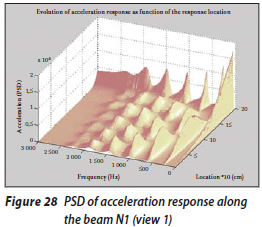
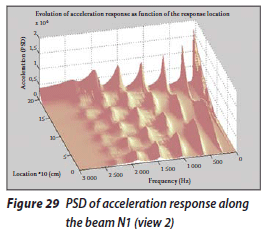
The following noteworthy results are obtained from these figures. The pattern of the response changes along the beam at the frequencies that coincide with the natural frequencies of the structure depends on the corresponding mode shape. For example, when the distance of a specific point from the fixed end of the beam is increased, the amplitude of response in the excitation frequency that coincides with the first natural frequency of oscillation will be increased and the associated response diagram will be quite similar to the first mode shape. This is also confirmed for higher natural frequencies. It must be noted that the response amplitude at excitation frequencies that coincide with the axial natural frequencies is very low (approximately zero).
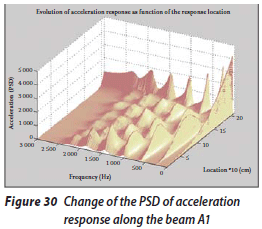
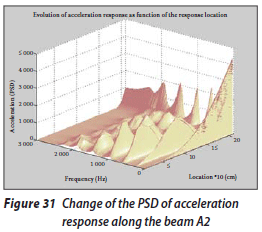
Figure 30 shows the change in the acceleration response along beam A1. In this figure, a peak is observed at a frequency of 1 500 Hz at the point located at a distance of 20 cm from the fixed end, which represents the location of the crack. Figure 31 shows the change in the acceleration response along beam A2. In this figure, a peak is observed at a frequency of 1 000 Hz at the point located at a distance of 40 cm from the fixed end, which represents the location of the crack.
CONCLUSIONS
The rate of frequency changes due to a reduction in the natural frequencies in a damaged member in comparison with an intact member. An increase in the depth of the crack leads to an increase in the decrement rate of the natural frequencies. Whenever the location of the crack comes closer to the free end of the beam, the rate of the frequency decrement is reduced because the rate of decrement of the beam stiffness is increased.
The rate of frequency changes due to the change in crack location depends on their corresponding mode shapes. When the crack location comes closer to those points for which the deformation amplitude is higher in a specific mode shape, the rate of the corresponding specific natural frequency decrement will be increased.
The creation of a crack can lead to some changes in the higher mode shapes of oscillation, but the lower mode shapes usually remain unchanged. The type of mode shape may be changed or two types may be combined. A study of the pattern of these changes can be useful for identifying the damage to the structures.
When the displacement, velocity and vertical acceleration responses are studied at different points along the beams, it can be seen that if the distance of the point from the fixed end is increased, the amplitude of the responses will be increased.
The displacement and velocity responses are approximately zero and are very small at high frequencies in comparison with the low-frequency responses. However, the acceleration response is more illustrative and has a high amplitude at high frequencies. Investigating the acceleration PSD diagrams is therefore a suitable way to study the change of the frequency response.
The amplitude of the responses at the points located to the right of the crack is higher than that at the points to the left of the crack. The reason is that these points are closer to the free end of the beam.
The pattern of the response changes along the beam at the frequencies that coincide with the natural frequencies of the structure depends on the corresponding mode shape. For example, when the distance of a specific point from the fixed end of the beam is increased, the amplitude of response in the excitation frequency that coincides with the first natural frequency of oscillation will be increased and the associated response diagram will be quite similar to the first mode shape. This is also confirmed for higher natural frequencies.
The normal changes in the amplitude of the acceleration response along the beam will be changed in the vicinity of the crack, resulting in a local peak which can be useful for identifying the location of the crack.
REFERENCES
ACI Manual of Concrete Practice 1996. Part 3, Use of concrete in buildings design, Specification and related topics, American Concrete Institute. [ Links ]
Bensalem, A, Fairfield, C A & Sibbald, A 1996. Vibration condition monitoring of brickwork columns. J Shock and Vibration, USA. [ Links ]
Bensalem, A, Fairfield, C A & Sibbald A 1997. Non-destructive evaluation of the dynamic response of a brickwork arch. J Structures and Buildings, ICE. [ Links ]
Castellani, A 1992. Concrete toughness after 20 years. J Struct Engng, ASCE 118: 1402-1412. [ Links ]
COSMOS/M Advanced Modules (Vol. 4, Part 1) 1995. Structural Research & Analysis Corp, Version 1.75, 1st edition. [ Links ]
Doebling, S W, Farrar, C R, Prime, M B & Shevitz, D W 1996. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: A literature review. Los Alamos National Laboratory Report LA-13070-MS. [ Links ]
Ewins, D J 1986. Modal testing: Theory and practice. New York: Wiley. [ Links ]
Liew, K L & Wang, Q 1998. Application of wavelet theory for crack identification in structures. J Engng Mech, ASCE, 124(2): 152-157. [ Links ]
Litorowicz, A 2006. Identification and quantification of cracks in concrete by optical fluorescent microscopy. Cement and Concrete Res: 1508-1515. [ Links ]
Maeck, J & De Roeck, G 1999. Dynamic bending and torsion stiffness derivation from modal curvatures and torsion rates. J Sound and Vibration 225(1): 153-170. [ Links ]
Maia, N M M et al 1997. Theoretical and experimental modal analysis. Taunton, UK: Research Studies Press. [ Links ]
Ndambi, J M, Vantomme, J & Harri, K 2002. Damage assessment in reinforced concrete beams using eigen frequencies and mode shape derivatives. Engng Structures 24(4): 501-515. [ Links ]
Penzien, J & Hansen, R K 1954. Static and dynamic elastic behavior of reinforced concrete beams. ACI J Proc 50: 545-567. [ Links ]
Salawu, O S 1997. Detection of structural damage through changes in frequency: A review. Engng Structures 19(9): 718-723. [ Links ]
Sohn, H, Farrar, C R, Hemez, F M, Shunk, D D, Stinemates, D W & Nadler B R 2003. A review of structural health monitoring literature: 1996-2001. Los Alamos National Laboratory Report LA-13976-MS. [ Links ]
Theoretical Manual for COSMOS/M, 2nd edition 1993. Structural Research and Analysis Corp. [ Links ]
Torigoe, I, Mori, K & Spagnoli, A 2005. Signal processing procedure for non-destructive test of concrete structure integrity. NDT&E International, 38: 575-581. [ Links ]
Wang, Z, Man, X T C, Finch, R D & Jansen, B H 1998. The dynamic behavior and vibration monitoring of reinforced concrete beams. J Testing and Evaluation 26(5): 405-419. [ Links ]
Wauer, J 1990. On the dynamics of cracked rotors: A literature survey. Appl Mech Rev, 43(1): 13-17. [ Links ]
Zembaty, Z 1997. Vibrations of bridge structure under kinematic wave excitations. J Struct Engng, ASCE 123: 479-488. [ Links ]
 | PROF MOHAMMAD ALI LOTFOLLAHI-YAGHIN, Associate Professor of Off shore Structural Engineering at the University of Tabriz, has a BSc degree in civil engineering from the Isfahan University of Technology, Iran, an MSc degree in structural engineering from the University of Tabriz, Iran, and a PhD degree in off shore structural engineering from Heriot-Watt University, UK. He is the author of more than 60 technical papers and reports, and two books on fi nite element analysis and the dynamics of off shore structures. |
 | REZA SHAHINPAR, Construction Engineering Manager and Site Deputy in the Urmia Lake Causeway Project being undertaken by the company SADRA in Iran, has a BSc degree in civil engineering from the University of Tabriz, Iran, and an MSc degree in structural engineering from the Urmia University, Iran. He is a lecturer in the Civil Engineering Department of Azad University of Urmia. |
 | HAMID AHMADI, PhD candidate in off shore structural engineering at the University of Tabriz, has a BSc in civil engineering and an MSc degree in offshore structural engineering from the University of Tabriz, Iran. He is the author of eight technical papers and a book on the dynamics of offshore structures. He is a member of the Iranian Association of Naval Architecture and Marine Engineering. |
 Contact details:
Contact details:
Faculty of Civil Engineering University of Tabriz
29 Bahman Blvd
Tabriz 51664 Iran
T: 98 914 418 6490; F: 98 411 334 4287
a_lotfollahi@yahoo.com; lotfollahi@tabrizu.ac.ir
Contact details:
SADRA Company's Site No 1 in the Urmia Lake Causeway Project
24th kilometer of Shahid Kalantari Highway
after Zanbil Mountain
Urmia Iran
T: 98 914 341 2805 / 98 443 487 6000~2; F: 98 411 334 4287
shahinpar77@yahoo.com; R.Shahinpar@urmia.sadragroup.com
Contact details:
Faculty of Civil Engineering University of Tabriz
29 Bahman Blvd
Tabriz 51664 Iran
T: 98 912 542 7829; F: 98 411 334 4287
h_ahmadi_81@yahoo.com; h-ahmadi@tabrizu.ac.ir














