Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.5-6 Pretoria May./Jun. 2008
BIOLOGICAL MODELLING
Modelling the dynamics of animal groups in motion
Christophe LettI, *; Vincent MirabetII
IInstitut de Recherche pour le Développement (IRD), UR GEODES, and Oceanography Department, University of Cape Town, Private Bag, Rondebosch 7701, South Africa
IICNRS; UMR 5558, Laboratoire de Biométrie et Biologie Evolutive, Université de Lyon, 43 boulevard du 11 novembre 1918, Villeurbanne F-69622, France; IRD, UR GEODES
ABSTRACT
Animal groups in motion, examples being fish schools, bird flocks, insect swarms and mammal herds, can exhibit spectacular collective behaviour. Attempts at formalizing the basic individual behaviour that accounts for the complex dynamics of an animal group began over 50 years ago. Numerous models of these dynamics have since been published. We review this information, starting with an overview of various approaches that have arisen from mathematical, physical, and computer-modelling methods. Our focus is on individual-based models of animal groups. Individuals are assumed to exert three types of local interactions with their neighbours in these models, namely attraction, alignment, and repulsion. We review these models according to their main objectives: to compare modelled results with observational data; to analyse the influence of model parameters on simulated group properties; and to investigate group response to any change in environment, or to divergent behaviour of some of the group members.
Introduction
Animal groups, such as fish schools, bird flocks, insect swarms and mammal herds, can exhibit spectacular collective behaviour.1,2 Being part of a group induces multiple changes in individual links with the environment and to siblings.3 Some of these changes are associated with the 'many eyes–many mouths' trade-off,4,5 namely collective benefits (many eyes, and hence a reduced risk of predation) and collective deficits (many mouths, creating increased competition for food). Complex group behaviour may emerge from simple local interactions between individuals. A fish school is not regarded as having a social leader, and individuals do not perceive the school as an entity of which they are a part, yet fish schools display complex coordinated collective behaviour.6 Attempts to formalize basic individual behaviour leading to complex group dynamics began over 50 years ago.7 Numerous models of the dynamics of animal groups have since been reported in the literature.
Models of animal groups in motion have been published in ecological8,9 and fish dynamic modelling reviews,10 and in reviews1,2 or theoretical notes11–13 on collective animal behaviour. Several examples of these models have also been reported in books on individual-based models14 or self-organization.15 To our knowledge, however, there is no specific review on modelling of the dynamics of animal groups. This paper addresses this shortcoming. We present an overview of various modelling approaches that arise from mathematical, physical, and computational methods. We then focus on individual-based models of animal groups, and report on these studies according to their main objectives: to compare model results with observational data; to analyse the effects of model parameters on the simulated group properties; to investigate group response to a change in its environment, or to divergent behaviour of some of its members.
Different modelling approaches
Mathematics
A simple mathematical model used to describe aggregative movements is the 'aggregation–diffusion equation'16:

in which u is the density of individuals at time t and space location x along a line. Different shapes of the ø(u) function correspond to different types of interactions between individuals: a linear function ø(u) = Du corresponds to the absence of interaction, resulting in diffusion dynamics, the continuous-time equivalent of a discrete-time random walk; a convex (conversely concave) function results in over-dispersion (conversely under-dispersion), and corresponds to a repulsive (conversely aggregative) interaction. But these dynamics are all 'diffusion-like', in the sense that a steady state of the system has a uniform density u = u0 along the line, where u0 is specified by the boundary conditions u(0,t) = u(L,t) = u0, L being the length of the line. But when ø(u) functions are such that the equation ø(u) = ø(u0) has three roots (Fig. 1, left panel), then the aggregation–diffusion equation gives rise to 'clumping-like' dynamics, where the steady state of the system consists of a succession of both low density and high density zones along the line (Fig. 1, right panel).

Other terms can be added to the aggregation–diffusion equation, in particular, advection and 'reaction' terms, to take into account any environmental (such as sea currents) and demographic (such as growth and mortality) factors, respectively.17–19 For example, see the advection–diffusion–reaction models that have been developed as representing the dynamics of tuna.20–22
Physics
Vicsek et al.23 developed a model of 'self-propelled particles' in which 'at each time-step a given particle driven with a constant absolute velocity assumes the average direction of motion of the particles in its neighbourhood of radius r, with some random perturbation'. The position of each particle i is given by

Its velocity is given a constant value and a direction determined by the angle

In Equation (3), 〈ν(t)〉 denotes the average direction of the velocities of particles located in radius r around particle i, and ξ is a random number chosen from a uniform distribution.
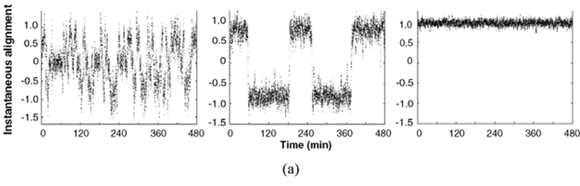
Transitions from disordered motion in this model to discrete groups moving coherently in random directions (Fig. 2, left panel), and thereafter, completely ordered motion (Fig. 2, right panel), occur as particle density increases.23 A model similar to this one has been applied to examine the transition from disorder to order occurring in populations of desert locust nymphs at critical densities.24 Evidence of a similar transition has also been reported for schools of young fish.25

Originally developed in two dimensions, the model23 has been extended to three dimensions,26 and a synthesis of the results obtained from experiments conducted in one to three dimensions has also been published.27 The density of particles in these models has been kept constant by using closed simulation domains, and collective motion does not occur in an open domain because the systems are in a disordered state at low particle density. This argument has led to the addition of an attraction–repulsion 'force' to the alignment component in Equation (3).28
Computer science
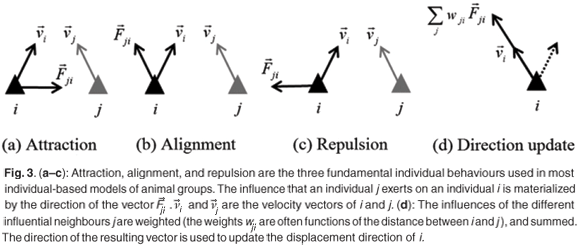
Reynolds29 is often cited as the first exponent of a computer model applied to the simulation of the dynamics of animal groups. His model is individual-based, where he considers a collection of individuals, whose behaviour is explicitly executed at the individual level. Focusing on bird flock simulation, Reynolds introduced the concept of a bird-oid, or 'boid', as a virtual equivalent to a real bird. The three fundamental individual behaviours used in Reynolds' model, namely cohesion, alignment and separation,30 are related closely to those used afterwards in most individual-based models (IBMs) of animal groups: attraction, alignment, and repulsion. These behaviours reflect the different types of interaction that an individual j may exert on an individual i. This is illustrated in Fig. 3 by the directions of the vector  . This vector is orientated towards (conversely away from) j in the case of an attraction (conversely repulsion) behaviour, and is aligned on the velocity vector,
. This vector is orientated towards (conversely away from) j in the case of an attraction (conversely repulsion) behaviour, and is aligned on the velocity vector,  , of j, for the alignment behaviour. Generally, each individual i has several influential individuals j in its neighbourhood (termed influential neighbours). In most IBMs the (potentially conflicting) influences of these are weighted by functions of the distance between i and j, and are summed. The resulting vector is used to determine the displacement direction of the individual i at the next time-step (Fig. 3d), and its position is updated using Equation (2). Different types of weighting functions have been used with different IBMs. These functions share some common properties, particularly reflecting the tendency for attraction, alignment and repulsion behaviour to be predominant at large, medium and small distances, respectively. But they also differ in a number of aspects, and the consequences on simulated group characteristics of favouring one type of function over another have been reported in a number of papers.6,31–34
, of j, for the alignment behaviour. Generally, each individual i has several influential individuals j in its neighbourhood (termed influential neighbours). In most IBMs the (potentially conflicting) influences of these are weighted by functions of the distance between i and j, and are summed. The resulting vector is used to determine the displacement direction of the individual i at the next time-step (Fig. 3d), and its position is updated using Equation (2). Different types of weighting functions have been used with different IBMs. These functions share some common properties, particularly reflecting the tendency for attraction, alignment and repulsion behaviour to be predominant at large, medium and small distances, respectively. But they also differ in a number of aspects, and the consequences on simulated group characteristics of favouring one type of function over another have been reported in a number of papers.6,31–34
Most IBMs rely on the fundamental principles discussed above, and are therefore conceptually similar to the reported model of self-propelled particles.28 But most IBMs also use additional parameters or processes to improve their biological realism. These are detailed below.
Individual-based models of animal groups
Overview
Of 31 papers on individual-based models of animal groups examined in this review, 20 deal with the dynamics of fish schools.6,35–53 The tendency to select fish in these models has already received attention.54 Individuals in most fish-school IBM studies have been given some specific characteristics of fish, such as dead angle limitation of their field of perception,36,40,43,44,46,49–53 varying fields of perception related to different sensory systems (vision and lateral line)36,44 or a fairly sophisticated spring-mass sub-model for locomotion.49 Seven papers have dealt with animal groups in general,31,33,34,55–58 leaving one paper on animal herds,59 one on human crowds,60 and two previously-mentioned publications on bird flocks29 and insect swarms.24
The objective of early work was to demonstrate that use of IBMs, with simple individual behaviour, allows for simulation of various types of group behaviour40,45,46 and can create realistic animations.29,49 The publications that we examine can be assigned to four categories in terms of their main objectives: a comparison of model results with experimental data, an analysis of the effects of model parameters on the simulated group properties, and an investigation of the simulated group response to a change in its environment, or to divergent behaviour of some of its members.
Comparison of model results with data
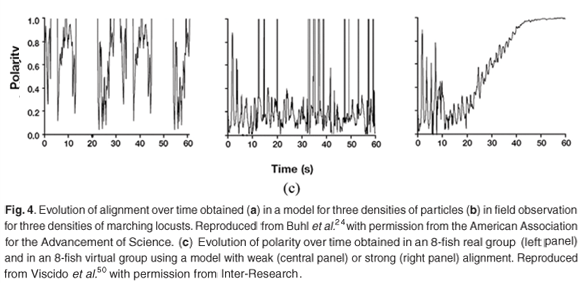
The evolution with time of variables that characterize the alignment of particles in a model, and the alignment of locusts in field observation, have been compared for three different densities.24 Impressively similar patterns of low alignment at low density, high alignment at high density, and shifting low–high alignment at intermediate density (Fig. 4a and b), are obtained. Moreover, the transitions between the different states occur at approximately the same critical densities. Similarly, the evolution of polarity, another variable characterizing the coherence of the displacement of individuals, has been measured over time, in 8-fish real groups and virtual groups.50 A strong alignment behaviour in the model results in a fast increase of polarity over time, which is not evident from the data. Weak alignment behaviour produces patterns more in accordance with data (Fig. 4c). Several characteristics of simulated fish schools (the distances to nearest neighbours, the degree of polarity, the frequency of the time spent by a fish at the front of a school) are in general good agreement with observed data.42 A good fit is also obtained for the number of fish per group, and for the number of groups, as observed in laboratory experiments and in a model.37 But the fit is poor in the field where there are much fewer and much larger schools than predicted by the model. Video analyses of fish schooling in a tank have been used to estimate the parameters of an IBM that included attraction and repulsion behaviour towards the tank wall and central structure.48 Use of video recording provides information on the long-distance attraction and short-distance repulsion behaviours that are the core of IBMs.61
Effects of model parameters on group properties
Analyses of the effects of different types of attraction–alignment–repulsion weighting functions on the simulated group properties31,33 reveal that functions resulting in a smooth transition from one type of behaviour to another (for example, from attraction to repulsion) lead to more cohesive33 and more homogeneous31 groups. A shift from slow moving groups (swarms) to highly polarized, faster-moving ones (schools) has been reported as increasing the strength of the alignment behaviour,55 or decreasing strength of randomness in movement of individuals.45 Only a tiny alignment force can create highly polarized groups, whereas a large degree of randomness is required for a group to disintegrate.52 Groups with higher polarity are also obtained when the alignment zone used in a model is enlarged.40 Increasing the number of influential neighbours (i.e. the number of j individuals that influence the behaviour of individual i, Fig. 3) results in smaller and more-polarized groups.6,40 A larger variability in individual spacing within the group is obtained6 for large numbers of influential neighbours, and may arise from the structures (concentrations of individuals in subgroups or lines) observed under such conditions.31 An asymptotic relationship between simulated group size and the number of individuals has been established,51 which suggests that increasing the number of individuals will result in several groups of similar size, rather than a single large group.
Group response to environment
Simple additions to the basic rules used in IBMs allows for the simulation of fish schools when feeding,35,41 swimming along environmental gradients,38,41 avoiding obstacles,38,41,48 and escaping predators.43,53,57,58 A decrease in speed and an increase in the random movement of individuals located in the vicinity of food patches allows one to simulate schools shifting from straight polarized dynamics, while cruising, to loose swarm-like dynamics, while feeding.41 A decrease (conversely increase) in individual speed within (conversely outside) food patches leads to individuals reacting collectively to the distribution of food, and thus spending a significantly longer time in favourable areas than in the case of solitary individuals.35 Another additional rule states that if a fish perceives an improvement in the environmental conditions, it will maintain its direction and will accelerate slightly,41 resulting in simulated fish schools swimming along a region that offers the best conditions (Fig. 5a). A similar approach has been used to simulate the migration of fish schools between spawning and feeding grounds.38 Repulsion from obstacles has been added to individual behaviour in order to simulate fish schools swimming around obstacles,41 and potentially being split by such obstacles (Fig. 5b).
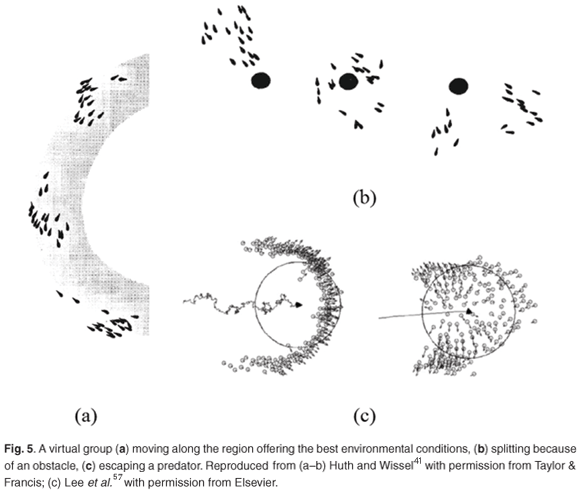
Obstacles can also be represented by unfavourable and avoidable environmental conditions for fish schools.38 Individual attraction and repulsion behaviour towards a tank wall is needed to account for small groups of fish observed swimming along such wall.48 Similar behaviour has been modelled to simulate the dynamics of a crowd escaping out of a room.60 Finally, adding repulsion behaviour away from a predator enables one to investigate the dynamics of animal groups in the presence of predators.43,53,57,58 Typical patterns of fish school responses to predators described in the literature have been identified through simulations.43 Movement of the predator will influence the group response:57 a split-type response is obtained when the predator has a direct movement (Fig. 5c, right); a herd-type response arises when the predator has a more erratic movement (Fig. 5c, left). The interplay between collective escape and 'selfish escape' (when a fish ceases to interact with its neighbours, due to the proximity of the predator) has also been examined.53 The group dynamics of predators chasing groups of prey has been investigated by means of an evolutionary IBM that includes scores for individuals, based on the number of predator–prey encounters and a selective process, where only the most successful individuals are able to reproduce.58
Group response to individual differences
IBMs have also been used largely to study the effects on the group dynamics of some members with different properties, or different behaviour from the others. Various speeds, maximum turning rates, sizes of alignment and repulsion areas, have influence on the positions of individuals relative to the front and/or centre of a group.55 Some individuals that have different attraction–repulsion functions exert an impact on the turning rate and velocity of whole group.47 Two categories of individuals have been introduced in an IBM,36 having properties such that individuals were more attracted towards, less repulsed by, and aligned more with individuals from their category. This has led to sub-groups of homogeneous categories becoming randomly distributed within a group. However, when the two categories differ in specific properties (the attraction–alignment–repulsion functions, in this case), sub-groups acquire privileged locations within the group. Groups that are initially composed of fast and slow individuals eventually fragment into a fast and a slow sub-group.59 Group fragmentation has not been obtained in another similar experiment; instead, the result has been fast individuals circling around slow ones.47 Several authors have used IBMs to investigate the effects of a few individuals with biased movement direction on group dynamics.39,47,56,59 In a modelling experiment where only a small proportion of the fish is attracted towards the source of a stimulus, a critical transition occurs at ~5% of stimulated individuals.39 At a lower percentage, almost no fish reach the stimulus source, and above this value, almost all fish succeed. The effects of conflicting preferred movement directions have also been studied.56 N1 and N2 individuals have a biased direction towards 0° and x° (x є [0º, 180º]) respectively in a group of 100 individuals moving in a two-dimensional area. With N1 = N2 = 5, and under a critical value of x, the group as a whole is most likely to follow an in-between direction x/2°, whereas above this critical value, it is equally likely to move collectively towards 0° (the preferred direction of the N1 individuals) or x° (the preferred direction of the N2 individuals). In contrast, with N1 = 6 and N2 = 5 there is minimal chance for the group as a whole to move towards x°, and no chance with N1 = 6 and N2 = 4.
Discussion
We have considered models of the dynamics of animal groups using mathematical, physical, or computational methods. Because we focus on individual-based models, our review is biased towards the computational approach (most IBMs considered here have been developed and used in a context of numerical ecology). Spatially explicit IBMs typically employ continuous variables for space. For this reason, we have excluded models that use discrete space, most of them being cellular automata networks developed from physical62–65 or computational66–70 methods.
The effects of changing parameter values in most IBMs on simulated group properties have been assessed. This review devotes a particular section to research in which this assessment was the main objective. Sensitivity analysis is crucial, but time-consuming, as it is based on series of simulations that use various sets of parameter values. There is a lack of theoretical background with respect to IBMs, compared with mathematical and physical modelling. Research that aims to establish links between mathematical or physical models and IBMs32,71–74 is thus of importance.
Individuals are assumed to move at constant speed with most IBMs that we have reviewed, or at a speed randomly chosen from a constant statistical distribution. A Newtonian description of movement has been used for a few IBMs, where the acceleration of each individual has been calculated as the sum of forces applied to it, divided by its mass.6,32,48–52,57 Forces have included social forces (attraction, alignment and repulsion), a drag force that impedes individuals when moving too quickly, and other potential attraction–repulsion forces for individuals that interact with their physical environment48 or with predators.57 On first impression, the acceleration approach would seem to be more satisfactory, as it allows individuals to vary their speed, and this relates to real life. Including a drag force, however, effectively sets a constant velocity. Individuals initially change in relative positions until they are at locations where all forces cancel. This steady state is likely to correspond to a condition where attraction and repulsion on one side, with alignment and drag on the other side, cancel one another, as these forces have opposing influences on movement.
It is often claimed that parameters and variables used in IBMs are more biologically meaningful, and easier to estimate than those used for mathematical models. A reason is that IBMs deal with individuals, which are entities that are generally easier to identify than populations, the level at which most mathematical models operate. This said, some parameters and functions used in IBMs of animal groups are notably difficult to estimate. Finding evidence for the existence of attraction–alignment–repulsion zones has already been a challenge.61 Determining attraction– alignment–repulsion weighting functions from data is difficult. Video analysis24,25,37,48,50,61 is expected to play a major role in this regard. The number of influential neighbours has been identified as a crucial parameter in many projects. Estimating such a parameter from data remains an open question. The number of individuals in a group is also an important parameter. Laboratory research thus far confines its work to small groups of individuals. Comparison of these results with larger groups in the field is complex.37 It is encouraging, however, to see how well model and data comparisons can agree.24 The fact that simulated groups avoid predators with dynamical patterns similar to observed ones43,57 is also a valuable qualitative validation of the models.
We have detailed investigations of a group's response to a change in its environment, and to the different behaviour of some of its members. Individuals with potentially different properties or behaviour exert local interactions with one another, and with their environment. Accounting for local interactions and the diversity of individuals have been two main reasons that have been advanced for the need of IBMs.75 Results that show how a few individuals can influence the behaviour of a whole group39,56 reinforce the view that IBMs are an appropriate method. IBMs of animal groups can also be used to explore other group phenomena. One is a fish school's reaction to shipping. This behaviour has been well documented, and compares the reported responses: avoidance,76–78 attraction,79 or no reaction.80 Another scenario is individuals that try systematically to avoid particular positions within a group. Location at the periphery of a group, for example, will lead to larger exposure to predators, or to adverse environmental conditions (for instance, colder temperatures in penguin colonies). This affords methods that explore not only the manner in which an individual influences a group, but also how the group has influence on individuals. In the South African context, one can consider the spectacular collective marine fish migration phenomenon named 'the sardine run' (a series of papers on the subject are in preparation for the African Journal of Marine Science). The step from the current models that simulate groups of hundreds of individuals to modelling a school of hundreds of millions of sardines is a massive challenge.
1. Parrish J.K. and Edelstein-Keshet L. (1999). Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science 284, 99–101. [ Links ]
2. Sumpter D.J.T. (2006). The principles of collective animal behaviour. Phil. Trans. R. Soc. B 361, 5–22. [ Links ]
3. Lett C., Auger P. and Gaillard J.M. (2004). Continuous cycling of grouped vs. solitary strategy frequencies in a predator-prey model. Theor. Popul. Biol. 65, 263–270. [ Links ]
4. Giraldeau L-A. (1988). The stable group and the determinants of foraging group size. In The Ecology of Social Behaviour, ed. C.N. Slobodchikoff, pp. 33–53. Academic Press, New York. [ Links ]
5. Ritz D.A. (1997). Costs and benefits as a function of group size: experiments on a swarming mysid, Paramesopodopsis rufa Fenton. In Animal Groups in Three Dimensions, eds J.K. Parrish and W.M. Hamner, pp. 194–206. Cambridge University Press, Cambridge. [ Links ]
6. Parrish J.K., Viscido S.V. and Grünbaum D. (2002). Self-organized fish schools: an examination of emergent properties. Biol. Bull. 202, 296–305. [ Links ]
7. Breder C.M. (1954). Equations descriptive of fish schools and other animal aggregations. Ecology 35, 361–370. [ Links ]
8. DeAngelis D.L. and Mooij W.M. (2005). Individual-based modeling of ecological and evolutionary processes. Annu. Rev. Ecol. Evol. Syst. 36, 147–168. [ Links ]
9. Grimm V., Revilla E., Berger U., Jeltsch F., Mooij W.M., Railsback S.F., Thulke H.H., Weiner J., Wiegand T. and DeAngelis D.L. (2005). Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310, 987–991. [ Links ]
10. Giske J., Huse G. and Fiksen O. (1998). Modelling spatial dynamics of fish. Rev. Fish Biol. Fish. 8, 57–91. [ Links ]
11. Vicsek T. (2001). A question of scale. Nature 411, 421–421. [ Links ]
12. Grünbaum D. (2006). Align in the sand. Science 312, 1320–1322. [ Links ]
13. Couzin I. (2007). Collective minds. Nature 445, 715–715. [ Links ]
14. Grimm V. and Railsback S.F. (2005). Individual-based Modeling and Ecology. Princeton University Press, Princeton, NJ. [ Links ]
15. Camazine S., Deneubourg J-L., Franks N.R., Sneyd J., Theraulaz G. and Bonabeau E. (2001). Self-organization in Biological Systems. Princeton University Press, Princeton, NJ. [ Links ]
16. Turchin P. (1989). Population consequences of aggregative movement. J. Anim. Ecol. 58, 75–100. [ Links ]
17. Okubo A. (1980). Diffusion and Ecological Problems: Mathematical models. Springer-Verlag. [ Links ]
18. Okubo A. (1986). Dynamical aspects of animal grouping: swarms, schools, flocks, and herds. Adv. Biophys. 22, 1–94. [ Links ]
19. Grünbaum D. and Okubo A. (1994). Modelling social animal aggregations. In Frontiers in Mathematical Biology. Lecture Notes in Biomathematics Vol. 100, ed. S.A. Levin, pp. 296–325. Springer-Verlag. [ Links ]
20. Sibert J.R., Hampton J., Fournier D.A. and Bills P.J. (1999). An advection-diffusion-reaction model for the estimation of fish movement parameters from tagging data, with application to skipjack tuna (Katsuwonus pelamis). Can. J. Fish. Aquat. Sci. 56, 925–938. [ Links ]
21. Maury O. and Gascuel D. (2001). 'Local overfishing' and fishing tactics: theoretical considerations and applied consequences in stock assessment studied with a numerical simulator of fisheries. Aquat. Living Resour. 14, 203–210. [ Links ]
22. Adam M.S. and Sibert J.R. (2002). Population dynamics and movements of skipjack tuna (Katsuwonus pelamis) in the Maldivian fishery: analysis of tagging data from an advection-diffusion-reaction model. Aquat. Living Resour. 15, 13–23. [ Links ]
23. Vicsek T., Czirók A., Ben-Jacob E., Cohen I. and Shochet O. (1995). Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229. [ Links ]
24. Buhl J., Sumpter D.J.T., Couzin I.D., Hale J.J., Despland E., Miller E.R. and Simpson S.J. (2006). From disorder to order in marching locusts. Science 312, 1402–1406. [ Links ]
25. Becco C., Vandewalle N., Delcourt J. and Poncin P. (2006). Experimental evidences of a structural and dynamical transition in fish school. Physica A 367, 487–493. [ Links ]
26. Czirók A., Vicsek M. and Vicsek T. (1999). Collective motion of organisms in three dimensions. Physica A 264, 299–304. [ Links ]
27. Czirók A. and Vicsek T. (2000). Collective behavior of interacting self-propelled particles. Physica A 281, 17–29. [ Links ]
28. Grégoire G., Chaté H. and Tu Y. (2003). Moving and staying together without a leader. Physica D 181, 157–170. [ Links ]
29. Reynolds C.W. (1987). Flocks, herds and schools: a distributed behavioral model. In Proc. 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, California, pp. 25–34. ACM Press, New York. [ Links ]
30. Reynolds C.W. (1999). Steering behaviors for autonomous characters. In Proc. 1999 Game Developers Conference, San Jose, California, pp. 763–782. [ Links ]
31. Mirabet V., Auger P. and Lett C. (2007). Spatial structures in simulations of animal grouping. Ecol. Model. 201, 468–476. [ Links ]
32. Mogilner A., Edelstein-Keshet L., Bent L. and Spiros A. (2003). Mutual interactions, potentials, and individual distance in a social aggregation. J. Math. Biol. 47, 353–389. [ Links ]
33. Warburton K. and Lazarus J. (1991). Tendency-distance models of social cohesion in animal groups. J. Theor. Biol. 150, 473–488. [ Links ]
34. Warburton K. (1997). Social forces in animal congregations: interactive, motivational, and sensory aspects. In Animal Groups in Three Dimensions, eds J.K. Parrish and W.M. Hamner, pp. 313–336. Cambridge University Press, Cambridge. [ Links ]
35. Breckling B., Reuter H. and Middelhoff U. (1997). An object oriented modelling strategy to depict activity pattern of organisms in heterogeneous environments. Environ. Model. Assess. 2, 95–104. [ Links ]
36. Hemelrijk C.K. and Kunz H. (2005). Density distribution and size sorting in fish schools: an individual-based model. Behav. Ecol. 16, 178–187. [ Links ]
37. Hensor E., Couzin I.D., James R. and Krause J. (2005). Modelling density-dependent fish shoal distributions in the laboratory and field. Oikos 110, 344–352. [ Links ]
38. Hubbard S., Babak P., Sigurdsson S.T. and Magnusson K.G. (2004). A model of the formation of fish schools and migrations of fish. Ecol. Model. 174, 359–374. [ Links ]
39. Huse G., Railsback S. and Ferno A. (2002). Modelling changes in migration pattern of herring: collective behaviour and numerical domination. J. Fish Biol. 60, 571–582. [ Links ]
40. Huth A. and Wissel C. (1992). The simulation of the movement of fish schools. J. Theor. Biol. 156, 365–385. [ Links ]
41. Huth A. and Wissel C. (1993). Analysis of the behavior and the structure of fish schools by means of computer simulations. Comments Theor. Biol. 3, 169–201. [ Links ]
42. Huth A. and Wissel C. (1994). The simulation of fish schools in comparison with experimental data. Ecol. Model. 75/76, 135–145. [ Links ]
43. Inada Y. and Kawachi K. (2002). Order and flexibility in the motion of fish schools. J. Theor. Biol. 214, 371–387. [ Links ]
44. Kunz H. and Hemelrijk C.K. (2003). Artificial fish schools: collective effects of school size, body size, and body form. Artif. Life 9, 237–253. [ Links ]
45. Niwa H.S. (1994). Self-organizing dynamic model of fish schooling. J. Theor. Biol. 171, 123–136. [ Links ]
46. Reuter H. and Breckling B. (1994). Self-organization of fish schools: an object-oriented model. Ecol. Model. 75/76, 147–159. [ Links ]
47. Romey W.L. (1996). Individual differences make a difference in the trajectories of simulated schools of fish. Ecol. Model. 92, 65–77. [ Links ]
48. Suzuki K., Takagi T. and Hiraishi T. (2003). Video analysis of fish schooling behavior in finite space using a mathematical model. Fish. Res. 60, 3–10. [ Links ]
49. Tu X. and Terzopoulos D. (1994). Artificial fishes: physics, locomotion, perception, behavior. In Proc. 21st Annual Conference on Computer Graphics and Interactive Techniques, Orlando, Florida, pp. 43–50. ACM Press, New York. [ Links ]
50. Viscido S.V., Parrish J.K. and Grünbaum D. (2004). Individual behavior and emergent properties of fish schools: a comparison of observation and theory. Mar. Ecol.–Prog. Ser. 273, 239–249. [ Links ]
51. Viscido S.V., Parrish J.K. and Grunbaum D. (2005). The effect of population size and number of influential neighbors on the emergent properties of fish schools. Ecol. Model. 183, 347–363. [ Links ]
52. Viscido S.V., Parrish J.K. and Grünbaum D. (2007). Factors influencing the structure and maintenance of fish schools. Ecol. Model. 206, 153–165. [ Links ]
53. Zheng M., Kashimori Y., Hoshino O., Fujita K. and Kambara T. (2005). Behavior pattern (innate action) of individuals in fish schools generating efficient collective evasion from predation. J. Theor. Biol. 235, 153–167. [ Links ]
54. Grimm V. (1999). Ten years of individual-based modelling in ecology: what have we learned and what could we learn in the future? Ecol. Model. 115, 129–148. [ Links ]
55. Couzin I.D., Krause J., James R., Ruxton G.D. and Franks N.R. (2002). Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11. [ Links ]
56. Couzin I.D., Krause J., Franks N.R. and Levin S.A. (2005). Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516. [ Links ]
57. Lee S-H., Pak H.K. and Chon T-S. (2006). Dynamics of prey-flock escaping behavior in response to predator's attack. J. Theor. Biol. 240, 250–259. [ Links ]
58. Nishimura S.I. and Ikegami T. (1997). Emergence of collective strategies in a prey-predator game model. Artif. Life 3, 243–260. [ Links ]
59. Gueron S., Levin S.A. and Rubenstein D.I. (1996). The dynamics of herds: from individuals to aggregations. J. Theor. Biol. 182, 85–98. [ Links ]
60. Helbing D., Farkas I. and Vicsek T. (2000). Simulating dynamical features of escape panic. Nature 407, 487–490. [ Links ]
61. Tien J.H., Levin S.A. and Rubenstein D.I. (2004). Dynamics of fish shoals: identifying key decision rules. Evol. Ecol. Res. 6, 555–565. [ Links ]
62. Csahók Z. and Vicsek T. (1995). Lattice-gas model for collective biological motion. Phys. Rev. E 52, 5297–5303. [ Links ]
63. Bussemaker H.J. (1996). Analysis of a pattern-forming lattice-gas automaton: mean-field theory and beyond. Phys. Rev. E 53, 1644–1661. [ Links ]
64. Bussemaker H.J., Deutsch A. and Geigant E. (1997). Mean-field analysis of a dynamical phase transition in a cellular automaton model for collective motion. Phys. Rev. Lett. 78, 5018–5021. [ Links ]
65. Deutsch A. (2000). A new mechanism of aggregation in a lattice-gas cellular automaton model. Math. Comput. Model. 31, 35–40. [ Links ]
66. Vabø R. and Nøttestad L. (1997). An individual based model of fish school reactions: predicting antipredator behaviour as observed in nature. Fish. Oceanogr. 6, 155–171. [ Links ]
67. Stöcker S. (1999). Models for tuna school formation. Math. Biosci. 156, 167–190. [ Links ]
68. Morale D. (2001). Modeling and simulating animal grouping – Individual-based models. Futur. Gener. Comp. Syst. 17, 883–891. [ Links ]
69. Schönfisch B. (2001). Simple individual based models of movement, alignment and schooling behaviour. Futur. Gener. Comp. Syst. 17, 873–882. [ Links ]
70. Hancock P.A., Milner-Gulland E.J. and Keeling M.J. (2006). Modelling the many-wrongs principle: the navigational advantages of aggregation in nomadic foragers. J. Theor. Biol. 240, 302–310. [ Links ]
71. Grünbaum D. (1994). Translating stochastic density-dependent individual behavior with sensory constraints to an Eulerian model of animal swarming. J. Math. Biol. 33, 139–161. [ Links ]
72. Flierl G., Grünbaum D., Levin S. and Olson D. (1999). From individuals to aggregations: the interplay between behavior and physics. J. Theor. Biol. 196, 397–454. [ Links ]
73. Adioui M., Treuil J.P. and Arino O. (2003). Alignment in a fish school: a mixed Lagrangian-Eulerian approach. Ecol. Model. 167, 19–32. [ Links ]
74. Moon S.J., Nabet B., Leonard N.E., Levin S.A. and Kevrekidis I.G. (2007). Heterogeneous animal group models and their group-level alignment dynamics: an equation-free approach. J. Theor. Biol. 246, 100–112. [ Links ]
75. Huston M., DeAngelis D. and Post W. (1988). New computer models unify theoretical ecology. BioScience 38, 682–690. [ Links ]
76. Gerltto F., Castillo J., Saavedra A., Barbieri M.A., Espejo M. and Cotel P. (2004). Three-dimensional structure and avoidance behaviour of anchovy and common sardine schools in central southern Chile. ICES J. Mar. Sci. 61, 1120–1126. [ Links ]
77. Handegard N.O. and Tjøstheim D. (2005). When fish meet a trawling vessel: examining the behaviour of gadoids using a free-floating buoy and acoustic split-beam tracking. Can. J. Fish. Aquat. Sci. 62, 2409–2422. [ Links ]
78. Skaret G., Slotte A., Handegard N.O., Axelsen B.E. and Jorgensen R. (2006). Pre-spawning herring in a protected area showed only moderate reaction to a surveying vessel. Fish. Res. 78, 359–367. [ Links ]
79. Røstad A., Kaartvedt S., Klevjer T.A. and Melle W. (2006). Fish are attracted to vessels. ICES J. Mar. Sci. 63, 1431–1437. [ Links ]
80. Skaret G., Axelsen B.E., Nøttestad L., Fernö A. and Johannessen A. (2005). The behaviour of spawning herring in relation to a survey vessel. ICES J. Mar. Sci. 62, 1061–1064. [ Links ]
* Author for correspondence. E-mail: christophe.lett@ird.fr