RESEARCH PAPER

 

Architectural optimization of a multilayer perceptron (MLP) neural network enhanced by the Levenberg-Marquardt algorithm for predicting relative humidity: application to Tangier, Morocco

 

 

Abdellah Ben yahia; Iman Kadir; Abdelaziz Abdallaoui; Kaoutar Elazhari

Processes and Environment Team, Analytical Chemistry and Electrochemistry, Faculty of Sciences, Moulay Ismail University, Meknes, Morocco

Correspondence

 

 

---

ABSTRACT

This study aimed at establishing a powerful model, using multilayer perceptron (MLP) artificial neural networks, while optimizing database distribution, hidden layer quantity, and node number with the Levenberg-Marquardt learning algorithm, to predict relative humidity in Tangier city, Morocco. The study used a meteorological database with daily readings of 7 variables to predict the output of relative humidity, recorded between January 1985 and December 2022 (13 869 days). The efficacy of the developed models was evaluated by contrasting performance metrics, including coefficient of correlation and mean square error. The best MLP model for the prediction of relative humidity in Tangier has a [7-13-1] architecture, where the hidden layer uses the 'Tansig' function and the output layer uses the 'Purelin' function. The optimized model's efficiency is demonstrated by performance metrics: R = 0.983 and MSE = 0.00295. This MLP model is more efficient than the models established by multiple linear regression, S-MLR and MLR (R ~ 0.930; MSE ~ 10.12). These results have practical applications for better understanding and adapting to climate variations in this region.

Keywords: meteorology, artificial neural networks, multilayer perceptron, activation functions, Levenberg-Marquardt learning, algorithm, relative humidity, Tangier

---

 

 

INTRODUCTION

Meteorology is a complex scientific field, stemming from the range macroscopic and microscopic atmospheric phenomena. Relative humidity (RH) is a pivotal factor and plays a key role in our daily lives. The consequences of climate change are manifold, impacting human health (Arundel et al., 1986; Baldwin et al., 2023), environmental behaviour (Barreca, 2012), material degradation (Chamas et al., 2020; Ho et al., 1999; Laouina, 2017), and energy consumption (Kheiri et al., 2023), particularly in coastal regions such as Tangier, Morocco, where land-sea interactions give rise to distinctive humidity patterns. The significance of relative humidity in governing a region's meteorology necessitates highly precise modelling of this parameter to support sectors such as agriculture, energy management, and public health, and to offer significant insights into climate change (Gunawardhana et al., 2017).

The relationship between relative humidity (RH) and pollutant dynamics, as well as human comfort, is a complex and multifaceted phenomenon. Low RH has been demonstrated to alter the behaviour of airborne substances (Goad and Gawkrodger, 2016), facilitate the spread of influenza, and increase mortality (Barreca, 2012). Additionally, low RH has been shown to cause skin, eye, and mucous dryness (Onozuka and Hashizume, 2011). While elevated relative humidity (RH) has been shown to increase the risk of hand, foot and mouth disease and asthma in children (Yang et al., 2017), it has also been demonstrated to promote hepatitis A survival (Mbithi et al., 1991), prolong the viability of influenza and SARS-CoV-2 (Deng et al., 2022), and correlates with higher suicide rates among youth and women (Deisenhammer, 2003). Low relative humidity conditions have also been demonstrated to result in impaired nasal function in senior citizens (Sunwoo et al., 2006) and to increase illness susceptibility in children. Beyond the realm of health, RH fluctuations have been observed to accelerate material degradation and energy dissipation (He et al., 2021), impede plant transpiration and growth, yet alleviate iron deficiency in soybeans (Amin et al., 2021), and at levels above 70% to induce heat stress, reduced fertility, and disease in livestock (Gaughan et al., 2008). As indicated by the extant literature, moisture has been demonstrated to be a driving force behind a variety of processes, including, but not limited to, corrosion of metals and electronics (Rice et al., 1980), wood decay (Svensson and Toratti, 2002), polymer deterioration (Copinet et al., 2004), alterations to chemical reaction pathways (Yang and Holmén, 2007), diminished engine efficiency, and effects on evapotranspiration (Kim et al., 2021). In addition, the potential for nanoporous materials to offer renewable energy has been identified (Liu et al., 2024). These effects of relative humidity are especially pronounced in a humid environment like Tangier.

A plethora of approaches have been developed with the objective of predicting various meteorological factors (Singh et al., 2019). In numerous instances, multi-layer perceptron (MLP) neural networks have demonstrated a consistent superiority over other artificial neural network (ANNs) and traditional methods, such as multiple linear regression (MLR), in numerical simulations (Kişi, 2007; Motahari Nezhad, 2022). These networks of MLP have gained widespread application in the field of relative humidity prediction (Bialobrzewski, 2008). It has been demonstrated in previous studies that the MLP model exhibits superior performance in the prediction of meteorological parameters.

For instance, Ben El Houari et al. (2016) found that the optimized MLP model outperformed radial basis function (RBF) and MLR models in predicting air temperature in Morocco. The MLP model's effectiveness in predicting relative humidity in Chefchaouen (El Badaoui et al., 2017), from the same region in Morocco as Tangier, supported its use in our study for Tangier. The Levenberg-Marquardt algorithm is renowned for its effectiveness in training ANN models, owing to its proven ability in forecasting and predictive modelling (Abdullah et al., 2016; Alomari et al., 2018; Awan et al., 2018; Samsuri et al., 2016). When applied to parameter modelling in a Mediterranean context analogous to our Tangier study, the Levenberg-Marquardt algorithm estimated global solar radiation in the eastern Mediterranean with a noteworthy regression coefficient of 0.99 (Çelik et al., 2016). Recent other studies have also confirmed the robustness of ANN models, especially MLP and long short-term memory (LSTM) models, in predicting relative humidity across diverse regions and climates (Abdelsattar et al., 2025; Zarin and Mayorga, 2021). However, the application of these models to the humid western Mediterranean environment of Tangier, the focus of this study, has not yet been conducted. The objective of our study was to address this research gap.

The objective of this study was to develop an efficient MLP ANN model for predicting relative humidity levels in Tangier. The model utilizes explanatory variables such as temperature, shortwave radiation, direct shortwave radiation, total precipitation, evapotranspiration, vapour pressure deficit, and wind speed. The process entails the optimization of the MLP configuration through the judicious selection of the data distribution, number of hidden layers, number of neurons, and regularization parameter, with consideration for the relationship between independent and dependent variables. The performance of the model is evaluated by means of statistical regression indicators, such as the correlation coefficient (R) and the mean square error (MSE).

This provides a comprehensive overview of the most effective way to parameterize the optimal size in an MLP model for the purpose of making accurate predictions. Tangier's western Mediterranean locale (B, 1940) underscores the novelty and significance of this inaugural mathematical meteorological modelling study. To the best of our knowledge, no study has hitherto focused on RH prediction in a western Mediterranean climate like Tangier's, thus creating a significant gap in the existing research.

 

METHODOLOGY

Study area

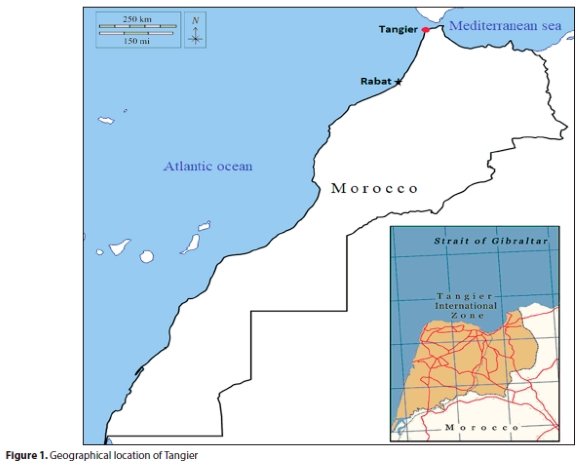
The city of Tangier (35°47' N. 5°49' W) has a coastal location, known for its very high levels of relative humidity and its industrial and economic impacts on Morocco in general and in particular its northern region. The city covers an area of11 570 km², 1.6% of the total area of the Kingdom of Morocco (Bourouhou et al., 2018).

Tangier is bordered by the Mediterranean Sea to the north, the Atlantic Ocean to the west (Fig. 1), the Taza-Al Hoceima-Taounate region to the east, and the Gharb-Chrarda-Beni Hssen region to the south (Laghzal et al., 2016). The city's climate is influenced by the air masses originating from these two bodies of water, resulting in a unique geographical location. Meteorological phenomena, such as sea breezes and temperature inversions, have been observed to exert a substantial influence on relative humidity in this region (Eick et al., 2023; Emmanuel and Johansson, 2006).

 

 

Characterizing the database

The database studied contains the values of 8 meteorological parameters recorded every hour between 1 January 1985 and 21 December 2022, i.e., 332 856 x 8 values. For the present study, we transformed these data to obtain daily values, by averaging the values of each parameter for each day. For precipitation, however, we have calculated the accumulated hourly values over the day. As a result, we produced a global database of 13 869 records, each with 8 columns representing the different meteorological parameters. The meteorological parameters, their units and designations used in this study are listed in Table 1.

 

 

Table 2 shows the statistical indicators for 8 daily variables. The standard deviations show a more pronounced dispersion for the parameters of RH, T, PT, VP and WS, indicating a greater variability in these values. On the other hand, the rest of parameters are relatively stable. Simply put, the more dispersed parameters are more volatile than the others and can experience more significant fluctuations over time.

Figure 2 shows the average annual RH during the study period. According to this graph, the maximum annual value of RH reached 82.9% in 2004, while the minimum annual value recorded was 75.1% in 1994. These annual variations, with higher values in 2004 and relatively lower values in 1994, illustrate the fluctuation in RH over time. The yearly profiles indicate that the data's variability is non-stationary. This non-stationarity makes it challenging to accurately capture and express the data's variability.

Figure 3 is a plot of the variation in monthly RH percentages over the study period, averaged for each month over 38 years. The maximum monthly value of RH reaches 83.3% (December), while the minimum monthly value is 67.7% (July); hence the monthly RH decreases from January (83.1%) until July, after which the RH starts to increase to reach the maximum value in December. The data show a general trend of monthly RH being higher in winter, early spring, and late autumn than in summer, early autumn, and late spring. These observations are consistent with the Mediterranean climate of the region, where RH is generally high due to the influence of air masses from the Mediterranean Sea.

Database preprocessing

It is imperative to normalize the database compositions, inputs, and targets in order to effectively train an artificial neural network to optimize its dispersion (Cabello-Solorzano et al., 2023), using the following formula:

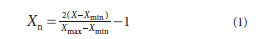
For a given variable: X = observed value; X_n = normalized value; X_max = maximum value; X_min = minimum value.

Statistical analysis

Statistical indicators

The performance of the models is determined by calculating and comparing the metrics of correlation coefficient (R) and mean squared error (MSE).

Correlation is defined as the term used to describe a relationship between phenomena or mathematical variables that tend to vary, are related to, or occur together in a way that cannot be predicted by chance (Akoglu, 2018). The equation used to calculate the Pearson correlation coefficient (Asuero et al., 2006) in this study was as follows:

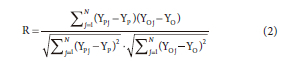
where: Y_O = average of the observed values; Y_P = average of the predicted values; Y_Pj and Y_Oj = predicted and observed values on observation j, respectively; N = number of observations.

MSE is commonly used as a performance indicator for constructing ANNs. The average squared difference between actual and estimated values is what this indicator is defined as. In this work, we aim to minimize the MSE by modelling the most efficient architecture (MSE ~ 0). The mathematical formula consists of (Ben El Houari et al., 2015):

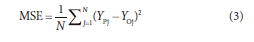
Multiple linear regression

Multiple linear regression (MLR) is a flexible system designed to examine the relation between a group of independent variables (or predictors) and a single dependent variable (or criterion) (Aiken et al., 2003).

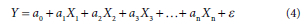
where: Y = dependent variable; X_i = independent variables (i =1, 2, ..., n); a_i = regression coefficients (i = 1, 2, ..., n); a_o = regression constant; ε = error; n = number of independent variables.

Stepwise multiple linear regression

Stepwise multiple linear regression (S-MLR) is an extremely valuable calculation technique for data analysis problems (Breaux, 1967). This approach allows for iterative selection of variables that contribute the most to the prediction of the result, with no inclusion of redundant or insignificant variables. Getting an accurate and effective prediction requires determining the optimal number of variables to include in the model. This iterative method is particularly suitable for cases where there are a large number of independent variables, simplifying the MLR model while maintaining its predictive performance.

Artificial neural networks (ANN)

ANN is an attempt to assimilate the functioning of the biological brain. The computing system of ANNs is massively parallel, composed of a large number of simple processors with many interconnections (Asadollahfardi, 2015). The high accuracy of neural networks in predicting numerical data of various physical parameters is well known (Abdallaoui and Badaoui, 2015, 2011; Ajina et al., 2023; Al-Shawwa et al., 2018; Chaal and Aboutafail, 2021; Elazhari et al., 2017; Sharma and Sahoo, 2022).

Therefore, network predictions are also a probability distribution (Hamid, 2009; Lourakis, 2005). Numerous units and processes contribute to the performance of the ANN architecture. These components include the number of hidden layers, the number of neurons per layer, the input layer, and the output layer. The relationship between units necessitates mathematical procedures involving algorithms and transfer functions. The signal comes from a node called the synaptic weight (weight W_i). Bias enhances the input sharpness of the activation function. Mathematically, we can describe a neuron k by the equation (Hyakin, 1994):

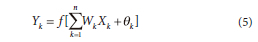
where W_k = synaptic weight; X_k = input variable (k = 1, 2, ..., n); 0_k = neuron bias; f = transfer function; Y_k = output variable.

Multilayer perceptron

The multilayer perceptron (MLP) is a derivation of the perceptron model created by Rosenblatt in the 1950s (Rosenblatt, 1958).

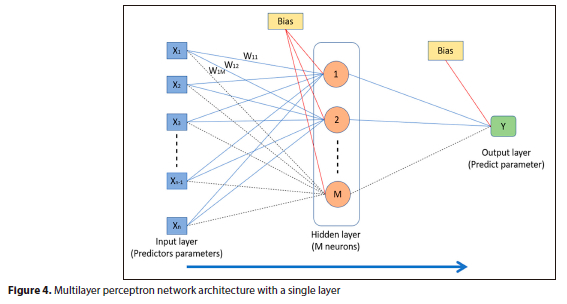
The fully connected MLP structure is of the «Feed-Forward» type with 3 layers, including the input layer, the output layer, and the hidden layers. It uses the learning algorithm of backpropagation (Asadollahfardi, 2015). The architecture in MLP networks holds significance, as a lack of connectivity can render the network incapable of solving the problem and insufficiently adjusting the parameters, while an excess of connections can lead to overfitting of training data (Lins and Ludermir, 2005). The simplicity of the non-linear relationship between the independent variables and the dependent variable can also lead to underfitting of the data. Figure 4 shows the architecture of the MLP model with a single hidden layer.

 

 

Regularization L2

Regularization is an essential technique to improve the ability to generalize machine learning models. It is frequently used to manage the complexity of advanced models. Such models demand marked regularization to prevent overfitting. In contrast, simpler models may need less.

One of the most prevalent forms of regularization is L2 regularization, which usually yields superior outcomes (Gupta et al., 2018; Phaisangittisagul, 2016). To apply this method, we include the summation of the square of all parameters (weight and bias) to the cost/loss function. By minimizing the total cost function using an optimizer, each weight W¡ undergoes modification through a XW² regularization term, where λ represents the regularization parameter. This term of L2 regularization enables the reduction of each weight to zero, thereby controlling the model's complexity and preventing overfitting and underfitting to the training data.

The mathematical expression for the L2 regularization term:

Then, in order to calculate the regularized mean squared error values, it is imperative to include the regularization term for every cost/loss function value of the MSE. This can be achieved by using the following formula:

 

RESULTS AND DISCUSSION

Multiple linear regression

It is well known that multiple linear regression is a modelling technique that attempts to improve the relationship between inputs and outputs. This part of the study attempts to build a model to predict the dependent variable, relative humidity, from the 7 predictors already mentioned, using multiple linear regression:

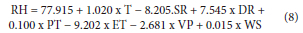
The performance obtained with this model of MLR is: MSE = 10.120; R = 0.93001.

To optimize the number of independent variables, we can use the S-MLR method, which tries to minimize the number of explanatory variables, with a model performance more or less similar to that of MLR.

The equation for the best model provided by the calculations when applying S-MLR is:

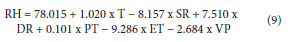
The performance obtained with this model of S-MLR is: MSE = 10.121; R = 0.93000.

This last model from S-MLR keeps 6 explanatory parameters, with the exception of the parameter of wind speed, compared to the MLR, with both methods giving a very similar performance. The current data does not show a linear relationship between wind speed (WS) and RH.

Both of the MRL models above are less accurate for predicting RH, have relatively high MSEs, and have correlation coefficients with potential for improvement in order to increase the accuracy of prediction. For this reason, we looked for a more efficient neural model than these linear regression related models.

Development of the MLP model

The goal of building a learning model is not to train the model to produce an exact representation of the training data, but to build a model that is capable of understanding the process that generates the relationship between inputs and outputs. In addition, the learning model must have good generalization to accurately predict input data. The development of a perfect ANN model is challenged by the multiplicity of choices over multiple probable configurations, depending on many parameters, mathematical processes, and data management options (O'Leary, 1993).

In this work, we studied the effects of data distribution, number of hidden layers, number of nodes on each layer, and activation functions 'Tansig' and 'Purelin', on the performance of ANN models, while using the Levenberg-Marquardt (LM) learning algorithm. In each phase, we considered the default options proposed by the program (Matlab) with the option obtained by the calculation of the previous step, thus considering the average of 10 computational tests to ensure the quality and reliability of the results. We start with the default settings: number of similar neurons in each layer and function couples, 'Tansig' in the hidden layers and 'Purelin' in the output layer, with the Levenberg-Marquardt backpropagation algorithm. Also, many applications have found a perfect performance for prediction of RH utilizing the LM algorithm with the configuration with the transfer function 'Tansig' in the hidden layer and 'Purelin' in the output layer (Elazhari et al., 2022; Ben El Houari et al., 2016).

Initially, we used 34 input parameters, but after analysing the data and to avoid overfitting, we reduced this number to 7 inputs. This simplifies the structure of the model while preserving its ability to capture important data patterns, thus promoting better generalization to new data. Thus, the computation is penalized by a regularization of type L2, in such a way that the regularization coefficient λ is adjusted to the value λ = 0.01, so that the computation time is minimal, the number of iterations is minimal (between 2 and 10), and that the performance of the models is optimal, avoiding overfitting and underfitting.

Step 1: Optimize database distribution

Distributing a given dataset is part of developing ANN models. It arbitrarily (randomly) divides the database into 3 parts: one for learning, one for validation, and one for testing. The first part is used to adjust the connection weights. The validation group is used to evaluate the performance of the model after successful training (Shahin et al., 2004). The test portion is used to check the performance of the network at different stages of learning, and training is stopped if the error in the test set increases.

We ran 5 different splits to select the best data distribution for optimal performance. The results (Table 3) show that a distribution of 80% for learning, 10% for validation, and 10% for testing gives the best results, with an MSE of0.0076 and R of0.9671. This allows the model to generalize well and is recommended to achieve optimal performance. However, it is important to consider the context and size of the data and explore different distributions to ensure model robustness and performance.

Step 2: Optimize the number of hidden layers

During this phase, we tested architectures consisting of 1 to 5 hidden layers. The results in Table 4 show that a single hidden layer was satisfactory, avoiding excessive complexity and unnecessary connections. This approach provides good performance while maintaining the simplicity and interoperability of the model.

Step 3: Optimize the number of neurons in the hidden layer

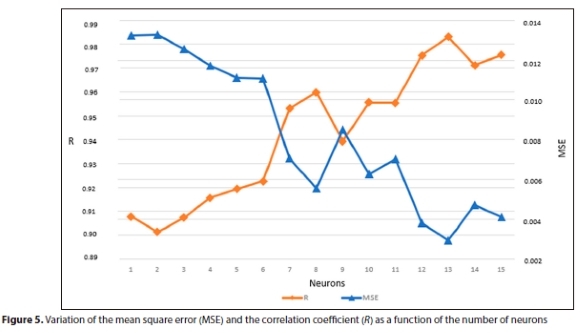
This part aims to optimize the number of neurons in the hidden layer. Figure 5 shows the variation of the number of neurons from 1 to 15 according to the average of 10 tests of the computations of the evaluators MSE and R. It shows that there is a general increase in performance as a function of increasing the number of neurons; however, the use of 13 neurons in the hidden layer achieves optimal efficiency compared to other numbers of neurons, with an accuracy of MSE = 0.00295 and R = 0.983.

 

 

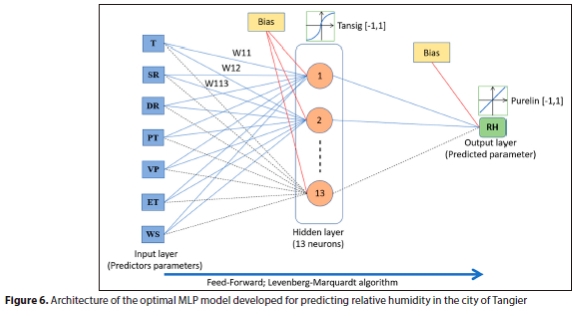
The developed architecture proposed for predicting RH levels in Tangier city is shown in Fig. 6 and constitutes:

• The input layer related to predictive variables such as T, SR, DR, PT, ET, VP, and WS

• The hidden layer, which is made up of 13 neurons, each of which is activated by the 'Tansig' function, which plays a crucial role in the learning process

• The output layer, which is dedicated to the RH dependent variable and uses the 'Purelin' activation function to generate the final predictions

 

 

The 3-layer architecture was meticulously selected to optimally depict the intricate interrelationships between the input variables and the RH output variable. The employment of the 'Tansig' function in the hidden layer facilitates the capture of nonlinear patterns, while the 'Purelin' function in the output layer guarantees an adequately linear response. The integration of these components within the model facilitates the attainment of precise and consistent outcomes in predicting the RH variable, contingent upon the presence of predictors.

The significance ofthis study lies in its contribution to meteorology, as evidenced by the development of a highly accurate predictive model for relative humidity. This model is a critical component in the field of meteorological observations and forecasting, as RH is a pivotal atmospheric variable. This work enhances the precision and reliability of humidity estimation based on multiple daily meteorological inputs by leveraging the multilayer perceptron (MLP) optimized with the Levenberg-Marquardt algorithm. This provides a robust computational tool that can support calibration processes, reduce observational uncertainty, and assist in the design of measurement systems in climates with high variability, such as Tangier. The high correlation coefficient (R = 0.983) and low mean square error (MSE = 0.00295) indicate the model's strong performance, positioning this overview as a potential reference for digital methods in atmospheric sciences.

 

CONCLUSION

The study was developed by examining the relative humidity values of the city of Tangier, as recorded over a span of13 869 days, commencing on 1 January 1985, and concluding on 21 December 2022. In order to execute this process, it is necessary to implement a multilayer perceptron architecture (MLP) in conjunction with the Levenberg-Marquardt algorithm and 2 transfer functions. The term 'Tansig' is employed for the hidden layer, while 'Purelin' is utilized for the output layer. This modelling was accompanied by a rigorous evaluation, in which model performance was compared with statistical indicators, such as correlation coefficients and mean squared error.

The findings indicated that the MLP model exhibited superior performance in comparison to multiple linear regression, thereby substantiating its capacity to establish more intricate nonlinear relationships between explanatory variables and the dependent variable, relative humidity. This flexibility in the modelling process enables the creation of more accurate and reliable predictions.

Through meticulous analysis of the optimal parameters, it was ascertained that the most efficient configuration consists of 7 inputs in the input layer, a hidden layer with 13 nodes activated by the 'Tansig' function, and the linear function 'Purelin' in the output layer for the dependent variable. The implementation of the Levenberg-Marquardt algorithm proved instrumental in mitigating the overfitting of the model, enhancing the efficiency of the computations, and fortifying the model's overall reliability. The employment of L2 regularization has been shown to play a critical role in the reduction of computation time and iterations, thereby enhancing the robustness of the model and preventing overfitting.

The MLP model developed has been shown to be a powerful tool for predicting the relative humidity in Tangier over an extended period. This study underscored the pivotal role of architectural design and the parameters selected during the modelling process, thereby facilitating the attainment of results that surpass those of multiple linear regression methods. These encouraging results suggest the potential for machine learning methods to be utilized in the domain of meteorology, particularly in the context of climate data prediction and analysis.

 

DECLARATION

The authors declare that no funds, grants, or other supports were received during the preparation of this manuscript.

 

AUTHOR CONTRIBUTIONS

The intricate nature of the interactions between the various elements of our project renders it challenging, if not impossible, to accurately quantify the individual contribution of each co-author. It is imperative to reiterate that each author played a pivotal role in the design, production, analysis, and writing of the article, and all of us participated in the validation of the final version submitted.

 

ACKNOWLEDGEMENT

We would like to express our gratitude to the Laboratory of Analytical Chemistry and Electrochemistry, Research Team Processes and Environment at Moulay Ismail University in Morocco.

 

ORCID

Abdellah Ben yahia: https://orcid.org/0000-0002-5585-1481

 

REFERENCES

ABDALLAOUI A and EL BADAOUI H (2015) Comparative study of two stochastic models using the physicochemical characteristics of river sediment to predict the concentration of toxic metals. J. Mater. Environ. Sci. 6 445-454.         [ Links ]

ABDALLAOUI A and EL BADAOUI H (2011) Prediction of toxic levels of heavy metals in sediments from the river Beht physical-chemical parameters. Phys. Chem. News 58 90-97.         [ Links ]

ABDELSATTAR M, ABDELMOETY A and EMAD-ELDEEN A (2025) Comparative analysis of machine learning techniques for temperature and humidity prediction in photovoltaic environments. Sci. Rep. 15 15650. https://doi.org/10.1038/s41598-025-98607-7        [ Links ]

ABDULLAH S, ISMAIL M, FONG SY and AHMED AN (2016) Neural network fitting using Levenberg-Marquardt training algorithm for PM10 concentration forecasting in Kuala Terengganu. J. Telecommun. Electron. Comput. Eng. 8 27-31.         [ Links ]

AIKEN L, WEST S and PITTS S (2003) Multiple Linear Regression. John Wiley & Sons. https://doi.org/10.1002/0471264385.wei0219        [ Links ]

AJINA A, G JCK, BHAT DN and SAXENA K (2023) Prediction of weather forecasting using artificial neural networks. J. Appl. Res. Technol. 21 205-211. https://doi.org/10.22201/icat.24486736e.2023.21.2.1698        [ Links ]

AKOGLU H (2018) Turkish Journal of Emergency Medicine user's guide to correlation coefficients. Turk. J. Emerg. Med. 18 91-93. https://doi.org/10.1016/j.tjem.2018.08.001        [ Links ]

ALOMARI MH, YOUNIS O and HAYAJNEH SMA (2018) A predictive model for solar photovoltaic power using the Levenberg-Marquardt and Bayesian regularization algorithms and real-time weather data. Int. J. Adv. Comput. Sci. Appl. 9. https://doi.org/10.14569/IJACSA.2018.090148        [ Links ]

AL-SHAWWA M, AL-ABSI AAR, HASSANEIN SA, BARAKA KA and ABU-NASER SS (2018) Predicting temperature and humidity in the surrounding environment using artificial neural network. Int. J. Acad. Pedagog. Res. 2 1-6.         [ Links ]

AMIN B, ATIF MJ, WANG X, MENG H, GHANI MI, ALI M, DING Y, LI X and CHENG Z (2021) Effect of low temperature and high humidity stress on physiology of cucumber at different leaf stages. Plant Biol. 23 785-796. https://doi.org/10.1111/plb.13276        [ Links ]

ARUNDEL AV, STERLING EM, BIGGIN JH and STERLING TD (1986) Indirect health effects of relative humidity in indoor environments. Environ. Health Perspect. 65 351-361. https://doi.org/10.1289/ehp.8665351        [ Links ]

ASADOLLAHFARDI G (2015) Artificial neural network. In: Water Quality Management. SpringerBriefs in Water Science and Technology. Springer, Berlin. 77-91. https://doi.org/10.1007/978-3-662-44725-3_5        [ Links ]

ASUERO AG, SAYAGO A and GONZÁLEZ AG (2006) The correlation coefficient: an overview. Crit. Rev. Anal. Chem. 36 41-59. https://doi.org/10.1080/10408340500526766        [ Links ]

AWAN SM, KHAN ZA and ASLAM M (2018) Solar generation forecasting by recurrent neural networks optimized by Levenberg-Marquardt algorithm. In: Proceedings of IECON 2018 - 44^th Annual Conference of the IEEE Industrial Electronics Society. 276-281. https://doi.org/10.1109/IECON.2018.8591799        [ Links ]

B M (1940) The Western Mediterranean. Bull. Int. News 17 701-709.         [ Links ]

BALDWIN JW, BENMARHNIA T, EBI KL, JAY O, LUTSKO NJ and VANOS JK (2023) Humidity's role in heat-related health outcomes: a heated debate. Environ. Health Perspect. 131 055001. https://doi.org/10.1289/EHP11807        [ Links ]

BARRECA AI (2012) Climate change, humidity, and mortality in the United States. J. Environ. Econ. Manage. 63 19-34. http://doi.org/10.1016/j.jeem.2011.07.004        [ Links ]

BEN EL HOUARI M, ZEGAOUI O and ABDELAZIZ A (2015) Development of an artificial neural network model to predict the monthly air temperature in the region of Meknes (Morocco). Int. Res. J. Comput. Sci. 2 18-27.         [ Links ]

BEN EL HOUARI M, ABDALLAOUI A and ZEGAOUI O (2016) Forecasting of the ambient air temperature using the artificial neural networks. Int. J. Multi-Discip. Sci. 3 14-19.         [ Links ]

BIALOBRZEWSKI I (2008) Neural modeling of relative air humidity. Comput. Electron. Agric. 60 1-7. https://doi.org/10.1016/jxompag.2007.02.009        [ Links ]

BOUROUHOU I, SALMOUN F and GEDIK Y (2018) Characteristics of Mediterranean Sea water in vicinity of Tangier region, north of Morocco. Environment, Green Technology and Engineering International Conference (EGTEIC 2018), 18-20 June 2018, Cáceres, Spain Proceedings 2 (20) 1291. https://doi.org/10.3390/proceedings2201291        [ Links ]

BREAUX HJ (1967) On stepwise multiple linear regression. Army Ballistic Research Lab Aberdeen Proving Ground MD. https://doi.org/10.21236/AD0658674        [ Links ]

CABELLO-SOLORZANO K, ORTIGOSA DE ARAUJO I, PEÑA M, CORREIA L and TALLÓN-BALLESTEROS AJ (2023) The impact of data normalization on the accuracy of machine learning algorithms: a comparative analysis. In: García Bringas P, Pérez García H, Martínez de Pisón FJ, Martínez Álvarez F, Troncoso Lora A, Herrero Á, Calvo Rolle JL, Quintián H and Corchado E (eds) 18^th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2023). Springer Nature Switzerland, Cham. 344-353. https://doi.org/10.1007/978-3-031-42536-3_33        [ Links ]

ÇELİK Ö, TEKE A and YILDIRIM HB (2016) The optimized artificial neural network model with Levenberg-Marquardt algorithm for global solar radiation estimation in eastern Mediterranean region of Turkey. J. Clean. Prod. 116 1-12. https://doi.org/10.1016/j.jclepro.2015.12.082        [ Links ]

CHAAL RE and ABOUTAFAIL MO (2021) Development of stochastic mathematical models for the prediction of heavy metal content in surface waters using artificial neural network and multiple linear regression. In: 6^th edition of the International Conference on GIS and Applied Computing for Water Resources (WMAD21). E3S Web of Conferences 314 02001. (2021)        [ Links ]

CHAMAS A, MOON H, ZHENG J, QIU Y, TABASSUM T, JANG JH, ABU-OMAR M, SCOTT SL and SUH S (2020) Degradation rates of plastics in the environment. ACS Sustain. Chem. Eng. 8 3494-3511. https://doi.org/10.1021/acssuschemeng.9b06635        [ Links ]

COPINET A, BERTRAND C, GOVINDIN S, COMA V and COUTURIER Y (2004) Effects of ultraviolet light (315 nm), temperature and relative humidity on the degradation of polylactic acid plastic films. Chemosphere 55 763-773. https://doi.org/10.1016/j.chemosphere.2003.11.038        [ Links ]

DEISENHAMMER EA (2003) Weather and suicide: the present state of knowledge on the association of meteorological factors with suicidal behaviour. Acta Psychiatr. Scand. 108 402-409. https://doi.org/10.1046/j.0001-690X.2003.00209.x        [ Links ]

DENG R, MA P, LI B, WU Y and YANG X (2022) Development of allergic asthma and changes of intestinal microbiota in mice under high humidity and/or carbon black nanoparticles. Ecotoxicol. Environ. Saf. 241 113786. https://doi.org/10.1016/j.ecoenv.2022.113786        [ Links ]

EICK CF, MAHIN M, CHEN G and ZHANG H (2023) On threshold correlation with application to studying the relationship of temperature and relative humidity. In: Proc. 6^th ACM SIGSPATIAL Int Workshop AI for Geographic Knowledge Discovery (GeoAI '23), 7-10 November 2023. ACM, New York. 53-62. https://doi.org/10.1145/3615886.3627741        [ Links ]

ELAZAHRI K, EL BADAOUI H, ABDALLAOUI A and ZINEDDINE H (2017) Optimization of neural architectures for prediction of heavy metal concentrations in Red Sea sediments. Int. J. Sci. Eng. Res. 8 906-912.         [ Links ]

EL AZHARI K, ABDALLAOUI B, DEHBI A, ABDALLOUI A and ZINEDDINE H (2022) Development of a neural statistical model for the prediction of relative humidity levels in the region of Rabat-Kenitra, North West Morocco. J. Water Land Dev. VII-IX 13-20. https://doi.org/10.24425/jwld.2022.141550        [ Links ]

EL BADAOUI H, ABDALLAOUI A and CHABAA S (2017) Optimization numerical the neural architectures by performance indicator with LM learning algorithms. J. Mater. Environ. Sci. 8 169-179.         [ Links ]

EMMANUEL R and JOHANSSON E (2006) Influence of urban morphology and sea breeze on hot humid microclimate: the case of Colombo, Sri Lanka. Clim Res. 30 189-200. https://doi.org/10.3354/cr030189        [ Links ]

GAUGHAN JB, MADER TL, HOLT SM and LISLE A (2008) A new heat load index for feedlot cattle. J. Anim. Sci. 86 226-234. https://doi.org/10.2527/jas.2007-0305        [ Links ]

GOAD N and GAWKRODGER DJ (2016) Ambient humidity and the skin: the impact of air humidity in healthy and diseased states. J. Eur. Acad. Dermatol. Venereol. 30 1285-1294. https://doi.org/10.1111/jdv.13707        [ Links ]

GUNAWARDHANA LN, AL-RAWAS GA and KAZAMA S (2017) An alternative method for predicting relative humidity for climate change studies. Meteorol. Appl. 24 551-559. https://doi.org/10.1002/met.1641        [ Links ]

GUPTA S, GUPTA R, OJHA M and SINGH KP (2018) A comparative analysis of various regularization techniques to solve overfitting problem in artificial neural network. In: Panda B, Sharma S and Roy NR (eds) Data Science and Analytics, Communications in Computer and Information Science. Springer Singapore, Singapore. 363-371. https://doi.org/10.1007/978-981-10-8527-7_30        [ Links ]

HAMID S (2009) Comparaison de méthodes de classification réseau RBF, MLP et RVFLNN. Int. Res. J. Comput. Sci. 1 119-129.         [ Links ]

HE X, ZHANG H, QIU L, MAO Z and SHI C (2021) Hygrothermal performance of temperature-humidity controlling materials with different compositions. Energ. Build. 236 110792. https://doi.org/10.1016/j.enbuild.2021.110792        [ Links ]

HO KLG, POMETTO AL and HINZ PN (1999) Effects of temperature and relative humidity on polylactic acid plastic degradation. J. Environ. Polym. Degrad. 7 83-92. https://doi.org/10.1023/A:1021808317416        [ Links ]

HYAKIN S (1994) Neural Networks: A Comprehensive Foundation (2^nd edn.) Prentice Hall, Upper Saddle River, NJ.         [ Links ]

KHEIRI F, HABERL JS and BALTAZAR JC (2023) Impact of outdoor humidity conditions on building energy performance and environmental footprint in the degree days-based climate classification. Energy 283 128447. https://doi.org/10.1016Zj.energy.2023.128447        [ Links ]

KIM Y, GARCIA M, MORILLAS L, WEBER U, BLACK TA and JOHNSON MS (2021) Relative humidity gradients as a key constraint on terrestrial water and energy fluxes. Hydrol. Earth Syst. Sci. 25 5175-5191. https://doi.org/10.5194/hess-25-5175-2021        [ Links ]

KISI Ö (2007) Streamflow forecasting using different artificial neural network algorithms. J. Hydrol. Eng. 12 (5) 532-539. https://doi.org/10.1061/(ASCE)1084-0699(2007)12:5(532)        [ Links ]

LAGHZAL A, KHADDOR M, CHERROUD S and FIHRI M (2016) Evaluation of physico-chemical and bacteriological quality of water springs by using a principal component analysis (PCA): A case study of Tingitane Peninsula (Morocco). J. Mater. Environ. Sci. 7 456-462.         [ Links ]

LAOUINA A (2017) Coastal vulnerability, risks of degradation and of climate change impact on the coastal zone of Morocco, GIS approach of the Tangier Peninsula. Rev. Marocaine Géomorph. 1 62-77.         [ Links ]

LINS APS and LUDERMIR T (2005) Hybrid optimization algorithm for the definition of MLP neural network architectures and weights. In: Fifth International Conference on Hybrid Intelligent Systems (HIS'05), 6-9 November 2005, Rio de Janeiro. https://doi.org/10.1109/ICHIS.2005.61        [ Links ]

LIU X, GAO H, SUN L and YAO J (2024) Generic air-gen effect in nanoporous materials for sustainable energy harvesting from air humidity. Adv. Mater. 36 2300748. https://doi.org/10.1002/adma.202300748        [ Links ]

LOURAKIS MIA (2005) A brief description of the Levenberg-Marquardt algorithm implemented by levmar. Matrix 4 2.         [ Links ]

MBITHI JN, SPRINGTHORPE VS and SATTAR SA (1991) Effect of relative humidity and air temperature on survival of hepatitis A virus on environmental surfaces. Appl. Environ. Microbiol. 57 1394-1399. https://doi.org/10.1128/aem.57.5.1394-1399.1991        [ Links ]

MOTAHARI NEZHAD M (2022) Comparison of MLP and RBF neural networks for bearing remaining useful life prediction based on acoustic emission. Proc. Inst. Mech. Eng. J. Eng. Tribol. 236 (Part J):237. https://doi.org/10.1177/13506501221106556        [ Links ]

O'LEARY DE (1993) The impact of data accuracy on system learning. J. Manage. Inf. Syst. 9 83-98. https://doi.org/10.1080/07421222.1993.11517979        [ Links ]

ONOZUKA D and HASHIZUME M (2011) The influence of temperature and humidity on the incidence of hand, foot, and mouth disease in Japan. Sci. Total Environ. 410-411 119-125. https://doi.org/10.1016/j.scitotenv.2011.09.055        [ Links ]

PHAISANGITTISAGUL E (2016) An analysis of the regularization between L2 and dropout in single hidden layer neural network. In: 7^th International Conference on Intelligent Systems, Modelling and Simulation (ISMS). 174-179. https://doi.org/10.1109/ISMS.2016.14        [ Links ]

RICE DW, CAPPELL RJ, KINSOLVING W and LASKOWSKI JJ (1980) Indoor corrosion of metals. J. Electrochem. Soc. 127 891. https://doi.org/10.1149/1.2129780        [ Links ]

ROSENBLATT F (1958) The perceptron: a theory of statistical separability in cognitive systems (Project Para). Report No. 85-460-1. Cornell Aeronautical Laboratory, Buffalo, NY.         [ Links ]

SAMSURI A, MARZUKI I, SI YUEN F and ALI NAJAH A (2016) Neural network fitting using Levenberg-Marquardt training algorithm for PM concentration forecasting in Kuala Terengganu. J Telecommun. Electron. Comput. Eng. 8 (12) 27-31.         [ Links ]

SHAHIN MA, MAIER HR and JAKSA MB (2004) Data division for developing neural networks applied to geotechnical engineering. J. Comput. Civ. Eng. 18 (2) 105-114. https://doi.org/10.1061/(ASCE)0887-3801(2004)18:2(105)        [ Links ]

SHARMA P and SAHOO BB (2022) Precise prediction of performance and emission of a waste derived biogas-biodiesel powered dual-fuel engine using modern ensemble boosted regression tree: a critique to artificial neural network. Fuel 321 124-131. https://doi.org/10.1016/j.fuel.2022.124131        [ Links ]

SINGH N, CHATURVEDI S and AKHTER S (2019) Weather forecasting using machine learning algorithm. In: 2019 International Conference on Signal Processing and Communication (ICSC), IEEE, Noida, India. 171-174. https://doi.org/10.1109/ICSC45622.2019.8938211        [ Links ]

SUNWOO Y, CHOU C, TAKESHITA J, MURAKAMI M and TOCHIHARA Y (2006) Physiological and subjective responses to low relative humidity in young and elderly men. J. Physiol. Anthropol. 25 229-238. https://doi.org/10.2114/jpa2.25.229        [ Links ]

SVENSSON S and TORATTI T (2002) Mechanical response of wood perpendicular to grain when subjected to changes of humidity. Wood Sci. Technol. 36 145-156. https://doi.org/10.1007/s00226-001-0130-4        [ Links ]

YANG H, WU J, CHENG J, WANG X, WEN L, LI K and SU H (2017) Is high relative humidity associated with childhood hand, foot, and mouth disease in rural and urban areas? Public Health 142 201-207. https://doi.org/10.1016/j.puhe.2015.03.018        [ Links ]

YANG W and HOLMÉN BA (2007) Effects of relative humidity on chloroacetanilide and dinitroaniline herbicide desorption from agricultural PM2.5 on quartz fiber filters. Environ. Sci. Technol. 41 3843-3849. https://doi.org/10.1021/es062692i        [ Links ]

ZARINKAMAR RT and MAYORGA RV (2021) Outdoor relative humidity prediction via machine learning techniques. J. Environ. Inform. Lett. 6 (2) https://doi.org/10.3808/jeil.202100074        [ Links ]

 

 

Correspondence:
Abdellah Ben yahia
Email: abd.benyahia@edu.umi.ac.ma
abdo.fsdm123@gmail.com

Received: 28 July 2024
Accepted: 7 July 2025