Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Education (University of KwaZulu-Natal)
On-line version ISSN 2520-9868
Print version ISSN 0259-479X
Journal of Education n.70 Durban 2017
RESEARCH ARTICLES
A sociological analysis of the pictures used in the South African foundation phase numeracy workbooks and their mathematical implications
Peter Pausigere
Rhodes University. peterpausigere@yahoo.com
ABSTRACT
About half of South Africa's Department of Basic Education foundation phase numeracy workbooks' content consist of pictures (Pausigere, 2016), yet the implications of these pictures to the different lower grades is not clear. To analyse the types of pictures, and the inferences to be drawn upon learners' mathematical understanding this article is theoretically informed by Dowling's (1996; 1998) sociology of mathematics education, specifically drawing from his textual description concepts. A sociological qualitative content analysis of the numeracy workbook pictures led to the development of a model capable of classifying key mathematical pictures used in mathematical workbooks and applicable to conventional maths textbooks. The analytical framework's pictorial categories show abstract and concrete-abstract mathematical pictures as being effective in translating generalising, context-independent mathematical principles. On the other hand concrete and abstract-concrete mathematical pictures through situational activities exhibit context-dependent numerical strategies. Given the analytical framework the study discusses the mathematical implications of its findings across the foundation phase.
Introduction
This paper analyses the types of pictures used in the South African foundation phase numeracy workbooks. The interest in analysing visual pictures comes from my earlier study (Pausigere, 2016), which found that on average 51% of the foundation phase numeracy learner workbooks consists of pictures. Visual illustrations such as pictures, photographs and drawings influences and shapes the way learners think about school mathematics. Thus pictures have implications on how learners understand mathematical concepts and skills (Thompson, 2008; Harries & Sutherland, 1999). Most studies have analysed how pictures are used in mathematical textbooks and there has been limited research on how pictorial visual representation are deployed in workbooks. This is because numeracy/mathematics workbooks were recently introduced both locally and in most countries' education systems. Since workbooks are a contemporary innovation, this paper textually analyses the kinds of visual pictorial representations used in these customised learner resources. It draws theoretically from Dowling's (1996; 1998) textual description concepts of esoteric-domain and public-domain messages; abstract and concrete modalities of practice; context-dependent and context-independent order of meanings and generalising and localising textual strategies.
The numeracy workbooks are intended to be supplementary to the textbooks purchased annually by schools (Department of Basic Education (DBE), 2012). There are two numeracy workbooks per grade consisting of 128 worksheet activities across the four terms. The South African government believes that workbooks have some advantages when used in addition to conventional textbooks. Firstly, it has been reported that numeracy workbooks provide learners with relevant worksheet activities to independently practice numeracy skills at home (DBE, 2012). Secondly, developers of the workbooks assume that these materials increase teachers instructional time as educators do not have to write maths exercises on the chalkboard (Fleisch, Taylor, N., Herholdt, R. & Sapire, 2011). Thirdly, because of the economic benefits of mass publication and the use of cheap material, the workbooks' production cost - to the national government - is less than R10.00 per book. Didactically, the workbooks are also suited for mixed-group, multi-grade and multilingual class teaching (DBE, 2012).
Given these numerous benefits of workbooks and the local primary maths challenges, the South African Department of Basic Education (DBE) introduced the Rainbow numeracy workbooks in 2013 for all primary school learners. The universal provision of numeracy workbooks and their enforcement in public schools is one of the department of education's measures aimed at both improving the performances of South African learners in the first six grades and offers learners the opportunity to acquire key mathematical concepts and skills (DBE, 2013; DBE, 2012). However, it must be noted that this study only analysed the English version of the local numeracy workbooks, though its findings are applicable to the other ten languages versions of the workbooks as their form, contents and structure is similar.
Given the national importance of the numeracy workbooks, this study qualitatively analyses the types of mathematical pictures used in the learner worksheet activities using Dowling's (1996; 1998) sociology of mathematics education theory. Specifically drawing from his textual description elements, my content analysis of the foundation phase numeracy workbooks will consider;
- the type of mathematical pictures which learners engage with in the South African foundation phase numeracy workbooks;
- the implications of the type of pictures on the learners' understanding of mathematical concepts and skills on different foundation phase grades.
My main focus is on the textual analysis of the local primary maths workbooks in relation to the nature of pictures, photographs and drawings used to convey and represent numerical concepts and skills. My unit of analysis consist of both the pictures and the subsequent mathematical activities that learners engage with in the workbooks.
In the section below I initially review literature relating to the types and the characteristics of visuals used to represent mathematical concepts in texts. The next sections present the sociological theoretical scheme, followed by the methodological approach undertaken to analyse the workbooks. The fourth section analyses and presents the key findings of this study, illuminated by the discussed sociological concepts and literature insights. The study identifies four key mathematical pictorial categories of abstract; concrete; concrete-abstract and abstract-concrete and illustrates the nature and characteristics of the mathematical pictorial classifications. The arising pictorial model and each mathematical pictorial category's influence on learners' mathematical understanding and the impact and limitations of the findings are discussed.
Literature review
Studies in primary maths education have started to investigate how different types of textual-pictorial visuals interfere or contribute to children's mathematical learning. There are concurrences that external pictorial representations in textbooks are crucial to developing mathematical understanding (Thompson, 2008; Harries and Sutherland, 1999; Botsmanova, 1972). This is similar to the DBE's (2012, p.39) claims that colourful pictures in the workbook project "motivate learners to love mathematics. . .and to appreciate the beauty and elegance of mathematics". Such proclamations must be carefully considered, for some forms of picture have been reported as distracting learners' mathematical attention (Harries & Sunderland, 1999; Botsmanova, 1972; Jellis, 2008; Dowling, 1998). Given the contradictory claims on the advantages and disadvantages of icon visuals in helping understanding mathematical tasks it is paramount therefore for this study to investigate the nature of pictorial representations and their implications in the learning of primary mathematical concepts to different foundation phase grades. Whilst there have been various classifications of pictures I present the main categories commonly found in educational literature. In primary maths psychology literature it is widely acknowledged that objective-illustrative (Botsmanova, 1972); decorative or cosmetic (Jellis, 2008) pictorial illustrations bear little or no relationship to the mathematical structure of the problem, with numbers being proclaimed to be a secondary feature of the mathematical task (Walkerdine, 1988). On the other hand objective-analytical (Botsmanova, 1972); essential, related and relevant illustrations (Jellis, 2008; Mayer, Sims & Tajika, 1995) help in solving mathematical problems, with ". . .numbers being an explicit focus of the task" (Walkerdine, 1988, p.81). This classification bears some features of the pictorial theoretical distinctions in this study and elaborates on the empirical definition of concrete- and abstract- mathematical pictures elucidated herein.
Furthermore, the limitation of this pictorial categorisation lies in the fact that such studies focuses on one aspect of the elementary mathematics, such as problem-solving (Botsmanova, 1972; Mayer et al., 1995), multiplication (Harries and Sutherland, 1999) or non-routine problems (Jellis, 2008). Thus they have never been a study classifying pictorial illustrations across the primary maths curriculum. Secondly most of the empirical studies have been in- or are informed by- the psychology of education (Botsmanova, 1972; Mayer et al., 1995; Harries & Sutherland, 1999) and do not theoretically draw from the sociology of education. Dowling (1998) study which drew from educational sociology focused on the limitation of using pictorial illustration in secondary school mathematics textbooks. Closely related to the impending theoretical analysis have been the use of the words concrete and abstract either to imply speech forms (Bernstein, 1971), order of meanings (Bernstein, 2000) or numeracy learners working strategies (Ensor, Hoadley, Jacklin, Kuhne et al., 2009). Besides using the words concrete and abstract to imply learners' mathematical strategies Ensor et al. (2009) referred to the use of concrete pictures in primary classes as entailing the manipulation of visual icons for mathematical strategies with abstract modes of representation being used to decipher and produce abstract mathematical statements. As with other previously mentioned studies, the research of Ensor et al., (2009) focused only on the teaching of numbers in the foundation phase. Furthermore, these sociological studies did not specifically explore the potential of textual pictures in facilitating mathematical concepts on different grades of learners in the foundation phase. Additionally, empirical research in primary maths education has focused mainly on textbook analysis and there haven't been any studies specifically on the sociological role of pictures in numeracy workbooks. This article is motivated by these limitations and gaps in literature in responding to its research questions.
Theoretical framing
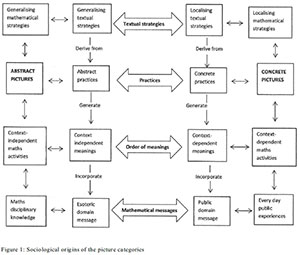
This study draws on Dowling's (1996; 1998) sociology of mathematics education theory which was developed through an analysis of British secondary school mathematics textbooks. It is specifically informed by Dowling's (1998) textual description scheme through his notion of domain messages, modality of practices aspects, order of meanings and textual strategies constructs. The opposition in the generalising and localising textual strategies are illustrated by Bernstein's (2000) context-independent and context-dependent meanings. On the other hand, abstract and concrete practices are respectively indexed by the contradicting esoteric-domain and public-domain messages. These textual strategies are key concepts used in representing forms of knowledge and relaying meanings within textual resources. I also relate esoteric-domain and public-domain messages; abstract and concrete modalities of practice; context-dependent and context-independent order of meanings as they are noted as being amongst a "repertoire of resources implicated in localising and generalising" mathematical content or tasks (Dowling, 1998, p.151; 1996). The textual descriptive principles are seamlessly intertwined and you can hardly explain any one of these concepts independent of the others. Below I explain these interrelated textual sociological theoretical concepts which will be used to analyse the nature of mathematical pictures in the local numeracy workbooks.
Generalising and localising textual strategies
Dowling's opposing scheme of generalising and localising aspects which he borrows from the work of Bernstein (1971), is relevant for the impending analysis, especially in relation to the nature of mathematical knowledge and meanings within numeracy workbook pictures. Dowling (1996, p.402) acknowledged that generalising- and localising-textual strategies "have a particular importance in the language of description" involved in the analysis of school mathematics texts. Sociologically it is the textual strategies which dually and simultaneously reproduce the types of meanings and features of school subject activities (Dowling, 1998; Hoadley, 2007). Thus generalising strategies generate context-independent texts characterising the esoteric-domain which relates to the principles and practices of school mathematics knowledge (Dowling, 1996; Hoadley, 2007). Localising strategies depict context-dependent texts which engenders public-domain knowledge relating broadly to everyday common sense knowledge (Dowling, 1996; Hoadley, 2007).
Abstract and concrete practices
Dowling (1996) also essentially noted that generalising and localising strategies have meanings associated by the contradiction between abstract and concrete practices. Dowling (1996, p.402) explicitly stated that textual strategies ". . .derive from a modality of practice which can be indexed by the opposition abstract/concrete". Sociologically and within concrete practices ". . .learning is achieved and regulated by observation" or "situational thinking" (Dowling, 1998, pp.29 & 93). Reinterpreting the term 'concrete' from the work of Piaget, Dowling explained that concrete/formal operations have meanings associated with practical or physical experiences. Similarly, Bernstein (1971, p.34) explains that a higher proportion of concrete rather than abstract symbols ". . .have little concern with processes and generalizations except of a causal order".
On the other hand, Dowling (1998, p.94) defined abstract thinking as entailing practices in which learning occurs "independent of any immediate context". In comparison to concrete discourse, Bernstein (1971) elaborates that abstract practices are analytical and emphasises on the elaboration of processes. Broadly relating the opposition in the modality of practices to other textual strategies shows that concrete practices are associated with context-dependent localisations whilst abstract thinking indicates context-independent generalisations. The latter exhibit high mathematical discursive saturation whilst the former indicates low mathematical discursive saturation (Dowling, 1998). Recontextualising Dowling's (1998) work mathematics discursive saturation refers to the extent to which the practices and principles of the mathematical academic discipline are explicitly available. The distinction between abstract and concrete; and the differences between concrete-localising context-dependent thinking and abstract-generalising context-independent practices is crucial for the impending analysis as it helps to illuminate the two main categories of pictures; namely abstract and concrete pictures - used in the local primary maths workbooks.
Context-dependent and context-independent strategies
The distinction in the textual distributing strategies is a central feature of Dowling's (1998; 1996) thesis which implies the types of meanings and forms of mathematical knowledge relayed in textbooks. Related to workbook pictorial representations such strategies indicate the extent or degree of mathematical engagements - implied in worksheets. Bernstein (1971, p.10) defined context-independent meanings as 'universalistic' as they do not rely on critical features of the context, whilst context-dependent meanings are considered 'particularistic' as they are "available only to particular types of speakers; those who share an implicit understanding of the context". In his later writing Bernstein (2000) highlighted that context-bound meanings lack the power of relations outside a context as they are wholly consumed and embedded by that context. Throughout his work Dowling emphasised that context-dependent mathematical texts mythologises mathematics as being implicated within other activities. Thus context-dependent mathematical problems include accomplishment in which numbers are an incidental feature of the task (Dowling, 1998; Walkerdine, 1988). On the other hand in context-independent mathematical problems, numbers are the main focus of the task (Walkerdine, 1988). Both Bernstein and Dowling concur that context-dependent meanings are highly localised whilst context-independent texts are more generalised.
Esoteric-domain and public-domain messages
The most crucial elements in Dowling's sociology of school mathematics textbooks is the dual dimension of esoteric and public domain knowledge. Esoteric-domain knowledge refers to the specialised disciplinary knowledge structures with public-domain knowledge relating to non-specialised everyday world experiences (Dowling, 1998; Bernstein, 2000). In relation to this study its esoteric-domain knowledge are the principles and practices of primary school mathematics knowledge (Hoadley, 2007), which in South Africa primary maths education consists of recontextualised numeracy content areas of algebra, arithmetic (number theory), geometry, measurement and statistics. Public domain knowledge consists of everyday experiences such as shopping, baking, dieting, drawing, play or street vending practices (Dowling, 1998), which can be used in elementary mathematical textbooks to help give expression to mathematical content (Pausigere, 2016). However, according to Dowling (1998), in secondary school mathematics translating non-mathematical elements to illustrate mathematical content has limitations.
Domain messages distinguish between high and low discursive saturation. Esoteric domain mathematics practices generate context-independent texts which exhibit high discursive saturation and generalising textual strategies (Dowling, 1996; 1998). On the other hand public domain experiences reproduce context-dependent meanings characterising low discursive saturation and localising textual strategies. Developing these theoretical elements for this foundation phase primary maths study, esoteric-domain picture features entail those pictorial representations which autonomies mathematical content, whilst public-domain pictures employ everyday experiences to exemplify mathematical concepts.
I thus relate the opposing textual expressions of generalising abstract context-independent esoteric-domain knowledge and localising concrete context-dependent public-domain knowledge to the features and meanings implied in the categories of numeracy workbook pictures. The explained sociological textual strategies both deductively and inductively informed the interpretation and classification of pictures used in the South African foundation phase numeracy workbooks. Figure 1 below reveals how this study connects Dowling's textual descriptive elements to my analysis and the origins of the names of the picture categories (and their features) used in the numeracy workbooks.
Figure 1 below reveals Dowling's textual descriptive elements which are used in my analysis to develop the names of the picture categories (and their features) used in the numeracy workbooks.
Research methodology - sociological qualitative textual analysis
The research methodology used in this study could be termed sociological qualitative textual analysis and derives from Dowling's (1996; 1998) broader project of sociologically analysing school mathematics textbooks. This methodological approach has its origins both in content/textual analysis and the modern sociologists of education (especially Bernstein). For this reason, the study analysed the content of South African foundation phase Rainbow numeracy workbooks, using Dowling's four main textual description elements. The empirical texts analysed, overall consisted of six foundation phase numeracy workbooks, each comprising 64 worksheets, translating to a total of 384 worksheets that primary maths learners use across the junior primary grades 1 to 3.
The textual analysis focused mainly on the types of pictures used in representing and translating mathematical knowledge and skills in the numeracy workbooks and how they may affect students' mathematical thinking. The workbooks' appendix cut-outs were excluded from the analysis as they did not include any pictorial representations; instead they had geometrical shapes which learners were instructed to cut out. The visual icon header and the ruler-footer on each page of the workbook were also excluded as these were repeated several times in the worksheets. The cover pages were also exempted from the analyses as they did not contain mathematical activities that the learners were supposed to engage with. Below I specify the mathematical pictorial text for analysis.
The unit of analysis
Dowling's (1998) notion of visual icon modes of signification and his idea of bounding the text (Dowling, 2009) helps in defining the numeracy workbook pictures' unit of analysis. Bounding the text entails delineating and specifying the text for analysis. Dowling (1998) defined icon signification as consisting of photographs, drawings and cartoons used in textbooks to represent mathematical knowledge and skills. Thus this study empirically analysed photographs, drawings and cartoons used in the South African foundation phase numeracy workbook pictures. In establishing the extent of the dataset I considered the mathematical picture including its immediate subsequent details such as verbal descriptions, questions, learners' activities, numerical figures, or a heading concerning the given portrait. Figure 2 and the workbook pictures below exemplify how the mathematical picture dataset was established.
Analysis of the numeracy workbook pictures
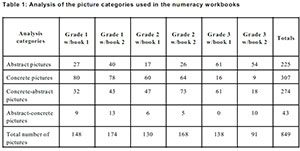
Based on the above mentioned criterion a total of 849 units of analysis were identified across the numeracy workbook foundation phase mathematical pictures. The study did employ both a deductive and an inductive analysis of the workbooks, which yielded four categories of pictures namely: - abstract; concrete; abstract-concrete and concrete-abstract. These picture categories are shown in Table 1 below. An initial theoretically-informed deductive qualitative analysis of the numeracy workbooks carried out using Dowling's (1998) practices categories revealed abstract and concrete pictures as the two main mathematical pictorial classifications. Noticing some inconsistencies in the initial categorisations led to more inferential scrutiny of the pictures. Thus a further reflective and close inductive empirical analysis of the numeracy workbooks gave rise to the emerging sub-categories of concrete-abstract and abstract-concrete pictures. The names of the picture categories show that Dowling's abstract and concrete distinction provided the study with conceptual, descriptive and analytical tools to interrogate and examine the illustrations used to represent mathematical concepts and skills used in the numeracy workbooks.
Rooted in both sociological textual descriptions and textual empirical analysis I explain the characteristics and features of each mathematical pictorial category.
Abstract pictures
The most notable feature of abstract mathematical pictures is their emphasis on the elaboration of logical and abstract mathematical processes. Because of their power to represent school mathematics algorithms, abstract pictures are naturally context-independent illustrations which point to specialised mathematical knowledge. As suggested earlier by the work of Walkerdine (1988) in context-independent mathematical pictures and in the accompanying activities numerical figures and mathematical algorithms are the obvious focus of the tasks. Their representation of school mathematical relations embeds universal generalisable meanings which establish mathematics as a systemic knowledge (Dowling, 1998). Furthermore, and most importantly, context-independent pictures do not suggest or illustrate to learners how to carry out mathematical computations for a given mathematical task. The nature of abstract picture is similar to what Botsmanova (1972, p.106) calls object-illustrative pictures as "they do not reflect the mathematical structure of the problem". Thus abstract mathematical icons activities show what Dowling (1998, p.7) called "the power of mathematics as a currency".
Abstract pictures consist of about 25% of the pictures in the foundation phase mathematics learner resources. What is commendable and encouraging is the increased use of these types of mathematical pictures in the Grade 3 workbooks as learners make a transition into the intermediate phase where mathematical abstraction is critical.
The mathematical task in Figure 3 above requires learners to solve an arithmetic problem that involves subtraction. The learner has to subtract or minus 67 tickets from 92 tickets to show that Musa had sold 25 tickets. The school concert picture does not in any way help the learner to carry out the mathematical computation of; 92 - 67 = 25. The school concert picture is literally context-independent of the mathematical task as it does not illustrate to learners the mathematical operation of subtracting 67 tickets from a collection of 92 tickets. Secondly the accompanying numerical activities' focus is the basic arithmetical operation of subtraction and not about depicting people paying for and entering into a concert. The underlying mathematical skill being inculcated through engaging in this problem solving exercise is developing the learners' knowledge about mathematical subtraction generalisations. The mathematical pictorial task in Figure 3 is an example of an abstract mathematical picture which shows the power of mathematics as a currency, with the concert entrance pictorial illustration containing no information pertinent to the subtraction mathematical problem.
Concrete pictures
As learners engage with mathematical concrete pictures their mathematical learning is regulated through observations or physical experiences. Borrowing from Dowling's (1998) sociology I explain that through concrete pictorial representations the mathematical learning process is highly localised and context-dependent, thus concrete pictorial visuals emphasise and culminate in concrete situations. Concrete context-dependent mathematical pictures also include settings in which numbers are secondary aspects (Walkerdine, 1988), with learners being engaged in some mechanical undertakings. The physical attributes of concrete pictures enables such visual representations to be used for concrete counting and undertaking concrete operations or calculations. Concrete pictures have characteristics akin to Botsmanova's (1972, p.106) object-analytical pictures as they "reflect the mathematical structure of the problem" This has mathematical disadvantages for the upper grades and advantages for the lower grades as it orientates learners to localised context-dependent strategies as objects in the pictures can be used in the algorithm solution process.
Empirically most of the concrete pictures are used in the first two grades with a decline in their use in Grade 3. Compared to other forms of pictures, concrete mathematical illustrations are used the most, as they consist of 36% of the total pictures used in the foundation phase numeracy workbooks. Like abstract-concrete pictures, concrete pictures have mathematical tasks in which learners partake in manual or physical and which mainly require the learners to 'draw' concrete objects when solving arithmetical problems. Theoretically, such lithographic artistic engagements (Pausigere, 2016), implicitly implicate elementary mechanical-mathematical activities. Thus in the mathematical picture in Figure 4 learners concretely add up to 5 using-, by means of- or through the objects/items in the pictures with tacitly culminating answers. Similarly in the Figure 5's 'sharing activity' the learners are required to physically draw - thus dividing - the fruits that each of the learners get.
In both instances learners' answers exemplify numerical symbols, and this provides incidental elementary school mathematical procedure opportunities. Such implicit numerical leveraging is clearly exemplified in the pictorial illustrations below, which involves localised context-dependent mathematical strategies. However such in-situ-mathematical operations suit the lower foundation phase learners or grades.
Concrete-abstract pictures
Concrete-abstract workbook pictures facilitate learners' transition from concrete into abstract mathematical strategies. Such arithmetical expedition and facilitation is noted as key in elementary primary mathematics (Ensor et al., 2009; DBE, 2012). The concrete-abstract mathematical pictures also positively relate with the departmental policy documents of ensuring that numeracy workbooks activities promote the 'representation-to-abstract sequence' under which learners ultimately use "only numbers and mathematical symbols" (DBE, 2012, p.41). Thus the transition from concrete workbook pictures to abstraction provides opportunities for learners to use numbers, numerical and mathematical symbols most appropriate for arithmetical manipulation. Theoretically this evolvement, involves a shift from localising context-dependent into generalising context-independent strategies; public domain messages into esoteric school mathematics domain knowledge. Thus concrete-abstract mathematical pictures are essential mathematical representations which are critical for enabling mathematical abstraction. Borrowing from the language of Muller and Taylor (2000) such forms of pictures are central to inducting learners into the practices and discipline of mathematics and its related algorithm solutions.
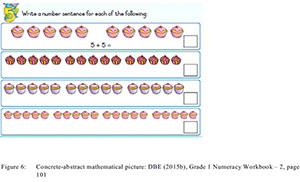
Close to a third of these types of pictures are used in the foundation phase numeracy workbooks, with a steady increase in the use of these pictures across the phase, except in the final Grade 3 workbook where more abstract pictures are deployed. In most of the examples of concrete-abstract mathematical pictures learners are instructed to ultimately '. . .write a sum. . .' or '. . .write a number sentence. . . .', after physically counting the objects or items in a given workbook picture. Thus in Figure 6 below, learners concretely count the number of scones in groups of fives after which they write the mathematical sum and its numerical answer in the workbook. Similarly, in Figure 7 learners physically count the stated items, perform the multiplication mathematical operations and finally write down the times-tables of 4 in the boxes provided. In both instances the concrete-abstract pictorial representations visually support learners to perform mathematical operations, with learners being initiated into solving and writing their answers in numerical figures. This is the mathematical potency of concrete-abstract pictures which allows for the transition from concrete to abstract mathematical strategies, which is a key mathematical process and skill for primary maths learners.
Abstract-concrete pictures
Theoretically abstract-concrete mathematical pictures are noted as reversing the mathematical abstraction process leading and inducting learners into concrete mathematical strategies. Such forms of pictures and their respective tasks supposedly defer and channel learners into 'situational thinking'. Ideally, this implies that the mathematical practices promoted by such pictures are "regulated by and within the concrete situation" (Dowling, 1998, p.29). Through their illustration of situational experiences these kinds of pictures proffer context-dependent mathematical approaches. Bernstein (2000, p.30) highlights the nature of context-tied particularistic meanings of the kind purportedly epitomised in abstract-concrete pictures as "they lack the power of relation outside a context because they are totally consumed by that context". In theory, because of their illustration and reflection of the mathematical structure of the problem these pictures are apparently perceived as foreground localising strategies and context-bound mathematical meanings.
However from an analytical numerical perspective, abstract-concrete mathematical pictures have the ability to show the 'reverse transition' (Botsmanova, 1972, p.105), mathematical relationships as they provide access to both concrete and abstract ways of working with numbers. Accordingly these types of pictures indirectly strengthen learners' mathematical generalisation process. Thus these pictures when used in the lower foundation phase maths textual resources promote elementary mathematical inverse processes as it allows learners to check their answers whilst alternating between situational and abstract numerical strategies.
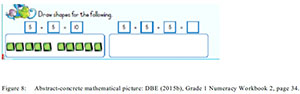
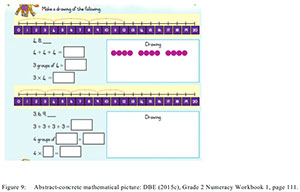
The writers of the foundation phase numeracy workbooks used these forms of pictures sparingly. Five percent, that is 43 of the 849 pictures used in the elementary workbooks, consists of these types of mathematical illustrations. In addition abstract-concrete pictures are used inconsistently across the foundation phase numeracy workbooks. Given their simultaneous support of concrete mathematical strategies and "mathematico-logical experiences" (Dowling, 1998, p.36), abstract-concrete illustrations are important in the early foundation phase maths grades. Figures 8 and 9 below illustrate abstract-concrete mathematical pictures.
In the two mathematical tasks above the learner initially engaged with abstract mathematical concepts and conclude the exercise with concrete activities. In the first task, after doing repeated addition and multiplication, the learner moves to drawing activities which is an inverse process between concrete and abstract strategies. The same is also evident in the second task where learners use number lines to solve the multiplication problem. The learner goes to write multiples of 4 and 3, then do repeated addition and multiplication. In both exercises, what is encouraging is the learners' simultaneous engagement in both abstract mathematical tasks and context-dependent activities of drawing, thus reinforcing the mathematical abstraction skills initially introduced. Generally, most of the abstract-concrete mathematical pictures have tasks in which learners engage in physical activities with learners being required to "draw, colour, circle, trace and cut-out". Thus these pictures include artistic and public domain aptitudes which are manual, physical and mechanical and are favoured by the younger learners. These I earlier described as 'lithographic skills' (Pausigere, 2016, p.582). The lithographic skills in abstract-concrete pictures are preferred by elementary foundation phase learners for their encouragement of concrete activities which in these instances strengthens abstract mathematical strategies.
Discussion
A cross-case analysis of pictorial categories based on their features, meanings and strategies translated shows a steady increase of abstract and concrete-abstract pictures whilst there is a steady decline of concrete and abstract-concrete pictures as the numeracy learner resources prepares learners for mathematical abstraction in the intermediate phase. This trend is quite marked from the first up to the fifth - (DBE, 2015e) - workbook, where there are 15% more abstract and concrete-abstract than concrete and abstract-concrete pictures. A higher proportion of concrete and abstract-concrete pictures may be desirable for workbooks designed for the first two primary grades as this enables context-dependent mathematical approaches for the elementary primary maths learners. In the final grade 3 learner workbook (DBE, 2015f) there is general decline in the use of pictorial illustrations in order to prepare learners for more abstract mathematical formulations and strategies. My earlier study also confirms to this pattern as it reports an increase in the use of alphanumeric symbols1 as one moves up the foundation phase grades (Pausigere, 2016). Thus generally in the initial stages of the foundation phase there is a higher prevalence of the numerically necessary concrete and abstract-concrete pictures so as to facilitate localising and context-dependent strategies for the lower grades with the mathematical domain translating effectiveness of abstract and concrete-abstract being recognised and acknowledged in the later stages of the numeracy workbooks.
Besides these pictorial combinations patterns this study proposes four key mathematical pictorial categories that benefited from both the theoretical sociological deductive and the textual inductive analysis of the numerical workbooks. The four pictorial categories of abstract; concrete; concrete-abstract and abstract-concrete were informed by Dowling's (1998) textual description codes of localising and generalising textual strategies, context-independent and context-dependent meanings and public- and esoteric-domain messages. The diagram below illustrates the nature and characteristics of the mathematical pictorial classifications.
These textual illustrative categories are not only limited to numeracy workbooks. They can also be extended to conventional primary maths textbooks or other primary textual resources used in the classroom such as charts and chalkboard mathematical expressions. There is also potential for widening the pictorial classification to secondary school mathematics textual resources. However this categorisation is of limited value for the content analysis of literacy textual resources or any other school subjects, either at primary or secondary level, though it could offer sociological insights worth considering.
Conclusion
This study identified a sociological textual analysis-informed framework for categorising primary mathematical pictures. The unit of analysis comprised of both the pictorial illustration(s) and the ensuing/subsequent mathematical learner exercise(s) or task(s). In the process of the sociological content analysis across the primary maths curriculum four clearly defined categories were identified for classifying numeracy workbook illustrations within the local foundation phase. The study was prompted by the numerous pictures within the local foundation phase numeracy workbooks and the need to identify mathematical pictures which can enable learners to understand mathematical concepts and skills across the different grades in the foundation phase. The Department of Basic Education, textbook writers, curriculum material developers, publishers of numeracy workbooks and primary maths teachers must consider the mathematical effectiveness of generalising context-independent strategies in abstract and concrete-abstract pictures, especially for the upper foundation phase grades. Whilst the exemplification mathematical potential for the early grades within concrete and abstract-concrete pictures that translate localising context-dependent strategies must also be contemplated. The mathematical translating strength and restrictions within the pictorial categories in relation to the different foundation phase grades must be explored for other mathematical related textual resources and for classroom pedagogical instructions.
Given these pictorial categorisations there is need for empirical studies to interrogate the frequency or amount of abstract, concrete, concrete-abstract and abstract-concrete pictures needed in the workbooks at the different primary phases - that is pre-primary, foundation and intermediate? Relatedly, and also worth empirically verifying, is which types of pictures suit different grades across the primary maths curriculum. Furthermore there is also a need to investigate how these different forms of mathematical pictures and the resultant tasks might relate to or distract learners from different social class groups. The theoretical and textual analysis herein could initially help inform such further interrogations.
Though this workbook textual sociological analysis offers insights worth considering there is need for more empirical research to supplement the content analysis and the findings of this study. Such empirical enquiry could involve classroom, experimental and home-based investigations of learners engaging in the numeracy workbook activities. These complementary studies could inform the mathematical pictorial categorisations proposed herein and enable the identification of forms of illustrations that enhance or constrain learners' conceptual understanding.
Acknowledgement
This work is supported by the FirstRand Foundation (with the RMB), Anglo American Chairman's Fund, the Department of Science and Technology and the National Research Foundation. However the opinions expressed herein are independent of the funders.
References
Bernstein, B. (1971). Class, codes and control, Volume I: Theoretical studies, towards a sociology of language. London: Routledge. [ Links ]
Bernstein, B. (2000). Pedagogy, symbolic control and identity theory, research, critique (Revised ed.). New York: Rowman & Littlefield Publishers. [ Links ]
Botsmanova, M. (1972). The forms of pictorial aid in arithematics problem solving. In J. Kilpatrick & I. Wirzsup (Eds), Soviet studies in the psychology of learning and teaching mathematics (105-110). Chicago: Doklady. [ Links ]
Department of Basic Education. (2012). Workbook Training Manual. Pretoria: Department of Basic Education. [ Links ]
Department of Basic Education. (2015a-f.) The Rainbow Workbooks: Mathematics English Grade 1-3. Pretoria: Department of Basic Education. [ Links ]
Dowling, P. (1996). A sociological analysis of school mathematics texts. Educational Studies in Mathematics, 31(4), 389-415. [ Links ]
Dowling, P. (1998). The sociology of mathematics education: Mathematical myths/pedagogic texts. London: RoutledgeFalmer. [ Links ]
Dowling, P. (2009). Sociology as method: Departures from the forensics of culture, text and knowledge. Rotterdam: Sense Publishers. [ Links ]
Ensor, P., Hoadley, U., Jacklin, H., Kuhne, C., Schmitt, E., Lombard, L. & Van den Heuvel-Panhuizen, M. (2009). Specialising pedagogic time and text in foundation phase mathematics classroom. Journal of Education, 47, 4-30. [ Links ]
Fleisch, B., Taylor, N., Herholdt, R., & Sapire, I. (2011). Evaluation of back to basic mathematics workbooks: A randomised trial of the Primary Mathematics Research Project. South African Journal of Education, 31, 488-504. [ Links ]
Harries, T., & Sutherland, R. 1999. The representation of mathematical concepts in primary mathematics textbooks: a focus on multiplication. Mathematics for living: The mathematics education into the 21st Century project (142-146). Amman, Jordan: MECP. [ Links ]
Hoadley, U. (2007). The reproduction of social class inequalities through mathematics pedagogies in South African primary schools. Journal of Curriculum Studies, 39(6), 679-706. [ Links ]
Jellis, R. (2008). Primary children's interests and use of illustrations in school mathematics textbooks and non-routine problems: A school-based investigation .Unpublished PhD thesis. London: Durham University. [ Links ]
Mayer, R.E., Sims, V., & Tajika, H. (1995). A comparison of how textbooks teach mathematical problem solving in Japan and the United States. American Educational Research Journal, 32(2), 443-460. [ Links ]
Muller, J., & Taylor, N. (2000). The well-tempered learner: Self-regulation, pedagogical models and teacher education policy. In J. Muller (Ed.), Reclaiming knowledge: Social theory, curriculum and education policy (57-74). London: Routledge Falmer. [ Links ]
Pausigere, P. (2016). A sociological analysis of the South African foundation phase numeracy workbooks. Proceedings of the 24th Annual National Conference of the Southern African Association for Research in Mathematics, Science and Technology Education (578-589). Tshwane University of Technology, Pretoria: SAARMSTE. [ Links ]
Thompson, I. (2008). Understanding and representation in early mathematics. In A.Harries, P. Barmby, & J. Suggate (Eds), Teaching and learning early number (160-175). London: Open University Press. [ Links ]
Walkerdine, V. (1988). The mastery of reason. London: Routledge. [ Links ]
Received 4 July 2016
14 September 2017
1 Alphanumeric symbols are a key resource remarked for facilitating generalising, context-independent, esoteric domain strategies of high discursive saturation