ARTICLES

 

Mathematics conceptual errors in the learning of a linear function- a case of a Technical and Vocational Education and Training college in South Africa

 

 

Lorraine Sehole^I; David Sekao^II; Lindiwe Mokotjo^III

^ITshwane North TVET College, South Africa
^IIUniversity of Pretoria, South Africa
^IIIThe Independent Institute of Education, South Africa

 

 

---

ABSTRACT

In this case study, we explored the conceptual errors that National Certificate (Vocational) Level 2 mathematics students at a Technical and Vocational Education and Training (TVET) College in South Africa experience in learning functions. Qualitative data were sourced from a sample of Level 2 (L2) mathematics students (n=17) from a TVET college through test responses and interviews. The findings revealed that the students find it difficult to: recognise a linear function, translate between different representations of a linear function, and identify particular components of a linear function. The findings generally indicated that the students lack conceptual understanding of the linear function. From the interviews, the students pointed to the teachers' instructional practices as a major contributory factor to the identified difficulties they experienced. Specifically, a lack of exposure to instruction and assessment tasks that involved all representations of functions hindered a deep conceptual understanding of functions.

Keywords: National Curriculum (Vocational) L2, mathematics students, linear function, conceptual knowledge, conceptual errors

---

 

 

INTRODUCTION

The concept of function is inarguably one of the most important concepts in school mathematics and beyond. As a building block of calculus, the concept plays a fundamental role in creating a pathway for related concepts in calculus such as the limit, differentiation, and integration. Also, the function concept contextualises mathematics in the real world (Bardini et al., 2014). For this reason, a firm grasp of this concept is essential. Sound understanding of function includes being able to: identify a function in its various representations and flexibly move between the representations. This knowledge facilitates students' ability to view the different representations of a function as a uniform object (Doorman et al., 2012), i.e., it is being understood conceptually.

One of the students' first encounters with the function concept is through the linear function. Although linear function might come across as the most uncomplicated compared to other algebraic functions, our view is that students tend to struggle to understand it conceptually. Assessing the depth of students' knowledge and understanding of linear function requires instructional tasks that strategically target conceptual understanding. Situational tasks that depict real life and involve elements familiar to the students are ranked highly in this regard. Such tasks can precede instruction on functions as a means to institute sound knowledge of the components where students will be relying solely on intuition and informal functional knowledge (Brendefur et al., 2015). The tasks can also be utilised in formal assessment, such as summative assessment, to evaluate the extent to which the concept has been grasped. This study forms part of a larger study which explored the difficulties that ¹NC(V) L2 students (n = 17) from a TVET college in South Africa encounter with regard to the conceptual knowledge of functions. With the current study, we sought to investigate students' conceptual knowledge difficulties regarding the linear function. We further explored the possible sources of these difficulties.

Problem statement

NC(V) L2-L4 is a vocational programme which offers an alternative pathway to mainstream high school Grades 1 0-1 2. Hence the entry requirement is Grade 9 (DHET 201 4). This being the case, most, if not all, NC(V) Level 2 classes house a combination of students who passed Grade 9 from the mainstream schooling system and those who come from ELSEN² schools. In addition, students who completed Grade 12 enrol for the programme due to two factors: (i) the level at which these students pass disqualifies them from university entry, and (ii) the limited number of universities in South Africa cannot handle a large influx of these students. In fact, in relation to the students who come from Grade 9 and/or ELSEN schools, they are likely to present knowledge gabs in certain mathematics concepts. One of these gaps is the students' insufficient knowledge of the linear function - the first function they were introduced to i n Grade 8. Although linear function appears to be the easiest to understand, some parts of this concept are problematic for students (Rakhudu, 2017). Legrande and Psycharis (2014) attest that such gaps exist due to imbalanced emphasis on procedural knowledge at the expense of conceptual understanding and the compromised foundation of mathematics concepts.

Purpose and research questions

In this paper, we explored the conceptual knowledge difficulties, and the sources experienced by NC(V) L2 students with the linear function in one TVET college in Gauteng province, South Africa. To gain insight into the students' conceptual knowledge difficulties and the sources thereof, we were guided by the following two research questions:

• What conceptual errors are experienced by NC(V) L2 mathematics students in the learning of a linear function?

• What are the possible sources of the conceptual errors that NC(V) L2 mathematics students experience in the learning of a linear function?

 

THE THEORETICAL FRAMEWORK

We used Sfard's (1991) 'Dual nature of mathematical conceptions' as a theoretical lens to explore the students' conceptual difficulties when learning linear functions. The theory outlines the cognitive processes through which knowledge and understanding of mathematical concepts such as functions develop. For Sfard (1991), a concept develops through two complementary stages: operationallyas a process or structurallyas an object. The two processes, both significant for the concept to be fully developed, occur through three stages: Interiorization, Condensation and Reification. Interiorization (operational): Learning procedures through which the new concept is constructed. For instance, the student is able to generate a graph using a set of ordered pairs or use a contextual/algebraic formula to generate a table of values. Condensation(moving from operational, working towards structural): The student can condense steps and use shortcuts to arrive at a solution. For instance, the student can identify the y-intercept and the gradient from an algebraic or contextual representation without first substituting χ by zero. Reification (structural): The student perceives various representations as a unified object. The student can identify a functionusing any of its representations and can compare and contrast functions.

The process view of a function is associated with a function as a machine which changes input values into corresponding output values, while the structural view is aligned to the function as a set of ordered pairs. Whether a representation of a function evokes a process view, a structural view, or both, depends on the type of teaching that the student receives and his/her understanding (Septyawan et al., 2019). Therefore, for students to be fully competent in working with functions and have a deep conceptual knowledge of the concept, they must have reached the reification stage. Notwithstanding the framing of our paper on Sfard's work on the nature of mathematical conceptions, we have also invoked constructivist views to gain insights into how conceptual errors are likely to arise when students learn linear functions. We support the Piagetian view that learning is characterised by construction of new knowledge in authentic contexts (Alanazi, 2016; Major & Mangope, 2012) through the twin constructs of assimilation and accommodation (Taber, 2019). Essentially, in the process of constructing knowledge, there exist two possibilities of making connections with the existing knowledge: (i) the newly-acquired knowledge can be connected with and fit into the relevant already-existing knowledge thereby enhancing conception, or (ii) the newly-acquired knowledge can erroneously be connected with and fit into the discordant already-existing knowledge thereby creating a misconception. Clearly, in the process of constructing knowledge, therefore, misconceptions are likely to be the product of knowledge construction; however, they should be viewed as an opportunity to learn (Mulungye et al., 2016).

 

LITERATURE REVIEW

The importance of teaching and learning functions for conceptual understanding is widely documented. Most of the available research highlights the difficulties experienced in teaching and learning this concept at the school and university levels (Zandieh et al., 2017; Chimhande et al., 2017). We acknowledge a few studies focusing on the teaching and learning of functions at TVET Colleges in South Africa (Mofolo-Mbokane, 2011; Rakhudu, 2017). We have noted the scarcity of similar studies which draw attention to the linear function, specifically at TVET colleges in the NC(V) programme. The study seeks to highlight conceptual errors that mathematics students experience when learning the concept of functions. In the next sections we discuss the conceptual understanding and common conceptual errors committed by students when working on mathematical tasks involving functions.

Representations of the linear function

Exposure to all representations of functions encourages structural conception, which results in a conceptual understanding of functions (Septyawan et al., 2019). We scanned the NC(V) L2 mathematics curriculum document (Subject Guidelines, henceforth referred to as SG) together with three prescribed textbooks to find out how they present a linear function different representation. The discoveries we made are discussed in the next two paragraphs.

The types of representations displayed in the three textbooks are now indicated, with the number in brackets indicating the number of texts from which a particular representation is found: a mapping (2), a graph (3), an equation (3), and a table (3). The absence of contextual representations in three of the four documents was found to be peculiar. By contextual representations, we are referring to what is commonly known as word problems. Only one of the textbooks (Daniels et al., 2010) contains one contextual representation of a linear function as an assessment task. We also found it odd that a few more of these contextual representations appear in another chapter, which is simultaneous equations. Secondly, instead of the two closely related topics being taught in succession, they are separated by another topic. This separation makes integrating the two topics difficult and denies students the opportunity to make formidable links between the two.

Daniels et al. (2010) address conceptual knowledge in two of the six tasks on graphical representations in their textbook, while the other tasks address students' knowledge of procedures to draw a graph using various options. The other two textbooks (van Rensburg & Mapaling, 2017; Hurjunlal et al., 2012) address only the knowledge of procedures as far as graphical representations are concerned. This analysis reveals that the prescribed textbooks mainly address procedural knowledge of a linear function, promoting the process conception while neglecting structural conception.

Students' errors in representation of a function

Undoubtedly, contextual representations are significant in developing a deep knowledge of functions. These are, however, marred by interpretation errors. Students who are not first-language English speakers face the dual hurdle of interpreting the English language and the mathematical language in the problem (Sepeng & Madzorera, 2014; Martin, Suryadi & Juandi, 2019). Early exposure becomes important to promote familiarity with the representations. Powell and Fusch (2014) suggest screening students for difficulties with contextual problems as early as second grade to assist them in reasoning algebraically.

Converting from one representation of a function to another is termed translation (Nitsch et al., 2015). Brendefur et al. (2015) established that students tend to struggle with some translations, particularly when working with contextual representations. For example, students might write correct algebraic and descriptive rules from a contextual representation and yet present incorrect graphs for the same task (Brendefur et al., 2015). Similarly, Wilkie and Ayalon (2018) also observed that students could determine the correct gradient value from a real-life tabular representation yet could not identify the value of the same gradient from graphical and algebraic representations. The students' fixation on situational dynamics might have possibly led them to lose the mathematics embedded in the task (Brendefur et al., 2015). A lack of exposure to contextual representations might also make it difficult for students to transfer knowledge of the same concept across different formats (Wilkie & Ayalon, 2018).

One of the requisite mathematical skills for learners to solve context-rich or unstructured problems is conceptual understanding (Ogilvie, 2009). Conversely, context-rich problems have been linked to improving learners' conceptual understanding (Gijsbers, 2020). It can, therefore, be concluded that translating functions represented in context-rich formats to other representations such as numeric, graphical and/or algebraic/equation representations requires students to be well grounded in conceptual understanding of the concept of function, including linear function.

Components of a linear function and their conceptual errors

In order to understand a function as a coordinated, intact structure, the components involved in its construction should first be known. For a linear function, such fundamental components are the gradient (slope) and the y-intercept, which can be easily identified from the linear equation y = mχ + c or y = ax + b or y = ax + q. Since these components are abstract mathematical constructs (Sfard, 1991), same as the linear function, it becomes difficult to teach or even assess them conceptually (Ackakin, 201 8). Nitsch et al. (201 2) contend that there are errors that are associated with the students' understanding of the purpose of the different components of the graphs in the context of understanding of a function. There are errors that relate to the understanding of the gradient, such as failure to interpret the meaning of the gradient of a line graph in real-life contexts (Roux et al., 201 5).

Understanding and conceptual errors of the gradient

Moore-Russo et al. (2011) state that the gradient can be perceived as an algebraic ratio 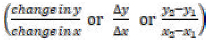a physical property (property of line often described using expressions like incline, pitch, steepness, slant, and tilt), or a functional property (rate of change between variables). In the school mathematics curriculum in South Africa, students are introduced to the gradient at Grade 9 as an algebraic ratio of the vertical distance to the horizontal distance or 'rise over run', using a right-angled triangle (Department of Basic Education [DBE], 2011). Crawford and Scott (2000) lament that this introduction makes it difficult for students to understand the gradient as the rate of change of two related quantities. Instead, the suggestion is for this introduction to be taught through practical examples that depict students' real-life contexts. For example, pricing a particular item from a local grocery store could serve as the rate of change, which is the cost per unit item. The task can be based on one item, with students noticing the constant increase in the cost as the number of the same item increases. Different translations can be performed within the task, with the gradient being interpreted in each case to benefit students' understanding. The rise-over-run formula (algebraic representation) can be brought into the lesson after completing the task, as an understanding of the gradient would have been established.

One of the indicators of conceptual understanding is the ability to recognise the same concept in different contexts. Such competence was found to be lacking among high school students who participated in a Croatian study (Planinic et al., 2012). The students were presented with a pair of questions on the positive gradient of a line and another pair on the negative gradient. In each pair, one question was asked from a mathematical context, while the other was asked from a physics context. The findings revealed that the students performed better in the mathematics questions in comparison with the physics questions. It is assumed that using the word 'slope' (synonym of gradient) assisted the students in responding correctly to the mathematics questions (Planinic et al., 2012).

Conversely, the physics question required students' understanding of acceleration as the rate of change of velocity, which students could not interpret as the gradient. Also, the students could identify the graphs with positive and negative gradients in the physics question but could not motivate their answers. This might indicate that the students memorised the relationship between the gradient and the shape of the line without real understanding (Birgin, 2012).

Using tasks familiar to students' contexts appears to be an effective strategy to enhance understanding of the gradient. It is, however, equally important to facilitate the ability to apply this knowledge in all functional representations. Stump (2001) used situational problems in words, pictures, and graphs to investigate high school students' understanding of gradients. The pictures presented a gradient as a measure of steepness, while the word problems and graphical representations focused on a gradient as a measure of the rate of change. The students presented a better understanding of the gradient as a measure of the rate of change than as a measure of steepness. It was further observed that the students provided more accurate descriptions of rates of change from the problems compared to graphical representations. Bannerjee (201 6) also reported that students found it difficult to interpret the rate of change of variables from practical problems in graphical and tabular form. This discussion highlights the difficulties that students seem to have with interpreting the gradient in different representations.

Understanding and conceptual errors of the y-intercept

The y-intercept is not usually emphasised much during teaching a linear function (Hattikudur et al., 2012). Teachers seem not expect students to struggle with the concept of y-intercept since it can be easily identified from the equation y = mx+ c as the value of c when x= 0. Difficulties with this component, if present, might go unnoticed due to the type of tasks used to assess it. Students are usually given simple tasks to identify the y-intercept from a graph or an equation. It has, however, emerged from some studies (Crawford & Scott, 2000; Hattikudur et al., 2012; Thomson, 2015) that assessing knowledge of the y-intercept in other means, such as verbal situations, might reveal gaps in students' understanding of the y-intercept.

Most of the increasing linear functions at the introductory level have a y-intercept at zero, leading students to believe that all linear graphs must start at the origin (Hattikudur et al., 2012). This practice handicaps students because they struggle to position the y-intercept on a graph if it is elsewhere except the origin. Another observation was that the students could view qualitative graphs as objects while working with quantitative graphs evoked a process conception. Once data are presented in numerical form, students become fixated on discrete points and hence lose the object conception (Hattikudur et al., 2012). Crawford and Scott (2000) suggest that the power of visualisation might assist students in understanding the y-intercept. Tasks, where students have to draw and compare several graphs while verbalising their observations might help establish knowledge of the y-intercept (Crawford & Scott, 2000). In other words, visualisation and verbalisation should precede the definition, description and computation of the y-intercept instead of the order being reversed as is usually the case.

Acquiring a sound knowledge of functions requires a teacher who is knowledgeable of the content and pedagogy. Such a teacher will demonstrate a complete conception of a function (Septyawan et al., 2019) in the planning, pacing and presentations of the lessons. Concerns are raised that some teachers' content knowledge of functions is inadequate due to the type of preparation programmes they have undergone (Adler 201 7; Makonye, 201 1). These limitations make it difficult for the teachers to recognise the students' misconceptions and to design assessments that elicit students' thinking (Ibeawuchi 2010; Makonye, 2011).

 

RESEARCH METHODOLOGY

Seventeen (17) NC(V) L2 students were conveniently sampled to participate in this case study. Qualitative data were collected through an achievement test and interviews. The self-designed achievement test, first used in a larger study, originally consisted of three (3) questions. For this study, we focused on question 1.3 of the original test, as it focused solely on the linear function. For this study, the question (original 1.3) will be referred to as question 1. The question, a contextual representation of a linear function followed by five (5) sub-questions, was meant to assess students' knowledge of a linear function in its different representations (see Table 1).

Students were required to demonstrate their competence in performing the three different translations (switching between three different representations) of a linear function as a prominent indication of conceptual understanding, which may lead to conceptual errors when not acquired. Sfard's (1991) stage (that each translation represents is indicated next to each question.

• contextual-numeric: translation between a contextual representation and a numeric table (question 1.1) - Interiorisation. Interiorisation, demonstrated by a student's ability to find the output values by means of substituting the input values into the formula in the learning of linear function concept.

• contextual-algebraic: translation between a contextual representation and an algebraic expression (question 1.2) - condensation. In the context of linear functions problem solving, this stage is characterised by activities such as generating a graph from its algebraic formula, as well as combining various functionsand see the relationship between them.

• contextual-graphical: translation between a contextual representation and a graph (questions 1.3, 1.4 and 1.5) - reification. The student who has reached this stage is able to identify a functionby means of any of its representations, provide an accurate, correct definition of a function, and determine the values of unknown parameters in the equation of a function, among other competencies.

After marking the test, six (6) students were purposively sampled for the subsequent interviews as they responded to almost all the questions in the test. The semi-structured, open-ended interviews assisted us in gaining an in-depth understanding of students' misconceptions about the linear function and corroborated the data obtained from the analysis of written responses (Wahyuni, 2012). The students were interviewed in pairs due to time constraints while preparing for the mid-year examinations. The pairs were as follows: Student E with Student K, Student D with Student G, and Student H with Student L. The videotaped interviews, which were later transcribed, took place over two consecutive days.

Data analysis took the form of thematic analysis of the students' test scripts. Thematic codes (Gibbs, 2013) were created from the students' responses and aligned with Sfard's levels of concept development which were considered helpful in answering the research questions. Drawing from the work of Braun and Clarke (2006) on conducting thematic analysis, our analysis was characterised by both the inductive and deductive analysis; however, gravitated more towards the latter due to our understanding of Sfard's levels of conceptualisation which include interiorisation, condensation and reification. The three (3) stages of conception, aligned to the codes and sub-questions of the test are presented in Table 2 as follows:

 

FINDINGS

This section discusses the findings based on the three categories used to analyse the data. Snapshots of some of the students' work from the test and extracts from the interviews are used as illustrations to contextualise the findings. The findings revealed some conceptual errors, indicating that most of the sampled students found it difficult, if not impossible, to link the different representations of a linear function.

Firstly, we present a summary of the students' responses to the test items in Table 3.

None of the students responded correctly to all four sub-questions. Sub-question 1.5 was not responded to by all 17 students. Dissemination of the findings, according to Sfard's levels of conceptualisation the three categories which were used for data analysis, follows.

Condensation Levels - Identification and recognition of functions

Sub-question 1.3required the students to write down the graph type that best represents the scenario. Six of the 1 7 students correctly identified a linear graph as the best scenario representation.

Oddly, turning to sub-question 1.1, four of the six students who presented correct table values could not recognise that the table represented a linear graph. The students were asked during the interviews whether they attempted to draw the graph in response to the sub-question. All four of the six students who presented the correct table values in sub-question 1.1 said the idea did not occur because the question did not ask them to sketch the graph. They also indicated that they wrote the first name they remembered because they got confused and did not understand what the question actually required. Although all four of the six students who presented correct tables in sub-question 1.1 recognised the table as representing a linear function, they were unable to justify their responses. The students committed a conceptual error in the manner in which they linked the numeric table to a linear graph.

Combination of Interiorisation, Condensation and Reification Levels - Knowledge of different representations (translations)

Conceptual knowledge of functions is characterised by students' flexibility to relate different representations of a concept (Kilpatrick, Swafford & Findell, 2001; Nitsch et al., 2015; Sfard, 1991). The study focused on three translations: contextual-numeric, contextual-algebraic, and contextual-graphical.

Contextual-numeric translation

Sub-question I.I required the students to complete a table by determining output values (amount earned) for the given input values (number of hours) using the scenario (contextual representation of a linear function). Some of the responses are presented in Figure 1.

Six of the 17 students presented correct output values, while 11 students presented a variety of conceptual errors. Two of the six students were among those who were interviewed, and they explained their calculations this way:

Student E WelL.the plumber charges a 1 50 call-out fee plus 60 rands neh? This means if she works for one hour she will be paid 1 50 + 60 which is 210. For two hours it will be double that amount, and so on and so on.

Student O: For one hour, Mmabatho charges 60 rands...but there is an additional charge of 150 rands which means you have to pay her 210. When she works for two hours she will charge double, which is 420. For three hours it become (sic) three times the previous charge.

Both Student E and student O did not understand that the call out fee was separate from the charge-per-hour fee.

Contextual-algebraic translation

Sub-question 1.2 required the students to write the expression that best represented the scenario. Some of the students' conceptual errors are shown in Figure 2. It would be a contextual-algebraic translation for students who used the scenario to respond to this question. On the other hand, for those students who could have used the table (item 1.2) in their response, it would be a numeric-algebraic translation.

Correct expressions were presented by three of the seventeen students, two of them in words, while the third student used symbols. For two of these three students, the expression correlated with their table of values (sub-question 1.1), while the third student could not link the correct expression with the calculated values.

The interviewer asked for Student D's understanding of the link between the numeric table and the equation she presented.

Interviewer: How did you use the information in the table to help you with the equation?

Student D I just filled the table using the given information. For 1.2 I used the T_n formula, and substituted a by 21 0, because it is the first term.

Interviewer. What about the other 21 0 you used to substitute d?

Student D I said 420 minus 21 0, that's how I got 21 0. The common difference.

Interviewer Did you get the same 210 when using the last two amounts (for 2 hours and 3 hours) from your table to obtain the common difference?

Student D I didn't check.

Student H also said that he did not verify whether the table of values matched the expression he wrote.

Both Student D and Student H demonstrated that they lacked the competence of linking a contextual linear function with the algebraic representation. Of the same function. The two students therefore displayed conceptual errors through their workings and explanations.

Contextual-graphical translation

Sub-question 1.3 addressed the first category (recognition of functions) and the contextual-graphical translation since it required students to match the scenario to a relevant graph. Other students could have possibly used the algebraic expression (sub-question 1.2) in their response, meaning they instead performed an algebraic-graphical translation. For students who used the table of values (sub-question 1.1) to respond to sub-question 1.3, they performed a numeric-graphical translation. The findings regarding responses to sub-question 1.3 have already been presented under category 1.

Condensation Level- Knowledge of components and behaviour of a function

Sub-questions 1.4 and 1.5 were about the components of the function, namely the gradient and y-intercept. The students were required to state what components were represented by the call-out fee and the hourly rate, respectively. No correct response was recorded for both sub-questions. While four students responded incorrectly to sub-question 1.4, all seventeen did not respond to sub-question 1.5.

The interviewer was curious about Student K's response that the call-out fee charged by the plumber represents the y-axis. She asked him what he meant, and his response was:

Student K The 150 call-out fee is charged to all clients for transport, I guess. So, if the job takes less than one hour, she will charge you 150 anyway. So, I used the table to draw the straight-line graph, and it cross on 150.

When asked to point to the y-axis on a graph with the y-intercept at (0;2), Student K pointed to the y-intercept and said:

Here, where the graph cuts.

The interviewer then handed Student K his script and asked him to calculate the gradient he correctly referred to in sub-question 1.3 using the numeric table. The student used the formula m = --- with two pairs of points to arrive at 60 as the gradient.

Interviewen What is that which you have just calculated?

Student K: The gradient of the straight line.

Interviewer What does that represent in terms of the plumber scenario?

Student K: How much she charges per hour, err...her rate.

Interviewer: So why did you not give that correct answer in the test?

Student K I didn't know at that time that it was the gradient, it just occurred to me now when you asked. They don't teach us the gradient like that, only the formula to find it, and that it is positive when and negative when...that sort of thing.

Students K's verbal response revealed a lack deep knowledge of the gradient and the y-intercept. The students' inability to identify the gradient and the y-intercept from the contextual linear function shows fragmented knowledge, which led to the conceptual error that the student committed.

 

DISCUSSION

Knowledge and understanding of a concept occur through three cognitive stages: interiorisation, condensation, and reification (Sfard, 1991). Students must go through all three stages to achieve both the process and structural views of concepts such as functions. It is only then that it can be established that the concept is fully developed and is being understood conceptually. Students' flexibility characterises this full development with all representations in terms of identification and behaviour of the function itself and its components.

The test's highest number of correct responses was 6/1 7 (35,3%), achieved in sub-questions 1 and 3. In sub-question 1, the students had to construct a table of values using the information from the word problem, a low cognitively demanding task. The interviewed students revealed that the correct responses in sub-question 3 were mostly coincidental because the linear graph was the first name that they could think of, which happened to be correct. It, therefore, became apparent that there was little or no thought process involved since the students did not perform any translation in their responses. There were three correct responses in sub-question 2, which required an algebraic representation, a medium cognitive demand task. The last two sub-questions, high cognitive demand tasks, did not yield any correct response. From this observation, it appears that most students' conception of a linear function is at the interiorisation stage - the first of the three stages. Although sub-question 3 also received an equal percentage as sub-question 1 in terms of responses, a revelation by the interviewed students that they just guessed the correct answer suggests that they are not yet at the reification stage of conception (Sfard, 1991) of a linear function.

In line with previous studies (Cansiz, Küçük & Isleyen, 201 1; Bardini et al., 2014), the students appear to regard each representation in isolation from the others. Constructing a numerical table appears to be easier for students than other translations (Ronda 2015, Brendefur et al., 2015). Similar to Adu-Gyamfi, Bosse and Chandler's (201 7) findings, determining the algebraic expression proved to be a more cognitively demanding task than working from the expression to the numeric table and then to the graph. The students' ability to present the correct table of values but failing to translate the information into a correct algebraic expression is evidence of superficial knowledge of the linear function (Doruk, 2019). This finding shows that the students have not yet reached the condensation stage of conception (Sfard, 1991) of a linear function.

Interviewing the students provided first-hand information regarding their thinking, knowledge and misconceptions about the linear function. The students revealed that they struggled to respond to the test items correctly as they were not familiar with contextual representations of a function (Thomson 2015). These obstacles also appeared to have a lot to do with the type of instruction the students received from the current level and previous grades. Functions were taught according to the textbook they used, as follows:

algebraic expression given-> table of values/critical points-> sketch a graph.

This finding implies that the type of teaching the students are exposed to impedes their ability to understand the linear function conceptually as a unified object with different representations. The students struggle with other representations of a linear function, particularly the contextual representation, which appears to be a consequence of a lack of exposure to such representations. This calls for mathematics teachers to strive for instructional practices that harness procedural knowledge and conceptual understanding of functions and other related mathematical concepts.

It is puzzling that even the students who presented correct equations were unable to recognise the call-out fee and hourly rate as the y-intercept and gradient, respectively. This difficulty confirms the findings by Wilkie and Ayalon (2018) that students could calculate the correct gradient value from a real-life table but did not understand it as the rate of the change. It became apparent that the students memorised procedures without understanding the meaning behind those procedures' concepts. Confusing the y-intercept with the y-axis also indicated a struggle with the vocabulary used in functions. These difficulties are, therefore, indicative of language challenges (Sepeng & Madzorera, 2014) and teaching practices that emphasise procedural rather than conceptual knowledge (Birgin, 2012). Teachers should, therefore, structure their instruction such they identify or design purposeful instructional tasks to facilitate students' understanding. While memorisation, often through drill and practice, of mathematical facts has a role to play in mathematics learning, it should be preceded by in-depth understanding of the concepts (Sfard, 1991). It is equally important to emphasise the vocabulary of such concepts within context-rich word problems so that the mathematics does not become lost in translation.

The findings indicate that six students' conception of a function is at the Interiorisation stage (Sfard, 1991) since they could calculate correct output values using the given input values. This is the entry-level of concept development. Three of these six students who could present correct algebraic expressions of the word problem appear to be at the condensation stage (Sfard, 1991). This second level of concept development is demonstrated by students' ability to relate different representations of the same function. Although these students were competent in performing the two translations, they could not identify the gradient and y-intercept of the linear function from the word problem. This finding indicates that none of the students has reached the reification stage, which enables viewing a function in all its representations as a unified object (Sfard, 1991). The findings generally indicate that the students' concept development is incomplete.

 

CONCLUSION

The ability to identify a function and its components in various representations means that the function is viewed as a unified object. This is evidence of a fully developed function concept (Sfard, 1991). The students in this study found it difficult to (1) correctly identify a linear function in its contextual representation, (2) translate between the different representations of a linear function, and (3) identify components of a linear functionsuch as gradient and y-intercept from a contextual representation. The findings are a testimony of the students' underdeveloped linear function conception. The students' incapacity to perceive different representations of a function as a unified whole indicates that they have not yet advanced to the reification stage of function conception (Sfard, 1991). Only three of the 1 7 students demonstrated that they were at the condensationstage of understanding a linear function, while the rest were still at the interiorisationstage. The identified difficulties might be attributed to traditional teaching practices, which strongly rely on the textbook, focusing on limited representations of functions (Birgin, 2012). Neglecting other representations incites a narrow conception of functions (Thomson, 2015). Extensive explanations and real-life examples might help deepen students' understanding of concepts.

These observations highlight the role teachers' instructional practices play in students' knowledge and understanding of constructs such as the linear function (Tchoshanov et al., 2017). Watson and Harel (2013) assert that teachers themselves should have a complete, structural conception of functions in order to be able to drive students' understanding in the same direction. Teachers need to reinforce their pedagogical content knowledge of functions so that they will be better equipped to enhance students' full conception of the linear function.

 

REFERENCES

Adler, J. (2017) Mathematics in mathematics education. South) African Journal of Science 11 3 pp.3-4.         [ Links ]

Adu-Gyamfi, K., Bosse, M.J., Chandler, K. (2017) Student connections between algebraic and graphical polynomial representations in the context of a polynomial relation. International Journal of Science and Mahematics Education 15 pp.91 5-938.         [ Links ]

Alanazi, A. (2016) A critical review of constructivist theory and the emergence of constructionism. American Research Journal of Humanities and Social Sciences 2 pp.1 -8.         [ Links ]

Aydin,U. & Özgeldi, M. (2019) The PISA tasks: Unveiling prospective elementary mathematics teachers' difficulties with contextual, conceptual, and procedural knowledge. Scandinavian Journal of Education Research 63(1) pp.105-123. https://doi.org/10.1080/00313831.2017.1324906        [ Links ]

Bannerjee, P. (2016) Thie Development of the Concept of Rates of Change and its Impact on Students' Understanding of Functions (Doctoral dissertation Texas A& M University-Corpus Christi: USA).         [ Links ]

Bardini, C., Pierce, R., Vincent, J. & King, D. (2014) Undergraduate mathematics students' understanding of the concept of a function. Indonesian Mahematical Society doi: 10.22342/jme.5.2.1495.85-107

Birgin, O. (2012) Investigation of eighth-grade students' understanding of the slope of the linear function. Bolema 26(42) pp.139-162.         [ Links ]

Braun, V. & Clarke, V. (2006) Using thematic analysis in psychology. Qualitative research in psychology 3(2) pp.77-101.         [ Links ]

Brendefur, J.L., Hughes, G. & Ely, R. (2015) A glimpse into secondary students' understanding of functions. International Journal for Mathematics Teaching and Learning 16(1) pp.1 -22.         [ Links ]

Cansiz, S., Kügük, B. & Isjeyen, T. (2011) Identifying the secondary school students' misconceptions about functions. Procedia Social and Behavioral Sciences 15 pp.2827-2842.         [ Links ]

Chimhande, T., Naidoo, A. & Stols, G. (2017) An analysis of Grade 1 1 learners' levels of understanding of functions in terms of APOS theory. Africa Education Review 14(2-3) https://doi.org/10.1080/18146627.2016.1224562        [ Links ]

Crawford, A.R., Scott, W.E. (2000) Algebra for all: Making sense of slope. The Mathematics Teacher 93(2) pp.203-233.         [ Links ]

Daniels, J., Solomon, N. & Taljaard, M. (2010) Mathematics hands-on training National Certificate Vocational Level 2. Cape Town, SA: Future managers.         [ Links ]

Department of Basic Education. (2011) Curriculum and Assessment Policy Statement Grades 7-9: Mathematics. DBE: Pretoria, South Africa.

Department of Education. (2007) National Certificate (Vocational)-Subject Guidelines Mathematics NQF Level 2. DoE: Pretoria, South Africa.

Department of Higher Education and Training. (2014) Tshwane South TVET College Admission Policy. DHET: Pretoria, South Africa.

Doorman, M., Drijvers, P., Gravemeijer, K., Boon, P. & Reed, H. (2012) Tool use and the development of the function concept: From repeated calculations to functional thinking. International Journal of Science and Mathematics Education 10 pp.1243-1267.         [ Links ]

Doruk, M. (2019) Examination of freshmen's conceptual knowledge of function in the context of multiple representations. International Journal of Research in Education and Science 5(2) pp.587-599.         [ Links ]

Gibbs, G.R. (2013) Using software in qualitative analysis. In U.W. Flick, W. Scott & K. Metzler (Eds.) The Sage handbook of qualitative data analysis. London: Sage, pp.277-94.         [ Links ]

Gijsbers, D., de Putter-Smits, L. & Pepin, B. (2020) Changing students' beliefs about the relevance of mathematics in an advanced secondary mathematics class. International Journal of Mathematical Education in Science and Technology 51 (1) pp.87-102.         [ Links ]

Hattikudur, S., Prather, R.W., Asquith, P., Alibali, M.W., Knuth, E.J. & Nathan M. (2012) Constructing graphical representations: Middle schoolers' intuitions and developing knowledge about slope and y-intercept. School Science and Mathematics 1 12(4) pp.230-240.         [ Links ]

Hurjunlal, A., Junak, H. & Naicker, A. (2012) Mathematics for NQF Level 2: Student's Book. South Africa: Pearson Education.

Ibeawuchi, E.O. (2010) The role of pedagogical content knowledge in the learning of quadratic functions. University of South Africa. pdfs.semanticsholar.org (Accessed 13 February 2018).

Kilpatrick, J., Swafford, J. & Findell, B. (2001) The strands of mathematical proficiency. In J. Kilpatrick, J. Swafford & B. Findell (Eds.) Adding it up: Helping chiildren learn mathematics. Washington, DC: National Academy Press, pp.11 5-1 55.         [ Links ]

Lagrange, J.B. & Psycharis, G. (2014) Investigating the potential of computer environments for the teaching and learning of functions: A double analysis from two research traditions. Technology, Knowledge and Learning 1 9 pp.255-286.         [ Links ]

Major, T.E. & Mangope, B. (2012) The constructivist theory in Mathematics: The case of Botswana primary schools. International Review of Social Sciences and Humanities 3(2) pp.1 39-147.         [ Links ]

Makonye, J.P. (2011) Learner mathematical errors in introductory differential calculus tasks: A study of misconceptions in the senior schiool certificate examinations. Unpublished doctoral thesis, University of Johannesburg, South Africa.         [ Links ]

Merriam-Webster Dictionary (2016) https://www.merriam-webster.com/dictionary/linear%20function. (Accessed 27 April 2020).

Moore-Russo, D., Conner, A. & Rugg, K.I. (2011) Can slope be negative in 3-space? Studying concept image of slope through collective definition construction. Educational Studies in Mathematics 76(1) pp.3-21.         [ Links ]

Martin, S.N., Suryadi, D. & Juandi, D. (2018) Students' difficulties in solving the mathematics word problems with the context of Education for Sustainable Development (ESD). Journal of Physics Conference Series(4)1157 pp.1-6, doi 10.1088/1742-6596/1157/4/042051        [ Links ]

Mofolo-Mbokane, B.L.K. (2012) Learning difficulties involving volumes of solids of revolution: A comparative study of engineering students at two colleges of furher education and training in South Africa Doctoral dissertation, University of Pretoria, South Africa.         [ Links ]

Nitsch, R., Fredebohm, A., Bruder, R., Kelava, A., Naccarella, D. et al. (2015) Students' competence in working with functions in secondary mathematics education-Empirical examination of a competence structure model. International Journal of Science and Mathematics Education 13 pp.657-682.         [ Links ]

Ogilvie, C.A. (2009) Changes in students' problem-solving strategies in a course that includes context-rich, multifaceted problems. Physical Review Special Topics-Physics Education Research 5(2) pp.0201 02 1-14.         [ Links ]

Planinic, M., Milin-Sipus, Z., Katic, H., Susac, A. & Ivanjek, L. (2012) Comparison of student understanding of line graph slope in physics and mathematics. International Journal of Science and Mathematics Education 10(6) pp.1393-13414.         [ Links ]

Powell, S.R. & Fusch, L.S. (2014) Does early algebraic reasoning differ as a function of students' difficulty with calculations versus word problems? Learning Disabilities Research & Practice, 29(3) pp.106-116.         [ Links ]

Raja, S., Pugalee, D.K. & Wickliff, A. (2015) How teacher knowledge and perceptions in representations of linear functions translate into their classroom teaching. In A. Rogerson (Ed.) The mathematics education for the future project. Paper presented at the 1 3^th international conference 'Mathematics in a connected world', Catania, Sicily.

Rakhudu, N.F. (2017) Exploring challenges faced by level 3 National Certificate vocational students in understanding hyperbolic functions in mathematics, Doctoral dissertation, University of South Africa. Pretoria, South Africa.

Ronda, E. (2015) Growth points in linking representations of function: a research-based framework. Educational Studies in Mathematics 90(3) pp.303-31 9.         [ Links ]

Roux, A., Nieuwoudt, H. & Nieuwoudt, S. (2015) Conceptual learning of functions in a technologically enhanced environment. African Journal of Research) in Mathematics, Science and Technology Education 19(3) pp.289-305.         [ Links ]

Sepeng, P. & Madzorera, A. (2014) Sources of difficulty in comprehending and solving word problems. International Journal of Educational Science 6(2) pp.21 7-225.         [ Links ]

Septyawan, S.R., Suryadi, D. & Nurjanah. (2019) Learning obstacles on the concept of functions: A hermeneutic phenomenological study. Journal of Physics: Conference Series. 1280(4) pp.1-8, doi 10.1088/1742-6596/1280/4/04204        [ Links ]

Sfard, A. (1991) On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics 22(1) pp.1 -36.         [ Links ]

Stump, S.L. (2001) High school precalculus students' understanding of slope as measure. School Science and Mathematics 101 (2) pp.81 -89.         [ Links ]

Taber, K.S. (2019) Constructivism in Education: Interpretations and Criticisms from Science Education. In Information Resources Management Association (Ed.) Early Childhood Development: Concepts, Methodologies, Tools, and Applications Hershey. Pennsylvania: IGI Global, pp.312-342.         [ Links ]

Tchoshanov, M., Cruz, M.D., Huereca K., Shakirova, K., Shakirova, L. & Ibragimova, E.N. (201 7) Examination of lower secondary mathematics teachers' content knowledge and its connection to students' performance. International Journal of Science and Mathematics Education 15 pp.683-702.         [ Links ]

Thomson, S.A. (2015) Algebral students' ability to relate the definition of a function to its representations. Electronic Theses, Projects, and Dissertations. 215, California State University: USA. Van Rensburg, M.J.J. & Mapaling, G.I. (2017) TVET First Matheematics NQF Level 2 Student's Book. South Africa: Macmillian.

Wahyuni, D. (2012) The research design maze: Understanding paradigms, cases, methods and methodologies. Journal of Applied Management Accounting Research 10(1) pp.69-80.         [ Links ]

Watson, A. & Harel, G. (2013) The role of teachers, knowledge of functions in their teaching: A conceptual approach with illustrations from three cases. Journal of Science, Mathematics and Technology Education 13(2) pp.154-168.         [ Links ]

Wilkie, K.J. & Ayalon, M. (2018) Investigating years 7 to 12 students' knowledge of linear relationships through different contexts and representations. Mathiematics Education Research! Journal 30 pp.499523.         [ Links ]

Zandieh, M., Ellis, J. & Rasmussen, C. (2017) A characterisation of a unified notion of mathematical function: the case of high school function and linear transformation. Educational Studies in Mathematics 95 pp.21-38.         [ Links ]

Zulnaidi, H. & Zakaria, E. (2012) The effect of geoGebra on conceptual and procedural knowledge of high school mathematics students. Asian Social Science 8(11) pp.1 02-106. https://doi.org/101.5539/ass.v8n11p102        [ Links ]

 

 

1 NC(V) L2-L4: National Curriculum (Vocational), a three-year programme offered at TVET colleges in South Africa as an alternative pathway to high school Grade 10-12.
2 ELSEN: Education for Learners with Special Educational Needs.