ARTICLES

 

The teaching and learning of trigonometry

 

 

Annatoria Zanele Ngcobo^I; Sethembiso Promise Madonsela^I; Deonarain Brijlall^II

^IUniversity of KwaZulu-Natal, South Africa
^IIDurban University of Technology, South Africa

 

 

---

ABSTRACT

A major desire of many African nations today is to be technologically developed. In South Africa there tends to be an acute shortage of skilled manpower in the Field of science, engineering and technology. The fundamental importance of mathematics to humans could be explained in terms of the interrelationship between mathematics and the development of humans to advance the cause of humanity. Science and technology rely on the application of trigonometry in real life situations which affect the daily lives of people. In this paper, we report on a qualitative study which explored the mental constructions made by Grade 12 learners when solving for the unknown properties of triangles in trigonometry. The study was carried out at a school in KwaZulu-Natal (n=30) in South Africa. The data were collected from written responses of students to a structured activity sheet consisting of questions on 2-dimensional shapes, and subsequently analysed using Action, Process, Object and Schema (APOS) theory. Findings emanating from the data analysis informed a modification of the initial genetic decomposition, which raised some didactical implications for basic education, specifically for the learning and teaching of trigonometry.

Keywords: teaching, learning, trigonometry, APOS theory

---

 

 

INTRODUCTION

Brijlall and Maharaj (2015) assert that mathematics, as part of the broader family of sciences such as physical science, for example, has as a result of its fundamental importance and significance to humans and their advancement and development received increased attention both at policy level and teaching and learning practice around the world. In other words, this explains the reasons behind the emerging and growing interest and debate among policy-makers and other related stakeholders with regard to how mathematics as a formal school subject has to be designed and also be dispatched for learning in various school systems around the world. Particularly the construction and understanding of knowledge by learners when responding to mathematical tasks (Jojo, 2014).

To enable learners to perform at the highest level in mathematics, learners need to be taught the relevant mathematical knowledge and skills, coupled with effective teaching strategies that can help learners exercise their reasoning powers or imaginations in the mathematics classroom. Mathematics as a body of knowledge embodies problem solving, deductive and inductive reasoning, among other things. Proficiency and competencies in these areas are essential when pursuing studies in science, engineering and technology (Orhun, 2010). Ndlovu & Brijlall (2015) state that the ability to reason mathematically can only develop once an individual or learner cognitively constructs the necessary mental schema needed to make sense of a particular mathematical concept.

The poor mathematical performance of many students as evidenced in literature (see, for example, Dündar, 2015; Orhun, 2010) suggests the need to ensure that students' achievement in mathematics is improved. In South Africa, among other factors, the problem of students' underachievement in mathematics has been attributed to the poor strategies employed by school teachers in the teaching and learning of mathematics, and teachers' lack of appropriate depth in pedagogical content knowledge (Brijlall & Maharaj, 2015). In South Africa, the situation is very critical; there is so much evidence of students' poor performance in mathematics (Makgato, 2007). In 2018, Motshekga (DoBE, 2018) in her national report compared grade 12 learner performance. The lowest performance was in Mathematics. The percentage pass rate for the 2017 senior certificate examinations appears in Table 1.

The overall pass rate for 2017 was 65%. This means that 35% of the learners failed mathematics. This is based on the pass rate being greater than or equal to 30%. If we had to consider the pass rate as 40%, we observe that more than half the number of learners would have failed. A recent survey shows that most learners find a number of topics in mathematics difficult to learn - particularly Trigonometric rules (Atagana et al., 2009). In their study, 103 out of the sample of 222 learners between Grades 10-12 (representing 46% of the sample) reported that they find it difficult to learn Trigonometry. Many students tend to encounter difficulties with trigonometry, particularly the trigonometric functions (Siyepu, 2015) and concepts related to 2-D shapes (Department of Education diagnostic report, 2017).

Trigonometry is a fundamental topic in mathematics that finds several applications in other branches of mathematics as well as in statistics, economics, surveying, architecture and many branches of engineering (Weber, 2005). Developing understanding based on trigonometric links is not easy for learners, and traditional ways of teaching trigonometry do not overcome students' difficulties (Demir, Sutton-Brown & Czermiak, 2012). The traditional ways involved a teacher-centred approach with the teacher as giver of knowledge and the use of chalk-and-talk.

The research work we report on is an original attempt of exploring an APOS study of Grade 12 learners solving problems on 2D shapes. Literature survey has shown that there are no Action, Process, Object and Schema (APOS) studies on trigonometrical concepts either nationally or internationally. This study also contributes to APOS theory in providing a modified model on the solution of triangles. Further its contribution is made for pedagogy of the solution of triangles in Trigonometry.

 

LITERATURE REVIEW

The concept of mental constructions as learning processes has roots in ancient times, going back to Socrates's dialogues with his followers in which he asked directed questions that led his learners to realise for themselves the weaknesses in their thinking (Baartman & De Bruijn, 2011). The Socratic dialogue is still an important tool in the way constructivist educators assess their students' learning and plan new learning experiences. Psychologists have made different philosophic assumptions about the nature of the learning process (Baartman & De Bruijn, 2011). For example, Dewey (1938: 89) asserted that 'It is that reconstruction or reorganization of experience which adds to the meaning of experience, and which increases ability to direct the course of subsequent experience'.

Piaget (1979) pointed out that every normal student is capable of good mathematical reasoning if attention (and care) is directed to activities of their interest, and if by this method the emotional inhibitions that too often give them a feeling of inferiority in lessons in mathematics are removed. Building on Piaget's ideas of reflective abstraction, Dubinsky (1991) introduced APOS theory, which is a theory aiming to explain the mental construction of mathematical concepts.

The descriptions of action, process, object and schema that follow are based on those given by Weller, Arnon & Dubinsky (2009) and Maharaj (2010, 2013). A transformation is first conceived as an action, when it is a reaction to stimuli which an individual perceives as external. It requires specific instructions, and the need to perform each step of the transformation explicitly. As an individual repeats and reflects on an action, it may be interiorised into a mental process. A process is a mental structure that performs the same operation as the action, but wholly in the mind of the individual. Specifically, the individual can imagine performing the transformation without having to execute each step explicitly. If one becomes aware of a process as a totality, realises that transformations can act on that totality and can actually construct such transformations (explicitly or in one's imagination), then we say the individual has encapsulated the process into a cognitive object. A mathematical topic often involves many actions, processes and objects that need to be organised and linked into a coherent framework, called a schema. It is coherent in that it provides an individual with a way of deciding, when presented with a particular mathematical situation, whether the schema applies. In the schema stage the learner has a collection of actions, processes, objects and other schemas that the learner understands in relation to calculus. According to Arnon et al. (2014) a genetic decomposition is a hypothetical model that describes the mental structures and mechanisms that students might need to construct in order to learn a specific mathematical concept.

There are many studies on learners' mental constructions, which are done using APOS theory in South Africa and abroad (e.g. Bansilal, Brijlall & Trigueros, 2017; Bijlall & Ndlovu, 2013; Brijlall & Maharaj, 2015; Dubinsky, 1991). These studies indicate that students' difficulties with construction of correct schema emanate from the incorrect conception of pre-requisite concepts, for example, continuity, differentiability and integration, are related to their difficulties with limits. Brijlall and Ndlovu (2013) investigated high school learners' mental construction during solving optimisation problems in Calculus in a rural Umgungundlovu District school in KwaZulu-Natal, South Africa. In that study, 10 learners who did Mathematics as a subject on grade 12 level participated, and data were collected through structured activity sheets and semi-structured interviews. Structured activity sheets with three tasks were given to 10 learners; these tasks were done in two groups of three and one group of four and the group leaders were interviewed.

Brijlall and Ndlovu (2013) also formulated itemised genetic decompositions for particular tasks, which contribute to APOS theory as also adopted for the theoretical framework for this study. The study revealed that most students did not operate at the object level and so did not formulate effective schema. Ndlovu and Brijlall (2015) investigated the level of mental constructions of concepts in matrix algebra by pre-service teachers. The study was guided by the belief that understanding the mental constructions the pre-service teachers make when learning matrix algebra concepts, leads to improved instructional methods. The findings revealed that the mental constructions made by pre-service teachers in most cases concur with the preliminary genetic decomposition. This study is aligned with the two studies (Brijlall & Ndlovu, 2013; Ndlovu & Brijlall, 2015) in that we extend the use of APOS as an analytic tool and formulate a genetic decomposition. Furthermore, Ndlovu and Brijlall (2013) emphasise the need to analyse learners' difficulties by means of research and this study adopts the use of genetic decomposition to analyse learners' difficulties in trigonometric concepts.

Jojo (2014) reports on a study that used APOS theory that the key mechanism for an individual to obtain new mathematical meaning is for him/her to construct mental constructions of direct experiences relevant to that concept. She asserts that a structured set of mental constructs, which might describe how the concept can develop in the mind of an individual, is called the genetic decomposition of that particular concept. Jojo (2014) also used mental constructions as a tool to explore how first-year engineering students conceptualise mathematical learning in the context of calculus with specific reference to the chain rule in South Africa.

In their study, Ndlovu and Brijlall (2015) uses preliminary genetic decompositions in APOS theory to explain mental constructions made or not made by learners. They noted that those students who had a weak schema of basic algebra were not able to make the necessary mental constructions or vice versa. Ndlovu and Brijlall (2015) revealed that the mental constructions made by pre-service teachers, in most cases, concur with the preliminary genetic decompositions for problems involving optimisation in Calculus. The findings from the study by Arnawa et al. (2007) have indicated that students who were taught how to prove that a maximum or minimum exists when solving optimisation problems using the APOS approach performed better than those taught using a traditional method such as a teacher-centred approach with the teacher as giver of knowledge and the use of chalk-and-talk.

Dubinsky (1991), on the other hand, proposed that in mental constructions the learner might include Actions, Processes, Objects and Schemas. APOS ascertains that for learners to understand a mathematical concept, they must begin with manipulating previously constructed mental or physical objects in their minds to form actions; actions would then be interiorised to form processes, which are then encapsulated to form objects (Dubinsky 1991). Therefore, these objects could be de-encapsulated back to the processes from which they were formed, which would be finally organised in schemas. Understanding the chain rule was explored in relation to the schema relevant to it.

Trigueros, Oktaç and Kú (2010) conducted a study to determine the role of mental constructions of undergraduate students in understanding the concept of a spanning set in Linear Algebra. In the study they used APOS theory to propose a genetic decomposition for the concept of a spanning set in Linear Algebra. One of the results that was obtained in their research is in line with the results reported by Nardi (1997) and Arnawa et al. (2007) on the difficulty in distinguishing a spanning set from a basis which was also explored by Mutumabara and Bansilal (2018). Nardi (1997) states that students have varying levels of difficulty when working with different types of vector spaces. Similarly, Mutumabara et al. (2018) confirmed that students' mental construction of vector space is at the action level, suggesting weak schema evolution. In the findings of the study exploring connections students make among concepts of linear independence/dependence, basis, linear combination, dimension, spanning set and generated vector space, Mutumabara et al. (2018) argue that the concept of linear combination plays a very important role in the understanding of the notion of 'spanning'. Their analysis so far indicates that it will be necessary to make certain modifications in the preliminary genetic decomposition, but the general model is in line with data.

The effective design of genetic decompositions in the APOS studies discussed in this literature survey suggested the formulation of the research question: How can the solving of problems involving 2-dimensional shapes inform the teaching and learning of trigonometry in schools?

To unpack this critical research question, we asked the following sub-questions:

1) What is the nature of Grade 12 learners' mental constructions of solutions of triangles?

2) To what extent do learners' mental constructions of triangles align with genetic decomposition?

3) Why do these mental constructions arise?

 

METHODOLOGY

Qualitative research methodology by its nature permits the use of different research strategies to gather data. It allows the voice of the participant to be heard. Cohen, Manion & Morrison (2013) asserted that research design is qualitative if there are no numbers used in categorising, organising and interpreting relevant information that has to be gathered. Flick (2006: 79) described this type of research as follows

Qualitative approaches allow for more diversity in responses as well as the capacity to adapt to new developments or issues. In qualitative methods, the data collected can include interviews and reflection, field notes, various texts, pictures and other materials.

This study was located within the interpretative quality research paradigm. Learners' performance on solutions of triangles was explored by means of an activity sheet. According to Dhlamini and Mogari (2013) knowledge is constructed as opposed to how it was created. In order to verify or interrogate the learners' mental constructions, written responses and interviews were used to analyse learners' responses to a particular set of questions. Ndlovu and Brijlall (2015) point out that having a correct answer does not necessarily mean an individual has constructed the necessary mental constructions and further that the written responses in mathematics need to be verified by means of an interview.

The study reported in this paper was conducted at one of the high schools in the Umlazi District. The school comprises black African learners and educators. Most of the learners are from nearby townships and some are shack dwellers, from low socio-economic backgrounds. Thirty Grade 12 learners who took Mathematics as a subject participated in this study. Activity sheets were given to all of them to work individually so as to get their mental construction on the solution of triangles. After they had completed their tasks, results were analysed using APOS. After the analysis of the written response, in some cases we needed to verify the APOS stages the learners were at as we could not with certainty deduce this. In these cases the affected learners were selected for interviews. Also, we selected one learner from each category of achievement. These categories were 'achieved', 'not achieved' and 'no response'.

Purposive sampling was adopted in this study. This sampling was chosen as it is not planned to generalise the findings with other schools. The researcher's choice to use a Grade 12 class was because of easy access to the participants since she was the one who was teaching that particular group. According to Bertram (2012), purposive sampling means that the researcher makes specific choices about which people to include.

Cohen, Manion and Morrison (2013) state that qualitative analysis frequently concerns individual cases and unique instances, and may involve personal and sensitive matters. It raises the question of identifiability, confidentiality and privacy of individuals. The researcher has an ethical obligation to reflect on the principle of primum non nocere be addressed first, do no harm (to participants). Permission was obtained from parents and guardians as well as from the learners to voluntarily participate in the study without any rewards. Participation was totally voluntary and had no impact or bearing on evaluation or assessment of the learner in any studies or course while at school. Participants were asked to take part in the interviews after the worksheets had been completed. All participants were written on transcripts and data collections by a pseudonym (i.e. fabricated names). The identities of the interviewees were kept strictly confidential.

All data were kept secured and were not used for any other purpose except for the research. Participants were allowed to leave the study at any time by notifying the researcher. Gatekeeper's permission was sought with Department of Education and ethical clearance no HSS\0320\016m was granted. According to Cohen et.al. (2013), the essence of anonymity is that information provided by participants should in no way reveal their identity. They further state that a participant is considered anonymous when neither the researcher nor another person can identify the participant from the information provided. In this study, the learner activity worksheets contained a learner number, not the names of participants and for the sake of the research, names were given privately. Their privacy was guaranteed. Cohen et al. (2013) explain that a research instrument that has no identifying marks such as names, addresses, occupational details or coding symbols ensures complete and total anonymity.

Cohen et al. (2013) state that the way of protecting a participant's right to privacy is through the promise of confidentiality: not to disclose information about a participant in any way that might enable the individual to be traced. The boundaries surrounding the shared information will be protected. The researcher explained to the participants the meaning of confidentiality. The consent letters explain in detail the steps taken to ensure confidentiality; data collected were stored in a secure place. The issue of reliability and trustworthiness was addressed through triangulation.

Table 2 provides details on how data collected were used to answer the research questions and, in addition, the possible limitations that each method had.

Learners' written responses to the 2-D problems were categorised into three categories which were:

• Achieved - represents those learners who made some or all mental-constructions proposed by genetic decomposition regarding the concept tested.

• Not Achieved - in this category learners made fragments of mental constructions of concepts, incomplete responses with computational errors in between steps. There was no reasoning to justify their responses, and others used wrong formulas to solve problems.

• Not Attempted - Learners who failed to attempt questions. Based on written responses, there was no mental construction of concepts since there were no written responses. However, they were probed through an interview.

Data presentation and discussion of written response to question one

Question one (see Figure 1) had three sub-questions. In this paper, the sub-questions will be referred to as items. All three items focused on solving a right-angled triangle (finding angles and sides). Item 1 intended to provide insight into whether the learner had developed at least an action conception of the sum of angles of a triangle. Items 2 and 3 sought to explore if the learners were beyond the action conception of trigonometric ratios of sine, cosine and tangent. In terms of APOS stages, mental constructions are hierarchical. The learners at Grade 12 level are expected to be at least at the process of understanding of the solution of right-angled triangles. Therefore, all learners were expected to solve all items in Question one, since these items mainly required the learners to perform external transformations.

In question one, which is shown in Figure 1, the triangle ABC has a right angle at A with BC = X and angle C = θ

In Figure 2, the itemised genetic decomposition (IGD) (Brijlall & Ndlovu, 2013) for question one is illustrated. The researchers used the IGD to explain the mental constructions evident in a learner's response and used the IGD as a basis to probe learners' responses during the interview.

Within this IGD, as part of his/her schema of solutions of right-angled triangle a learner should:

• Perform the sum of angles of a triangle to solve for an interior angle (item 1) Use trigonometric ratios to solve sides of triangles (items 2 and 3) Apply the knowledge of solving equations (items 2 and 3).

• The responses were first grouped according to categories in Table 3. This was purposely done in order to assist the researcher to present the analysis of the mental constructions evident in the responses per category.

• The IGD (Brijlall & Ndlovu, 2013) in this study is not for statistical purposes but is used to reveal the mental constructions that learners made or failed to make, and to discuss the impact of the analysis in relation to the development of the concepts assessed. Table 3 shows the performance of learners to each item of question one.

Analysis and discussion of Item 1 of question one

For Item 1, a learner with fully developed action conception would use the formula of finding the sum angles of a triangle correctly in order to find one angle when given two other angles. He/she would carry out all the steps of finding the sum angles of a triangle, in order to solve the third angle in terms of θand provide a correct response.

What we noticed in question one was that all learners attempted all the items and more than 83% showed evidence of making the mental constructions as specified in the IGD. In Item 1 the results revealed that 28 learners were categorised as achieved, which meant that they had made the necessary mental constructions as indicated in the IGD. However, only six learners made all the necessary mental constructions. These six learners displayed the process conception. Their responses showed that they had interiorised the geometric actions and algebraic actions to find the third angle into a process, which made it possible to interpret the magnitude of angle B in terms of the quadrants. According to Arnon et al. (2014), when a learner invents appropriate shortcuts, he/she is thus showing the evolution of the process conception of the concept. At this level, learners could easily write the formula of finding angles in a right-angled triangle without struggling to think about the formula as evident in the written and interview response below.

The written response in Extract 1 displayed that Suzuki could successfully find the third angle when given two angles in a triangle without performing all the steps, thus confirming that she had interiorised the action into a process.

Suzuki's interview response

While Suzuki's response seemed to emphasise the theorem instead of paying particular attention in explaining the concept, her response confirmed that she had developed a process understanding of the solution of the sum of angles of a triangle as she performed the steps cognitively to represent her solution. The probing by the interviewer made Suzuki reflect on her thought processes in keeping with the claims made by Baartman & De Bruijn (2011). From the response it was evident that Suzuki must have performed these actions repeatedly until she had constructed the relationship between the geometric actions and algebraic actions and was then able to coordinate these into the single process of determining the magnitude of a third angle and explained its meaning without the numerical values.

Unlike the six learners who displayed the process conception, 22 learners' responses revealed that they had the action conception of finding the sum of interior angles of a triangle. These learners applied the formula of finding the sum of a triangle and no step was omitted until they determined the solution. Nevertheless, Melly's response lacked accuracy (see Extract 2). While this could be considered as a slip, it in fact confirms the finding by Brijlall and Maharaj (2015) that learners do not engage with what they wrote. Having angle B = 90°+ θcontradicts the theorem that holds that the 'sum of angles of a triangle = 180°', which is the rule she was applying.

 

 

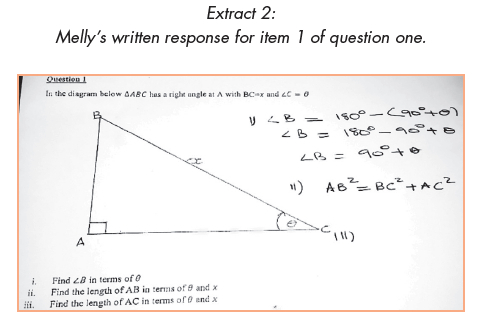
During the interview, Melly did identify the procedural error she had made which thus confirms that she had an action conception. Nevertheless, she could not explain the meaning of the answer in relation to the question, thus showing that although she can perform the actions, those actions have not been interiorised into a process. Having the process conception would have allowed her to formulate the concept image informed by the correct concept definition of the meaning of the properties of the triangle.

Analysis and discussion of item 2 of question one

Item 2 (see Figure 3) focused on learners' understanding of the concept of trigonometric ratios. They were expected to determine the unknown side unlike Item 1 where they had to find the unknown angle.

Item 2 intended to provide insight into whether a learner had developed an action and process conception of the concept of trigonometric ratios. A learner must be able to find the length of AB using trigonometric ratios and be able to solve equations. A learner on action level (Weller, Arnon & Dubinsky, 2009) of APOS will be also able to carry out all the steps of finding AB using trigonometric ratios. However, a learner at process stage will work out her responses mentally and express side AB = χSinθwithout physically writing down all the steps.

In Item 2 the analysis displayed that 25 learners were categorised as achieved. These learners' responses displayed the evolution of the necessary mental constructions. However, similar to Item 1, the majority displayed the action conception of solution of triangles. We observed that in Item 2, the numbers of achieved learners dropped as compared to Item 1. The main reason was that many learners were making errors. Three learners out of the 28 who were categorised as achieved in Item 1 could not determine the unknown sides because they tried to use Pythagoras theorem while only given one side instead of using trigonometric ratios (see Extract 3.)

 

 

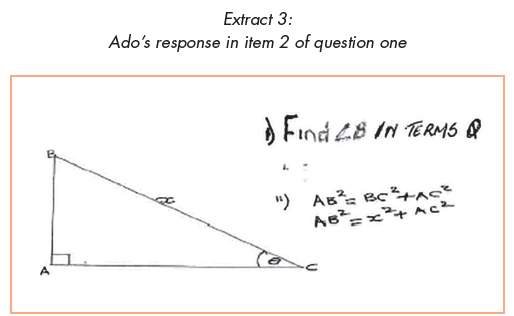
The question required the angle but Ado determined the side using Pythagoras theorem. His response confirms that previous knowledge when instrumentally understood can negatively impact on the construction of new knowledge. The above response showed Pythagoras theorem has been instrumentally understood, as a result, it was used in the wrong context and incorrectly.

Analysis and discussion of Item 3 of question one

In Item 3 (see Figure 4), learners were expected to find the lengths of AC in terms of θand X using trigonometric ratios. While Item 3 seemed to be similar to Item 2, in Item 3 learners needed to integrate concepts before determining an answer to Item 3. They needed the schema of co-functions and reduction formula if they were to use trigonometric ratios to solve the sum or just use the sine rule. Learners limited to an action level (Weller, Arnon & Dubinsky, 2009) will apply trigonometric ratios without identifying the need to apply co-functions. In addition, they would be limited to using trigonometric ratios since the triangle given is a right-angle triangle without seeing the possibility of applying the sine rule. Such constructions are possible to be made by learners with process understanding of solution of triangles.

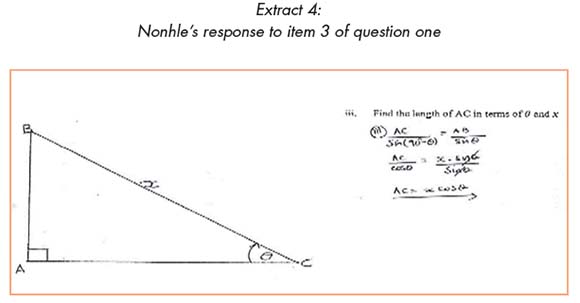
The analysis of learners' responses to Item 3 showed that 26 learners had a procedural conception to determine the solution. This meant that they had made at least an action conception of the concept as specified in the IGD (Brijlall & Ndlovu, 2013) for question one. As it was shown in Table 2, 26 learners provided correct responses to Item 3. While 26 learners provided the correct responses, only six learners displayed a process conception as explained in Figure 2 (IGD) of the concept assessed. The action of applying the sine rule and the action of determining the unknown was coordinated into a single action which was interiorised as process. These learners performed the steps internally and could determine the answer without explicitly writing down the steps. Contrary to the six learners, 20 displayed an action conception. This was evident as they carried out a step-by-step procedure for determining the solution as evident in Nonhle's response in Extract 4.

 

 

Data presentation and discussion of written response to question two

Question two differed from question one in that it assessed the learners' understanding of the solution of non-right-angle triangles.

In Figure 6 we present the IGD for question two. Within this IGD, as part of his/her schema of solution of triangle a learner should:

• Have the action understanding of solving interior angles of a triangle Have a schema of trigonometric ratios

• Have the process understanding of application of the sine rule

• Have the schema of solving algebraic fractions and different algebraic equations.

The above IGD (Brijlall & Ndlovu, 2013) describes the mental constructions a learner should make in order to provide correct solutions and construct conceptual understanding of solutions of a non-right-angle triangle. A learner who has constructed an action conception of finding the sum of interior angles will perform all the steps for finding the third angle when given other two angles. However, for a learner to display a process stage, they will present the solutions without performing steps or do appropriate constructions to relate the non-right angle triangle to a right-angled triangle. It is expected that such a learner would have interiorised (Weller, Arnon & Dubinsky, 2009) the solution of right-angle triangle to construct a complete concept image of the solution of non-right-angle triangle. The process of deconstructing and reconstructing the triangle is coordinated with the action of solving for interior angles to generate a new process of constructing a relationship between acute and obtuse angle; thus seeing angle D as the difference between 180 degrees and the sum of the two acute angles. When determining the sides, a learner with an action conception would identify the appropriate rule and apply it correctly when given numerical values of the given sides and angles. However, the learner with a process conception would have identified the appropriate rule and generalised the formula of solution of triangles given numerical values to solving triangles with abstract information.

The analysis of the participants' responses was grouped according to the categories in Table 4. The categories assist in presenting the analysis of the learners' performance in terms of determining correctness/ incorrectness of the solution. It reveals the nature of their mental constructions within the IGD (Brijlall & Ndlovu, 2013). The categories are necessary in order to explore the various APOS stages at which the learner could be operating. The IGD then would reveal the level of each learner.

Item 1 (see Figure 7) was aimed at revealing the APOS level learners could be operating at and how this links with the IGD.

 

The results showed that 26 out of 30 learners could solve for the third angle when given the two angles. In this item, we observed that the majority were operating at the process stage, which shows some evolution of the concept schema. Of the 26 learners who provided the correct answer, four showed the action conception of the solution of interior angles of a triangle. These learners correctly performed step-by-step procedures in order to find the third angle. The other 22 presented their solution without carrying out all the steps, indicating an interiorisation of action level. Extract 5 shows one of the responses of learners who displayed process conception of the solution of interior angles of a triangle.

Lolly's response to Item 1 displayed a process conception as it is portrayed that the whole idea of finding the third angle had been interiorised as she expressed the third angle as 180° - (β + θ), without explicitly showing all the steps. During an interview she was asked to explain why she only gave the answer without showing her manipulations, she responded as follows:

Lolly displayed an understanding of sum angles of a triangle as it was evident from her response that she had interiorised the action of finding the third angle when given two other angles in a triangle into a process. The probing by the interviewer made Lolly reflect on her thought processes in keeping with the claims made by Baartman & De Bruijn (2011). Even during the interview, Lolly was clear on the concept of solving triangles when given two angles. This was evident as she explained the steps mentally and expressed the answer as a whole entity without writing down all the steps. Other than Lolly, the researchers noticed that 25 other learners displayed a process understanding of Item 1 in question two. In question one the learners had to seek the one angle in terms of the other two angles in the right-angled triangle provided. In question two the triangle is now an obtuse angled one. The reasons for the developmental understanding from action to process may be attributed to the similarity in the application of the angle sum of a triangle in both questions and question one was already discussed in class. In this way the learners might have improved their understanding of the concepts from action to process.

The aim of Item 2 (see Figure 8) was to explore learners' mental constructions of determining the sides of a triangle using the sine rule. That was to understand the level at which learners were able to integrate the sine rule with an angle that is in terms of symbols. The ability of learners to integrate concepts and determine the solution of triangles in its abstract form would mean that such learners have developed the process understanding of the concept.

In Item 2 learners who were at an action level were expected to identify the appropriate rule. They must know that the sine rule is used when you are given two angles and one side of which must be opposite to the given angle. Learners who have constructed a process understanding were expected to use the rule to determine the solution in its abstract form. In other words, these learners must be able to use the reduction formulas and be able to make BC the subject of the formula through cross multiplication. All these procedures needed to be comprehended mentally in order to arrive at the process stage. For this item, the analysis (see Table 4) displayed that 11 learners were categorised as achieved, of which five were at an action stage. They were able to identify the correct rule, which is the sine rule. Six of the 11 learners displayed a process conception as mentioned in the IGD in Figure 6. These learners identified and used the correct formula to determine the solution in fewer steps. An illustration of this type of response appears in Figure 9.

Eli identified the correct formula and solved the equation in its abstract form as indicated in the IGD. Moreover, he identified the side BC and the corresponding angle, which is Sin[180° - (β + 0)] and was able to convert it to sin(ß + θ) and find solutions of triangles in its abstract form. Although Item 2 was abstract, Eli completed certain steps implicitly, thus showing the interiorisation of the concept.

In answering the research question, what is the nature of Grade 12 learners' mental constructions of solutions of triangles? We observed that for Item 1 of question one a learner (under the category of achieved) with fully developed action conception would use the formula of finding the sum angles of a triangle correctly in order to find one angle when given two other angles. He/she would carry out all the steps of finding the sum angles of a triangle, in order to solve the third angle in terms of 0 and provide a correct response. For item 2 of question one, 85% of the learners' responses displayed the evolution of the necessary mental constructions. However, similar to Item 1, the majority displayed the action conception of solution of triangles. For item 3 of question one, 20 learners displayed the action conception whereas six learners demonstrated that they were operating at the process conception (Weller, Arnon & Dubinsky, 2009) of APOS. For item 1 of question two, the results showed that 26 out of 30 learners could solve for the third angle when given the two angles. In this item, we observed that the majority (87%) were operating at the process stage, which shows some evolution of the concept schema. For item 2 of question two, only 37% of the participants achieved the mathematically correct solutions. Learners therefore did not reach an object stage of APOS. This meant that learners could operate at the lower conceptions of APOS but challenges arose when problems demanded higher order thinking.

In answering the research question to what extent do learners' mental constructions when dealing with problems involving triangles align with the IGD, the data analysis shows that the IGD (Brijlall & Ndlovu, 2013) was an effective analytic tool. We could place the learners' written response in the corresponding category and we were able to identify the APOS conception of the participants via their written or verbal responses. For instance, we noticed in question one that all learners attempted all the items and more than 83% showed evidence of making the mental constructions as specified in the IGD. For question two, the analysis helped us identify that five learners were at an action stage and six of the 11 learners displayed a process conception as mentioned in the IGD in Figure 6. In answering the research question why do these mental constructions arise, we deduce from the analysis of the data that certain previous mathematical conceptions are necessary for successful problem solving of problems involving 2D shapes in trigonometry.

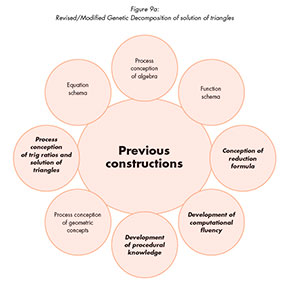
Many APOS studies (Bansilal, Brijlall & Trigueros, 2017; Bijlall & Ndlovu, 2013; Brijlall & Maharaj, 2015; Dubinsky, 1991) indicate that students' difficulties with the construction of correct schema emanate from the incorrect conception of pre-requisite concepts. For example, continuity, differentiability and integration are related to their difficulties with limits. The necessary mathematical conceptions for solution of triangles for our study are presented in Figure 9a below.

 

Figure 9a - Click to enlarge

 

The prerequisite mathematical conceptions, which we identified from the data discussion and the mental constructions we identified from the learners' written and verbal responses helped us modify our previous IGDs (Figures 2 and 6). This modified genetic decomposition is shown in Figure 9b below.

 

Figure 9b - Click to enlarge

 

CONCLUSION AND RECOMMENDATION

APOS theory was used as the theoretical framework to underpin this study. Based on the findings it was concluded that the majority of the participants were still operating at the action stage. While the action stage is necessary for the development of the other stages, such as process and object, it was rather troubling that 67% of the participants at Grade 12 level had not even developed the object conception. The main concern was the lack of the development of necessary schemas of the prerequisite concepts, thus showing that while learners progress from grade to grade, their conceptualisation of mathematical concepts remains at the action stage for many. In addition, the nature of the mental construction displayed by the participants in this study revealed that the development of schemas as prerequisites (see Figure 9a) are needed in the development of conceptual understanding by Grade 12 learners when solving problems involving triangles.

It was further evident that having the genetic decomposition for problems involving 2D shapes as a data analytic tool assists immensely with explaining the mental constructions made and also helps in understanding the difficulties learners have with a concept. As pointed out by Ndlovu and Brijlall (2015), it is critical for teachers of mathematics to have appropriate tools to use to understand how learners learn and, therefore, in this study we presented a genetic decomposition for the solution of triangles. The data

analysis findings helped us formulate the revised genetic decomposition as illustrated in Figure 9. The revised genetic decomposition is empirically based and hence is a realistic tool to inform mathematics teachers, curriculum developers and other relevant stakeholders of more meaningful ways of teaching this section in trigonometry. This study is hoped to contribute to the better performance by school learners in their senior certificate examinations. It is hoped that it will lead to a better grounding for school learners entering into tertiary education when studying engineering, computer science and other related fields of study which depend on mathematics. These disciplines are vital in developing a better technological South Africa.

 

REFERENCES

Arnawa, I. M., Sumarno, U., Kartasasmita, B. & Baskoro, E.T. (2007). Applying the APOS theory to improve students ability to prove in elementary algebra. Journal for Indonesia Mathematics Society 13(1) pp.133-148.         [ Links ]

Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S.R., Trigueros, M. & Weller, K. (2014) A Framework for Research and Curriculum Development in Mathematics Education. New York: Springer.         [ Links ]

Atagana, H.I., Mogari, L.D., Kriek, J., Ochonogor, E.C., Ogbonnaya, U.I. & Makwakwa, E.G. (2009) An analysis of educators' and learners' perceived difficult topics in mathematics, physical science and life science at the Further Education and Training (FET) band in Gauteng province: A Report of the ISTE 2009 Winter School. A research report. University of South Africa.

Baartman, L.K. & De Bruijn, E. (2011) Integrating knowledge, skills and attitudes: Conceptualising learning processes towards vocational competence. Educational Research Review 6(2) pp.125-134.         [ Links ]

Bansilal, S., Brijlall, D. & Trigueros, M. (2017) An APOS study on pre-service teachers' understanding of injections and surjections. Journal of Mathematical Behaviour 48 pp.22-37.         [ Links ]

Bertram, C. (2012) Exploring an historical gaze: A language of description for the practice of school history. Journal of Curriculum Studies 44(3) pp.429-442.         [ Links ]

Brijlall, D. & Ndlovu, Z. (2013) High school learners' mental construction during solving optimisation problems in Calculus: a South African case study. South African Journal of Education 33(2) doi: 10.15700/ saje.v33n2a679        [ Links ]

Brijlall, D. & Maharaj, A. (2015) Exploring Pre-service Teachers' Mental Constructions when solving problems involving infinite sets. International Journal of Educational Sciences 9(3) pp.273-281.         [ Links ]

Cohen, L., Manion, L. & Morrison, K. (2013) Research Methods in Education. 7th ed. London and New York: Routledge.         [ Links ]

Demir, K., Sutton-Brown, C. & Czerniak, C. (2012) Constraints to changing pedagogical practices in higher education: An example from Japanese lesson study. International journal of science education 34(11) pp.1709-1739.         [ Links ]

Dewey, J. (1938) Philisophy of Education; problems of men. Paterson, New Jersey. Litlefield: Adams & Co, pp.48-49.         [ Links ]

Dhlamini, J. & Mogari, D. (2013) The effect of a group approach on the performance of high school mathematics learners. Pythagoras 34(2) pp.1-9.         [ Links ]

Department of Basic Education. (2018) The 2017 National Senior Certifícate Schools Subject Report. Pretoria: National Department of Education.         [ Links ]

Dubinsky, E. (1991) Reflective abstraction in advanced mathematical thinking. In D. Tall (Ed.) Advanced mathematical thinking. Dordrecht: Kluwer, pp.231-250.         [ Links ]

Dündar, S. (2015) Mathematics Teacher-Candidates' Performance in Solving Problems with Different Representation Styles: The Trigonometry Example. Eurasia Journal of Mathematics, Science & Technology Education 11(6) pp.1379-1397.         [ Links ]

Flick, U. (2006) An introduction to qualitative Research. 3rd ed. London: Sage.         [ Links ]

Jojo, ZMM. (2014) Instructional design in the formation of mental images and the genetic decomposition of a concept. Journal of Educational and Social Research 4(3) pp.139-148.         [ Links ]

Maharaj, A. (2010) An APOS Analysis of Students' Understanding of the Concept of a Limit of a Function. Pythagoras 71 pp.41-52.         [ Links ]

Maharaj, A. (2013) An APOS analysis of natural science students' understanding of derivatives. South African Journal of Education 33(1) pp.146-164.         [ Links ]

Makgato, M. (2007) Factors associated with poor performance of learners in mathematics and physical science in secondary schools in Soshanguve, South Africa. Education Review 4(1) pp.89-103 http://dx.doi.org/10,1080/181466201412183        [ Links ]

Mutambara, L.H.N. & Bansilal, S. (2018) Dealing with the Abstraction of Vector Space Concepts. In S. Stewart, C. Andrews-Larson, A. Berman & M. Zandieh (Eds.) Challenges and Strategies in Teaching Linear Algebra ICME-13 Monographs. Springer: Cham.

Nardi, E. (1997) El encuentro del matemático principiante con la abstracción matemática: Una imagen conceptual de los conjuntos generadores en el análisis vectorial. Educación Matemática 9(1) pp.47-60.         [ Links ]

Ndlovu, Z.A. & Brijlall, D. (2015) Pre-service teachers' mental constructions of concepts in matrix algebra: A South African case. African Journal of Research in Mathematics, Science and Technology Education doi: 10.1080/10288-457.2015.1028717

Orhun, N. (2010) The gap between real numbers and trigonometric relations. Quaderni di Ricerca in Didattica 20 pp.175-184.         [ Links ]

Piaget, J. (1979) The Child's conception of the World. (J. & A. Tomlinson, Trans.). New Jerssey. Litlefield: Adams & Co.         [ Links ]

Siyepu, S.W. (2015) Analysis of errors in derivatives of trigonometric functions. International Journal of TEM Education 2(16) doi: 10.1186/s40594-015-0029-5        [ Links ]

Trigueros, M., Oktaç, A. & Kú, D. (2010) Spanning set: an analysis of mental constructions of undergraduate students. Prelminary Research Report. http://www.math.kent.edu/~edd/ICMIPaper.pd (Accessed 15 January 2017).

Weber, K. (2005) Students' Understanding of Trigonometric Functions. Mathematics Education Research Journal 17(3) pp.91-112.         [ Links ]

Weller, K., Arnon, I., Dubinsky, E. (2009) Preservice teachers' understanding of the relation between a fraction or integer and its decimal expansion. Canadian Journal of Science, Mathematics and Technology Education 9(1) pp.5-28.         [ Links ]

 

 

Date of submission 12 October 2018
Date of review outcome 7 February 2019
Date of acceptance 25 September 2019