RESEARCH ARTICLE

 

DDLV: A system for rational preferential reasoning for Datalog

 

 

Michael Harrison^{I, II}; Thomas Meyer^{I, II}

^IDepartment of Computer Science, University of Cape Town
^IICentre for Artificial Intelligence Research, South Africa. Email: Michael Harrison hrrmic014@myuct.ac.za (corresponding), Thomas Meyer tmeyer@cair.org.za

 

 

---

ABSTRACT

Datalog is a powerful language that can be used to represent explicit knowledge and compute inferences in knowledge bases. Datalog cannot, however, represent or reason about contradictory rules. This is a limitation as contradictions are often present in domains that contain exceptions. In this paper, we extend Datalog to represent contradictory and defeasible information. We define an approach to efficiently reason about contradictory information in Datalog and show that it satisfies the KLM requirements for a rational consequence relation. We introduce DDLV, a defeasible Datalog reasoning system that implements this approach. Finally, we evaluate the performance of DDLV.
CATEGORIES: • Computing methodologies ~ Artificial intelligence • Theory of computation ~ Logic

Keywords: datalog, non-monotonic reasoning, preferential reasoning, knowledge representation

---

 

 

1 INTRODUCTION

Datalog (Abiteboul et al., 1995) is a rule-based language that was originally designed as an effort to integrate efforts from the Artificial Intelligence and Database communities (Ceri et al., 1989). The aim of Datalog was to provide a deductive database querying language that extended conjunctive queries with recursion (Abiteboul et al., 1995), thereby allowing a relation (predicate) to be present in both the head and body of a rule. Datalog was derived from logic programming (Lloyd, 2012), with a key distinction being that Datalog does not contain functions.

Datalog has been around since the 1980s, but interest in it waned as there did not seem to be many compelling uses for it. Datalog has experienced some renewed interest in the past decade as the world moves towards greater levels of automation in most industries. Some of the areas where Datalog is currently being used include data integration, declarative networking, program analysis, information extraction, network monitoring, security, and cloud computing (Huang et al., 2011). Datalog has been used as the core of some very expressive and efficient Knowledge Representation and Reasoning systems, such as DLV (Leone et al., 2002) and RDFox (Nenov et al., 2015). DLV is a Disjunctive Logic Programming (DLP) system that uses an extended Disjunctive Datalog (Eiter & Gottlob, 1997) as its kernel language. DLV is one of the most successful and widely used DLP engines.

Most of these reasoning systems have limited applicability to real-world problems, though, as they can usually not reason about inconsistent or contradictory information. Contradictions often occur in domains that contain exceptions. Many systems cannot handle these contradictions due to the systems being monotonic (Ben-Ari, 2012). Monotonicity is a property of logical languages that states that previously concluded information cannot be revoked in light of new, contradictory information. Monotonicity is usually a desirable property for a logical language to possess. The information concluded in a monotonic system can only ever be added to and never taken away. Systems capable of dealing with contradictions need to, therefore, be nonmonotonic. DLV is nonmonotonic, but only in the way that it can represent and reason about incomplete information. We desire a system that can model rules that will generally hold true but also permit exceptions without the user having to perform additional knowledge engineering.

We present a simple example of a case where we would want to be able to represent and reason about exceptional information:

Example 1. Classical mammal knowledge base

• Mammals don't lay eggs.

• Platypusses are mammals.

• Platypusses lay eggs.

If we wanted to query the knowledge base in Example 1 to find out if platypusses lay eggs, traditional Datalog reasoning systems (including DLV) would conclude that platypusses lay eggs and platypusses don't lay eggs, thereby returning no possible models (essentially saying that there can be no platypusses). This is clearly not a desirable result. We would like to extend Datalog to represent defeasible knowledge. A defeasible rule is a non-classical rule that typically holds. A defeasible version of Example 1 would be:

Example 2. Defeasible mammal knowledge base

• Mammals typically don't lay eggs.

• Platypusses are mammals.

• Platypusses typically lay eggs.

Defeasible rules, unlike classical rules, would not have to hold if they are contradicted by classical information.

Defeasible reasoning has been successfully applied to the fields of inconsistency management (Martinez et al., 2014), planning (Garcia et al., 2007), agent negotiations (Dumas et al., 2002), business rules (Morgenstern, 1998), contracting (Grosof et al., 1999), and legal reasoning (Antoniou et al., 1999). Defeasible versions of Datalog have been utilised in many of these applications. Most of the previous approaches to defeasible Datalog require additional information or are not very computationally feasible. An approach that requires no additional input and is computationally efficient would provide further value in these fields.

A seminal approach to reasoning about defeasible knowledge is the preferential approach, as defined by Kraus et al. (1990) and Lehmann and Magidor (1992) (often referred to as the KLM approach). The KLM approach looks at nonmonotonic reasoning from a general and abstract point of view. The framework defines the requirements that a nonmonotonic inference procedure should meet in order to be considered a rational consequence relation. The KLM approach is defined in the propositional logic setting. The KLM approach has been successfully lifted to Description Logics (Casini & Straccia, 2010) as a way to extend the Description Logic language ALC with nonmonotonic reasoning capabilities. A practical defeasible reasoning system (Moodley, 2015) using the KLM approach has even been implemented in the form of a plugin for Protégé, an ontology engineering program.

The KLM approach's abstract framework and computational tractability make it an appealing candidate for application to the Datalog setting. In this paper, we define a defeasible extension to Datalog. We define an algorithm that performs a defeasible entailment check for our extended defeasible Datalog language, as well as defining the supporting algorithms required to perform this kind of reasoning. We show that our approach meets the KLM requirements for a rational consequence relation.

We then introduce DDLV, a system that can create, edit, and, critically, query a defeasible Datalog program. We give an overview of the design of DDLV, delve into how DDLV implements our preferential reasoning approach for defeasible Datalog, and evaluate the performance of the DDLV system.

This paper is an extension of a conference paper, "Rational preferential reasoning for Data-log" (Harrison & Meyer, 2020), which was presented at the South African Forum for Artificial Intelligence Research in 2019.

 

2 LANGUAGE

We will first define vanilla Datalog before we propose our extensions to it. A Datalog program consists of a set of Datalog rules. Datalog rules are expressions of the form

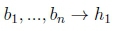
where b₁,...,b_nand h₁are literals. The left-hand side of the rule is the body and the right-hand side of the rule is the head¹. Traditionally, the head of a Datalog rule contains only one literal but the body is made up of a conjunction of any finite number of literals. If all the literals in the body are true in a model of a Datalog program, then the literal in the head is implied and added to the model. In vanilla Datalog, a literal is just an atom p. An atom is an expression p(_1i ,...,t_m), where p is a predicate with arity m and t₁,...,t_mare terms. A term can either be a constant or a variable.

Datalog follows a model-theoretic semantics where the Datalog program is viewed as a set of first-order sentences that describes the desired answer (Abiteboul et al., 1995). A Datalog interpretation is an assignment of concrete meaning to all constant and predicate symbols in the Datalog program (Ceri et al., 1989). A Datalog statement is entailed (denoted =) by a Datalog program if that fact is true under every model of the Datalog program.

We define two language extensions to Datalog:

1. A practical defeasible Datalog language that is used in our implemented defeasible Data-log reasoning.

2. A theoretical defeasible Datalog language enriched with additional operators that is used purely to prove how our approach meets the KLM requirements for a rational consequence relation (defined in Section 4).

2.1 Practical defeasible Datalog language

We need to define an extension to Datalog that is capable of expressing defeasible knowledge. The first essential extension to the language is negation, -². Any literal in the head or body can now be an atom p or a negated atom -p. Negation is necessary in order to be able to express any contradictory information. Our next extension is disjunction V. We include disjunction as a nice-to-have, purely because our system is built on top of DLV, which uses disjunctive Datalog as its underlying language. We, therefore, also only allow disjunction in the head between literals. Our final extension is an essential one - we add a defeasible implication operator ->³. This operator can be used in place of the traditional classical implication operator - when we want to express a defeasible rule.

2.2 Theoretical defeasible Datalog language

We define further extensions to our defeasible Datalog language, purely to express the postulates that characterise the language and in proving that the postulates hold for our approach.

We introduce disjunction in the body between literals and conjunction in the head between literals. The defeasible Datalog rule

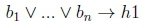
corresponds to the logical sentence

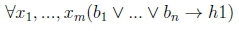
where x₁,...,x_mare all the variables occurring in all the literals of the rule. Similarly, the defeasible Datalog rule

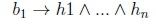
corresponds to the logical sentence

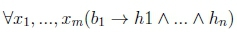
where x₁,...,x_mare all the variables occurring in all the literals of the rule.

Furthermore, we introduce bottom _L, which can be seen as shorthand for p A -p. Bodies of rules are seen as equivalent = if they are modelled by the same interpretations. A defeasible Datalog rule a -> β is defeasibly entailed by a defeasible Datalog program if, knowing a is true and based on the information contained in the defeasible Datalog program, it would be sensible to (defeasibly) conclude that β is true. If we have a set of defeasible rules DR, then DR is a set of classical versions a - (β of all defeasible rules a -> β (( in DR.

 

3 A RATIONAL CONSEQUENCE RELATION FOR DEFEASIBLE DATALOG

Kraus, Lehmann, and Magidor studied preferential consequence relations as an approach to nonmonotonic reasoning (Kraus et al., 1990). Lehmann and Magidor looked at a more restricted class of consequence relations, rational relations (Lehmann, 1995). They argued that any reasonable nonmonotonic inference procedure should define a rational consequence relation. Rational relations are those that may be represented by a ranked preferential model. A ranked model is a preferential model for which there is a modular strict partial order (Lehmann, 1995).

A nonmonotonic inference procedure needs to meet properties known as the KLM postulates to be considered a rational consequence relation. The original KLM postulates were defined in propositional logic. These properties have been discussed at length in the literature. We define defeasible Datalog versions of the KLM postulates that characterise a rational consequence relation for ranked defeasible Datalog models:

K refers to a defeasible Datalog program (knowledge base). The variables to the left of the implication operators refer to defeasible Datalog bodies and the variables to the right of the implication operators refer to defeasible Datalog heads. For each postulate, if the statement(s) above the line hold, then the statement below the line must hold. These defeasible Datalog versions of the KLM postulates are elaborated upon in Section 5 of this paper.

 

4 DEFINING RATIONAL CLOSURE FOR DEFEASIBLE DATALOG

In this section, we emulate rational closure (a specific construction given by KLM (Kraus et al., 1990) that satisfies all the KLM postulates for a rational consequence relation) for our defeasible Datalog. Our rational closure will rely on a ranking of the defeasible Datalog rules in a defeasible Datalog program. We need to construct a ranking of our defeasible Datalog rules based on the exceptionality of each rule. If a rule is assigned a lower ranking, then that rule is more normal or general. If a rule is assigned a higher ranking, then that rule is more exceptional or specific. Only once we have this ranking can we perform rational closure to determine if a rule is defeasibly entailed by our knowledge base.

Firstly, we define an algorithm to determine which defeasible rules in a set of defeasible rules are exceptional with respect to that set of defeasible rules and an optional set of classical rules. A defeasible rule is exceptional with respect to a set of defeasible and classical rules if the body of the rule is not satifisfiable with respect to the set of defeasible and classical rules. Platypusses would not be satisfiable in Example 2, meaning that the defeasible rule with platypusses as the body ("Platypusses typically lay eggs"/platypus(X) -> lays_eggs(X)) will be exceptional with respect to the classical rule and the other defeasible rule in Example 2.

Next, we define an algorithm that computes the ranking of a set of defeasible rules. This algorithm starts by putting all the defeasible rules in rank 0. It then utilises Algorithm 1 to determine which rules are exceptional to rank 0 and a set of classical rules. The exceptional rules are moved from rank 0 to rank 1. The same process is then performed to determine which rules in rank 1 are exceptional relative to rank 1 and the classical rules. Those exceptional rules will be moved to rank 2. This process is continued until either there are no more exceptional rules in a rank or all the rules in a rank are exceptional. If all the defeasible rules in a rank are exceptional, then the defeasible rules are classical rules represented as defeasible rules. These rules will be moved to the set of classical rules and represented as classical rules.

Returning to Example 2, the two defeasible rules ("Platypusses typically lay eggs"/platypus(X) ~> lays_eggs(X) and "Mammals typically don't lay eggs"/mammal(X) -> -ilays_eggs(X)) would start on rank 0. "Platypusses typically lay eggs"/platypus(X) -> lays_eggs(X) would be found to be exceptional with respect to the other defeasible rules in its current rank ("Mammals typically don't lay eggs"/mammal(X) -> -lays_eggs(X)) and the classical rules ("Platypusses are mammals"/platypus(X) -> mammal(X)). "Platypusses typically lay eggs"/platypus(X) -> lays_eggs(X) would, therefore, be moved to rank 1.

Once we have computed the ranking for a defeasible Datalog knowledge base, we can go about checking if a defeasible rule is defeasibly entailed by the knowledge base. We do this by checking if the rule is in the rational closure of the knowledge base. Essentially, the rational closure algorithm considers the portion of the knowledge base for which the queried rule is not exceptional (using Algorithm 1). The algorithm then checks if the rule classically follows from this portion of the knowledge base.

Returning to Example 2 again, if we wanted to query that knowledge base to determine whether it defeasibly entailed the query "Platypusses typically lay eggs"/platypus(X) -> lays_eggs(X), we would first look at the portion of the knowledge base where the body of the query is satisfiable. Platypusses are not satisfiable when considering rank 0 ("Mammals typically don't lay eggs"/mammal(X) -> -ilays_eggs(X)), rank 1 ("Platypusses typically lay eggs"/platypus(X) -> lays_eggs(X)) and the classical rules ("Platypusses are mammals"/platypus(X) - mammal(X)). When considering just rank 1 and the classical rules, though, platypusses are satisfiable. We will then look at the classical version of the remaining defeasible rules and the classical rules and determine whether a classical version of our query is classically entailed, which it is in this case. Our approach can also check for defeasible entailment of classical rules. To do this, we check if the classical query is classicalally entailed by the classical portion of the knowledge base. This is worth mentioning but, it is beyond the scope of the paper, so it shall not be discussed further here.

 

5 RATIONAL CLOSURE FOR DEFEASIBLE DATALOG SATISFIES KLM'S RATIONAL CONSEQUENCE RELATION REQUIREMENTS

As stated in Section 4, a ranking of the defeasible Datalog program must be constructed before it can be queried. Once a ranking has been computed using Algorithm 2 (which, in turn, makes use of Algorithm 1), Algorithm 3 can be used to answer defeasible entailment queries on the defeasible Datalog program. This section gives proofs showing how this approach satisfies each of the defeasible Datalog versions of the KLM postulates.

Postulate 1 (Reflexivity)

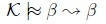
Reflexivity is satisfied universally by any kind of reasoning that is based on some notion of consequence (Kraus et al., 1990). Our defeasible entailment check for the given defeasible rule is eventually reduced to a classical entailment check for a classical version of the rule, which will always be reflexive.

Proof:

1. In order for RationalClosure(K, p ~> p) to terminate, we have to break out of the while loop on line 2 of Algorithm 3, so we will either have Case 1 where 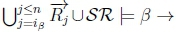no longer holds or Case 2 where ip < n is no longer true.

Case 1:

2. (a) Since , we must have 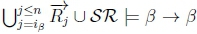by classical inference.

(b) Line 4 of Algorithm 3 will then return True for RationalClosure(K, β ~> β), meaning 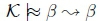for this case.

Case 2:

3. (a) Since iβ > n, we will only be dealing with the classical portion of the Datalog program. SR |=β->β will hold by classical inference.

(b) Line 4 of Algorithm 3 will then return True for RationalClosure (K, β ~> β), meaning for this case.

Postulate 2 (Left Logical Equivalence)

 

Left Logical Equivalence expresses the requirement that logically equivalent formulas have exactly the same consequences (Kraus et al., 1990). Since 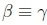, Algorithm 3 will consider the same portion of the knowledge base for both ( and 7 where they are not exceptional. Since K |≈ β ; η, we know that β → η holds for this portion of the knowledge base. Since β ≡ γ and we are considering the same portion of the knowledge base, 7 - n will hold. Algorithm 3 will, therefore, return True when checking K |≈ γ ; η.

Proof:

1. Given K |≈ β ; η, RationalClosure (K, β ; η) returns True.

2. In order for RationalClosure (K, β ; η) to terminate, we have to break out of the while loop on line 2 of Algorithm 3, so we either have Case 1 where no longer holds or Case 2 where i_β < n is no longer true.

Case 1:

3. (a) Sinceβ ≡ γ, RationalClosure (K, γ ; η) must giv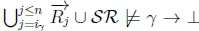e where

i_Y = i_pfor which 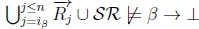in RationalClosure(K, γ ; η).

(b) Given 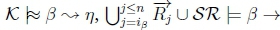must hold on line 4 of Algorithm refalg3 in RationalClosure(K, γ ; η).

(c) 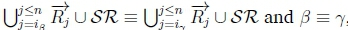therefore must hold on line 4 of Algorithm refalg3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ γ ; η for this case.

Case 2:

4. (a) If i_β >n,then .

(b) If and given K |≈ β ; η, then SR |= β → ηmust hold on line 4 of Algorithm refalg3.

(c) Since β ≡ γ,, RationalClosure(K, γ ; η) must not have any number i_Yfor which , therefore i_Y > n.

(d) If Iy > n, then .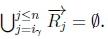

(e) If SR |= β → η and β ≡ γ, then SR |= γ → η must hold on line 4 of Algorithm refalg3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ γ ; η for this case.

Postulate 3 (Right Weakening)

 

Right Weakening implies that we may replace logically equivalent formulas in the head of the rule (Kraus et al., 1990). The portion of the knowledge base that Algorithm refalg3 considers for both K |≈ β ; η and K |≈ β ; γ is the same due to exceptionality being determined by the body of a rule and these two rules have the same body. We know that 3 - n holds for this portion of the knowledge base and we know that = |= η → γ.. Due to transitivity of classical implication, we know that β → γ will also hold for this portion of the knowledge base, so Algorithm 3 will return True when checking K |≈ β ; γ.

Proof:

1. Given K |≈ β ; η, RationalClosure(K, γ ; η) returns True.

2. In order for RationalClosure(K, γ ; η) to terminate, we have to break out of the while loop on line 2 of Algorithm 3, so we either have Case 1 where 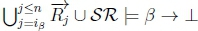no longer holds or Case 2 where ip < n is no longer true.

Case 1:

3. (a) Given 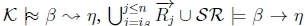must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(b) With we will get 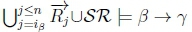due to the transitivity of classical Datalog implication.

(c) Thus, 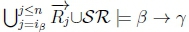will hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η) and cause RationalClosure(K, γ ; η) to return True, meaning K |≈ β ; γ for this case.

Case 2:

4. (a) If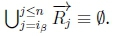

(b) If and given K |≈ β ; η, then SR |= β → η

(c) With SR |= β → η and given |= η → γ, we will get SR |= β → γ due to the transitivity of classical Datalog implication

(d) Thus, SR |= β → γ will hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η) and cause RationalClosure(K, γ ; η)to return True, meaning K |≈ β ; γ for this case.

Postulate 4 (And)

 

And expresses the fact that the conjunction of two plausible consequences is also a plausible consequence (Kraus et al., 1990). The portion of the knowledge base that Algorithm 3 considers for K |≈ β ; γ, K |≈ β ; η, and K |≈ β ; γ ∧ η is the same due to exceptionality being determined by the body of a rule and all of these rules having the same body. For this portion of the knowledge base, we know that both β → γ and β → η.Due to classical conjunction introduction, β → γ ∧ η must also hold for this portion of the knowledge base. Algorithm 3 will, therefore, return True when checking K |≈ β ; γ ∧ η..

Proof:

1. Given K |≈ β ; γ and K |≈ β ; η, RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η) both return True.

2. In order for RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η)to terminate, we have to_Ubreak out of the while loop on line 2 of Algorithm 3, so we either have Case 1 where 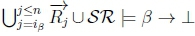no longer holds or Case 2 where iβ ≤ n is no longer true.

Case 1:

3. (a) Given 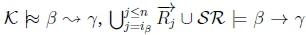must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(b) Given 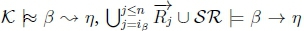must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) If we have and then 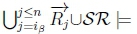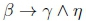must hold due to classical conjunction introduction.

(d) If we have on line 4 of Algorithm 3, then RationalClosure(K, γ ; η) will return True, meaning K |≈ β ; γ ∧ η for this case.

Case 2:

4. (a) If >n,then .

(b) If 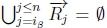and given K |≈ β ; γ, then SR |= β → γmust hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) If 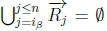and given K |≈ β ; η, then SR |= β → η must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(d) If we have SR |= β → γ and SR |= β → η, then SR |= β → γ ∧ η must hold due to classical conjunction introduction.

(e) If we have SR |= β → γ ∧ η on line 4 of Algorithm 3, then RationalClosure(K, β ; γ ∧ η) will return True, meaning K |≈ β ; γ ∧ η for this case.

Postulate 5 (Or)

 

Or states that any formula that is, separately, a plausible consequence of two different formulas, should also be a plausible consequence of their disjunction (Kraus et al., 1990). For K |≈ β ; η, Algorithm 3 considers the portion of the knowledge base where β is not exceptional; r classically follows for this portion of the knowledge base. For K |≈ γ ; η, Algorithm 3 considers the portion of the knowledge base where y is not exceptional; r classically follows for this portion of the knowledge base. When Algorithm 3 checks if K |≈ β ∨ γ ; η, it will consider the largest portion of the knowledge base where at least one of β or y is no longer exceptional. We know that at the point where at least one of β or y is no longer exceptional, r classically follows for this portion of the knowledge base. So we know that β ∨ γ → η for this portion of the knowledge base. Algorithm 3 will, therefore, return True when checking K |≈ β ∨ γ ; η.

Proof:

1. Given K |≈ β ; η and K |≈ γ ; η, RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η) both return True.

2. In order for both RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η)to terminate, both calls to Algorithm 3 need to break out of the while loop on line 2, so we can have 4 different cases. For Case 1 RationalClosure(K, γ ; η) reaches a point where 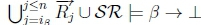no longer holds and RationalClosure(K, γ ; η) reaches a point where 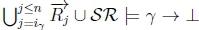no longer holds. For Case 2 RationalClosure(K, γ ; η) reaches a point where is no longer true and RationalClosure(K, γ ; η) reaches a point where 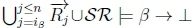no longer holds. For Case 3 RationalClosure(K, γ ; η) reaches a point where 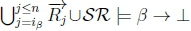no longer holds and RationalClosure(K, γ ; η) reaches a point where i_Y < n is no longer true. For Case 4 RationalClosure(K, γ ; η) reaches a point where ip < n is no longer true and RationalClosure(K, γ ; η) reaches a point where i_Y < n is no longer true.

Case 1:

3. (a) Given K |≈ β ; η, we know that 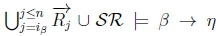holds on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(b) Given K |≈ γ ; η, we know that 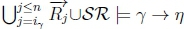holds on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) We now have 3 subcases. We have Case 1a where ip <i_Y. We have Case 1b where ip > i_Y. We have Case 1c where ip = i_Y.

Case 1a:

(d) i. Since ip < i_Y, RationalClosure(K, γ ; η) will break out of the while loop on line 2 of Algorithm 3 at a point when no longer holds.

ii. Since we know that 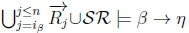holds, we then know that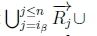 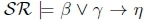must hold on line 4 of Algorithm 3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Case 1b:

(e) i. Since ip > i_Y, RationalClosure(K, γ ; η) will break out of the while loop on line 2 of Algorithm 3 at the point when 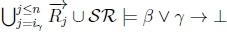no longer holds.

ii. Since we know that 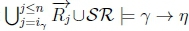holds, we then know that must hold on line 4 of Algorithm 3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Case 1c:

(f) i. Since ip = i_Y, we will have , so RationalClosure(K, γ ; η) will break out of the while loop on _Sline 2 of Algorithm 3 at a point when both 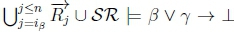and no longer hold.

ii. Since we know that 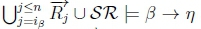and both hold, we know that both and 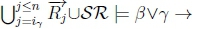n must hold on line 4 of Algorithm 3, thus returning True for RationalClosure (K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Case 2:

4. (a) Since ip > n and i_Y < n, it must be that i_Y < ip, so RationalClosure(K, γ ; η) will break out of the while loop on line 2 of Algorithm 3 at the point when 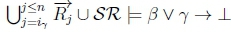no longer holds.

(b) Given K |≈ γ ; η, we know that 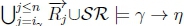holds on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) Since 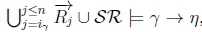then 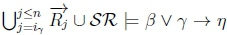must hold on line 4 of Algorithm 3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Case 3:

5. (a) Since i_Y > n and ip < n, it must be that ip < i_Y, so RationalClosure(K, γ ; η) will break out of the while loop on line 2 of Algorithm 3 at the point when 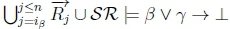no longer holds.

(b) Given K |≈ β ; η, we know that holds on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) Since 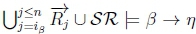, then 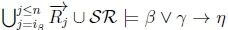must hold on line 4 of Algorithm 3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Case 4:

6. (a) Since ip > n, then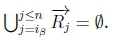

(b) If 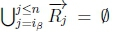and given K |≈ β ; η, then SR |= β → η holds on line 4 of Algorithm 3.

(c) Since Iy > n, then .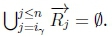

(d) If and given K |≈ γ ; η, then SR |= γ → η holds on line 4 of Algorithm 3.

(e) Therefore SR |= β ∨γ → η also holds on line 4 of Algorithm 3, thus returning True for RationalClosure(K, γ ; η), meaning K |≈ β ∨ γ ; η for this case.

Postulate 6 (Cautious Monotonicity)

 

Cautious Monotonicity expresses that learning a new fact that could have been plausibly concluded should not invalidate previous conclusions (Kraus et al., 1990). For K |≈ β ; γ and K |≈ β ; η, Algorithm 3 considers the portion of the knowledge base where β is not exceptional. We know that β -> y and β -> n for this portion of the knowledge base. Since β -> Y, we know that β A y will not be exceptional for this same portion of the knowledge base. Algorithm 3 will, therefore, consider this same portion of the knowledge base when checking K |≈ β ∧ γ ; for this portion of the knowledge base, ( A y - r will also hold for this portion of the knowledge base due to classical monotonicity. Algorithm 3 will, therefore, return True when checking K |≈ β ∧ γ ; η.

Proof:

1. Given K |≈ β ; γ and K |≈ β ; η, RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η)of K, β ; η) both return True.

2. In order for RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η) to terminate, both calls to Algor_Uithm 3 have to break out of the while loop on line 2, so we either have Case 1 where 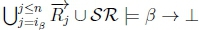no longer holds or Case 2 where ip < n is no longer true.

Case 1:

3. (a) Given K |≈ β ; γ we know that 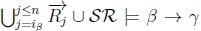must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η)

(b) Given K |≈ β ; η, we know that 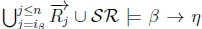must hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) Since we have , we equivalently have 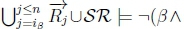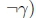. Therefore cannot hold, so the equivalent 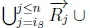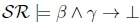will not hold on line 2 of Algorithm 3 in RationalClosure(K, γ ; η).

(d) Since 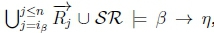, then 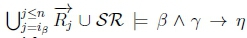must hold by classical monotonicity on line 4 of Algorithm 3.

(e) Since 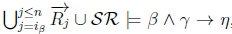, then RationalClosure(K, γ ; η) must return True, meaning K |≈ β ∧ γ ; η for this case.

Case 2:

4. (a) Since i_p > n, then .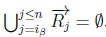

(b) If 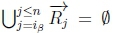and given K |≈ β ; γ, then SR |= β → γ holds on line 4 of Algorithm 3.

(c) If 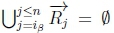and given K |≈ β ; η, then SR |= β → η holds on line 4 of Algorithm 3.

(d) Since SR = p - y, we equivalently have SR |= ¬(β∧¬γ). Therefore, SR |= β∧¬γ cannot hold, so the equivalent SR |= β∧γ → ⊥ does not hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(e) Since SR |= β → η, then SR |= β ∧ γ → η must hold by classical monotonicity on line 4 of Algorithm 3.

(f) Since SR |= β ∧ γ → η, then RationalClosure(K, γ ; η) must return True, meaning K |≈ β ∧ γ ; η for this case.

Postulate 7 (Rational Monotonicity)

Rational Monotonicity expresses the fact that only the negation that only additional information that negates a previously drawn plausible conclusion should force us to withdraw that plausible conclusion (Kraus et al., 1990). For K |≈ β ; η and K ̸|≈ β ; ¬γ, Algorithm 3 considers the portion of the knowledge base where p is not exceptional. We know that β → η and that is is not the case that β → ¬γ for this portion of the knowledge base. We, therefore, know that p A y will not be exceptional for this same portion of the knowledge base. Algorithm 3 will, therefore, consider this same portion of the knowledge base when checking K |≈ β ∧ γ ; η Since p - n for this portion of the knowledge base, p A y - n will also hold for this portion of the knowledge base due to classical monotonicity. Algorithm 3 will, therefore, return True when checking K |≈ β ∧ γ ; η.

Proof:

1. Given K |≈ β ; η, RationalClosure(K, γ ; η) returns True.

2. Given K ̸|≈ β ; ¬γ, RationalClosure(K, γ ; η) returns False.

3. In order for RationalClosure(K, γ ; η) and RationalClosure(K, γ ; η) to terminate, both calls to Algorithm 3 have to break out of the while loop on line 2, so we either have Case 1 where no longer holds or Case 2 where ip < n is no longer true.

Case 1:

4. (a) Given K |≈ β ; η, we know that 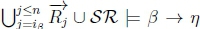must hold on line 4 ofAlgorithm 3 in RationalClosure(K, γ ; η).

(b) Given K ̸|≈ β ; ¬γ, we know that 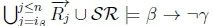does not hold on line 4 of Algorithm 3 in RationalClosure(K, γ ; η).

(c) In order to have K |≈ β ∧ γ ; η, RationalClosure(K, γ ; η) must return True.

(d) Since 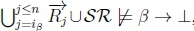, we will have 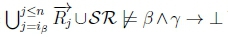by classical monotonicity.

(e) Since we have , RationalClosure(K, γ ; η)will progress out of its while loop on line 2 of Algorithm 3.

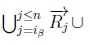
(f) Since and , we can have by classical monotonicity.

(g) By having 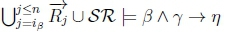on line 4 of Algorithm 3, RationalClosure(K, γ ; η) will return True, thereby giving K |≈ β ∧ γ ; η for this case.

Case 2:

5. (a) Since ip > n, then .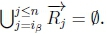

(b) If 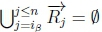and given K |≈ β ; η, then SR |= β → η.

(c) If 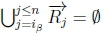and given K ̸|≈ β ; ¬γ, then SR ̸|= β → ¬γ.

(d) Since there is no number ip < n such that 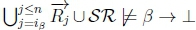, there will be no number ip < n such that 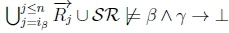due to classical monotonicity.

(e) Since there is no number ip < n such that 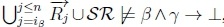, we will have ip > n, so RationalClosure(K, γ ; η) will progress out of its while loop on line 2 of Algorithm 3.

(f) Since SR |= β → η and SR ̸|= β → ¬γ, we can have SR |= β ∧ γ → η by classical monotonicity.

(g) By having SR |= β ∧ γ → η on line 4 of Algorithm 3, RationalClosure(K, γ ; η) will return True, thereby giving K |≈ β ∧ γ ; η for this case.

 

6 DDLV: DEFEASIBLE DLV

We now introduce DDLV. DDLV is a system that performs preferential reasoning for defeasible Datalog programs. The defeasible Datalog language for defeasible Datalog programs is defined in Section 2.1 of this paper. Defeasible Datalog programs can be edited in DDLV for convenience, but its main feature is the capability to query whether or not a defeasible Data-log rule is entailed by a defeasible Datalog program. DDLV achieves this by implementing the algortithms defined in Section 4 of this paper. DDLV is written in Java and uses the DLV Wrapper (Ricca, 2003) to interact with DLV programatically. DLV is used to perform the classical Datalog entailment checks that are required in our algorithms. The source code for DDLV is freely available online⁴, along with instructions on how to install, run, and use DDLV.

Figure 1 gives a simplified view of the architecture of DDLV. A model-view-controller (MVC) design pattern was used. All the computation is performed by the classes in the models package. The "views" package currently contains a single class that provides a command-line interface (CLI) for the user to interact with the system. The controllers package also currently contains a single class that handles the input from the CLI, requests the appropriate functions from the models, and calls on the CLI to give the appropriate output. The system uses this design package to allow all of the computational components to be contained and provides the capability for additional views (input and output interfaces) and their respective controllers to be added in a modular fashion if and when desired.

The raw defeasible Datalog program is stored as a DDLVProgram. A DDLVProgram is made up of StrictRules and DefeasibleRules. The RankedModel class contains most of the crucial functionality. A RankedModel takes a DDLVProgram as input and creates a ranking using implementations of Algorithm 1 and Algorithm 2. The RankedModel class also contains the functionality to then check if a defeasible Datalog rule is defeasibly entailed by the DDLVProgram using an implementation of Algorithm 3.

Figure 2 is a simplified sequence diagram that shows how a user would typically interact with the DDLV system. As can be seen, when the user opens the application, the user has the choice to either load an existing DDLV program (which would be stored as a text file) or to create a new DDLV program. Once the user has either created or loaded a program, the system presents the option to either view, edit, or query the program. By choosing to view the program, the user will initially be presented with the ranks of the RankedModel of the current DDLVProgram. The user can then select a rank and be shown all the rules in the selected rank. By choosing to edit the program, the user will be presented with the option to either add a new rule, edit an existing rule, or remove an existing rule. When choosing to edit or remove a rule, the user is able to navigate to the desired rule in the same way as when viewing the program. By choosing to query the program, the user is able to enter either a classical or defeasible Datalog rule. The system will then return whether the rule is entailed by the program or not.

 

7 IMPLEMENTING RATIONAL CLOSURE IN DDLV

DDLV uses implementations of Algorithm 1 and Algorithm 2 to create a RankedModel (which represents a defeasible Datalog ranking construction) of a DDLVProgram (which represents a defeasible Datalog program). This ranking is computed when a defeasible Datalog program is loaded into DDLV or edited in DDLV. Algorithm 1 is implemented using two functions, isExceptional and getExceptionalRank. The pseudocode for these functions is given below.

The isExceptional function takes a rule and a program as arguments. DLV is invoked to perform a classical entailment check to determine if the rule is exceptional with respect to the program. DDLV uses DLV (Leone et al., 2002) to perform these classical Datalog entailment checks in co-NP. One of the greatest appeals to the KLM approach is its computational tractab-ility and that is largely because the preferential reasoning process can be reduced to classical reasoning. This feature allows us to leverage the years of development that has been put into DLV to make it a highly efficient Datalog reasoning system.

The getExceptionalRank function constructs a program by combining a classical representation of a rank (a set of defeasible rules) and all the classical rules in the whole DDLV program. Note that all the defeasible rules in the DDLV program are initially set as rank 0. getExceptionalRank then creates a function call to isExceptional for each of the rules in the defeasible rank and passes the respective rule and the constructed program in as arguments. All of these calls to isExceptional are then executed concurrently. Each execution of isExceptional either returns the rule that was passed to it if the rule is exceptional with respect to the program that was passed to it or returns nothing if the rule is not exceptional. getExceptionalRank then returns the set of the results of all of the isExceptional executions.

Implementing Algorithm 1

function isExcEPTiONAL(currentRule, currentProgram)

inputProgram currentProgram

inputProgram inputProgram U grounded body of currentRule

dlvInvocation new DLV Invocation

Set inputProgam as the input for dlvInvocation

Set number of models for dlvInvocation to 1

Run dlvInvocation

if dlvInvocation does not compute any models then

L return currentRule

else

L return null

end function

Require: strictRules

Require: defeasibleRanks <r- {0 : allDef easibleRules}

function getExceptionalRankO

currentProgram strict representation of def easibleRules at rank U

strictRules

exceptionalRankFutures list isExceptional(rule, currentProgram)

for each rule in defeasibleRanks at rank

return results of all isExceptional calls in exceptionalRankFutures

end function

Algorithm 2 is implemented by the computeRanking function. The first step in the computeRanking function is to call getExceptionalRank on rank 0, which initially contains all the defeasible rules in the whole DDLV program. The result of this call to getExceptionalRank is the set of all the defeasible rules that are exceptional to rank 0. These rules are put into rank 1.

If rank 1 is equal to rank 0 (all the rules are exceptional), then the rules are actually what we call hidden classical rules. These are rules that are represented as defeasible rules but actually convey strict information. In this case, the function will jump to its end where it will remove all of these hidden classical rules form the defeasible rules and add them to the classical rules.

If rank 1 is not equal to rank 0, all the rules that are in rank 1 are moved out of rank 0. This process is then repeated by calling getExceptionalRank on rank 1 to obtain rank 2, and so on. The process will terminate when the exceptional rank that is obtained is either empty (contains no rules) or is equal to the rank that it is exceptional to (the rank below it). If the most exceptional rank is empty then we have no more exceptional rules and the ranking process is complete. The empty rank is simply removed from the ranking. If the most exceptional rank is equal to the rank below it, then we have the same case as mentioned earlier with hidden classical rules. These rules are moved to the set of classical rules and removed from the ranking.

Taking an asynchronous approach to the getExceptionalRank function by making all of its calls to the isExceptional function concurrently allows the computeRanking function to reach completion much quicker than a sequential approach would allow.

Implementing Algorithm 2

function computeRanking

counter - 1

def easibleRanks at counter - getExceptionalRank(counter - 1)

if def easibleRanks at (counter - 1) = def easibleRanks at counter then

def easibleRanks at (counter - 1) - def easibleRanks at (counter - 1)\

defeasibleRanks at counter

while def easibleRanks.get(counter - 1) = def easibleRanks.get(counter) A

defeasibleRanks.get(counter).getRules().size() > 0 do

counter - counter + 1

def easibleRanks at counter - getExceptionalRank(counter - 1)

if defeasibleRanks.get(counter - 1) = defeasibleRanks.get(counter) then

def easibleRanks at (counter - 1) def easibleRanks at (counter - 1)\

|_ def easibleRanks at counter

if number of rules in defeasibleRanks at counter = 0 then

|_ Remove def easibleRanks at counter from def easibleRanks

else

Remove def easibleRanks at counter from def easibleRanks

forall rule € def easibleRanks at (counter - 1) do

|_ strictRules - strictRules U strict representation of rule

_ Remove def easibleRanks at (counter - 1) from def easibleRanks

end function

Algorithm 3 is implemented by the rationalClosure function. DDLV uses this function to perform a defeasible entailment check. The function takes in a defeasible rule as an argument. The function checks if this rule is defeasibly entailed by the defeasible Datalog program.

This function initialises a counter to 0. While the value of the counter is less than the number of defeasible ranks, the function uses classical entailment calls to DLV to check if the query rule is exceptional with respect to all the defeasible rules contained in the rank at the value of the counter and all the more exceptional ranks (including the classical rules). When the function gets to a subset of the defeasible rules for which the query rule is no longer exceptional, it uses DLV to check whether the head of the query rule is classically entailed by this subset of rules. If the DLV check returns true, then the query rule is in the rational closure of the defeasible Datalog program and it is, therefore, defeasibly entailed. If the DLV check returns false, then the query rule is not in the rational closure of the defeasible Datalog program and it is, therefore, not entailed.

Implementing Algorithm 3

Require: inputProgram

while rank < ranks do

Clear inputProgram

inputProgram - inputProgam U defeasibleRanks from rank to (ranks - 1)

inputProgram - inputProgam U strictRules

inputProgram - inputProgam U grounded body of queryRule

dlvInvocation - new DLVInvocation

Set inputProgam as the input for dlvInvocation

Run dlvInvocation

if dlvInvocation computes a model then

L break

else

L rank - rank + 1

inputProgram - inputProgam U head of queryRule as a query

dlvInvocation - new DLV Invocation

Set inputProgam as the input for dlvInvocation

Run dlvInvocation

if dlvInvocation computes a model then

L return true

else

|_ return false

end function

 

8 EVALUATION

This section evaluates the performance of DDLV. Other defeasible Datalog reasoning implementations typically use an argumentation-based approach, which require additional information, such as constraints or override axioms. These other approaches also typically do not handle classical negation. These other approaches would, therefore, require a different set of rules that does not use classical negation and has additional information which the other approaches require to solve inconsistencies. Since there are no other preferential reasoning systems for defeasible Datalog, we compare DDLV with DIP, the Defeasible-Infererence Platform for Description Logics (Meyer et al., 2014). Although Datalog and Description Logics are different languages with different levels of expressivity and different approaches to classical reasoning, the preferential reasoning approach of DIP is very similar to DDLV. It is worth comparing DIP and DDLV to illustrate the computational benefits of utilising Datalog as an underlying language rather than Description Logics. Classical Datalog reasoners benefit from database optisation techniques, such as join order optimisations and the magic sets transformation. (Hustadt & Motik, 2005; Hustadt et al., 2007; Leone et al., 2002)

DIP performs KLM-style rational closure for ALC. The exceptionality check for DIP terminates in EXPTIME. Moodley built and then evaluated DIP for his PhD (2015) thesis. He synthesised ontologies to evaluate. No repository or collection of defeasible Datalog programs exists, so we must synthesise defeasible Datalog programs to evaluate as well. We follow Moodley's parameters and techniques for the synthesised programs in order to have defeasible Datalog programs that are as comparable as possible to his defeasible ontologies. Hardware with identical specifications is also used (Intel i7, 4 cores, 3GB RAM).

Moodley evaluated 10 groups of defeasible ontologies. Each group had a different percentage of defeasible statements in the ontologies in the group, starting from 10% and going up to 100% in intervals of 10%. Each group contained 35 ontologies, with the smallest ontology containing 150 statements and the largest ontology containing 3500 statements. The ontology sizes were uniformly distributed between the smallest and largest ontologies. To perform a similar evaluation of DDLV's performance, we synthesised and evaluated 10 groups of defeasible Datalog programs. As with the evaluation of DIP, each group of defeasible Datalog programs has a different percentage of defeasible rules in the programs in the group, starting from 10% and going up to 100% in intervals of 10%. Still following Moodley's parameters for the evaluation of DIP, our groups contain 35 programs, with the smallest program containing 150 rules and the largest program containing 3500 rules. The program sizes are uniformly distributed between the smallest and largest programs.

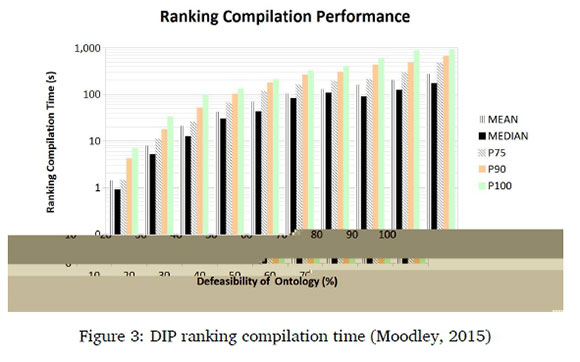
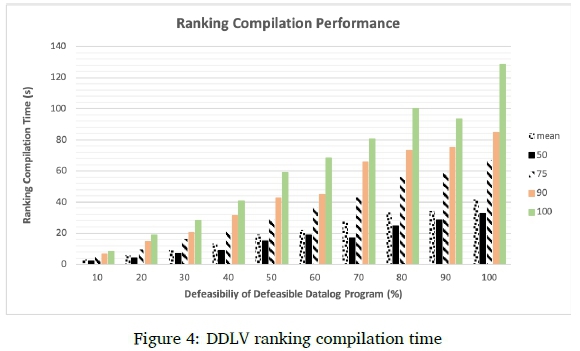
Figures 3 and 4 show the ranking compilation time of DIP and DDLV respectively. Figure 3 shows the ranking compilation time for DIP for each of 10 groups of defeasible ontologies, while Figure 4 shows the ranking compilation time of DDLV for the 10 groups of defeasible Datalog programs. Moodley used percentile plots because they give a good general picture of the performance and reveal outliers quickly (Moodley, 2015). For example, if the value for the P90 bar is 40 seconds then it means that 90% of the ontologies (in the case of DIP) or programs(in the case of DDLV) could have their ranking computed in 40 seconds or less. Note that the vertical scale for Figure 3 is logarithmic whereas the vertical scale for Figure 4 is linear.

 

 

 

 

Computing the ranking is the greatest bottleneck with this approach. Once the ranking has been computed, defeasible entailment checks can be performed very quickly. We will first compare DDLV's ranking compilation time with DIP's.

As with DIP, the time that DDLV takes to compute rankings increases with the level of defeasibility present in the program. DDLV seems to perform favourably against DIP, though. DIP already takes about 100 seconds on average to compute a ranking for an ontology with 60% defeasibility. DDLV, in the worst case of Datalog programs with 100% defeasibility, only takes just over 40 seconds on average to compute a ranking. The longest DIP takes to compute a ranking is nearly 1000 seconds. The longest DDLV takes to compute a ranking is less than 130 seconds.

Next, we will compare the time DDLV takes to perform a defeasible entailment check with the time DIP takes to perform a defeasible entailment check. Figure 5 shows the time DIP takes to perform a defeasible entailment check using Rational Closure on the same groups of defeasible ontologies that it performed the ranking compilation on, while Figure 6 shows the time DDLV takes to perform a defeasible entailment check using Rational Closure on the same groups of defeasible programs that it performed the ranking compilation on. Note that the vertical scale for Figure 5 is logarithmic whereas the vertical scale for Figure 6 is linear.

 

 

 

 

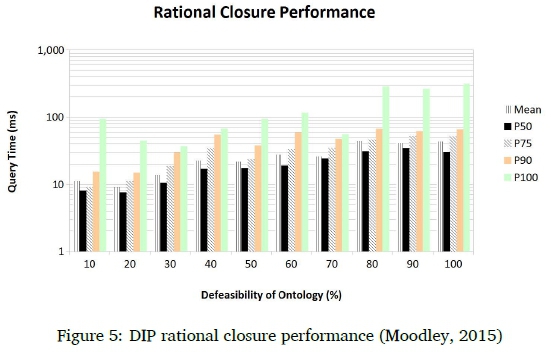
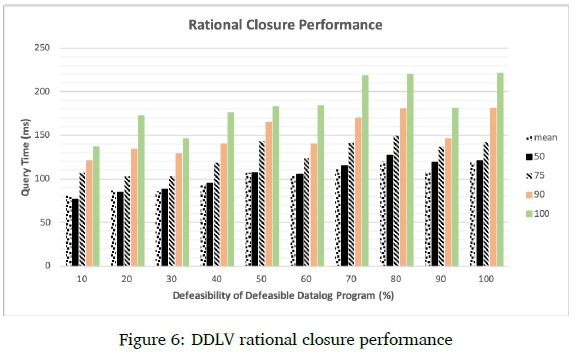
DDLV does not outperform DIP on average when it comes to defeasible entailment checks. DIP's average query time is less than 50 milliseconds, even for ontologies with 100% defeas-ibility. DDLV's average query time is about 120 milliseconds in the worst categories. In the worst cases, however, DDLV outperforms DIP. The longest DIP takes to perform a defeasible entailment check is just over 300 millisconds whereas the longest DDLV takes to perform a defeasible entailment check is about 220 milliseconds. Even though DDLV's average query time is slower than DIP, the difference is very small in terms of real units of time and almost negligible when single queries are performed in isolation. The performance of DDLV's ranking computation is of value, because reducing the typical bottleneck imposed by a long ranking computation time will greatly increase the usability of the system. To test how well DDLV will scale up, we also present stress tests.

For the size stress test, we recorded the ranking compilation time for 20 defeasible Data-log programs varying uniformly in size from 5000 rules to 10000 rules, with all 20 programs having a 20% level of defeasibility. For the ranking depth stress test, we recorded the ranking compilation time for 20 defeasible Datalog programs of 5000 rules and a 20% level of defeasibility, while the number of ranks in each program varied from 2 to 21. These two tests were performed because the number of rules in a program and the number or defeasible ranks have shown to have the greatest impact on ranking time. The two stress tests were performed on an Intel Xeon processor with 96 cores. DDLV performs the exceptionality checks for each rule in a rank asynchronously. This allows DDLV to perform as many exceptionality checks in parallel as the number of cores available. We believe this approach contributes to the performance demonstrated in Figure 7 and Figure 8. The longest DDLV took to compute a ranking in the size stress test is just under 7 seconds for 8750 rules. The longest DDLV took to compute a ranking in the ranking depth stress test is just under 6.5 seconds for 19 ranks.

 

9 RELATED WORK

The KLM preferential reasoning approach has been lifted to the Description Logic setting a few times in different flavours (Britz et al., 2009; Britz et al., 2008; Britz et al., 2011; Casini & Straccia, 2010). DIP is the most similar work and the only other known implementation of KLM-style preferential reasoning. There is research into handling incomplete knowledge in Datalog programs (Eiter et al., 1997), but that is not the same type of nonmonotonicity that we are dealing with.

The nonmonotic approach we are taking is to elegantly deal with inconsistencies. There has been other work on handling inconsistency in Datalog programs. The existing work in inconsistency handling in Datalog has generally used an argumentation approach. Hecham et al. implemented a defeasible Datalog± reasoning system called DEFT (2017). Seeing as DEFT uses Datalogi as an underlying language, it does not use classic negation and, therefore, requires additional negative constraints to represent inconsistencies. Hecham et al. also proposed a new Statement Graphs formalism for defeasible reasoning based on argumentation (2018). This approach uses defeater rules that can prevent defeasible rules from being concluded. Deagustini et al. take an argumentation approach to defeasible reasoning for Datalogi (2018). The inconsistency they deal with arises from incoherence and is resolved using comparison criterion to establish which argument is preferred amongst arguments that attack each other. Wan et al. define a framework for dealing with defeasibility in disjunctive logic programs (2015). This approach requires additional override axioms to explicitly define the preference or priority of defeasible rules. Morris et al. (2020) consider a KLM approach to enriching Datalog with defeasibility by defining relevant closure and lexicographic closure. Their considerations are purely theoretical.

 

10 CONCLUSIONS AND FUTURE WORK

We have identified the need for an extension to Datalog that can handle inconsistent information in order to deal with exceptions. We introduced the defeasible Datalog language that is able to express defeasible Datalog rules and contradictory Datalog rules.

We lifted the KLM preferential reasoning framework to our defeasible Datalog setting. We defined versions of the rational closure algorithm and its supporting ranking and exceptionality algorithms for defeasible Datalog. We defined defeasible Datalog versions of the KLM postulates and proved that our rational closure algorithm meets these KLM requirements to be considered a rational consequence relation.

We introduced DDLV, a system for rational preferential reasoning for defeasible Datalog. We showed how our approach was implemented as a software tool in DDLV. We demonstrated the value of this approach by being able to reduce the critical functions of DDLV to classical entailment checks, thereby being able to leverage the performance of the well-established DLV. The evaluation of DDLV made the performance benefits of this approach quite clear whilst introducing espressive power that Datalog has not previously enjoyed.

In this paper, our preferential reasoning approach was very syntactic. Future work would involve clearly defining a semantics for this work and demonstrating the correspondence between the syntactic and semantic approaches.

 

References

Abiteboul, S., Hull, R. & Vianu, V. (1995). Foundations of databases (Vol. 8). Addison-Wesley Reading.

Antoniou, G., Billington, D. & Maher, M. J. (1999). On the analysis of regulations using defeasible rules. Proceedings of the 32nd Annual Hawaii International Conference on Systems Sciences. 1999. HICSS-32. Abstracts and CD-ROM of Full Papers, 7-pp. https://doi.org/10.1109/hicss.1999.772631

Ben-Ari, M. (2012). Mathematical logic for computer science. Springer Science & Business Media. https://doi.org/10.1007/978-1-4471-4129-7

Britz, K., Heidema, J. & Labuschagne, W. (2009). Semantics for dual preferential entailment. Journal of Philosophical Logic, 38(4), 433-446. https://doi.org/10.1007/s10992-008-9097-z        [ Links ]

Britz, K., Heidema, J. & Meyer, T. (2008). Semantic preferential subsumption. Eleventh International Conference on Principles of Knowledge Representation and Reasoning, 476-484.

Britz, K., Meyer, T. & Varzinczak, I. (2011). Semantic foundation for preferential description logics. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 7106 LNAI, 491-500. https://doi.org/10.1007/978-3-642-25832-9\_50

Casini, G. & Straccia, U. (2010). Rational Closure for Defeasible Description Logics. European Workshop on Logics in Artificial Intelligence, 77-90. https://doi.org/10.1007/978-3-642-15675-5\_9

Ceri, S., Gottlob, G. & Tanca, L. (1989). What You Always Wanted to Know About Datalog (And Never Dared to Ask). IEEE Transactions on Knowledge and Data Engineering, 1(1), 146-166. https://doi.org/10.1109/69.43410        [ Links ]

Deagustini, C. A., Martinez, M. V., Falappa, M. A. & Simari, G. R. (2018). How does incoherence affect inconsistency-tolerant semantics for Datalog±? Annals of Mathematics and Artificial Intelligence. https://doi.org/10.1007/s10472-016-9519-5

Dumas, M., Governatori, G., Ter Hofstede, A. H. & Oaks, P. (2002). A formal approach to negotiating agents development. Electronic Commerce Research and Applications. https://doi.org/10.1016/S1567-4223(02)00016-9

Eiter, T. & Gottlob, G. (1997). Disjunctive Datalog. ACM Transactions on Database Systems, 22(3), 364-418. https://doi.org/10.1145/261124.261126        [ Links ]

Eiter, T., Leone, N., Mateis, C., Pfeifer, G. & Scarcello, F. (1997). A deductive system for non-monotonic reasoning. International Conference on Logic Programming and Nonmonotonic Reasoning, 363-374. https://doi.org/10.1007/3-540-63255-7\_27

Garcia, D. R., Garcia, A. J. & Simari, G. R. (2007). Planning and defeasible reasoning. Proceedings of the International Conference on Autonomous Agents. https://doi.org/10.1145/1329125.1329393

Grosof, B. N., Labrou, Y. & Chan, H. Y. (1999). A declarative approach to business rules in contracts: Courteous logic programs in XML. ACM International Conference Proceeding Series. https://doi.org/10.1145/336992.337010

Harrison, M. & Meyer, T. (2020). Rational preferential reasoning for datalog. Proceedings of the South African Forum for Artificial Intelligence Research, 232-243.

Hecham, A., Croitoru, M. & Bisquert, P. (2017). Argumentation-based defeasible reasoning for existential rules. Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS, 3, 1568-1569.         [ Links ]

Hecham, A., Bisquert, P. & Croitoru, M. (2018). On a flexible representation for defeasible reasoning variants. Proceedings ofthe International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS.

Huang, S. S., Green, T. J. & Loo, B. T. (2011). Datalog and emerging applications. Proceedings of the 2011 international conference on Management of data - SIGMOD '11, 1213. https://doi.org/10.1145/1989323.1989456

Hustadt, U. & Motik, B. (2005). Description logics and disjunctive Datalog : The story so far. CEUR Workshop Proceedings, 147.

Hustadt, U., Motik, B. & Sattler, U. (2007). Reasoning in description logics by a reduction to disjunctive Datalog. Journal of Automated Reasoning, 39(3), 351-384. https://doi.org/10.1007/S10817-007-9080-3        [ Links ]

Kraus, S., Lehmann, D. & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44(1-2), 167-207. https://doi.org/10.1016/0004-3702(90)90101-5        [ Links ]

Lehmann, D. (1995). Another perspective on default reasoning. Annals ofMathematics and Artificial Intelligence, 15(1), 61-82. https://doi.org/https://doi.org/10.1007/BF01535841        [ Links ]

Lehmann, D. & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55(1), 1-60. https://doi.org/10.1016/0004-3702(92)90041-U        [ Links ]

Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S. & Scarcello, F. (2002). The DLV System for Knowledge Representation and Reasoning. ACM Transactions on Computational Logic (TOCL), 7(3), 499-562. https://doi.org/10.1145/1149114.1149117        [ Links ]

Lloyd, J. W. (2012). Foundations of logic programming. Springer Science & Business Media.

Martinez, M. V., Deagustini, C. A. D., Falappa, M. A. & Simari, G. R. (2014). Inconsistency-tolerant reasoning in Datalog± ontologies via an argumentative semantics. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 8864, 15-27.

Meyer, T., Moodley, K. & Sattler, U. (2014). DIP: A defeasible-inference platform for OWL ontologies. CEUR Workshop Proceedings.

Moodley, K. (2015). Practical Reasoning for Defeasible Description Logics (Doctoral dissertation). University of KwaZulu-Natal.

Morgenstern, L. (1998). Inheritance comes of age: Applying nonmonotonic techniques to problems in industry. ArtificialIntelligence. https://doi.org/10.1016/s0004-3702(98)00073-3

Morris, M., Ross, T. & Meyer, T. (2020). Defeasible disjunctive datalog. Proceedings of the South African Forum for Artificial Intelligence Research, 208-219.

Nenov, Y., Piro, R., Motik, B., Horrocks, I., Wu, Z. & Banerjee, J. (2015). Rdfox: A highly-scalable rdf store. International Semantic Web Conference, 3-20. https://doi.org/10.1007/978-3-319-25010-6_1

Ricca, F. (2003). A Java wrapper for DLV. CEUR Workshop Proceedings, 78, 305-316.         [ Links ]

Wan, H., Kifer, M. & Grosof, B. (2015). Defeasibility in answer set programs with defaults and argumentation rules. Semantic Web. https://doi.org/10.3233/SW-140140

 

 

Received: 31 May 2020
Accepted: 11 November 2020
Available online: 08 December 2020

 

 

1 Datalog is often written with the head on the left and the body on the right, with a full stop at the end of each rule. :- is also often used to represent the implication operator instead of -. This more traditional representation is used for the syntax of our implementation.
2 - is used to represent negation in our implementation.
3 :~is used to represent defeasible implication in our implementation.
4 https://github.com/MindfulMichaelJames/DDLV