RESEARCH ARTICLE

 

Defeasibility applied to Forrester's paradox

 

 

Julian Chingoma^{I, II}; Thomas Meyer^{I, II}

^IDepartment of Computer Science, University of Cape Town, South Africa Email: Julian Chingoma chingy.j@hotmail.com (corresponding), Thomas Meyer tmeyer@cair.org.za
^IICentre for Artificial Intelligence Research, South Africa

 

 

---

ABSTRACT

Deontic logic is a logic often used to formalise scenarios in the legal domain. Within the legal domain there are many exceptions and conflicting obligations. This motivates the enrichment of deontic logic with not only the notion of defeasibility, which allows for reasoning about exceptions, but a stronger notion of typicality that is based on defeasibility. KLM-style defeasible reasoning is a logic system that employs defeasibility while Propositional Typicality Logic (PTL) is a logic that does the same for the notion of typicality. Deontic paradoxes are often used to examine logic systems as the paradoxes provide undesirable results even if the scenarios seem intuitive. Forrester's paradox is one of the most famous of these paradoxes. This paper shows that KLM-style defeasible reasoning and PTL can be used to represent and reason with Forrester's paradox in such a way as to block undesirable conclusions without completely sacrificing desirable deontic properties.
CATEGORIES: • Theory of computation ~ Logic • Theory of computation ~ Semantics and reasoning

Keywords: deontic logic, defeasible reasoning, propositional typicality logic, Forrester's paradox

---

 

 

1 INTRODUCTION

Logic has for a long time been used to formalise legal norms and study legal reasoning (Grossi & Rotolo, 2011). The difference between "what is the case" and "what should be the case" is fundamental to law and this naturally translates to deontic logic and its notions of obligation, permission and prohibition. This paper is part of a research study which focuses on introducing the notion of defeasibility into a deontic setting, a task that has been investigated for many years within the deontic logic community. Defeasibility allows for reasoning about exceptions in a domain, distinguishing between "what is normally the case" and "what is actually the case" (Makinson, 1993, 2005). It is important to note there are already notions of defeasibility in the world of legal reasoning. The introduction of new information or a new regulation can cause laws to conflict and/or present exceptions which make existing laws inapplicable (Grossi & Rotolo, 2011). Therefore the further exploration of the use of defeasibility and defeasible techniques within a deontic context is of interest. KLM-style defeasible reasoning is a logic system which allows for conclusions to be retracted and therefore allows for dealing with exceptions (Casini & Straccia, 2012; Kraus et al., 1990). Typicality is based on defeasibility and is a notion used in Propositional Typicality Logic (PTL) where its extra expressivity makes it a more powerful version of defeasibility (Booth et al., 2015). In deontic logic research, it is common for systems to be validated with the use of deontic paradoxes (van der Torre, 1997). One of the famous paradoxes is Forrester's paradox, also known as the Gentle Murder paradox (Pigozzi & van der Torre, 2017; van der Torre, 1997). The semantic connection between deontic logic and the logic systems of defeasibility and typicality will be discussed later in the paper. This paper will present the paradox and also examine the effectiveness of KLM-style defeasible reasoning and PTL when applied to the paradox. This examination will mainly consist of three steps. To begin with, we must find a representation of the deontic statements for each of KLM-style defeasible reasoning and PTL. Then we must determine which of the deontic properties that we deem to be desirable are satisfied by these logic systems. We then must examine whether Forrester's paradox and its issues can be dealt with in a reasonable manner using these logic systems.

Now we outline the structure of the paper. We begin by presenting propositional logic as this is the logic that forms the foundation of the logic systems we will be working with. We then detail the following logic systems: KLM-style defeasible reasoning, deontic logic and pro-positional typicality logic. The deontic logic section will be where Forrester's paradox and its issues are detailed. Once these have been detailed we then look at the analysis of Forrester's paradox using KLM-style defeasible reasoning and PTL. During this analysis we show that, for both logic systems, we can find sensible representations for the paradox and can subsequently deal with the paradox's issues in a reasonable manner. Finally, we present the conclusions. This paper is an extended version of a paper published in the proceedings of the South African Forum for Artificial Intelligence Research (Chingoma & Meyer, 2019).

 

2 PROPOSITIONAL LOGIC

Propositional logic is a logic used to formalise statements that can either be true or false (Booth et al., 2015). These statements are usually represented using propositional letters such as p,q and r. Given a set of propositional letters $, the language of propositional logic can be formed with the following constants and operators (Booth et al., 2015; Parent & van der Torre, 2018; Pigozzi & van der Torre, 2017). ± is a constant which represents a contradiction while - and A are operators which represent negation and conjunction respectively. V is the disjunction, - represents implication which makes o the double implication/"if and only if" and T is the tautology (Parent & van der Torre, 2018; Pigozzi & van der Torre, 2017). These various parts of the language can be combined to create propositional formulas, usually represented by a, β, Y, etc. For example, p - -q and (p A q) V -r are propositional formulas. Since the reasoning aspect is of interest, it is important to mention the notion of entailment. Entailment refers to what conclusions logically follow from a set of premises (Booth et al., 2015). The classical way to do this in propositional logic is to look at the truth assignments of the propositional letters, usually denoted using valuations. A valuation is an assignment of either true or false to each propositional letter. For example, {p, -q} is a valuation where p is true and q is false. Let's take W to denote the set of all valuations. Given a valuation s e W, a propositional letter p and a propositional formula a, we can define the satisfaction in the language as follows (Parent & van der Torre, 2018):

• s = p iff p is true in the valuation s

• s = -a iff not s = a, as in a is false in s

• s = a A ( iff s = a and s = (, as in a and ( are both true in s

• s = a V j( iff s = a or s = (5, as in at least one of a and (5 are true in s

• s = a - 5 iff s = -a V 5, as in at least one of -a and (5 is true in s

• s = a o 5 iff s = a - 5 and s = ( - a

Classical entailment commonly denoted using =, tells us what logically follows from a set of premises such as a knowledge base. A classical knowledge base, let's say KB, is a set of propositional formulas. If all the valuations that model KB, modelling a knowledge base means the valuation satisfies all the formulas in KB, also satisfy a formula a, then we say that KB entails a. This can be represented by KB = a.

 

3 KLM-STYLE DEFEASIBLE REASONING

The logic system, proposed by Kraus et al. (1990), is a form of non-monotonic reasoning, which is reasoning that allows for conclusions to be retracted. The property of monotonicity is one that classical logic systems satisfy which states that the addition of new, and possibly contradictory, information strictly leads to more conclusions. This does not align with the usual thinking of humans who can deal with exceptions and thus this system allows us to reason defeasibly. Take for example, we have the statements "Students do not pay tax" and "John is a student and a part-time worker", so we can conclude that John does not pay tax. Now we add the statement "Students who are part-time workers pay tax". Without non-monotonicity, this addition would cause a contradiction as John both pays tax and does not pay tax. But intuitively, we should be able to retract the first conclusion that John does not pay tax as we now know of an exception, namely that students who are part-time workers pay tax. This aligns more with the commonsense reasoning of humans.

3.1 Language

The language of the KLM-style defeasible reasoning is formed by a set of propositional letters $, the operators and constants of propositional logic with the addition of the following defeasible implication operator, |~. Thus the language of the KLM approach is an enriched version of propositional logic where we can form defeasible implications such as a \^ (, which can be read as "a usually implies (" where a and ( are propositional formulas.

3.2 Semantics

The semantics for the KLM approach is defined in the form of ranked interpretations. A ranked interpretation, R, is a set of valuations, let's say V ç W, along with a binary relation < where the valuations are ranked, with some valuations being preferred to others. We have that < is reflexive, antisymmetric, connected and transitive. And given a ranked interpretation R and a formula a, the set of valuations that satisfy a are represented as [aJ^R, where [aJ^R= {v e V | v = a} (Booth et al., 2015). We say that a defeasible implication, let's say a \^ (, is satisfied in a ranked interpretation if the minimal valuations where a is true are the valuations where ( is also true, min<[aJ^Rç [(J^R(Booth et al., 2015; Lehmann & Magidor, 1992). That is to say that given [aJ^R, for every v' in V, if we have v' e {v e [aj^R : v < w for every w in [aJ^R}, then v' = (. v < w means that v is at least as preferred as w.

3.3 Properties of rational defeasible entailment relation

We now present the defeasible counterpart to the classical entailment relation, =, that we have seen in the previous section. We will use this defeasible entailment relation to denote what we can derive from a defeasible knowledge base. A defeasible knowledge base being a set which includes classical propositional formulas such as a, -a, a V ( and a - (, along with defeasible implications such as a \^ (. Defeasible entailment will be denoted using the relation fc and for example, a statement such as KB a \^ (( tells us that a \^ ( follows from the knowledge base KB. Below we list some of the properties that the defeasible entailment relation, fc, ought to satisfy in order to be considered rational. Note that the below properties are not a complete list of those needed to consider a defeasible entailment relation to be rational. The remaining properties are omitted as they are not used when dealing with the issues of Forrester's paradox. The role of the below properties in the paradox's issues will be detailed in the following section. These properties are to be interpreted as if we have a defeasible knowledge base, let's say KB, which makes use of propositional formulas such as a, ( and 7.

Conjunction If we have KB |≈ α |∼ β and KB |≈ α |∼ γ then we can derive KB |≈ α |∼ β ∧ γ

If we have that α |∼ β follows from the knowledge base and also have that α |∼ γ follows from the knowledge base. If we have for example that "being a student usually implies having a student card" and also have "being a student usually implies paying the fees in full" then we would want it to be the case that "being a student usually implies having a student card and paying the fees in full".

Weakening If we have |= β → γ and KB |≈ α |∼ β then we can derive KB |≈ α |∼ γ

If we have ( - 7 as a tautology and that a \ ( follows from the knowledge base, this property tells us that we can conclude that a \ 7 follows from the knowledge base. If we have for example that 'being a student implies having a student card" and 'paying the fess in full usually implies being a student" then we should be able to derive 'paying the fess in full usually implies having a student card".

Rational Monotonicity If we have KB |≈ α |∼ β and KB ̸|≈ α |∼ ¬γ then we can derive KB |≈ α ∧ γ |∼ β.

If we have that α |∼ β follows from the knowledge base and also have that α |∼ ¬γ does not follow from the knowledge base, this property tells us that we can conclude that α ∧ γ |∼ β ( follows from the knowledge base. If we have for example that 'being a student usually implies having a student card" and also have 'being a student does not usually imply not paying the fees in full" then we would want it to be the case that 'being a student and paying the fees in full usually implies having a student card".

3.4 Lexicographic Closure

We now present the reasoning algorithm we will use when dealing with the KLM approach. Lehmann detailed a form of entailment for defeasible reasoning called lexicographic closure (Lehmann, 1995). This method satisfies the properties outlined in the previous section as well as those that were omitted which were required to consider an entailment relation as rational.

Now we present the steps for a lexicographic closure algorithm that we used during the paradox analysis. Let's take the following example knowledge base, {b \^ f,b\ w,p \^ -f,p - b,r - b}, and observe the algorithm's process more clearly. In the example, we have that p is a "penguin", r is a "robin", b is a 'bird", f is "to fly" and w is "has wings". For the purpose of the example, let's say we wish to observe whether we can derive p \^ w, "penguins have wings" from the knowledge base using lexicographic closure. The following are the summarised steps of a lexicographic closure algorithm for propositional logic by Casini et al., which was generalised in order to be implemented for Description Logics (Casini & Straccia, 2012). We will begin by separating the knowledge base into A = {p - b,r - b} and B = {b \^ f,b \^ w,p \^ -f}, which are the classical and defeasible parts of the knowledge base respectively. We will use A and B along with the entire knowledge base, KB, in various parts of the algorithm. When we refer to the premise, we are referring to the antecedent of the defeasible statement which we query. So if we were to query whether p \^ w is derived by lexicographic closure then p would be the premise. Intuitively, when determining what follows from a premise, we look to take into consideration as many statements of a 'better' rank as possible. Thus the algorithm will assign ranks to the statements and separate them into various subsets. Then it will look to determine which subsets to derive conclusions from, based on the number of statements, starting from the highest ranked statements, the subsets satisfy.

Step 1 We create a set of materialisations of the statements in the knowledge base and refer to it as kB. A materialisation is the converting of defeasible implications into classical implications so that we have ÏcB being the classical implications of KB along with {a - 3 | a \\ 3 e KB}. We must then check the consistency of the knowledge base using the materialisations set. If a knowledge base is inconsistent then anything will follow from it, which is not desired when reasoning. A knowledge base KB is inconsistent if and only if kB = _L. We have that kB in our example is {p - b,r - b,b - f,b - w,p - -f} which is consistent and we continue with the algorithm.

Step 2 We then give each statement in B a ranking based on their exceptionality. A formula a is exceptional in a defeasible knowledge base, let's say, KB if and only if ÏcB = -a (Giordano et al., 2015; Lehmann & Magidor, 1992). This tells us the materialisation set classically entails the negation of the formula. And a defeasible implication is exceptional if its antecedent is exceptional with respect to KB. For example, 3 is exceptional in KB if a is exceptional in KB. In order to determine the degree to which a defeasible implication is exceptional, we construct a non-increasing sequence of exceptional subsets of KB. We say that E (KB) is the set of the exceptional defeasible implications of KB (Giordano et al., 2015; Lehmann & Magidor, 1992). Now, we consider a sequence of subsets of KB, C_ifor i > 0, where C₀ = KB, and C_i = E(C_i_i). For a KB, there is an n > 0 such that C_n = 0 or for all m > n, C_m = C_n. We then say that the rank of a formula, let's say a, will be the smallest natural number, i, in the subset sequence such that a is not exceptional. If the formula is exceptional for all the subsets in the sequence then it is given an infinite rank. Classical statements are also given an infinite rank. This can be seen as we can turn a classical statement, such as a - (3, into a defeasible statement (a A-3) \^ _L, and for the antecedant, a A-3, to be exceptional, we would require ïcB = -a V (. This is equivalent to ïcB = a - 3 which will always be the case. Thus classical statements receive an infinite rank as they will always be exceptional. The ranks of the example's statements in B are as follows, {rk(b \^ f) = 0, rk(b \^ w) = 0, rk(p \^ -f) = 1}. The ranks for the statements in A will be infinite and for the example we have rk(p - b) = oo and rk(r - b) = oo.

Step 3 We define the set B to be {a\^ 3 e B | rk(a \^ 3) < oo}. So B will be all the defeasible implications in B with a rank less than infinity. The rank of B, rk(B), will be the highest rank among the defeasible implications in B. The example's B will be {b \^ f,b\^ w,p \^ -f} and

rk(B) = 1.

Step 4 We will now define T, which will be the set of the most preferred subsets of X which are consistent with our premises and A, where X = {a - ( | a \^ ( e B}. Take k to be the rank of B and define the subset Xⁱas the subset of statements in X which have rank i. So we can now give every subset D of X a sequence of natural numbers with each number representing a count of statements, which have a certain rank, that appear within that subset. For the sequence, ( n₀, ...,n_k)_D, the numbers are generally defined as n_i=| D n X^k-i|. It is with these sequences of numbers that we rank the subsets, where the number of statements they satisfy is important along with the exceptionality of statements they satisfy. Let's say we have that ( n₀,...,n_k) > ( m₀,...,m_k) iff (i) for every i (0 < i < k),n_i> mi or (ii) if ni < mi, then there is a j such that j < i and nj > mj. We can say that a subset D is preferred to a subset E iff ( n₀, ...,n_k)_D> ( n₀, ...,n_k)_Ewhere > refers to the above relation > but having ( no, ...,nk)d = ( no, ...,nk)s.

So now to define the set T for our example. We list the subsets of X along with their natural number sequence. Note again that rk(B) = 1.

• {p - -f, b - f,b - w} - (1,2) as one statement is of rank 1 while two are of rank 0.

• {b - f,b - w} - (0, 2)

• {b - f,p - -f} - (1,1)

• {b - w,p - -f} - (1,1)

• {b - f} - (0,1)

• {b - w} - (0, 1)

• {p - -f} - (1,0)

So for premise p and A = {p - b, r - b}, T will be {{b - w, p - -f}}.

Step 5 Finally, given the premise, p, we say p \^ w is in the lexicographic closure if p∪A∪D |= w for every D e T. So if we take p to be the premise, we can see that p\\ w is in the lexicographic closure and this can be denoted withp |∼lcK B w.

 

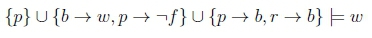
4 DEONTIC LOGIC

This section will formally present deontic logic and the specific logic system we will investigate. Deontic Logic is a field of logic which formalises normative concepts. These concepts include obligation ("what is an individual's duty", "what an individual ought to do"), permission ("what an individual may do") as well as other related concepts such as prohibition ("what an individual is forbidden from doing") (Hansson, 1969; Hilpinen & McNamara, 2013; Parent & van der Torre, 2018; Pigozzi & van der Torre, 2017). The system we will be working with is the traditional Dyadic Standard Deontic Logic (DSDL) approach (Parent & van der Torre, 2017, 2018; Pigozzi & van der Torre, 2017) although there are alternative approaches to deontic logic such as input/output logic (Hilpinen & McNamara, 2013; Makinson & van der Torre, 2000). The reason we opted for the more traditional approach was that it has a semantics based on valuations, similar to that of the other logic systems we deal with in this research study (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017).

4.1 Language

Given a set of propositional letters $, the language of Dyadic Standard Deontic Logic (DSDL) can be represented with the following operator added to the propositional logic language (Parent & van der Torre, 2018; Pigozzi & van der Torre, 2017): the O-operator is added which represents obligation. This operator in DSDL handles conditional obligations such as "if p is true then it ought to be the case that q is true". Such statements can be represented using the "I" notation which is usually seen in conditional probability. The above example would be translated to O(q I p) in DSDL. This operator can be used similarly to the negation operator, -, in that it can be placed in front of any propositional formula and can be applied in a nested fashion such as in the following example DSDL formula O(p I q AO(r I p)) (Parent & van der Torre, 2018). Since many legal statements are of the conditional form, the conventional DSDL will be the logic used when we are dealing in the deontic environment instead of Standard Deontic Logic (SDL) which does not have the "I " mechanism for conditional obligations. The notion of permission is related to obligation by Pp = -O-p and that of prohibition being similarly related by Fp = O-p. Pp is to be read as "p is permitted" while Fp can be read as "p is prohibited/forbidden" (Parent & van der Torre, 2018; Pigozzi & van der Torre, 2017). Obligations without a conditional can be written in the conditional form in the following manner Op = O(pI T) (Pigozzi & van der Torre, 2017).

4.2 Semantics

We can now formally define the preference-based semantics for DSDL which is presented with similar formal definitions by Parent and van der Torre (2018) and Pigozzi and van der Torre (2017). We have preference models defined as M = (V, <) where V ç W, with W being a nonempty set of possible valuations. Note that we will not allow for duplicate valuations. < is not

only a binary relation over V but a total preorder as it is reflexive, transitive and connected. The operator = represents the satisfaction of a formula. Given a model M, a valuation s e V as well as propositional formulas a and (, we can define the satisfaction of formulas in the deontic language as the usual notion for classical propositional satisfaction, covered in Section 2, along with the following (Parent & van der Torre, 2018):

• M,s = O(( I a) iff Vs¹e V, if s¹e {s e [a] : s < t, Vt e [a]}, then M,s' = ( (where [a] = {s e V : M,s = a}). So O(( I a) means that given a being true, then only if the "minimal" or "most typical" valuations that satisfy a also satisfy ( can we then can derive that ( is obligatory

4.3 Properties

The following is an outline of some of the desirable deontic properties that commonly occur in the deontic logic literature (Goble, 2013; Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017; van der Torre, 1997). These properties were chosen because they were presented as being important, or at least relevant, when assessing the usefulness of deontic logic systems. Thus they should be seen as properties that an ideal system of deontic logic would have. Note, this is not a full list of properties that can seem desirable for a deontic logic nor are they necessary properties for a reasonable deontic system. These are simply those needed for the analysis of Forrester's paradox in the paper.

Ought Implies Can ¬⃝(α ∧ ¬α)

This property could also be represented as - O_- as the conjunction of conflicting tasks, a A-a, will be a logical contradiction and can therefore be represented by _L. The property states that it is undesirable for contradictory tasks such as a and -a to be obligatory. Without "ought implies can", the derivation of a contradiction, e.g OL , would be acceptable and simply indicate that there has been a violation.

Factual Detachment If we have O(( I a) and a then we can derive O(

If we have an obligation to do a task ( when a is satisfied, once we have that a has happened then it is intuitive that we are now obligated to do (.

Restricted Strengthening of the Antecedent If we have O(( I a) then we can derive O(( I 7 A a) if 7 is true

Let's say we have the obligation to do ( when a is satisfied. It is intuitive that a more specific version of a being true would still make ( obligatory. Note that the restricted version of the property that we refer to requires the formula a A 7, of the derived obligation O(( I 7 A a), to be consistent. The property will also be occasionally referred to as RSA in this paper.

Conjunction If we have O(( I a) and O(7 I a) then we can derive O(7 A ( I a)

Let's say we have an obligation to do a task ( when a is satisfied. And we also have an obligation to do 7 when a is satisfied. By combining these two obligations, it is intuitive that we are now obligated to do both ( and 7 when we have a. We will be working with a restricted version of this property where we will require that ( A 7 be consistent.

Weakening If we have O(( A 7 | a) then we can derive O(( I a)

Let's say that we have the obligation to do both 7 and ( when a is satisfied. It is intuitive that we can derive an obligation to do only one of 7 or ( when a is satisfied. So Weakening can be applied in this scenario since we know ( A 7 - (5 is always true.

4.4 Forrester's paradox

Forrester's paradox is one of the most frequently occurring paradoxes in the deontic logic literature (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017; van der Torre, 1997). Although this is not a logical paradox in the usual sense, but rather a dilemma or problem, we will retain the terminology from the literature. One of the reasons that this paradox was chosen by us is that it is similar in structure to many other deontic examples as it is a contrary-to-duty scenario (van der Torre, 1997). As scenarios with the contrary-to-duty structure have challenged deontic logic researchers, another reason we look at the paradox is that it provides difficulties that the straightforward examples would not (Parent & van der Torre, 2017; van der Torre, 1997). For obligations O(ai I (₁) and O(a₂I (₂), we say that the obligation O(a₂I (₂) is a contrary-to-duty obligation of O(a₁I (₁) if its antecedent, (₂, is contradictory to the consequent of the first obligation, a₁. Intuitively, this means an obligation that informs us what must be the case when something forbidden has been done (Rönnedal, 2019).

This paradox comprises the following three statements. "You must not kill anybody", "Ifyou kill someone then you must kill them gently" and "You killed someone". With this we also have the background knowledge that "Killing gently implies killing" (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017; van der Torre, 1997). We will now detail two undesirable derivations that occur through the different combinations of the deontic properties on this paradox's set of statements. Both are presented as they illustrate different issues with the paradox and the properties. In the following figures, derivations of obligations are shown using an arrow with a subscript containing the abbreviation of the property which was used for the derivation. O(5 I a) -_WO(7 I a) would mean the Weakening property was used to go from O(( I a) to O(7 I a). Weakening would be an applicable property in this example if we knew ( - 7 to always be true. For derivations that involve more than one obligation as the premise, these obligations are displayed between braces and separated by a comma. {O(7 I a), O(5 I a)} -conj O(7 A ( I a) means that the Conjunction property was used on the obligations O(7 I a) and O(( I a) to derive O(7 A ( I a). The paradox's statements can be represented by the following deontic knowledge base: {O-k, O(g I k), k}

4.4.1 RSA, Weakening and Conjunction

The following table illustrates the derivations of the Restricted Strengthening of the Anteced-ant, Weakening and Conjunction properties.

The background knowledge is represented by g - k. When we apply Weakening to the first obligation "You must not kill anybody", we can then derive "You must not kill gently" since we have that "Killing gently implies killing" and the contrapositive that "Not killing implies not killing gently". This is an intuitive derivation since killing gently is still killing, which we want to be forbidden. Then using RSA and the fact that "You killed someone", we can go from "You must not kill gently" to "If you kill then you must not kill gently". This derivation is the issue with the paradox, an obligation becoming the premise from which its own contrary-to-duty obligation is derived is counter-intuitive (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017). Then using Conjunction we can derive a contradiction from the obligations "If you kill then you must not kill gently" and "Ifyou kill then you must kill gently". If we have the aforementioned "ought implies can" property then this would be undesirable (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017; van der Torre, 1997). Without it, we would be satisfied with the derivation of a violation but "ought implies can" states we don't want to settle for a contradiction but rather to act as best as possible in the case of a violation (van der Torre, 1997).

4.4.2 Factual Detachment and Conjunction

The following table illustrates the derivations of the Factual Detachment and Conjunction properties.

The rule of Factual Detachment gives us "You should kill gently" from the fact "You have killed" and the obligation "Ifyou kill then you should kill gently". Applying Conjunction to "You should kill gently" and the non-conditional obligation "You ought to not kill someone" gives us "You should not kill and you should kill gently" which is an undesirable derivation if one was to use the "ought implies can" principle (Parent & van der Torre, 2017; Pigozzi & van der Torre, 2017). And as in the previous derivation, if we do not have "ought implies can" then the derivation is not a problem.

 

5 PROPOSITIONAL TYPICALITY LOGIC

5.1 Language

Given a set of propositional letters $, the language of the propositional typicality logic, denoted by can be represented with the following «-operator added to the propositional logic language (Booth et al., 2015): There is «a with its intuition being that it represents the most typical situations where a holds. This operator can be used similarly to the negation operator - in that it can be placed in front of any propositional formula and can be applied in a nested fashion such as in the following example PTL formula «« p. This means that PTL is more expressive than KLM-style logic (Booth et al., 2015) from Section 3 and the bullet operator can be applied to both the antecedent and consequent side of a conditional. Note that the PTL statement «a - ( would be equivalent to the KLM statement a \^ (. The following example illustrates how it can be used. «a - «-(5 stands for "the most typical situations where a holds, imply the most typical situations where ( does not hold". Note, this is a similar reading to the semantics to that of DSDL conditionals as stated in Section 4.2.

5.2 Semantics

For the semantics of PTL, ranked interpretations are used. With W being the set of possible valuations, ranked interpretations are pairs < V, <>, where V ç W and < is a total preorder over V. Intuitively, the valuations pushed lower down the rankings are more typical than those that are higher (Booth et al., 2015). And given a ranked interpretation R and a formula a, the set of valuations that satisfy a are represented as \a\^R(Booth et al., 2015). Satisfaction of a formula is defined in the classical way, such as in Section 4.2, with the omission of the O-operator satisfaction and the addition of the following (Booth et al., 2015): v = «a iff v = a and there is not a V < v such that V = a. So the valuations that satisfy «a will be the minimal valuations that satisfy a. So {«a\^R:= min<(JaJ^R) for a ranked interpretation R.

Note that the typicality «-operator can express any KLM-style conditionals. That is, for every ranked interpretation R and every a, ( e L, R=a \ ( if and only if R = « a - (. There are L'-sentences that cannot be expressed using KLM-style |~-statements on L, so the converse does not hold (Booth et al., 2015). Now the method of entailment we will use, which is proposed by Booth et al. (Booth et al., 2015), is outlined.

5.3 LM-entailment

The first form of entailment to be looked at is one that produces a single ranked model that is constructed to be the LM-minimum model for the knowledge base. A sequence of ranked interpretations (R₀,Ri,R₂,...) constructed by the algorithm will be used to construct R*_KB, the ranked model, which will be used for entailment. The algorithm will make use of ranks in order to construct RK_B. The ranks represent a level in the ranked interpretation, where the rank of a valuation u is less than the rank of v if and only if u < v, as defined in Section 5.2 (Booth et al., 2015). The following is some of the notation used in the algorithm. In this algorithm, we say R^l_sis the ranked interpretation obtained when any valuation not in S, where S ç V^Rwhere is V^Rare the valuations given a ranked interpretation R, has its rank increased by 1. Similarly, RS? is the ranked interpretation obtained from R by setting the rank of all valuations not in S to oo (Booth et al., 2015). These would represent those at the highest level of RKc_Band deemed to be atypical. Intuitively, the reasoning of the algorithm is separating out the valuations which satisfy the knowledge base when taking a certain ranked interpretation into account and building the ranked model in that manner. Now to present the steps in the algorithm (Booth et al., 2015).

Step 1 Set the ranks of all valuations in the knowledge base to 0, define S₀which is initially empty and have variable i equal to 1.

Step 2 Find the valuations which satisfy the knowledge base with respect to the current ranked interpretation R₀, as in every knowledge base statement holds true in this valuation, and put them into the set Si.

Step 3 If S_iis equal to S_i_₁then there hasn't been a change so set the rank of all the valuations that do not satisfy the knowledge base with respect to Ri to o and return the interpretation that remains.

Step 4 Otherwise create a new ranked interpretation R_i, by increasing the rank of every valuation not in Si by 1.

Step 5 Find the valuations which satisfy the knowledge base with respect to the current ranked interpretation R_iand put them in the set S_i+1and finally, increment i. Step 6 Go to Step 3.

Example Now to present an example that illustrates the above steps. Let's take the knowledge base, {»p - -f, »b - f,p - b}. The conditionals can be read as "typical penguins do not fly", "typical birds do fly" and "penguins are birds". The situations that are most reasonable given the information we have would be the situations where there are no penguins while the most typical birds do fly. Such a scenario would satisfy all the statements. It seems reasonable that the next best situation is when the most typical penguins don't fly while we can have that non-typical birds also don't fly. Then we can have that non-typical penguins do fly. The least desirable situations are when we have penguins that aren't birds at all as this violates a classical conditional, p - b. Now to look if the reasoning matches our intuition.

We first note that because of the last statement we can immediately discount the valuations {p, -b, f} and {p, -b, -f} as having infinite rank, and therefore on the highest level, as they will never satisfy the set of statements. So we begin by setting the rank of all the valuations to 0. The valuations that satisfy all the statements are {-p, b, f}, {-p, -b, f} and {-p, -b, -f}. Therefore they become the first level of our model, S₁:= {KB}^R° = {{-p,b,f}, {-p, -b,f}, {-p, -b, -f}}.

All the valuations not in Si obtain a rank of 1. The valuations that satisfy all the statements w.r.t. R are {p,b, -f} and {-p,b, -f}. So we have S₂:= \KB\^Rl = {{p,b, -f}, {-p,b, -f}}. The remaining valuation {p, b, f} will be S₃and {p, -b, f} and {p, -b, -f} will be S₄. As previously mentioned the valuations in S₄will not satisfy the statements so S₄will remain the same as S₅and so on. The algorithm terminates at this stage. The ranked models for the Bird example generated during the execution of the LM-entailment algorithm are given in figure 1.

 

6 KLM ANALYSIS

This section aims to presents the analysis on the paradox using the KLM defeasible reasoning approach. The representation is chosen first, and then the properties are addressed. Then the problematic derivations of the paradox are investigated using the KLM approach.

6.1 Representation

We now present a guide to translate the deontic statements into their KLM equivalents. For the translation of deontic obligations into the language of the KLM defeasible reasoning, we say that 0(3 | a) is equivalent to a \\ 3. Non-conditional obligations such as Q)a will be represented as T \\ a. Facts are given in the usual way with no additional operators, such as a. This gives an appropriate method to handle the translation of deontic statements and allows for the analysis to continue.

6.2 Properties

In this section we look at which of the deontic properties that we deemed desirable are satisfied by the KLM-style defeasible reasoning approach. This begins with an analysis of the "ought implies can" principle's satisfaction and its subsequent impact on the way in which we reason within the KLM logic system.

6.2.1 Ought Implies Can Principle and Violations

When working with obligations, we ideally want to be able to explicitly state whether a certain fact brings up a violation with respect to our set of obligations. This will require the logic system we use to cater for the occurrence of conflicts. But when dealing with these KLM defeasible implications we will see that lexicographic closure cannot perform their reasoning with the presence of conflicts and thus satisfy the "ought implies can" principle. Ideally if one is obligated to perform a task then they should be able to do so, therefore the task should not be simultaneously obligatory and prohibited. This principle can be represented by the derivation of - O (a A -a) which tells us that there is no obligation to perform contradictory tasks. With conflicts being an explicit indication that a violation has occurred, the "ought implies can" principle means we must find a way to detect violations. To do this, we temporarily keep a fact in the knowledge base before the application of the lexicographic algorithm and check if the knowledge base is inconsistent. If so, then we check the fact against every obligation to identify which have been violated. We will then remove the fact from the knowledge base and determine which general obligations arise from the set of obligations we have along with the background knowledge. We then use the facts as a premise when examining the derivations of actual obligations. These actual obligations refer to the obligations which a hypothetical agent must act upon when certain facts are taken into consideration.

6.2.2 Deontic properties

In Section 3, we have that the following desired deontic properties used in Forrester's paradox are satisfied by the defeasible entailment relation of lexicographic closure, fc: Weakening and Conjunction. This allows us to look at the paradox's problematic derivations which involve these properties. Another of the desirable deontic properties which is satisfied is the Factual Detachment property. If we have KB fc a \\ ( and = a is a tautology, then either the knowledge base is inconsistent or we can derive that KB fc T \\ (. Note that we treat facts for this property differently than is usual, in that we do not consider it a possible or contingent fact, but rather, it has to be a tautology or known truth. The treatment will be similar in Section 7. We now move on to examine the remaining property of interest, Restricted Strengthening of the Antecedent.

6.2.3 Strengthening of the Antecedent

Recall that we will not have the Strengthening of the Antecedent property with lexicographic closure since the reasoning we will be using is non-monotonic (Kraus et al., 1990). We instead have the property of Rational Monotonicity in the KLM logic system which was outlined in Section 3.3. This property will serve as an alternative and is shown again below.

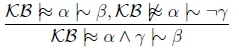
Although not having any version of the Strengthening of the Antecedent property blocks us from intuitive derivations, its omission also results in many issues within the paradoxes no longer arising.

6.3 Forrester's paradox analysis

This paradox comprises three statements. The obligations "You must not kill anybody" and "If you kill someone then you must kill them gently" as well as the fact "You killed someone". Along with these we also have the background knowledge, "Killing gently implies killing". The KLM equivalent of these obligations is given in the following set of KLM statements and this comes with the translated background knowledge, g - k and the fact k.

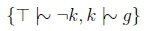
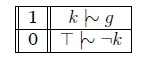
It is clear that the fact k causes the knowledge base to become inconsistent with respect to kÈ if it were included during reasoning and it is clear that T \\ -k is the obligation that is violated. We then continue to build a ranking based on exceptionality. We now have a consistent fcB to construct the ranking of the statements. We have B = {T \ -k, k \ g} with rk(T \\ -k) = 0 and rk(k \\ g) = 1 so the ranking would be the following:

Now we examine what can be gathered given the above ranking and compare this with the paradox's undesirable derivations.

6.3.1 Restricted Strengthening of the Antecedent, Weakening and Conjunction

We first want to check if we can derive O-g as a general obligation before we apply the fact. This was derived via the Weakening property as seen in the above table. As a non-conditional obligation, we assume the tautology, T as the premise and observe if we can derive -g. With T as the premise, we have D = {T - -k, k - g} and we include the background knowledge g - k in the set of statements which have infinite rank, A, where it is the only statement. We then have the following derivation which shows that -g follows from our knowledge base using lexicographic closure. This is clear through the contraposition of g - k, which is -k - -g.

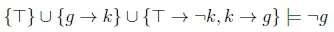
Now we look at whether we can derive the undesirable conditional obligation O(-g | k). This was derived using Restricted Strengthening of the Antecedent in the above table but recall that we do not have this property. It is thus of interest to observe whether the alternative, Rational Monotonicity, 'blocks' this undesirable obligation from being derived. This would be considered an actual obligation which occurs when we take the fact that killing has occurred. For this situation, we have k as the premise and D = {k - g}. This results in the following derivation which tells us that we cannot derive -g from the knowledge base given the fact k

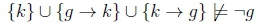
Intuitively, this tells us that although there we can originally derive O-g which tells us "do not kill gently" in general, once one kills then we retract that obligation. This seems reasonable since the individual will now be obligated to kill gently once they have killed.

6.3.2 Factual Detachment and Conjunction

For the first derivation, we examine whether we can derive Og given the fact k. With this being a non-conditional obligation, we would normally have the tautology as the premise but taking the fact k into account means we use k as a premise. We then have that D = {k - g} and A = {g - k}. The following derivation tells us that we can derive the obligation to do g.

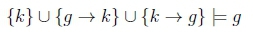
We can also see lexicographic closure also blocks the issues that come between Factual Detachment and Conjunction where O(-k A g) can be derived. We continue to take k as the premise since have already taking it into account. We still have D = {k - g} and A = {g - k}. While g follows from this lexicographic closure configuration, we cannot derive - k. Thus we cannot derive the undesirable O(-k A g) using lexicographic closure.

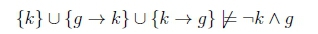
This tells us that although we originally had the non-conditional obligation to not kill, if one does kill then we can retract that non-conditional obligation, avoiding a violation. Then we can aim for the next best scenario which would be for one to kill gently.

 

7 PTL ANALYSIS

This section aims to presents the analysis on the paradox using PTL, LM-entailment specifically. Similarly to Section 6, the order of analysis will be the representation of statements, the desirable properties and then the problematic derivations of the paradox.

7.1 Representation

It is important to note that we restrict ourselves to the use of only a subset of PTL for this analysis. We will only allow PTL statements of the form, «a - ( or «a - •(, where a and ( could be any combination of the PTL language except «-operator. The reason being that the examples we deal with can be represented reasonably with this limited language and this limiting also reduces the complexity of the analysis. Statements of the form a - •( do not have the intuitive reading we desire. Since we do not want the properties of (, whether they are the most typical or not, to apply to all a valuations. This is why we require that the antecedent have a bullet operator. We can represent the statements with the typicality bullet on antecedent side only where «a - ( reads as "the most typical a are (". As previously stated, bullets on the antecedent-side only make the conditionals equivalent to the KLM-style conditionals, the results of which we have already explored. Thus we will use the alternative representation to examine typicality and its added expressive power. This is «a - •( and can be read as "the most typical a are the most typical (". This is a stronger reading where the most typical ( worlds are in a sense tied to a worlds. Intuitively, this obligation states not only that "the most typical a are (" but also that "the most typical ( should possibly be a result of a occurring". For example, let's say we have «d - «l where "d" reads as "driving" and "l" reads as "having a license". «d - «l not only tells us that in the most typical driving scenario that you have a license, but it also states that in the most typical license-having scenarios, we cannot have that you can only be a non-driver.

7.2 Properties

We check whether our restricted PTL satisfies the aforementioned desirable properties using LM-entailment. In other words, we check if the properties can be applied when we have obligations of the form similar to that of Forrester's paradox. We are not assessing whether these are general properties that are satisfied by PTL. Except for the "ought implies can" principle, we do the check for the different representations of obligations that we have, which are cases which first involve non-conditional obligations and then conditional obligations. We will investigate these two cases for each property, where applicable. For each property, we present the knowledge bases and their corresponding LM-entailment models.

7.2.1 Ought Implies Can and Violations

Let's say we have a knowledge base that contains the conditionals »T - »a and »T - -a. There will be no valuations that satisfy the knowledge base because of the conflicting conditionals, therefore we cannot reason with this knowledge base. This implies that we have the "ought implies can" property. Since having contradictory facts in the knowledge base stops us from using the LM-entailment reasoning, we will not have any facts in the knowledge base when using the LM-entailment algorithm. But similarly to the previous section, we can observe which obligations have been violated by a certain fact by checking each obligation against the fact. When there is an inconsistency and thus no valuations that satisfy the knowledge base, that indicates that we can proceed to check the obligations to determine which have been violated. After determining the violated obligations, we will then only use the facts after the LM-entailment algorithm constructs the ranked model. We will strip valuations from the model that contradict the facts we are presented with and then reason with the resultant model. This will give the best case scenario whenever an obligation has been violated.

7.2.2 Restricted Strengthening of the Antecedent

We assume that we have O(5 I a) and then check if O(5 I 7 A a) can be derived.

1. We have {»T - •(} and ideally want to derive »a - •( when a holds.

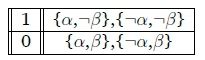
In the case where a holds then it is clear that the most typical a valuation is also the most typical ( valuation. This would be blocked if we had »a - in the knowledge base.

2. We have {»a - •(} and ideally want to derive »(a A 7) - •( when 7 holds.

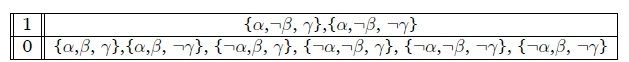
In the case where 7 holds then it is clear that the most typical a A 7 valuation is also the most typical ( valuation. This would be blocked if we had -(a A 7) - •( in the knowledge base.

7.2.3 Weakening

We assume that we have O(( A 7 | a) and then check if O(( I a) can be derived.

1. We have {»T - •(( A 7)} and ideally want to derive »T -

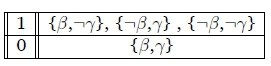
It is clear that the most typical valuation is the most typical ( valuation which allows for the derivation of •T - The most typical valuation in the model is also the most typical 7 valuation thus the derivation of •T - •7 also holds.

2. We have {•a - •(( A 7)} and ideally want to derive •a - •(.

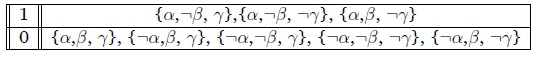
It is clear that the most typical a valuation, which is {a, (,7}, is also the most typical ( valuation as well as the most typical 7 valuation. This means that both •a - •( and •a - •7 also holds.

7.2.4 Factual Detachment

We assume that we have O(( | a) and a, and then check if O( can be derived when using LM-entailment. There is only one case to look at as the non-conditional obligation check is trivial.

1. We have {•a - •(} and ideally want to derive •T - •( when a holds.

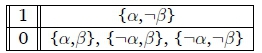
When a is true then the most typical valuation is {a, (} therefore the derivation holds.

7.2.5 Conjunction

We assume that we have O(( I a) and O(7 I a), and then check if O(( A7 | a) can be derived. The cases with non-conditional obligations aren't checked since they will be equivalent to Deontic Detachment.

1. We have {•T - •(, •T - •7} and ideally want to derive •T - •(( A 7).

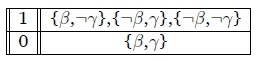
It is clear that we get •T - •(( A 7) as the best valuation is {(, 7}.

2. We have {•a - •(, •a - •7} and ideally want to derive •a - •(( A 7).

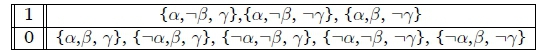
There is only one best a valuation and it is {a, (, 7} therefore we can derive •a - •(( A7).

7.3 LM-entailment analysis

We present the paradox once again and then translate it into a PTL version. The LM-entailment model is then presented and afterwards we show that the undesirable derivations, from Section 4.4, can no longer be derived. This is despite the satisfaction of all the properties. The paradox's statements are translated into the following PTL knowledge base, {«T - «-k, «k - «g}. With this knowledge base comes the background knowledge g - k and the fact k. The background knowledge means that the valuation {g, -k} must be omitted from the model. It is also clear that the violated obligation is «T - «-k when k holds.

7.3.1 RSA, Weakening and Conjunction

Now using Weakening we can go from «T - «-k to «T - «-g as the model shows that the most typical valuations are -g valuations. This is equivalent to the derivation of "You must not kill gently" from "You must not kill anybody" in Section 4.4.1. But unlike in Section 4.4.1, one cannot derive «k - «-g using RSA. The model blocks this derivation since the best k valuations are g valuations in this model.

7.3.2 Factual Detachment and Conjunction

The issue presented in Section 4.4 is blocked because once we assume the fact k in the model, the -k valuations are removed as seen in the following model. The model shows that the derivation of «T - «-k, which means "You must not kill anybody", is not possible, and thus when k is assumed the derivation of «T - «(-k A g) is blocked in the model shown in the above Figure 2.

 

 

8 CONCLUSION

This paper explored the extent that KLM-style defeasible reasoning and Propositional Typicality Logic (PTL) can be used to deal with the issues found with Forrester's paradox. Along with detailing the paradox and its issues, we formally presented the two logic systems we used to analyse the paradox, KLM-style defeasible reasoning and PTL. The sections which show the paradox analysis for KLM-style defeasible reasoning and PTL, sections 6 and 7 respectively, followed the same analysis process. A representation for the paradox in each logic system's language was determined. Then we showed the desirable properties which were satisfied by the logic systems. These are the properties which are the source of the paradox's issues. Then lexicographic closure and LM-entailment algorithms were used in the respective sections to reason with the paradox and show that the undesirable derivations from Section 4.4 are avoided using these reasoning methods. This shows us that we can reasonably represent and deal with the issues of Forrester's paradox using these logic systems without having to drop the desirable deontic properties. This shows the potential that both KLM-style defeasible reasoning and PTL possess when applied in a deontic setting and this paper serves to highlight any such potential for further use. These two techniques mainly differ in the reading of the obligations but also in potential to represent other obligations. PTL provides more expressive power which could offer greater potential in dealing with other types of deontic scenarios, such as those with exceptional obligations, according-to-duty obligations or multiple levels of violations. These approaches differ from other Forrester's paradox solutions such as those by Sinnott-Armstrong (1985) and Meyer (1987) in that they avoid the need for the expansion of the representative language using actions and/or logic quantifiers. So the question to be asked is if KLM-style defeasible reasoning and PTL can be used on a variety of other examples with similar effectiveness.

 

References

Booth, R., Casini, G., Meyer, T. & Varzinczak, I. (2015). On the entailment problem for a logic of typicality. Proceedings of the 24th International Conference onArtificialIntelligence, 2805-2811.

Casini, G. & Straccia, U. (2012). Lexicographic closure for defeasible description logics. Proc. of Australasian Ontology Workshop, 969, 28-39.         [ Links ]

Chingoma, J. & Meyer, T. (2019). Forrester's paradox using typicality. http://ceur-ws.org/Vol-2540/FAIR2019_paper_54.pdf

Giordano, L., Gliozzi, V., Olivetti, N. & Pozzato, G. L. (2015). Semantic characterization of rational closure: From propositional logic to description logics. Artificial Intelligence, 226, 1-33. 10.1016/j.artint.2015.05.001        [ Links ]

Goble, L. (2013). Prima facie norms, normative conflicts, and dilemnas. Handbook of deontic logic and normative systems (pp. 241-352). College Publications.

Grossi, D. & Rotolo, A. (2011). Logic in the law: A concise overview. Logic and Philosophy Today, 2, 251-274. http://hdl.handle.net/11585/132834        [ Links ]

Hansson, B. (1969). An analysis of some deontic logics. Noûs, 3(4), 373-398. http://www.jstor.org/stable/2214372        [ Links ]

Hilpinen, R. & McNamara, P. (2013). Deontic logic: A historical survey and introduction. Handbook of deontic logic and normative systems (pp. 3-136). College Publications.

Kraus, S., Lehmann, D. & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167-207. https://doi.org/10.1016/0004-3702(90)90101-5        [ Links ]

Lehmann, D. (1995). Another perspective on default reasoning. Annals of Mathematics and Artificial Intelligence, 15, 61-82. https://doi.org/10.1007/BF01535841        [ Links ]

Lehmann, D. & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55, 1-60. 10.1016/0004-3702(92)90041-U        [ Links ]

Makinson, D. (1993). Five faces of minimality. Studia Logica: An International Journal for Symbolic Logic, 52(3), 339-379. http://www.jstor.org/stable/20015680        [ Links ]

Makinson, D. (2005). Bridges from classical to nonmonotonic logic. King's College Publications.

Makinson, D. & van der Torre, L. (2000). Input/output logics. Journal of Philosophical Logic, 29, 383-408. https://doi.org/10.1023/A:1004748624537        [ Links ]

Meyer, J.-J. (1987). A simple solution to the "deepest" paradox in deontic logic. Logique et Analyse, 30, 81-90.         [ Links ]

Parent, X. & van der Torre, L. (2017). Detachment in normative systems: Examples, inference patterns, properties. IfCoLog Journal of Logics and Their Applications, 4(9), 2295-3039. https://orbilu.uni.lu/bitstream/10993/33555/1/ifcolog-paper.pdf        [ Links ]

Parent, X. & van der Torre, L. (2018). Introduction to deontic logic and normative systems. College Publication, UK.

Pigozzi, G. & van der Torre, L. (2017). Multiagent deontic logic and its challenges from a normative systems perspective [L'article est en libre accès et disponible sur le site Web de College Publications : http://www.collegepublications.co.uk/]. The IfCoLog Journal of Logics and their Applications, 4(9). https://hal.archives-ouvertes.fr/hal-01679130

Rönnedal, D. (2019). Contrary-to-duty paradoxes and counterfactual deontic logic. Philosophia. 10.1007/s11406-018-0036-0

Sinnott-Armstrong, W. (1985). A solution to Forrester's paradox of gentle murder. The Journal of Philosophy, 82.3, 162-168. 10.2307/2026353        [ Links ]

van der Torre, L. (1997). Reasoning about obligations, defeasibility in preference-based deontic logic (Doctoral dissertation). Erasmus University Rotterdam. https://icr.uni.lu/leonvandertorre/papers/thesis.pdf

 

 

Received: 30 May 2020
Accepted: 30 Oct 2020
Available online: 08 December 2020