RESEARCH ARTICLE

 

Algorithmic definitions for KLM-style defeasible disjunctive Datalog

 

 

Matthew Morris^{I, II}; Tala Ross^I; Thomas Meyer^{I, II}

^IDepartment of Computer Science, University of Cape Town, South Africa. Email: Matthew Morris matthewthemorris@gmail.com (corresponding), Tala Ross rsstal002@myuct.ac.za, Thomas Meyer tmeyer@cs.uct.ac.za
^IICentre for Artificial Intelligence Research, South Africa

 

 

---

ABSTRACT

Datalog is a declarative logic programming language that uses classical logical reasoning as its basic form of reasoning. Defeasible reasoning is a form of non-classical reasoning that is able to deal with exceptions to general assertions in a formal manner. The KLM approach to defeasible reasoning is an axiomatic approach based on the concept of plausible inference. Since Datalog uses classical reasoning, it is currently not able to handle defeasible implications and exceptions. We aim to extend the expressivity of Datalog by incorporating KLM-style defeasible reasoning into classical Datalog. We present a systematic approach for extending the KLM properties and a well-known form of defeasible entailment: Rational Closure. We conclude by exploring Datalog extensions of less conservative forms of defeasible entailment: Relevant and Lexicographic Closure. We provide algorithmic definitions for these forms of defeasible entailment and prove that the definitions are LM-rational.
CATEGORIES: • Theory of computation ~ Automated reasoning • Theory of computation ~ Logic and databases • Computing methodologies ~ Nonmonotonic, default reasoning and belief revision

Keywords: knowledge representation and reasoning, defeasible reasoning, KLM approach, Rational Closure, Relevant Closure, Datalog

---

 

 

1 INTRODUCTION

The KLM approach, proposed by Kraus et al. (1990), is a well-known framework for defeasible reasoning. The KLM properties can be used to determine the rationality of different forms of defeasible entailment. While rationality can often be understood intuitively, a common definition is required in order to avoid confusion between different conflicting or assumed definitions. Lehmann and Magidor's definition of rationality (1992) is used extensively in the literature and we use it throughout the paper. The framework has been discussed at length in the literature for propositional logic (Kraus et al., 1990; Lehmann, 1995; Lehmann & Magidor, 1992) and description logics (Casini et al., 2014; Casini et al., 2013; Moodley, 2015; Straccia & Casini, 2013). We present what we believe to be the first theoretical approach for extending the KLM framework to Datalog. We consider an extended form of Datalog, Disjunctive Datalog, which allows for disjunction in the head of Datalog clauses. We do not consider a semantic characterisation for the Datalog case. Instead, we provide algorithmic definitions of defeasible entailment.

There are two well-known forms of defeasible entailment that satisfy the KLM properties: Rational Closure (RC) (Lehmann & Magidor, 1992) and Lexicographic Closure (LC) (Lehmann, 1995). Both are rational (Casini et al., 2019), with RC being the most conservative form of rational defeasible entailment among the popular proposals, and LC a more permissive form. Another form of defeasible entailment, Relevant Closure (RelC) (Casini et al., 2014), has been proposed for description logics. It intuitively seems rational but does not satisfy all of the KLM properties. We provide algorithmic definitions of RC, LC and RelC, showing that RC and LC are still rational when converted to Datalog and that RelC is not.

Our results demonstrate that the KLM approach can be extended to operate in Datalog and that rational definitions of defeasible entailment exist within the language. This shows promise for the extension of KLM-style defeasible entailment to other more expressive logics, as well as providing evidence for the possibility of a semantic definition of defeasible entailment in Datalog.

In the next section we provide the relevant background material, after which we present our work on KLM-style defeasible entailment for the Datalog case. We conclude with a discussion of related work and suggestions for future work. This work is an extension of that done by Morris et al. (2019).

 

2 BACKGROUND

2.1 Propositional Logic

Propositional logic Ben-Ari, 2012 is a simple logic which is built up from a finite set V of propositional atoms, denoted by meta-variables p,q,.... The language L of propositional logic is the set of all formulas, denoted by a, (3,..., which are recursively defined as usual: a ::= T | ± | p | -a | a A a | a V a | a - a | a o a.

An interpretation is a function I : V - {T, F} which assigns a single truth value to each atom. A formula a e L is satisfied by an interpretation I, denoted I ¥ a, if it can be evaluated to true by I in the usual recursive truth-functional way. We define the models of a finite set of formulas X to be [X] = {I : I ¥ a, a e X}. We say that a set of formulas X entails a formula a, denoted by X = a, if [X] ç {{a}].

2.2 The Failures of Monotonicity

Classical reasoning systems, such as propositional logic, are monotonic. This means that all information is certain and adding new information does not change the conclusions that you could draw before. This form of reasoning can be too weak to model certain systems. To illustrate this, consider an example where the following statements are made:

Example 1

From this, we can conclude that "students pay taxes", which may in fact be incorrect. However, each of these statements is perfectly reasonable from a human perspective. What we actually meant was "typically, people pay taxes". Then, when we add the extra information that students do not pay taxes, we want the system to retract its conclusion that "students pay taxes". However, a monotonic, classical reasoning system cannot change previous conclusions, and knowing that "students do not pay taxes" and "students pay taxes", it must then conclude that no students can exist, otherwise we would get a contradiction. In non-monotonic systems, defeasible statements of the form "typically, something is the case" are permitted. This allows for a more "common sense" approach to reasoning than in the approach of classical reasoning (Casini et al., 2013).

2.3 KLM-style Defeasible Entailment

The KLM approach (Kraus et al., 1990) is based on the concept of plausible inference, which is represented by defeasible implication operators of the form a \^ ((. This is read as "typically, if a, then ( ".

Let a knowledge base K be a finite set of defeasible implications. The KLM framework answers the question: "What does it mean for a defeasible implication ( to be entailed by a knowledge base K?". This is referred to as defeasible entailment, and denoted by a \^ ((.

Unlike classical entailment, it is well-accepted that defeasible entailment is not unique. There are multiple formalizations of defeasible entailment, such as Rational Closure (Lehmann & Magidor, 1992), Lexicographic Closure (Lehmann, 1995), and Relevant Closure (Casini et al., 2014). Lehmann and Magidor (Lehmann & Magidor, 1992) proposed a set of rationality properties known as the KLM properties. They argue that if a defeasible entailment algorithm satisfies all the properties it is believed to be an acceptable form of defeasible entailment. We adopt this approach and refer to these forms of defeasible entailment as LM-rational. The KLM properties for propositional logic are stated below:

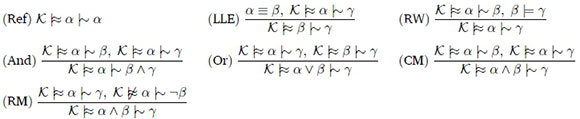
All of these properties have a fairly intuitive meaning. Consider the two defeasible implications: "typically, tutors are employees" (t \^ e) and "typically, tutors are students" (t \^ s). It seems rational to conclude that "typically, tutors are employees and students" (t |~ e A s). This is exactly what the And property enforces. Kraus et al. (Kraus et al., 1990) provide detailed descriptions of the intended meaning of each property.

2.4 Rational Closure

Rational closure is the most conservative form of defeasible entailment. This means that anything entailed by rational closure will also be entailed by the other common forms of defeasible entailment. We use the algorithmic definition (Freund, 1998), which we refer to as the Rational Closure Algorithm, as the sole definition of Rational Closure.

The algorithm is split into two distinct sub-algorithms, proposed by Casini et al. (Casini et al., 2019). The BaseRankProp algorithm, Algorithm 2, is used to construct a ranking of the classical versions (CC) of the statements in the defeasible knowledge base (/C). For example, the classical version of defeasible statement a \ (5 would be a - (5. Intuitively, the more "typical" statements are placed further down in the ranking, corresponding to the notion that some typical implications are more typical than others.

 

 

The RationalClosureProp algorithm, Algorithm 1, is used to compute whether a defeasible implication is entailed by the knowledge base and uses the BaseRankProp algorithm. Also note that the RationalClosureProp algorithm just reduces to a sequence of classical entailment checks.

We can express any classical sentence a as a defeasible implication -a \ ± (Casini et al., 2019). For example, the rank of the statement (5 - y corresponds to the rank of the statement (5 A-y\\^. This means that we can use the BaseRankProp algorithm to rank knowledge bases which include classical sentences and the RationalClosureProp algorithm can be used to check classical queries as well. Note that this also means that the BaseRankProp algorithm will put all classical sentences on the bottom (infinite) level.

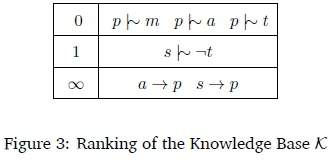
To illustrate how the algorithm works, consider the following example knowledge base K.

Example 2

1. Adults are people (a - p)

2. Students are people (s - p)

3. Typically, people pay taxes t)

4. Typically, students do not pay taxes (s \ -t)

Figure 1 shows the ranking of K according to the BaseRankProp algorithm. Throughout the paper, we illustrate the ranking of a knowledge base with all sentences in their original form for ease of understanding.

 

 

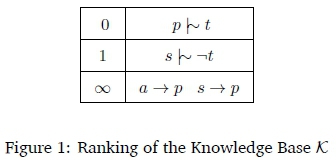
Suppose we asked; "Do students typically pay taxes?", corresponding to the query s \^ t. Then at the start of the algorithm when i = 0, R_o U R = -s, since we have s - p - t and s - -t. So the top level (R₀) is thrown away. Now when i = 1, U R = -s. Also, Roo U R = s - t, so the algorithm returns false for the query. This makes sense, and the algorithm has computed the intuitively correct result.

2.5 Disjunctive Datalog

Datalog (Ceri et al., 1989) is a more expressive logic than propositional logic and a popular query language for deductive databases Pasarella and Lobo, 2017; Shkapsky et al., 2016. Data-log is a simplified version of general logic programming. It allows us to represent statements about specific individuals as well as generic concepts which can be associated with many individuals. For example, in Datalog we can represent the statements in Example 3, whereas in propositional logic we can only represent tutors in general.

Example 3

1. For all X, X is a tutor.

2. For all X, if X is an under-graduate, then X is a student.

3. Tyler is a tutor.

It is often useful to be able to represent statements that involve the disjunction "or", since these type of statements allow us to model incomplete knowledge. It is also useful to represent statements about falsehood. Disjunctive Datalog (Datalog^v), as defined in this section, allows us to make the same statements as standard Datalog as well as statements involving disjunction and negation, such as the following:

Example 4

4. For all students X, X is an undergraduate or a postgraduate.

5. Tyler is not a lecturer.

The language of Disjunctive Datalog is made up of function-free Horn clauses (Ceri et al., 1989), which are formulas with the general structure: l₀ A h A - • • A l_m - l_m+\ V l_m+₂ V • • - V l_n. Each literal l_iis either ± or is a positive atom of the form p_i(t₀,... ,t_ki), where pi is a predicate symbol and t₀,... ,t_kiare terms. A term is either a constant or a variable. In our version of Datalog, the left-hand side of the clause is referred to as the body and the right-hand side as the head. Horn clauses with a body are called rules and those without a body are called facts.

We can represent the statements from Example 3 and 4, using variable X, constant Tyler and predicates s, t, u, p and l which represent students, tutors, under-graduates, post-graduates and lecturers respectively:

We say that clauses, such as t(Tyler), are ground since they do not contain any variables. A Herbrand Base B^Pis the set of all ground facts constructible from the symbols in a Datalog program P. For example; Tyler is the only constant in the program P, defined in Example 3 and 4, so the set of all possible ground facts that we can form is:

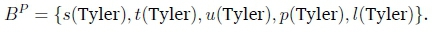
A Herbrand interpretation t is simply a subset of a Herbrand Base: t ç B^p. For any Herbrand interpretation t, we define that ± is not in t. So, following our example, a possible Herbrand interpretation is:

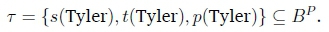
A rule /₀A l_i A- • • A l_m - l_m+i V l_m+₂ l_nis true for Herbrand interpretation t if and only if, for each substitution 9 which replaces variables by constants, if l₀9 e t,1₁9 e t,. .., l_m9 e t then at least one of l_m+i9 e t, l_m+₂9 e t,. .. ,l_n9 e t holds. For example; t(X ) A p(X ) - l(X ) is not true for t , since t (Tyler) e t and p(Tyler) e t but l (Tyler) e t .A fact l₀ A l_i A - • • A l_mis true for Herbrand interpretation t if and only if, for each substitution 9 which replaces variables by constants, l₀9 e t,1₁9 e t,. ..,l_m9 e t all hold. For example; s(X) is true for t but u(X) is not. A Herbrand interpretation t is a Herbrand model of a set of Horn clauses X if and only if every clause in X is true for t. For example; t is a Herbrand model of P.

2.5.1 Entailment of Horn Clauses

Entailment is defined in the standard way: a set of Horn clauses X entails Horn clause a, denoted by X = a, if and only if each Herbrand model of X is also a model of a.

2.5.2 Molecules as Combinations of Literals

We introduce the idea of molecules as a shorthand for a combination of literals. A disjunctive molecule, denoted a^v, is a combination of literals of the form: l_i V l₂V • • • V l_n. A conjunctive molecule, denoted a^A, is a combination of literals of the form: l_i A l₂ A • • • A l_n. A molecule, denoted a, is either a disjunctive molecule or a conjunctive molecule. Now a Disjunctive Datalog rule can be written as a^A - ( ^v.

 

3 DEFEASIBLE DISJUNCTIVE DATALOG

3.1 KLM-style Defeasible Rules

We represent plausible inference in Disjunctive Datalog using defeasible rules of the form: b_i A • • • A b_m Y h_i V • • • V h_n, where each bi, h_iis a literal. This is read as "typically, if all of b_i,... ,b_mare true, then at least one of h_i,... ,h_nis true". We do not consider a semantic definition of defeasible rules. We will instead define defeasible rules by adapting rational defeasible entailment algorithms for Disjunctive Datalog.

3.2 Defeasible Entailment

Let knowledge base K be a finite set of defeasible rules. The main question of this paper is to algorithmically analyse defeasible entailment K a^A Y (5^v. That is, how do we answer the question: "Can we conclude a^A Y (^vfrom a defeasible knowledge base K?". When analysing different defeasible entailment algorithms, Lehmann and Magidor (Lehmann & Magidor, 1992) advocate that the KLM properties be used to assess the rationality of these algorithms. We adopt this approach for Datalog and provide an extension of the KLM properties for Disjunctive Datalog.

3.2.1 A Motivation for Extending Disjunctive Datalog

We find that, due to the restrictive nature of Datalog's syntax, none of the KLM properties can be expressed using Disjunctive Datalog without violating the syntax. However, we need to ensure that LM-rational forms of defeasible entailment satisfy all of the KLM properties. We argue that this is necessary, even though the reasoning described by some of these properties will never be computed by defeasible entailment algorithms for Disjunctive Datalog.

Let us consider an example where we can come to a conclusion that cannot be expressed in Datalog's syntax. Even though we cannot express that conclusion, we still want the algorithm to be able to compute it, otherwise the algorithm would not be rational. For example, if tutor(X) Y student(X) and tutor(X) Y employee(X) both hold, then we would want to be able to conclude tutor(X) Y student(X) A employee(X) holds as well.

As another example, if tutor(X) Y teacher(X) and lecturer(X) Y teacher(X) both hold, then we would want to be able to conclude tutor(X) V lecturer(X) Y teacher(X) holds as well. These examples illustrate the KLM properties of And and Or respectively. Note that in the conclusions of these examples, the syntax of Datalog, restricting disjunction to only be allowed in the head and conjunction in the body, is violated.

3.2.2 Datalog+

Our proposed extension to Datalog, Datalog + , introduces the idea of compounds. Compounds, denoted by A,B,..., are recursively defined from base literals l as follows: A ::= l | -A | AAA | A V A. In Datalog+ a fact is a compound A and rules have the form A - B.

Let t be a Herbrand interpretation and consider some substitution 9 which replaces variables by constants. We say that compound A is in t under 9, denoted A9 e t, if and only if one of the following conditions holds, where B, r are compounds and l is a literal:

• A = l and 19 e t

• A = -B and B9 e t

• A = B A r, B9 e t and r9 e t

• A = B V r and B9 e t or r9 e t

Herbrand interpretation t is a model of fact A if and only if A9 e t for every possible 9. Herbrand interpretation t is a model of rule A - B if and only if, whenever A9 e t for some 9, then B9 e t for the same 9. A knowledge base K entails Datalog+ Horn clause (rule or fact) a, denoted by K = a, if and only if each Herbrand model of K is also a model of a.

3.2.3 The KLM Properties Expressed in Datalog+

We state the KLM properties (in Defeasible Datalog + ) for Datalog below, where compounds a, ((, y are used as a shorthand. Note that the defeasible implication operator \^ has been added to the language of Datalog + . These properties are used to define the rationality of a defeasible entailment algorithm for Datalog. Only an algorithm which satisfies all of these properties is considered rational and acceptable.

 

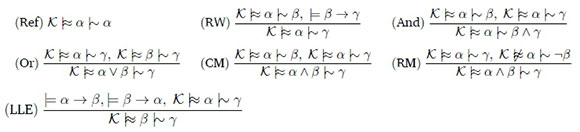
4 RATIONAL CLOSURE FOR DATALOG

In this section we propose a simple adaptation to the Rational Closure algorithms for the Disjunctive Datalog case.

4.1 Base Rank Algorithm

In the propositional case, we can rewrite a classical statement a as the defeasible statement -a \\ ± and, hence, we can assume that all of the statements in our knowledge base are defeasible. It is not possible to rewrite classical clauses as defeasible rules for the Datalog case. Instead, the adapted version of the BaseRankProp algorithm, BaseRankDatalog, ranks the statements in a knowledge base K = D U C, where D is the set of defeasible rules and C the set of classical clauses. It forms a ranking using only the defeasible statements by setting E₀:= ^-on line 2. Then, since the classical statements are all definite, it adds them to the most typical level (the infinite level).

In the propositional case, a statement a is exceptional with respect to a set of statements X if X = -a. Datalog^v's syntax does not include the negation connective -, so we use the ± literal to define a notion of falsehood, and hence exceptionality.

Proposition 1 Let t be a Herbrand interpretation. Then, t is a model of -a under Datalog+ semantics iff t is a model of a - ± under Datalog^v semantics.

The exceptionality of molecule a is now assessed using the entailment check Ei U C = a - ± on line 4. Finally, when all the defeasible rules are ranked, BaseRankDatalog adds the classical clauses to the infinite level by setting R_o := E_i-i U C on line 8.

 

Algorithm 3

 

4.2 Rational Closure Algorithm

As with the BaseRankDatalog algorithm, we choose to represent falsehood using the ± literal. The RationalClosureDatalog algorithm now uses the entailment check R_o U R = a - ± on line 4. Under the assumption that we can compute classical entailment for Datalog^v, this adapted version of the RationalClosureProp algorithm can be used to check whether a rule a \^ (3 is defeasibly entailed by the knowledge base K = D U C.

 

Algorithm 4

 

Proposition 2 The adapted RationalClosureDatalog algorithm is LM-rational.

The proof of LM-rationality is provided in Appendix A.

4.3 Interactions Between Variables and Constants

While it is certainly important that RationalClosureDatalog is LM-rational, the KLM properties do not capture the full expressivity of Datalog. In particular, they do not express the interactions between constants and variables in rules. While a set of properties that fully express how defeasibilty should work with respect to this is certainly useful, it is beyond the scope of this paper. Instead, we provide an example that illustrates the basics of how RationalClosureDatalog fails to deal correctly with rules involving constants and variables.

Example 5 Consider the following knowledge base K:

1. Birds typically fly: b(X ) ^ f (X )

2. Tweety is a non-flying bird : b(t) A -f (t)

3. Chirpy is a bird : b(c)

When ranked according to the BaseRankDatalog algorithm, we would want the statements to appear as shown in Figure 2. Classical statements should have infinite rank and the defeasible statement should have a finite rank. However, instead of this, all statements get ranked on the same level, as this is in fact an inconsistent knowledge base. To see this, notice that the classical version of b(X) \ f (X) is b(X) - f (X). We also know b(t) is true, so we can use this to conclude that f (t) must be in any Herbrand interpretation satisfying our knowledge base. But we know that -f(t) must also be true, so f(t) is not in any such Herbrand interpretation, a contradiction.

 

 

5 RELEVANT CLOSURE FOR DATALOG

It seems unnecessary for the Rational Closure algorithm to throw away an entire level of statements when there is a conflict. While it is true that a statement within the level is causing the conflict, there are other statements in the level that may have no effect on the conflict occurring. Relevant closure takes a finer-grained approach to removing statements, only removing the "relevant" statements in a level. In this section we give the definition for Relevant Closure as provided by Casini et al. (Casini et al., 2014). The algorithm is based on RationalClosureProp, with some slight changes.

5.1 Motivation for Relevant Closure

In this subsection we argue, by means of an example, that not all statements in a level are responsible for being able to prove R_o U R = -a, given the query a \ j.

Example 6

Figure 3 shows the ranking of these statements according to the BaseRankProp algorithm.

 

 

Let us now consider what happens when we ask the question; "Do students typically watch movies?", corresponding to the query s \^ m. In the algorithm, when i = 0, we can conclude that s - t and s - -t. That is, students both pay and don't pay taxes, leading us to conclude that there are no students. Thus, R_o U R = - s, so we throw away the entire top level of the ranking and check again.

Now, Roo U R = -s, so we check if s - m holds. It does not, since the statement p - m was thrown away in the previous iteration. Thus, the algorithm returns false. This intuitively feels wrong, since the conclusion "Students typically watch movies" seems like a very reasonable one to make from the given information. The issue arises from throwing away the statement p - m in the previous iteration, even though it had nothing to do with us being able to conclude that there were no students.

We used the following statements to conclude - s;

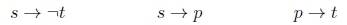
One could argue that since the statement p - m was not relevant to us concluding - s, it should not have been thrown away with the top level. This is the idea behind Relevant Closure.

5.2 Algorithmic Definition

 

Algorithm 5

 

in R as eligible for removal. We say that a statement a Y 5 is in the Relevant Closure of K if and only if the RelevantClosureProp algorithm returns true when given a Y 5 and K.

5.3 Defining Relevance

Now that the algorithm has been defined, the only work remaining is to define how to calculate the partition < R, R^- > for a given query a Y 5. Based on the ideas explored by Casini et al. (Casini et al., 2014), we would want R to contain exactly all the statements used to prove -a. To formalize this, we present a sequence of definitions to gradually build up the idea of relevance.

Definition 1 a is said to be exceptional for K if K = -a.

Definition 2 Let K be a knowledge base, J ç K such that J only contains defeasible implications, and a a propositional sentence. Then J is said to be an a-justification w.r.t. K if a is exceptional for J and for any J¹c J, a is not exceptional for J'.

Definition 3 For a sentence a and knowledge base K, let J^K(a) = {J I J is an a-justification w.r.t. K}. Then a Y 5 is said to be in the Basic Relevant Closure of K if it is in the Relevant Closure of K w.r.t [J J^K (a).

5.4 Minimal Relevant Closure

It could be argued that for Basic Relevant Closure, we are still considering too many statements as relevant to the query. This is because we consider all the statements in all a-justifications as relevant to proving that a is exceptional. However, we could instead consider only the statements of minimal rank from each a-justification as relevant, and still fix the exceptionality of a.

Definition 4 For some set of justifications J ç K, let J^K_in= {a Y 5 I r_K(a) < r_K(7 ) for every 7 Y A eJ}.

^{ForasentencealetJ}m_%n^(a) = UJJK(a) ^JLn^.

Then a Y 5 is said to be in the Minimal Relevant Closure ofK ifit is in the Relevant Closure of K w.r.tU J^Kin(a).

5.5 Relevant Closure for Datalog

In terms of adapting the RelevantClosureProp algorithm for Datalog, no further work needs to be done beyond what has already been said for Rational Closure. To define a molecule a being exceptional, we simply need to be able to check entailment of negated molecules, which is something we already know how to do. The remainder of the definitions for both Basic and Minimal Relevant Closure only entail manipulating sets and checking the rankings of statements.

 

Algorithm 6

 

5.6 LM-Rationality

For this, we will use Minimal Relevant Closure as the definition for Relevant Closure. As shown by Casini et al. (Casini et al., 2014), Relevant Closure for propositional logic satisfies the properties Ref, LLE, And, and RW, and does not satisfy Or, CM, or RM. We will show that the same holds true for Relevant Closure for Datalog.

Let us consider the proofs that show that Rational Closure fulfills the KLM properties of Ref, RW, and And. The only difference RelevantClosureDatalog has from RationalClosureDatalog is the inclusion of the "relevance partition". Thus, the proofs can be re-used without editing, provided that the relevance partition is the same throughout the various queries.

The relevance partition is fully determined by the antecedent of the query (e.g. a in a \ ( ), as can be seen in the definition of Minimal Relevant Closure. In the aforementioned properties, the antecedent is the same in all queries made to the algorithm. Hence, the proofs can be directly re-used to show that Relevant Closure fulfills the KLM properties of Ref, RW, and And.

The proof for satisfaction of the property LLE and the counter-examples for satisfaction of the properties Or, CM, and RM can be found in Appendix C. The counter-examples were adapted from the ALC case (Casini et al., 2014).

 

6 LEXICOGRAPHIC CLOSURE

In Section 5 we argue that it is unnecessary for the Rational Closure algorithm to throw away an entire level of statements when there is a conflict, since some of the statements may have no effect on the conflict occurring. Unfortunately the Relevant closure definition of defeasible entailment is not LM-rational. Instead of attempting to define "relevant" statements, Lexicographic closure (Lehmann, 1995) considers all possible subsets of worst-ranked statements and removes the smallest possible subset such that there is no longer a conflict. The semantic and algorithmic definitions of Lexicographic Closure for propositional logic are known and have been shown to be LM-rational (Lehmann, 1995). In this section we provide an extension of Lexicographic Closure to the Datalog^v case.

6.1 Lexicographic Closure for Propositional Logic

We adapt the definition of Lexicographic Closure for propositional logic provided by Casini et al.(Casini et al., 2019). The new definition, in terms of the sub-algorithms SubsetRankProp and LexicographicClosureProp, can easily be adapted for Datalog^v.

The SubsetRankProp algorithm, Algorithm 7, constructs a new ranking of statements by using the base ranks R₀,..., R_n-i, R_ocomputed by the BaseRankProp algorithm. It adds new rank levels D_in._-1, D_in._-2D_it1in between each existing rank level R_iand R_i+i. Each level D_ij represents all the different ways of removing | R_i| -j statements from R_i. The Subsets (X, k) function finds all possible subsets of size k <n of a set X of size n.

 

 

As seen in Section 5, when the knowledge base in Example 6 is ranked according to the BaseRankProp algorithm, the statements appear in the ranking shown in Figure 4.

 

 

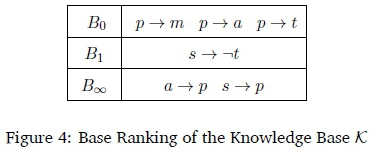
Let us look at B₀. Finding all the different ways of removing 1 statement from B₀, is the equivalent of finding all the subsets of B₀of size 2 using S₀₂= Subsets(B₀,2) = {{p - m,p - a}, {p - m,p - t}, {p - a,p - t}}. Now, using {p - m,p - a} is equivalent to using the single statement (p - m) A (p - a). And, using at least one of the statements (p - m) A (p - a), (p - m) A (p - t) or (p - a) A (p - t) is equivalent to using the single statement ((p - m) A (p - a)) V ((p - m) A (p - t)) V ((p - a) A (p - t)). So, all the different ways of removing 1 statement from B₀can be represented by this one statement. If we follow the algorithm for all possible subset sizes (from \Bi\ to 1) for each B_i, then we get the following ranking:

 

 

The LexicographicClosureProp algorithm ranks the statements in the input knowledge base C using the SubsetRankProp algorithm. It then checks whether the defeasible implication a\\ (5 is defeasibly entailed by CC in a manner equivalent to that used by the RationalClosureProp algorithm (LexicographicClosureProp is the same as RationalClosureProp, barring the use of SubsetRankProp instead of BaseRankProp.)

Let us again consider what happens when we ask the question; "Do students typically watch movies?" (s \ m). In the algorithm, when i = 0, we can conclude that s - t and s - -t so we throw away R₀and check again. Now, for i = 1, R_o U R = -s, so we check if s - m holds and it does. Thus, the algorithm returns true.

6.2 Lexicographic Closure for Datalog

In this section we extend the Lexicographic Closure algorithm for the propositional case to the Datalog case. We conclude the section by showing that our extended algorithm is LM-rational.

6.2.1 Rephrasing SubsetRank for Datalog

The definition of Lexicographic Closure for the propositional case cannot directly be applied to the Datalog case. The statement D_i-jis formed by combining statements from subset Sousing A and V connectives. It will violate Datalog^v's syntax if S_ij contains multiple rules or multiple subsets of facts. However, the statement D_íj can be transformed into Conjunctive Normal Form (CNF) D_itj := D₁ A D₂ A ... A D_n, where:

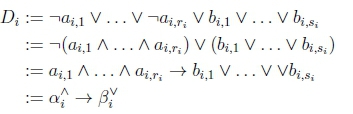
Thus, D_ijj can be rewritten as a conjunction of Disjunctive Datalog rules. Checking entail-ment from a conjunction of rules is equivalent to checking entailment from a set of the same rules. Hence, we can replace each statement D_ij with a set of Datalog^v rules. On line 7 of the SubsetRankProp algorithm, Algorithm 7, we now set R_k := RNF(D_ij). The Rule Normal Form function RNF(r) takes an "extended" Disjunctive Datalog statement r as input and does the following:

1. Computes the Conjunctive Normal Form CNF(r).

2. Converts CNF(r) into a conjunction of clauses of the form (a¹ - (3^v) A (a% - 320 A ... A

3. Converts the conjunction of clauses into a set of clauses {ai - P^v,^2 - 3^v,... ,a£ -

4. Returns the set of clauses.

 

Algorithm 8

 

6.2.2 Rephrasing Lexicographic Closure for Datalog

LexicographicClosureDatalog is the same as RationalClosureDatalog, with the exception that the adapted SubsetRankDatalog algorithm is used to rank statements on line 1 instead of the BaseRankDatalog algorithm.

Proposition 3 The adapted LexicographicClosureDatalog algorithm is LM-rational.

Proof of Proposition 3: Notice that the proofs for the satisfaction of each KLM property by the RationalClosureDatalog procedure, in Appendix A, are independent of the ranking produced by the BaseRankDatalog procedure. Furthermore, notice that the only difference between the LexicographicClosureDatalog procedure and the RationalClosureDatalog procedure is the use of the SubsetRankDatalog procedure to rank statements instead of the BaseRankDatalog procedure. Thus, the proofs for the satisfaction of each KLM property in Appendix A can be used to prove the satisfaction of each KLM property by the LexicographicClosureData] procedure.

 

7 CONCLUSIONS & FUTURE WORK

The main focus of this paper was to provide versions of defeasible reasoning for Disjunctive Datalog. To be able to express the KLM properties and the algorithm in Datalog, we motivated for extensions that would have to be made to the syntax and semantics of Datalog. We proved that Rational Closure for Datalog was LM-rational (i.e. it conforms to the KLM properties), but showed by example that it does not seem to capture the relationship between variables and constants in Datalog.

We introduced Relevant Closure and Lexicographic Closure as alternatives for computing defeasible entailment and adapted both of the algorithms for Datalog. We found that Lexicographic Closure is still LM-rational, but that Relevant Closure does not satisfy some of the KLM properties.

This paper is a first step towards defining defeasible entailment for more expressive logics. Future work on this topic would most definitely include finding a semantic definition of Rational Closure for Datalog, based on minimal models. Other future work could include an attempted adaptation of the Relevant Closure method for computing defeasible entailment, done in such a way that it satisfies the KLM properties, while still maintaining the basic ideas of Relevant Closure.

As another option, Casini et al. (Casini et al., 2019) showed that LM-rationality is necessary but not sufficient to define acceptability of defeasible entailment forms. The additional properties for Basic Defeasible Entailment proposed by Casini et al. (Casini et al., 2019) can be extended to Datalog. Furthermore, other properties that are specific to defeasible entail-ment for Datalog should be explored. These properties would likely lead to a revision of our proposed algorithm, as it does not fully capture how variables and constants should interact in defeasible Datalog.

 

References

Ben-Ari, M. (2012). Mathematical logic for computer science. Springer Science & Business Media. 10.1007/978-1-4471-4129-7

Casini, G., Meyer, T., Moodley, K. & Nortje, R. (2014). Relevant closure: A new form of defeasible reasoning for description logics. JELIA 2014: Logics in ArtificialIntelligence, 92-106. 10.1007/978-3-319-11558-0_7

Casini, G., Meyer, T., Moodley, K. & Varzinczak, I. (2013). Towards practical defeasible reasoning for description logics. Proceedings of the 26th International Workshop on Description Logics, 587-599. http://researchspace.csir.co.za/dspace/handle/10204/7039

Casini, G., Meyer, T. & Varzinczak, I. (2019). Taking defeasible entailment beyond rational closure. JELIA 2019: Logics in Artificial Intelligence, 182-197. 10.1007/978-3-030-19570-0_12

Ceri, S., Gottlob, G. & Tanca, L. (1989). What you always wanted to know about datalog (and never dared to ask). IEEE Transactions on Knowledge and Data Engineering, 1, 146-166. 10.1109/69.43410        [ Links ]

Freund, M. (1998). Preferential reasoning in the perspective of Poole default logic. Artificial Intelligence, 98, 209-235. 10.1016/S0004-3702(97)00053-2        [ Links ]

Kraus, S., Lehmann, D. & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167-207. 10.1016/0004-3702(90)90101-5        [ Links ]

Lehmann, D. (1995). Another perspective on default reasoning. Annals ofMathematics and ArtificialIntelligence, 15, 61-82. 10.1007/BF01535841        [ Links ]

Lehmann, D. & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55, 1-60. 10.1016/0004-3702(92)90041-U        [ Links ]

Moodley, K. (2015). Practical Reasoning for Defeasible Description Logics (Doctoral dissertation). University of KwaZulu-Natal. 10.31237/OSF.IO/DW5P2

Morris, M., Ross, T. & Meyer, T. (2019). Defeasible disjunctive datalog. Proc. of the South African Forum for Artificial Intelligence Research FAIR, 208-219. http://ceur-ws.org/Vol-2540/FAIR2019_paper_38.pdf

Pasarella, E. & Lobo, J. (2017). A Datalog Framework for Modeling Relationship-based Access Control Policies. Proceedings ofthe 22nd ACM on Symposium on Access Control Models and Technologies - SACMAT '17 Abstracts, 91-102. 10.1145/3078861.3078871

Shkapsky, A., Yang, M., Interlandi, M., Chiu, H., Condie, T. & Zaniolo, C. (2016). Big Data Analytics with Datalog Queries on Spark. Proceedings of the 2016 International Conference on Management of Data - SIGMOD '16, 1135-1149. 10.1145/2882903.2915229

Straccia, U. & Casini, G. (2013). Defeasible inheritance-based description logics. Journal of Artificial Intelligence Research, 48, 415-473. 10.1613/jair.4062        [ Links ]

 

 

Received: 30 May 2020
Accepted: 26 Aug 2020
Available online: 08 December 2020

 

 

APPENDICES

 

A LM-RATIONALITY OF RATIONAL CLOSURE

Let CC = D u C be a Datalog knowledge base, where D is a set of defeasible rules and C is a set of classical clauses. Let a, (5, y be molecules. We provide proofs below for the satisfaction of each KLM property by the RationalClosureDatalog procedure. That is, we prove that RationalClosureDatalog is LM-rational. We start by showing that while checking CCfc a\\ (5, if it is always the case that R_o U R = -a, then the algorithm returns true.

Lemma 1 Let CC be a Datalog knowledge base and a, (5 molecules such that when checking CC fc a \\ (, it is always the case that R_o U R = -a. Then, the RationalClosureDatalog algorithm returns true.

Proof of Lemma 1: Since, in the checking, it is always the case that R_o U R = -a, the while loop on line 4 will keep looping, until R = 0. Then the algorithm will jump to line 7, and return R_o U R = a - (.

But, since R_o U R = -a, we know that a9 e t for every substitution 9 and model t (of Roo U R). Thus, a - ( is true under every substitution 9 and model t. Hence, the query Roo U R = a - 5 must return true. So the algorithm itself returns true.a

A.1 Ref

We want to show that CC fc a\\ a. We will make use of Lemma 2 to do so. Lemma 2 The defeasible rule a - a is a tautology.

Proof of Lemma 2: Let t be any Herbrand interpretation and 9 a substitution which replaces variables by constants. In the proofs, we refer to such a substitution as a grounding substitution. If a9 e t then a9 e t. So t is a model of a - a. Hence, a - a is a tautology.^

Let t be a Herbrand interpretation of CC and 9 a grounding substitution. We now consider 2 cases below:

Case 1: At some point (when i e [0,n]) in the CC fc a \\ a checking, R_o U R = -a for the first time. Then, since a - a is a tautology, any model of R_o U R must satisfy a - a so Ro U R = a - a. Thus, the algorithm returns true.

Case 2: It is always the case in the CC fc a \\ a checking that R_o U R = -a. Then, the algorithm returns true, by Lemma 1.b

A.2 LLE

Suppose = a - (,= ( - a and CC fc a \\ y. We want to show that CC fc (5 \\ y. We will make use of Lemma 3 to do so.

Lemma 3 Let t be a Herbrand interpretation and 9 a grounding substitution. Then, = a - (5 and = 5 - a iff a9 e t and (9 e t, or, a9 e t and (9 e t.

Proof of Lemma 3: Let t be some Herbrand interpretation and 9 some grounding substitution. Suppose that a9 e t. Since = a - ( we must have that t satisfies a - ( and so (9 e t. Now suppose that a9 e t. We know that t satisfies ( - a since = ( - a. So we must have (9 e t . Similar arguments hold for when (9 e t and (9 e t m

Claim: At each level, Ro U R = -( iff Ro U R = -a.

Proof of Claim: Suppose that, at some point i e [0, n], R_o U R = -a. Let t be a model of Roo U R and 9 some grounding substitution. So t is a model of -a and, hence, a9 e t. Thus, by Lemma 3, (9 e t so t is a model of -(. Hence, R_o U R = -(. Similarly, we can show that if at some point i e [0, n], R_o U R = -(, then R_o U R = -a.

Now suppose that, at some point i e [0, n], R_o U R = -a. Then, there is some model t of R_o UR such that t is not a model of -a. So there must be some substitution 9 such that a9 e t. Hence, by Lemma 3, (9 e t so t is not a model of -(. Thus, R_o U R = -(. Similarly, we can show that if at some point i e [0, n], R_o U R = -(, then R_o U R = -am

We now consider 2 cases below:

Case 1: At some point (when i e [0, n]) in the Kfc a\\ y checking, R_o U R = -a for the first time. Then, at point i, since Kfc a\\ y, R_o U R = a - y. As shown above, at the same point i, Roo U R = -( for the first time. The algorithm now checks that R_o U R = ( - y. Let t be a model of R_o U R and 9 a grounding substitution. Suppose (9 e t then, by Lemma 3, a9 e t too. And, since R_o U R = a - y, we must have y9 e t. So R_o U R = ( - y and the algorithm returns true.

Case 2: It is always the case in the K fc a \ y checking that R_o U R = -a. Then, in the K ( i\\ y checking, as shown above, it is also always the case that R_o U R = -(. So the algorithm returns true, by Lemma 1.b

A.3 RW

Suppose = ( - y and Kfc a \ (. We want to show that K a\\ y. Consider the 2 cases below:

Case 1: At some point (i e [0, n]) in the K fc a \ ( checking, R_o U R = -a for the first time. Then, at that point i, since K fc a\\ (, we have that R_o U R = a - (. When checking Kfc a\\ y, the algorithm reaches that same point i, where R_o U R = -a for the first time and then checks whether R_o U R = a - y.

Let t be a model of R_o U R and 9 a grounding substitution. Suppose a9 e t then, since R_o U R = a - (, we have that (9 e t. Since ( - y is a tautology, we must also have that y9 e t. So R_o U R = a - y and the algorithm returns true.

Case 2: It is always the case in the Kfc a \ ( checking that R_o U R = -a. Then, in the Kfc a i\\ y checking, it is also always the case that R_o U R = -a. So the algorithm returns true, by Lemma 1m

A.4 And

Suppose CC fc a\\ ( and CC fc a\\ y. We want to show that CC fc a\\ ( A y. Consider the 2 cases below:

Case 1: At some point (i e [0, n]) in the CC fc a\\ ( checking, R_o UR = -a for the first time. Then, at the same point i in the CC fc a \\ y checking, R_o U R = -a for the first time. Now, since CC fc a\\ ( and CC fc a\\ y, at point i we have that R_o UR = a - ( and R_o UR = a - y. So, at point i in the CCfc a\\ ( A y checking, R_o U R = -a for the first time and the algorithm checks whether R_o U R = a - ( A y.

Let t be a model of R_o U R and 9 a grounding substitution. Suppose a9 e t then, since R_o U R = a - 5 and R_o U R = a - y, we must have (9 e t and y9 e t. So (( A y)9 e t. Thus, R_o U R = a - ( A y and the algorithm returns true.

Case 2: It is always the case in the C c a \ ( checking that that Ro U R = -a. Then, in the CC fc a \\ ( A y checking, it is also always the case that R_o U R = -a. So the algorithm returns true, by Lemma 1.a

A.5 Or

Suppose CC fc a\\ y and CC fc (5 \\ y. We want to show that CC fc a V (5 \\ y. Consider the 2 cases below:

Case 1: It is always the case (for all i e [0,n]) that in the CCfc a\\ y checking, R_o U R = -a and, in the CC fc (5 \\ y checking, R_o U R = -(. Let t be a model of R_o U R at some point (i e [0,n]) and 9 a grounding substitution. Then, at point i, we must have that a9 e t and (9 e t so (a V 5)9 e t. Thus, Ro U R = -(a V () at point i. Hence, in the CC fc a V /3^ y checking, it is always the case that R_o UR = -(a V() so the algorithm returns true, by Lemma 1.

Case 2: There is some point (i e [0,n]) at which, without loss of generality, R_o U R = -a for the first time and at each point before point i (for each 0 < j < i), R_o U R = -(. That is, R_o U R = -a for the first time either at the same level or a higher level than the level at which R_o U R = -( for the first time. Since we know that CC fc a\\ y, at point i we must have that R = a - y.

At point i, since R_o U R = -a, there is some model t of R_o U R which is not a model of -a. Thus, there is some substitution 9 such that a9 e t. Thus, (a V ()9 e t so (-(a V ())9 e t. Hence, at point i in the CCfc a V ( \\ y checking, R_o U R = -(a V ( ).

Furthermore, at any point j < i, we have that Ro U R \= -a and Ro U R \= -(. Thus, as shown above in Case 1, we must have that R_o U R = -(a V () at point j. So point i is the first point at which R_o U R = -(a V ().

We again let t be a model of R_o U R at point i and 9 a grounding substitution. Now we consider 2 sub-cases below:

i At point i, Ro U R = -(. Then (9 e t. Suppose that a9 e t. Then, (a V ()9 e t so a V5 - y is true under t for substitution 9. Now suppose that a9 e t. Then, (a V ()9 e t and, since R = a - 7, 76 e t. So, a V 3 - 7 is true under t for substitution 9. Hence, R = a V 3 - 7 and the algorithm returns true.

ii At point i, Roo U R = -3 (and this is not the case for any j < i, otherwise it would violate our assumption for case 2). So, since Kfc 3 Y 7, we have that R_o U R = 3 - 7. Suppose that a9 e t and 39 e t. Then, (a V 3)9 e t so a V 3 - 7 is true under t for substitution 9. Now suppose that, without loss of generality (since both R = a - 7 and R = 3 - 7), a9 e t. Then, (a V 3)9 e t and, since R = a - 7, 76 e t. So, a V 3 - 7 is true under t for substitution 9. Hence, R = a V 3 - 7 and the algorithm returns true.a

A.6 CM

Suppose Kfc a Y 3 and Kfc a Y 7. We want to show that Kfc a A 3 Y 7. We will make use of Lemma 4 to do so.

Lemma 4 Suppose Kfc a Y 3 and Kfc a Y 7 for some knowledge base K. Then, the following holds:

i IfR_o U R = -a at some point i in the RationalClosureDatalog algorithm, then R_o U R = -(a A 3) at that point i.

ii IfR_o U R = -a for the first time at some point i in the RationalClosureDatalog algorithm, then R_o U R = -(a A 3 ), also for the first time, at that point i.

Proof of Lemma 4:

i Suppose that R_o U R = -a at some point i. Let t be a model of R_o U R at point i and 9 a grounding substitution. Then a9 e t so (a A 3)9 e t and, hence, (-(a A 3))9 e t. Hence, Ro U R = -(a A 3).m

ii Suppose that, at point i, R_o U R = -a for the first time. Then, since K fc a Y 3, we have that R_o U R = a - 3. And, since R_o U R = -a, there is some model t of R_o U R which is not a model of -a. Thus, there is some substitution 9 such that a9 e t. Since R_o UR = a - 3, we must have that 39 e t too. So (a A3)9 e t and, thus, (-(a A3))9 e t. Hence, at point i, R_o U R = -(a A 3).

Now, it remains to show that point i is the first point at which R_o UR = - (a A3). Assume, to the contrary, that at some point j < i, R_o U R = -(a A 3). But, then at this point, we know Ro U R = -a, so Ro U R = -(a A 3), which is a contradiction. Thus, point i is the first point at which R_o U R = -(a A 3).■

Now we consider 2 cases below:

Case 1: At some point (i e [0, n]) in the K a Y 3 checking, R_o U R = -a for the first time. Then, at the same point i, in the Kfc a Y 7 checking, R_o U R = -a for the first time.

Thus, at this point i we have that R_o U R = a - 5 and R_o U R = a - 7. And, by Lemma 4, at point i in the K fc a A 5 Y 7 checking, R_o U R = -(a A 5) for the first time.

Let t be a model of R_o U R at point i and 9 a grounding substitution. Suppose that a9 e t. Then, (a A 5)9 e t so a A 5 - 7 is true under t for substitution 9. Suppose now that a9 e t so, since Roo UR = a - 5 and R_o UR = a - 7, we have that 59 e t and 79 e t. Thus, (a A5)9 e t and 79 e t so a A 5 - 7 is true under t for substitution 9. Hence, R_o U R = a A 5 - 7 so the algorithm returns true.

Case 2: It is always the case in the K fc a Y 5 checking that R_o U R = -a. Then, by Lemma 4, in the K fc a A 5 Y 7 checking, it is always the case that R_o U R = -(a A 5) and so the algorithm returns true, by Lemma 1.a

A.7 RM

Suppose that K fc a Y 7 and K fc a Y -5. We want to show that K fc a A 5 Y 7. Consider the 2 cases below:

Case 1: At some point (i e [0, n]) in the K fc a A 5 Y 7 checking, R_o U R = -(a A 5). We claim that we must have that both R_o U R = -a and R_o U R = -5. Suppose, to the contrary, R_o U R = -a. Let t be a model of R_o U R at point i and 9 a grounding substitution. Then a9 e t so (a A 5)9 e t. Thus, R_o U R = -(a A 5), a contradiction. Similarly, if R_o U R = -5 then Ro U R = -(a A 5), a contradiction.

Claim: Point i is the first point at which R_o U R = -a.

Proof of Claim: Assume to the contrary that there exists some j < i such that R_o U R = -a, where j is minimal. Based on the assumptions of Case 1, we know that R_o U R = -(a A 5) at point j. And, since Kfc a Y -5, we know that R_o U R = a - -5 at point j. Let t be a model of Roo U R and 9 a substitution that replaces variables with constants. Now, either a9 e t or a9 e t. We consider 2 sub-cases below:

i If a9 e t. Then, a - -5 must be true under t for 9.

ii If a9 e t. Then, we must have that 59 e t. Otherwise, we would have (a A 5)9 e t, and, hence, R_o U R = -(a A 5), a contradiction. Thus, -59 e t and so a - -5 must be true under t for 9.

Either way, a - -5 is true under t for 9, so R_o U R = a - -5, a contradiction. Thus, no such j < i exists.b

So, since Ro U R |= -a at point i (and not before) and K |c a |Y 7, we know that Ro U R |= a - 7 at this point. Suppose that at least one of a9 e t or 59 e t holds. Then, (a A 5)9 e t so a A 5 - 7 is true under t for substitution 9. Now suppose that both a9 e t and 59 e t. Then, (a A 5)9 e t and, since R_o U R = a - 7, we know that 79 e t too. So a A 5 - 7 is true under t for substitution 9. Hence, R_o U R = a A 5 - 7 and the algorithm returns true.

Case 2: It is always the case in the K |c a A 5 |Y 7 checking that Ro U R |= -(a A 5). Then, the algorithm returns true, by Lemma 1m

 

B LM-RATIONALITY OF LEXICOGRAPHIC CLOSURE

In this section, for completeness, we provide proofs for the satisfaction of each KLM property by

the LexicographicClosureDatalog procedure. That is, we prove that LexicographicClosureDatalog is LM-rational.

Notice that the proofs for the satisfaction of each KLM property by the RationalClosureDatalog procedure, in Appendix A, are independent of the ranking produced by the BaseRankDatalog procedure. Furthermore, notice that the only difference between the LexicographicClosureDatalog procedure and the RationalClosureDatalog procedure is the use of the SubsetRankDatalog procedure to rank statements instead of the BaseRankDatalog procedure.

Thus, the proofs for the satisfaction of each KLM property in Appendix A can be used to prove for the satisfaction of each KLM property by the LexicographicClosureDatalog procedure.

 

C LM-RATIONALITY OF RELEVANT CLOSURE

Here we provide a proof that Minimal Relevant Closure satisfies the KLM property of LLE. We also provide counter-examples to show that it does not satisfy the properties of Or, CM, and RM.

C.1 LLE

Let us start by examining the KLM property of LLE:

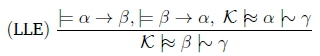
The proof (in Appendix A.2) that Rational Closure satisfies LLE does not directly translate to a proof for Relevant Closure, since the relevance partitions in the two queries are different. The two queries in question are Kfc a \ 7 and Kfc (3 \^ 7. The relevance partitions for these queries are fully determined by a and ( respectively, since the K in both instances is the same K.

Thus, to allow the proof to translate, we just have to prove that (J Jm_in(a) = {J J^K_in(P) (i.e. the relevance partitions for the two queries are the same). To do this, we start by showing that Jk(k) = Jk(3). We first prove that J_K(a) ç Jk(3).

Let J e J_K(a); then J is an a-justification. This means that J = -a. Now since = (3 - a, J = -3.

Assume to the contrary that there is some J' c J such that J' = -3. Then since = a - (3, J' = -a, contradicting J being an a-justification. So J is also a 3-justification. This means that J e Jk(3) as required, proving that Jk(a) ç Jk(3). The proof that Jk(3) Ç Jk(o) is very similar.

Thus, we have that J_K(a) = J_K((). Since these are exactly equal, it must also be the case then that IJ Jm_in(a) = U JmnW). The proof (in Appendix A.2) that Rational Closure satisfies the property of LLE can now be used directly to show that Relevant Closure also satisfies the property.

C.2 Or

For the upcoming three counter-examples, we will use the symbol a to represent the Datalog molecule a(Tyler), b to represent b(Tyler), and so on. In this case, Tyler is just some constant in our Datalog program. This way, truth can be assigned to these molecules in the same way that it is for propositional logic.

We need to find a knowledge base K and molecules a, g, e such that Kfc a \\ e and Kfc g\\ e, but Kfc a V g \ e. Define:

This can be represented neatly by a lattice, where a \ b would be represented by a line going upwards from a to b and a \^ -b by a dashed line.

 

 

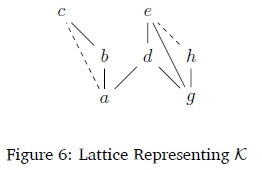
When ranked according to the base rank algorithm, the statements would appear as follows. Note that there is no "infinite rank", since there are no classical statements in the knowledge base.

 

 

To compute Relevant Closure, we first need to compute the justification sets for each of the queries we will be making:

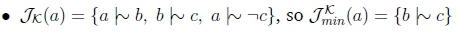
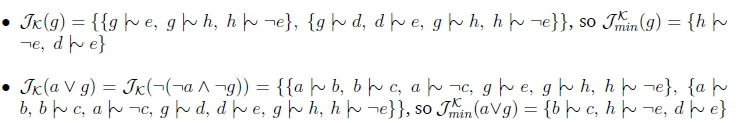
From this, it can be clearly seen that K fc a Y e and K fc g Y e. We now consider what happens when the algorithm is passed the query a Vg Y e. When i = 0, R^- UR = K = - (a Vg), so the algorithm proceeds to the next iteration. When i = 1, R^- U R = -(a V g), so we check if R^- U R = a V g - e. At this point:

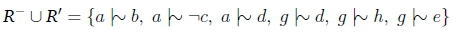
Consider a Herbrand interpretation t such that a,b,d,h e t and c,g,e e t. Then t \\- R^- UR, but T\f a V g - e. Thus R^- U R = a V g - e, and the algorithm returns false. So Kfc a V g Y e as required.

C.3 CM

We now need to find K, c, d, and e such that Kfc cY d, Kfc cY e, but Kfc c A d Y e. Define:

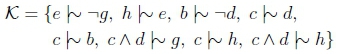
This can be represented by a lattice, where a |Y b would be represented by a line going upwards from a to b, a |Y -b by a dashed line, and a A b by thinly dotted lines from a, b to a A b.

 

 

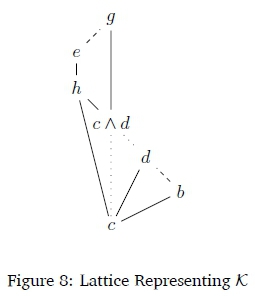
When ranked according to the base rank algorithm, the statements would appear as shown in Figure 9.

 

 

We now compute the justification sets for each of the queries we will be making:

 

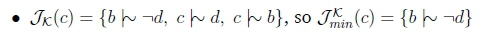
Thus Kfc c\\ d and Kfc c\\ e. Now we consider the justification set for c A d, which consists of three different c A d-justifications:

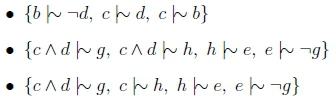
Thus J^K_in(c A d) = {b i\\ -d, e \\ -g, h \ e}. Thus, when processing the query c A d \\ e, the 0th rank is entirely thrown away, leaving only the 1st rank in R^- U R. So when i = 1, R^- U R = -(c A d), so we check if R^- U R = c A d - e.

Consider a Herbrand interpretation t such that c, b,d,h,g e t and e e t. Then t lh R^- U R, but T\f c A d - e. Thus R^- U R = c A d - e, and the algorithm returns false. So Kfc c A d\ e as required.

C.4 RM

We now need to find K, c, d, and e such that Kfc c \ -d, Kfc c\\ e, but Kfc c A d \\ e. Consider the same counter-example as above for CM. Since K c c \ d, it is also the case that Kfc c\\-d.

To see this, assume to the contrary that Kfc c\ -d. Then at some point i when R^- U R = -c, R^- U R = c - -d. However, this stopping point i is the same stopping point for the query c\\ d, so R^- U R = c - d. But then R^- U R = c --d and R^- U R = c - d, so R^- U R = -c, a contradiction.

Thus, we have that Kfc c\ -d, Kfc c\\ e, but Kfc c A d\\ e as before. So the previous counter-example is also a counter-example for RM.

 

D OTHER PROOFS

D.1 Proposition 1

Let t be a Herbrand interpretation. Then, t is a model of -a under Datalog+ semantics iff t is a model of a - ± under Datalog^v semantics.

Proof of Proposition 1 : Let t be a Herbrand interpretation and 9 a substitution which replaces variables with constants. We want to show that t is a model of -a under Datalog + semantics iff t is a model of a - ± under Datalog^v semantics.

Suppose t is a model of -a under Datalog+ semantics. Then, a9 e t under Datalog + semantics. Clearly, we also have that a9 e t under Datalog^v semantics. So, a - ± is true under t for 9. Hence, t is a model of a - ± under Datalog^v semantics.

Suppose t is a model of a - ± under Datalog^v semantics. We claim that a9 e t under Datalog^v semantics. Suppose, to the contrary, that a9 e t. Notice that it is always the case that ±9 e t. Thus, a - ± is not true under t for 9, contradicting the assumption that t is a model of a - ±. Thus, our claim holds - a9 e t under Datalog^v semantics. Clearly, we also have that a9 e t under Datalog+ semantics. Thus, -a is true under t for 9. Hence, t is a model of -a under Datalog+ semantics.^