RESEARCH ARTICLE

 

An assessment of algorithms for deriving failure deterministic finite automata

 

 

Madoda Nxumalo^I; Derrick G. Kourie^{II, III}; Loek Cleophas^{II, IV}; Bruce W. Watson^{II, III, I}

^IDepartment of Computer Science, University of Pretoria, South Africa. mddnxml@gmail.com, bruce@fastar.org
^IIFastar Research Group, Department of Information Science, Stellenbosch University, South Africa. dkourie@fastar.org, loek@fastar.org, bruce@fastar.org
^IIICentre for Artificial Intelligence Research (CAIR), CSIR Meraka, Pretoria, South Africa. dkourie@fastar.org, bruce@fastar.org
^IVSoftware Engineering and Technology Group, Eindhoven University of Technology, The Netherlands. loek@fastar.org

 

 

---

ABSTRACT

Failure deterministic finite automata (FDFAs) represent regular languages more compactly than deterministic finite automata (DFAs). Four algorithms that convert arbitrary DFAs to language-equivalent FDFAs are empirically investigated. Three are concrete variants of a previously published abstract algorithm, the DFA-Homomorphic Algorithm (DHA). The fourth builds a maximal spanning tree from the DFA to derive what it calls a delayed input DFA. A first suite of test data consists of DFAs that recognise randomised sets of finite length keywords. Since the classical Aho-Corasick algorithm builds an optimal FDFA from such a set (and only from such a set), it provides benchmark FDFAs against which the performance of the general algorithms can be compared. A second suite of test data consists of random DFAs generated by a specially designed algorithm that also builds language-equivalent FDFAs, some of which may have non-divergent cycles. These random FDFAs provide (not necessarily tight) lower bounds for assessing the effectiveness of the four general FDFA generating algorithms.

Keywords: Failure deterministic finite automata, random automata

---

 

 

1 INTRODUCTION

Deterministic finite automata (DFAs) are widely studied and used in Computer Science. Each DFA defines a set of strings, its language, from the class of string sets known as the regular languages. Each string consists of a sequence of symbols drawn from a finite set of symbols called the alphabet of the DFA. A simple algorithm is available to very efficiently determine whether or not an arbitrary finite string is a member of the language of a given DFA. As a result, DFAs are extensively used in many practical string processing applications that relate to the regular languages. These include searching through natural language texts (Drozdek, 2008, p. 702), network intrusion detection (Roesch, 1999; Zha & Sahni, 2008), lexical analysis (Aho, Lam, Sethi, & Ullman, 2006; Lesk & Schmidt, 1990) and biological sequence data processing (Roy & Aluru, 2014).

A DFA is commonly implemented as a graph. Graph nodes correspond to the so-called states of the DFA and transitions between states are labelled by symbols from its alphabet. In practice, the size of a DFA can grow very large, both in terms of the number of states, and in terms of the number of transitions. As a result, strategies for limiting the size of implemented DFAs-and, hence, of limiting their memory requirements-are of significant practical concern. The problem of converting an arbitrary DFA to a language equivalent DFA that has a minimal number of states has been well-studied. (See, for instance, Brzozowski (1962), Hopcroft (1971), Revuz (1992), Daciuk (2014).) In addition, Chapter 8 of Daciuk (2014) offers a useful overview of strategies for compressing the representation of DFAs in memory.

An orthogonal approach to reducing memory requirements is to somehow reduce the number of transitions to be stored. This approach has not been as widely studied as the state minimisation problem. For reasons that will later be apparent, we use so-called failure transitions to reduce the overall number of transitions and call the resulting structures failure DFAs (FDFAs).

A brief recent history of FDFA research is provided in Section 2. Section 3 then describes the purpose of a study we have undertaken into FDFAs and points to our overall methodological approach. Section 4 gives formal definitions of relevant concepts. In Section 5 an overview is given of the FDFA generating algorithms that have been implemented. Findings with respect to the empirical effectiveness of these algorithmic variants are then described. In Section 6 empirical results are given with respect to data for which optimal transition reduction performance is known a priori. In Section 7, an algorithm is described that produces random data for which optimal transition reduction performance is not known. The relative performance of FDFA generating algorithms against this data is described in Section 8. Section 9 then concludes, highlighting further research work needed.

 

2 BRIEF HISTORY OF FDFAS

In general, there are no redundant transitions in a DFA, so one cannot simply remove transitions without changing the language of the remaining DFA. An alternative way of reducing transitions is to replace an appropriately chosen set of DFA transitions with a single new transition of a different type, called in many texts a failure transition for reasons indicated below. In so doing, the remaining formalism is no longer a DFA. Nevertheless, by assigning appropriate semantics to the failure transitions, the resulting graph structure can still be made to define a regular language.

The use of graphs embedding such failure transitions can be traced back to the 1970's. For example, they are implicit in the data structure used in the Knuth-Morris-Pratt (KMP) algorithm (Knuth, Morris Jr, & Pratt, 1977)-an algorithm that locates a single pattern in a text string¹. Also well known is a generalisation of the KMP algorithm, due to Aho and Corasick (1975), that is widely used for multiple keyword pattern matching.

Aho and Corasick relied on the fact that a finite set of strings (i.e. a set of keywords) may be viewed as the language of a DFA whose transition graph is a tree. In the context of DFA theory, such a tree is called a trie. By ensuring that each state in this trie has appropriate additional transitions for each symbol in the alphabet (the precise details are not relevant here), a DFA is obtained whose language is a superset of the keywords. Since the resulting DFA is optimal in the sense that it has minimal states with respect to the language that it recognises, the algorithm used to construct this DFA will be referred to in this text as AC-opt. This DFA can be used to identify keywords in an arbitrary text by relying on a well-known efficient classical string recognition algorithm.

In many practical applications, the number of states and of transitions in AC-opt DFAs can be extremely large. Aho and Corasick devised an algorithm that mitigates this problem by building the DFA trie instead of the full AC-opt DFA. Thereafter, the algorithm prescribes how failure transitions are to link states of this trie 'backwards' to shallower states of the trie². The resulting graph structure is of course no longer a DFA, but it can nevertheless be used to define the same regular language as the AC-opt DFA. In fact, it is transition-minimal in the sense of replacing the maximum number of DFA transitions with failure transitions. A slightly modified version of the classical DFA-based string recognition algorithm is now required to identify keywords in an arbitrary text.

Aho and Corasick did not give a specific name to their resulting graph structure. However, the reason for calling these new transitions failure transitions is clear: these transitions are taken at a point when the next symbol of the input string being parsed "fails" to match an expected keyword symbol. In this text, we will refer to the Aho and Corasick algorithm to build this graph as AC-fail.

Note that AC-fail does not address the problem of replacing groups of DFA transitions with failure transitions in an arbitrary DFA. Such an algorithm was proposed by Kourie, Watson, Cleophas, and Venter (2012) for input DFAs that are complete³. The resulting graph structure was named an FDFA for the first time. The algorithm was called the DFA-Homomorphic Algorithm (DHA) because the FDFA output has the same state structure as the input DFA. The FDFA defines the same language as the DFA, where the semantics of a failure transition is the same as an AC-fail failure transition. However, unlike AC-fail, the resulting FDFA may not necessarily be transition-minimal with respect to the language that is defined. Indeed, Björklund, Björklund, and Zechner (2014) have shown that it is computationally hard to derive a language-equivalent transition minimal FDFA from an arbitrary DFA.

In broad terms, DHA may be described as follows⁴: It identifies all sets of DFA transitions that are suitable candidates for failure transition replacement. It iterates through these sets, using a greedy heuristic to select the next DFA transition set to be processed. The selection is based on a metric called arc redundancy. Processing entails replacing all DFA transitions whose origin is at a common state in such a set, with a single failure transition, also originating at that state. In general one of several possible states may serve as the destination for such a failure transition. DHA allows for an arbitrary selection from amongst these possible destination states.

Subsequent to the presentation of DHA in 2012 in a stringology context, an earlier article by Kumar, Dharmapurikar, Yu, Crowley, and Turner (2006) was discovered in the literature on network intrusion detection. It describes how to transform DFAs to so-called delayed-input DFAs, abbreviated to D²FAs. Upon closer inspection, it turned out that a D²FA is simply an FDFA by another (somewhat counter-intuitive) name. Their technique for generating failure transitions to replace DFA transitions is based on finding the maximal spanning tree (Kruskal, 1956) of a suitably weighted undirected graph that reflects the structure of the underlying DFA. The nodes in the graph correspond to the states of the DFA and the weights correspond to the arc redundancy measure between pairs of states (as opposed to maximal sets of states, used in the DHA case). The data sets used to test their algorithms are (state) minimised DFAs built from standard regular expressions that are used in network intrusion detection applications. Although they do not explicitly say so, it seems reasonable to conjecture that these DFAs are akin to AC-opt DFAs.

Further FDFA related research has been conducted for certain limited contexts. See Crochemore and Hancart (1997) for an overview of some earlier studies. A more recent example is discussed in Cleophas, Kourie, and Watson (2013, 2014). It is shown how DFA transitions in so-called factor oracle automata can be replaced with failure transitions to achieve a savings of up to 9% of DFA transitions. More recently, in Bille, G0rtz, and Skjoldjensen (2016), failure transitions were applied in the context of subsequence automata to form smaller subsequence automata.

 

3 PURPOSE AND METHODOLOGY

The overall purpose of this paper is to bring together the results of empirical experiments examining how effective various FDFA generating algorithms are in reducing the number of transitions held by their language-equivalent DFAs⁵.

Historically, we started by investigating DHA's effectiveness in respect of the greedy heuristic based on the arc redundancy metric. A specific heuristic was also used to select the destination of failure arcs from among several possibilities. Subsequently we proposed and investigated two alternative metrics to arc redundancy. Then, when the Kumar et al. study was discovered, we also included one of their two algorithms in our empirical experiments. It will be referred to here as the D² FA algorithm. Since the second Kumar et al. algorithm focuses on minimising lengths of failure transition paths - a consideration which was not of direct concern in our study - it has not been implemented here.

For our data sets, two distinct types of data sources were used. The first was based on randomly generated sets of keywords. AC-opt was used to generate DFAs from these and AC-fail, to obtain language equivalent FDFAs. The DHA variants and the Kumar et al. algorithm were then applied to the generated DFAs and the resulting FDFAs compared against the AC-fail FDFAs. Because AC-fail FDFAs are known to be transition-minimal, they provide an objective benchmark for the transition-reduction performance of the implemented FDFA generating algorithms. We presented the empirical results in Nxumalo et al. (2015a) and give them again in Section 6.

However, we also wanted to examine the performance of the implemented FDFA generating algorithms against generalised input data. Early experiments with classically generated random DFAs as input indicated that the opportunities for introducing failure transitions were typically rather limited and therefore not too interesting. Instead, therefore, a special algorithm was developed for generating 'random' DFAs for which there are many opportunities for replacing DFA transitions with failure transitions. Its structure was briefly outlined in Nxumalo et al. (2015b). We give it again in Section 7 here in more detail, including correctness arguments that were not previously made explicit. The algorithm simultaneously develops a language-equivalent FDFA to each 'random' DFA that is generated. The extent to which such FDFAs attain the ideal of minimising the number of transitions is not known. Nevertheless, these FDFAs are useful because they provide a peg against which to assess the performance of the other FDFA generating algorithms. Results that rely on this random data are presented in Section 8.

The various implementations and experiments in this study were conducted on an Intel i5 dual core CPU machine, running Linux Ubuntu 14.4. Code was written in C++ and compiled under the GCC version 4.8.2 compiler. Source code is available online⁶.

 

4 PRELIMINARIES

An alphabet is a finite non-empty set of symbols, denoted Σ, and of size |Σ|. A string (or word), s, is a finite sequence of characters drawn from the alphabet and its length is denoted |s|. An empty string is denoted e and |e| = 0. Σ* denotes the set of strings over this alphabet, including e. The concatenation of strings p and q is represented as pq. If s = pqr then q is a substring of s, p and pq are prefixes of s and q and qr are suffixes of s. Moreover, q is a proper substring iff -(p = e V r = e). Similarly, pq is a proper prefix iff r = e and qr is a proper suffix iff p = e.

4.1 DFAs versus FDFAs

A DFA, 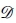, is classically defined as follows:

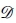= (Q, Σ, δ, F,qs), where:

Q is a finite set of states; Σ is an alphabet; q_s e Q is the start state; F C Q is a set of final states; and δ : Q χ Σ → Q is a transition function.

In general, δ maybe a partial function. Let δ( q,a) = _L indicate that δ^,a) is undefined (there is no symbol transition on a in state q) and let 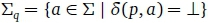(the set of symbols for which there are no symbol transitions in state q).

When δ is a total function, the DFA is called complete. If δ is not a total function, can easily be converted into the complete DFA 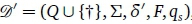, where t is a special so-called sink state such that 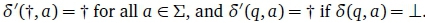. In all other cases δ' has the same mapping as δ.

Given a complete DFA, the extension of δ is defined as 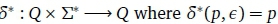and if 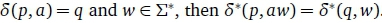A finite string, w, is said to be accepted by the DFA iff , w) ε F. The language of a DFA is the set of accepted strings.

The following formal definition of an FDFA, &, was given in Kourie et al. (2012):

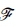= (Q, Σ, δ,f, F,qs), where:

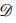= (Q, Σ, δ, F, q_s) is a DFA and f ε Q - Q is a (possibly partial) failure transition function. Let a ε Σ and p ε Q, if δ(p, a) is undefined, f(p) = q for some q ε Q.

In this text we shall refer to the mappings defined by δ as symbol transitions, and those defined by f as failure transitions.

The extension of δ in an FDFA context is a mapping: δ*: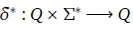 such that

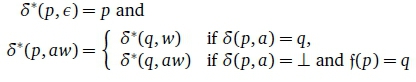
An FDFA accepts 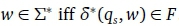. The language of an FDFA is its set of accepted strings. It can be shown that every DFA has a language-equivalent FDFA and vice versa.

The sequence of FDFA states (p₀, p₁,... p_n) such that f(p_i) = p_i+1, for all 0 < i < n, is called a failure path and is denoted 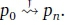. The failure alphabet 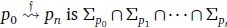. A failurecycle is a failure path such that, for any state, , in the path, 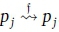. A divergent failure cycle is a cycle whose failure alphabet is non-empty. When constructing an FDFA, divergent cycles should be avoided because they lead to an infinite sequence of failure traversals in string processing algorithms.

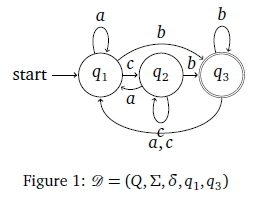
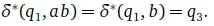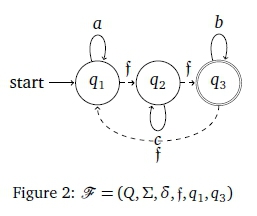
Figure 1 depicts a complete DFA for which Q = {q₁, q₂, q₃} and Σ = {a, b, c}. Its start state is q₁ and q₃ is the only final state. Its symbol transitions are depicted as solid arrows between states. Figure 2 shows a language-equivalent FDFA where dashed arrows indicate the failure transitions. Note, for example, that ab is in the language of both automata. In the DFA case,. In the FDFA case,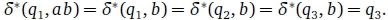

 

 

 

 

Notice the failure cycle in Figure 1 where by . The respective failure alphabets are = , the failure cycle is not divergent.

4.2 Brief introduction to FCA

Because DHA relies on formal concept analysis (FCA), a brief introduction to FCA is given here. A more complete and formal introduction can be found in standard texts such as Ganter, Stumme, and Wille (2005), Ganter and Wille (1999).

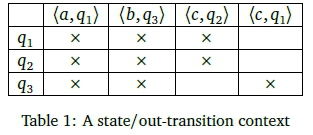
A table can be used to connect a finite set of discrete entities (also known as objects), and discrete attributes as follows. A row is allocated to each object and a column to each attribute. Each table cell is assigned a binary value to indicate whether or not the row's object has the column's attribute. In formal concept analysis (FCA), such a table is called a context. Table 1 is an example that will be further discussed below.

 

 

FCA concerns the study of formal concepts that can be inferred from a context. A concept, C, is a pair (ext(C), int(C)) where ext(C) is a set of entities (context rows) and int(C) is a set of attributes (context columns) possessed in common by these entities. ext(C) and int(C), called the extent and intent of C respectively, are further characterised by being maximal⁷. In FCA, concepts are partially ordered by set containment of extents-i.e. concept D is considered smaller than concept C (written as D < C) if and only if ext(D) c ext(C). It can be shown that there is the following dual relationship between intents and extents: (D < C) if and only if int(C) c int(D). Thus, in general, concepts high up in the lattice ordering have large extents and small intents and vice-versa.

FCA algorithms and tools are available for inferring concepts from a given context. They rely on this partial order to construct a concept lattice from the inferred concepts.

In Kourie et al. (2012) a specific context is inferred from a given DFA as follows. The context rows (objects) represent Q, the DFA states. The context columns (attributes) are pairs of the form (a,p) ε Σ χ Q. A state q is deemed to have attribute (a,p) if and only if 5(q, a) = p. Table 1 shows such a context for the DFA in Figure 1. The concept lattice line diagram that can be derived from this

context is shown in Figure 3. The diagram has four nodes, each of which represents a concept in the lattice. Attribute and object annotations are attached to certain concepts and can be used to infer the respective intents and extents of concepts. The bottom concept is below all the object labels and

 

 

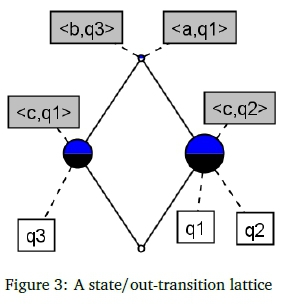
so is construed to have 0 as its extent. Conversely, because the top concept is above all objects it has Q as extent. The bottom concept is below all the attribute labels and so is construed to have all the attributes as its intent. The top concept is below the labels of attributes in its intent, i.e. its intent is {(a,q₁), (b,q₃)}. In effect, the bottom concept informs us that no state possesses all the attributes, whereas the top concept informs us that all objects have the same two out-transition/destination pairs described in its intent.

Figure 3 also shows the two intermediate concepts. Note that they are not commensurate with one another. The right-hand side intermediate concept depicts the fact that states in its extent ({q₁, q₂}) are similar in that each has a transition on symbol a to q₁, b to q₃ and on c to q₂ - i.e. the concept's intent is {(a, q₁), (b, q₃), (c,_q2)}. Similarly, the left-hand side intermediate concept depicts the fact that only the single state in its intent, {q₃}, has intent {(a,q₁), (b,q₃), (a,q₂)}.

In Kourie et al. (2012), the lattice in Figure 3 is called a state/out-transition lattice. Each concept C is characterised by an integer called its arc redundancy, denoted by ar(C). It is defined as

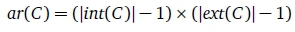
ar(C) represents the number of arcs that may be saved by doing the following to the originating DFA:

1. Select one of the states in ext(C).

2. At all the remaining states in ext(C), remove all out-transitions mentioned in int(C).

3. Insert a failure arc from each of the states in step 2 to the singled out state in step 1.

The expression, | ext(C)| - 1 represents the number of states in step 2 above. At each such state, \int(C)| symbol transitions are removed and a failure arc is inserted. Thus, \int(C)| - 1 is the reduction in total number of transitions at each of ^xt(C)| - 1 states so that ar(C) is indeed the total number of arcs reduced by the above transformation.

 

5 FDFA ALGORITHMS

This section focuses on a description of the DHA algorithm, first in its abstract form and then in its implemented versions. Thereafter a very brief description of D²FA is given.

For DHA to convert a DFA, 3, into a language equivalent FDFA, a staged transformation of 3 is undertaken. Firstly, the state/out-transition context is derived from 3. Then the concept lattice is generated⁸ and PAR, the set of concepts that have positive arc redundancies, is computed. We next give an outline of the abstract version of DHA proposed in Kourie et al. (2012). After that, the heuristics used in concrete implementations of DHA are discussed.

5.1 The abstract DHA version

The abstract DHA version is outlined in Algorithm 1. It requires 3 as input, as well as PAR. It provides a language-equivalent FDFA, &, by removing selected symbol transitions, δ, of 3 and replacing them with failure transitions in f, a set variable that is initialised to the empty set.

 

 

DHA maintains a variable, O, to keep track of states that are not the source of any failure transitions to date. This is to ensure that a state is never the source of more than one failure transition. Initially all states qualify, so O is initialised to Q. For as long as O and PAR are non-empty, the algorithm iteratively performs the following transformation step on the input DFA.

A concept c is selected from the PAR set, abstractly specified here as c := selectConcept(PAAR). To ensure that c is no longer available in subsequent iterations it is removed from PAR. From c's extent, one of the states, t, is chosen to be a failure transition target state. This is indicated by the abstract statement t :=getAnyState(ext(c)). The remaining set of states in ext(c) is denoted by ext'(c).

Then, each state s in both ext'(c) and O is considered as a possible source of a new failure transition. (Of course, states in ext'(c) but not in O are already the source of a failure transition and so do not qualify to be the source of a new failure transition.) A new failure transition is inserted from s to t, provided such insertion will not create a divergent failure cycle. In addition, all symbol transitions in int(c) are removed from s. Because state s has become a failure transition source state whose target state is t, it may no longer be the source of any other failure transition, and so is removed from O.

Thereafter PAAR is recomputed to reflect changes in arc redundancy before another transformation step is carried out. The algorithm terminates when it is no longer possible to install any more failure transitions.

5.2 Implementing DHA

In order to actually implement the above abstract version of DHA, several concrete choices had to be made.

For pragmatic reasons, a simplifying choice was made. It was decided not to recompute PAR in each iteration. This choice does not affect the correctness of the algorithm, but may affect its optimality. Investigating such effects was left for future study.

The selection of c from PAAR that is abstractly expressed in Algorithm 1 as c := SelectConcept (PAAR) was concretely tested against three different heuristics:

1. The MaxAR heuristic: c is a PAR concept with a maximum arc redundancy.

2. The MaxIntent heuristic: c is a PAR concept with a maximum intent size.

3. The MinExtent heuristic: c is a PAR concept with a minimum extent size.

In each case, the selection was done greedily, i.e. an element from PAR was selected on the basis of the indicated maximal or minimal feature, without regard to the potential lost opportunities in the forthcoming iterations resulting from these selections. An arbitrary choice was made in the case of tied values.

After selecting a concept, c, based on one of these heuristics, Algorithm 1 allows for any state t in ext(c) to become the target state of failure transitions from each of the remaining states in ext(c). Instead of selecting t randomly, we decided to take a queue from AC-fail and direct all failure arcs towards the start state. For ease of implementation a reasonably simple criterion was chosen, namely to select t as the closest state in ext(c) to the start state.

In the case of AC-opt DFAs, the distance of states from the start state is well defined in the underlying trie, providing an easy basis for selecting the closest state in ext(c) to the start state. In the case of more general DFAs, there could be multiple alternative paths from start state to a given state. As a result, it was necessary to use Dijkstra's well-known algorithm for computing the shortest path between two nodes in a graph (Dijkstra, 1959) to find the closest state in ext(c) to the start state.

5.3 Motivating the heuristics

Since these heuristics were iteratively evolved during our experiments, it is appropriate to indicate briefly the intuition that lies behind them. This is explained with reference to Table 2 giving information about three concepts labelled A, B and C, in some fictitious example. The table shows the size of the extents and intents of these concepts, and the resulting arc redundancy. Recall that after DHA selects a concept, a transformation results in the following: failure transitions are introduced that are one less in number than the size of the extent; the size of the intent corresponds to the number of DFA symbol transitions that are replaced per failure transition introduced; and the arc redundancy is the overall decline in transitions per transformation.

 

 

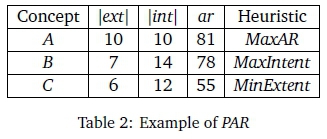
The final column of the table shows which of the three heuristics would select the concept in the given row over the other concepts. Thus, MaxAAR would select A, resulting in the maximal decline of 81 transitions in the transformation. This seemed like the most obvious heuristic to apply, and was in fact proposed in Kourie et al. (2012). After a few initial experiments, we decided to consider MaxIntent as an alternative. In the example, it would select B, resulting in a slightly smaller overall decline of transitions (78), but replacing the largest possible number of symbol transitions per state (namely 14 symbols per state) during the transformation step. The final heuristic, MinExtent, was proposed because of the known dual relationship in concept lattices between extent and intent sizes. In the example, this heuristic selects C, thereby replacing more symbol transitions per state (12) during the transformation step than MaxAAR but fewer than MaxIntent. It results in the smallest overall decline in the number of transitions (55), leaving further transition replacements to transformation steps to come in subsequent iterations.

5.4 The D²FA Algorithm

Kumar et al. (2006) refer to default transitions instead of failure transitions. Their algorithm computes the arc redundancy between each pair of states-i.e. the transition (and thus space) reduction that can be achieved by removing appropriate outbound symbol transitions at either one of the states of the pair and inserting a failure transition from that state to the other one in the pair. It then constructs a fully connected undirected graph (called a space reduction graph) whose nodes are states and whose arcs are weighted by the arc redundancy computed for the relevant pair of states. Following this, it computes the maximum spanning tree over this graph. Each arc in this maximal spanning tree indicates where to place a failure transition in the transition graph and appropriately remove symbol transitions.

In a concrete implementation, a choice may have to be made between alternative spanning trees that have the same maximum weight but different roots. Decisions also have to be made about the orientation of the failure transitions. A heuristic recommended by Kumar et al. (2006) is that all failure transitions should be directed towards the spanning tree's selected root. In our implementations, we took the starting state of the DFA as the root of the spanning tree. This coheres with our DHA heuristic of closest-to-the-start-state.

5.5 Key differences between DHA and D²FA

The algorithm of Kumar et al. (2006) avoids failure cycles. However, Figures 4 and 5 present an example indicating this to be potentially suboptimal.

 

 

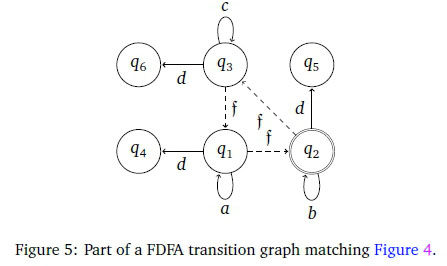
The two figures show parts of a transition graph of a DFA and the corresponding parts of the transition graph of a language-equivalent FDFA. The FDFA contains three failure transitions in a non-divergent cycle. Leaving out any one of these failure transitions to avoid the cycle would mean more transitions overall in the FDFA.

DHA, in contrast, allows for non-divergent cycles.

Furthermore, because D²FA compares DFA states on a pairwise basis, it tends to result in long failure paths. Such long paths render the FDFA less efficient when being used to check whether a string is in its language.

DHA, by way of contrast, identifies sets of DFA states that have common transition behaviour (represented by the extent of a concept), selecting one as the target, and then installing failure arcs from all the other states in the set to the target. This tends to avoid such long failure paths.

 

6 THE AHO-CORASICK EXPERIMENT

It can easily be demonstrated that if there are no overlaps between proper prefixes and proper suffixes of keywords in a keyword set, then the failure transitions of the associated Aho-Corasick FDFA will all loop back to its start state, and the ClosestToRoot heuristic will behave similarly. To avoid keyword sets that lead to such trivial AC-fail FDFAs, the following randomised keyword set construction algorithm was devised. Note that all random selections described below are based on a pseudo-random number generator.

Keywords (also referred to as patterns) from an alphabet of size 10 were generated. The keyword lengths varied between 5 and 60 characters. Keyword sets whose size-ranges are 5,10,15,..., 100 were constructed. For each of these 20 different set sizes, twelve different keyword sets were generated. Thus in total 12 χ 20 = 240 keyword sets were available.

To construct a keyword set of size N, an initial N random strings were generated. Each such string has random content taken from the alphabet and random length in the range between 5 and 30. However, for reasons given below, only M of these N strings were directly inserted into the keyword set where M < N. The set was then incrementally grown to the desired size, N, by repeating the following:

• Randomly selected a string in the current keyword set.

• Select a prefix, say p, of random length from this string.

• Create a string, say w, not yet in the keyword set.

• Insert either pw or wp into the keyword set.

Steps are taken to ensure that there is a reasonable representation of differently constructed keywords in a given keyword set.

These keyword sets served as input to the SPARE Parts toolkit (Watson & Cleophas, 2004) to create the associated AC-fail FDFAs and the language-equivalent state-minimal AC-opt DFAs. A routine was written to extract state/out-transition contexts from the AC-opt DFAs. These contexts were used as input data to FCART (Buzmakov & Neznanov, 2013; Neznanov & Parinov, 2014). The DHA variants under test generated FDFAs using as input the AC-opt DFAs as well as PAR derived from the resulting concept lattices. The D²FA algorithm was also implemented and run, also with the AC-opt DFAs as input.

6.1 Results

Figure 6 reflects the reductions in total transitions (i.e. symbol and failure transitions) to be had when building an FDFA that is language equivalent to an AC-opt DFA. FDFAs were built ab initio from a keyword set using AC-fail algorithm. FDFAs were also derived from the AC-opt DFA using each of the DHA variants as well as D²FA. In each case, the difference between the total number of AC-opt DFA transitions and the total number of FDFA transitions was found, and this difference was expressed as a percentage of the total number of AC-opt DFA transitions. For each of the set sizes, the percentage was computed for each of the 12 keyword set samples and then the average percentage over those 12 samples was found and plotted.

The figure shows that the optimal transition reduction attained by AC-fail FDFAs is about 80% over all sample sizes. The MaxIntent, MinExtent and D²FA FDFAs almost identically track this performance. By way of contrast, the MaxAR heuristic barely achieves a 50% reduction in transitions for small sample sizes, and the reduction declines below 20% for a sample size of about 75, after which there is some evidence that the reduction might become somewhat more significant.

However, the fact that the overall savings of the MaxIntent, MinExtent and D²FA FDFAs closely correspond to savings attained by AC-fail FDFAs does not guarantee that the failure and symbol transitions in the respective language-equivalent FDFAs will be arranged in exactly the same way.

Figures 7 and 8 give alternative views of how the arrangements of transitions differ. These figures each contain a subfigure for the FDFAs derived using MaxIntent, another for FDFAs derived using MinExtent, yet another for FDFAs derived using MaxAR and finally a subfigure for FDFAs derived from D²FA. Each subfigure is built up out of a 20 box-and-whisker plots, one for each of the pattern set sizes 5,10,... 100. Each box-and-whisker plot shows data relating to the 12 sample keyword sets of the given size, namely the median, the 25^th and the 75^thpercentiles as well as outliers. The data shown differs in the two figures. Figure 7 shows the count of non-equivalent symbol transitions, that do not correspond with symbol transitions in AC-fail FDFAs. This count is made with respect to a given FDFA, say &, by running through all symbol transitions in the language-equivalent AC-fail FDFA and incrementing the count every time a transition is not found in & that transitions from the same source state to the same destination state on the same symbol.

Figure 8 shows similar data, but with respect to equivalent failure transitions instead of non-equivalent symbol transitions. In this case, however, the data is presented as a percentage of the total number of failure transitions in the AC-fail FDFA under consideration.

6.2 Discussion of Results

Overall, Figures 6 to 8 reveal that there is a variety of ways in which failure transitions may be positioned in an FDFA that lead to good, or in many cases even optimal, transition reductions. It is interesting to note that even for the D²FA FDFAs, the total number of transition reductions is close to optimal, despite relatively large differences in the positioning of the transitions. However, the results also show that this flexibility in positioning failure transitions to achieve a good reduction in the number of transitions eventually breaks down, as in the case of the MaxAR FDFAs.

The overall rankings of the output FDFAs of the various algorithms to AC-fail FDFA could broadly be stated as

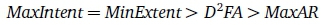
This ranking is with respect to closeness of transition placement to AC-fail FDFA. Since the original focus of this study was to explore heuristics for the DHA, further comments about the D²FA algorithm are reserved for the general conclusions in Section 9.

As was previously noted, all the heuristics used in the DHA approach are greedy and greedy strategies are not guaranteed to produce optimal results. Nevertheless, it was clearly seen that MaxIntent FDFAs and MinExtent FDFAs practically reproduced AC-fail FDFAs in respect of symbol transitions, despite their greedy nature. On the other hand, the MaxAR heuristic failed in removing large numbers of symbol transitions, paying an apparent price for following this opportunistic selection strategy.

The rationale for the MaxAR heuristic is clear: it will cause the maximum reduction in transitions in a given iteration. It is therefore somewhat surprising that it did not perform well in comparison to other heuristics. It would seem that, in the present context, it is too greedy - i.e. by selecting a concept whose extent contains the set of states that can effect maximal reduction in one iteration, it unfavourably eliminates from consideration concepts whose extent contain some of those states in subsequent iterations. Note that, being based on the maximum of the product of extent and intent sizes, it will tend to select concepts in the middle of the concept lattice diagram.

As previously noted, preliminary trials showed up the relatively poor performance of MaxAR and led to the introduction of the MaxIntent heuristic. Its effect is to maximise in every transformation step the number of symbol transitions to be removed per state. Because of the dual nature of extents and intents, MinExtent and MaxIntent heuristics frequently select the same concept for the next transformation step. This explains why the results are similar, though not identical. Note that these latter two heuristics prioritise 'small' concepts in the partial order - i.e. concepts that lie towards the bottom region of the line diagram of the concept lattice.

One of the reasons for differences between AC-fail FDFAs and the other FDFAs is that some implementations of the AC-fail algorithm, including the SPARE Parts implementation, inserts a failure arc at every state (except the start state), even if there is an out-transition on every alphabet symbol from a state. Such a failure transition is, of course, redundant. Inspection of the data showed that some of the randomly generated keyword sets lead to such "useless" failure transitions, but they are so rare that they do not materially affect the overall observations.

The heuristic of choosing failure transition destinations as close as possible to the start state approximates the AC-fail FDFA action in so far as it also directs failure transitions backwards towards the start state. However, by selecting a failure transition's target state to be as close as possible to the start state, it also contrasts with the AC-fail algorithm actions. As briefly described in footnote 2, AC-fail chooses a state for the failure transition destination that is as far as possible from the start state. It is interesting to note in Figure 8 that MinExtent FDFA and MaxIntent FDFA show a rapid and more or less linear decline in failure transition equivalence with respect to AC-fail FDFAs when pattern set size reaches about 65. We conjecture that for smaller keyword sizes, our 'closest-to-the-start-state' heuristic does not conflict significantly with AC-fail algorithm's actions because there is little to choose in the backward direction; and that when keyword set sizes become greater, there is more choice, and consequently less correspondence between the failure transitions. This is but one of several matters that has been left for further study.

 

7 GENERATING GENERALISED DATA

In order to test the DHA variants and D² FA against general DFAs (not subject to the constraints of AC-opt DFAs), early experiments were conducted with 'randomly' generated DFAs⁹. These experiments showed that the percentage reduction in transitions of DHA FDFAs from random DFAs was generally less than 10%. This is because such randomly generated DFAs typically do not offer much scope for introducing failure transitions. An alternative way of generating more interesting DFA test data was therefore sought.

However, there is a further difficulty to be confronted in generating DFA test data. How should one determine the effectiveness of algorithms that generate language-equivalent FDFAs since Björklund et al. (2014) have proved that it is computationally hard to determine whether a given FDFA has maximally reduced the number of transitions? Starting with some randomly generated complete DFA, there is no self-evident way of deciding how well or badly DHA has performed.

In order to mitigate these issues, an algorithm was devised that constructs an FDFA in lockstep with the construction of a language-equivalent DFA. The DFA and FDFA states and alphabet are assumed to be predefined. The FDFA symbol and failure transitions are randomised, yet guaranteed to remain free of divergent failure cycles. The DFAs are random in some broad sense, yet should nevertheless provide many opportunities for replacing symbol transitions with failure transitions. The randomness therefore pertains to the structural graph of the FDFA and the DFA and not the language. The independently generated random FDFA offers a useful (not necessarily tight) lower bound for assessing the effectiveness of other algorithms that generate a language-equivalent FDFA from an arbitrary DFA.

Algorithm 2 constructs such a DFA/FDFA pair. It is inspired by the proof in Björklund et al. (2014) of the following claim: "Given an FDFA, we can construct an equivalent DFA with the same number of states in polynomial time." The FDFA, & = (Q, Σ, δ, f, F, q₀), is constructed to have various random features and alongside it, a language equivalent DFA, ® = (Q, Σ, δ', F, q₀). The entities Σ, Q, F and q_sare common to the two automata, and are global constants to the algorithm. It is assumed that the states are named as Q = {q₀, q₁,... q_n}. The transitions δ, δ' and f are global variables.

 

 

To influence the number of failure transitions in the final FDFA, the algorithm is invoked with a user-assigned integer input parameter k < |Q|. It serves as an upper bound on the length of any failure path that may appear in the FDFA, thus constraining the number of failure transitions in the FDFA that need to be traversed before a symbol transition on any given symbol is encountered. Hence, when k = 0 the result will be a degenerate FDFA i.e., & = ®. Note that, because of various random features built into the algorithm, the extent to which the value of k influences the number of failure transitions is not known or predictable a priori. All that can be said is that the larger the value of k, the fewer symbol transitions and the more failure transitions are likely to be present in the final FDFA, and vice versa.

The algorithm starts by ensuring all states are connected. To do this, δ and δ' transitions are defined from each state q¡ to state q_i+1 on some randomly selected alphabet symbol, a for i e [0, n). All the remaining symbol and failure transitions are then initialised to the undefined symbol, L.

The algorithm loops over each state, q¡, for each alphabet symbol, a. If δ'^_{, a) is already defined, then no further action is taken. Otherwise T, h and I are initialised ahead of a loop that constructs a failure path from q_iof maximum length I whose head is h and whose states are accumulated in state set T. The initialised values of these variables are {q¡}, q¡ and a random value from [0, k + 1) respectively.

Note that |T| - 1 gives the length of the failure path. The loop therefore terminates if |T| - 1 = I. It also terminates if there is already a δ' transition from h or if there is already a failure transition from h to one of the states in T. If none of these conditions apply, the loop body constructs a failure transition from h to some randomly selected state that is not in T, provided no failure transition from h already exists. T and h are then updated accordingly.

After the loop, a δ' symbol transition from h on a to some random state is defined if such a transition was undefined at that stage. A δ transition from h on symbol a matching the δ' transition from h is also defined. As noted in the second comment after the loop, the loop's condition guarantees that no state in T other than possibly the head, h, has a transition defined on a. Therefore all these states in T are also assigned the same δ' transition on a as state h.

The algorithm terminates with a complete DFA - i.e. when there is exactly one symbol transition on every symbol in the alphabet from every state. It ensures that upon termination δ and f are such that the FDFA defines the same language as the DFA. A detailed example about the execution of this algorithm is available at Nxumalo et al. (2015b).

Note that the FDFA generated may indeed contain failure cycles. This will happen when the inner do-loop ends with h such that f(h) e T. Although the frequency of this happening cannot be predicted, it can be shown that such a cycle will not be divergent.

To see this, it is sufficient to consider the outcome at the end of each iteration of the for-loop over a e Σ. Because δ(/ι, a) is defined at that stage, it is assured that a is not in the failure alphabet of the failure path from q_ito h (irrespective of whether or not a failure cycle has been formed). When the for-loop over alphabet symbols has run its course, all symbols in Σ will have been removed from the failure alphabet of the failure path out of q_i. Thus, any cycle formed that incorporates state q_i cannot be divergent. Since this claim holds for every q_ie Q, it must be the case that all failure cycles are non-divergent.

 

8 THE GENERAL CASE EXPERIMENT

An experiment was carried out to monitor the transition reductions resulting from the FDFAs that are derived from 'random' DFAs generated by Algorithm 2. The main differences between these DFAs and FDFAs and those produced by AC-opt and AC-fail are as follows:

• An AC-opt DFA for the keyword set K over alphabet Σ is the state-minimal DFA defining a particular regular language (specifically Σ*K). The random DFAs define arbitrary regular languages and are not guaranteed to be state minimal.

• An AC-fail FDFA for keyword set K is a transition-minimal language-equivalent version of the AC-opt DFA. It will never contain a failure cycle. The Algorithm 2-generated random FDFAs are language-equivalent versions of their DFA counterparts but may or may not be transition-minimal. The random FDFAs may possibly contain non-divergent failure cycles.

• An AC-opt DFA has an underlying trie structure (i.e. all states other than the start state have exactly one inbound transition) that reflects the longest common prefixes of the underlying keyword set. This can be used to characterise the distance of a state from the start state. All remaining transitions are 'backward' from a state deeper in the trie to a state closer to the start state. A random DFA has an arbitrary structure that does not offer a clear notion of a state's distance from the start state.

The DFA/FDFA pairs generated by Algorithm 2 used natural numbers as identifiers for the states, Q, starting with 0 to designate the start state. |Q| ranged over 250,500,... 2500 and k ranged over 10,20... 100. There were therefore 10 possible values for both |Q| and k. One random DFA/FDFA pair was generated for each possible (|Q|, k) combination. An alphabet of size |Σ| = 10 was used. Since the DFAs are complete, the total number of symbol transitions is given by |Q| χ |Σ|, in this case yielding values in the range [2500, 5000, ... 25000].

For each DFA/FDFA pair, the difference between their respective total number of transitions was computed and expressed as a percentage of the total DFA transitions.

The DFAs were then used for input to the three DHA variants and also to the D²FA algorithm. In each case, the associated language-equivalent FDFA was obtained and the percentage differences between the FDFA transitions and DFA transitions were computed as before.

Inspection of these percentage differences indicated that they were insensitive to the value of |Q|. Consequently, for each k, the average of the percentage differences over all |Q| values was computed. These results are displayed in Figure 9.

For all FDFA types cases other than MaxAR, the percentage transition differences increase quite definitively as k increases from 10 to 30 and thereafter increase much more slowly. D² FA reduces the average number of transitions in the DFA by more than the DHA heuristics as well as by more than randomly generated FDFAs. (Recall that the randomly generated FDFAs are not claimed to be optimal in terms of transition savings, but serve as a lower bound for the possible transition savings.) For k > 30 the D² FA FDFAs show transition reductions of about 75% whereas DHA MaxIntent and MinExtent are just above 65%. In contrast to these trends, the percentage transition reductions for the MaxAR heuristic remains below 30% for all points plotted.

For k < 30, the MaxIntent and MinExtent FDFAs were smaller than the random FDFAs. However, for k > 30, the graph associated with the random FDFAs is bound from above by that of the D² FA graph and from below by the MaxIntent and MinExtent graphs.

 

9 CONCLUSION AND FUTURE WORK

Generally, the empirical investigation provided a comparison of various FDFA types, tested in two different domains. They were firstly tested against the AC-fail FDFAs and later against the general case FDFAs. As a by-product of general case FDFA tests, an algorithm for generating pairs of random FDFA and language equivalent DFA was proposed. An alternate failure-DFA generating algorithm called D² FA algorithm was also included in all experiments conducted.

The empirical results revealed that the modified DHA FDFAs bring about reasonably good transition reduction of minimal Aho-Corasick DFAs, producing FDFAs that are very close in structure to the AC-fail FDFAs. They also perform satisfactorily in the general context, though not quite as well as the D² FA algorithm. The FDFAs produced by D² FA, though near optimal in terms of minimising the number of transitions of AC-opt DFAs, were nevertheless rather different from AC-fail FDFAs in structure.

The relatively small alphabet size of 10 was dictated by unavoidable growth in the size of the associated concept lattices. This effect can possibly be mitigated in various ways - for example, by not generating concepts with arc redundancy less than 2. Nevertheless, it is recognised that use of DHA will always be constrained by the potential for the associated lattice to grow exponentially.

From a theoretical perspective, however, a lattice-based DHA approach to FDFA generation is attractive because it encapsulates the entire solution space in which a minimal FDFA might be found - i.e. each ordering of its concepts maps to a possible language-equivalent FDFA that can be derived from a DFA and at least one such ordering will map to a minimal FDFA.

The MaxAR heuristic, initially thought to be promising, turned out to be not so effective in reducing transitions. Perhaps it could be used to derive FDFAs that lie in between the minimal FDFA and a DFA. Such FDFAs might have value in some applications in striking a balance between reducing space and processing time efficiency. This, of course, is a tradeoff to be made.

The D² FA generation approach is not as constrained by space limitations as the DHA approach and in the present experiments it has performed reasonably well. Nevertheless, it is known that the algorithm locks out the possibility of failure cycles and will thus perform sub-optimally when non-divergent cycles are in the optimal solution. In the original publication Kumar et al., 2006, a somewhat more refined version is reported that attempts to avoid unnecessary chains of failure transitions. (Long failure chains are undesirable because they cause a computational cost when using the FDFA for string processing.)

Future research should examine the potential of this refined version using generalised DFAs as input and should explore more fully the relationship between these D² FA based algorithms and the DHA algorithms. It should also explore possible modifications to Algorithm 2 to enhance the probability of generating FDFAs with non-divergent cycles, as this would work in favour of the DHA-based algorithms.

 

ACKNOWLEDGEMENTS

This work was partially supported by the NRF (South African National Research Foundation) under grants 92187 and 93063.

 

References

Aho, A. V & Corasick, M. J. (1975). Efficient string matching: An aid to bibliographic search. Commun. ACM, 18(6), 333-340. https://doi.org/10.1145/360825.360855        [ Links ]

Aho, A. V, Lam, M. S., Sethi, R., & Ullman, J. D. (2006). Compilers: Principles, techniques, and tools (2nd edition). Addison Wesley. Retrieved from http://www.amazon.ca/exec/obidos/redirect?tag=citeulike09-20%5C&amp;path=ASIN/0321486811

Bille, P, G0rtz, I. L., & Skjoldjensen, F. R. (2016). Subsequence automata with default transitions. In SOFSEM (Vol. 9587, pp. 208-216). Lecture Notes in Computer Science. Springer. https://doi.org/10.1007/978-3-662-49192-8_17

Björklund, H., Björklund, J., & Zechner, N. (2014). Compression of finite-state automata through failure transitions. Theor. Comput. Sci. 557, 87-100. https://doi.org/10.1016/j.tcs.2014.09.007        [ Links ]

Brzozowski, J. A. (1962). Canonical regular expressions and minimal state graphs for definite events. Mathematical Theory of Automata, 12, 529-561.         [ Links ]

Buzmakov, A. & Neznanov, A. (2013). Practical computing with pattern structures in FCART environment. In FCA4AI@IJCAI (Vol. 1058, pp. 49-56). CEUR Workshop Proceedings. CEUR-WS.org.

Cleophas, L., Kourie, D. G., & Watson, B. W. (2013). Weak factor automata: Comparing (failure) oracles and storacles. In J. Holub & J. Zd'árek (Eds.), Proceedings of the Prague Stringology Conference 2013 (pp. 176-190). Czech Technical University in Prague, Czech Republic.

Cleophas, L., Kourie, D. G., & Watson, B. W. (2014). Weak factor automata: The failure of failure factor oracles? South African Computer Journal, 53, 1-14. Retrieved from http://reference.sabinet.co.za/document/EJC161394        [ Links ]

Crochemore, M. & Hancart, C. (1997). Automata for matching patterns. In S. A. Rozenberg G. (Ed.), Handbook of Formal Languages (Vol. 2, Linear Modeling: Background and Application, pp. 399-462). Springer. https://doi.org/10.1007/978-3-662-07675-0_9

Daciuk, J. (2014). Optimization of automata. Gdansk University of Technology Publishing House.

Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numerische Mathematik, 1(1), 269-271. https://doi.org/10.1007/BF01386390        [ Links ]

Drozdek, A. (2008). Data structures and algorithms in Java (3rd). Delmar Learning.

Ganter, B., Stumme, G., & Wille, R. (Eds.). (2005). Formal Concept Analysis, Foundations and Applications, Springer, 3626.

Ganter, B. & Wille, R. (1999). Formal Concept Analysis-Mathematical Foundations. Springer. https://doi.org/10.1007/978-3-642-59830-2

Hopcroft, J. (1971). An n log n algorithm for minimizing states in a finite automaton. STAN-CS-71-190. https://doi.org/10.1016/b978-0-12-417750-5.50022-1

Knuth, D. E., Morris Jr, J. H., & Pratt, V R. (1977). Fast pattern matching in strings. SAM J. Comput. 6(2), 323-350. https://doi.org/10.1137/0206024        [ Links ]

Kourie, D. G., Watson, B. W., Cleophas, L., & Venter, F. (2012). Failure deterministic finite automata. In Stringology (pp. 28-41). Department of Theoretical Computer Science, Faculty of Information Technology, Czech Technical University in Prague.

Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical Society, 7(1), 48-50. https://doi.org/10.1090/S0002-9939-1956-0078686-7        [ Links ]

Kumar, S., Dharmapurikar, S., Yu, F., Crowley, P, & Turner, J. S. (2006). Algorithms to accelerate multiple regular expressions matching for deep packet inspection. In SIGCOMM (pp. 339-350). ACM. https://doi.org/10.1145/1151659.1159952

Lesk, M. E. & Schmidt, E. (1990). Lex-A lexical analyzer generator. In A. G. Hume & M. D. Mcllroy (Eds.), Unix vol. ii (pp. 375-387). Philadelphia, PA, USA: W. B. Saunders Company. Retrieved from http://dl.acm.org/citation.cfm?id=107172.107193

Neznanov, A. & Parinov, A. (2014). FCA analyst session and data access tools in FCART. In AIMSA (Vol. 8722, pp. 214-221). Lecture Notes in Computer Science. Springer. https://doi.org/10.1007/978-3-319-10554-3_21

Nxumalo, M., Kourie, D., Cleophas, L., & Watson, B. (2015a). An Aho-Corasick based assessment of algorithms generating failure deterministic finite automata. In Proceedings of the 12th International Conference on Concept Lattices and their Applications (CLA 2015). Clermont-Ferrand, France.

Nxumalo, M., Kourie, D., Cleophas, L., & Watson, B. (2015b). On generating a random deterministic finite automaton as well as its failure equivalent. In Proceedings of Russian and South African Workshop on Knowledge Discovery Techniques based on Formal Concept Analysis (RuZA 2015) (pp. 47-57). Retrieved from http://ceur-ws.org/Vol-1552/paper5.pdf

Revuz, D. (1992). Minimisation of acyclic deterministic automata in linear time. Theor. Comput. Sci. 92(1), 181-189. https://doi.org/10.1016/0304-3975(92)90142-3        [ Links ]

Roesch, M. (1999). Snort-Lightweight intrusion detection for networks. In Proceedings of the 13th USENIX Conference on System Administration (pp. 229-238). LISA'99. Seattle, Washington: USENIX Association. Retrieved from http://dl.acm.org/citation.cfm?id=1039834.1039864        [ Links ]

Roy, I. & Aluru, S. (2014). Finding motifs in biological sequences using the Micron automata processor. In 2014 IEEE 28th International Parallel and Distributed Processing Symposium, Phoenix, AZ, USA, May 19-23, 2014 (pp. 415-424). https://doi.org/10.1109/IPDPS.2014.51

Watson, B. W. & Cleophas, L. (2004). SPARE Parts: A C++ toolkit for string pattern recognition. Softw., Pract. Exper. 34(7), 697-710. https://doi.org/10.1002/spe.590        [ Links ]

Zha, X. & Sahni, S. (2008). Highly compressed Aho-Corasick automata for efficient intrusion detection. In Proceedings of the 13th IEEE Symposium on Computers and Communications (ISCC 2008), July 6-9, Marrakech, Morocco (pp. 298-303). https://doi.org/10.1109/ISCC.2008.4625587

 

 

Received: 12 February 2016
Accepted: 3 February 2017
Available online: 9 July 2017

 

 

1 In this case, so-called binary automata are built from an originating DFA in which the successor states of a state are represented as a linked list. A binary automaton is essentially an FDFA that has a single symbol transition and a failure transition at every state. Its language (but not its states) corresponds to that of the originating DFA. Daciuk (2014) references sources that discuss compaction strategies for binary automata.
2 Essentially, the algorithm is based on the fact that the path from source to each state, say q, in the trie maps out a string, say s_q. The failure transition from q goes to a some other state p where the path leading from source to p maps out a string, s_p, that corresponds identically to a suffix of s_q. In fact, p is chosen from among trie states to ensure that s_p is the longest possible suffix of s_q.
3 A DFA is complete if it has a transition on every alphabet symbol in every state. The interpretation of a failure transition that replaces transitions in a DFA that is not complete is unclear and not a concern in this paper.
4 A fuller description is given in Section 5.
5 Initial results have been published in Nxumalo, Kourie, Cleophas, and Watson (2015a) and Nxumalo, Kourie, Cleophas, and Watson (2015b), the former being the proceedings of Formal Concept Analysis conference and the latter being an output of a private workshop between two research groups. Since these were both highly specialised forums, it seems appropriate to repeat the results here, together with subsequent results, so that all relevant findings are readily available to a wider community in one place.
6 http://madodaspace.blogspot.co.za/2016/02/a-toolkit-for-failure-deterministic.html
7 i.e. all objects not in ext(C) lack at least one attribute in int(C); and all attributes not in int(C) fail to characterise at least one object in ext(C).
8 FCART version 0.9 was used Buzmakov and Neznanov (2013), Neznanov and Parinov (2014).
9 To generate such a random DFA, decide on the number of states, and then for each state and for each symbol, assign a transition whose destination is some randomly selected state, while ensuring that the resulting transition graph does not contain any unreachable states.