Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
R&D Journal
On-line version ISSN 2309-8988
Print version ISSN 0257-9669
R&D j. (Matieland, Online) vol.37 Stellenbosch, Cape Town 2021
http://dx.doi.org/10.17159/2309-8988/2021/v37a7
ARTICLES
Over-attemperation and Short-term Overheating in Pendant-type Superheaters
N. BassonI; W. F. FulsII
IMSAIMechE. Mechanical, Industrial & Aeronautical Engineering, Faculty of Engineering & the Built Environment, University of Witwatersrand, South Africa. E-mail: Nilkri.basson@wits.ac.za
IIMechanical Engineering, Faculty of Engineering & the Built Environment, University of Cape Town, South Africa. E-mail: wim.fuls@uct.ac.za
ABSTRACT
A water-wedge is often suspected to be the root cause for short-term overheating in fossil-fuelled boiler superheaters. However, it can be argued that evaporation of the water-wedge would cool the tube sufficiently and prevent overheating. This study aims to determine if the thermo-physical conditions occurring at low loads support this claim by studying the transient behaviour of a representative superheater segment under postulated conditions. A flow model was constructed to facilitate direct comparison with a boiler pendant superheater of a full-scale fossil-fuelled power plant. Several scenarios of water-wedges sustained by attemperation spraywater were simulated at low load operating conditions. The temperature evolution of the tube wall was tracked and, together with calculated equivalent stresses including thermal stress, was compared to the yield strength of the material. The results show that the stresses exerted over the tube wall and throughout the tube length are not sufficient to overcome the yield strength of the tube material, even for an aged tube under severe process conditions of boiler overfiring. Evaporation of the water-wedge provides sufficient cooling to the superheater tube to prevent failure. It was concluded that water-wedging alone is unlikely to be the root cause of short-term overheating at low boiler loads.
Additional keywords: Short-term overheating; water-wedge; boiler superheater tube; attemperation; thermal stress, evaporation.
Nomenclature Roman
f Friction factor [-]
h Effective heat transfer coefficient [W/m2.K]
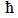 Enthalpy [kJ/kg]
Enthalpy [kJ/kg]
m Mass flow rate [kg/s]
D Diameter [m]
E Modulus of elasticity [-]
Nu Nusselt number [-]
Pr Prandtl number [-]
Q Heat rate [W]
Re Reynold number [-]
T Temperature [°C / K]
Greek
σ Stress [MPa]
αt Stress concentration factor [-]
ßlin Linear expansion coefficient [°C-1]
ν Poisson's ratio [-]
ε Material roughness [μm] / Emissivity factor [-]
Subscripts
att Attemperation
con Convective conditions
fg Flue gas conditions
l Fluid conditions
0 Ambient conditions rad Radiative conditions t Tube side
th Thermal
w Water side
H Hydraulic
1 Introduction
Short-term overheating is one of the most common and destructive boiler failures that occur in fossil-fuelled power plants. The damage and associated cost of repair has led to in situ cases being studied extensively to determine the root cause of these failures [1,2,3,4]. Short-term overheating is a premature failure that occurs when the tube is exposed to higher than its design temperature, reducing the material's lifetime drastically until it ruptures. The tube material can exceed its design temperature (either by a lack of cooling or due to abnormally high furnace temperatures) and will fail over a short period of time. Short-term overheating can occur within minutes or over a few days, depending on the temperature reached [5].
At Eskom, Africa's largest power utility, short-term overheating is the fourth-largest cause of boiler tube failures and accounts for approximately 8% of all unplanned boiler outages [6]. Of these recent short-term overheating events, approximately 45% of the root causes have been attributed to water-wedging, steadily increasing from 36% in 2012. One of the most prominent incidents in Eskom occurred in 2000 due to short-term overheating [7]. A unit was taken off load for a boiler tube inspection that was to last five days. After the unit was returned to service, it ran for only 7.5 hours before a boiler tube leak was detected. Upon inspection of the final stage superheater, six tubes were found to have burst along with multiple other adjacent tubes. All six of the bursts were attributed to short-term overheating due to over-attemperation that caused a water-wedge.
Investigative plant reports have claimed that most short-term overheating occurrences are due to condensate formation in the boiler tube when the unit was force-cooled after a shutdown [8]. According to Babcock & Wilcox short-term overheating most commonly takes place during a unit start-up [9]. During the start-up procedure, the condensate that is still present in the bends of the tubes obstructs the steam flow, causing the tubes to overheat. This is known as steam starvation. It is suspected that, at low load, a similar scenario may occur. In an attempt to reduce the possibility of short-term overheating, a plant operator may manually increase the spraywater flow from the attemperation system [7]. This has been suspected to cause excessive condensate formation, preventing steam flow through the superheater tubes. This means that when enough condensate forms in the superheater tubes, it creates a plug of water known as a water-wedge. If the pressure difference between the superheater inlet and outlet is not sufficient to transport the water-wedge through and out of the tubes, the tube may experience steam starvation. It is also suspected that tube fouling reduces the steam outlet temperature of the tubes, which can increase the attemperation spray mass flow rate [10].
Investigative boiler failure reports show that in a twin pass type boiler, short-term overheating due to water-wedging only occurred in the front gas pass of the boiler, which is where the pendant-type superheaters are situated [8]. In tower-type boilers (once-through boilers), the sling-type tubes were mainly affected, which are similar to pendant tubes. Short-term overheating due to oxide scaling was more likely to occur in horizontal superheaters. These patterns are consistent with findings reported in the literature [2,11,4,12]. Some plant operating procedures attempt to reduce the risk of short-term overheating occurrences by constantly monitoring saturation temperatures within the boiler and ensuring that steam temperatures remain above saturation temperatures. The purpose of this is to prevent the condensation of steam within the boiler tubes, which should then prevent liquid collection that could cause water-wedging [7].
The claim of a water-wedge being the root cause for short-term overheating during low boiler loads can be challenged for two main reasons. Firstly, the main steam temperature in fossil-fuelled superheaters is typically in the range of 530550 °C, whereas condensate will only start to form at approximately 350 °C. For this to occur, the temperature of the superheater should be drastically reduced. Secondly, if water droplets should start to form, the high furnace temperature would be sufficient to cause evaporation, preventing a complete water-wedge. Thus, the water would not exist in the tubes long enough to cause steam starving that leads to short-term overheating. The rate at which the water evaporates could also be sufficient to cool the tubes.
Short-term overheating can be recognized by inspecting the failed tube visually. The first visible indication of short-term overheating is the tube rupture itself, which would have a thin-lipped fish-mouth appearance [13]. This type of rupture is a result of the longitudinal fracture that occurs during failure. The tube will also show some discolouration due to localized heating [2]. These indications make it easy to distinguish the failure from long-term overheating (also known as creep), which is a more common failure mechanism in both fossil fuel and renewable energy plants [14].
Boiler tubes are generally designed to operate within the ASME oxidation limits to prevent solid blockages. However, such blockages are still common [15]. Pramanick et al. presented an experimental study on short-term overheating caused by a partial blockage due to oxide deposits [16]. Similar studies were conducted on the water-wall tubes of a
power plant [3] and boiler tubes of a petrochemical plant [17]. These studies indicate that complete or even partial blockages due to solid deposits could cause failure due to an increase of hoop stresses over the tubes. Included in the hoop stress is the thermal stress over the tube wall, which is linearly correlated to the tube thickness [18]. A heat transfer study found that the temperature distributions over boiler tube walls become highly non-linear due to overfiring in the furnace, which could also increase the tube hoop stresses and contribute to failures [19]. A more recent computational fluid dynamics study confirms this possibility by indicating that the flame shape over the water wall tubes of an industrial boiler leads to overheating of these tubes [20]. Another numerical study on the downcomer tubes of a 600 MW thermal plant boiler evaluated the heat flux and wall temperature distribution over the tubes to identify overheating conditions [21].
The final rupture of a tube is owed to a combination of the resulting radial, axial and circumferential stresses. These include thermal-induced stresses over the tube wall due to the thermal gradient. A review of the available literature shows that very few studies have been conducted that specifically consider the thermal stresses during short-term overheating events. In a study conducted by Mertens et al. [22], the design impact of frequent natural-circulation boiler start-ups was investigated and the temperature gradients in terms of thermal stresses of critical components were analysed. Thermal stresses over a tube wall were determined using a general thermal stress calculation [23]:

The variable ßünrefers to the linear expansion coefficient, Εis the modulus of elasticity, νis Poisson's ratio and ΔT is the difference between the average wall temperature and the tube's inner surface temperature. The variable atis a factor for stress concentration, which considers the geometry of the connected piping and welding joint specifications and how these weaken the tube wall. This stress concentration was not relevant to this study, since the pipe studied had no discontinuities, and can thus be approached as having a value equal to 1. The modulus of elasticity is calculated at the average wall temperature.
Unlike oxide deposits, water blockages can evaporate due to increased furnace temperatures. Though short-term overheating events have been extensively studied, none of these studies clarifies whether the evaporation from a water-wedge could provide sufficient cooling within the tube to prevent overheating at low boiler loads.
Additionally, no such transient simulation models are available. This paper presents a methodology to determine if the evaporation of the water-wedge at low loads would cool the tube sufficiently to prevent short-term overheating with the aid of a transient thermofluid model and tube material stress analysis. Since any tube from any boiler component transporting water or steam can be subjected to short-term overheating, the methodology presented in this study is generic and can be applied to any power plant, including those using renewable energy sources.
2 Methodology
2.1 Description of Boiler Geometry
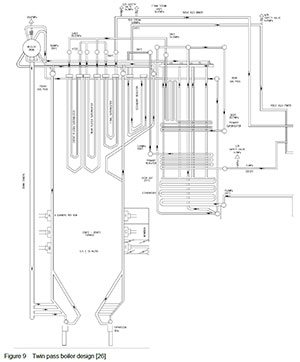
The boiler considered for this project is known as a twin-pass boiler (previously called a Carolina boiler) and the steam flow path is shown in figure 9 provided in Appendix A. The primary superheater is the first component in the boiler to receive saturated steam to convert into superheated steam. The steam produced exits through a vertical outlet bank to the primary superheater outlet headers.
The first stage attemperation takes place between the primary superheater outlet headers and the platen superheater inlet headers. Attemperation is achieved via a high-pressure spraywater system supplied by the line from the feedwater system to the economizer. The platen superheater consists of two groups of pipe elements that are suspended above the furnace in the form of loops. The front steam loops are configured in parallel flow with the flue gas while the loops at the rear are counter-flow. After the steam completes its progression through these loops to the outlet headers, it is attemperated (second stage attemperation) before being transported to the final superheater inlet manifolds.
The third and final superheater is located in the front gas pass after the platen superheater. As shown in figure 1 (created in Solidworks®), the final superheater is a pendant type consisting of 28 elements, of which each element is made up of 34 tubes in a U-shape. Element tubes are stacked next to one another via common inlet and outlet headers. The material used to construct these tubes is specified as 10CrMo910 and is simply referred to as grade 22 steel.

Each element is made up of three sections, namely the inlet section (blue), the intermediate section (green), and the outlet section (purple). The inlet section is connected to the inlet header, which receives the steam from the platen superheaters. The first part of the inlet section is inside a dead space, referring to the tube areas located in the boiler roof, which receives minimal exposure to the heat emitted from the furnace. These tubes have a length of 339 mm with an outer diameter (OD) of 44.5 mm and wall thickness of 6.3 mm. Following are the inlet tubes with a length of 7761 mm which are exposed to the flue gas. Some tubes are an exception to this tube length, as some of them are extended to wrap around some of the other tubes for alignment purposes. This is also true for the outlet section.
The outlet section feeds to the outlet header. This segment also includes an outlet dead space of tube length 339 mm, OD of 44.5 mm, and wall thickness of 11 mm. The exposed outlet section length is 8 261 mm, with the exception of wraparound tubes. The intermediate section is where the bends are located, connecting the inlet and outlet sections. This segment also contains wrap-around tubes and each tube differs in length with an OD of 44.5 mm and a wall thickness of 8.8 mm. The total length of the intermediate section is 16 626 mm.
Notice how at each consecutive section the inner diameter (ID) decreases. This was so designed to increase the wall thickness of the tube as the steam flows through the component, thus protecting the material as the temperature increases.
2.2 Model development
To simulate transient events of short-term overheating, a thermofluid network software tool known as Flownex Simulation Environment was used. Flownex is a 1D simulation environment with built-in fluid mechanics and heat transfer modelling capabilities that can indicate a system's behaviour for both steady-state and transient processes. The specific need for a transient model is to determine how temperatures and pressures change with time while a tube is blocked.
For the purpose of this study two scenarios were considered. Firstly, a scenario with an unblocked tube was simulated and verified with analytical calculations to determine the boundary conditions of the superheater tube under low-load conditions. These conditions include the pressure drop over the superheater, which, in turn, defined the minimum height of a water column that cannot be forced out of the pendant-type tube. It also defined the steam and pipe initial temperatures at the start of a water-wedge event.
The analysis assumed a quasi-steady operation before the blockage. Next, various conditions were simulated for a water-wedged tube for a range of boiler load conditions. These were transient analyses, where the temperature evolution of the pipe wall was analysed. Specific transient conditions were required to simulate the heating of the water-wedge as well as the rate of evaporation. The water-wedge would have to be replenished by attemperation spray, remaining in the tube for at least ten minutes to replicate the effects of sudden onset overheating.
The load conditions chosen for this study are at 4 %, 12 %, 20 %, and 32 % of full boiler load (BL). The boiler used in this study has a maximum continuous rating (MCR) of 618 MW. These loads were identified as the low boiler loads where short-term overheating is likely to occur. The resulting excess steam temperatures might prompt the operator to over-attemperate, which may result in water-wedging.
It is also possible for an operator to overfire (OF) the boiler at a higher rate than required for a specific load to "boil out" a suspected water-wedge, which may result in a shorter time before short-term overheating would occur. For this reason, overfiring conditions were imposed upon the four load scenarios previously mentioned. Overfiring scenarios were simulated at 0 %, 25 %, 50 %, 100 %, and 200 % of the set boiler load by adjusting the flue gas mass flow rate and temperature.
Design data from the pendant-type superheater previously described was used for this study and is thus a practical approach to establishing if short-term overheating is possible on such a tube. The longest (outer-most) tube element of the final superheater tube bundle was selected for the case study. The longer the tube, the greater the possibility for short-term overheating to occur since a larger area is exposed to the heat of the furnace.
For this study, it is initially assumed that a stationary water column can form within the tube. A worst-case scenario will be simulated, which requires the height difference of the water-wedge to be at its maximum length. To do this, the start of the water-wedge is assumed to begin at the lowest part of the tube.
Depending on the boiler load, the pressure difference over the inlet and outlet header would differ, which will allow for different lengths of water-wedges. As previously mentioned, the tube is divided into three sections, each with a different ID. This means that there are three possible cases in which the water-wedge can lie within the tube (illustrated in figure 2) namely (a) the water-wedge ends somewhere within the intermediate section, (b) the water-wedge ends on the boundary between the intermediate and outlet section, or (c) the water-wedge ends somewhere within the outlet section. The system to be simulated will be that section just above the water-wedge up to the outlet of the tube, as indicated by the dashed line boundary.
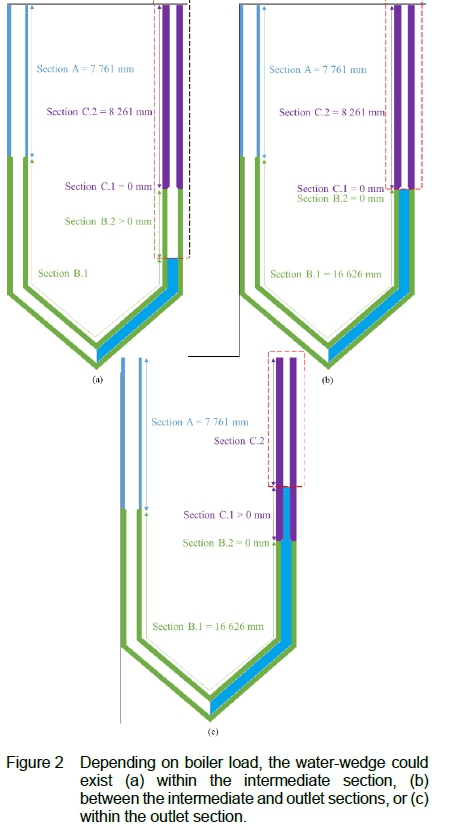
The length of section A, which is the inlet section shown in blue, would stay constant at 7 761 mm for all cases as shown in figure 2. The total length of the intermediate section (green) is 16 626 mm. This section is divided into two parts - section B.1 and section B.2. Section B. 1 represents that part of the intermediate tube from where it connects at the inlet section to the point where the water column ends, which varies depending on the boiler load. This is done to determine the boundary conditions just where the water-wedge ends, and the final length of the tube being starved of steam for different boiler load scenarios. Section B.2 represents the part of the intermediate tube remaining should the water-wedge not fill up the whole intermediate section. Similarly, the outlet section in purple, with a total length of 8 261 mm, is divided into two parts.
Section C. 1 is that part of the outlet tube that is filled with water if the water column extends past the intermediate section. Section C.2 is the remaining part of the tube being starved of its cooling medium.
In other words, if section B.2 is greater than 0 mm, it means that a part of the intermediate section is exposed to possible overheating, and this section is included in the simulation as illustrated in figure 2(a). Then section C.1 will be 0 mm since no water-wedge exists past the intermediate section and section C.2 will be the entire length of the outlet section. If section B.2 is calculated to be 0 mm, then the entire intermediate section is filled up with water and the length of section B.1 will be equal to the entire length of the intermediate section. If section C.1 is greater than 0 mm, it means that the water-wedge extends past the intermediate section, and only a part of the outlet tube is exposed to overheating, for which the length is indicated by section C.2, as illustrated in figure 2 (c). If both section B.2 and section C. 1 are equal to 0 mm, it means that the water-wedge ends at the intersection between the intermediate and outlet section, as illustrated in figure 2 (b).
To determine the boundary conditions for a superheater tube before a water-wedge occurs, an initial Flownex model was created, as shown in figure 3. The intermediate and outlet sections are each divided into two separate regions to distinguish between the region with water in it and the region exposed to overheating later if water-wedging occurs, as described above. Figure 3 indicates where the water-wedge would present for a worst-case scenario. However, for the initial steady-state case, it is assumed that no water-wedge is present.
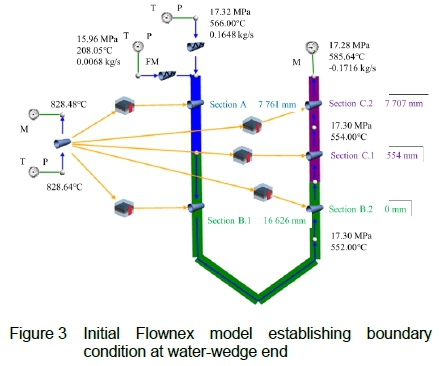
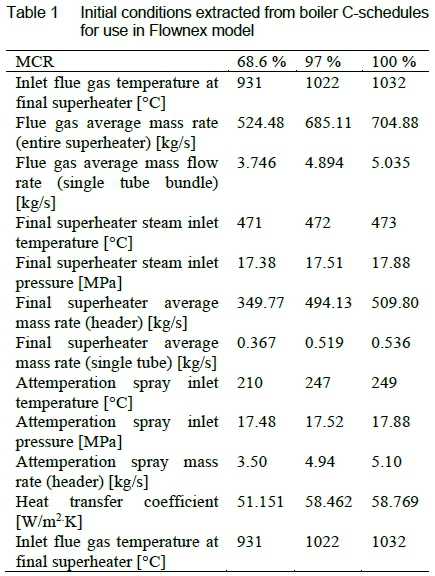
The inlet conditions for each load case were provided from the boiler C-schedules, which provide the final superheater inlet and outlet conditions at 100 %, 97 % and 68.6 % MCR [24]. For the Flownex model, the superheater inlet and flue gas conditions are provided, while the outlet conditions are simulated. The properties used, as extracted from the boiler C-schedules, are provided in table 1. As the lowest boiler load condition provided is at 68.6 %, the conditions for lower boiler loads were extrapolated from this data. As a simplified assumption, the mass flow rates used in the model were divided depending on the number of relevant elements and tube bundles to allow for the flow rate over a single tube.
The superheater inlet conditions are divided into two parts, namely (i) steam from the preceding platen superheater and (ii) attemperation spray. The conditions for the steam flow and attemperation spray are specified via the incoming steam pressure and temperature for the chosen load case. At the superheater outlet, a fixed mass flow rate boundary is specified.
The flue gas is represented by a pipe element with specified inlet pressure and temperature boundary values together with a fixed mass flow rate boundary value at the outlet based on the chosen firing condition. The furnace (flue gas side) and superheater pipe (steam side) elements are connected using composite heat transfer elements. These elements represent the heat transfer taking place between the flue gas and the steam through the boiler tube, including the tube wall resistance and thermal mass.
For each section of tubing described, the Reynolds number (Re) is calculated using fluid properties that are approximated as constant throughout the tube element. The assumption is reasonable for highly superheated steam. This assumption is not valid for a blocked tube scenario where water is gradually heated from saturated steam. Hence the pipe will be discretized into small sections to track the variation in fluid properties.
In the same way, the friction factor can be determined through each tube section. The friction factor is calculated using the Swamee-Jain equation:
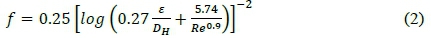
This equation is only valid for 5000 < Re < 108, which implies that the flow is turbulent, and 10-6< e/DH< 10-2, where εis the tube roughness and DHis the hydraulic diameter. The typical roughness value for boiler tubes is approximately 60 μm.
The pressure drop over each segment is calculated and secondary friction losses occurring due to tube bends, entrances and exits, as well as an increase or decrease of the tube wall thickness, are taken into account. The total pressure drop through the superheater tube will be the sum of the pressure drops through each tube section. This pressure drop determines the height of a possible stationary water column.
The tube specific to this study is the first tube exposed to convective heat transfer from the flue gas. For cross-flow scenarios, the convection coefficient for a tube in the first row of the tube bundle is approximately equal to that of a single tube in cross-flow, whereas larger heat transfer coefficients are associated with tubes of the inner rows. Thus, the convective heat transfer coefficient for cross-flow over a tube bundle can be determined. For crossflow over a single tube, the Nusselt number (Nu) was calculated using the Churchill-Bernstein correlation (eq. (3)), which depends on the Reynolds number determined for the flue gas flow over the tube under specific load conditions.
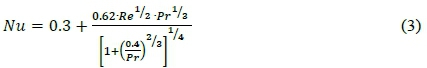
For a transient study conducted over the short period of ten minutes, the value of the convective heat transfer coefficient on the flue gas side is assumed to remain unchanged. This is because the flue gas velocity used to calculate the Reynolds number remains constant during this time period. The Reynolds number calculated is then used to determine the appropriate Nusselt number. Due to the high gas temperatures, radiation also takes place between the flue gas and the boiler tubes. The effective heat transfer coefficient for radiation in the convective pass of a boiler can be determined as the functional equation
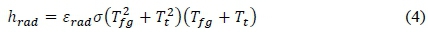
where eradis the relevant emissivity factor, σis the Stefan-Boltzmann constant, Tfgis the temperature of the flue gas and Ttis the temperature of the surface of the tube wall. If this radiative coefficient should be added to the convective coefficient, the result would be the total heat transfer coefficient of the external fluid over the tube. In this case, the coefficient for the flue gas over the boiler tube. It can thus be assumed that

It is then concluded that the value for h0 considers both the convection and radiation heat transfer emitted from the furnace. Since the radiative heat transfer coefficient is a function of the flue gas temperature, which remains constant during the transient simulation, it can be assumed that the total external heat transfer coefficient on the flue gas side remains constant for a specific boiler load.
In other words, the total heat transfer coefficient in the boiler changes due to variations in the boiler load but is unaffected by the possibility of a water-wedge in a tube during the transient simulation. Thus, the value of the heat transfer coefficient calculated at a specific load for an unblocked tube can also be applied for a water-wedged tube.
2.3 Model validation
The steady-state Flownex model was verified with an analytical model written in Mathcad. To ensure that the steady-state Flownex model is valid, the model results at the outlet leg were compared with that of the boiler commissioning C-schedules available at three different boiler load conditions (100 %, 97 % and 68.6 % MCR).
Table 2 compares the results from the steady-state Flownex model with the values provided in the boiler C schedules [24]. The properties selected for validation are the temperature and pressure at the outlet header of the final superheater. These properties indicate whether the outlet leg is being modelled reliably.

From table 2, it can be concluded that the Flownex model is an acceptable representation of the superheater's design data. The C-schedules provide the superheater outlet temperature at the outlet header after all of the steam from the tube bundle has mixed. The Flownex model only models the longest tube in the tube bundle. Due to the length of the tube, the steam is exposed to the boiler heat for a longer period compared to the other tubes. This results in a higher temperature in the modelled outlet leg than the final outlet header temperature, resulting in the minor temperature errors provided in table 2. If all of the tubes in the tube bundle were modelled and the resulting steam mixed in the outlet header, the final temperature of 540 °C is expected.
The steam outlet pressure errors observed could be a result of minor differences in the built-in fluid property and component characteristic relationships used in the Flownex software package. When calculating the Reynolds number, Flownex takes a correction factor into account based upon the number of bends throughout the pipe, leading to minor errors in the tube outlet properties.
2.4 Blocked boiler tube
To manage the outlet temperature, water from the attemperation spray enters the tube at sub-cooled conditions. If heating of the tube is not sufficient to evaporate the water and carry it through the tube with the superheated steam, a water column can temporarily form in the outlet leg of the tube. If the pressure difference over the tube inlet and outlet is not large enough to force the water-wedge out through the tube and excessive spray water is continually introduced, then a stationary column of water can plug the tube.
It should also be noted that, in a transient simulation, the water need not be in thermal equilibrium with the surrounding steam, i.e. it is possible to have liquid in a system that exists at temperatures above the saturation temperature. The mass flow rate of evaporation is the rate at which the water evaporates from the water column and is calculated as

The variable Qwrepresents the heat transfer to the water-wedge and hfg represents the difference between the enthalpies for saturated steam and saturated water at the pressure inside the boiler tube element. If the attemperation mass flow rate is equal or more than this calculated amount, the water column will remain. A lower attemperation flow will result in a decrease of the column height, which would then be forced out by the prevailing pressure difference between the inlet and outlet header. On the other hand, a higher attemperation mass flow rate will increase the water column height, thus reducing the length of the starved section of the tube.
The steam produced by evaporation will flow along the pipe towards the outlet, which would be the only cooling flow available to protect the pipe from overheating. A low evaporation rate could result in a larger temperature excursion of the outlet tube, where the top-most part of the tube would experience the highest temperatures (assuming uniform flue gas heating all along the tube length).
While the water column remains, the spray water entering the tube will result in improved cooling on the inlet side, because of the much colder conditions of the water compared to the tube wall conditions before the event. The worst-case scenario is, therefore, when the water column is at a maximum height and remains there for the full ten-minute duration.
A ten-minute period was selected since the evaporation rate for all of the simulated scenarios falls within this period. The time required for the water column to heat up from original attemperation spray conditions to saturated steam conditions (to begin evaporating) is calculated as

Here, 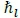 is the enthalpy of the fluid in the superheater tube at saturated liquid conditions and
is the enthalpy of the fluid in the superheater tube at saturated liquid conditions and 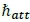 is the enthalpy of the sub-cooled attemperator spraywater. The purpose of the time calculated here is to gradually increase the rate of evaporation, to emulate the delay caused by the heat-up process.
is the enthalpy of the sub-cooled attemperator spraywater. The purpose of the time calculated here is to gradually increase the rate of evaporation, to emulate the delay caused by the heat-up process.
Now that the steady-state conditions have been modelled and validated, the required information can be carried over to the transient model. The need for a transient model is to determine how temperatures and material stresses change as time passes while a tube is blocked. The methodology developed to anticipate whether a failure will occur or not is described by the flowchart provided in figure 4.
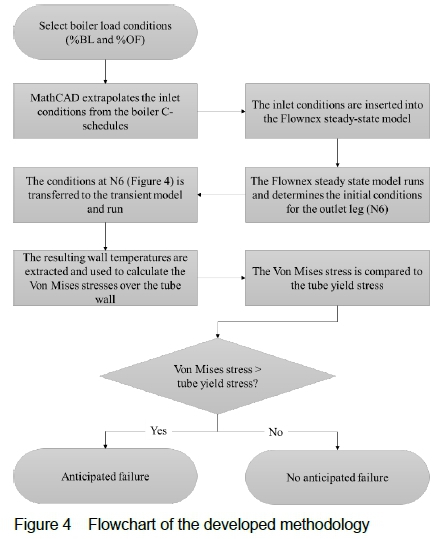
The Flownex model required for this theoretical study was constructed as illustrated in figure 5. Only the portion of the exposed tube above the assumed water wedge needs to be modelled, as short-term overheating is expected to happen only in this segment of the tube.
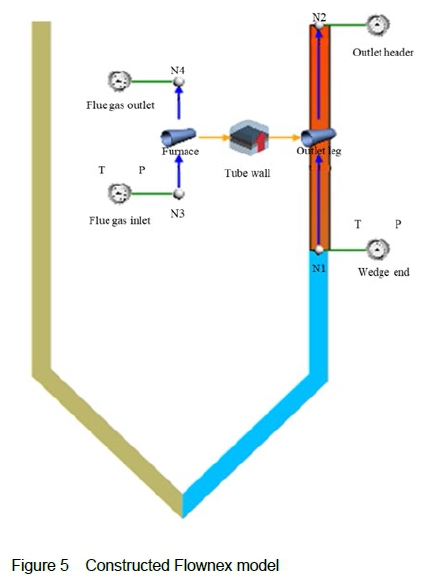
A Flownex tube element was used to represent the outlet leg and contains the geometry for the chosen superheater component. The top boundary condition attached to the pipe element is for the outlet header of the tube leg, which would then allow the steam to flow into a manifold before it enters the main steam line going to the turbine. The boundary condition at the bottom simulates flow conditions at the point in the tube where the stationary water-wedge ends. The length of the outlet leg depends on the height of the water-wedge column that would be formed should the pressure difference over the tube be insufficient to transport the water through to the outlet header.
The flue gas flow is also represented using a pipe element, for which the flue gas inlet and outlet boundaries are set. The flue gas and superheater outlet leg elements are connected using a composite heat transfer element, representing the thermal resistances and thermal mass of the tube wall where heat transfer takes place between the steam in the tube and the flue gas, and also represents the tube internal convection. It is at this element where the tube is divided into increments throughout the tube length and wall thickness to track the temperature evolution through the tube wall.
During this transient simulation, various events were replicated to mimic the sequence during and after the water-wedge formation.
For each scenario, the transient state starts by simulating the low load steam flow through a single boiler tube as if no blockage occurs. This is similar to the steady-state initial condition and ensures that the wall temperatures are at the correct initial condition.
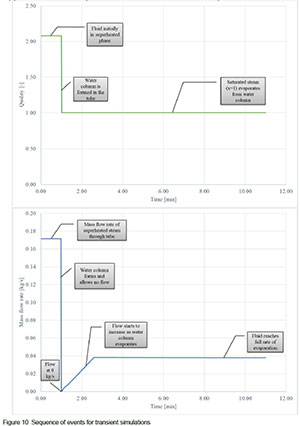
After 60 seconds, the steam mass flow rate is reduced to 0 kg/s to simulate a water-wedge blocking the flow of steam. The fluid conditions at the tube inlet change from normal superheated steam at the specific load, to saturated vapour to prepare the model for evaporation of the water-wedge. The evaporation rate starts to increase until it eventually reaches the rate required to maintain the water column as calculated in eq. (6). The time it takes to reach the full rate of evaporation is determined using eq. (7). The boundary condition labelled as "Wedge end" in figure 5, which is where the water blockage would occur in the outlet pipe of the boiler superheater tube, is initially set up with an input for a temperature value. When the simulation creates the water wedge (after 60 seconds), the temperature boundary condition is changed to a quality boundary, which is then set to a value of 1. This indicates that the water being evaporated has now reached its boiling point, and saturated steam is moving along the tube. The sequence of events is visually explained on the graph provided in figure 10 in Appendix A.
2.5 Superheater tube materials
The Flownex simulation results provide the tube wall temperatures at various locations, but do not specify the yield strength of the material at certain points while operating at different temperatures. To determine if the material will fail under certain conditions, the combined yield strength for the various scenarios was calculated using the thick wall cylinder theory. Taking into consideration the study conducted by Mertens et al [22], together with its formulation for the calculation of thermal stress as in eq. (1), the circumferential thermal stress for the application of this study can be determined. The stress concentration factor as mentioned in the study is assumed to have a value equal to one, based upon the MacGregor and Crossman study [25]. The circumferential stress is calculated according to the thick-walled cylinder and the final hoop stress is calculated as a combination of the circumferential stress and the thermal stress. The Von Mises yield criterion was used to find the final value of the combined stresses, including the hoop stress, radial stress, and axial stress acting on the tube.
High-temperature yield tests were conducted on actual boiler tubes utilizing an integrated thermomechanical system known as the Gleeble 3800 to find their yield strengths. A used piece of tube (approximately 200 000 hours), as well as a piece of virgin tube, was tested. The lab test results will be used to determine if the combined von Mises stresses exceed these yield strengths, indicating a tube failure.
2.6 Results and discussion
For each load scenario (4 %, 12 %, 20 %, and 32 % of full boiler load), the water column length that would exist in the pipe due to the differential pressure over the superheater tube was calculated, as well as the starved length of the tube exposed to elevated temperatures. These were the values used in the Flownex model to finally determine the superheater tube wall temperatures.
A sensitivity analysis was performed to determine the minimum number of increments for reliable results. The tube is discretized into thirty increments along the tube length as well as through the tube wall thickness. Increment one is at the lowest part of the tube outlet leg and increment 30 is at the top-most part of the tube outlet leg.
An example (32 % boiler load, 50 % overfiring conditions) of how the internal tube wall temperatures change over the ten minutes as calculated from the transient model at specific tube increments is shown in figure 6, with the other scenarios showing similar trends. The simulation is run under normal boiler load conditions before the water-wedge is introduced. From the graph in figure 6, the lower part of the tube (increment 1) then suddenly starts cooling down. The water wedge starts to evaporate, and the lower part of the tube continues to cool down. However, from the graph, the top part (increment 30) is not yet receiving the evaporated steam for cooling and gradually increases in temperature.
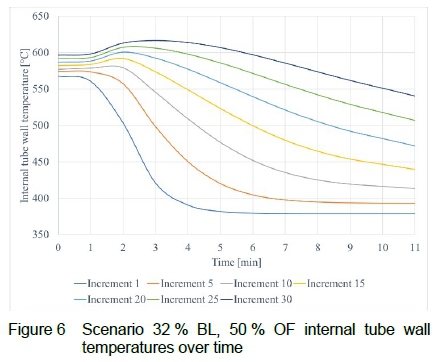
Once the evaporated steam makes contact with the top part of the tube, it gradually starts cooling down as well. The graph shows that the inner wall temperatures and outer wall temperatures do differ by a few degrees. This temperature distribution over the wall thickness is what contributes to the hoop stresses in the form of thermal stress. There is a clear difference in temperature between the lower part of the outlet leg (closest to the water-wedge) and the top part of the outlet leg. This is an indication of how the top part of the tube becomes susceptible to short term overheating, since it is starved of steam for a longer time and receives hotter steam than the bottom due to the low flow rate.
However, for this specific scenario, short-term overheating will not occur, regardless of the time, because of the cooling from the saturated steam which brings the temperature below the initial conditions. This simulation was reproduced for the boiler load scenarios of 4 %, 12 %, 20 %, and 32 % of full boiler load.
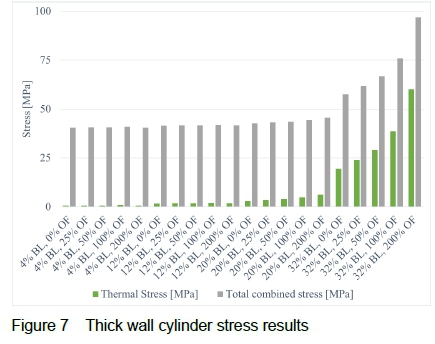
Additionally, overfiring in the furnace was also simulated to determine if this could assist in causing short-term overheating within ten minutes of boiler start-up. Overfiring was simulated for each boiler load scenario at 0 %, 50 %, 100 %, and 200 % of normal load conditions. With the material elasticity modulus and thermal expansion coefficient properties known along with the information extracted from the transient results, the possibility of short-term overheating can be examined. The thick wall cylinder calculations determined the axial, circumferential, radial, thermal, and finally the combined stresses over the tube wall for the various scenarios. The results for the thermal and Von Mises stresses are given in figure 7, showing how the combined stress increases as overfiring in the furnace take place. The thermal stresses are relatively small during extremely low load conditions and have very little effect on the overall combined Von Mises stress. However, the thermal stress becomes more significant as the boiler load is increased.
Utilizing the stress results and the tested lab results of old and new tube materials, a tube failure prediction can be made. The corresponding yield strength for the average wall temperature was determined and compared with calculated combined stress results for each scenario considered.
If the yield strength of the tube material (either for the old or for the new tube samples) at the hottest tube temperature was less than the combined tube stress, it could be established that a tube failure might occur. These results are given in figure 8.
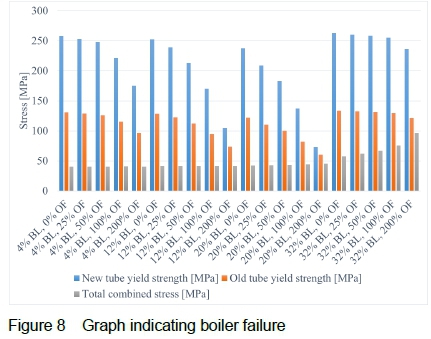
From figure 8, the combined stress in the tube increases as the exposed outlet length of the pipe increases. Observing figure 8, it appears that no boiler failure would occur due to water-wedging for any scenario under the specific circumstances, whether it is on a piece of virgin tube recently installed, or on a tube that has been in service for several hundred thousand hours.
The results do, however, indicate that a short-term overheating event is more likely to occur on an old tube. The yield strength of the old tube material is approximately half that of the virgin tube material for every temperature indicated.
Taking the scenario indicating that the tube is close to failure (for this study it would be scenario 20 % BL, 200 % OF) a failure might occur if the outlet leg of the superheater tube is lengthened enough to further restrict the cooling capabilities of the evaporating water-wedge. This can be simulated by lengthening the outlet tube in the Flownex® model. Such a parametric study show that, for the specific scenario mentioned, the tube needs to be lengthened by approximately 80 m and combined with unlikely overfiring conditions before it might fail after ten minutes. Alternatively, the event needs to remain for longer than 11 hours. Both of these extreme conditions are unrealistic. This shows that it is unlikely that a boiler failure would occur during boiler low load due to poor operation and water-wedging alone.
3 Conclusions
This study aimed to determine if short-term overheating due to water-wedging caused by over-attemperation can occur in a fossil-fuelled boiler at low boiler loads. A transient simulation model was created for the various boiler load scenarios. The pressure difference over the boiler tube under low load conditions is small enough to allow for a stationary water column.
The results show that short-term overheating is unlikely to occur at the superheater outlet tubes due to water-wedging alone, even at low boiler loads subjected to extreme overfiring conditions. The stresses exerted over the tube wall and throughout the tube length are not large enough to overcome the yield strength at elevated temperatures of the superheater tube material. This is true for both the virgin and the aged boiler tube materials. It is therefore concluded that evaporative cooling from the water-wedge is sufficient to cool the tube to prevent short-term overheating events.
It may be possible for overheating to occur under the conditions studied if the exposed tube length was significantly lengthened. However, this will only occur with unrealistic superheater geometries and therefore does not represent a real-plant situation. Alternatively, the duration must be substantially more than ten minutes, which is highly unlikely. Future studies may take into account the effects of tube fouling, which may decrease the effectiveness of heat transfer to the steam, causing less rapid evaporation and increasing the risk of a short-term overheating failure.
The methodology presented in this study can be applied to other industrial boilers, as well as boilers in renewable energy plants.
Acknowledgements
The authors would like to thank the staff of Eskom SOC Ltd for providing crucial data used for model simulation and validation. Material yield stress tests were performed by the Centre for Materials Engineering at the University of Cape Town.Special thanks go to Eskom Power Plant Engineering Institute (EPPEI) for partially sponsoring the research.
References
[1] R. K. Hosseini. Root cause failure analysis of superheated steam tube at a petrochemical plant. In Structural Integrity Procedía, 13:232-7, 2018. [ Links ]
[2] J. Ahmad, J. Purbolaksono and L. C. Beng. Tube failures due to cooling process problem and foreign materials in power plants. Nuclear Engineering and Design, 240(7):1882-1886, 2010. [ Links ]
[3] S. W. Liu, W. Z. Wang, and C. J. Liu. Failure analysis of the boiler water-wall tube. Case Studies in Engineering Failure Analysis, 9:35-39, 2017. [ Links ]
[4] J. Purbolaksono, J. Ahmad, L. C. Beng, A. Z. Rashid, A. Khinani, and A. A. Ali. Failure analysis on a primary superheater tube of a power plant. Engineering Failure Analysis, 17(1):158-167, 2010. [ Links ]
[5] D. N. French. Short-Term High Temperature Failures. The National Board of Boiler and Pressure Vessel Inspectors, URL https://www.nationalboard.org/Index.aspx?pageID=16&ID=186.
[6] Eskom. GPSS Data. Unpublished results.
[7] Confidential. Special permission obtained from Eskom Holdings Ltd, Unpublished results.
[8] Eskom. Boiler Tube Leak Investigation Reports. Unpublished results, 2007-2019.
[9] Finding the Root Cause of Boiler Tube Failures. Babcock & Wilcox. URL https://www.babcock.com/resources/learning-center/finding-the-root-cause-of-boiler-tube-failure.
[10] P. Madejski, T. Janda, J. Taler, D. Nabagło, R. Węzik, and M. Mazur. Analysis of fouling degree of individual heating surfaces in a pulverized coal fired boiler. Journal of Energy Resoures Technology, 140(3):032003, 2018. [ Links ]
[11] J. J. Perdomo and T. D. Spry. An overheat boiler tube failure. Journal of Failure Analysis and Prevention, 2:25-28, 2005. [ Links ]
[12] W. Liu. The dynamic creep rupture of a secondary superheater tube in a 43 MW coal-fired boiler by the decarburization and multilayer oxide scale buildup on both sides. Engineering Failure Analysis, 53:1-14, 2015. [ Links ]
[13] P. Munda, M. M. Husain, V. Rajinikanth, and A. K. Metya. Evolution of microstructure during short-term overheating failure of a boiler water wall tube made of carbon steel. Journal of Failure Analysis and Prevention, 18(1):199-211, 2018. [ Links ]
[14] C. O'Hagan, R. Barrett, S. Leen and R. Monaghan. Effect of high-temperature corrosion on the service life of P91 piping in biomass co-firing. Journal of Pressure Vessel Technology, 138(2):021407, 2016. [ Links ]
[15] ASME Standards Technology, LLC, Design Guidelines for the Effects of Corrosion, Erosion and Oxidation for Boiler Tube Components, New York, 2011.
[16] A. K. Pramanick, G. Das, S. K. Das, and M. Ghosh. Failure investigation of super heater tubes of coal fired power plant. Case Studies in Engineering Failure Analysis, 9:17-26, 2017. [ Links ]
[17] R. K. Hosseini and S. Yareiee. Failure analysis of boiler tube at a petrochemical plant. Engineering Failure Analysis, 106:104146, 2019. [ Links ]
[18] K. Peng, F. G. Qin, R. Jiang, and S. Kang. Effect of tube size on the thermal stress in concentrating solar receiver tubes. Journal of Solar Energy Engineering, 142(5):051008, 2020. [ Links ]
[19] L. W. Swanson and D. K. Moyeda. A thermal model for concentric-tube overfire air ports. Journal of Thermal Science and Engineering Applications, 1(1):011004, 2009. [ Links ]
[20] G. Tang, B. Wu, K. Johnson, A. Kirk, and C. Q. Zhou. Simulation of an industrial tangentially fired boiler firing metallurgical gases. Journal of Thermal Science and Engineering Applications, 7(1):011003, 2015. [ Links ]
[21] N. M. Hossain, K. Ghosh, and N. K. Manna. A two-phase flow model for thermal design of the riser-downcomer system pertaining to a 600 MW subcritical boiler. Journal of Thermal Science and Engineering Applications, 13(1):011021, 2021. [ Links ]
[22] N. Mertens, F. Alobaid, R. Starkloff, B. Epple, and H. G. Kim. Comparative investigation of drum-type and once-through heat recovery steam generator during start-up. Applied Energy, 144:250-260, 2015. [ Links ]
[23] J. Taler and P. Duda. Solving Direct and Inverse Heat Conduction Problems. Springer-Verlag, BerlinHeidelberg, 2006.
[24] Eskom. [Redacted] Power Station Boiler C-schedules, Unpublished results, 1982.
[25] C. W. MacGregor and N. Grossman. Effects of Cyclic Loading on Mechanical Behavior of 24S-T4 and 75S-T6 Aluminum Alloys and SAE 4130 Steel. NACA TN 2812, Washington, 1952.
[26] Eskom. Boiler Module 6: Boiler Steam System, 2006.
Received 8 April 2021
Revised form 24 August 2021
Accepted 14 September 2021
Appendix A. Power plant boiler flow path
Appendix B. Visual representation of transient event sequence for Flownex model