Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
R&D Journal
On-line version ISSN 2309-8988
Print version ISSN 0257-9669
R&D j. (Matieland, Online) vol.34 Stellenbosch, Cape Town 2018
ARTICLES
Four-point bending fatigue test specimen design by FEA
JP Jordaan
SAIMechE Member, CSIR Mechanical Testing Laboratory, Meiring Naudé Road, Pretoria, South Africa. E-mail: jjordaanl@csir.co.za
ABSTRACT
The FEA method is utilised in the geometric design of test specimens for use in four-point plane beam bending fatigue testing. A purpose-designed and -made testing jig is employed in the test routines. The specimen geometry is adjusted from a standard, prismatic, rectangular cross-section to a unique or nonstandard, non-prismatic, complex geometry that nearly ensures fatigue crack initiation on the free surface of the specimen away from areas of contact. The proposed method enables the engineer to retain the in-service or prevailing surface condition of the specimen material, while evaluating fatigue properties of interest at full force reversal. Due to the relatively complex specimen geometry, simple analytical methods typically used for average stress calculations in mechanical testing routines are substituted by the FEA method, allowing for accurate predictions of bending stresses, as well as reliable predictions of the location of fatigue crack initiation. The process of interaction between analysis and testing is demonstrated, resulting in a specimen design that is easy to manufacture and simple to test. Several test specimens are subjected to fatigue testing, demonstrating the accuracy and predictability of results.
Nomenclature
Roman
A Cross-sectional area [m2]
F Force [N]
FEA Finite Element Analysis
I Moment of inertia of beam cross-sectional area [m4]
L Length of beam [m]
Μ Bending moment in beam [Nm]
Ν Number of load cycles until fracture [-]
Ρ Applied load on beam [N]
R Force ratio [-]
Sf Fatigue limit (endurance limit) [Pa]
SN Fatigue strength [Pa]
V Shear force in beam [N]
χ Distance along beam length [m]
y Distance from beam neutral axis [m]
Greek
σ Stress (normal) [Pa]
1 Introduction
The application of the finite element analysis (FEA) method in the geometric design of fatigue testing specimens used in four-point plane beam bending mode is demonstrated and reported on in this paper.
The specimen geometry is adjusted from a standard, prismatic, rectangular cross-section to a unique or nonstandard, non-prismatic, complex geometry which increases the probability that fatigue cracks initiate on the free surface of the specimen away from areas of contact.
The proposed method enables the engineer to test for fatigue properties of interest, while simultaneously retaining the prevailing in-service surface condition of the material from which the specimen is extracted, as well as being able to fluctuate the stress on the specimen surface fully between tension and compression. The extent of stress fluctuation is described by the force ratio, which is defined as the minimum force divided by the maximum force in one force cycle [1], as follows:
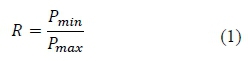
Complete load reversal per force cycle therefore implies a force ratio of R = -1.
2 Fatigue testing
Fatigue testing encompasses a wide spectrum of types of tests, ranging from (small specimen) materials testing through component testing to assembly or system testing such as complete aircraft weighing many tons [2]. It is quite easy to visualise that the extent of standardisation reduces as one progresses from materials fatigue testing through to systems fatigue testing.
The concept of fatigue testing of materials gave cause to the notion that fatigue strength generally, and the endurance limit (fatigue limit) specifically, are inherent material mechanical properties similar to, say, the modulus of elasticity or the yield strength of the material under investigation. For example, in the textbook by Shigley [3], the fatigue strength of wrought aluminium alloys is listed alongside yield and tensile strength values in a table of mechanical properties.
The fatigue strength of a material, SN, is defined as the maximum value of the stress range which causes a test specimen of the material of interest to fracture after the application of Ν completely reversed load cycles [1]. As one would expect, Ν varies as SN is adjusted.
The correlation between SN and Ν is negative, that is the number of cycles until fracture generally increases as the stress range or load range decreases. A collection of fatigue test results consisting of several pairs of stress range vs. number of cycles to failure data, is conveniently presented in graphical format, referred to as an S-N curve [1].
As an example, the S-N curve of normalised SAE 4130 chrome-moly steel is constructed in figure 1 from test data contained in NACA Technical Note 3866 [4].
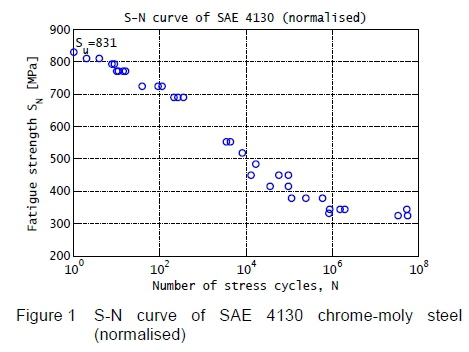
Due to the exponential nature of the S-N relationship, results are typically plotted on a log scale for number of cycles, and often for stress amplitude as well. It is noted that the left-most data point in figure 1 represents the tensile strength result of a static tensile test.
In the case of steel, furthermore, it is observed that the negative correlation between SNand Ν ceases to exist at a critical stress range below which it can be declared that an infinite number of load cycles can be applied without specimen fracture. This critical stress range is defined as the fatigue limit (Sf) of the material [1]. The fatigue limit of the steel tested in figure 1 appears to be slightly larger than 300 MPa, but smaller than 350 MPa.
The difficulty with fatigue strength as a mechanical property seems to be the amount of variability or scatter present in the test data. Schijve [5] furthermore states that the distribution function of the endurance limit is unknown. The natural consequence of this scatter is that fatigue testing requires many more test specimens than, say, tensile testing, in order to arrive at useful and sound conclusions from a statistical point of view.
The rotating beam fatigue testing machine is commonly used for generating the required large amount of material fatigue test data [2].
2.1 Rotating beam fatigue testing
Rotating beam fatigue testing is a simple, accurate, fast and cost effective method employed for fatigue testing of engineering materials. The frequency of load cycling is typically twice as large as that attainable with servo-hydraulic equipment.
The mechanical design of a rotating beam testing machine is such that the test specimen assembly resembles a horizontal beam structure that can be loaded by vertical forces in one plane. This beam is allowed to deflect or bend in the plane only, and by rotating the specimen assembly through the vertical plane of bending, stresses that fluctuate fully between compression and tension are induced in the specimen.
Specifically, the arrangement of applied forces is designed to ensure a symmetrically loaded beam in a state of four-point plane beam bending, supported at two outer points and loaded at two inner points (the test specimen resides between the two inner loading points).
Let Ρ denote the total applied load and L denote the overall length of the beam, then the shear force and bending moment diagrams of a symmetrically loaded beam, divided into thirds, can be constructed as shown in figure 2.
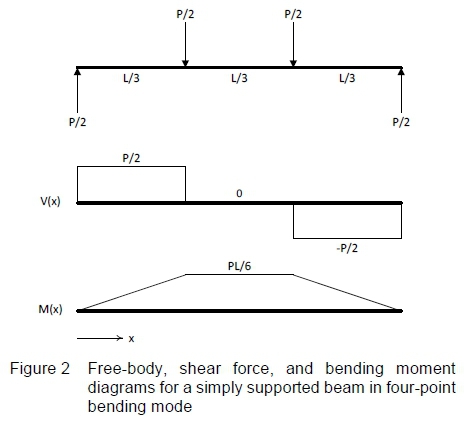
From figure 2 one observes that the maximum bending moment (PL/6) is present and uniform in the centre third of the beam. This region of the beam also experiences pure bending, that is shear forces are absent, as can be seen from the shear force diagram. The bending moment in the beam induces bending stresses in the beam material. These bending stresses are typically of prime interest to the test engineer, and can be calculated from the well-known flexure formula [6].

From the flexure formula it is evident that the calculated stress is a function of the bending moment (M), vertical distance (y) of the point of interest from the beam neutral axis, and the moment of inertia (I) of the beam cross-sectional area about the appropriate transverse axis that intersects the neutral axis. It is further evident that, for a cross-section at a particular location on the beam neutral axis, the stress is maximum when y is maximised, that is, the maximum stress (tensile or compressive) is located on the beam surface.
It goes without saying that the test specimen is the weakest part of the (rotating) beam. The specimen is deliberately machined into a characteristic dog-bone or hourglass shape on a lathe. In this way, the region of maximum bending stress is shifted to precisely the centre of the specimen where the diameter of the specimen is the smallest. The geometric transitions on the specimen are also very gradual in order to eliminate stress concentrations, so that the actual maximum stress corresponds well with the calculated maximum stress according to equation (2).
The disadvantage, however, of rotating beam testing, for the purpose of the work presented here, is the inability to retain the prevailing surface condition of the structure from which the specimen is extracted. It is thus not possible to investigate the effect of actual surface condition on fatigue life while simulating actual, fully reversed, load cycles experienced by the structure.
2.2 Four-point bending fatigue testing
Although rotating beam fatigue testing is in fact four-point bending, reference to four-point bending fatigue testing is understood to mean testing in a servo-hydraulic testing machine with a vertical load-line.
The specimen in four-point bending fatigue testing constitutes the entire beam, which means that the bending moment and shear force vary in the longitudinal direction of the specimen (recall that the rotating beam specimen is only part of the centre section of the beam, being in a state of constant pure bending). The specimen also does not rotate during testing, hence the specimen is constructed to obtain flat surfaces which help to stabilise the orientation of the specimen with respect to the testing machine. The cross-section of a specimen employed in four-point bending is rectangular in shape.
It appears that four-point bending is not often employed in fatigue testing of metals, especially when full force reversal is required. Instead, four-point bending is used to characterise the flexure properties of non-metallic materials, as described in ASTM D6272 [7].
Various configurations are possible to achieve four-point bending in a vertical load-line machine. Zhai et al. [8] describe the application of a four-point bending fatigue testing rig used to test for fatigue properties of an Al-Li alloy material, but only by loading in one direction (that is R = 0.1). They listed several apparent advantages of four-point bending, and also mentioned that a standard for four-point bending fatigue testing is not available (in 1999), causing specimen geometry to differ among mechanical testing laboratories.
Hassan and Liu [9] highlight the differences in fatigue strengths obtained from rotating bending, four-point bending, and cantilever bending tests of stainless steel pipe specimens, which they attribute to differences in strain ranges for equal stress ranges. While all three testing methods are analysed by FEA, only rotating bending tests are actually performed.
Four-point bending fatigue testing results of aerospace grade steel are also reported by Baxter etal. [10]. Once again, loads were applied at a force ratio of R = 0.1. Their focus was detection of crack growth by means of acoustic emission techniques, which required a rectangular shaped specimen that enabled the mounting of sensors at various distances from the crack location.
Fatigue testing results of forged titanium alloy Ti-6Al-4V in four-point bending mode are reported by Oberwinkler et al. [11]. A testing jig was developed with the aid of FEA and loads were applied at a force ratio of R = -1. The frequency of load application appear to be quite high, as mention was made of a resonant machine, and up to 107 load cycles were applied to specimens. The effect of surface condition, that is as-forged vs. machined, was investigated.
For the current work, a purpose-designed testing jig is manufactured because of the unique requirements for fatigue testing in a full force-reversal mode, as well as the ability to retain the prevailing surface condition of the specimen material.
2.2.1 Testing jig
A photograph of the installed testing jig is displayed in figure 3.

The testing jig comprises of four u-sections that contain the smaller jig components. These components are eight shafts of 25 mm diameter (ground surface) that interface with the specimen (machined surface). The shaft-ends are allowed to rotate inside 16 needle roller bearings in order to facilitate rolling motion between the shafts and the specimen surface during force actuation while minimising relative sliding between the surfaces.
The needle roller bearings are fitted into 16 eccentric rings which, in turn, are fitted in the u-sections. The eccentric rings can rotate in the u-sections. The eccentric rings are also actuated in pairs by mating rack gears, the positions of which are adjusted by set screws. By adjusting the set screws, the racks are translated, thereby rotating the pair of eccentrics via the meshed gear teeth, causing the centrelines of paired shafts to either close in or drift out. In this way all shafts are adjusted until intimate contact with the specimen is attained, allowing for force reversal in a smooth and controlled manner that minimises the disturbance to the control system of the testing machine. The testing jig therefore enables fatigue testing with a force ratio of R = -1.
The testing jig interfaces with a Schenk servo-hydraulic testing machine of capacity 250 kN operational in the lab. The jig is structurally able to carry an externally applied total force of 150 kN maximum.
2.2.2 Test specimen standard geometry
The standard specimen geometry is a prismatic bar with a rectangular cross-section of nominal width 20 mm and nominal height 40 mm. The distance between the outer beam supports, that is the length L in figure 2, is 210 mm.
The testing jig displayed in figure 3 accepts a rectangular cross-section specimen of width between 10 and 25 mm, height between 39 and 41 mm, and length between 230 and 276 mm. While the bending moment only depends on the loading arrangement (loading sizes and positions), the moment of inertia depends on the specimen cross-section only, bearing in mind that the maximum vertical distance from the neutral axis is for practical purposes constant (the testing jig allows for specimen height variation between 39 and 41 mm).
Changes or variation in the moment of inertia along the specimen neutral axis cause variation in the stress distribution in the specimen. In particular, the specimen cross-section could conceivably be modified or designed in such a way that the maximum surface stress is located in a preferred region of the specimen. This process is explored further below.
2.2.3 Contact and fretting
The basic disadvantage of a four-point bending arrangement is the regions of contact between the testing machine/jig and the test specimen. Stresses induced in these areas by contact can only be accurately calculated or measured with great difficulty, which means that a test result is unreliable if fracture occurs in a region where contact exists.
A specimen that bends causes regions in the beam to experience tension stresses and other regions to experience compressive stresses. Tension and compression regions are separated by the neutral plane. In the case of static testing where the surface in tension is of interest, a reliable test result can readily be recorded because the points of contact reside on the surface in compression (the opposite surface). If, however, the surface in compression is of interest, a problem arises because of contact due to specimen loading.
In the case of dynamic testing (with a view to evaluate material fatigue properties, often simply referred to as fatigue testing) at a force ratio of R = -1, the contact problem remains acute because fatigue cracks are likely to originate precisely in these regions of contact. This may happen owing to fretting between the jig rollers and the specimen surface on the lines of contact, or because of local plastic deformation (indentation) of the specimen material on the lines of contact. Nevertheless, it was desired to develop a test method that is independent of special lubrication requirements or the need for shimming between surfaces in contact.
3 Analysis and fatigue test results
Stress analysis is necessary in order to provide force target values during testing. Simple analytical models or equations are utilised because standard specifications on specimen geometry are followed. The calculation for average normal stress for a bar in tension, σ = F/A, is well-known and regularly used in tensile testing.
Deviation from standard specimen geometry requires caution, because the maximum stress in a specimen may deviate significantly from the average stress calculated by the simple equation. Stress analysis by FEA, however, solves this problem efficiently, and the author believes that much more information can presently be inferred from mechanical testing by duplication of the test set-up in FEA.
3.1 Specimen material properties
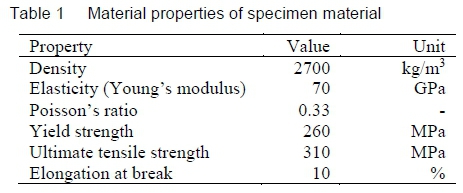
Aluminium alloy 6082-T6 is a medium strength structural alloy available in 20 mm plate, and is the alloy most commonly used for machining [12].
The material properties of the alloy are listed in table 1 [12],[13].
3.2 Standard test specimen geometry
3.2.1 Stress calculation
In order to ensure fatigue fracture within a reasonable (from a testing time point of view) number of cycles (< 106), a target maximum stress of at least 60% of yield stress is selected, that is 156 MPa. Substitution into the flexure formula, equation (2), yields
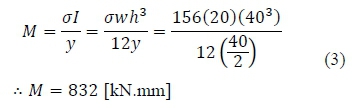
From figure 2 the peak force is calculated as

Based on this result, a slightly higher force amplitude of 25 kN is selected for the fatigue test. This increase in force raises the peak stress to 164 MPa (calculated from eq. (2)).
3.2.2 FEA result
Two planes of symmetry intersect the load line of the machine at right angles to each other. One of these is utilised such that only one half of the jig/specimen assembly is modelled as solids in the FEA software [14], as shown by the meshed model displayed in figure 4.
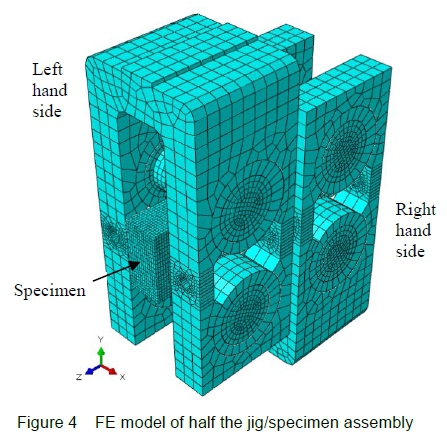
The jig structures are also modelled due to a simultaneous requirement to assess the strength of the jig, determined at 150 kN stated in section 2.2.1.
A vertical load of -12.5 kN (in the y-direction as defined in figure 4) is applied to the left hand side of the jig model, which is also constrained to allow movement in the y-direction only. The right hand side section is fixed in space.
A contact formulation is defined between the cylindrical shaft surfaces and the specimen surfaces. An exponential pressure is defined for contact normal to the surfaces, while frictionless tangential behaviour is selected.
The specimen is meshed by 13091 quadratic hexahedral elements of type C3D20. The bending stress contours in the specimen at equilibrium conditions are displayed in figure 5 in two dimensions.
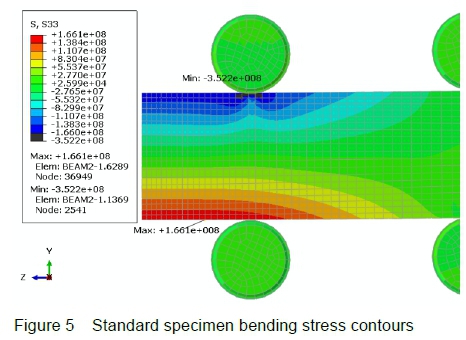
A maximum tension stress of 166 MPa is recorded on the bottom surface of the specimen, while the maximum compressive stress due to bending is 161 MPa (not indicated in the figure).
The maximum compressive stress due to the combination of bending and contact is given as 352 MPa, as shown beneath the shaft, although this number is quite dependent on the specifics of the contact formulation and not considered to be accurate.
There is good agreement between the stress calculation of section 3.2.1 of 164 MPa (both tension and compression) and the FEA results of 161 MPa compression and 166 MPa tension.
3.2.3 Test results
In order to verify calculated strain and stress against measured quantities, a strain gauge is attached to the surface of the specimen, right in the middle, measuring the strain in the z-direction defined in figure 4.
The strain results as a function of total applied force (which is varied across the complete range of interest) are displayed in figure 6. From the graph it is evident that the relationship between the applied force and the measured strain is linear, and that it runs through the zero point.
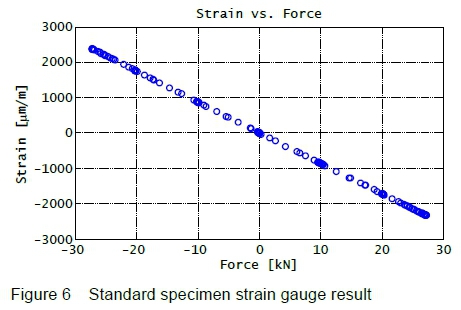
The values at the two extreme data points in figure 6 are listed in table 2.
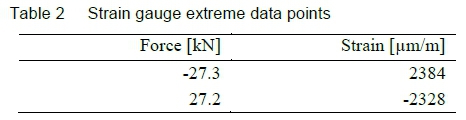
Assuming a linear relationship between force and strain, one can interpolate between the above two sets of data points for the estimated strain at 25 and -25 kN. The stress estimates are subsequently calculated employing the modulus of elasticity (which is used in the linear elastic FEA as well), as shown in table 3.
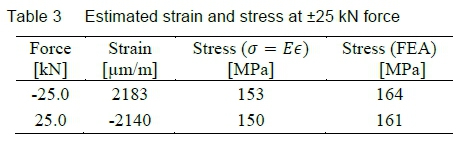
The difference between the measured and computed strains (and hence stresses) of about 7% can be attributed to the specifics of the contact formulation between the jig and the specimen. The FEA assumes frictionless contact between the shafts and the specimen, while a specified friction coefficient between these bodies of 0.1 reduces the solved strains to within 1.5% of the measured values listed in table 3.
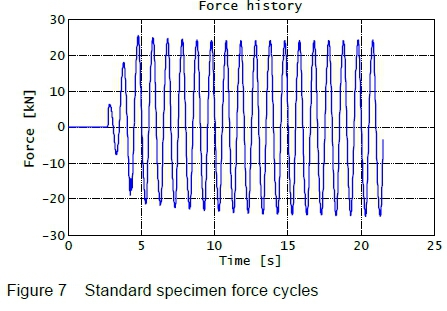
Upon invoking the fatigue routine, the data of the first few force cycles is recorded and displayed in figure 7. The force amplitude is 25 kN, the mean force is 0 kN, and the initial frequency is 1 Hz (the frequency is subsequently raised to 5 Hz in order to speed-up the test).
Specimen fracture occurred after 127 748 force cycles. A photograph of the fractured specimen is displayed in figure 8.

The fatigue crack initiated from the line of contact between the specimen and the jig shaft closest to centre of the specimen, as expected.
3.3 First modified test specimen geometry
3.3.1 FEA result
The first modification to the standard test specimen introduced in section 3.2 is machining of a 15 mm diameter centre hole transverse and horizontal to the length-axis of the specimen. The idea of the hole is to reduce the strength of the specimen in a region away from the contact zones, thus causing the stress to rise in this region.
The applied force is kept unchanged at -12.5 kN (y-direction). The bending stress contours in the specimen at equilibrium conditions are displayed in figure 9.
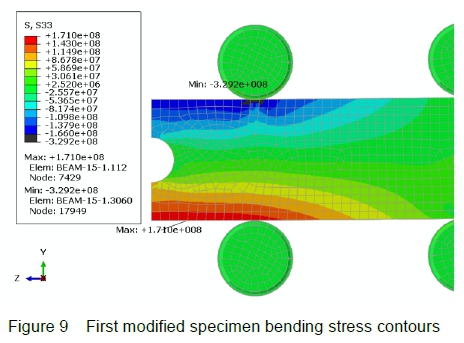
The maximum tension stress increases from 166 MPa to 171 MPa, and its location shifts slightly towards the centre of the specimen away from the areas of contact.
3.3.2 Fatigue test results
The target force profile has a mean value of 0 kN and an amplitude of 25 kN. The force signal is applied at a frequency of 5 Hz.
Specimen fracture occurred after 188 178 completed force cycles. Although the number of cycles increased from the previous test, the value is not of any importance in this work.
A photograph of the fractured specimen is displayed in figure 10.

Figure 10 Photograph of fractured specimen (first mod.)
Once again, the fatigue crack initiated on the line of contact between the jig shaft and the specimen. The proposed modification therefore proved inadequate.
3.4 Second modified test specimen geometry
3.4.1 FEA result
As an intermediate modification step, the diameter of the transverse hole is substantially enlarged in order to reduce the applied load, and hence the contact stresses, while still maintaining a maximum stress of about 164 MPa. In fact, the diameter is increased as much as possible (up to 28 mm) until the location of the maximum stress shifts from the specimen outside surface to the hole inside surface. This situation is of course undesirable since the probability is increased that the crack initiates in the hole and propagates to the outside surface.
The applied force is reduced to -8 kN (y-direction), equivalent to 16 kN in the actual test, in order to obtain bending stresses of similar magnitude to those calculated in sections 3.2.2 and 3.3.1. The bending stresses for this intermediate case at equilibrium conditions are displayed in figure 11.
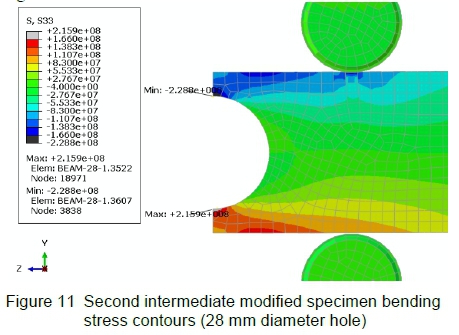
From the graph of stress contours it is witnessed that both the maximum tension and compressive stresses are located on the inside surface of the hole. The maximum tension stress is 216 MPa, while the maximum compressive stress is 229 MPa.
In order to mitigate this new development, the hole is translated or sweeped (as a final modification step) through a distance of 14 mm along the length of the specimen in order to create a slot. The corresponding bending stresses for the same load (-8 kN) are displayed in figure 12.
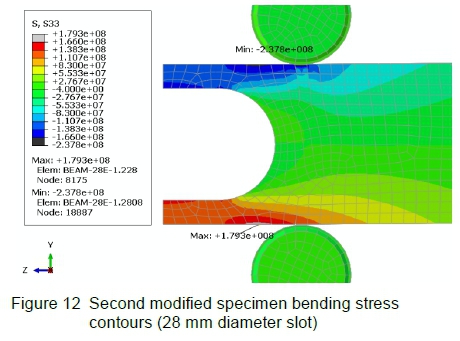
The maximum tension stress is reduced from 216 MPa to 179 MPa, and resides on the outside surface of the specimen as desired. The compressive stress at the same point - when the load is reversed - is 177 MPa.
3.4.2 Fatigue test results
Four test specimens are prepared from the specified material and subjected to the test routine.
The applied force amplitude is reduced to 16 kN, while the frequency is increased to 10 Hz (reducing the time required to test). The results are summarised by the data presented in table 4.
A photograph of the fractured specimens is displayed in figure 13. The specimens are numbered from the far side to the near side, in chronological order.

One specimen (no. 1) fractured from a crack that originated at the line of contact beneath the jig shaft. Three out of the four specimens, however, fractured in the desired and expected region as predicted by the FEA effort. These specimens can be identified from the photograph as specimens no. 0, 2, and 3.
It is also noted that the fatigue cracks indeed initiated on the outside surfaces of the specimens. Photographs of the fracture surfaces of specimens no. 0 and no. 2 are displayed in figures 14 and 15, respectively.


4 Conclusion
The predictive capability of FEA is utilised in a process where the geometry of a standard test specimen is modified into a nonstandard geometry that is still suitable for mechanical testing.
The standardisation of specimen geometry in mechanical testing enables the utilisation of analytical equations to calculate induced stresses in the specimen for a known applied force. Deviation from a standard geometry necessitates the employment of an alternative method of analysis, such as FEA, since analytical solutions to the stress distribution in this nonstandard geometry are not available.
The process is successfully demonstrated in a four-point bending fatigue testing arrangement. Induced stresses due to the applied load, as well as the location of crack initiation and fracture, can be predicted (by FEA) and manipulated to a satisfactory extent - three out of four test specimens fractured in the desired region from a crack that initiated on the outside, free surface of the specimen.
Acknowledgement
The effective integration of the testing jig with laboratory equipment, as well as professional execution of the fatigue test routines by the experienced and able test officers resident at the mechanical testing lab of the CSIR, Messrs. Erich Güldenpfennig and Chris McDuling, are gratefully acknowledged.
The Department of Science and Technology provided funding for this work under a Parliamentary Grant of the Republic of South Africa.
References
[1] ASTM E1823-13. Standard Terminology Relating to Fatigue and Fracture Testing. ASTM International, West Conshohocken, PA, 2013.
[2] S. R. Swanson (Editor). Handbook of Fatigue Testing. ASTM Special Technical Publication 566, 1974.
[3] J. E. Shigley. Mechanical Engineering Design. First Metric Edition, McGraw-Hill, 1986.
[4] W. Illg. Fatigue Tests on Notched and Unnotched Sheet Specimens of 2024-T3 and 7075-T6 Aluminum Alloys and of SAE 4130 Steel With Special Consideration of Life Range from 2 to 10,000 Cycles. NACA Technical Note 3866, December 1956.
[5] J. Schijve. Fatigue of Structures and Materials in the 20th Century and the State of the Art. International Journal of Fatigue, 25(8):679-702, 2003. [ Links ]
[6] J. M. Gere and S. P. Timoshenko. Mechanics of Materials. Third SI Edition, Chapman & Hall, 1991.
[7] ASTM D6272-10, Standard Test Method for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials by Four-Point Bending, ASTM International, West Conshohocken, PA, 2017.
[8] T. Zhai, Y. G. Xu, J. W. Martin, A. J. Wilkinson and G. A. D. Briggs. A Self-aligning Four-point Bend Testing Rig and Sample Geometry Effect in Four-point Bend Fatigue. International Journal of Fatigue, 21(9):889-894, 1999. [ Links ]
[9] T. Hassan and Z. Liu. On the Difference of Fatigue Strengths from Rotating Bending, Four-point Bending, and Cantilever Bending Tests. International Journal of Pressure Vessels and Piping, 78(1):19-30, 2001. [ Links ]
[10] M. G. Baxter, R. Pullin, K. M. Holford and S. L. Evans. Detection of Fatigue Crack Growth in Aircraft Landing Gear, 4 Point Bend Test Specimens. Key Engineering Materials, 293:193-200, 2005. [ Links ]
[11] B. Oberwinkler, M. Riedler, H. Leitner and A. Javidi. Four Point Bending Fatigue Tests of Forged Ti 6Al 4 V. Materials Testing, 51(9):580-586, 2009. [ Links ]
[12] Aluminium Alloy 6082-T6, Aalco Metals Ltd, 25 High Street, Cobham, Surrey KT11 3Dh, www.aalco.co.uk.
[13] Aluminium 6082-T6, MatWeb Material Property Data, www.matweb.com.
[14] Abaqus Version 6.14-1 2014, Dassault Systèmes Simulia Corp., Providence, RI, USA.
Received 30 October 2017
Revised form 19 January 2018
Accepted 16 February 2018














