PROFESSIONAL TECHNICAL AND SCIENTIFIC PAPERS

 

Prediction of rock fragmentation using the Kuznetsov-Cunningham-Ouchterlony model

 

 

E.K. Mutinda^I; B.O. Alunda^I; D.K. Maina^I; R.M. Kasomo^II

^ISchool of Mines and Engineering, Taita Taveta University, 657-80300, Voi, Kenya
^IICollege of Resource and Environmental Engineering, Wuhan University of Technology, Wuhan 430070, China

Correspondence

 

 

---

SYNOPSIS

Assessment of blast fragment size distribution is critical in mining operations because it is the initial step towards mineral extraction. Different empirical models and techniques are available for predicting and investigating the consequences of blasting, one of which is the Kuznetsov-Cunningham-Ouchterlony (KCO) model. In this paper we summarize the advances in the empirical models from inception until now, and explore the improvements that have been made so far with particular emphasis is on the most recent KCO model. Utilization of the model and the errors that arise between expected and the actual outcomes are analysed. The results indicate that the KCO model remains useful for predicting the blast fragmentation at limestone mine sites, despite the availability of other advanced prediction models. It is also a valuable instrument for pre-surveying the impact of varying certain parameters of a blast plan.

Keywords: blasting, rock fragmentation, modelling, prediction.

---

 

 

Introduction

The initial stage of ore excavation in limestone mines is drilling and blasting, the aim of which is to reduce the rock to easily handleable fragments (Ouchterlony, 2005; Monjezi et aí., 2010). It is essential that the blast fragments have the required size distribution as this affects the loading, hauling, and crushing processes (Ouchterlony, 2003). Accurate measurement of blasted rock fragmentation is of great importance in hard rock drilling and blasting (Fourney and Dick, 1996). The post-blast rock size distribution dramatically influences the efficiency of all the downstream rock processes, including comminution. In cases where there are too many boulders, the mine operator will be faced with the need for secondary blasting, which will have unnecessary negative consequences for the company's cash flow. It also poses safety issues due to the increased risk of flyrock and air blast hazard because of the light stemming employed in secondary blasting (Abuhasel, 2019; Ouchterlony and Sanchidrián, 2019).

There are a number of parameters that influcence the outcome of any blasting exercise. They include parameters over which the operator has control and those that the operator does not. The former include blast design parameters such as geometrical and explosive parameters (Sharma et aí., 2019) whereas the latter depend on the inherent properties of the rock being blasted. The geometrical parameters that the mine operator can control during blasting are shown in Figure 1. They include the bench height, burden, spacing, hole depth, sub-drill, hole diameter, stem deck, and top stemming. The explosive parameters includes the type of explosive used, charge density, firing pattern, and blast initiation systems. The other parameters, which the operator has no control over, include the hardness factor, rock mass rating, and rock density.

 

 

A reliable rock fragmentation prediction model is an essential aspect of blasting operations for improved production. Several models have been developed to predict the particle size distribution from a blast. The development of fragmentation models emanates from the need to provide engineering solutions to blasting problems such as the optimization of run-of-mine (ROM) fragmentation (Esen, 2013; Petrosyan, 2018). However, none of these models accurately predicts the size distribution from a blast. To minimize the number of boulders produced during blasting, there is a need for blasts to be designed and fragment size distributions modelled. This will inform the mine operator of the suitable blast parameters that are likely to result in the desired fragment size distribution. This has the advantage of reducing the need for secondary blasting, which has a dual benefit of reduced the cost of operation to the mining company and increased safety for the operator.

The two most recent empirical fragmentation models were introduced in 2005 and both have undergone subsequent modification to better predict the size of rock fragments and minimize the occurrence of boulders. These are the KCO (Cunningham, 2005) and Modified Kuz-Ram models (Ouchterlony and Sanchidrián, 2019), and were developed to overcome the shortcomings of the Kuz-Ram model (Ouchterlony and Sanchidrián, 2019). One of the reasons for the KCO model's superiority to the other empirical models is the fact that the required input parameters are comparatively simple to obtain and apply in fragment size prediction. Newer techniques for analysing blast fragments have been recently proposed (Abuhasel, 2019), such as artificial neural networks (ANNs) and multivariate regression (MVR) (Cardu, Coragliotto and Oreste, 2019). However, building these techniques to a level such that they can accommodate the blast design variables as well as quantify the influence of inherent rock properties on the blast outcome is tiresome, time-consuming, and also expensive. On the other hand, secondary blasting due to the production of large boulders increases the cost and time required before any further size reduction can take place (Ouchterlony and Sanchidrián, 2019). Therefore, this research is focused on determining the possibility of applying the KCO model for predicting blast fragment size distribution in two limestone quarries in Kenya.

 

Theory

Development of fragmentation models

There are several blast fragment size distribution prediction models that have been developed, and these can be categorized as either empirical or mechanistic models, depending on the cause of the fines production (Babaeian et al., 2019; Ouchterlony and Sanchidrián, 2019). The empirical models assume that finer fragmentation is brought about by a higher powder factor (higher input energy of explosives) (Franklin and Maerz, 2018), whereas the mechanistic models link the production of fines to the proper understanding of the fundamental principles of physics or the dynamics of detonation, or sometimes a combination of the two, and transfer of the blast energy during blasting. This makes the mechanistic models less popular at mine sites because they are very complex and need more complex data (Dare-Bryan, Mansfield, and Schoeman, 2012).

Mechanistic models are at the apex of the modelling order demonstrating the progressive systems. They utilize a large number of numerical techniques and thus require considerable processing power and unnecessarily long computation times (Ouchterlony and Sanchidrián, 2019).

They predict blast outcomes by expressly mimicking changes in conditions (Cardu, Coragliotto, and Oreste, 2019). They can simulate bulk explosive loading and movement of rocks around the blast area by analysing stress or strain in the affected region. These models are considered the most complex models, that seek to explain the behavior of system components (thus being known as multi-material science codes). Owing to their complexity, they can take days or weeks to run even on powerful supercomputers (Ouchterlony and Sanchidrián, 2019). Also, the models are reported to be less site-specific, in addition to the difficulty in collecting the required rock and detonation data.

Empirical computer models, in contrast, depend on the straightforward fitting of scientific as well as computational articulations to data that has been obtained from field measurements or potential estimations (Ouchterlony and Sanchidrián, 2019). These models include the 1970 model by da Gama (Ouchterlony and Sanchidrián, 2019), which predicted fragment size distribution based on the energy and explosives needed and rock characteristics. This model had a disadvantage in that it neglects the effect of stemming length, spacing, bench height, and does not include non-uniformity and uniformity predictions factors (Babaeian et al., 2019). In 1973, Larsson (Ouchterlony, 2005) developed another model that utilizes burden, spacing, specific charge, and characteristics of the rock's discontinuities for prediction. However, this model did not perform much better in predicting particle size distribution. In 1973 Kuznetsov (Cunningham, 2005) developed an empirical model that factored in the type of explosives, rock mass classification, influence of applied blast energy, and evaluation of uniformity and non-uniformity of fragmentation. In this model, the fragmentation is determined in terms of mass percentage, powder factor (applied blast energy per unit volume of rock), and mean fragment size (Ouchterlony and Sanchidrián, 2019).

The Kuz-Ram model was introduced in 1983 by Cunningham (Ouchterlony and Sanchidrián, 2019). The model is capable of calculating both the average fragment size, x, and the uniformity index, n, for the muckpile of a bench blasting round whose sieving curve follows the Rosin-Rammler (RR) distribution (fragmentation curves for equal mean size) function (Ouchterlony and Sanchidrián, 2019). In 1987 Kou and Rustan (Cunningham, 2005; Sanchidrián, Segarra, and López, 2006) made an adjustment to Larson's model and named this new model Sve-DeFo (Chung and Katsabanis, 2000). The main parameters considered are the bench height, stemming length, the discontinuities' characteristics, and the rock's nature. This model also had its drawbacks, in that the assumption of the rocks' features was an approximation. Also, the predicted dimensions of fragmented rocks were smaller than the actual values (Babaeian et al., 2019) . In 2000, Chung and Katsabanis used data from Otterness and other researchers (Ouchterlony and Sanchidrián, 2019) collected in 1991 to verify the accuracy of the Kuz-Ram model (Chung and Katsabanis, 2000). They proposed that the RR (fragmentation curves for equal mean size) function describes the fragment size distribution data well enough (Ouchterlony and Sanchidrián, 2019).

The modified Kuz-Ram model, which was introduced in 2005 (Ouchterlony and Sanchidrián, 2019), resembles the preceding Kuz-Ram model. However, the difference is the modification of the Kuznetsov equation by applying a 0.073 multiplier to help the model perform better in predicting the mean fragmentation size (Gheibie et al., 2009). The Kuz-Ram uniformity index is also substituted by an upgraded uniformity index, which was initially proposed by Cunningham (Cunningham, 2005; Sanchidrián, 2019) and considers the blastability index, BI, of the rock in question (Gheibie et al., 2009; Ouchterlony, 2019).

KCO model

The Kuznetsov-Cunningham-Ouchterlony (KCO) fragmentation model is an extended form of the Kuz-Ram model. The KCO model replaces the Rosin-Rammler equation of the Kuz-Ram model with the Swebrec function, and was put into use in 2005 by Cunningham (Ouchterlony, 2005; Ouchterlony and Sanchidrián, 2019). This model was developed to help minimize two important weaknesses of the Kuz-Ram model: the poor prediction ability for fragments with high fines content and the upper limit cut-off of block sizes (Bhandari, 2012; Ouchterlony and Sanchidrián, 2019).

The Swebrec function that replaced the Rosin-Rammler equation in the Kuz-Ram model is shown in Equation [1]. The Swebric function includes three parameters; the 50% of the material size (X₅₀) passing through the crusher gap, the maximum block size (X_Max), and b which is a curve undulation parameter which is similar to and depends on the uniformity index of the Kuz- Ram model ( Hekmat, Munoz, and Gomez, 2019; Ouchterlony and Sanchidrián; 2019 Sanchidrián and Ouchterlony 2017).

where P(x) is the percentage fraction of fragments passing sieve size X, and b is the curve undulation parameter. X_Maxis the minimum (in-situ block size; S or B). The system of equations that make up the KCO model is shown in Equations [2, 6, and 7].

where mean fragment size (X₅₀) is the 50% of the material passing through the crusher gap, A is a rock factor as shown in Equation [3], q is the specific charge/powder factor (kg/m³), Q is the explosive weight per drill-hole (kg), and 5_ANFO is the weight strength of the explosive relative to ANFO.

 

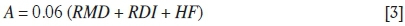
where RMD is the rock mass description. When rock is powdery and friable RMD is 10, when joints are vertical RMD is JF; when the rocks mass is massive, RMD is 50. JF is the joint factor, calculated using Equation [4]:

where JCF is joint condition factor which assumes the value of 1 for tight joints, 1.5 for relaxed joint, and 2 for gouge-filled joints. JPS is the vertical joint plane spacing; which relates to joint spacing S_jand 'reduced pattern' VBS as follows. JPS is 10 when Sj < 0.1 m, 20 if S is 0.1-0.3 m, 50 if S_jis 0.3-0.95 VBS, and 80 if S_j> VBS. JPA is the joint plane angle; when the joints dip out-of-face, the value is 20, when striking perpendicular to the face, 30, and when the joints dip into the face it is 40. RDI is the rock density influence in kg /m³, defined by Equation [5].

where ρ is the density of the rock, and HF is the hardness factor. The curve undulating paramters, b, is defined by using Equation [6] :

Alternatively, b can be established by Equation [7], as reported by Choudhary and Gupta (2012).

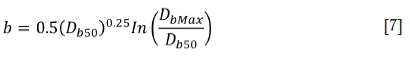
where D_bMaxis the least burden, spacing, or maximum in-situ block size and D_b50 is the least burden, spacing, or maximum in-situ block size, as suggested by Ouchterlony (2005).

 

Materials and methods

This research paper presents a case study of Bisil and Simba quarries in Kenya. Data was collected on recognition of pushbacks, bench faces, and geological measurement to determine the pre-existing fractures and their orientation, and spatial and explosive parameters for each blast. The joints present on each bench face were identified and their spacing measured so as to determine the rock mass rating (RMR). The Bisil quarry has four mining faces while Simba quarry has two mining faces. Extraction is done in benches. The information gathered was used to predict the blast fragmentation using the KCO model so as to ascertain the pre-blast particle size distribution at the two quarries. After data acquisition the blast was performed and fragmentation images were taken as shown in Figure 2a for analysis using Split-Desktop. The images were subsequently processed by first delineation as shown in Figure 2b, followed by the generation of the particle size distribution curves. Six blasts were carried out in each quarry, and the fragment size distributions analysed.

 

Results and discussion

Table I shows the rock parameters obtained for six blasts at each quarry. Table II shows the geometrical parameters used in the blast rounds, and the explosive parameters, including the powder factor and explosive weight, are presented in Table III. The rock mass classification was based on Bieniawski's geomechanical rock classification (Bieniawski, 1988). For the prediction, a Python code was developed to assist in the determination of the model's particle size distribution. Split-Desktop an industry-standard software for image analysis was used to measure the after-blast fragment size distribution. The Split-Desktop is an image processing software package that uses grayscale to determine the particle size distribution of the blast rock fragments (de Souza, da Silva, and Rocha, 2018). Digital images are normally acquired using a digital camera or smartphone (Maerz, 1996). Ten images were captured using a smartphone fitted with Split-Camera application.

The images were transferred to a computer and high-quality images with a resolution of 600 dpi delineated to help determine measured rock size distribution using Split-Desktop 4.1 software. After delineation, fragment size distribution was generated, representing the measured blast fragment particle size distribution. Graphs of the predicted and measured particle size distributions were plotted, as shown in Figure 3.

The regression results from the two sites were 99.0% and 98.1%, respectively, as shown in Figure 4. These high regression values indicated that the predictions from the model correlated well with the actual results from the blasts studied. The KCO model seemed to have shown a better relationship between the predicted and the actual results for the Simba quarry than for Bisil quarry.

The percentage of boulders predicted and produced per blast was determined from the difference of total material and material passing the crusher gape. The crusher gape for both Simba and Bisil quarries was 50 cm, and any material larger than this was considered as a boulder. Generally, the model predicted boulders with error of less than 10% for all of the studied blast rounds in both quarries. Figure 5 shows the varying trends of the KCO model in predicting boulders.

It was noted that the model underestimated the amount of boulders from most of the blast rounds at the Bisil quarry, and overestimated boulders for most of the rounds at Simba. This can be ascribed to the difference in the rock mass characteristics at the two quarries.

 

Conclusion

The Kuznetsov-Cunningham-Ouchterlony (KCO) model, being an empirical model, provides a reliable guide to the expected blast fragment particle size distribution, depending on the geology and blast design applied. The findings of this paper could act as a datum for investigating the impact of changing blast variables. Well-studied geology and correct choice of explosives with a properly designed and modelled blast round can yield the desired fragment size, hence optimizing the cost of excavation of limestone. Moreover, the straightforwardness of the model and the overall simplicity of obtaining model input places the KCO model at the cutting edge of rock fragmentation models. The most significant application of KCO is to guide the blast engineer in considering the impact of different parameters when endeavouring to improve blast round output.

 

Acknowledgments

The support from Split-Engineering for this project is highly appreciated (award of software license). We also thank the Exploration and Tertiary Material Department of East African Portland Cement Company (EAPCC) and Mining Department of Simba Cement Company for their cooperation and provision of their personnel, equipment, and laboratory facilities for this research work.

 

References

Abuhasel, K.A. 2019. A comparative study of regression model and the adaptive neuro-fuzzy conjecture systems for predicting energy consumption for jaw crusher. Applied Sciences, vol. 9, no. 18. pp. 3916.         [ Links ]

Babaeian, M., Ataei, M., Sereshki, F., Sötöudeh, F., and Möhammadi, S. 2019. A new framework for evaluation of rock fragmentation in open pit mines. Journal of Rock Mechanics and Geotechnical Engineering, vol. 11, no. 2. pp. 325-336.         [ Links ]

Bhandari, S. 2012. Fines and dust generation and control in rock fragmentation by blasting. Rock Fragmentation by Blasting. CRC Press, Boca Raton, FL. pp. 511-520.         [ Links ]

Bieniawski, Z.T. 1988. The Rock Mass Rating (RMR) system (geomechanics classification) in engineering practice. Rock Classification Systemsfor Engineering Purposes. Kirkaldie, L. (ed.) ASTM International, West Conshohocken, PA. pp. 17-34.         [ Links ]

Cardu, M., Coragliotto, D., and Oreste, P. 2019. Analysis of predictor equations for determining the blast-induced vibration in rock blasting. International Journal of Mining Science and Technology, vol. 29, no. 6. pp. 905-915.         [ Links ]

Chung, S.H. and Katsabanis, p.D. 2000. Fragmentation prediction using improved engineering formulae. Fragblast, vol. 4, no. 3. pp. 198-207.         [ Links ]

Cunningham, C.V.B. 2005. The Kuz-Ram fragmentation model - 20 years on. Proceedings of the 3rd European Federation of Explosives Engineers World Conference on Explosives and Blasting, Brighton, 2005. vol. 4. pp. 201-210.         [ Links ]

Dare-Bryan, p., Mansfield, S., and Schoeman, J. 2012. Blast optimisation through computer modelling of fragmentation, heave and damage. Rock Fragmentation by Blasting. CRC Press, Boca Raton, FL. pp. 95-104.         [ Links ]

De Souza, J.C., da Silva, A.C.S., and Rocha, S.S. 2018. Analysis of blasting rocks prediction and rock fragmentation results using Split-Desktop software. Tecnología em Metalurgia Materiais e Mineragao, vol 15, no. 1. pp. 22-30.         [ Links ]

Esen, S. 2013. Fragmentation modelling and the effects of ROM fragmentation on comminution circuits, Proceedings of the 23rd International Mining Congress & Exhibition of Turkey. Chamber of Mining Engineers of Turkey, Ankara. pp. 252-260.         [ Links ]

Fourney, W.L. and Dick, R.D. 1996. Explosive fragmentation. High-Pressure Shock Compression of Solids II. Springer.         [ Links ]

Franklin, J.A. and Maerz, N.H. 2018. Empirical design and rock mass characterization. Measurement of Blast Fragmentation. Routledge.         [ Links ]

Gheibie, S., Aghababaeia, H., Hoseinieb, S.SH., and pourrahimianc, Y. 2009. Modified Kuz-Ram fragmentation model and its use at the Sungun Copper Mine. International Journal of Rock Mechanics and Mining Sciences, vol. 46. no. 6. pp. 967-973.         [ Links ]

Hekmat, Α., Munoz, S., and Gomez, R. 2019. Prediction of rock fragmentation based on a modified Kuz-Ram model. Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection - MPES 2018. Springer International, Cham, Switzerland. pp. 69-79.         [ Links ]

Maerz, N.H. 1996. Image sampling techniques and requirements for automated image analysis of rock fragmentation. Proceedings of the FRAGBLAST 5 Workshop on Measurement of Blast Fragmentation, Montreal, Quebec, Canada. Balkema, Rotterdam. pp. 115-120.         [ Links ]

Monjezi, M., Amiri, H., Farrokhi, Α., and Goshtasbi, K. 2010. Prediction of rock fragmentation due to blasting in Sarcheshmeh Copper Mine using artificial neural networks. Geotechnical and Geological Engineering, vol. 28, no. 4. pp. 423-430.         [ Links ]

Ouchterlony, F. Influence of blasting on the size distribution and properties of muckpile fragments, a state-of-the-art review. Technical report Project P2000-10. Luleá University of Technology. https://wvww.diva-portal.org/smash/get/diva2:995258/FULLTEXT01.pdf        [ Links ]

Ouchterlony, F. 2005. The Swebrec© function : Linking fragmentation by blasting and crushing. Mining Technology, vol. 114. pp. 29-44.         [ Links ]

Ouchterlony, F. and Sanchidrián, J.A. 2019. A review of development of better prediction equations for blast fragmentation. Journal of Rock Mechanics and Geotechnical Engineering, vol. 11, no. 5. pp. 1094-1109.         [ Links ]

petrosyan, M.I. 2018. Model investigations of parameters of rock breakage by blasting. Rock Breakage by Blasting. Routledge. pp. 75-104.         [ Links ]

Sanchidrián, J.A. and Ouchterlony, F. 2017. A distribution-free description of fragmentation by blasting based on dimensional analysis. Rock Mechanics and Rock Engineering, vol. 50, no. 4. pp. 781-806.         [ Links ]

Sanchidrián, J.A., Segarra, p., and López, LM. 2006. A practical procedure for the measurement of fragmentation by blasting by image analysis. Rock Mechanics and Rock Engineering, vol. 39, no. 4. pp. 359-382.         [ Links ]

Sharma, Α., Mishra, Α., Choudhary, Β., and Meena, R. 2019. Impact of blast design parameters on rock fragmentation in building stone quarries. Current Science, vol. 116. pp. 1861.         [ Links ] ♦

 

 

Correspondence:
B.O. Alunda
Email: benard.ouma@ttu.ac.ke

Received: 11 Oct. 2020
Revised: 29 Jan. 2021
Accepted: 3 Feb. 2021
Published: March 2021

 

 

ORCID
E.K. Mutinda https://orcid.org/0000-0002-1012-9655
B.O. Alunda https://orcid.org/0000-0003-0283-6525
D.K. Maina https://orcid.org/0000-0002-8514-055X
R.M. Kasomo https://orcid.org/0000-0003-1850-0735