PROFESSIONAL TECHNICAL AND SCIENTIFIC PAPERS

 

Optimization of chlorite and talc flotation using experimental design methodology: Case study of the MCG plant, Morocco

 

 

K. Boujounoui^I; A. Abidi^II; A. Baçaoui^I; K. El Amari^III; A. Yaacoubi^I

^IFaculty of Sciences Semlalia, department of chemistry, Marrakech Morocco
^IIMining Institute of Marrakech (IMM), Marrakech, Morocco
^IIIGeoresources, Geo-environment and Civil Engineering Laboratory, Faculty of Sciences and Technologies Marrakech, Marrakech, Morocco

Correspondence

 

 

---

SYNOPSIS

Response surface methodology (RSM), central composite design (CCD), and desirability functions were used for modelling and optimization of the operating factors in chlorite and talc (collectively termed 'mica') flotation. The influence of pulp pH, cyanide (NaCN) consumption, and particle size was studied with the aim of optimizing ssilicate flotation while minimizing recoveries of galena, chalcopyrite, and sphalerite.
Flotation tests were carried out on a representative sample of a complex sulphide ore from Draa Sfar mine (Morocco). The model predictions for the flotation of each of the minerals concerned were found to be in good agreement with experimental values, with R² values of 0.91, 0.98, 0.99, and 0.90 for mica, galena, chalcopyrite, and sphalerite recoveries, respectively. RSM combined with desirability functions and CCD was successfully applied for the modelling of mica flotation, considering simultaneously the four flotation responses to achieve the maximum recovery of mica and minimal loss of Pb, Cu, and Zn to the flotation concentrate.

Keywords: chlorite, talc, flotation, response surface methodology, central composite design, optimization.

---

 

 

Introduction

The Mining Company of Guemassa (MCG), located 30 km southwest of Marrakech in Morocco, applies a selective flotation process to produce 13.812 t of lead (galena) concentrate, 16.755 t of copper (chalcopyrite) concentrate, and 72.970 t of zinc (sphalerite) concentrate per annum (Managem Group, 2014). The ore processed consists of sphalerite, galena, chalcopyrite, pyrite, pyrrhotite, chlorite, talc, amphibole, calcite, dolomite, and ankerite (Hibti, 2001). The flotation circuit comprises three stages - galena recovery, followed by chalcopyrite, and finally sphalerite recovery, using common processes for sulphide flotation (Cao and Liu, 2006), but the presence of chlorite and talc, which have a natural floatability, lowers the grade of the lead concentrate. An additional 'mica' flotation circuit, upstream of the lead flotation circuit, is used from time to time to reduce the content of these silicate minerals in the feed to lead flotation.

The statistical design of experiments (DOE) (Box, Hunter, and Hunter, 1978; Akhanazarova and Kafarov 1982; Obeng, Morell, and Napier-Munn, 2005; Napier-Munn 2012; Ennaciri et al., 2014), which has several advantages over the classical method of treating one variable at a time, is used for optimization and modelling process parameters in mineral processing. These statistical techniques have been used to study the flotation of minerals (Yalsin 1999; Rao and Mohanty 2002; Cilek and Yilmazer 2003; Martinez et al., 2003; Martyn et al., 2008; Mehrabani et al., 2010; Vazifeh, Jorjani, and Bagherian, 2010; Boujounoui et al., 2015, 2018) as well as in predicting performance in several plants using multivariable statistical modelling (Lind, Yalcin, and Butcher, 2003).

This study is a part of an overall project to improve the performance of the MCG flotation plant by optimizing the mica flotation, as well the recycling of process water. (Abidi et al., 2014, 2016, 2019; Boujounoui et al., 2015, 2017, 2018, 2019). Since the MGC plant is located in a semi-arid climate, improving the rate of process water recycling is still a serious target, despite the possible modification in the flotation conditions.

The aim of the present work is to apply DOE techniques for the optimization, at batch scale, of mica flotation ('natural flotation'). The study targeted the three most influential factors in flotation; i.e. the pulp pH, the consumption of cyanide (NaCN), and the particle size (d₈₀). The main effects and interactions of these factors on the flotation responses will be determined and modelled to find the optimum operating conditions, with the aim of selectively removing the mica minerals from galena, sphalerite, and chalcopyrite.

To achieve this goal, the response surface methodology (RSM) and the desirability functions were applied. RSM is a collection of statistical and mathematical techniques useful for the modelling and analysis of problems in which a response of interest is influenced by several variables and the objective is to optimize this response (Anderson and Whitcomb, 2000).

In this study the central composite design (CCD) was used extensively in building the second-order response surface models. CCD has been successfully used to design an experimental programme to provide data to model the effects of operating factors and cyclone geometry on the operational performance of a three-product cyclone (Obeng, Morrell, and Napier-Munn, 2005).

 

Experimental

Material and methods

Bench-scale flotation tests were carried out on a representative sample of the complex sulphide ore from MCG's Draa Sfar mine (Marrakech, Morocco). The ore used was the same as that used by Abidi et al. (2014) and Boujounoui et al. (2015, 2018, 2019). It was composed of sphalerite, galena, chalcopyrite, pyrrhotite, and gangue minerals consisting mainly of quartz, talc, chlorite, calcite, siderite, and ankerite.

A representative sample of 150 kg was taken from the feed belt of the primary ball mill at the flotation plant and crushed to 2 mm using laboratory roll crushers. The crushed sample was stored in vacuum-sealed bags to prevent oxidation of the sulphide minerals.

Prior to the flotation tests, samples of 500 g were milled in 250 ml of Marrakech drinking water using a Denver carbon-steel ball mill. The size fractions studied in this work were d₈₀ = 60, 120, and 180 μm.

Flotation experiments

Flotation tests were carried out on 500 g samples of milled ore using tap water in a Denver flotation cell with a capacity of 1.5 liters. The initial solid concentration was approximately 27% by weight. The impeller rotation speed was fixed at 1000 r/min. NaOH: was used as a pH regulator, with NaCN: as a depressant for sphalerite, chalcopyrite, and, pyrrhotite, and methyl isobutyl carbinol (MIBC) as frother (40 g/t).

The flotation time was 9 minutes for each test and the concentrates were recovered by automatic scraping every 30 seconds. The level of the pulp was constantly adjusted by water addition. The concentrate and tails were filtered, dried, weighed, and analysed by atomic absorption spectroscopy for Cu, Pb, Zn, Fe, SiO₂, Al₂O₃, and MgO. Elemental recoveries to the concentrates were calculated according to the following equation:

where R (%) is the recovery, t_C(%) is the concentrate element grade, t_f(%) is the feed metal grade; C is the concentrate weight, and A is the feed weight.

Talc and chlorites ('mica minerals') recovery was calculated as:

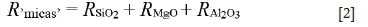
In this equation mica recovery could be overestimated due to the recovery of quartz by entrainment. However, this will not affect the target of the separation, i.e. removal of all the gangue.

Design of experiments

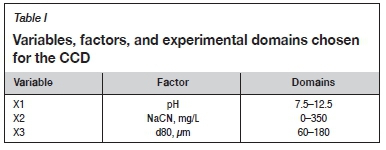
In order to determine the optimum operating conditions concerning mica flotation, and the corresponding metal losses (Pb, Cu, and Zn) in this step, the response surface methodology (MRE) (Bagaoui et al., 2002; Ennaciri et al., 2014; Boujounoui et al., 2018) was applied. This method allows the search for the optimum settings of the factors to achieve a desired response. Central composite design (CCD) was used to assess the relationship between the three more influential factors (X₁, X₂, and X₃) in mica flotation (i.e. pH, NaCN, and particle size) and the studied responses - the recoveries of micas (Y1, R_(Micas)), galena (Y2, RPb), chalcopyrite (Y3, RCu), and sphalerite (Y4, RZn). It consists of the following parts:

(1) A full factorial or fractional factorial design

(2) An additional design, often a star design in which experimental points are at a distance from the centre

(3) A central point (Mehrabani et al., 2010).

The number of experiments (N) for CCD is established according to the following relationship:

with N the number of tests, K the number of factors, and n the centre tests.

In this study, the three factors and five center tests correspond to 19 tests to be performed.

A second-order polynomial model was used, which contains only the terms (bi) and (bij) that will reflect the different effects (main and interactions) of factor on the four studied responses (Y1, Y2, Y3, and Y4).

The model can be written following Equation [4]:

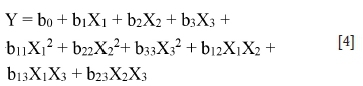
where

Y: studied response

X_i·: investigated factor (i varies from 1 to 3) b₀: a constant

b_i: main effect of the factor ii

b_ijinteraction coefficients between factors i and j

The CCD was processed by Nemrodw Software (Mathieu et al., 2000), in which the experimental sequence was randomized in order to minimize the effects of the uncontrolled factors. The CCD and the corresponding experimental conditions and responses are given in Tables I and II.

 

 

Results and discussion

The results in Table II show that mica recovery vary between 37% and 78% and the metals losses between 26% and 67% for lead, 16% and 55% for copper, and 13% and 27% for zinc.

The estimation coefficients of the postulated model (Equation [4]) were determined by the least-squares method. The interpretation of the coefficients, main effects of factors (b), and interaction effects (bj was done using statistical tests on the coefficients by using the estimated variance from replicates and Student's test (ta/2,d) (Boujounoui et al., 2015, 2018). Factors considered statistically significant are those with a significance level higher than 95% (p-value < 0.05). Positive coefficients (b_i or b_ij) indicate that the variables increase the studied response (Yi), and negative coefficients a decrease.

The considered mathematical models were validated using analysis of variance (ANOVA), F-test, and also checked by the correlation coefficient (R²) (Haider and Pakshirajan, 2007). When the values of R² are close to unity, the model offers an appropriate explanation of the variability of experimental values with respect to the predicted values (Liu and Wang, 2007). An adjusted determination coefficient (R²_Adj) was used as a measurement of the proportion of the total observed variability described by the model. After validation, the different models were used to graphically represent the response surfaces in the domain of interest (iso-response curves) to interpret the results (Boujounoui et al., 2018).

Analysis of Y responses

Factor effects and coefficients estimation

The coefficients estimated from the results obtained are displayed in Table III

 

 

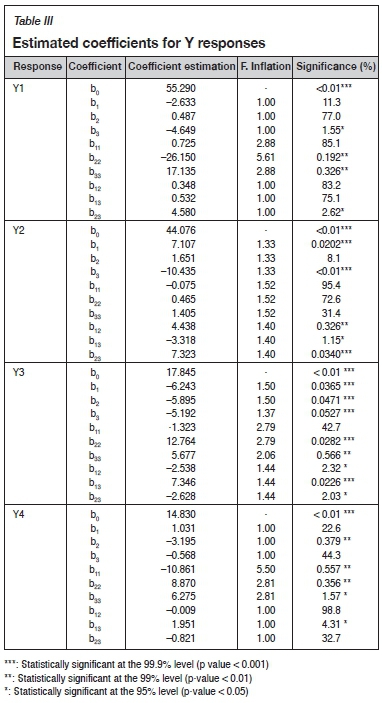
For Y1: The analysis of the different effects shows that the particle size (b₃ = -4.649) has a significant effect on the mica flotation (with a significance level of 95% (p-value 0.05). Furthermore, the more significant interaction effect (with a significance level of 95% (p-value < 0.05) is NaCN/particle size (b₂₃ = 4.580). From these results, the mica recovery can be described by the following model (Equation [5]):

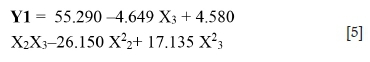
The mica recovery model presents a high determination coefficient R² = 0.91, explaining 91% of the variability in the response. The adjusted determination coefficient (R²_Adj = 0.80) and F-test = 7.97 were also satisfactory and confirmed the significance of the model.

For Y2: The pH (b₁ = 7.107) and particle size (d₈₀) (b₃ = -10.435) have a significant direct effect (with a significance level of 99.9%, p-value < 0.001) on the galena recovery. The pH favours losses of galena (Pb); on the other hand, the particle size (d₈₀) reduces the losses of Pb at the mica flotation stage. As regards the interactions between factors, the more significant interaction effect is NaCN/particle size (d₈₀) (b₂₃ = 7.323) followed by the pH/NaCN (b₁₂ = 4.438), and finally the interaction pH/ d₈₀(b₁₃ = -3.318). The galena recovery (response Y2) can be described by the following model (Equation [6]):

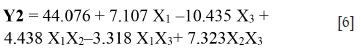
The correlation between the theoretical and experimental responses, calculated according this model, is satisfactory (R² = 0.98, R²_Adj = 0.97, and F-test = 50.28) (Sayyad et al., 2007).

For Y3: All factors (X₁, X₂ and X₃) are involved in different interactions. The most significant interactions are pH/d₈₀ (b₁₃ = 7.346), pH/NaCN (b₁₂ = -2.5381) and NaCN/d₈₀ (b₂₃ = -2.628). The mathematical model describing the response R_(Cu) (Y3) as a function of the significant factors can be written as follows (Equation [7]):

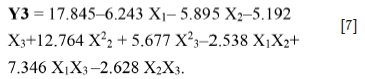
The correlation between the theoretical and experimental responses, calculated by the model, according to R² = 0.99, R²_Adj = 0.97, and F-test = 6.42, is satisfactory.

For Y4: The factor NaCN (b₂ = -3.195) has a significant effect on the sphalerite recovery (Zn), with a significance level of 99% (p-value < 0.01. Furthermore, the more significant interaction effect, with a significance level of 95% (p-value < 0.05), is pH/ particle size (b₁₃ = 1.951).

From these results, the sphalerite recovery can be described by the following model (Equation [8]):

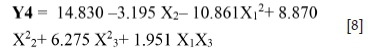
The sphalerite recovery model presents a high determination coefficient R² = 0.90, explaining 90% of the variability in the response. The adjusted determination coefficient (R²_Adj= 0.76) and F-test -4.48 were also satisfactory and confirmed the significance of the model.

Three dimensional (3D) responses surfaces and isoresponse curves

In order to visualize the relationship between the response and experimental levels of each variable, and the type of interactions between the variables, in order to deduce the operating conditions leading to optimal response (Tanyildizi, Ozer, and Elibol, 2005; Vazifeh, Jorjani, and Bagherian, 2010; Ebadnejad, Karimi, and Dehghani, 2013; Boujounoui et al., 2018), three-dimensional (3D) response surface and isoresponse curves were used. The objective is to maximize the selectivity of mica flotation over metallic elements such as Pb, Cu, and Zn.

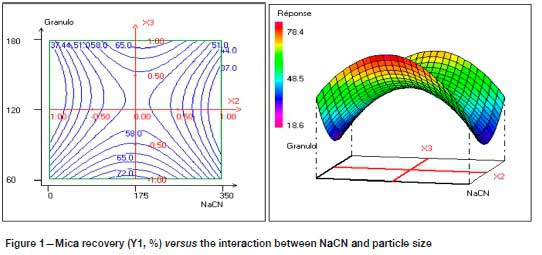
Figure 1 represents the variation in mica flotation according to the interaction NaCN (X₂) and particle size (d₈₀) (X₃), and shows that the effect of particle size on mica flotation depends on NaCN consumption. Indeed, the increase in cyanide consumption with a small particle size (d₈₀ = 60 μm) allows a maximum recovery of mica (Y1 > 65%). On the other hand, at a particle size of 180 μm the response is Y1 < 65%.

 

 

Figures (2a) and (2a') show that low galena recovery (Y2 < 36%) can be obtained when the consumption of NaCN (X₂) is maximal (220-350 g/t) and the pH value (X₁) a minimum (7.5-8). Increasing the pH to 12.5 with maximum cyanide consumption increases lead recovery (Y2 > 51%). This suggests that the alkaline pH favours lead flotation (Fornasiero and Ralston, 2006; Chandra and Gerson, 2009). On the other hand, cyanide has no action on the lead depression (Seke, 2005).

Figures 2b and 2b' show that the minimum lead recovery is obtained for a d₈₀ (X₃) between 150 and 180 μm and pH (X₁) between 7.5 and 9. The pH increase with decreasing particle size ( d₈₀) gives a maximum lead recovery, because the basic pH and the fragility of galena favour its flotation even in the absence of the collector (Seke, 2005). Figures 2c and 2c' also show that the lead recovery is minimal when the particle size (d₈₀0) (X₃) is between 150 and 180 μm and consumption of NaCN (X₂) is low.

Thus, to minimize the loss of Pb in the mica circuit, it is necessary to work at a d₈₀ of 150-180 μm, a moderately alkaline pH value (7.5-9), and low consumption of cyanide.

Figures 3a and 3a' show the 3D response surface curve for chalcopyrite (Cu) recovery (Y3) versus the interactions X₁X₃ (pH/d₈₀), X₁X₂ (pH/NaCN). It is obvious that a low chalcopyrite recovery could be achieved with an increase in particle size (d₈₀) and pH. Figures 3b and 3b' show that the low chalcopyrite recovery is obtained the higher levels of NaCN consumption (175-350 g/t) and pH between 11 and 12.5.

Generally, sodium cyanide is a depressant of chalcopyrite (Coetzer, du Preez, and Bredenhann, 2003; Seke, 2005; Lefèvre and Fédoroff, 2006; Ikumapayi, Johansson, and HanumanthaRao, et al. 2010, and this effect is more apparent at average concentrations.

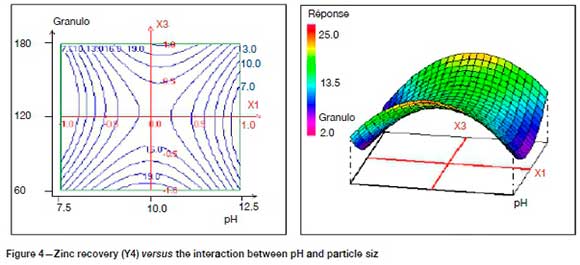
Figure 4 shows the response surface curve of Zn recovery (Y4) as a function of interaction X₁X₃ (pH/ d₈₀). It is found that the effect of particle size (d₈₀) on sphalerite flotation depends on pH. Indeed, the minimal recovery of Zn (< 13%) is reached at the extreme ranges of pH (X₁) and particle size (X₃).

 

 

Multi-criteria optimization using desirability function

To reach the targeted mica flotation and selectivity with respect to lead, copper, and zinc in the mica circuit, (Y) responses were simultaneously optimized by using the desirability functions approach to determine an acceptable compromise zone (Derringer and Suich, 1980). This method first converts each estimated response Y_i into an individual scale-free desirability function d_i that varies over the range of zero outside of the desired limits (if Y_i(x) < Y_i; min.) to unity -the target (desired) value (if Y_i(x) > Y_i; max.) where Y_i; min. and Y_i; max. are the lower and upper acceptability bounds for response i, respectively (Boujounoui et al., 2018). Once the function d_i (partial desirability of response Y_i) is defined for each response of interest, an overall objective function (D), representing the global desirability function, is calculated by determining the geometric mean of the individual desirabilities. Therefore, the function D over the experimental domain is calculated using Equation [9] as follows (Bruns, Scarminio, and de Barros Neto,. 2006):

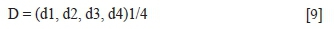
The maximum of the function D gives the best global compromise in the studied domain and corresponds to optimal experimental conditions.

The low and target values assigned to each goal and the partial desirability associated to the four responses are shown in Table IV The targeted value of mica recovery is 100%, and zero for galena, chalcopyrite, and sphalerite. The minimal acceptable value for mica recovery is 50%, and 25% is the maximal acceptable value for galena, chalcopyrite, and sphalerite recovery.

The global desirability function D was calculated using the Software NemrodW®, yielding a global degree of satisfaction for the four responses of 22%. The response surface corresponding to the global desirability function D is presented as contour and three-dimensional plots. It can be seen from Figure 5 that the acceptable compromise domain for better recovery of mica and low recoveries of galena chalcopyrite, and sphalerite was where pH values vary between 7.5 and 8.5, with average consumption of NaCN and a high particle size d₈₀of 160-180 μm.

The maximum recovery of mica (53%) and low recoveries of galena (28%), chalcopyrite (16%), and sphalerite (11%) were obtained with the optimal experimental conditions of pH 8, consumption of NaCN 180 g/t, and particle size d₈₀ of 180 μm.

To validate these results and to check the proposed model, three additional flotation tests were carried out under the predicted optimal operating conditions (pH = 8; NaCN: 180 g/t; d₈₀: 180 μm; test duration: 9 minutes; impeller rotation speed:

1000 r/min). The results, as well as the corresponding values calculated by the proposed model, are reported in Table IV It can be seen that the deviation between the experimental and the predicted values is lower than 5%, indicating the good accuracy of the model.

 

Conclusions

Central composite design, response surface methodology, and multi-criteria optimization using desirability functions were used to optimize the flotation of chlorite and talc ('mica') and minimize the loss of valuable metals (Pb, Cu, Zn) when there is a need to float the micas prior to the current process at CMG. The modelling and optimizing study, which concerned particle size, pH, and the amount of NaCN, indicated the following:

> Better recovery of micas and low recoveries of galena, chalcopyrite, and sphalerite were obtained at a moderately alkaline pH, average consumption of NaCN, and a high particle size (d80)

> Optimal operating conditions in this stage were: pH 8, 180 g/t NaCN consumption, and particle size d₈₀ of 180 μm. At these conditions, mica recovery was 53%, and valuable metals losses were Pb 28%, Cu 16 %, and Zn 11%.

> Flotation tests carried out with the optimal predicted operating conditions resulted in responses close to those calculated by the proposed model.

 

Recommendations

According to this study, the losses of Pb, Zn, and Cu in the mica circuit are high (especially for Pb), probably due to entrainment and not to true flotation.

Further studies should be undertaken to reduce these losses by (1) treating the mica concentrate to minimize Pb, Zn, and Cu losses in the final tailings, (2) focusing on the grinding-classification circuit in order to reduce the production of ultrafine particles, and (3) optimizing the hydrodynamic parameters within the flotation cells (agitation, air flow, and pulp density).

 

Acknowledgments

The authors thank the Mining Company of Guemassa for providing the sulphide ore sample and flotation reagents, and Reminex Society for the chemical analyses.

 

Compliance with ethical standards

The authors declare that they have no conflict of interest.

 

References

Akhanazarova, S. and Kafarov, V. 1982. Experiment Optimization in Chemistry and Chemical Engineering. Mir Publishers, Moscow.         [ Links ]

Anderson, M.J. and Whitcomb, P.J. 2000. DOE simplified: Practical tools for effective experimentation. Productivity Inc. Portland, OR.         [ Links ]

Abidi, A., Elamari, K., Bacaoui, a., and Yacoubi, A. 2014. Entrainment and true flotation of a natural complex ore sulphide. Journal of Mining Sciences, vol. 50. pp. 1061-1068.         [ Links ]

Abidi, A. 2016. Flottation des minerais sulfurés complexes: Cas de Draa Lasfar (Maroc). Thesis, Université Caddi Ayyad, Faculté des Sciences Semlalia, Morocco.         [ Links ]

Abidi, A., Boujounoui, K., El amari, K., Bacaoui, A., and Yacoubi, A. 2019. Contribution to improve water process recycling in the flotation plant of a complex Zn-Pb-Cu sulphide ore. Journal of Mining Sciences, vol. 55, no. 4. pp. 658-667.         [ Links ]

Box, G.E.P., Hunter, W.G., and Hunter, J.S. 1978. Statistics for Experiments. Wiley, New York.         [ Links ]

Baçaoui,A., Dahbi, A., Yaacoubi, A., Bennouna, C., Maldonado-HoädarF, Rivera-Utrilla, J., Carrasco-Marin, f., and Moreno-Castilla, C. 2002. Experimental design to optimize preparation of activated carbons for use in water treatment. Environmental Science and Technology, vol. 36, no. 3. pp. 844-3849.         [ Links ]

Bruns, R.E., Scarminio, LS., and de Barros Neto, B. 2006. Statistical design chemometrics. Data Handling in Science and Technology, vol. 25. Rutan, S. and Walczak, B. (eds). 1st edn. Elsevier.         [ Links ]

Boujounoui, K., Abidi, A., Bacaoui, A., El Amari, K., and Yaacoubi, A. 2015. The influence of water quality on the flotation performance of complex sulphide ores: Case study at Hajar Mine. Morocco. Journal of the Southern African Institute ofMining and Metallurgy, vol. 115, no.12. pp. 1243-1251.         [ Links ]

Boujounoui, K. 2017. Optimisation du potentiel de recyclage de l'eau de procédé dans les circuits de flottation des minerais sulfurés complexes: Cas de Draa Lasfar Sud (Maroc). Thesis, Université Caddi Ayyad, Faculté des Sciences Semlalia, Morocco.         [ Links ]

Boujounoui, K., Abidi, A., Bacaoui, A., El Amari, K., and Yaacoubi, A. 2018. Flotation process water recycling investigation for the complex Draa Sfar sulphide ore, Morocco. Mine Water and the Environment, vol. 37, no. 1. pp. 75-87. https://doi.org/10.1007/s10230-017-0471-3        [ Links ]

Boujounoui, K., Abidi, A., Bacaoui, A., El Amari, K., and Yaacoubi, A. 2019. Effect of water quality on the performance of the galena and blend flotation: case of Draa Sfar complex sulphide ore, Morocco. Moroccan Journal of Chemistry, vol. 7, no. 2. pp. 337-345.         [ Links ]

Cilek, E.C. and Yilmazer, B.Z. 2003. Effect of hydrodynamic parameters on entrainment and flotation performance. Minerals Engineering, vol. 16. pp. 745-756.         [ Links ]

Coetzer, G., du Preez, H.S., and Bredenhann, R. 2003. Influence of water resources and metal ions on galena flotation of Rosh Pinah ore. Journal of the Southern African Institute ofMining and Metallurgy, vol. 103. pp. 193-207.         [ Links ]

Cao, M. and Liu, Q. 2006, Reexamining the functions of zinc sulfate as a selective depressant in differential sulfide flotation - the role of coagulation. Journal of Colloid and Interface Science, vol. 301, no. 2. pp. 523-531.         [ Links ]

Chandra, A.P. and Gerson, A.R. 2009. 'A review of the fundamental studies of the copper activation mechanisms for selective flotation of the sulfide minerals, sphalerite and pyrite. Advances in Colloid and Interface Science, vol. 145. pp. 97-110.         [ Links ]

Derringer, G. and Suich, R. 1980. Simultaneous optimization of several response variables. Journal of Quality Technology, vol. 12. pp. 214-219.         [ Links ]

Ebadnejad, A., Karimi, G.R., and Dehghani, H. 2013. Application of response surface methodology for modeling of ball mills in copper sulphide ore grinding. Powder Technology, vol. 245. pp. 292-296.         [ Links ]

Ennaciri, K., Baçaoui, A., Sergent, M., and Yaacoubi, A. 2014. Application of fractional factorial and Doehlert designs for optimizing the preparation of activated carbons from Argan shells. Chemometrics and Intelligent Laboratory Systems, vol. 139. pp. 48-57.         [ Links ]

Fornasiero, D. and Ralston, J. 2006. Effect of surface oxide/hydroxide products on the collectorless flotation of copper-activated sphalerite. International Journal of Mineral Processing, vol. 78. pp. 231-237.         [ Links ]

Haider, M.A. and Pakshirajan, K.K. 2007 Screening and optimization of media constituents for enhancing lipolytic by a soil microorganism using statically designed experiments. Applied Biochemistry and Biotechnology, vol. 141. pp. 377-390.         [ Links ]

Hibti, M. 2001. Les amas sulfurés des Guemassa et des jebilets témoins del'hydrothermalisme précoce Dans le bassin mésetien. Thèse de Doctorat d'état, Faculté des Sciences Semlalia, Marrakech.         [ Links ]

Hay, M.P. 2008. Optimising froth condition and recovery for a nickel ore. Minerals Engineering, vol. 21. pp. 861-872.         [ Links ]

Ikumapayi, F., Johansson, B., and HanumanthaRao, K. 2010. Recycling of process water in sulfides processing and flotation selectivity. Proceedings of the XXV International Mineral Processing Congress, Brisbane, Australia, 6-10 September 2010. Australasian Institute of Mining and Metallurgy, Melbourne. pp. 4079-4088.         [ Links ]

Lind, P., Yalcin, T., and Butcher, J. 2003. Computer simulation of the Bullmose coal preparation plant. Coal Preparation, vol. 23. pp. 129-145.         [ Links ]

Lefèvre, G., and Fédoroff, M. 2006. Sorption of sulfate ions onto hematite studied by attenuated total reflection-infrared spectroscopy: kinetics and competition with other ions. Physics and Chemistry of the Earth, vol. 31. pp. 499-504.         [ Links ]

Liu, G.C. and Wang, X.L. 2007. Optimization of critical medium components using response surface methodology for biomass and extra cellular polysaccharide production by Agaricus blazei. Applied Biochemistry and Biotechnology, vol. 74. pp. 78-83.         [ Links ]

Mathieu, D., Nony, J., and Phan Tan Luu, R. 2000. Software NEMRODW. LPRAI, Marseille, France.         [ Links ]

Martinez, A.L., Uribe, A.S., Carrillo, F.R.P., Coreno, J.A., and Ortiz, J.C. 2003. Study of celestite flotation efficiency using sodium dodecyl sulfonate collector: Factorial experiment and statistical analysis of data. International Journal of Mineral Processing, vol. 70. pp. 83-97.         [ Links ]

Mehrabani, J.V., Noaparast, M., Mousavi, S.M., Dehghan, R., and Ghorbani, A. 2010. Process optimization and modelling of sphalerite flotation from a low-grade Zn-Pb ore using response surface methodology. Separation and Purification Technology, vol. 72. pp. 242-249.         [ Links ]

Managem Group. 2014. Annual report, Casablanca, Morocco. http://www.managemgroup.com/en/investisseurs/managem/annual-reports        [ Links ]

Napier-Munn, T.J. 2012. Statistical methods to compare batch flotation grade recovery curves and rate constants. Minerals Engineering, vol. 34. pp. 70-77.         [ Links ]

Obeng, D.P., Morrell, S., and Napier-Munn, T.J. 2005, Application of central composite rotatable design to modelling the effect of some operating variables on the performance of the three-product cyclone. International Journal of Mineral Processing, vol. 76. pp. 181-192.         [ Links ]

Rao, G.V., and Mohanty, S. 2002, Optimization of flotation parameters for enhancement of grade and recovery of phosphate from low-grade dolomitic rock phosphate ore from Jhamarkorta, India. Minerals and Metallurgical Processing, vol. 19. pp. 145-160.         [ Links ]

Seke, M.D. 2005. Optimization of the selective flotation of galena and sphalerite at Rosh Pinah Mine. PhD thesis, University of Pretoria, South Africa.         [ Links ]

Sayyad, S.A., Panda, B.P., Javad, S., and Ali, M. 2007. Optimization of nutrient parameters for lovastatin production by Monascus purpureus MTCC 369 under submerged fermentation using response surface methodology. Applied Microbiology and Biotechnology, vol. 73. pp. 1054-1058.         [ Links ]

Tanyildizi, M.S., Ozer, D., and Elibol, M. 2005. Optimization of α-amylase production by bacillus sp. using response surface methodology. Process Biochemistry, vol. 40. pp. 2291-2296.         [ Links ]

Vazifeh, Y., Jorjani, E., and Bagherian, A. 2010. Optimization of reagent dosages for copper flotation using statistical technique. Transactions of Nonferrous Metals Society of China, vol. 20. pp. 2371-2378.         [ Links ]

Yalsin, T. 1999. Evaluation of Box-Wilson experimental design in flotation research. Transactions of the Institution ofMining and Metallurgy, vol. 108. pp. 109-112.         [ Links ]

 

 

Correspondence:
K. Boujounoui
Email: boujounoui.kh@gmail.com

Received: 19 Apr. 2020
Revised: 15 Oct. 2020
Accepted: 20 Oct. 2020
Published: December 2020