Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.119 n.12 Johannesburg Dec. 2019
http://dx.doi.org/10.17159/2411-9717/17/375/2020
GENERAL PAPERS
Monte Carlo analytic hierarchy process for selection of the longwall mining method in thin coal seams
C. WangI, II; S. YangI; C-Y. JiangI; G-Y. WuI; Q-Z. LiuI
ISchool of Mines, Guizhou University, China
IIState Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology, Xuzhou, China
SYNOPSIS
Mining method selection is one of the most important decisions to be made by mining engineers. To solve the decision-making problem regarding selection of the optimal longwall mining method for thin coal seams, we propose an approach that combines Monte Carlo simulation and the conventional analytic hierarchy process (AHP). Economic, technical, and ergonomic factors are taken into consideration in the process. With this approach, the confidence level of each method's score, as calculated by AHP, is determined by Monte Carlo simulation. The proposed approach is applied to a panel in Liangshuijing coal mine in China and the appropriate mining methods for this panel are ranked.
Keywords: mining method selection, thin coal seam, Monte Carlo simulation, AHP, confidence level.
Introduction
The reserves contained in thin coal seams (less than 1.3 m in thickness) in China are enormous. The recoverable reserves in these seams are about 6.5 Gt, accounting for 19% of the total recoverable coal reserves (Wang and Tu, 2015). As the result of the historical mining method focusing on thick seams, the mineable reserves of these seams are depleted in eastern China. In order to increase the mineable reserves, it is of great importance to exploit thin seams in many coalfields, such as Zibo, Datong, Hancheng, Handan, and Yulin.
There are two major fully-mechanized longwall mining methods for thin seams: one method uses a coal shearer and the other one a coal plough (Wang et al., 2016). Each method has its advantages and disadvantages. This paper is focused on the decision-making process for choosing between these two methods.
The factors to be considered in deciding on the mining method include geological, economic, technical, and ergonomic factors. Decision-makers therefore have always some difficulties in making the right decision. Mining method selection is one of the multiple attribute decision-making (MADM) problems (Alpay and Yavuz, 2009).
Previous research
A large amount of research has been conducted on mining method selection. Alpay and Yavuz, 2009, developed a computer program for underground mining method selection based on the analytic hierarchy process (AHP) and Yager's method. This method can be used to select the best underground mining method for different deposit shapes and orebodies. Using the fuzzy cluster, AHP, and Delphi, Tan et al. (2014) obtained the ideal evaluation results in the primary selection of mining method. To select a mining method for a given orebody Guraya et al. (2003) developed a technique based on 13 different expert systems and one interface agent, which an inexperienced user can utilize to extend his/her knowledge about mining method selection. The technique for order preference by similarity to ideal solution (TOPSIS) method (Wang et al., 2013), principal component analysis and neural networks (Chen et al., 2010), the unascertained measure model (Yang, Deng, and Feng, 2014), the double base points and value engineering methods (Xiang, Zhang, and Guo, L. 2000), and fuzzy statistical and grey relational analysis (Gao and Yang, 20010 have been successfully applied for mining method selection.
For selecting the optimal mining method for thin seams, Lv (2010) developed an expert system using a neural network. Geological, human, and technical factors were considered in the system; however, the effects of economic factors were ignored during the decision-making process. No other research on the selection of thin seam mining methods is readily available in the literature (Wang, 2016).
Multi-attribute and multi-objective decision model
In general, selection of the mining method for thin seams proceeds in two stages, as shown in Figure 1. As the focus of this study, a detailed optimal selection process is performed mathematically in stage 2 on the basis of the primary selection in stage 1. By correlation analysis, a decision-making index system for selecting the optimal mining method is established in stage 2. The system is divided into four layers: the Goal (G) layer is selection of the optimal mining method; the Criteria (P) layer and the Indicator (C) layer; the Alternative (A) layer consists of the two alternative mining methods involving the shearer (A1) and plough (A2) (Wang et al., 2016).
Monte Carlo analytic hierarchy process approach
The analytic hierarchy process (AHP), proposed by operational research scientist T.L. Saaty (1980), is a decision-making tool incorporating qualitative and quantitative analysis. Based on the decision index system for mining method selection outlined above, the AHP is applied to assign weights for each criterion. The process normally includes three steps: constructing the hierarchy judgment matrices, calculating the hierarchy relative weights, and checking the consistency of the judgments (Alpay and Yavuz, 2009).
Generally, the traditional AHP approach uses an exact value to express the decision-maker's opinion in the comparison of alternatives. It has been criticized because of the unbalanced scale of judgments, inability to handle the inherent uncertainty adequately, and imprecision in the pairwise comparison. Moreover, agreement or disagreement between decision-makers about the element in the pairwise matrix is not considered in this approach. To overcome these shortcomings the MAHP approach, which combines a Monte Carlo simulation and the AHP method, is proposed.
In the MAHP method, the decision-maker's opinion can be expressed in the final results, and the effect of this opinion on the results can be ascertained. The confidence level allocated to the score for each alternative can be determined with respect to the variance of the decision-maker's opinion. For thin seam longwall mining method selection, the MAHP method is applied as outlined in Figure 2.
As shown in Figure 2, the alternative mining methods and indicators are gathered in stage 1. Then, Monte Carlo simulation is performed in stage 2. A 3D matrix with respect to all decision-makers' opinions is constructed, as shown in Figure 3. Two dimensions of this matrix express the number of criteria (n), and the third dimension is the number of decision-makers (k), which is equal to the number of the 2D pairwise matrices. The cumulative distribution function of each pairwise matrix array is determined. A sample between 0 and 1 is generated and the regard values of this sample are calculated from the cumulative distribution function. The consistency of the 3D matrix should be checked before the pairwise matrix is determined. In the last stage, the score of each alternative and its distribution function are calculated using the traditional AHP process (Alpay and Yavuz, 2009).
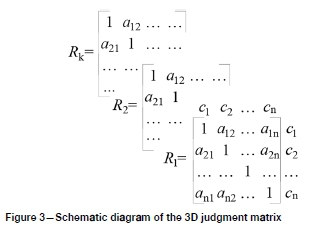
In the study, the MAHP approach with 10 indicators and 60 decision-makers is used. One of these pairwise comparisons matrixes is shown as an example:
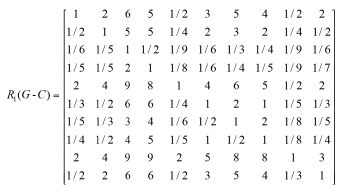
Monte Carlo simulation results
In the 3D matrix shown above, the array in the pairwise matrix is a kind of discrete random variable. Its probability distribution can be illustrated as shown in Table I. Then the array cumulative distribution can be determined.

The probability is pkwhen the value of the array X is xk(k = 0,1,...), as follows:
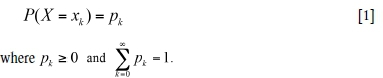
Then Monte Carlo simulation is performed (Rubinstein and Kroese, 2008): extracting a random number r obeying (0,1) uniform distribution; the sampling value of the discrete random variable X is xn, where
Taking array a12 as an example, its probability distribution is shown in Table II.
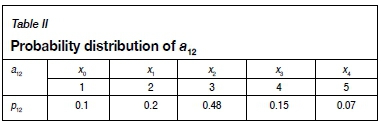
Then its cumulative distribution can be expressed as:
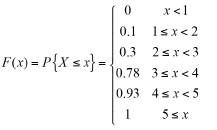
Then Monte Carlo simulation for array a12 is performed (Rubinstein and Kroese, 200: extracting random number r obeying (0,1) uniform distribution; the sampling value of the discrete random variable a12is shown in Table III.
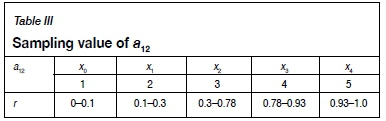
Random number r is defined as the input variable, and weight vector W and consistency criterion CRare defined as output variables. Crystal Ball (Wang, 2016) was applied to the Monte Carlo simulation with 3000 iterations. The weight probability and frequency distribution of each criterion was obtained, as shown in Figure 4a-j. At the same time, the consistency criterion CRof the judgment matrices was checked to measure its credibility, as shown in Figure 4k-l.
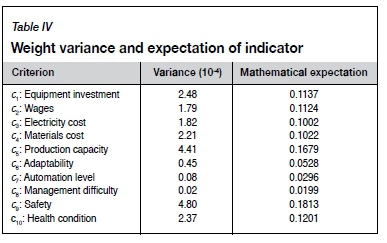
As the most important criterion, the safety criterion is assigned a weight of 0.1813. The weight vector W is W = (0.1137, 0.1124, 0.1002, 0.1022, 0.1679, 0.0528, 0.0296, 0.0199, 0.1813, 0.1201)T. The statistics from Monte Carlo simulation are shown in Table IV. Consistency index of less than 0.1 accounted for up to 89.87% (Alpay and Yavuz, 2009). The consistency of the matrix is considered to be acceptable and the weight vectors are credible.
Alternatives ranking
With respect to the alternative longwall mining methods, adaptability (c6), automation level (c7), management difficulty (c8), safety (c9), and health condition (c10) are the qualitative indices. Monte Carlo simulation was applied to determine their importance. The weight of the qualitative indices to the target layer was calculated as shown in Table V.
However, the quantitative index should be treated in another way. The quantitative index is divided into cost indices such as equipment investment wages (c2), electricity cost (c3), materials cost (c4), and the benefit index, including production capacity (c5). A judgment matrix about these indices can be constructed on the basis of their attribute values. The larger the benefit index and the smaller the cost index, the better the alternative. According to the values of these indices, the importance of the alternatives can be determined. Suppose alternative set a = [A1, A2, L, Am] is composed of m alternatives A1, A2,..., Am, and quantitative indicator set C including l quantitative indicators s1, s2,..., sk,..„ sl.. The pairwise judgment matrix Dsk (k =1,2,..., m) with respect to these indicators can be expressed as:

where bijk (i = 1,2,..,m;j = 1,2,.. m;) is the importance degree of alternative Airelative to Ajwith respect to the quantitative indicator sk.
The pairwise judgment matrix Dskshould be transformed from attribute value matrix Amxl of the quantitative indicator layer. For unification, the cost index is converted into the benefit index in Dsk. Supposing attribute value matrix Amxl is:
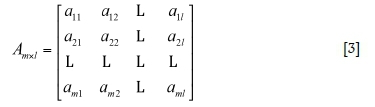
where aij (i = 1,2,...,m; j = 1,2,...,l;) is the value of quantitative indicator sjto alternative Ai, which can be obtained from field measurements. Assuming aij= aij-, and aij= 1/aijfor the benefit index and cost index, respectively, then intermediate matrix Amxl can be transformed from the value matrix Amxl:
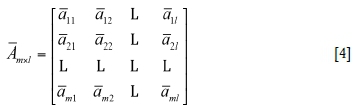
where aij (i = 1,2,...,m;j = 1,2,...,l;) is the transformed value of quantitative indicator sj to alternative Ai-. All elements in the matrix Amxl are benefit indices. Then the importance degree bijk of the alternative Aito Ajabout the quantitative indicator skcan be expressed:

Then the pairwise judgment matrix Dskcan be transformed into:
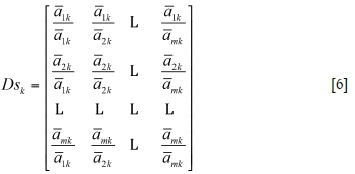
The judgment matrix Dskis a positive reciprocal matrix, which can meet the requirements of comparison in the AHP. Therefore, the ranking of alternatives can be calculated using the traditional AHP method.
Engineering verification
The Monte Carlo AHP and traditional AHP methods have been tested using 12 examples of thin seam mining in China. The Monte Carlo AHP method was validated in all thin seam working faces investigated. The precision of the MAHP predictions was 100% when compared to the actual applications. However, only 8 of 12 examples could be validated using traditional AHP. The precision of traditional AHP was only about 66.7%, as shown in Table VI. Compared with traditional AHP, the Monte Carlo AHP method has more adaptability and precision in selection of the optimal mining method.
Engineering application
Engineering geological conditions
Selection of the optimal mining method for panel 43101 in Liangshuijing coal mine, Yulin City, Shaanxi Province is used as an example. The no. 4-3 coal seam is the primary mineable seam, with an average thickness of 1.2 m and a dip of 1°. Fully mechanized full-height mining was adopted in the panel. That is to say, the average mining height is 1.2 m. The panel was designed to be 150 m long. Based on the geological evaluation and cluster analysis, the fully mechanized longwall mining method was selected in the primary selection. However, there was still no agreed optimal mining method for the seam.
Mining method selection
In the selection process, the quantitative indicators were quantified through field research at panel 43101, as shown in Table VII.
According to the value of these quantitative indices, the attribute value matrix Amxl can be obtained and expressed as:
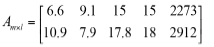
Then the intermediate matrix Amxlcan be calculated and expressed as:
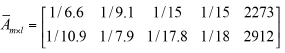
The weight vector w1, w2 of these quantitative indices with respect to alternative A1, A2 respectively can be obtained as follows:

Combining the weight vector of the qualitative indices with w1and w2, the weight w the alternative to indicator layer can be obtained. Weight vectors W and w were defined as input variables and alternative ranking results were defined as output variables. Crystal Ball was applied to the Monte Carlo simulation with 3000 iterations. The distribution of ranking results for the alternatives is shown in Figure 5.
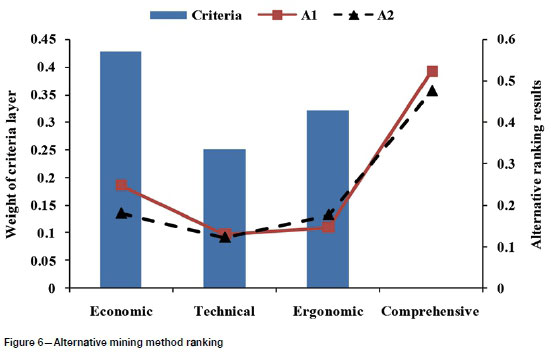
In economic terms, the interval of the evaluation score of A1 and A2 is (0.2040, 0.2992) and (0.1458, 0.2160), with mathematical expectations 0.2480 and 0.1799, respectively. The interval of value difference A1- A2 is (0.0497, 0.0871), which is consistently greater than zero. It is suggested that the mining method involving the shearer has a higher priority, the certainty of which is 100%.
In technical terms, the interval of the evaluation score of A1 and A2 is (0.0938, 0.1660) and (0.0800, 0.1602), with mathematical expectations 0.1298 and 0.1213, respectively. The interval of value difference A1- A2 is (-0.0080, 0.0871), in which the interval (0, 0.0871) accounts for up to 95%. It is suggested that the mining method involving the shearer has a higher priority, the certainty of which is 95%.
In ergonomic terms, the interval of the evaluation score of A1and A2is (0.1081, 0.1918) and (0.1290, 0.2364), with mathematical expectations 0.1447 and 0.1762, respectively. The interval of value difference A1- A2 is (-0.00446, -0.0218), which is less than zero consistently. It is suggested that the mining method involving the plough has a higher priority, the certainty of which is 100%.
Synthesizing the economic, technical, and ergonomic factors, the interval of the comprehensive evaluation score of A1 and A2 is (0.5094, 0.5413) and (0.4587, 0.4906) ,with mathematical expectations 0.5228 and 0.4752, respectively. The interval of value difference A1- A2 is (0.0189, 0.0825), which is greater than zero consistently. This indicates that the mining method involving the shearer will be the optimal method, the certainty of which is 100%. The rankings for alternative mining methods for panel 43101 in Liangshuijing coal mine are shown in Figure 6.
Conclusion
1. A multi-attribute decision model was developed for selecting the optimal mining method for thin coal seams. A total of 10 indicators encompassing economic, technical, and ergonomic criteria were selected for use in the evaluation, and their comprehensive weight vectors determined using Monte Carlo simulation.
2. Alternatives were ranked by traditional AHP, in which qualitative and quantitative indices are calculated separately. According to the engineering verification, the Monte Carlo AHP method has more adaptability and precision than traditional AHP.
3. The optimal mining method can be selected precisely using the MAHP technique. Using panel 43101 in Liangshuijing coal mine as an example, the ranking results and the certainty of the alternative mining methods for thin seam mining were calculated in terms of single and integral criteris.
Acknowledgments
Financial support for this work was provided by National Natural Science Foundation of China (No.51904081, No.51964008), First-class Professional Construction of Undergraduate Colleges in Guizhou Province (SJZY2017006), Guizhou Science and Technology Project (Platform talent of Qian Ke He[2018]5781), Funded by the Research Fund of The State Key Laboratory of Coal Resources and safe Mining, CUMT (SKLCRSM19KF010). Joint Funds of Department of Science & Technology of Guizhou Province and Guizhou University, Grant/Award Number: LH [2017] 7282. The authors gratefully acknowledge the financial support from the organizations mentioned above.
References
Alpay, s. and Yavuz, M. 2009. Underground mining method selection by decision making tools. Tunnelling and Underground Space Technology, vol. 24, no. 2. pp. 173-184. [ Links ]
Chen, J.H., Liu, L., Zhou, Z.Y., and Yong, X.-Y. 2010. Optimization of mining methods based on combination of principal component analysis and neural networks. Journal of Central South University, vol. 41, no. 5. pp. 1967-1972. [ Links ]
Gao, W. and Yang, L. 2001. Application of fuzzy synthetic evaluation method to geological conditions of fully mechanized mining. Systems Engineering Theory & Practice, no. 12. pp. 117-123. [ Links ]
Guraya, C., Celebia, N., Atalaya, V., Gunhan, A., and Pasamehmetoglu, G. 2003. Ore-age: a hybrid system for assisting and teaching mining method selection. Expert Systems with Applications, vol. 24, no. 3. pp. 261-271. [ Links ]
Lv, W. 2010. Research on the optimized selection of thin coal seam mining method and the optimization of mining face length. China University of Mining & Technology, Beijing. [ Links ].
Rubinstein, R.Y. and Kroese, D.P. 2008. Simulation and the Monte Carlo Method. Wiley. [ Links ]
saaty, T.L. 1980. The Analytic Hierarchy Process. McGraw-Hill, Pittsburgh. [ Links ]
Tan, Y., song, W., Li, T., and Zia, H. 2014. Application and research on consistency combination weights for mining method optimization by multi-objective decision. Journal of University of Science and Technology Beijing, vol. 36, no. 8. pp.1115-1122. [ Links ]
Xiang, W.A., Zhang, W.F., and Guo, L. 2000. Application of the similarity ratio value engineering method in optimization of mining method. Journal of Central South University of Technology, vol. 31, no. 4. pp. 94-96. [ Links ]
Yang, Y., Deng, X., and Feng, Y. 2014. Optimization of mining method based on uncertainty measurement theory and AHP. Journal of Central South University, vol. 45, no. 11. pp. 3936-3942. [ Links ]
Wang, X., Qin, J., Zhang, Q., Chen, W., and Chen, X. 2013. Mining method optimization of Gu Mountain stay ore based on AHP-TOPSIS evaluation model. Journal of Central South University, vol. 44, no. 4. pp. 1131-1137. [ Links ]
Wang, C. and Tu, s.H. 2015. Selection of an appropriate mechanized mining technical process for thin coal seam mining. Mathematical Problems in Engineering, vol. 2015. pp. 1-10. doi: 10.1155/2015/893232 [ Links ]
Wang, C., Tu, s.H., Chen, M., and Yuan, Y. 2016. Optimal selection of a longwall mining method for a thin coal seam working face. Arabian Journal for Science and Engineering, vol. 41, no. 9. pp. 3771-3781. [ Links ]
Wang, C. 2016. Key techniques and decision support system of automatic mechanised longwall mining face in thin coal seam. China University of Mining & Technology, Beijing. [ Links ]
 Correspondence:
Correspondence:
C. Wang
Email: cwang@gzu.edu.cn
Received: 15 Sep. 2018
Revised: 8 Mar. 2019
Accepted: 10 Oct. 2019
Published: December 2019














