Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of the Southern African Institute of Mining and Metallurgy
versão On-line ISSN 2411-9717
versão impressa ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.118 no.7 Johannesburg Jul. 2018
http://dx.doi.org/10.17159/2411-9717/2018/v118n7a7
PAPERS OF GENERAL INTEREST
Investigation and modelling of work roll temperature in induction heating by finite element method
L. BaoI; X-W. QiI; R-B. MeiI, II; X. ZhangI, II; G-L. LiIII
INortheastern University, Qinhuangdao, China
IIState Key Laboratory of Rolling and Automation,Northeastern University, China
IIIIronmaking Plant of Shougang Qian'an Iron and Steel Co Ltd, China
SYNOPSIS
An induction coil was designed successfully to heat a work roll online for hot or warm strip rolling. The surface temperature of the work roll was investigated through embedding a developed program into finite element (FE) software. A new model to describe the convective heat transfer coefficient between air and the work roll was proposed and the coefficient was obtained as a function of ambient and surface temperature. The influences of working frequency, source current density, air gap length, and coil distance on the mean and variance value of the surface temperature were investigated using the simulation results. The work roll surface temperature was significantly higher than that of the centre due to the skin effect. A longer induction heating time was beneficial for a more uniform temperature distribution on the work roll surface. The mean temperature increased exponentially with increased working frequency and coil distance. However, the mean temperature decreased with increased air gap between the coil and work roll surface. The mean value increased following a power function with increases in source current density, and increased linearly with induction heating time after the initial heating stage. A new formula was proposed and implemented to predict the mean work roll temperature based on induction heating parameters in order to control the surface temperature. The results predicted by the model agree well with measured values and the model proposed is reliable. Furthermore, the proposed equation is beneficial for calculating and controlling the value of any one influencing parameter, if the other three parameters and the ideal mean temperature of induced heating are known.
Keywords: finite element method, induction heating, temperature, work roll, strip rolling.
Introduction
Hot and warm rolling technology has been used widely to produce various metal strip products since 1880, when Japan first began steel production (Ataka, 2014). In hot rolling, the workpiece is usually heated in a furnace and the temperature decreases significantly during the subsequent slab or strip rolling process. The decreased surface temperature may cause non-uniform deformation and crack generation, especially in metals with poor plastic deformability, such as magnesium and high-silicon steel. Fischer and Yi, (1964) first proposed a rolling method with heating of the work roll to 538°C to avoid the rapid decrease in strip temperature. The advantage of rolling mills with heated equipment compared to conventional rolling mills was also discussed in detail. Cr3C2 was used as the roll sleeve and steel as the main body of the work roll (Fischer and Yi, 1964). After that, methods and equipment for rolling with a heated work roll were proposed and designed by different researchers (Kang, Wang, and Lv 2005; Zhang, Wang, and Wang, 2008; Li et al., 2012) in order to avoid surface oxidation and improve the plastic deformation limit of hard-to-form materials. The preheated work roll is significantly helpful for large plastic deformation and grain refinement. Jeong and Ha (2007) discussed the influence of the work roll temperature, initial thickness, thickness reduction, rolling temperature, and rolling velocity on the microstructure and texture of AZ31 magnesium alloy during warm rolling. No cracks were found in the strip with a reduction of 30%, rolling velocity of 30 m/min, rolling temperature of 200°C, and work roll temperature of 110°C. Furthermore, the grain size was refined significantly with a singlepass 50% reduction after preheating of the work roll. Kim et al. (2014) used a preheated work roll to realize continuous high-ratio differential speed rolling, maintaining the strip temperature within an ideal range for large plastic deformation and dynamic recrystallization. This method refined the grain size of the workpiece from 11.1 μm to 2.3 μm.
In the previous work, the resistance heating method was mainly used to heat the work roll. The lower heating efficiency of the resistance heating method causes difficulties in application to online rolling. Induction heating is widely used in hot or warm rolling processes (Lainati, 2015) because it offers high efficiency and heating rates (Davies, 1990). In order to assess the possibilities of obtaining the required parameters of induction heating, Barglik (2011) carried out three-dimensional analysis of electromagnetic and temperature fields in a transverse flux induction heater for thin strips using the finite element method (FEM) and compared the calculated results with the measured data. Ross (2003) investigated different solenoidal and transverse flux heating methods for strip heating and discussed their application to galvanizing and strip preheating based on experimental data. The higher heating efficiency and no need to make direct contact with the work roll are beneficial to rapid online heating and rolling processes. In order to optimize embossing process, a chiller-equipped heating roll system was developed by Kim et al. (2014). The work roll surface was heated by induction and the temperature was controlled using a temperature-margin-based control algorithm and the measured temperature. New heating equipment for the work roll using induction heating was designed and used in hot and warm rolling by Mei et al. (2016). Complete dynamic recrystallization occurred and ultrafine grains were obtained successfully after three passes of rolling with a cold strip and the heated work roll. However, many factors have an important influence on the temperature of the work roll, leadings to difficultly in controlling temperature in induction heating.
Numerical simulations are widely used to solve nonlinear problems, including thermal analysis to improve the accuracy of the predicted and controlled temperature. Local temperature variations induced in both longitudinal and transverse flux induction heaters were studied by Blinov et al. (2011). The temperature of a strip of AZ31 magnesium alloy during strip rolling with a heated work roll was analysed based on the thermal-structural numerical simulation (Mei et al., 2016). The temperature of the cold strip was increased to approximately 200°C after one rolling pass under the conditions of a work roll temperature of 300°C, initial thickness of 2 mm, 20% reduction, and rolling speed of 0.1 m/s. Yu et al. (2012) discussed the changes in strip temperature during AZ31 alloy rolling with a heated work roll and cold strip, and proposed a new model to predict the exit temperature of the strip. Induction heating at different frequencies was investigated by FEM and the calculated results agreed well with the experimental measurements. The transient temperature field of a heated strip or slab was simulated based on the coupled electromagnetic-thermal FEM (Mei et al., 2008, 2010). FEM simulations and experiments were performed to analyse edge defect generation in plate rolling; and it was proposed that increasing the temperature of the edge zone of the slab by induction heating could reduce the possibility of corner crack formation (Pesin and Pustovoytov, 2015). Cai et al. (2013) introduced the idea of warm rolling with a work roll heated by the induction heating method and analysed the temperature distribution of the work roll using a 2D FE model and the heat generation model proposed by Mei et al. (2010).
In the current work, the temperature distribution of the work roll was investigated during induction heating through an FEM 2D coupled electromagnetic-thermal analysis, giving detailed boundary conditions, FE mesh, and a flow chart of the program. The effects of various induction heating parameters, including working frequency, air gap between the coil and work roll surface, source current density, and distance between two coils, on the temperature were studied after changing the mean and variance of temperature based on the simulation results. Subsequently, a new model was proposed to predict the temperature of the work roll surface according to linear fitting and nonlinear induction, and the data predicted by the model was compared with the results calculated by FEM. Lastly, the model was verified by comparing the experimental data and simulation results. This study may be helpful in improving modelling methodology to simulate the work roll temperature in induction heating and accurately control it during roll processing.
FE Modelling
Initial and boundary conditions
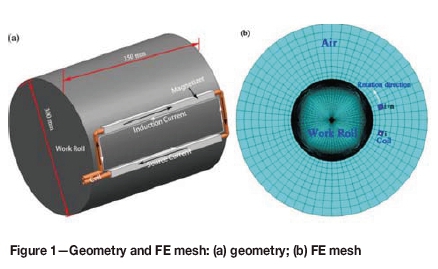
The parameters of the work roll were the same as those of the experimental rolling mill used to analyse induction heating (Figure 1). The induction coil consisted of a copper pipe forming a single circle on the work roll surface, with a cross-sectional area of 20 mm2. A magnetizer was installed at the outside of the coil (Figure 1a) to improve the magnetic field and heating efficiency. The material of the work roll was hot die steel (CG-2), whose properties are assumed constant (free-space permeability 4πχ10-7 H/m (Mei et al., 2008), expansion coefficient 13.1x10-6 °c-1 (Xu and Chen, 2001), and density 7900 kg/m3 (Xu and Chen, 2001)) for the purpose of analysing the electromagnetic-thermal field. The relative permeability values of the air and the coil were set to unity (Mei et al., 2008). The effects of temperature on the main electromagnetic-thermal properties (Xu and Chen, 2001) are given in Table I. In order to ensure an adequate service life and reduce the elastic deformation, the work roll is usually not heated to high temperature (Fischer, 1964). Therefore, these properties are given for temperatures less than 700°C, and those at temperatures of 740 to 1200°C can be obtained by linear extrapolation. The relative permeability of the steel changes to approximately unity by thermal demagnetization when the temperature reaches the Curie temperature of about 740°C (Xu and Chen, 2001). After this, the relative permeability decreases slowly to reach 1.0 at 1200°C (Xu and Chen, 2001; Mei et al., 2008). The initial temperature is set to 20°C. The induction heating parameters chosen to analyse the effects on temperature were: working frequency 5-100 kHz; current density 5.0x106 to 1.5x 107 A/m2; air gap between coil and work roll surface 530 mm; and coil conductor spacing 30-180 mm. The velocity of the work roll was set to 0.05 m/s and the consumed time was set to one rotation of the work roll.
Only the change of surface temperature was calculated during induction heating, and the boundary conditions included convective and radiative heat dissipation. Therefore, the heat transfer coefficient is written as
h = hrad = hconv [1]
where h (W/m2K) is the total heat transfer coefficient, while hrad (W/m2K) and hconv (W/m2K) are the heat transfer coefficients in the radiative and convective processes, respectively. The surface temperature of the work roll and the ambient temperature affect the heat transfer coefficient in radiative processes; the radiative heat transfer coefficient can be described as
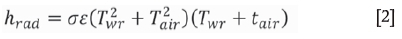
where Twr (K) is the surface temperature of the work roll, Tair (K) is the air temperature, and σ is the Stefan-Boltzmann constant, 5.67x10-8 w/m2K4. The surface emissivity (Zhou, 2003; Han, Lee, and Kim, 2002) ε is described as
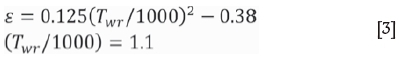
As forced convection is ignored because of the low speed of the work roll (Panjkovic, 2007), the heat transfer coefficient of natural convection can be written as (Dai, 2005)
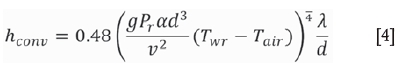
where g (m/s2) is the gravitational acceleration, d (m) the characteristic size (in this case equal to the work roll diameter), Prthe Prandtl number, a (K-1) the coefficient of expansion, ν (m2/s) the kinematic viscosity, and λ (W/m K) the conductivity of air at a characteristic temperature, in this case set to about 350°C (Dai, 2005). Referring to the equation given by Panjkovic (2007), and for an assumed mean value of characteristic temperature of air around the work roll surface, the convective heat transfer coefficient can be described as
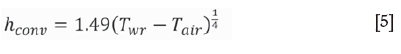
FE mesh
One cycle of the square induction coil is designed to heat the work roll. The experimental equipment was designed and the experiments were carried out in a similar fashion. The length of the coil in the axial direction of the work roll was larger than the radius, so the influence of the coil along the circular direction on the induction heating can be neglected. Accordingly, a 3D FE model can be simplified to a 2D problem to reduce the computational time. The distance between adjacent coil conductors in the axial direction is referred to here as the coil distance. The induction current is generated when the source current passes through the coil, which then heats the work roll. In Figure 1b, the red elements express one circular movement of the coil, whereas the fork and point are used to describe the source current direction at a given time during induction heating. The quadrilateral elements in the mapped mesh model provide higher solution precision than triangular elements in a free mesh model. Therefore, the outside of the work roll is modelled using a mapping mesh with quadrilateral elements, while the centre is modelled as a free mesh with quadrilateral elements. Furthermore, the skin depth should have been divided into three or four layers of elements to improve the predicted precision. However, in order to reduce the computational time, these elements were meshed more coarsely from the centre to the boundary (Figure 1b). There were a total of 10 122 elements and 30 427 nodes in the FE mesh, with the numbers of elements and nodes for the work roll being 9782 and 28 807 respectively.
The skin depth is greatly affected by the working frequency, resistivity, and permeability (Davies, 1990; Blinov et al., 2011), which can be expressed as

where δ is skin depth, μ is relative permeability, μ0 is free-space permeability, and ƒ the working frequency.
An electromagnetic-thermal coupling model
The interaction of the electromagnetic field with the thermal characteristics impedes the solving of the coupled electromagnetic-thermal field during induction heating. The temperature distribution has a significant effect on the magnetic properties of the material, which then generates different electromagnetic fields. Meanwhile, different induction currents give rise to different Joule heating effects. In addition, the relative positions of the induction coil and work roll surface change with the rotation of the work roll.
The electromagnetic-thermal model was developed in the ANSYS software environment, which employs an iterative solver to solve for the temperature and electromagnetic field. In order to solve problems for the rotation of the work roll by FEM, the induction coil was assumed to have the same velocity as the work roll, but in the opposite direction, and the work roll was assumed to be stationary. During induction heating, the movement of the source current causes the heat transfer boundary to change. Therefore, the transient temperature should be solved with different positions of the source current and boundary conditions through embedding the appropriate programs in the software.
The flow chart of the coupling methodology is shown in Figure 2. Firstly, the geometry and FE mesh were created according to the input parameters, including materials properties, element type, and heating parameters. A series of arrays for storage was defined and the number of elements and nodes on the surface of the work roll were reordered in order to simulate the rotation of the work roll, change of the boundary conditions, and loads. Secondly, the induction heating parameters were set and saved in the generated electromagnetic physics environment. Then the thermal analysis parameters for the elemental model of the work roll in the thermal physics environment were set and saved. In the solution of the electromagnetic field at ti+1, the temperature at ti was used to calculate the electromagnetic properties and the Joule heat was obtained for the solution of thermal analysis at ti+1. When the FTIME meets the setting value, the simulation has finished.
Results and discussion
Temperature analysis
Figure 3 shows the temperature distribution at different times, with an air gap of 10 mm, coil distance of 80 mm, source current density of 7.5x106 A/m2, and working frequency of 50 kHz, where MX and MN are expressed as the maximum and minimum values of the temperature, respectively. The position of maximum temperature changes with the rotation of the work roll. The temperature of the rotating work roll during induction heating was predicted through the developed program-coupled FE model. The maximum temperature occurred in the same region after one rotation, and the skin effect creates a significantly higher temperature at the surface than the centre. The layer distribution of the temperature caused by induction heating is beneficial for maintaining the strip temperature. With increasing induction heating time, the centre is heated by conduction. The temperature at positions closer to the induction coil increased quickly, and the temperature difference was obvious among these surface nodes. The surface temperature changed from 32°C to 88.8°C after one rotation and varied from 327°C to 394°C at 1200 seconds under the above specified conditions.
Both the distribution and homogeneity of the surface temperature have an important influence on the strip rolling process. In order to study the change in temperature with different induction parameters, ignoring edge effects, the mean temperature Ta and variance temperature ST2of the nodes in the work roll surface were used to describe the heating efficient and homogeneity (Marck et al., 2012)
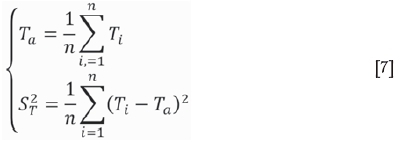
where n is the number of nodes on the work roll surface. In this study, eight nodes, including the typical nodes of A, B, C, and D (Figure 3f) and four others in the middle (E, F, G, and H), were selected to analyse the mean value and homogeneity.
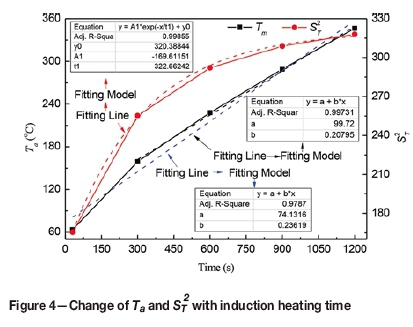
The change in Taand St with induction heating time is shown in Figure 4. It was found that the coefficient of determination was 0.9985 and that ST2increased exponentially with heating time. ST increased by 90 seconds from 60 seconds to 300 seconds, but only by 10 seconds within the range of 900 seconds to 1200 seconds. This indicated that STincreases more slowly with increased induction heating time. The Ta value increased significantly with the induction time, with an approximately linear relationship. Ta was approximately 155°C at 300 seconds and 335°C at 1200 seconds. Therefore, a lower temperature at a shorter induction time can be used for rolling with a hot strip. Meanwhile, the higher temperature after a longer induction time can easily meet the requirements for heat transfer from the heated work roll to a cold strip. Furthermore, the fitting curves show the coefficients of determination to be 0.9787 if the data point at Ta at 300 sec2onds is included, and 0.9973 without the data point. The ST2 value increases more slowly than Ta with increased time, contributing to the homogeneity of the surface temperature.
Influence ofinduction heating parameters on temperature
Due to the lower homogeneity early in heating, the effects of the induction heating parameters on induction heating after 300 seconds were studied. The induction heating parameters, including the working frequencyfw(kHz), air gap ga(mm) between coil and work roll surface, source current density cs (MA/m2), coil distance dc(mm) in the circumferential direction between the two coils, and the heating time have important influences on the changes in Ta and ST .
Working frequency (fw)
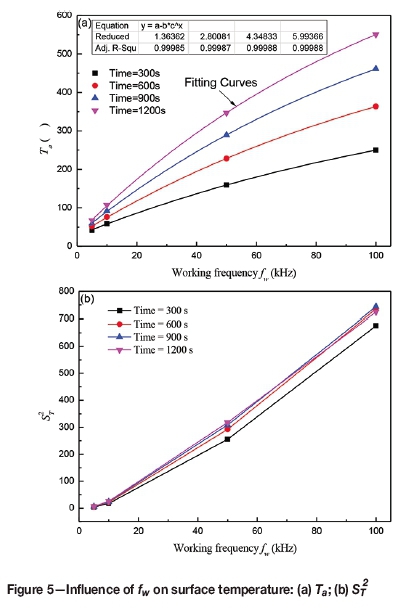
Figure 5 shows the influence of fwon the Taand STvalues of the surface temperature. A higher working frequency created a more significant skin effect and higher inductive current intensity. Ta increased exponentially with increased working frequency. The minimum of determination coefficients of fit curves was greater than 0.999. Consequently, the fitting model is valid. The mean temperature changed very slowly at 500 Hz. However, as the induction heating time increased from 300 seconds to 1200 seconds, the mean temperature increased significantly from 220°C to 550°C at 100 kHz. In addition, with increasing working frequency, sT first increased slowly from 500 Hz to 10 kHz, before increasing more quickly from 10 kHz to 100 kHz. The induction heating time has less influence on St thanfw. Despite the higher variance value, the ratio of the maximum temperature difference to the mean value decreased significantly with increased working frequency. Therefore, a higher working frequency is beneficial for the homogeneity of surface temperature.
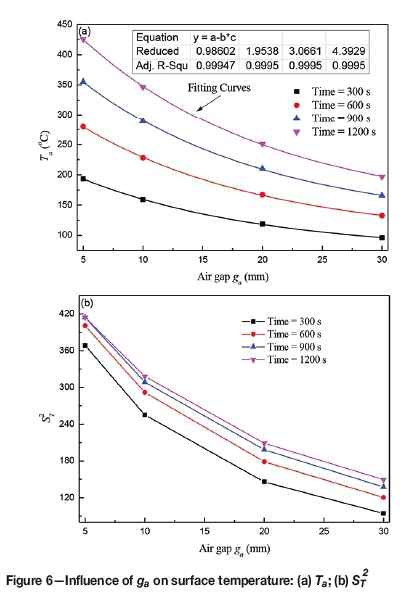
Air gap (ga)
The effect ofgaon Taand Stis shown in Figure 6. Ta decreased exponentially with increasing air gap length. The minimum of coefficient of determination was 0.99947, demonstrating that the fitting curves were effective. Increased distance from the coil to work roll surface decreased the intensity of the magnetic induction current and Ta decreased with increasing ga. However, the magnitude of increase was different and a smaller ga caused a stronger increase in Ta. As an example, the magnitude of increase was 100°C with a change of ga from 10 mm to 20 mm, and 50°C with a change of ga from 20 mm to 30 mm. The St value of the surface temperature decreases markedly with increased ga and decreased induction heating time. ST2 changes less at 1200 seconds than at 900 seconds with ga= 5 mm because of the higher temperature. Therefore, smaller ga values and longer induction heating times promote homogeneity.
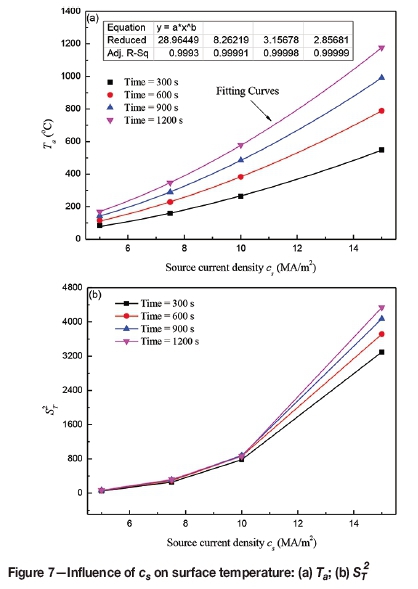
Source current density (cs)
The influence of cs on the Ta and St2 values of surface temperature is shown in Figure 7. Ta varied as a power function. The minimum coefficient of determination was 0.9993. A higher induction current intensity results from higher cs, so Taincreased significantly with increases of cs. The St value of the surface temperature increased exponentially with increasing cs. ST increased slowly in the cs range from 5.0 MA/m2 to 10.0 MA/m2, but for further increases in cs to 15 MA/m2, St increased to approximately four times the value at 10.0 MA/m2. Thus, the surface temperature became more homogeneous with increased heating time because the increase in sT was less than that of Ta.
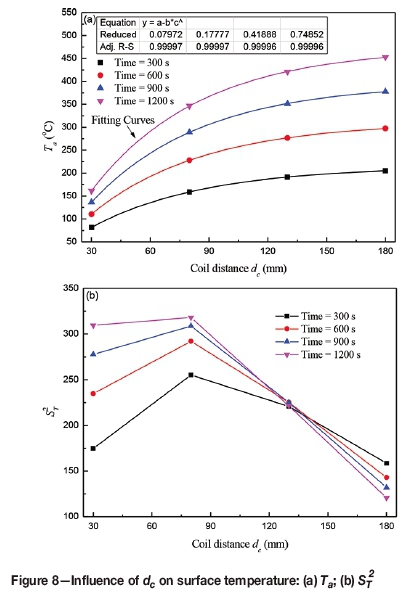
Coil distance (dc)
The value of dccan be controlled by changing the number of interval elements (Figure 1b). The influence of dcon Taand ST2of the surface temperature is shown in Figure 8, with the minimum value of the coefficient of determination being 0.99996. Ta increased significantly with increases in dc. This was mainly because the reversed direction of the source currents for elements i and i+1 (Figure 1) generates an induction current with a reversed direction. The interaction of the reversed induction current decreased the current intensity in the effective regions of the electromagnetic fields. The sT value increased initially for dcvalues below 80 mm, but decreased within the range of dc from 80 mm to 180 mm. Clearly, larger dcvalues benefit the homogeneity of the surface temperature. Furthermore, the surface temperature had a nearly constant ST with dc= 130 mm.
Modelling of induction heating
In order to predict Ta, a new function was proposed according to the curves in Figures 5 to 8. Ta varied exponentially with the air gap, coil distance, and working frequency, while varying according to a power law with increased source current density. Therefore, the function is described as
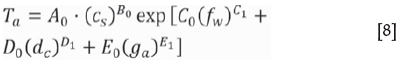
where A0, B0, C0, D0, E0, C1, D1, and E1 are constants.
Taking the natural logarithm of both sides of Equation [8] gives:
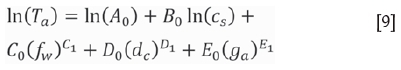
The values of C1, D1, and E1 are 0.1, -1, and 0.5, respectively, according to the linear fitting precision of the plots of 1n(Ta)-(fw)C1, ln(Ta)-(dc)D1, and ln(Ta)-(ga)E1.
Then, the values of B0, C0, D0, and Ξ0 can be obtained as:
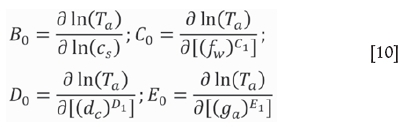
The values of the constants B0, C0, D0, and E0 were obtained as 1.748, 4.854, -35.663, and -0.231, respectively, from the mean slope of the lines in the plots of ln(Ta)-(ƒw)0, 1, ln(Te)-ln(c,), ln(Ta)-(dc)-1, and ln(Ta)-(ga)°.5 (Figure 9). Tais therefore described as:
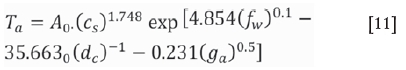
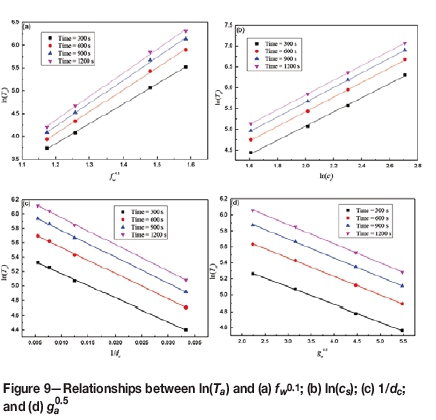
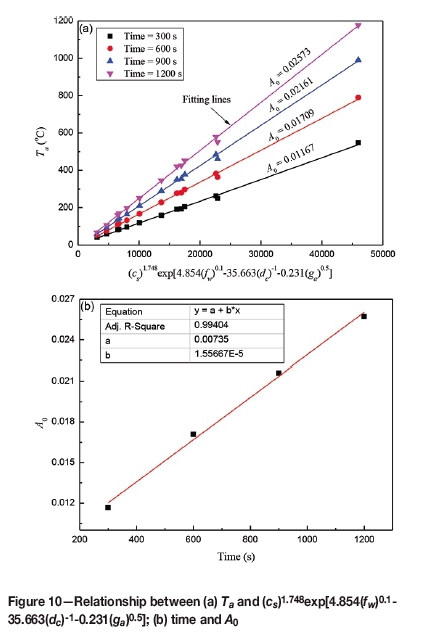
Subsequently, substituting different source current densities, work frequencies, coil distances, and air gaps into Equation [11] with different induction heating times provided the constant A0 as equal to the slope of the fitting curves, as shown in Figure 10. It can be seen that A0 decreased linearly with increased induction heating times. Through the linear fitting, the value is described as:
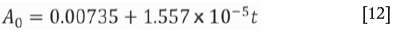
According to the above analysis, the model obtained for Ta in induction heating can be deduced as:
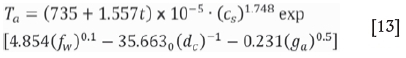
where t (s) is the induction heating time.
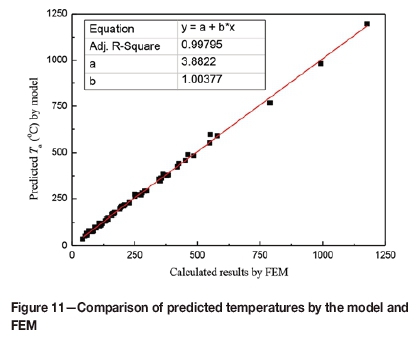
The temperatures calculated by the new model and ANSYS software were compared to validate the model predictions (Figure 11). The new predicted temperature agreed well with that obtained using the ANSYS software, with the coefficient of determination being 0.99301. Thus, the model proposed and obtained from the FEM data reliably predicted the temperature of the work roll in induction heating. The nonlinear analysis method is suitable for the solution of induction heating and constructing the mathematic model.
Furthermore, the modelling technique and methods are helpful for nonlinear analysis of engineering problems. For the known values of the working frequency, air gap, coil distance, and source current density during induction heating, the mean temperature at any time can be predicted by the model. Furthermore, Equation [13] can be used to calculate the critical value of any one influencing parameter if the other parameters and the ideal mean temperature of induction heating are known. As an example, when the air gap is 10 mm, the source current density is 10 MA/m2, coil distance is 100 mm, and ideal mean temperature is 300°C, the working frequency should be approximately 40 kHz for heating time of 450 seconds according to the model. Induction heating experiments have been also carried out to verify the model predictions with the same conditions as in the above example. The relationships between the critical working frequency and idea temperature, mean measured value, and predicted results are shown in Figure 12. In order to reduce error, the position located between typical points D and H was measured rapidly five times in 15 seconds and the mean value recorded. The five measurements for the above experimental conditions were 318°C, 321°C, 319°C, 323°C, and 324°C, and the relative error of these measured values was less than about 2%. Additionally, different experimental parameters were also selected as follows to verify the model: the source current was set to 7.5 MA/m2, working frequency was set to 25 kHz, the air gap was 30 mm, and the coil distance was 80 mm, with heating time from 300 seconds to 3600 seconds (Figure 12b). It can be seen that the temperature predicted by the proposed model was in good agreement with the measured value. The maximum error was about 12.4% and the average relative error was 3.9%. Therefore, the model derived from the FEM data is useful for predicting the temperature of the work roll in induction heating.
Conclusions
A program was developed and embedded into the FE software ANSYS to simulate the surface temperature of the work roll for metal strip rolling during induction heating. The skin effect created a higher temperature at the surface than that at the centre. The variance value increased exponentially with increased heating time. The mean temperature varied approximately linearly after the initial heating stage of approximately 300 seconds.
With increased working frequency, current density, and coil distance, and decreased air gap, the mean temperature increased exponentially. Furthermore, the variance value increased with increasing source current density and working frequency and decreasing air gap. However, the variance value first increased and then decreased with increasing coil distance, because of the change of the electromagnetic field. Despite the increased variance value of the surface temperature, longer induction heating times promoted temperature homogeneity because the surface temperature changed more dramatically than the variance value.
The relationship between the mean temperature and induction parameters was fitted according to the simulated data. A new formula was developed to predict the mean temperature of the work roll during induction heating, considering the working frequency, air gap, coil distance, source current density, and induction heating time. Furthermore, the formula could be used to calculate the critical value of any one parameter, given the influencing parameter with three known values and the ideal mean temperature of induction heating. The predicted results agreed well with the simulated data by FEM and the measured values from actual induction heating experiments.
Acknowledgements
The authors gratefully acknowledge the financial support from the Natural Science Foundation - Steel and Iron Foundation of Hebei Province (no. E2014501114 and E2018501016), Fundamental Research Funds for the Central Universities (No. N172304042), the Doctoral Scientific Research Foundation of Liaoning Province (No. 20170520314), and the Science and Technological Youth Foundation of Hebei Higher Education (no.20132007 and QN2016301)
References
Ataka, M. 2014. Rolling technology and theory for the last 100 years: the contribution of theory to innovation in strip rolling technology. Tetsu-to-Hagane, vol. 100. pp. 94-107. [ Links ]
Barglik, J. 2011. Induction heating of thin strips in transverse flux magnetic field. Advances in Induction and Microwave Heating of Mineral and Organic Materials. InTech, Rijeka,, Croatia. pp. 207-232. [ Links ]
Blinov, K., Nikanorov, A., Nacke, B., and Klopzig, M. 2011. Numerical simulation and investigation of induction through-heaters in dynamic operation mode. COMPEL, vol. 12. pp. 1539-1549. [ Links ]
Cai, B., Wang, H., Mei, R.B., and Lí, C.S. 2013. 2D-FEM analysis of rolls temperature field in induction heating process. AIP Conference Proceedings, vol. 1532. pp. 977-981. [ Links ]
Dai, G.S. 2005. Heat Transfer. Chinese Higher Education Press, Beijing. pp. 152-158. [ Links ]
Davies, E.J. 1990. Conduction and Induction Heating. Institute of Engineering Technology, London, UK, vol. 177. pp. 1567-74. [ Links ]
Fischer, R.B. and Yí, Q.Z. 1964. Rolling mill with the equipment to heat work roll. Heavy Machinery, vol. 13. pp. 30-32. [ Links ]
Han, H.N., Lee, J.K., and Kim, H.J. 2002. A model for deformation, temperature and phase transformation behavior of steels on run-out table in hot strip mill. Journal of Materials Processing Technology, vol. 128, no.1-3. pp. 216-225. [ Links ]
Jeong, H.T. and Ha, T.K. 2007. Texture development in a warm rolled AZ31magnesium alloy. Journal of Materials Processing Technology, vol. 187, no.12. pp. 559-561. [ Links ]
Kang, Y., Wang, Y., and Lv, B. 2005. A kind of equipment for heat the roll for warm rolling of magnesium alloy strips. Chinese patent 200510086721.X. [ Links ]
Kim, S., Son, S., Lee, S., Ham, S., and Kim, B. 2014. Hot roller embossing system equipped with a temperature margin-based controller. Review of Scientific Instruments, vol. 85. pp. 085117-085117-6. [ Links ]
Kim, W.Y. and Kim, W.J. 2014. Fabrication of ultrafine-grained Mg-3Al-Zn alloy sheets using a continuous high-ratio differential speed rolling technique. Materials Science and Engineering A, vol. 594. pp. 189-192. [ Links ]
Lainati, A. 2015. Advantages of induction heating, new possibilities of efficiency and flexibility for rolling mills for long products. Metallurgia Italiana, vol. 1. pp. 35-44. [ Links ]
Lí, C.S., Wang, H., Cai, B., and Zhu, T. 2012. Processing technology and development of 6.5%Si steel. Henan Metallurgy, vol. 20. pp. 1-6. [ Links ]
Marck, G., Nemer, M., Harion, J.L., Russeil, S., and Bougeard, D. 2012. Topology optimization using the SiMP method for multiobjective conductive problems. Numerical Heat Transfer Part B: Fundamentals, vol.61, no. 6. pp. 439-470. [ Links ]
Mei, R.B., Bao, L., Zhang, X., Lí, P.P., and Zhou, Y. Z. 2016. A new method to roll strip of magnesium alloy with heating equipment of work roll. Chinese patent 2016100775235. [ Links ]
Mei, R.B., Du, Y.X., Cai, B., Huang, M.L. and Lí, C.S. 2017. Numerical simulation of rolling process of AZ31 Mg alloy strip under different heating conditions. Hot Working Technology, vol. 46. pp. 113-116. [ Links ]
Mei, R.B., Lí, C.S., Han, B., and Liu, X.H. 2008. FEM Analysis of slab induction heating. Iron & Steel, 2008, vol. 43. pp. 56-60. [ Links ]
Mei, R.B., Lí, C.S., Liu, X.H., and Han, B. 2010. Analysis of strip temperature in hot rolling process by finite element method. Iron and Steel Research International, vol. 17. pp. 17-21. [ Links ]
Panjkovic, V. 2007. Model for prediction of strip temperature in hot strip steel mill. Applied Thermal Engineering, vol. 27. pp. 2404-2414. [ Links ]
Pesin, A. and Pustovoytov, D. 2015. Research of edge defect formation in plate rolling by finite element method. Journal of Materials Processing Technology, vol. 220. pp. 96-106. [ Links ]
Ross, N.V. 2003. Transverse flux induction heating of conductive strip. US patent 6570141. [ Links ]
Xu, J. and Chen, Z.Z. 2001. Mold Materials Manual and Application. Chinese Machine Press, Beijing. pp. 254-306. [ Links ]
Yu, H.L., Yu, Q.B., Kang, J.W., and Liu, X.H. 2012. Investigation on temperature change of cold magnesium alloy strips rolling process with heated roll. Journal of Materials Engineering and Performance, vol. 21, no. 9. pp. 1841-1848. [ Links ]
Zhang, P., Wang, S., and Wang, R. 2008. A heat system of roll for magnesium alloy strip rolling. Chinese patent 200810036132.4. [ Links ]
Zhou, S.X. 2003. An integrated model for hot rolling of steel strips. Journal of Materials Processing Technology, vol. 134. pp. 338-351. [ Links ] ♦
Paper received May 2017
revised paper received Dec. 2017














