PAPERS OF GENERAL INTEREST

 

A new open-pit mine planning optimization method using block aggregation and integer programming

 

 

N.L. Mai^I; E. Topalt^II; O. Ertent^II

^IWestern Australian School of Mines, Curtin University of Technology, Australia
^IISchool of Mining and Geosciences, Nazarbayev University, Astana, Kazakhstan

 

 

---

SYNOPSIS

Mathematical programming has been applied to optimizing open pit mine planning problems since the early 1960s. Nonetheless, it still remains challenging to obtain a life-of-mine plan with current computational hardware and software, mostly because of the scale of the input data, which is generally in the form of mining blocks. To overcome this challenge, one common practice is to aggregate blocks into larger units before formulating and solving mine planning models. However, the majority of available block aggregation techniques ignore the slope relation between blocks or are simply not capable of controlling the number of aggregates generated. In this study, a new optimization method for open pit mine planning is proposed, which consists of two stages. In the first stage, a new block aggregation algorithm is proposed, called the TopCone algorithm (TCA), where blocks are clustered into TopCones (TCs), which have two important features: (1) the cone shape and (2) the number of TCs that can be explicitly controlled. In the second stage, TCs form the basis of an integer programming model with a variety of operational constraints so that a high-quality production scheduling solution can be obtained in relatively quick computational time. The capability and novelty of the proposed method is demonstrated through the optimization of the long-term production schedule of a large-scale copper deposit. The case study shows higher NPV results compared to a commercial software package, and the entire mine planning process can be completed in less than 10 minutes.

Keywords: large-scale optimization, TopCone algorithm, production scheduling, open pit mine planning, integer programming.

---

 

 

Introduction

The fundamental input for open pit mine planning is a resource block model in three-dimensional space, which represents geological attributes i.e., grades of different minerals comprising the orebody, mineralogy, density, and tonnage. This model can then be converted into an economic block model by applying economic parameters such as operational costs and commodity price. A critical objective of mine planning is to determine the mine's production schedule, which basically is a plan indicating when and where to mine ore and waste blocks to maximize total discounted cash flows subject to various constraints, including blending grades, mining and processing capacity requirements, and slope safety. Optimizing the production schedule is a complicated task that involves processing a substantial amount of data constrained by many conditions, which is naturally the domain of mathematical programming techniques (Pendharkar, 1997; Topal and Ramazan, 2010, 2012).

The pioneering of the application of linear programming (LP) mathematical models in open pit mine production scheduling has been credited to Johnson (1968). In this type of model, linear variables represent mining proportions of blocks which lead to slope safety violations, as blocks at a lower level can be mined without the overlying blocks being completely removed. For this reason, integer programming (IP) and its variants, such as mixed integer programming (MIP), were developed, which consider integer variables to maintain the integrity of the mining blocks. For a block model including n blocks to be scheduled within p periods, each block will have p binary variables which enable that particular block to be scheduled (value of 1) in a period p or not (value of 0). In real mining projects, the total number of binary variables n*p is usually enormous, with magnitudes into the millions. Many studies have suggested different ways to deal with the problem of solving large-scale production scheduling using IP (Bienstock and Zuckerberg, 2010; Bley et al., 2010; Boland et at, 2009; Caccetta and Hill, 2003; Gershon, 1983; Ramazan and Dimitrakopoulos, 2004). However, the problem still seems to present significant challenges and it is generally impossible to solve considering the computational intensiveness.

Given the difficulty of achieving an exact solution from large-scale IP models, researchers have resorted to heuristic and metaheuristic techniques to obtain near-optimal solutions within a reasonable computation time. Several notable heuristic and metaheuristic algorithms developed recently can be found in the works of Chicoisne et al. (2012), Jélvez et al. (2015), Lamghari, Dimitrakopoulos, and Ferland (2015), and Lamghari and Dimitrakopoulos (2012). A common drawback of these models, apart from that of Lamghari, Dimitrakopoulos, and Ferland (2015), is that they are not able to incorporate a typical full set of operational constraints in mining, being the lower and upper bounds of mining capacity, processing capacity, and blending grade.

Block aggregation is another approximation approach, in which blocks are clustered to form larger units to reduce the scale of the data before formulating mathematical models. Reducing block resolution, or reblocking, is by far the simplest method but this also seriously compromises the quality of scheduling results. One common trend is to combine blocks on the same level based on their similarity of distance, material, or attributes, such as in the work of Tolwinski and Underwood (1996) and Tabesh and Askari-Nasab (2011). As slope constraints between blocks are not considered in the clustering stage but must be considered in the production scheduling stage, this conflict may severely compromise the possibility of obtaining an optimal solution. The two most well-known block aggregation algorithms where slope constraints are effectively introduced in the aggregating process are fundamental tree algorithm (FTA) (Ramazan, 2007) and Blasor (Froyland and Menabde, 2009). FTA deploys a clever LP formulation to cluster blocks into fundamental trees (FTs). However, in most instances, the number of FTs is slightly less than the number of ore blocks in the ultimate pit limit where FTA is applied. This is because most FTs consist of only one ore block, the so-called 'single tree problem'. Consequently, the number of FTs is still very large in real-life data-sets. Blasor uses a propagation procedure from the bottom up to cluster blocks into clumps with a cone shape, which considerably reduces the number of variables for downstream scheduling models. However, to our best knowledge, there is no evidence that Blasor can dictate or effectively control the number of clumps generated.

The above mentioned challenges are the motivation for our new algorithm, called the 'TopCone algorithm' or TCA. This algorithm is a hybrid of the ultimate pit limit technique and the clustering technique, where a near-optimal ultimate pit can be obtained during the clustering process. TCA aggregates blocks into 'TopCones' using LP in a manner such that the number of aggregates generated can be controlled to keep the size of the downstream IP-based scheduling model tractable. A schematic of a traditional and the new proposed mine planning framework is presented in Figure 1.

The remainder of this paper is organized as follows. The methodology of the TCA is presented, followed by a demonstration of the algorithm in a simple 2D case study. We then detail the methodology of a long-term production scheduling model using IP specially developed for TCs. Large-scale numerical experiments are discussed. Finally, conclusions are drawn.

 

Methodology of TopCone algorithm

TCs are groups of blocks having four properties:

(i) Can be mined without violating slope constraints

(ii) Total economic value of blocks as a TC must be positive

(iii) The TCs are subject to certain constraints

(iv) A TC cannot be split into smaller cones without violating (i), (ii), and (iii).

The constraints in property (iii) could be the minimum cone size (MCS) in terms of the number of member blocks or total ore or waste tonnage, average grade, material proportion, or any constraints that could appear in the downstream scheduling model. At the current stage of development, we set only the minimum number of blocks per cone as a condition for property (iii) to control the number of TCs generated. However, it would be promising to consider other attributes as they may have a beneficial impact on the result of solving the IP model.

 

Nomenclature

The following notations are defined for explaining the steps of the algorithm:

Indices and sets

I Є N Set of underlying nodes i found at current searching level

j Є M Set of overlying nodesj established at current network flow

J Є 0_i cM Subset of overlying nodes j that belong to cone of underlying node i

i Є Uj cN Subset of underlying nodes i which have their cone cover overlying node j

t Sink node

s Source node

Parameters

CV_i Cone value of underlying node i

C_i Coefficient of underlying node i

Vi Economic value of block i. If V_i> 0, block i is called a 'positive node', otherwise, a 'negative node'

ξ A very small decimal value, for example, 0.01

Variables

f_si Continuous variables: Flow from source node to underlying node i

f_ij Continuous variables: Flow from underlying node i to overlying node j

f_jt Continuous variables: Flow from overlying node j to sink node t

Figure 2 gives a two-dimensional illustration of a network consisting of the abovementioned nodes and flows.

Steps ofTCA

The algorithm starts from the top level of the block model and then progresses level by level until the bottom, aggregating blocks into TCs at each iteration. Steps are schematically illustrated in Figure 3 and discussed below.

 

 

Step 1. The level that the TCA is currently scanning is termed the 'current searching level' and all positive nodes at this level are termed 'underlying nodes'. All nodes (both positive and negative) that overlie the underlying nodes based on slope constraints are termed 'overlying nodes'. If no positive node is found at the current searching level, the algorithm goes to a lower level and repeats step 1.

Step 2. Generate a network flow consisting of source node, sink node, underlying nodes, overlying nodes, and flows, as illustrated in Figure 2.

Step 3. Calculate the cone values of underlying nodes by summing the economic values of all overlying nodes connected to that underlying node and the underlying node itself.

Step 4. Assign coefficients to Ν underlying nodes according to their cone values, starting from the highest and proceeding to the smallest with coefficients from 1 to Ν respectively. Specifically, the underlying node with the highest cone value has a coefficient of 1, the second highest has a coefficient of 2 and so on.

Step 5. Set up and solve the LP formulation. The aim of the LP model is to group positive and negative nodes into clusters (called TCs) so that in each cluster, positive nodes are strong enough to support negative nodes. That is, TCs always have a positive value. This is a minimization problem to minimize connections between nodes so that the size of the clusters is minimal.

Objective function

Subject to

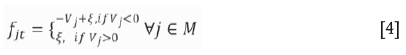
The objective function is a minimization of connections between underlying nodes and their corresponding overlying nodes. The role of the coefficients is to prioritize the creation of connections to high-value nodes so that they are available for mining before the lower value ones. This is critical to facilitate downstream scheduling models to yield a better NPV score. Constraint [3] ensures that an underlying node and its positive overlying nodes are unable to provide support greater than their value. Constraints [4] ensure that overlying nodes receive sufficient support. Note that positive overlying nodes can always be removed (i.e. just need a very small ξ value support) once the corresponding underlying nodes are removed. The addition of ξ is to prevent TCs from having zero value as this will require additional support from other underlying nodes. Constraints [5] and [6] enforce the mass balance of flows in and out of the underlying and overlying nodes. Constraint [7] defines all flows as non-negative linear variables.

As this is a pure linear problem, it can be solved quickly using a solver like CPLEX (CPLEX, 2009).

Step 6. Analyse the LP solution by checking all positive flows to find TCs. Once generated, TCs automatically respect and accommodate slope constraints as a result of step 1. Post-process all TCs by validating against properties (ii) and (iii) to find valid TCs. Condition (iii), i.e. the condition on minimum size of TCs, is relaxed for those positive values with TCs having no possibility of increasing their size, such as there is no positive nodes at the lower levels. This relaxation is to increase the ultimate pit value.

Step 7. Qualified TCs from step 6 are removed from the block model while nodes of unqualified TCs remain.

Step 8. If the current search level reaches the bottom, the algorithm moves to step 9, otherwise all variables are reset and the algorithm moves to a lower level and back to step 1.

Step 9. Print the results and stop.

Features of TCA

► The TCA generates TCs by scanning through all ore blocks available in the orebody, from the top level to the bottom level, and sequentially extracts as many ore blocks, together with the overburden, as possible, given that each time of extraction generates economic profit. By definition, this process results in an ultimate pit.

► By varying the properties applied on TCs, particularly a minimum number of blocks per cone or MCS, the number of aggregates is controlled. Theoretically, the TCA can reduce the number of TCs to close to, or equal to, unity when MCS is set large enough. The smallest number can be unity only if the shape of the ultimate pit limit allows all blocks to be connected to a root block according to the slope constraints. That theoretical ultimate pit limit has a cone shape with an appropriate slope angle and an ore block located at the bottom. This critical ability of the TCA ensures that there is always an appropriate number of variables in the IP scheduling model to make it tractable.

► The TCA is able to incorporate various constraints into TCs via its post-processing step. At the current development stage, only the minimum size of cones is considered.

► TCA is a linear programming method, therefore the computation time required for generating TCs is not a major concern if sufficient memory is available. Together with feature 2 above, dictating the number of TCs being controlled, the proposed mine planning framework using TCA and IP can be applied to any large-scale data-sets and a solution obtained within a relatively short computation time.

 

Demonstration of TCA in a 2D instance

The TCA is demonstrated in a 2D example using a hypothetical cross-sectional view of a mineral deposit, represented by nodes. The numbers inside circles (Figure 4) represent node indexes, and those outside are economic values. The MCS comprises two nodes.

 

 

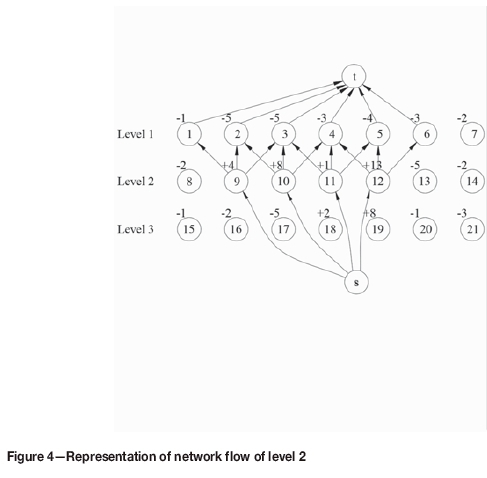
Step 1. Start from level 1, no positive node is found. Then, the algorithm moves to level 2 where there are four positive nodes, namely 9, 10, 11, and 12. They are now termed underlying nodes.

Step 2. Generate the network flow as shown in Figure 4. Steps 3, 4. The cone values of the four underlying nodes are -7, -5, -11, and +3. Therefore, their coefficients are 3, 2, 4, and 1, respectively.

Step 5. Formulate the LP model of level 2 (Figure 5) The solution is presented in Table I and Figure 6, showing positive flows only.

 

 

Step 6. Two TCs are found based on thLP solution, and they are valid according to the predefined properties. Considering precedence, TC 2 is removed after TC 1 to ensure slope safety.

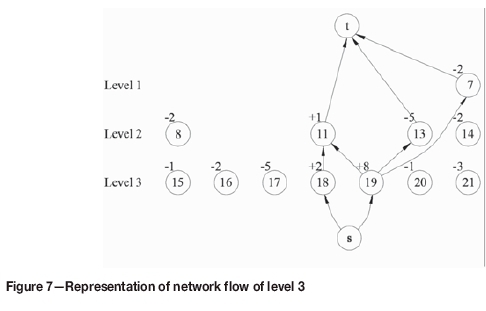
Steps 7, 8. Mine out two TCs found at step 6, go to level 3, and similarly repeat steps 1-8 to find more TCs. The network flow corresponding LP formulation and result of level 3 are presented in Figures 7, 8, and 9 and Table II, respectively. Note that the value +1 of positive overlying node 11 is transferred to underlying node 18 because it has a smaller coefficient than underlying node 19.

 

 

 

 

 

 

 

 

Step 9. As level 3 is the last level, the algorithm stops. All TCs found are presented in Figure 10.

Besides satisfying all four properties, other comments on TCs are as follows.

► TC 3 only consists of two positive nodes.

► The combination of all four TCs forms an ultimate pit limit.

► In TC 2, two positive nodes 9 and 10 have jointly supported three negative nodes 1, 2, and 3.

► When mining TCs follow their order of appearance, the slope constraints are always secured. This feature significantly reduces the number of sequencing constraints at IP formulation. > At level 3, the combination of node 11 with node 18 instead of node 19 to form cones provides the most beneficial scenario for scheduling in terms of NPV. This demonstrates the important role of coefficients in the LP formulation as discussed in step 5 of the TCA (setting up and solving the LP formulation). After generating TCs, the long-term production scheduling using the IP model is implemented using the formulation presented in the next section.

 

Optimization of long-term production scheduling using TopCones

In this section we discuss an open pit mine long-term production scheduling model using integer programming and TopCones. In the model, each TC can be taken at any scheduling period over the life of mine to maintain a global optimization. A TC's ore tonnage, waste tonnage, and economic value are calculated by summing from the constituting blocks, while the TC's grade is assumed to be homogeneous within the ore tonnage and calculated by averaging the grade of the TC's ore material. As the whole TC will be extracted at once when it is scheduled in a period, the assumption of homogeneity has no impact on the scheduling result.

Indices and sets

i ЄN Set of TCs i

j Є M, cN Subset of TCsjthat are predecessor TCs for TC i

t,t Є P Set of time periods t, t' in the horizon Parameters

d Economic discount rate

V_i Economic value of TC i

C_i^tExpected value of TC i when being extracted in period t

Gi Grade of TC i

O_i Ore tonnage of TC i

W_i Waste tonnage of TC i

G_min/G_max Minimum/maximum blending grade

PC_min/PC_max Minimum/maximum processing plant capacity

MC_min/MC_max Minimum/maximum capacity of the mine's equipment.

Binary variables

X_i^t equal to 1 if TC i is scheduled in period t; 0 otherwise.

Objective function

Subject to

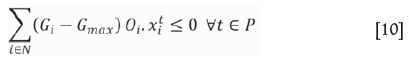
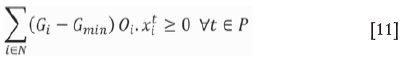
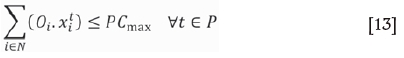
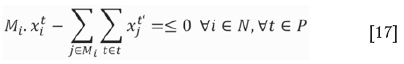
Objective function [9] maximizes the discounted cash flow. Constraints [10] and [11] ensure that the average grade of material sent to the mill is within the upper and lower bounds. Constraints [12] ensure that a TC is removed in one period only. Constraints [13], [14], [15], and [16] limit the production targets of processing and mining capacity in each period. Constraints [17] ensure the precedence between TCs, where a TC i is mineable at period t only if all of its M_ioverlying TCs are scheduled at previous periods or the same period. A TC is considered to be overlying the other if it has at least one block overlying any block of that underlying TC according to slope constraints. Constraints [18] ensure integrality of binary variables, as appropriate.

 

Numerical results

The two-phase mine planning method using TCA and IP proposed in this paper was applied to a hypothetical copper deposit. The block model characterizing the deposit consists of 1 568 250 blocks of size 20x20x20 m, 20 571 of which are ore blocks. The experiments were implemented using a normal office computer with an Intel^(R) Core^(TM) i7 with 3.4 GHz CPU processor and 8 GB of RAM. The hypothetical set of scheduling targets is presented in Table III.

 

 

In this study, the proposed mine planning method was implemented multiple times using seven MCS options of 1, 10, 75, 100, 200, and 300 blocks per TopCone. The MCS of 1 implies that there is no restriction on the minimum size of the TCs. The ultimate pit limit and production scheduling solutions yielded by the proposed method were validated against the Whittle Milawa NPV algorithm (Whittle, 2016). Those blocks inside the optimal Whittle ultimate pit limit are regarded as the original, non-aggregated problem. Table IV shows the results of the numerical experiments. For each run, the following parameters are reported:

► Number of TCs generated by TCA or blocks in the original problem

► Number of binary variables: Equal to number of TCs or blocks multiplied by number of time periods

► Number of precedences: Number of precedence arcs between TCs.

► Number of constraints: Include resource constraints, maximum processing capacity constraints, and slope constraints, as formulated by constraints [12], [13], and [17] respectively

► Gap to optimum ultimate pit (%): The ultimate pit values encapsulated by TCs are compared with the optimum solution

► NPV gap (%): The NPV obtained from solving TCs-based IP models is compared with the block-based Whittle Milawa NPV algorithm

► Solution time of TCA (minutes): The computing time of TCA in aggregating blocks into TCs

► Solution time of IP (minutes): The computing time of solving IP models built on TCs. CPLEX was used as the solver using standard parameters and an optimality tolerance gap of 5%.

As demonstrated in Table IV, the solution time for solving IP models increases exponentially with the number of TCs, and this emphazises the significance of controlling the number of aggregates while clustering blocks. Specifically, the aggregated problems are orders of magnitude (in the thousands) smaller than the original block-based problem. For instance, at a MCS of 300, only 239 TCs are generated together with 1912 binary variables, 483 precedences, and 2159 constraints for the corresponding IP model, a staggering reduction from the 562 800 binary variables of the original problem. Consequently, the whole two-stage mine planning process with a MCS of 300 was completed in just seven minutes. Considering the experiments were conducted with limited computing power, that time-frame is very practical. In the scenarios of MCS of 1 and 10, CPLEX did not obtain a solution within five days, so the experiments were terminated as this is no longer a practical time-frame.

The increase of 7 to 8% in NPV value with TCA-IP model compared to the popular Whittle Milawa NPV algorithm is also considerable. Although this is not a fair comparison, as IP is an exact method while Whittle Milawa NPV algorithm is a heuristic approach, the proposed methodology and the results of these experiments contribute to the application of mathematical programming-based optimization models in producing high-quality, large-scale scheduling solutions in a practical time-frame with the support of an appropriate block aggregation algorithm.

Selecting an appropriate MCS is a case-by-case exercise and likely involves a trial-and-error process. A small MCS would return a large number of TCs to provide a greater flexibility to the downstream IP model in favour of optimizing NPV value. This, however, comes with a cost of an exponential increase in computing time. The rule of thumb is to start with a reasonably small MCS, then if no solution is obtained in a desired time-frame, that implementation should be terminated and the process attempted again with a larger MCS option. Factors like computing power, size of the block model, and allowed time all contribute to the selection of a MCS.

The ability to obtain the ultimate pit limit using TCA was also validated in Table IV. Although a loss of 0.2 to 0.3% of pit value is relatively small, TCA can be implemented within a predefined optimal pit limit to completely eliminate this issue. Hence the experiments presented in this study are aimed at demonstrating the ability of TCA to find near-optimal pit limits only.

Figures 11 and 12 present detailed comparisons of the TCA-IP model with MCS of 300 and Whittle Milawa NPV's scheduling scenarios regarding tonnage production, NPV, and blending grade. To maximize NPV as defined in the objective function of the IP model, the proposed scheduling model maximizes the ore tonnage and copper grade while minimizing waste production in early periods. This explains the considerable improvement in NPV over the Whittle Milawa NPV's solution.

To illustrate the practicality of the solutions of the proposed model, the plan view and typical cross-sections of the production schedule generated by TCA-based IP model with MCS of 300 are presented in Figure 13.

 

Conclusions

A new optimization method for open pit mine planning has been introduced, expounding the idea of aggregating mining blocks using a TopCone algorithm and then deploying integer programming to find production scheduling solutions based on aggregated blocks. By clustering blocks in a controlled manner regarding both quantity and shape of aggregates, TCA provides a novel platform for the application of mathematical programming techniques to solve mine planning problems. The numerical experiments demonstrated that the proposed method could solve large-scale problems quickly, even with limited computing power. In addition, it is suggested that determining pushbacks is not necessary while a near-optimal ultimate pit can be obtained during block aggregation. These features make the proposed mine planning framework simpler and easier to implement than conventional approaches.

One limit of TCA is that some TCs become too large when the MCS is set too high, particularly those TCs generated near the pit bottom. These oversize TCs may reduce the flexibility of the IP scheduling model or even make it infeasible to solve, depending on the narrowness of the lower and upper bound constraints. In future work, we plan to mitigate the effect of oversize TCs via a post-processing step, such as by introducing a maximum cone size parameter or developing a MIP model for partial mining of TCs. Furthermore, incorporating a minimum width for mining benches would also be an interesting exercise.

 

References

Bienstock, D. and Zuckerberg, M. 2010. Solving LP relaxations of large-scale precedence constrained problems. Proceedings of the International Conference on Integer Programming and Combinatorial Optimization, Lausanne, Switzerland, 9-11 June 2010. Eisenbrand F. and Shepherd F.B. (eds). Lecture Notes in Computer Science, vol 6080. Springer, Berlin, Heidelberg. pp. 1-14.         [ Links ]

Bley, A., Boland, N., Fricke, C., and Froyland, G. 2010. A strengthened formulation and cutting planes for the open pit mine production scheduling problem. Computers and Operations Research, vol. 37, no. 9. pp. 1641-1647.         [ Links ]

Boland, N., Dumitrescu, I., Froyland, G., and Gleixner, A.M. 2009. LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity. Computers and Operations Research, vol. 36, no. 4. pp. 1064-1089.         [ Links ]

Caccetta, L. and Hill, S.P. 2003. An application of branch and cut to open pit mine scheduling. Journal of Global Optimization, vol. 27, no. 2-3. pp. 349-365.         [ Links ]

Chicoisne, R., Espinoza, D., Goycoolea, M., Moreno, E., and Rubio, E. 2012. A new algorithm for the open-pit mine production scheduling problem. Operations Research, vol. 60, no. 3. pp. 517-528.         [ Links ]

CPLEX, I.I. 2009. V12. 1: User's Manual for CPLEX. International Business Machines Corporation, vol. 46, no. 53. p. 157.         [ Links ]

Froyland, G.A., and Menabde, M. 2009. System and method(s) of mine planning, design and processing. US patent 7957941. BHP Billiton.         [ Links ]

Gershon, M.E. 1983. Optimal mine production scheduling: evaluation of large scale mathematical programming approaches. International journal of Mining Engineering, vol. 1, no. 4. pp. 315-329.         [ Links ]

Jélvez, Ε., Morales, N., Nancel-Penard, P., Peypouquet, J., and Reyes, P. 2015. Aggregation heuristic for the open-pit block scheduling problem. European Journal of Operational Research, vol. 240. pp. 1169-1177. doi: 10.1016/j.ejor.2015.10.044        [ Links ]

Johnson, T.B. 1968. Optimum Open Pit Mine Production Scheduling. University of California, Berkeley. 258 pp.         [ Links ]

Lamghari, A., and Dimitrakopoulos, R. 2012. A diversified Tabu search approach for the open-pit mine production scheduling problem with metal uncertainty. European Journal of Operational Research, vol. 222, no. 3. pp. 642-652.         [ Links ]

Lamghari, A., Dimitrakopoulos, R., and Ferland, J.A. 2015. A hybrid method based on linear programming and variable neighborhood descent for scheduling production in open-pit mines. Journal of Global Optimization, vol. 63, no. 3. pp. 555-582.         [ Links ]

Pendharkar, P.C. 1997. A fuzzy linear programming model for production planning in coal mines. Computers and Operations Research, vol. 24, no. 12. pp. 1141-1149.         [ Links ]

Ramazan, S. 2007. The new fundamental tree algorithm for production scheduling of open pit mines. European Journal of Operational Research, vol. 177, no. 2. pp. 1153-1166.         [ Links ]

Ramazan, S., and Dimitrakopoulos, R. 2004. Recent applications of operations research and efficient MIP formulations in open pit mining. Transactions of the Societyfor Mining, Metallurgy, and Exploration, vol. 316. pp. 73-78.         [ Links ]

Tabesh, M., and Askari-Nasab, H. 2011. Two-stage clustering algorithm for block aggregation in open pit mines. Mining Technology, vol. 120, no. 3. pp. 158-169.         [ Links ]

Tolwinski, B. and Underwood, R. 1996. A scheduling algorithm for open pit mines. IMA Journal of Management Mathematics, vol. 7, no. 3. pp. 247-270.         [ Links ]

Topal, Ε. and Ramazan, S. 2010. A new MIP model for mine equipment scheduling by minimizing maintenance cost. European Journal of Operational Research, vol. 207, no. 2. pp. 1065-1071.         [ Links ]

Topal, Ε. and Ramazan, S. 2012. Strategic mine planning model using network flow model and real case application. International Journal of Mining, Reclamation and Environment, vol. 26, no. 1. pp. 29-37.         [ Links ]

Whittle. 2016. Dassault Systèmes Canada Software Inc. Vancouver, BC, Canada. http://www.geovia.com/products/whittle ♦         [ Links ]

 

 

Paper received Jan. 2017
revised paper received Nov. 2017