Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.118 n.5 Johannesburg May. 2018
http://dx.doi.org/10.17159/2411-9717/2018/v118n5a12
PAPERS OF GENERAL INTEREST
Particle size distribution and energy consumption during impact crushing of single granite particles
H.Y. Fang; J.H. Yang; Q. Chen
College of Mechanical Engineering and Automation, Huaqiao University, China
SYNOPSIS
To study the effects of crushing parameters on particle size distribution and energy consumption of rock impact crushing, a custom-made experimental rig was used for impact crushing tests on single particles of granite. The particle size distribution of the crushed product was analysed, as well as the sand production ratio and energy consumption per unit sand product under different impact velocities and with different primary particle sizes. The results show that the particle size distribution of the crushed granite under different experimental parameters is in accordance with the Weibull distribution. With a decrease in the primary particle size, or a specified impact velocity, the discreteness of the particle size distribution of the fragments becomes greater. An optimal impact velocity exists at which the energy consumption per unit sand product is minimized. Also, it was found that the smaller the primary particle size, the lower the energy consumption per unit sand produced.
Keywords: granite, single-particle impact crushing, impact velocity, primary particle size, particle size distribution; specific energy consumption.
Introduction
In both civil and architectural engineering, sand is an important constituent of concrete, and the consumption of sand for such use is significant. In recent years, the supply of natural sand has become inadequate, resulting in a need to produce relatively large amounts of manufactured, high-quality sand. Research has shown that the vertical shaft impact (VSI) crusher can produce manufactured sand with high enough quality to compete with natural sands (Gopalakrishnan and Murugesan, 2015; Bengtsson and Evertsson, 2006; Johansson and Evertsson, 2014; Luo Yang, and Fang, 2014; Ákesson and Tjell, 2010).
There are many factors that affect the fragmentation characteristics of rock. Ovalle. (2014) analysed the effects of particle size on rock aggregate crushing strength, and concluded that strength decreases as particle size decreases. Nikolov (2002, 2004) presented a model for the particle size distribution of material crushed by hammer or VSI crusher, expressed as a function of the crusher rotor radius and angular velocity, the feed rate, and the feed size distribution. In the model of Bengtsson and Evertsson (2008), typical parameters of mass flow and absolute velocity of particles were incorporated to calculate the capacity and power of a VSI crusher. The model predictions were compared with experimental data obtained from a full-scale VSI crusher to select appropriate parameters to improve production of manufactured sand under conditions of minimum energy consumption. However, it was found that the conditions in the VSI crusher were not ideal for high-quality sand manufacturing, and instrumental monitoring of the sand-making process inside the crushing chamber was difficult.
From the research to date, it is evident that the velocity of particles ejected from the rotor is typically obtained theoretically, and based on many assumptions. In 2009 (Shi et al., 2009), the Julius Kruttschnitt Mineral Research Centre (JKMRC) comminution research team developed a Rotary Breakage Tester (JKRBT) for testing of rapid particle fragmentation. In the device, a high-speed video camera was used to measure impact velocity, although the interactions of rocks inside the crushing chamber are complex and chaotic. As a result, it is difficult to determine the main factors that influence particle fragmentation characteristics and energy consumption.
These challenges can be addressed by using the experimental method of single particle impact crushing. Laboratory material fragmentation studies can be broadly classified into two groups based on the role of external forces applied: compression crushing and impact crushing. The representative test methods for the former are the twin pendulum (Weedon and Wilson, 2000; Sahoo, Weedon, and Roach, 2004a, 2004b; Narayanan, 1985; Cai et al, 2016), drop weight tester (DWT) (Napier-Munn et al, 1996; Saeidi, et al, 2016; Hu et al., 2015; Li, Zheng, and Du, 2013), and split Hopkinson pressure bar (SHPB) (Deng, et al., 2016; Li et al., 2009; Zhang et al., 2000). The experimental device presented in the literature by Jiang, Du, and Liu (2013) belongs to the latter group, given that the particles were accelerated by a drive belt and then crushed on an impact plate. In compression crushing, two solid working surfaces move from opposite directions, and when the distance between them is reduced to a certain value, the compressive stress on the particles reaches its limiting value and fragmentation occurs. In this scenario, the strain of the particle occurs between two solid working surfaces. In impact crushing, high-speed particles impact fixed or moving targets, causing the particles to be subjected to extremely rapid impact loading. When the ultimate value of stress is reached, fragmentation occurs. In this scenario, the strain on the particle occurs on one working surface, such as in a VSI crusher, in which the particles are broken during impact.
Particle fragmentation characterization aims to quantify the size distribution of the product and establish the relationship between specific energy inputs and resultant product through laboratory testing (Napier-Munn et al., 1996). There are many published studies on particle size distribution of the rock product and the related energy consumption. Early in 1996, the relationship between t10 and specific comminution energy was developed by the JKMRC (Napier-Munn et al., 1996; Bearman, Briggs, and Kojovic, 1997; Delaney et al., 2015; Cleary et al., 2017), wherein the factor t10 is the percentage of material passing 1/10th of the original feed size, and thus represents the degree of fragmentation.
Another common function used to represent the rock product of mechanical comminution is the Rosin-Rammler distribution, or Weibull distribution (Rosin and Rammler, 1933; Weibull, 1939, 1951). A number of investigators report that the Weibull distribution can be used to describe the mass accumulation distribution of brittle material fragments (Sanchidrián et al., 2012, 2014; Paluszny et al., 2015; Jiang, Du, and Liu, 2013; Li, Zheng, and Du, 2013). In the study of Jiang, Du, and Li (2013), according to the Griffith theory of brittle fracture, the surface energy formula is used to calculate the fracture energy formed in the new surface, and from such it is evident that the energy dissipation rate increases with impact velocity. To date, the effect of impact velocity and primary particle size on product particle size distribution, and the energy consumption per unit sand product, have been rarely mentioned in the literature. The suitability of a Weibull distribution model for describing the distribution of rock product grain size from impact crushing is also in question.
In this paper, the results of impact crushing experiments on single granite particles are presented for different impact velocities and different primary particle sizes. Based on a Weibull distribution model, the particle size distribution of the product is analysed, and the energy consumption per unit sand product is also discussed. This research is aimed at the selection of parameters for sand manufacturing using a VSI crusher.
Modelling
Weibull distribution model
The definition of Weibull distribution was first put forward by Maurice Fréchet. Rosin and Rammler (1933) applied a Weibull distribution model for the first time when studying the particle size distribution of coal. A Weibull distribution model that describes the particle size distribution obtained from impact crushing of a granite single particle can be expressed as:

where R(d) is the cumulative mass percentage of particles ≤d in size after crushing. The factor d denotes any particles in the size range of the crushed product, while D is the particle size when R(d) = 63.2%. The Weibull modulus, n, can be used to characterize the uniformity of particle size distribution. To analyse the particle size distribution, a logarithmic transform is applied to both sides of Equation [1] to obtain the particle size distribution function after crushing:
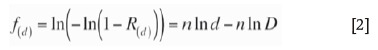
wherey(d) is defined as the cumulative mass distribution function of the crushed granite with particles no larger than d.
In order to predict the degree of granite fragmentation under different experimental parameters, the dimensionless parameter is defined as:

where D0 is the primary particle size of the granite.
Energy consumption per unit sand product model
Manufactured sand is mainly used in concrete with strength grade ≤C60 for building, municipal, transportation, and other construction projects. The required particle size for such concrete is ≤4.75 mm. In a VSI crusher, sand particles are produced by accelerating aggregate particles in a rotor to a specified velocity (the particles have relatively large kinetic energy) and ejecting them to impact on a static anvil made of liner material or wear-resistant metal. The impact results in crushing of the particles at high velocity as the fragments decelerate extremely rapidly.
The economic viability of manufactured sand production is closely related to the energy utilization ratio of the processes of particle acceleration and impact. For the latter, the kinetic energy of the particles is the energy input. The energy output includes the energy required to generate a new surface, the residual kinetic energy of fragments, the distributed heat energy, and friction energy, among other. Unfortunately, the ratio of fragmentation energy to input energy is difficult to determine. In this study, the energy input required to produce a unit of finished product is chosen as a measure of energy utilization, and is represented as energy consumption per unit sand product in kWh/t.
A particle with velocity (v) has a mass-specific kinetic energy (E), which is independent of the particle shape and mass, as shown below:

The sand production ratio (Sp) is defined as the mass percentage of fragments which are not larger than 4.75 mm in size. The value of Sp is expressed as:

where mi is the mass of fragments no larger than 4.75 mm in size and m0 is the total mass of the fragments. The energy consumption per unit sand product (Es) is expressed as:

Single particle impact crushing test on granite
Test apparatus and method
Single particle impact crushing experiments on granite were performed using a custom-made test platform constructed mainly of stainless steel, as shown in Figure 1. The apparatus uses high-pressure gas stored in a container to provide energy to the particles entering from a feeder into the launch tube. The gas pressure can be adjusted to control the launch velocity. The single granite particle enters the feeder, the gas valve is opened, and the particle is launched and is accelerated through the launch tube into the crushing chamber. In the chamber the particle impacts a hardened metal anvil at a high velocity and is crushed.
The front side of the crushing chamber includes a large transparent window of bulletproof glass, which enables photographs of particles to be taken before impact using a high-speed camera (up to 10 000 images per second). A ruler in the window is used to record the locations of the particle in the crushing chamber, as shown in Figure 2. The distance between the two positions shown can be determined to scale using the ruler, and the time between the two positions can be obtained from the frame numbers of the corresponding photographs, thus allowing the velocity of the particle to be calculated. After impacting the anvil with relatively high kinetic energy, the granite particle breaks into many fragments. Powder generated from the impact rises under its own buoyancy in the air and escapes to a dust collecting device mounted at the top of the crushing chamber. Under the force of gravity, the larger fragments fall from the discharge port into another collector located under the crushing chamber. The fragments from the two collectors are then sieved and weighed to obtain the mass of fragments within each range of particle sizes.

Test conditions
After coarse or medium crushing with a jaw or cone crusher, the broken granite particles have irregular shapes. Because the impact point on the surface of the particle when it strikes the anvil is usually random, the forces acting on the particle have different effects depending on the particle's orientation at impact, and the corresponding crushing effect will also be different. To reduce the influence of irregular shapes, the granite particles used in these tests were carefully processed beforehand so as to be as close to spherical as possible. Since granite is a brittle material a large number of samples was needed for reliable results to be obtained, thus 12 particles were used for each set of experiments.
Results and discussion
Influence ofimpact velocity on particle size distribution
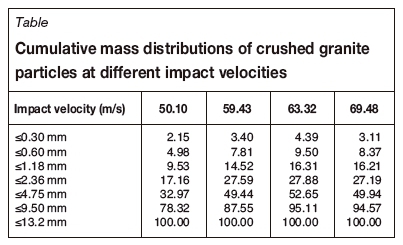
During sand manufacturing with a VSI crusher, the stone particles are accelerated by the rotor to a velocity of 50-70 m/s and are then ejected. To correspond to these conditions, the crushing experiments were conducted using four groups of granite particles with a primary particle size of about 15.30 mm, at velocities of 50.10 m/s, 59.43 m/s, 63.32 m/s, and 69.48 m/s. Repeatability tests were also conducted on each group to optimally control the velocity difference between each sample group. After comminution, the granite fragments of each group were collected, sieved, weighed, and the cumulative mass distributions were calculated, which are shown in Table I.
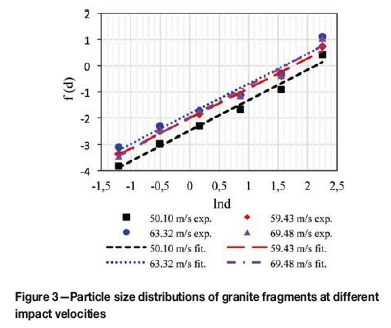
The least squares regression method was used for best-fit analysis of the particle size distributions at different impact velocities. The analysis was carried out on the cumulative mass distribution, and the results are shown in Figure 3. The distribution functions and correlation coefficients are presented in Table II. The distribution function is linear with respect to ln(d) under the experimental impact velocity. The correlation coefficients of the fitting equation are in the range 0.97-0.99, indicating that the Weibull distribution function can be used to describe the particle size distribution of the broken granite particles after impact crushing.
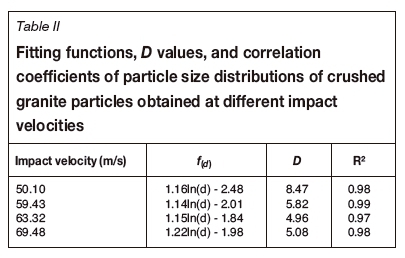
The relationship between the Weibull modulus n and the impact velocity is shown in Figure 4, from which it is evident that Weibull modulus initially decreases and then increases with increasing impact velocity. At an impact velocity of about 60 m/s, the discreteness of the particle size distribution reaches the maximum, suggesting that the mass distribution of progeny fragments in each size range is not uniform.
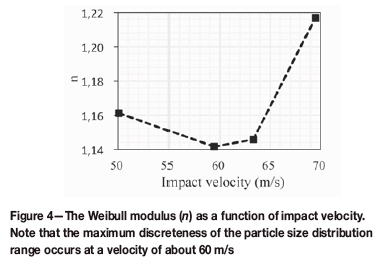
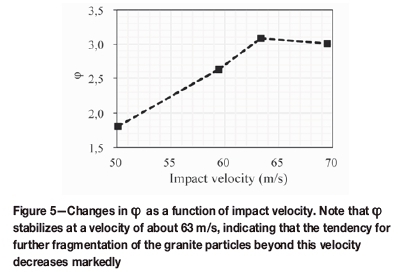
Figure 5 shows changes in the value of φ with changing impact velocity. As impact velocity increases, the value of φ increases rapidly and then tends to stabilize, demonstrating that the greatest fragmentation occurs at the highest impact velocity. As the degree of fragmentation increases, the ability of the granite particles to resist external forces gradually strengthens, and more energy is needed for further fragmentation. Thus, when the impact velocity reaches a relatively high value, about 63 m/s in this case, further increases in fragmentation decrease markedly.
Influence of primary feed size on particle size distribution
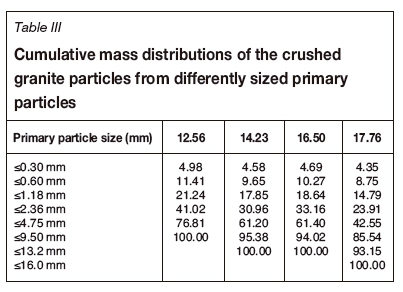
The average feed particle size of the granite used in VSI crushing is normally about 15 mm. To test the influence of feed particle size, a further four groups of spheroidal granite particles were prepared for further experimentation, with particle sizes of 12.56 mm, 14.23 mm, 16.50 mm, and 17.76 mm. The crushing experiments were conducted at impact velocities of about 60 m/s, with post-treatment of the granite fragments (collection, weighing and analysis) as before. The cumulative mass distributions of the sand products from these differently sized primary particles are shown in Table III.
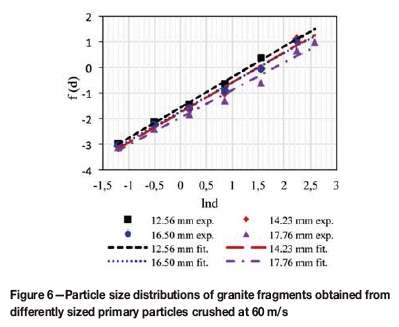
As before, the least squares regression method was used for best-fit analysis of the particle size distributions based on differently sized primary particles, carried out on the cumulative mass distribution (Figure 6). The distribution function and correlation coefficients are presented in Table IV. The distribution function is again linear with respect to ln(d), with high correlation coefficients (0.98-0.99). This provides further evidence that the Weibull distribution function can be used to describe the particle size distribution of fragmented granite particles subjected to impact crushing.
The relationship between the Weibull modulus n and the primary particle size is shown in Figure 7, which indicates that n decreases as primary particle size increases. The discreteness of the particle size distribution of the crushed granite therefore becomes greater.
Figure 8 shows the relationship between φ and the primary particle size, and it is evident that as the primary particle size increases, the φ value decreases. This indicates that when the impact velocity is around 60 m/s, the degree of fragmentation of the granite particles decreases as the primary particle size increases. This is because granite is a brittle material with a variety of defects, including cleavage surfaces, micro-cracks, and macro-cracks. The large primary particles contain more macro-cracks. Under the instantaneous impact force, macro-crack extension occurs first, to a certain extent, and the particle is broken, which results in a decrease in particle size. However, in this process, the kinetic energy of the progeny fragments decreases rapidly and becomes insufficient for further crushing, so the particle size of the final progeny fragments is relatively large. For the small primary particle sizes, there is sufficient initial kinetic energy to overcome the resistance to micro-crack propagation and cleavage surface damage, and the degree of fragmentation is high.
Energy consumption per unit sand product
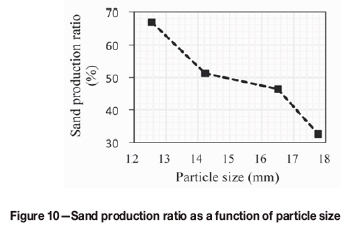
Particles no larger than 4.75 mm were isolated by sieving the fragments, and the mass percentage with respect to total fragments was calculated. The sand production ratio is shown as a function of impact velocity and particle size in Figures 9 and 10, respectively. Within the range of experimental parameters, the sand production ratio from granite particles by a single impact is in the 30-70% range. With increasing impact velocity, the sand production ratio first increases and then decreases. This trend is also evident with increasing particle size, as shown in Figure 10. There is an optimum impact velocity and primary particle size for obtaining the highest sand production ratio: 63 m/s and 15.30 mm, respectively. A high sand production ratio can also be obtained with the smaller primary particle sizes.
As the impact velocity increases, the initial kinetic energy of the particles increases accordingly. The effects of impact velocity and primary particle size on energy consumption per unit sand product are represented in Figures 11 and 12. The energy consumption per unit sand product for impact crushing is in the 0.70-1.60 kWh/t range, and as the impact velocity increases, the energy consumption per unit sand product first decreases, and then increases after about 60 m/s. This increase is also evident in relation to increasing particle size (Figure 12).
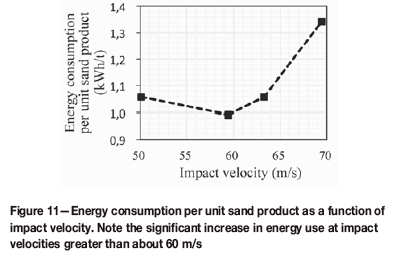
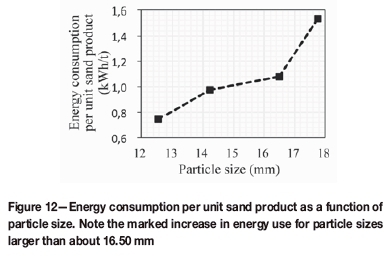
The minimum energy consumption per unit of finished product is at an impact velocity of about 60 m/s. It is also evident that small primary particle sizes should be selected to expend the least amount of comminution energy. However, this might be outweighed by the increased comminution energy required in the previous fragmentation stage to produce such small primary particles. Further study will be required to ascertain the balance between energy consumption in these two crushing stages.
Conclusion
In this study, we used single particle impact crushing to investigate the factors controlling rock fragmentation in VSIcrushing. A high-velocity impact comminution apparatus was designed and built to dynamically fragment granite particles in order to quantify the effect of impact velocity and primary particle size with the aid of a high-speed camera.
The experimental results show that the particle size distribution of the granite fragments accords with the Weibull distribution function. The impact velocity and primary particle size have little effect on the distribution function, but are closely associated with the degree of fragmentation and the uniformity of particle size distribution. The energy consumption per unit sand product can be reduced if an appropriate impact velocity and smaller primary particle size are selected.
Recommendations
The VSI crusher is the preferred equipment for industrial production of manufactured sand. The size of the feed (primary) rock and rotational speed of the rotor are two key factors that affect the fragmentation characteristics. Based on the research findings presented in this paper, in industrial-scale VSI crushing, rocks with smaller primary particle size are recommended. The optimum rotational speed of the rotor (nr) can be approximated by Equation [7]:

where Vp is the velocity of the particles ejected from the rotor, which is generally considered as the impact velocity of the particles, and r is the radius of the rotor.
Taking the minimum energy consumption per unit sand product as the major consideration, the impact velocity is set to about 60 m/s. The degree of fragmentation is moderate with this parameter. The required gradation of the manufactured sand can be achieved by further screening and recombination of the progeny fragments.
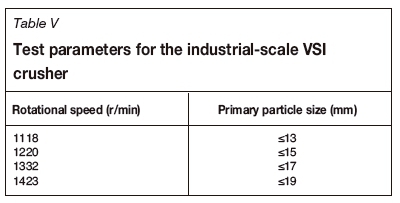
In order to verify the applicability of the research results to industrial-scale VSI crushing, some follow-up experiments should be done. For an existing VSI crusher with rotor radius of 470 mm, the recommended test parameters are shown in Table V. For all the experiments, the capacity of the VSI crusher will be set to the same value of approximately 100 t/h, and the rock used in the tests will be granite. The orthogonal experiment will be conducted, and the power consumption will be measured when the process is considered stable.
Acknowledgements
This work was financially supported by the Major Project Foundation of Science and Technology in Fujian Province (2014H6017, 2016H6013), a special project of the National and International Scientific and Technological Cooperation (2015DFA710402) and Joint Innovation Project of Industrial Technology in Fujian Province.
References
Akesson, U. and Tjell, B. 2010. Geological parameters controlling the improvement of manufactured sand using vertical shaft impact crushers instead of cone crushers. Proceedings of 1MPC2010: XXV International Mineral Processing Congress, vol. 1. pp. 547-553. [ Links ]
Bearman, R.A., Briggs, C.A., and Kojovic, T. 1997. Applications of rock mechanics parameters to the prediction of comminution behaviour. Minerals Engineering, vol. 10, no. 3. pp. 255-264. [ Links ]
Bengtsson, M. and Evertsson, C.M. 2008. Modelling of output and power consumption in vertical shaft impact crushers. International Journal of Mineral Processing, vol. 88, no. 1-2. pp. 18-23. [ Links ]
Bengtsson, M. and Evertsson, C.M. 2006. Measuring characteristics of aggregate material from vertical shaft impact crushers. Minerals Engineering, vol. 19, no. 15. pp. 1479-1486. [ Links ]
Cai, G.P., Liu, Z.G., Xu, Q., and Yu, S.K. 2016. Experimental study on impact energy and crushing effect. Mining Research and Development, vol. 36, no. 1. pp. 106-110 (In Chinese). [ Links ]
Cleary, P.W., Sinnott, M.D., Morrison, R.D., Cummins, S., and Delaney, G.W. 2017. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM. Minerals Engineering, vol. 100. pp. 49-70. [ Links ]
Delaney, G.W., Morrison, R.D., Sinnott, M.D., Cummins, S., and Cleary, P.W. 2015. DEM modelling of non-spherical particle breakage and flow in an industrial scale cone crusher. Minerals Engineering, vol. 74. pp. 112-122. [ Links ]
Deng, Y., Chen, Y., Jin, Y., and Zou, D.W. 2016. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. Journal of Natural Gas Science and Engineering, vol. 33. pp.231-239. [ Links ]
Gopalakrishnan, K.M. and Murugesan, R. 2015. Effect of rock fractured materials replacement in concrete-its strength and durability study. International Journal of Earth Sciences and Engineering, vol. 8, no. 1. pp. 470-475. [ Links ]
Hu, Z.Z., Zhuang, Y.M., Cai, T.Y., and Chen, X.P. 2015. Experimental study on energy consumption and particle size distribution of single particle coal under impact crushing. Journal of China Coal Society, vol. 40. pp. 230-234 (In Chinese). [ Links ]
Jiang, H.X., Du C.L., and Liu S.Y. 2013. The effects of impact velocity on energy and distribution of rock crushing. Journal of China Coal Society, vol. 38. pp. 604-609 (In Chinese). [ Links ]
Johansson, R. and Evertsson, M. 2014. CFD simulation of a centrifugal air classifier used in the aggregate industry. Minerals Engineering, vol. 63. pp. 149-156. [ Links ]
Li, J.P., Zheng, K.H., and Du, C.L. 2013. The distribution discipline of impact crushed on coal and gangue. Journal of China Coal Society, vol. 38. pp. 54-58 (In Chinese). [ Links ]
Li, X.B., Zhou, Z.L., Zhao, F.J., Zuo, Y.J., Ma, C.D., Ye, Z.Y., and Hong, L. 2009. Mechanical properties of rock under coupled static-dynamic loads. Journal of Rock Mechanics and Geotechnical Engineering, vol. 1, no. 1. pp. 41-47. [ Links ]
Luo, M., Yang, J.H., and Fang, H.Y. 2014. An investigation on sand production of vertical shaft impact crusher using EDEM. Advanced Materials Research, vol. 1004-1005. pp. 1226-1230. [ Links ]
Napier-Munn, T.J., Morrell, S., Morrison, R.D., and Kojovic, T. 1996. Mineral Comminution Circuits: their Operation and Optimisation. Julius Kruttschnitt Mineral Research Centre, University of Queensland. [ Links ]
Narayanan, S.S. 1985. Development of a laboratory single particle breakage technique and its application to ball mill scale-up. PhD thesis, university of Queensland (JKMRC), Australia. [ Links ]
Nikolov, S. 2002. A performance model for impact crushers. Minerals Engineering, vol. 15, no. 10. pp. 715-721. [ Links ]
Nikolov, S. 2004. Modelling and simulation of particle breakage in impact crushers. International Journal of Mineral Processing, vol. 74, Supplement. pp. 219-225. [ Links ]
Ovalle, C., Frossard, E., Dano, C., Hu, W., Maiolino, S., and Hicher, P.Y. 2014. The effect of size on the strength of coarse rock aggregates and large rockfill samples through experimental data. Acta Mechanica, vol. 225, no. 8. pp. 1-18. [ Links ]
Paluszny, A., Tang, X.H., Nejati, M., and Zimmerman, R.W. 2015. A direct fragmentation method with Weibull function distribution of sizes based on finite- and discrete element simulations. International Journal of Solids and Structures, vol. 80. pp. 38-51. [ Links ]
Rosin, P. and Rammler, E. 1933. The laws governing the fineness of powdered coal. Journal of the Institute of Fuel, vol. 7. pp. 29-36. [ Links ]
Saeidi, F., Tavares, L.M., Yahyaei, M., and Powell, M. 2016. A phenomenological model of single particle breakage as a multi-stage process. Minerals Engineering, vol. 98. pp. 90-100. [ Links ]
Sahoo, R.K., Weedon, D.M., and Roach, D. 2004a, Single-particle breakage tests of Gladstone Port Authority's coal by a twin pendulum apparatus. Advanced Powder Technology, vol. 15, no. 2. pp. 263-280. [ Links ]
Sahoo, R.K., Weedon, D.M., and Roach, D. 2004b. Degradation model of Gladstone Port Authority's coal using a twin-pendulum apparatus. Advanced Powder Technology, vol. 15, no. 4. pp. 459-475. [ Links ]
Sanchidrián, J.A., Ouchterlony, F., Moser, P., Segarra, P., and López, L.M. 2012. Performance of some distributions to describe rock fragmentation data. International Journal of Rock Mechanics and Mining Sciences, vol. 53. pp. 18-31. [ Links ]
Sanchidrián, J.A., Ouchterlony, F., Segarra, P., and Moser, P. 2014. Size distribution functions for rock fragments. International Journal of Rock Mechanics and Mining Sciences, vol. 71. pp. 381-394. [ Links ]
Shi, F.N., Kojovic, T., Larbi-Bram, S., and Manlapig, E. 2009. Development of a rapid particle breakage characterisation device - The JKRBT. Minerals Engineering, vol. 22, no. 7-8. pp. 602-612. [ Links ]
Weedon, D.M. and Wilson, F. 2000. Modelling iron ore degradation using a twin pendulum breakage device. International Journal of Mineral Processing, vol. 59, no. 3. pp. 195-213. [ Links ]
Weibull, W. 1939. A statistical theory of the strength of materials. Proceedings of the American Mathematical Society, vol. 151, no. 5. pp. 1-45. [ Links ]
Weibull, W. 1951. A statistical distribution function of wide applicability. Journal of Applied Mechanics, vol.18. pp. 293-297. [ Links ]
Zhang, Z.X., Kou, S.Q., Jiang, L.G., and Lindqvist. P. 2000. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning. International Journal of Rock Mechanics and Mining Sciences, vol. 37, no. 5. pp. 745-762. [ Links ]
Paper received May 2017
Revised paper received Jul. 2017














