Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.118 n.5 Johannesburg May. 2018
http://dx.doi.org/10.17159/2411-9717/2018/v118n5a6
PAPERS OF GENERAL INTEREST
Determination of stable spans in UG2 excavations
B.P. WatsonI; R. GerberII
IVisiting Professor - School of Mining Engineering, University of the Witwatersrand, Johannesburg
IIAnglo American Platinum, Amandelbult Complex, Thabazimbi
SYNOPSIS
The hangingwall of the UG2 Reef is characterized by stratification in the form of thin and weakly cohesive chromitite stringers that can vary in number and height above a stope. These stringers, in conjunction with shallow-dipping thrust faulting, endemic across the platinum-bearing reefs of the Bushveld Complex, affect the maximum span that can be safely mined. The paper describes the research that was carried out to determine the interaction of support with the rock mass in both conventional and mechanized workings, and provides insights into stable span determination where excavations are intersected by a shallow-dipping thrust structure. Four important issues are highlighted.
1. Mine pole and pack support has a greater influence on stability than span in the context of the studied database for conventional mines.
2. Shallow-dipping discontinuities are a dominant feature in stability analyses.
3. The height of the vertical tensile zone does not restrict the fallout height if persistent shallow-dipping structures are present.
4. In the context of the numerical modelling shown in the paper, a span of 6 m is safe when 1.8 m long, full-column resin bolts are used at a support resistance of 48 kN/m2, regardless of the k-ratio or height of the triplets (intersections must be dealt with separately).
Several leading practices have been developed in recent years to identify and timeously support hazardous structures.
Keywords: thrust fault, dome structure, stable span, triplets, conventional mining, mechanized mining, UG2 Reef, vertical tensile zone.
Introduction
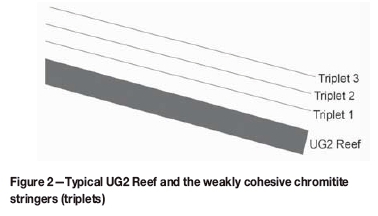
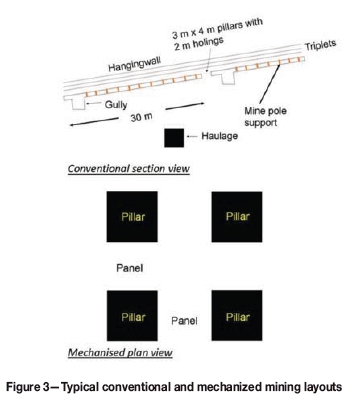
The UG2 Reef is widely mined in the South African Bushveld Complex (Figure 1). It is a tabular, gently dipping orebody as shown in Figure 2. The hangingwall of the UG2 Reef is characterized by stratification in the form of thin and weakly cohesive chromitite stringers (triplets) that can vary in number and height above a stope. Traditionally this reef has been extracted conventionally (Figure 3) using mine poles and packs as support. Increasingly it is extracted using mechanized (Figure 3) or partially mechanized mining methods, and these stopes or zones have to be supported on tendons.
The analyses described in this paper are based on work performed on a PlatMine project (Watson et al., 2007). Most of the original PlatMine work was done in conventional stopes, and was included in this paper to highlight the impact of persistent shallow-dipping discontinuities on stability. Sensitivity analyses were done on mechanized stopes supported on tendons. The paper describes stable span determination in both conventional and mechanized stopes where a shallow-dipping thrust structure has been intersected. There are some interesting findings that are applicable to both mining methods, which are highlighted in the conclusions. Significantly more work has been added to the original PlatMine project in the paper.
For any given situation, the stability of a UG2 hangingwall depends upon the presence or absence of shallow-dipping thrust structures, height and spacing of the chromitite bands (triplets) above the reef (Figure 2), the stoping span, the rock mass rating, the support resistance, and depth of penetration (if tendons are used). The conditions for stability, incorporating all these variables and their interactions, have to be determined in order to develop a design methodology to determine stable spans for the mining of the UG2 Reef.
Three research approaches were employed to evaluate the comparative significance of the stability parameters, and to determine stable panel spans:
► Rock mass rating systems
► Hangingwall failure mechanisms
► Numerical modelling, including calibration and sensitivity analyses.
The first approach involved a suitable rock mass rating system to address the unique problems associated with the chromitite bands above the UG2 Reef. Secondly, modes of failure were determined from documented collapses. Finally, numerical modelling was used to perform sensitivity analyses on various stability parameters and support configurations.
Literature review
Kirkaldie (1988) identified a total of 28 parameters that may influence the strength, deformability, permeability, or stability behaviour of rock masses. Of these parameters 10 are related to rock material properties, 10 to properties of discontinuities, and 8 are hydrogeological properties. Because it is often difficult or impossible in a general characterization to include the many variables in such a complex natural material, it is necessary to develop suitable systems or models in which the complicated reality of the rock mass can be simplified through the selection of a limited number of representative parameters.
Rock mass classification systems are empirical methods (based on case studies) that quantify the integrity of the rock mass and which can be used to estimate mechanical properties for excavation and support design. Rock mass classification systems consider combinations of some of the following components making up a rock mass:
► Intact rock strength
► Field stresses
► Joint persistence
► Joint spacing
► Joint surface condition
► Joint orientation
► Groundwater.
Some important considerations required for rock mass evaluations in shallow-dipping, tabular stopes are discussed below.
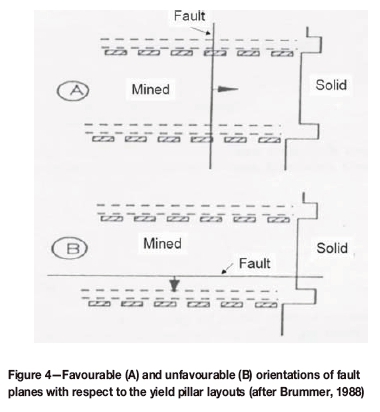
► Discontinuity orientation. Brummer et al. (1988) suggested that faults or persistent joints striking parallel to pillar lines (Figure 4) are considerably less stable than those perpendicular to the pillar lines.
► Joint alteration. Instability often occurs when the joint filling is thicker than 3 mm (Watson, 2003).
► Joint dip angle with respect to the orientation of the stope hangingwall. This is an important consideration for the evaluation of shallow-dipping, tabular stopes (Watson, 2003).
► Joint persistency. This factor would be in multiples of 10 m. It was suggested that a factor of 2 or greater would be considered persistent enough to cause a panel collapse if pillar lines were sub-parallel to such a joint set (Roberts, 2002).
► Stress condition. High horizontal stress can create fractures that curve into the hangingwall, providing release surfaces for large falls of ground (FOGs). Very low stress conditions can also be problematic, resulting in blocks sliding out of the hangingwall even in otherwise good rock mass conditions (Watson, 2003).
►Presence of water. Water lubricates and hence reduces the frictional resistance of joints to movement.
Fourteen rock mass rating systems were assessed by Watson (2003). Of these rock mass classification systems, four were considered relevant for the evaluation of stability in shallow-dipping, tabular panels. These findings agree with an assessment by Swart et al. (2000) for the Bushveld Complex chrome mines. The systems are:
► the Geomechanics Classification or Rock Mass Rating (RMR) system developed by Bieniawski (1989)
► the Norwegian Geotechnical Institute rock quality index (Q) system developed by Barton, Lien, and Lunde (1974)
► the Mining Rock Mass Classification or Modified Rock Mass Rating (MRMR) system developed by Laubscher (1990)
► the Modified Stability Graph method through the use of the Modified Stability Number (N'), originally developed by Mathews et al. (1981) and later modified by Potvin (1988) and others.
The N' system was found to correlate consistently to observed conditions underground (Watson, 2003) and is simple to use. This system was employed as a basis for development of the New Modified Stability Graph Method (N"), specifically for the platinum industry (Watson, 2003). The N" method was used in rock mass rating analysis and a database of evaluated stable, unstable, and collapsed sites was collected for the UG2 Reef by a number of rock engineers across the Bushveld Complex. Statistical analyses were performed on the collected data to determine the relevance of each parameter.
Statistical analyses of geotechnical data
A database of records, including the parameters that make up N", along with depth, physical dimensions, and support arrangements was collected for 159 panels - ample data for back-analysis by regression. All of the data was from conventional mining stopes with various configurations of mine pole and pack support (a full description of the database is provided in the PlatMine report (Watson et al., 2007). The aim was to determine the comparative influence of the rating parameters, span, and support on stability. The physical dimensions of the panels were described by hydraulic radius (HR) as shown in Equation [1].

where w and h are the width and length of a panel.
The relative contributions of the parameters in the N" system to stability were determined by logistic regression analysis. It was established that the relationship between HR and the probability of panel collapse does indeed effectively correlate with panel failure (Figure 5): fitted into a logistic regression model with HR, it predicts collapse with an accuracy of around 77%, although with a large overlap.
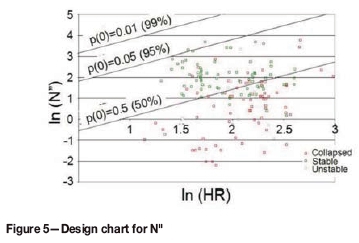
The overlap could have arisen because the range of spans in the database was limited to what would normally be stable. Conversely, the analysis showed a relatively strong relationship between support resistance and probability of stability.
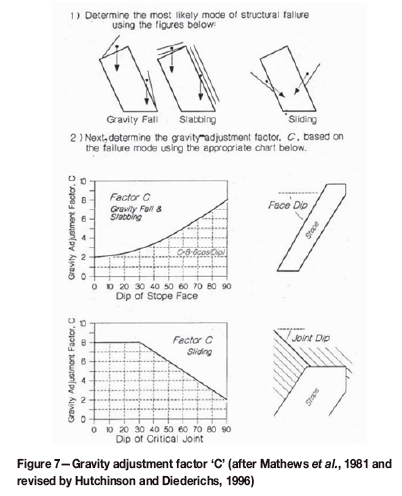
A statistical evaluation and reworking of the N" equation (Equation [2]) was done to provide a best fit between collapsed and stable panels. A significantly better fit was found (confidence level: about 93 %) when Equation [5] (N(3)) was compared to support resistance (SR) and a factor describing the joint filling. The analysis suggests that support resistance plays a more influential role than span for a given discontinuity condition, within the context of the spans in the database. Note that the dominant parameter in this equation is the B-value, which is a factor accounting for the dip orientation of the most influential discontinuity (Figure 6). The The C-value (Equation [1]) accounts for the influence of gravity on the hangingwall blocks (Figure 7).


where

RQD is calculated from the Palmström (1982) equation (Equation [4]).

where Jv is the average number of joints in a cubic metre. Ja, Jr, Jn, Jw, and SRF are the parameters used in the Q rock mass rating system originally developed by Barton, Lien, and Lunde (1974) and modified slightly to suit local conditions (Watson, 2003).
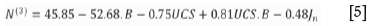
where UCS is the uniaxial compressive strength of the rock.
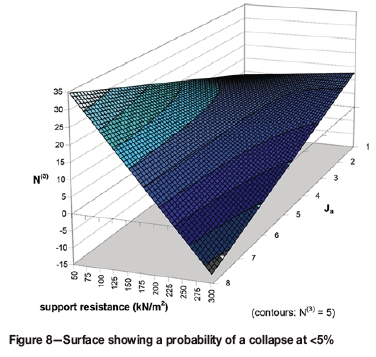
Note that although Ja was important in influencing the statistical evaluation, N(3) did not depend on this factor. The evaluation showed a synergistic effect of SR and Ja and because of it, these two factors could not be completely separated. Therefore, three variables were involved, and a single two-dimensional chart was insufficient. In Figure 8, the blue surface separates upper and lower regions of stability and instability, respectively (probability of collapse < 5%). Importantly, the analysis shown in the figure did not depend on HR. The derivation of Equation [5] is well described in the original PlatMine report (Watson et al., 2007).
Evaluation and summary of the empirical RMR approach
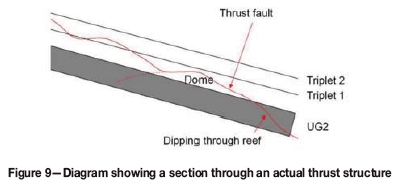
The statistical evaluation of the geotechnical data suggested that the most significant stability parameter is persistent, shallow-dipping or curved discontinuities. Generally, these features are associated with thrust fault structures, which appear to be endemic across the platinum-bearing orebodies of the Bushveld Complex. These discontinuities dip in and out of the reefs, resulting in the development of dome structures in the hangingwall during mining (Figure 9).
The results of the empirical evaluation also indicate that, under the conditions of the panels in the database, changing the support resistance would yield better results than changing the panel span. However, this should be understood in the context of a maximum minor span of 30 m, the mine pole support used in the evaluated panels, and the depth below surface range of between 32 m and 970 m.
Analyses of panel collapse reports
Reports on 69 collapsed sites in the database were investigated to determine the most common causes of panel collapse.
The majority of collapse occurred on persistent, shallow-dipping or curved discontinuities (thrust faulting features). None of the collapses could be positively connected to high stress conditions or fracturing. In some cases, visible sagging of the hangingwall towards the centre of the panel suggested parting on the triplets some 3.5 m above the stope, indicating excessive panel spans for this middling between the stope and the triplets. The heights of collapses recorded without the assistance of shallow-dipping or curved joints were invariably controlled by the Leader seam or triplets. Parting in the hangingwall can theoretically occur only within the vertical tensile zone (VTZ). The FOGs with a fallout thickness greater than the VTZ height all occurred on shallow-dipping or curved structures, showing that the height of the VTZ does not restrict the fallout height if these structures are present. Since most of the FOGs studied in the PlatMine project involved shallow-dipping or curved discontinuities as the primary release surface, it was considered necessary to include the effects of such discontinuities on stability in the numerical models.
Numerical modelling to determine the effects of a shallow-dipping discontinuity
Case study on a conventional stope
A highly appropriate 2D case study was made available at 'mine A'. Stopes were mined from one side of a raise line, from 2 m to a planned 30 m width on strike and about 120 m on dip (Figure 10). A shallow-dipping thrust fault dipped in and out of the reef, causing several panel collapses that were used to calibrate the model. The joint sets at the site were similar to the common joints observed generally across the platinum mines.

2D UDEC models (Shi and Goodman, 1987) were set up with the Barton-Bandis joint addition. The models incorporated the two commonly observed joint sets, the triplets, and a thrust fault structure at 20° to the strata. The analyses were performed using laboratory-derived input parameters and actual measurements made at the mine (Tables I-III). A k-ratio of 0.16 was assumed due to the proximity of the workings to the side of a mountain.
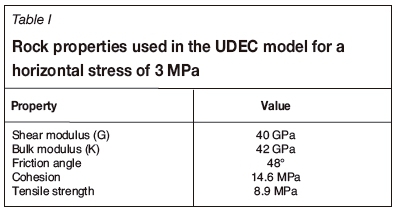
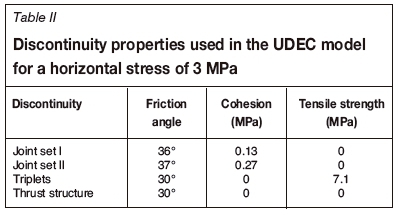
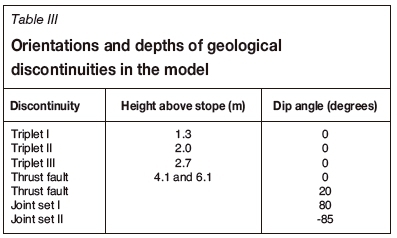
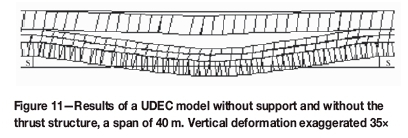
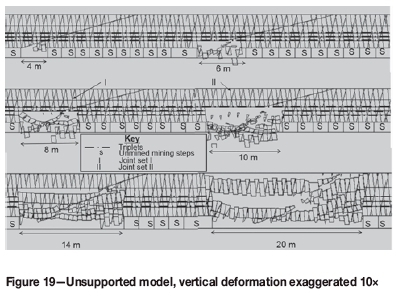
A suite of models was run without the thrust structure and without support. The models were set up using the input parameters provided in Tables I-III so that an initial span of 3 m could be increased in steps of 2 m. The models were terminated when the unsupported span reached 40 m. No failure occurred (stable conditions), although parting took place on the triplets and the plane at 4.1 m above the stope, as shown in Figure 11. The maximum vertical deformation was 15 mm at a minor span of 40 m.
The model above was modified to include thrust faults and a suite of tests was run without support as shown in Figure 12. Blocks that formed between the shallow-dipping thrust fault and the two joint sets fell out as the span was increased, showing that there is no stable, self-supporting span. At a span of 5 m the rock mass collapsed up to triplet I (1.3 m above the stope). An increase of the span by 2 m resulted in a migration of the unstable zone up to triplet II at 2.0 m above the stope. The conditions at spans of both 5 m and 7 m were observed underground at mine A in unsupported or under-supported panels. At a span of 9 m, the entire rock mass below triplet III (at a height of 2.7 m) became unstable. At a span of 15 m, a collapse occurred up to the horizontal thrust fault at 4.1 m above the stope.
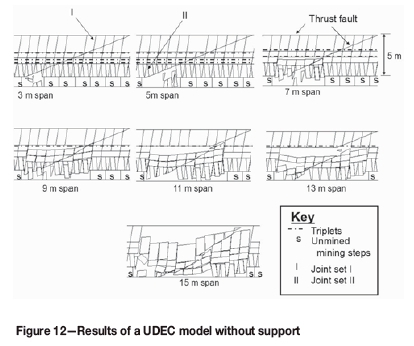
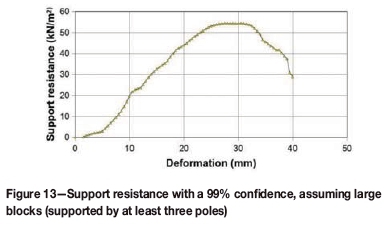
A support system of 170 mm diameter mine poles spaced 2 m χ 2 m on dip and strike was originally used at the mine. A downrated support resistance of 50 kN/m2 was assumed from underground measurements. A curve for the elongate support system is provided in Figure 13. The results of the models are shown in Figure 14. Stable conditions were predicted up to a span of 9 m. At a span of 11 m the model showed that parting had occurred on all three triplets as well as at 4.1 m above the stope. A collapse occurred up to triplet III at a span of 13 m, which is a modest improvement of 4 m over the unsupported scenario.

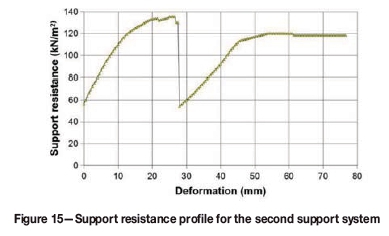
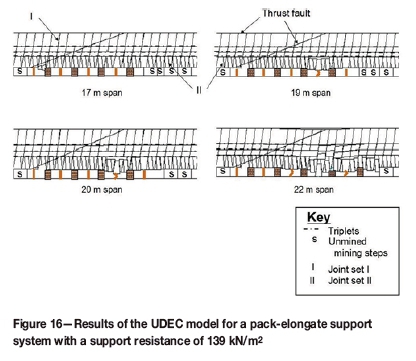
A new support system was introduced to the mine, which included larger diameter mine poles and packs. This condition was modelled assuming a downrated support resistance of 135 kN/m2. In the model, only the mine poles were prestressed (to 150 kN) and the profile of support resistance to closure was determined from underground measurements (Figure 15). A great improvement, both in stable panel span and rock mass conditions, was achieved by this support system (Figure 16). Unstable conditions occurred at a span of 19 m and a final collapse at 22 m. Note that parting initiated at 4.1 m above the hangingwall, when the span reached 17 m. The modelled unstable conditions were observed underground.
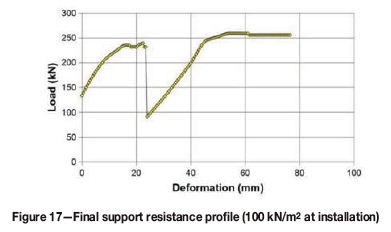
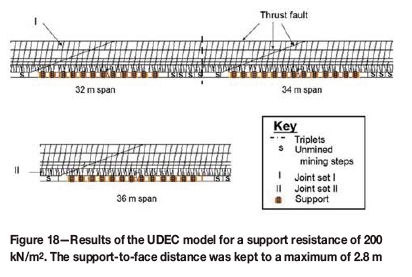
A support system which was prestressed to 100 kN/m2 at installation and provided a peak resistance of 200 kN/m2 (Figure 17) was introduced to the mine. This support system was technically able to support a rock height of 5 m, with only about 5 mm deformation. To ensure worst-case conditions in the model, a second horizontal discontinuity, with properties similar to the thrust fault, was set up at 6.1 m above the stope. This was slightly higher than the support capacity. The results are shown in Figure 18. Spans were increased in the model to a maximum of 36 m and stable conditions were predicted in all runs. However, it should be noted that FOGs occurred in the face area when the maximum support-to-face distance was 3.6 m. These FOGs did not occur in the model when the support-to-face distance was reduced to 2.8 m, and this was also confirmed by underground observations. The peak support resistance used at this mine was very high, and it may be unrealistic to apply as a best practice for preventing large-scale instabilities. Mitigation strategies based on knowledge of the height and behaviour of potentially hazardous structures are preferred.
Sensitivity analyses on mechanized scenarios
The calibrated model used in the case study was modified to provide a better representation of the general UG2 Reef conditions and to cater for mechanized stopes where only roofbolts are used:
► The second set of joints that only extended up to the first triplet at mine A was extended up to 6.1 m above the model to provide a worst-case scenario
► k-ratios of 0.5 and 2 were applied
► Models were run at depths of 200 m, 400 m, and 1000 m below surface.
All models included thrust structures that were inclined at 0° and 20° or 30° to the strata. The horizontal structures were located at 4.1 m and 6.1 m above the stope. Note that the models do not cater for intersections, where most collapses occur. This issue will be discussed later in the paper. Tunnel widths were increased in 2 m span intervals to determine the maximum stable span with the imposed conditions. A vertical exaggeration of ten was used to highlight vertical deformation in all the diagrams from Figures 19 to 28.
Sensitivity analyses were performed on:
► The height of the parting planes
► Length and spacing of bolts
► Prestressing of bolts
► Depth of workings below surface
► k-ratio.
The first model (Figure 19) shows the unsupported base case. All the parameters shown in Table I to Table III were applicable to this model. The tunnel was progressively mined wider to determine the spans at which panel collapses are likely to occur.
The models depicted in Figure 19 show that FOGs occur at every tunnel width, as expected, because of the shallow-dipping thrust structure. At a span of 6 m a collapse occurred up to triplet I, a height of 1.3 m. The collapse height migrated up to 2.0 m (triplet II) at a span of 8 m, and up to 2.7 m (triplet III) at a span of 10 m. Collapse heights of 4 m and 6 m occurred at spans of 14 m and 20 m respectively.
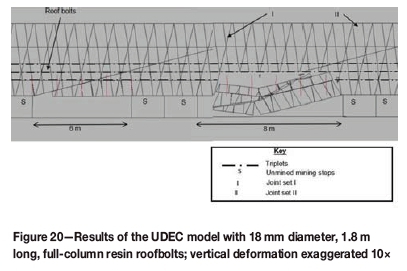
A set of models was run with 18 mm diameter, 1.8 m long full-column resin roofbolts, spaced 1.5 m χ 1.5 m. The reinforcement properties shown in Table Table IV were applied in the models, which provided a support resistance of 48 kN/m2 over the length of the bolts. The results of the investigation are shown in Figure 20.
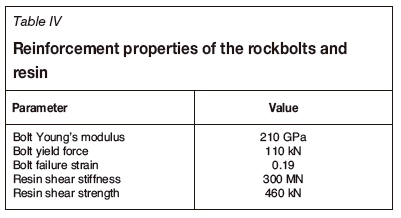
Stable conditions with minor FOGs were observed until a span of 8 m. Note that the reach of the bolts extended to just beyond triplet I. The panel collapse occurred up to triplet II at exactly the same span as in the unsupported models. Importantly, the supported models were able to control most of the FOGs. Suitable surface support is needed to control the small falls between the bolts.
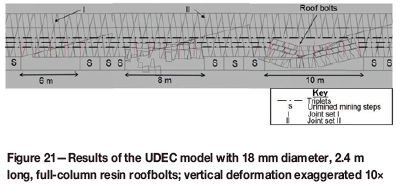
A set of models was run to test the effects of increasing the bolt length to 2.4 m. The results showed unstable conditions at a span of 8 m and a collapse at 10 m (Figure 21). The unstable conditions at 8 m were probably the result of parting on triplet II and bolt yield. A collapse occurred up to triplet III at a span of 10 m; again as observed in the unsupported model.
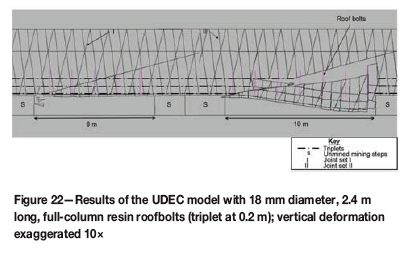
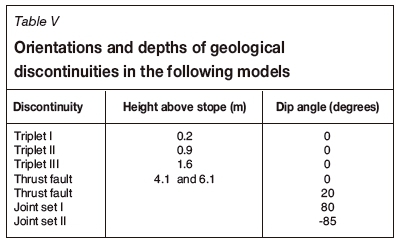
Some models were run to determine the behaviour of supported rock where the triplets are much closer to the excavation. The triplets were shifted down by 1.4 m, but the distances between the triplets remained unchanged. The thrust faulting and jointing were kept the same as in the previous models. A list of orientations and depths of the geological discontinuities in the new models is shown in Table V. The model results (Figure 22) show more stable conditions at a span of 8 m than the case where the bolts did not penetrate through the third triplet (Figure 21). However, a panel collapse still occurred up to the third triplet at a span of 10 m. The collapse occurred because the thrust fault extended above the reach of several rows of roofbolts.
A similar set of models was run with the thrust fault angle adjusted up to 30° to the strata. The results were the same as for the 20° fault, and again a collapse occurred at a span of 10 m.
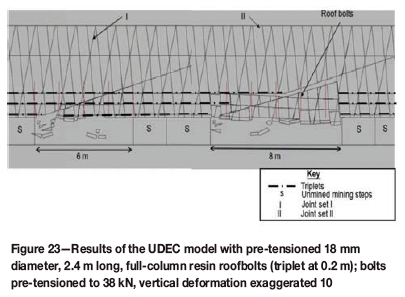
The model shown in Figure 22 (thrust fault at 20°) was re-run once more with a pre-tension of 38 kN on each bolt at installation. A collapse occurred at a smaller span (Figure 23). The reason for the earlier failure is not clear. Previous modelling work by consultants showed that a small pretension on tendon support elements definitely improves deflection and thus stability. However, the thrust structure was not included in those models.
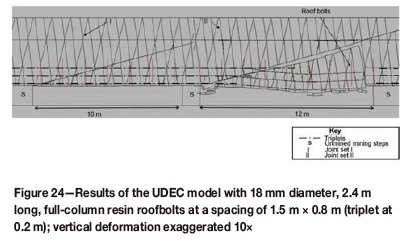
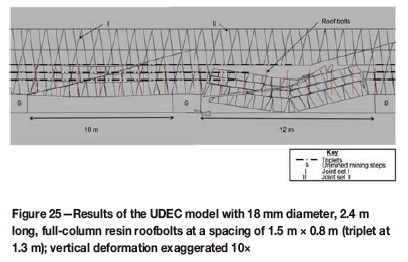
An investigation was conducted to determine the effect of changing the support resistance on stability. The spacing of roofbolts used in Figure 21 was reduced to 1.5 m χ 0.8 m. The support resistance was thus increased from 48 kN/m2 to 92 kN/m2, but the length and diameter of the bolts were kept the same. The results showed an improvement in span with support resistance, with the critical span increasing from 10 m to 12 m (Figure 24). A similar set of models (with the higher support resistance) was run with the triplets at 1.3 m (same as in Figure 21). In this instance the bolts did not penetrate through the upper triplet, but the critical span remained at 12 m (Figure 25). However, significantly more vertical displacement was calculated at a span of 10 m in this model than when the triplets were closer to the reef, due to parting on the upper triplet. Parting took place on this upper triplet at the same span as a collapse in the unsupported scenario (10 m), but the support was able to prevent a collapse and increased the critical span by 2 m.
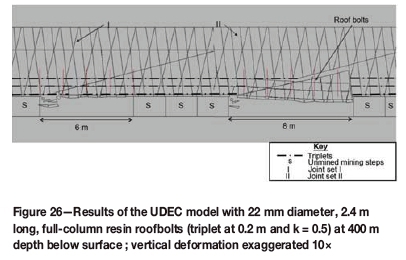
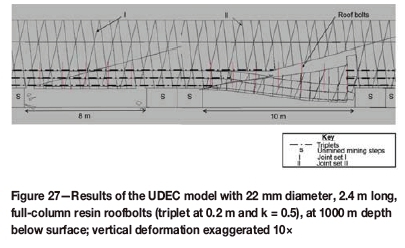
A set of models was run to determine the effect of k-ratio on stability. The height and orientations of discontinuities were as shown in Table V, and all parameters as for the model depicted in Figure 22, except the k-ratio, which was reduced to 0.5. The results show that k-ratio does affect stability conditions, and the decrease in k-ratio resulted in a decrease in stable-span width (Figure 26) for the given support and geotechnical conditions. A collapse occurred at 8 m (2 m less than in Figure 22). A similar set of models was run at depths of 200 m and 1000 m, keeping the k-ratio at 0.5. The stable span was the same at 200 m, but there was an improvement at 1000 m (Figure 27).
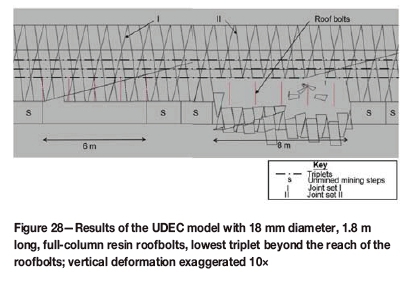
For completeness, a model was run with the triplets shifted up. Triplet I was adjusted to 1.9 m above the hangingwall, i.e. just above the reach of the 1.8 m long roofbolts (Figure 28). The results were the same as when triplet I was at 1.3 m (Figure 20).
Evaluation of the numerical modelling results
The models were calibrated on conventional stopes where elongate and pack support was used. Shallow-dipping thrust faults were included in all the analyses as these structures occurred at the calibration site and have been observed across the Bushveld Complex platinum reefs. At the calibration site, stable conditions were predicted up to minor spans of 40 m, if an active support system, of 100 kN (at installation) and a maximum capacity of 200 kN was installed early. This support resistance was sufficient to maintain stability over the said minor span, even when parting planes existed above the reach of the support.
The conventional mining model was modified to cater for more general UG2 mining conditions. The aim of this exercise was to determine safe mining spans in a mechanized environment where roofbolts are used. Shallow-dipping thrust structures were again included in the sensitivity analyses. The results of the investigation show that provided 1.8 m long full-column resin roofbolts are installed early on a support resistance of 48 kN/m2 (bolt spacing of 1.5 m χ 1.5 m), a span of 6 m can be safely mined, irrespective of the height of the triplets or magnitude of the k-ratio. However, it should be noted that this finding is restricted to the conditions and parameters used in the models and described here. There may be conditions that were not modelled, and those cases should be treated differently.
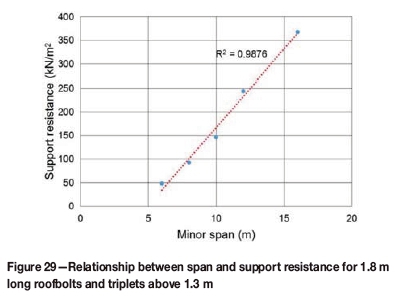
The models show that surface support is required between bolts where shallow-dipping thrust structures cut through the hangingwall or if triplet 1 is close to the hangingwall. It is interesting to note that the less intense vertical jointing above triplet I in the conventional models resulted in similar collapse spans as in the mechanized models when comparing the unsupported results (Figures 12 and 19). The finding agrees with the statistical evaluation of the rock mass ratings, which shows that shallow-dipping, persistent discontinuities are the predominant factor in stable span determination and overshadow the other geotechnical parameters when they are present. An increase in bolt length to penetrate the second triplet at 2.0 m improved conditions, with a collapse at 10 m, although unstable conditions were predicted at 8 m. When the heights of the triplets were dropped to ensure that the bolts were able to penetrate all the triplets, stable conditions were shown at 8 m and a collapse occurred at 10 m. An improvement in critical span was also observed when the support resistance was increased, even though the elements remained the same length and did not penetrate all the triplets. A sensitivity analysis was done on support resistance by progressively reducing the spacing of support elements. In this analysis the support length was 1.8 m and the height of triplet l was 1.3 m. In these models the bolts penetrated only through triplet I, as shown in Figure 20. The results indicate an almost linear relationship between span and support resistance for the given geotechnical conditions and support type (Figure 29).
The angle of the shallow-dipping thrust fault was changed to 30° to the strata to determine if a slightly steeper angle would increase the height of instability at a particular span, and thus reduce the stable span for a given set of conditions. However, no discernible difference was observed. Hutchinson and Diederichs (1996) also show equal severity across the range of dip angles between 10° and 30° to the strata, and suggest that the worst discontinuity angles are within that range (Figure 5).
Pre-tensioning of the bolts resulted in premature unstable ground conditions at 8 m. The reason for the earlier collapse is not clear. Note that much larger lumps fell out during the collapses, which is also observed underground in areas supported with roofbolts.
Interestingly, the models using roofbolt support showed two failure mechanisms: beam failure and wedge failure.
If a collapse occurred on a plane above the reach of the bolts, beam failure took place. Where this plane was below the bolt penetration (and the support resistance was sufficient to carry the weight of the rock below the plane), wedge failure was noted. This wedge failure occurred when a shallow-dipping thrust structure cut through the parting planes. Failure initiated in the zone where the structure was above the reach of the bolts and subsequently caused the bolts that penetrated the plane in tension to fail, one row at a time under a cantilever action.
Under ideal conditions, the maximum achievable stable span with a bolt spacing of 1.5 m χ 1.5 m (48 kN/m2) was shown to be about 8 m. Larger stable spans are often observed underground, even with the same tendon support as used in the models. It should be emphasized, though, that the shallow-dipping thrust fault is not always in the vulnerable position modelled. The models are showing a worst-case scenario. Should it be possible to determine where these structures exist with a high degree of confidence, it would be possible to mine safely at larger spans, accounting for these structures where they exist. At mine B the thrust structures were easily identifiable. Spans of 10 m were mined successfully in areas where the thrust structure did not intersect the stope hangingwall. This scenario agrees with the results shown by the model without a thrust structure (Figure 11). However, the areas affected by the thrust structure had to be properly supported on a separate support system using 4.5 m and 6.0 m long anchors on a close spacing. The actual length and support resistance were calculated at the height of the structure above the hangingwall. Since the introduction of this system, instances of large FOGs have reduced almost to zero, except for instances of human error.
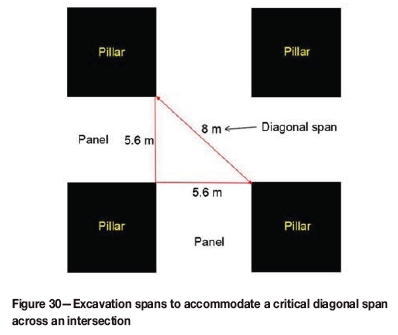
It should be noted that the model assumed an infinitely long panel (into the page). However, in reality there are intersections, or holings, between orthogonal panels. These intersections represent areas of larger span and should also be treated differently, or the spans of the panels should be reduced to ensure that the diagonal across the intersection does not exceed the critical span. For an 8 m critical span, a safe panel span for two equal sized panels intersecting would be 5.6 m (Figure 30).
Leading practices to combat FOGs
Several leading practices have been developed over the past 10 years to enable the early detection of potentially hazardous structures, as well as to determine appropriate local support in the hangingwall of stopes. Some of these practices are summarized below.
► Triggered Action Response Plan (TARP) systems were developed as a hazard identification tool to assist production personnel in the identification of potentially hazardous ground conditions. A TARP consists of a set of documented and known workplace hazards that need to be continuously identified (MOSH, 2017).
► Ground-penetrating radar (GPR) is a risk management tool that can facilitate the identification of potential parting planes and/or critical block-, slab- or wedge-forming discontinuities (Godden, 2011). Potentially unstable ground can often be identified for a distance of approximately 5.0 m above a cut stope hangingwall. Other instrumentation such as borehole cameras in regularly spaced boreholes is also increasingly being used in mechanized stopes to develop isopach plans of potential parting planes.
► Identification of deformation event precursors (Hartzenberg et al., 2017). Effective identification of the precursors can assist in the planning and design processes to ensure appropriate design and layout strategies.
► Support design from a mechanistic understanding of the rock behaviour (Hartzenberg, du Plessis, and Friese, 2016).
► An understanding of instabilities from an understanding of the structural geology (du Plessis, Hartzenberg, and More O'Ferrall, 2017).
Summary and conclusions
The analysis of the FOG reports studied for the PlatMine project showed that FOG height is not restricted by the VTZ if a shallow-dipping fault structure cuts through the strata. Most FOGs have been shown to be connected with shallow-dipping or curved structures. Generally, these structures are associated with thrust faulting, which appears to be endemic across the Bushveld Complex. Dome structures are formed where this structure dips in and out of the reef hangingwall.
The results of the statistical evaluation of the rock mass ratings indicate that, under the conditions of the conventionally mined panels in the database, changing the support resistance would yield better results than changing the panel span. However, this should be understood in the context of a maximum minor span of 30 m, the type of support used in the evaluated panels, and the depth below surface ranging between 32 m and 970 m. The effect of increasing support resistance on stable span was also shown by the stope modelling. In a conventional mining scenario, stable conditions were predicted up to a minor span of at least 36 m if a prestressed mine pole and pack support system was installed at an average prestress load of 100 kN/m2 and a peak resistance of 200 kN/m2, regardless of the height of parting planes. This model was tested on the same mine and the collapses that had been regularly occurring ceased.
Both the FOG reports and the RMR database showed the importance of considering the effects of shallow-dipping thrust faulting on stability. A 2D UDEC model was calibrated on a conventional mining case study at mine A and subsequently modified to cater for generalized bolted, mechanized sections. Sensitivity analyses assumed the worst-case scenario, with a thrust structure present, and were done on:
► The height of the parting planes
► Length and support resistance of bolts
► Prestressing of bolts
► Depth below surface
► k-ratio.
The results of the investigation showed that 6 m is a safe panel span when 1.8 m long, full-column resin bolts are used at a support resistance of 48 kN/m2. This span was found to be safe regardless of the k-ratio or height of the triplets. However, it should be noted that there could be conditions not considered in the models. Any conditions dissimilar to those described in the report should, therefore, be treated differently. Surface support is required between bolts where shallow-dipping discontinuities cut through the hangingwall or the lowest triplet is near the stope surface. Under ideal conditions, i.e. bolt penetration of all three triplets, a maximum span of 8 m seems feasible at the same support resistance. However, an increase in support resistance can improve stability and increase the stable span, even if the triplets are not penetrated by the bolts. It should be noted, though, that the 2D model does not account for intersections, which should be treated separately. Alternatively, the critical span at an intersection should be calculated by using the diagonal across the intersection.
In areas where there are no thrust structures, much larger spans can be mined with less support, but the structures need to be supported separately where they occur. Several leading practices have been developed in recent years to identify hazardous structures and determine appropriate support for localized hazards.
Acknowledgements
The CSIR and PlatMine are acknowledged for facilitating the success of the original research work described in this paper.
Dr J.A. Ryder and Dr D.P. de Carcenac are thanked for the guidance provided in the statistical evaluations of the Rock Mass Rating system. Mine management and rock engineering personnel on the mines are acknowledged for the assistance provided during data collection.
References
Barton, N., Lien, R., and Lunde, J. 1974. Engineering classification of rock masses for the design of tunnel support. Rock mechanics, vol. 6, no. 4. pp 189-236. [ Links ]
Bieniawski, Z.T. 1989. Engineering Rock Mass Classifications. Wiley, New York. [ Links ]
Brummer, R.K., Gay, N.C., Jager, A.J., McKinnon, S.D., Piper, P.S., Roberts, M.K.C., Ryder, J.A., Spottiswoode, S.M., and Wojno, L.J. 1988. An industry guide to methods of ameliorating the hazards of rockfalls and rockbursts. Chamber of Mines of South Africa, Johannesburg. [ Links ]
Du Plessis M., Hartzenberg, A.G., and More O'Ferrall G. 2017. Rock mass instability associated with the formation of regional geological structures along the Bushveld Complex as encountered during the extraction of the UG2 chromitite layer at Lonmin PLC. Proceedings of the 13th 1SRM International Congress of Rock Mechanics, Montreal, Canada, 10-13 May. https://www.onepetro.org/conference-paper/ISRM-13CONGRESS-2015-185 [ Links ]
Godden, S. 2011. The use of remote sensing techniques on the AQPSA mines. S. Godden & Associates Ltd. [ Links ]
Hartzenberg, A.G., du Plessis M., and Friese, A.E.W. 2016. Structurally-related hangingwall alterations contributing to UG2 stope instabilities at Lonmin. Proceedings of EUROCK2016, the 2016 International Symposium of the International Society/or Rock Mechanics (ISRM 2016), Ürgüp, Cappadocia Region, Turkey, 29-31 August 2016. CRC Press. [ Links ]
Hartzenberg, A.G., du Plessis M., and Friese, A.EW. 2017. Unravelling the structural mysteries of the 'Bermuda Triangle' at Lonmin's Saffy Shaft. Proceedings of Rock Mechanics/or Africa (AfriRock 2017), Cape Town, 3-5 October. Southern African Institute of Mining and Metallurgy, Johannesburg. [ Links ]
Hutchinson, D.J. and Diederichs, M.S. 1996. Cablebolting in Underground Mines. BiTech, Vancouver. 406 pp. [ Links ]
Kirkaldie, L. 1988. Rock classification systems for engineering purposes. STP 984. ASTM International, West Conshohocken, PA. 167 pp. [ Links ]
Laubscher, D.H. 1990. A geomechanics classification system for the rating of rock mass in mine design. Transactions of the Institution of Mining and Metallurgy, vol. 90. pp. 257-273. [ Links ]
Mathews, K.E., Hoek, E., Wyllie, D.C., and Stewart, S.B.V. 1981. Prediction of stable excavations for mining at depths below 1000 m in hard rock. CANMET Report. DSS Serial no. OSQ80-00081, DSS File no. 17SQ.23440-0-9020. Deptartment of Energy, Mines and Resources, Ottawa. [ Links ]
MOSH (Mining Industry Occupational Safety and Health). 2017 Chamber of Mines, Johannesburg. http://www.mosh.co.za [ Links ]
POTVIN, Y. 1988. Empirical open stope design in Canada. PhD thesis, Department. of Mining and Mineral Processing, University of British Columbia. 343 pp. [ Links ]
Roberts, M.K.C. 2002. Addressing the problem of joints sub parallel to pillar lines. Contract report number 2002-0339. Johannesburg. [ Links ]
Swart, A.H., Stacey, T.R., Wesseloo, J., Joughin, W.C., le Roux, K., Walker, D., and Butcher, R. 2000. Investigation of factors governing the stability/instability of stope panels in order to define a suitable design methodology for near surface and shallow mining operations. SIMRAC Project Report OTH 501. Safety in Mine Research Advisory Committee (SIMRAC), Johannesburg. [ Links ]
Shi, G. and Goodman, R.E. 1987. Block theory and its application to rock engineering. Prentice Hall, Englewood Cliffs, NJ. [ Links ]
Watson, B.P. 2003. The feasibility of using rock mass ratings for the design of panel spans and support in the shallow to intermediate depth Bushveld platinum mines. MSc thesis, Department of Mining Engineering, University of the Witwatersrand, Johannesburg. [ Links ]
Watson, B.P., de Carcenac, D.P., Roberts, D.P., and Roberts, M.K.C. 2007. The determination of stable spans in stratified UG2 excavations. PlatMine project report 3.9. Miningtek Division of CSIR, Johannesburg. [ Links ]
Paper received Oct. 2017
Revised paper received Apr. 2018














