Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.118 n.4 Johannesburg Apr. 2018
http://dx.doi.org/10.17159/2411-9717/2018/v118n4a8
PAPERS OF GENERAL INTEREST
Application of optimized models through direct block scheduling in traditional mine planning
P.H.A. CamposI; C.E. ArroyoII; N. MoralesIII
IFederal University of Ouro Preto, Brazil
IIDelphos Mine Planning Laboratory
IIIAMTC & DIMIN - Universidad de Chile
SYNOPSIS
Many papers have been published by the scientific community on the development of techniques that use direct block scheduling (DBS) to solve open pit production scheduling problems, and have compared the results obtained with DBS to those obtained with conventional methods for mine planning. The most significant advantage of using DBS is the possibility of maximizing the economic value to each project. However, until recently, the computational complexity of DBS has prevented it from being used to solve problems on an industrial scale, where there are a large number of mine blocks to deal with and many constraints.
While much research has already been conducted and many new tools and algorithms have been developed to solve this global open pit production-scheduling problem, this article proposes the use of optimized models obtained through DBS as part of the conventional medium-term planning methodology to take advantage of its benefits without being hindered by its limitations.
Three different approaches to medium-term planning were compared. First, a renowned software package that is used in the mineral industry was used to execute conventional medium-term scheduling. Then, DBS was used to perform the same task. Finally, a combination of DBS and conventional scheduling was tested. Using the results provided by DBS, sectorization of specific areas was included in the conventional methodology to guide the scheduling and thus allow this combination to produce real benefits, even for large projects.
Keywords: Block scheduling, open pit mining, mine planning, production scheduling.
Introduction
Open pit mine production scheduling is the process of defining and scheduling mine production with the objective of obtaining the maximum possible net present value (NPV) for the project, subject to spatial precedence and various operational constraints (Espinoza , 2012).
It is common practice in the mining industry to represent a mineral deposit as a set of three-dimensional blocks, known as a block model. The production scheduling then consists of defining when, if ever, to extract each of these blocks and the destination to which they should be sent.
There are two methodologies that are mainly used to optimize this form of scheduling, namely 'block-level resolution' and 'aggregation' (Elkington and Durham, 2011). The block-level resolution optimization approach was first proposed by Thys Johnson (1968) and evolved to be known as direct block scheduling (DBS). The aggregation approach splits the scheduling problem into several smaller sub-processes which include, for example, the definition and optimization of the ultimate pit, intermediate pushback selection, and finally, production scheduling. This last approach became known as the conventional planning approach (Elkington and Durham, 2011; Morales et al., 2015).
Research into DBS and its use as a method for solving scheduling problems in open pit mine planning has recently been gaining increasing interest as an alternative to the conventional methodology, which is based on nested pits. In DBS, however, an entire production plan can be obtained in only one step, which can maximize the economic value of a mining project.
Among the advantages offered by this method is that it considers the temporality of the problem and the opportunity cost when sequencing mining blocks, i.e., it searches for the next best block to mine considering its implication for other periods. As such, it is able to present users with the best NPV possible, subject to constraints such as operation, capacity, and metallurgy.
However, this methodology is still being developed, and all of the existing operational constraints have not yet been fully implemented in the method, which can result in unfeasible long-term production plans. To address this gap, this paper proposes using DBS as a tool for medium-term planning.
Medium-term planning is important for operational purposes; it also encompasses the quality and quantity of intermediate-period goals required to accomplish the strategic/global project goals. The aim of this study was to utilize the advantages of DBS for improving economic outcomes in a reasonable solution time with feasible outcomes and flexible results, which could be adjusted manually if desired by the planner. For this, DBS was used together with conventional methods. First, the project was divided in portions or periods, according to the results obtained using traditional strategic planning (for this study, we chose to work with a time span of approximately five years). Then, the first portion was segmented into sectors, each one with a mining priority, according to the results provided by DBS. Because the model size was reduced and the restrictions were easier to follow, scheduling within each sector will produce the best result possible.
Literature review
Traditional mine planning process
Because it is hard to solve the entire problem of overall open pit planning in one step, the traditional planning process (which has been in use by the industry since the 1960s) divides the main problem into several sub-problems, such as determination of the ultimate pit limit, pushback generation, scheduling, blending, and cut-off grade optimization. Over time, approaches have been developed to optimize these decisions individually. For instance, Lerchs and Grosmann (1965) created an algorithm that guarantees optimality with respect to defining pit limits that maximize undiscounted cash flow. They also proposed a technique for creating nested pits to guide the creation of pushbacks. Subsequent improvements on this have been made (for example, Picard (1976), Hockbaum and Chen (2000), and Amankwah, Larsson, and Textorius (2014)). However, this approach has three problems: (1) it considers a fixed cut-off grade that depends on an arbitrary delineation between waste and ore; (2) it uses notional prices in determining the nested pits; and (3) it incorporates the piecemeal approach to the entire optimization problem, thus disregarding the temporal interaction of resource requirements (Newman et al., 2010).
The DBS method
In 1968, Johnson presented a general mathematical formulation based on mixed integer programming as the solution to the block scheduling problem that defines when a block should be extracted, if it is to be extracted, and the destination to which it should be sent. This formulation represented a great advance with the incorporation of a 'time' factor, that is, all decisions on a period are taken considering the implications for the others, thus considering the temporal interaction of resources requirements. Furthermore, discounting can be used to more accurately reflect the value of a block as a function of its extraction date and the cut-off grade definition made dynamic.
This would be the most ideal method to solve open pit block scheduling problems were it not for its computational complexity and the excessive processing time required to generate the solutions. These issues prevent the application of these techniques in large models. To obtain a reasonable resolution time, many variations of this method have been proposed (see, for example, Chicoisne et al. (2012) and Cullenbine, Wood, and Newman (2011)).
A further problem is the large number of constraints and aspects that have to be considered when sequencing. Different applications of DBS have been explored in several studies with different focuses. Jélvez et al. (2016) used heuristics based on incremental and aggregation approaches to solve the problem. Saavedra-Rosas et al. (2016) developed a block scheduling technique for an exposed ore reserve. Morales and Reyes (2016) proposed an approach that takes the mining system into account to solve mine scheduling issues related to short-term planning. Studies by Morales and Rubio (2010) and Eizavy and Askari-Nasab (2012) also focused on the short term.
Iron ore mine case study
The developed case study was based on a block model (which is already in operation) of an existing iron ore mine located in Brazil. This model contains 38 172 regular blocks of dimensions 50 m x 50 m x 20 m. Each block has, in addition to its three dimensional coordinates, other relevant attributes: tonnage, iron grade, and contaminants, and possible destination (processing plant or waste dump). For the economic evaluation, some economic parameters are necessary: iron price, iron recovery, selling cost, processing cost, and mining cost. Thus, the block economic value (BV) is calculated for each possible destination. If a block is sent to the processing plant,
BV = (Metalprice - Selling cost) x
Metal grade x Metal recovery x
Tonnage - (Mines cost + Processing cost) x TonnageIf a block is sent to the waste dump,
BV = - (Mine cost + Processing cost) x Tonnage
The slope angle depends on the region: 45° for a bearing between 0° and 120°; 35° for a bearing between 120° and 240°; and 30° for a bearing between 240° and 360°. The mining and processing capacities were 55 and 36.5 Mt/a, respectively. Table I summarizes the main economic and technical parameters.

Case study
The methodology used in this study was to develop a strategic planning project using the Whittle software package with nested pits based on a revenue factor (factor multiplying the ore price) between 0.6 and 1.0, while the definition of the ultimate pit limit and subsequent selection of pushbacks were made based on the planner's experience. A sequencing algorithm based on 'Milawa Balanced' was used, which aims to optimize the utilization of resources, as it is the most commonly used algorithm in the mining industry. Therefore, the output from the strategic plan was the ultimate pit and how the pushbacks were to be mined.
With the strategic planning taken care of, the medium-term planning was then conducted. Medium-term planning differs from strategic planning in its level of sophistication. It is important to ensure that the intermediate targets to be achieved over shorter periods of time are operationally feasible; once these are achieved, they can contribute to achieving a strategic objective (e.g. the excavator mining rate in tons per hour is an intermediate target that, once complied with, can help to achieve the desirable quantity of material mined in a year). For comparison purposes, evaluating the performance of medium-term plans in the initial years of mining is enough. Therefore, only the sector that corresponds approximately to the first five years of mining was selected and scheduled in three different ways:
► Scheduling using a renowned software package in the mineral industry (Deswik). This software package is very flexible, as it gives autonomy and freedom to the planner to perform scheduling. To reproduce what is done in industry, medium-term scheduling was conducted considering operational issues, such as the maximum number of resources (excavators), their mining rate and utilization, the maximum number of mining fronts, and the access and bench level considered when assigning priorities. To create dependencies, constraints were placed on bench face angle, and the main objective was to keep the mining rate around 55 Mt/a, with 36.5 Mt/a being sent to the processing plant. Table II shows some constraints that were applied to medium-term planning.
► Scheduling with DBS. DBS always seeks to maximize the NPV. It is not flexible regarding existing constraints, and a lack of such constraints may yield non-operational results, such as the extraction of blocks very distant from one another.
► Scheduling using Deswik aided by DBS. This is an attempt, shown in this study, which seeks to use the results of DBS to adjust the sequencing generated by Deswik to add economic value while remaining operational. This was done as follows: the extracting period assigned to each block by DBS was analysed visually. Then, extraction-period sectors of blocks were manually defined. This sectorization was done according to the proximity of blocks with the same extraction period, e.g. if a block with extraction period of 1 is surrounded by blocks with extraction period of 2, then this block will be add into the second extraction period sector.
Results and discussion
The strategic planning of the whole project produced the life-of-mine production plan, shown in Figure 1. The low stripping ratio is justified by the fact that the mine is already in operation and most of the overburden has already been removed.

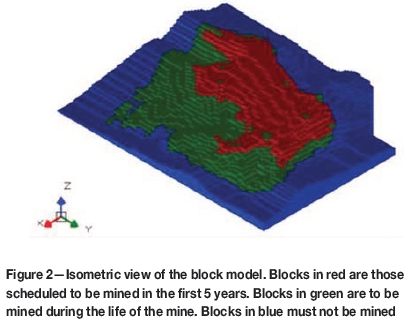
Based on this result, the mass extracted in the first five years (approximately 281 Mt) was taken to be medium-term sequenced in another software package. Figure 2 shows this mass highlighted in red; the blocks that belong to the final pit are shown green, and the remaining blocks of the block model in blue.
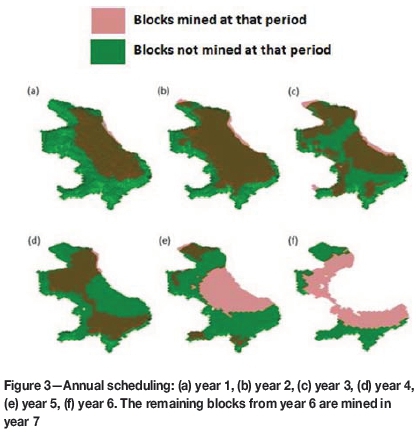
The red blocks were rescheduled using the Deswik software package to obtain an annual plan that complies with intermediate targets that have already been defined. Figure 3 shows this scheduling in which blocks to be extracted in that specific period are pink, and the green region represents the remaining mass for the period.
Scheduling of the same mass was performed using DBS, as shown in Figure 4. Note the colour scale to distinguish the periods of extraction of the blocks. Because this methodology is not based on nested pits, blocks extracted during the same period may be very far from each other. To fix that and use DBS as a medium-term planner, operational and physical constraints such as the horizontal and vertical rates of advance, the minimum mining width, and the maximum number of mining fronts, as well as resource characteristics such as the mining rate, utilization, and availability should be implemented.

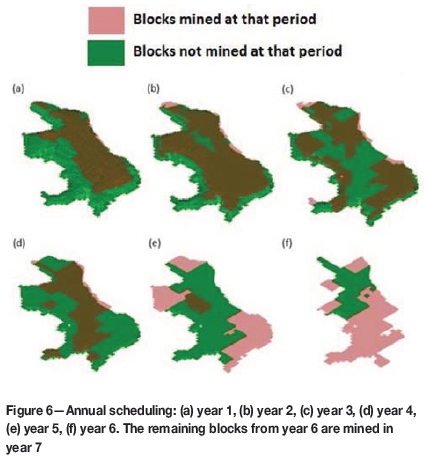
To use the DBS results to aid the scheduling process reported in schedule (iii) above, the blocks in Deswik were manually divided into sectors defined according to the highest proportion of blocks with the same extraction period (shown in Figure 5). These sectors were used as a priority in mining. All constraints, priorities, and dependencies created in production plan (i) were also fulfilled. The final scheduling is shown in Figure 6, in which blocks to be extracted in that specific period are pink, and the green region represents the remaining mass. Note the difference between Figures 3 and 6 and see how the scheduling of the blocks changes.

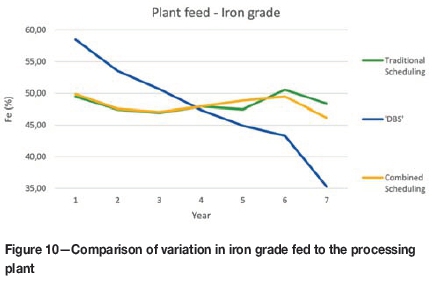
Figures 7, 8, and 9 as well as Tables III, IV, and V show the results in terms of tonnage, economic value, stripping ratio, and iron grade of each scheduling way: plans (i), (ii), and (iii).
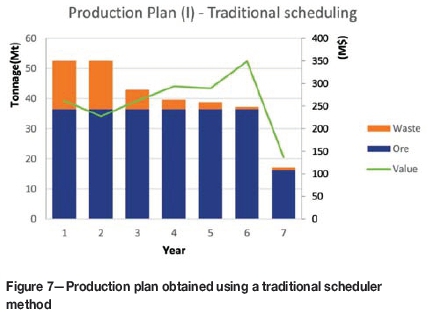

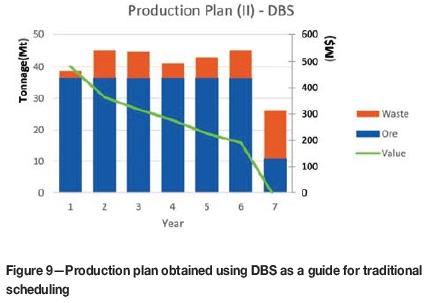
From the comparison of the results, it is clear that in plan (ii), when trying to maximize the NPV, the DBS delays the removal of overburden and tries to achieve a decreasing undiscounted value over time while increasing the stripping ratio. As there is a constraint to mine all blocks, the last period has more waste to mine and a negative economic value, causing the cumulated NPV to decrease. In plan (i), however, the biggest concern is that the plan should obey certain mining priorities and operational constraints. The stripping ratio is decreased while the total mass is mined (the small difference of 0.01% in total tonnage mined between the production plans is due to design operationalization). The result of plan (iii), therefore, is a combined action to comply with priorities and medium-term constraints while trying to increase the total value. Table VI shows the NPV of each production plan.

Scheduling by DBS plan (ii) has a NPV increase of 10.57% compared with traditional scheduling (i). However, plan (ii) is an operationally unfeasible scheduling, and there is no way of knowing if there is any real improvement. However, the combined sequencing (iii) increases the NPV by 0.43%; this improvement is real and possible to comply with. As the stripping ratios of plan (i) and (iii) are almost the same, the increase in NPV is mostly due to the slightly higher iron grade in years 1 to 5; this is a smooth variation in iron grade over time, as it can be seen in Figure 10.
Conclusion
It has become clear that the conventional method based on nested pits is no longer the ideal method of mine planning. However, although DBS can provide the best economic results possible, the current state of the DBS method means that it is not the most ideal method to plan mining either. Software programmes based on DBS techniques still lack important operational parameters and thus yield unfeasible results.
Until computer technologies are advanced enough to tackle these restrictions, a way must be found to take maximum advantage of the benefits of the current tools.
The main objective of this study was to verify the use of the DBS technique to improve medium-term results while maintaining the flexibility adjustments and operational feasibility provided by software based on conventional planning methodology. The technique used herein, which is the simplest possible, consisted of a visual definition of priority sectors based on the extraction period for the largest proportion of blocks in each sector according to results provided by DBS. An increase in economic output of 0.43% was obtained. The results could potentially be improved further through the compartmentalization of blocks by means of aggregation techniques not based on human subjectivity, such as visual analysis.
Acknowledgements
This research was supported by the AMTC, Universidad de Chile, CONICYT Basal Grant FB0809.
References
Amankwah, H., Larsson, T., and Textorius, B. 2014. A maximum flow formulation of a multi-period open-pit mining problem. Operational Research, vol. 14, no. 1. pp. 1-10. [ Links ]
Chicoisne, R., Espinoza, D., Goycoolea, M., Moreno, E., and Rubio, E. 2012. A new algorithm for the open-pit mine production scheduling problem. Operations Research, vol. 60, no. 3. pp. 517-528. [ Links ]
Cullenbine, C., Wood, K., and Newman, A. 2011. Improving the tractability of the open pit mining block sequencing problem using a sliding time window heuristic with lagrangian relaxation. Optimization Letters, vol. 88, no. 3. pp. 365-377. [ Links ]
Elkington, T. and Durham, R. 2011. Integrated open pit pushback selection and production capacity optimization. Journal of Mining Science, vol. 47, no. 2. pp. 177-190. [ Links ]
Espinoza, D., Goycoolea, M., Moreno, E., and Newman, A. 2013. Minelib: a library of open pit mining problems. Annals of Operations Research, vol. 206, no. 1. pp. 93-114. [ Links ]
Hochbaum, D. and Chen, A. 2000. Performance analysis and best implementation of old and new algorithms for the open-pit mining problem. Operations Research, vol. 48. pp. 894-914. [ Links ]
Jélvez, Ε., Morales, N., Nancel-Penard, P., Peypouquet, J., and Reyes, P. 2016. Aggregation heuristic for the open-pit block scheduling problem. European Journal of Operational Research, vol. 49, no. 3. pp. 1169-1177. [ Links ]
Johnson, T.B. 1968. Optimum open-pit mine production scheduling. PhD thesis, Operations Research Department, University of California, Berkeley. [ Links ]
Lerchs, H. and Grosmann, I.1965. Optimum design for open pit mines. CM Bulletin, vol. 58. pp. 47-54. [ Links ]
Morales, N., Jélvez, Ε., Nancel-Penard, P., Marinho, Α., and Guimaraes, O. 2015. Α comparison of conventional and direct block scheduling methods for open pit mine production scheduling. Proceedings of the 37th International Symposium on Application of Computers and Operations Research in the Mineral Industry, Fairbanks, AK. Society for Mining, Metallurgy & Exploration, Littleton, CO. pp. 1040-1051. [ Links ]
Morales, N. and Reyes, P. 2016. Increasing the value and feasibility of open pit plans by integrating the mining system into the planning process. Journal of the Southern African Institute of Mining and Metallurgy, vol. 116. pp. 663-672 [ Links ]
Newman, Α., Rubio, Ε., Caro, R., Weintraub, Α., and Eurek, K. 2010. Α review of operations research in mine planning. Interfaces, vol. 40, no. 3. pp. 222-245. [ Links ]
Picard, J. 1976. Maximal closure of a graph and applications to combinatorial problems. Management Science, vol. 22, no. 11. pp. 1268-1272. [ Links ]
Saavedra-Rosas, J., Jélvez, Ε., Amaya, J., and Morales, N. 2016. Optimizing open-pit block scheduling with exposed ore reserve. Journal of the Southern African Institute of Mining and Metallurgy, vol. 116. pp. 655-662. [ Links ] ♦
Paper received Apr. 2017
revised paper received Oct. 2017















