Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.115 n.12 Johannesburg Dec. 2015
http://dx.doi.org/10.17159/2411-9717/2015/v115n12a12
PAPERS OF GENERAL INTEREST
The accuracy of calcium-carbonate-based saturation indices in predicting the corrosivity of hot brackish water towards mild steel
A. PalazzoI; J. van der MerweII; G. CombrinkIII
IBuckman Africa (Pty) Ltd, Hammarsdale, South Africa and part-time MSc student at the School of Chemical and Metallurgical Engineering, Faculty of Engineering and the Built Environment, University of the Witwatersrand, Johannesburg, South Africa
IIUniversity of the Witwatersrand, Johannesburg, South Africa
IIIUniversity of Johannesburg, South Africa
SYNOPSIS
Industry has always relied on water's inherent ability to inhibit mild steel corrosion by virtue of its levels of calcium hardness and total alkalinity. This research seeks to verify the application of this principle to brackish water used in industrial systems at moderately elevated temperatures. A brief review is first given of the conventional calcium-carbonate-based scale or corrosion predictive indices. Laboratory corrosion tests were performed at various levels of calcium hardness and total alkalinity, resulting in the generation of an empirically derived nonlinear regression model. The newly developed model and the existing indices were then compared statistically in predicting the corrosivity of brackish water in contact with mild steel at 45°C. The accuracy, broader application, and relevance of the indices are also discussed.
Keywords: saline water, brackish water, cooling, corrosion prediction, computer modelling, Langelier Saturation Index, Ryznar Stability Index, mild steel, calcium carbonate saturation.
Introduction
Between 1960 and the mid-1990s the Langelier Saturation Index (LSI) (Equation [1]) (Langelier, 1936) attracted adverse commentary from the municipal potable water community. It was stated that the LSI had no correlation with corrosion rate (Stumm, 1960; Larson and Sollo, 1967; Singley, 1981; Schock, 1984; Piron et al., 1986; Pisigan and Singley, 1987), and based on the empirical evidence it was suggested that the use of the LSI for corrosion prediction should be abandoned (AWWARF and DVGW, 1996). The same sentiment applied to the Ryznar Stability Index (RSI) (Ryznar, 1944) (Equation [2]) and the various other 'corrosion prediction indices' that emerged during this period and that were also grounded on the same principle:
> Momentary Excess (ME) (Dye, 1958)
> Calcium Carbonate Precipitation Potential (CCPP) (Merrill and Sanks, 1978)
> Aggressiveness Index (AI) (Millette et al., 1980)
> Driving Force Index (DFI) (Rossum and Merrill, 1983).
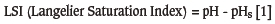
where the variables and their range of applicability are as follows:
pH: measured pH (7.0-9.5), temperature: 25-80°C, total dissolved solids <800 mg/l. pHs: the pH at which the cooling water will be saturated. This value is calculated based on the solubility product for calcite, the second dissociation constant for carbonic acid and calcium concentrations, and total alkalinity of the cooling water Positive LSI values indicate 'oversaturation' and a tendency for a protective CaCO3 coating to form, whereas negative values indicate the tendency to dissolve an existing CaCO3coating.

Puckorius uses an equilibrium pH for this index rather than the actual cooling water pH. The index applies for temperatures up to 93°C.
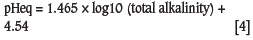
Total alkalinity: mg/l CaCO3.
RSI or PSI values 6 and higher indicate increasingly severe corrosive tendencies, whereas values 6 and lower indicate more CaCO3scaling tendencies.
The PSI (Puckorius and Brooke, 1990), calculated using Equations [3] and [4], is a refinement of the RSI, in which an empirical alkalinity function is derived to modify the calculated pH of saturation for calcium carbonate (pHs). In large industrial and power station cooling systems, either the LSI of PSI is still used to control acid feed or the cycles of concentration for calcium carbonate scale control. This supports their continued role in predicting the impact of water-soluble species on industrial water systems.
Early research (Larson and Skold, 1957) confirmed that the precipitation/dissolution of calcium carbonate is not the only water quality parameter relevant to the corrosion of distribution systems. Other factors such as the ratios of anions, flow velocity, pH, and calcium concentration also contribute to corrosion rates, but perhaps the best researched is the Larson and Skold Index, also known as the Larson Ratio (LR) (Larson and Skold, 1957, 1958) (Equation [5]). This index includes the corrosive effects attributable to the chloride and sulphate concentrations.
Larson-Skold Index, Larson ratio (LR) or Corrosivity
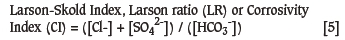
where
[Cl-], [SO42-] and [HCO3-]: meq/litre of chloride, sulphate, and total alkalinity respectively. The water studied approximated the quality of the Great Lakes waters of North America. The higher the index the more corrosive the water.
Feigenbaum et al. (1978) demonstrated poor correlation between the already-mentioned calcium-carbonate-based indices and the saline waters of the Negev Desert, and therefore developed an empirical index that included the effect of calcium carbonate solubility and the ions of the LR.
The reported lack of a definite correlation between the LSI and corrosion rates evident in both the drinking water industry and laboratory-scale closed-loop experiments prompted Pisigan and Singley (1984) to embark on a series of jar tests. The results of the laboratory tests permitted them to empirically derive a four-variable model (Equation [6]) and an eight-variable model (Equation [7]) that could account for 98% of the variations in corrosion rate under the experimental conditions explored. The equations hypothesized indicated that the corrosion rate of mild steel was in fact influenced by factors beyond just the precipitation or dissolution of calcium carbonate.
Pisigan and Singley 4-variable equation:

where
TDS (total dissolved solids): mg/l, Ca (calcium): mg/l as Ca, Mg (magnesium): mg/l as Mg, Na(sodium): mg/l as Na, Cl (chloride): mg/l as Cl, SO4 (sulphate): mg/l as SO4, Alk (alkalinity): mg/l as CaCO3, β (buffer capacity): mg/l as CaCO3/pH, DO (dissolved oxygen): mg/l as O2.
Pisigan and Singley's eight-variable model (1984) suggests that increasing chloride, sulphate, alkalinity, and dissolved oxygen levels would accelerate corrosion, whereas increases in calcium concentration, buffer capacity, saturation index, and exposure time would lead to decreasing corrosion rates. In this hypothetical equation, the alkalinity is declared to accelerate rather than reduce corrosion, as is commonly known. The authors attributed this contradiction to the overwhelming influence of the increased ionic strength over the effect of alkalinity with increasing dosages of sodium bicarbonate while attempting to raise the alkalinity during the laboratory experiments.
The first use of the buffer capacity (β) appeared in the literature pertaining to the subject of corrosion prediction in the work by Stumm (1960). Laboratory tests with synthetic solutions helped explain the mutual interaction of corrosion-stimulating and -inhibiting factors of natural waters, namely: pH, buffer capacity, CaCO3deposition, and alkalinity. This study was thought to at least partially explain the increase in corrosion rates with increasing pH between the values of 7.0 and 8.5.
Several studies found that as the pH approached 8.4, either from a higher or lower pH value, the corrosion rate of cast iron increased with decreasing buffer intensity. It is presumed that this effect occurs as a result of there being fewer but larger cathodic and anodic areas, thereby encouraging the electrochemical cell (Stumm, 1960).
Based on the independent studies reported by Pisigan and Singley (1987) and Imran et al. (2005a), it was possible to propose a modified Larson ratio (LRM) that would compensate for the increase in total dissolved solids with the increasing alkalinity by including the sodium ion concentration.
Imran continued his work on potable water distribution systems and published an article (Imran et al., 2005a) that included a wider range of parameters in an empirically derived nonlinear model. The model is based on the change in apparent colour (AC in cpu) as a measure of corrosion in distribution lines, as it was found to be a reliable surrogate measurement of total iron. Calcium and pH were not deemed significant during the statistical modelling, because all tests were performed in waters stabilized for CaCO3 solubility. Alkalinity was the only variable that could be effectively controlled by chemical addition.
In the arena of oilfield brines, where the high salinity affects the ionic strength and influences the calcium carbonate solubility, the Stiff-Davis Index (SDI) (Equation [8]) has been used (Stiff and Davis, 1952) in place of the Langelier Index. Waters with total dissolved solids levels higher than 4000 mg/l require that the SDI is used.

where
pH: pH measured, pCa = -log (Ca in mg/l as Ca2+), and pAlk = -log (M alkalinity in mg/l as CaCO3), K = constant based on the total ionic strength and temperature.
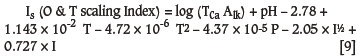
where
I (ionic strength): moles/l, TCa (calcium): moles/l as Ca, Alk (alkalinity): moles/l as HCO3-, T (temperature): 0F, P (pressure): psi.
As with the Langelier Saturation Index, positive SDI or Isvalues indicate 'oversaturation' and a tendency for a protective CaCO3 coating to form, whereas negative values indicate the tendency to dissolve an existing CaCO3coating
Higher CR values indicate higher corrosion rates in mils per year (mpy).
The Stiff-Davis (Stiff and Davis, 1952) method is one of the easiest ways to calculate calcium carbonate scaling tendencies (Calcite Saturation Index) in brines and it is valid for temperatures from 0-90°C and ionic strengths from 0-4. This index does not take into account the pressure and carbon dioxide concentration. It requires that the pH is measured on a fresh sample to avoid inaccuracies. As ionic strength and/or the temperature increase, so the K value decreases, resulting in a higher SDI, indicating a higher calcium carbonate scaling tendency. Higher concentrations of calcium or alkalinity would also lead to higher SDI values, also resulting in increased scaling tendencies. Calculating the SDI requires a calculation of the ionic strength, knowing the temperature of the operation, and looking up the K value in a K versus ionic strength graph (Stiff and Davis, 1952).
The Oddo-Tomson (1982) method is an alternative index applicable to high ionic strength waters for predicting the formation of calcium carbonate and various sulphate scales. It is valid between temperatures of 0-200°C, ionic strengths of 0-4.0, and pressures of 1-1380 bar (0-20000 psig) (Equation [9]). The calculation was reported by Oddo and Tomson (1982) to be accurate at high and low temperatures and pressures. The calculation can be easily performed in the field and is said to work well when applied to geopressured wells.
The prediction of the corrosivity of underground minewaters towards mild steel was also explored by White and Higginson (1985). It was reported that the corrosion takes place under cathodic control, with the metal acting as a substrate for the cathodic reaction. Thus the corrosivity of minewaters is largely dependent upon on the oxygen concentration and the pH of the water.
Equipment and methodology
In determining the relationship between the calcium hardness and alkalinity and the corrosion rate of mild steel in brackish water at elevated temperatures (35-45°C), numerous laboratory tests were conducted with synthetic solutions.
The main aim of the laboratory evaluation was to determine the impacts of temperature (between 35°C and 45°C), calcium hardness (between 50 mg/l and 100 mg/l as Ca2+), and total alkalinity (between 55 and 220 mg/l as CaCO3) on the corrosivity of brackish water towards mild steel. Thus, the limiting conditions for the applicability of this study are waters having a quality range defined in Table I.
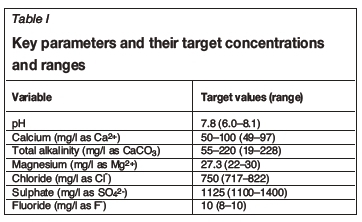
C1010 (mild steel) corrosion coupons were subjected to synthetic test solutions (4000 ml) stirred at 100-110 revolutions per minute (r/min) for 72 hours. The coupons were then removed, cleaned with a water wash to finger-touch, followed by an ethanol wipe; and then oven-dried, weighed and the corrosion rates calculated based on their weight loss. The methods followed were based on ASTM methods:
> G31-72 (Reapproved 1999): Standard Practice for Laboratory Immersion Corrosion Testing of Metals
> G1-90 (Reapproved 1999: Standard Practice for Preparing, Cleaning, and Evaluating Corrosion Test Specimens.
A Corrater® (Rohrback Cosasco) was used to measure the general corrosion rate and imbalance (i.e. indicator of the tendency for localized corrosion). The test solutions were also tested for their total iron concentrations and compared against the coupon method and Corrater® readings. Each set of tests was performed in a batch of six tests in a 'Laboratory Scale and Corrosion Test Station', a Buckman proprietary corrosion testing device, over a period of three days (refer to Figures 1 and 2).
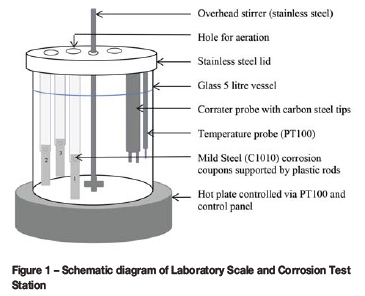
Each of the six stations has its dedicated 5-litre beaker and an overhead paddle stirrer, dedicated temperature probe, hot plate, three coupon holders, and a Corrater® probe
Results
Table II lists the target calcium and total alkalinity concentrations, the temperatures explored, and the total iron concentrations of the test solutions. Table III summarizes the corrosion coupon results and the Corrater® readings taken over the three days.
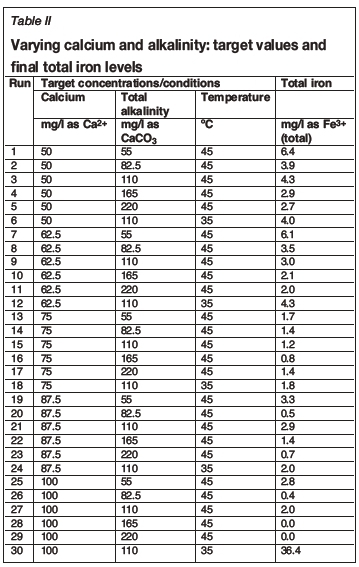
Figure 3 compares the mild steel coupon corrosion rates (mm/a) for the two positions, and Figure 4 provides a three-dimensional view of the correlations between the three corrosion measurements: the average coupon corrosion rate, the average Corrater® general corrosion rate, and the total iron concentrations.
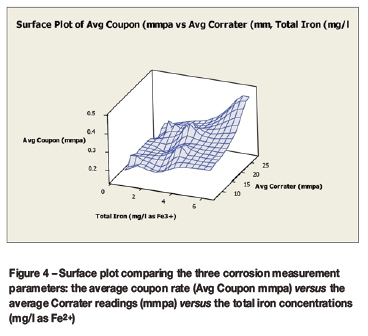
Figure 5 reflects the impact of a 10°C difference in temperature on the corrosion rates as well as the impact of higher and lower alkalinity. It includes the error bars based on the maximum standard deviation - that is, a value of 0.07 mm/a - for the entire set of coupon data recorded during the 30 test runs.
Statistical correlations were performed between the average coupon corrosion rate and the various parameters measured during the experiment. Statistically significant linear model correlations, with a 95% confidence level, were found between the average coupon corrosion rate and the following parameters: the initial and final calcium concen-trations, the initial total alkalinity, the average Corrater® general corrosion rates, and the total iron levels. Inverse relationships were evident between the average coupon corrosion rate and the calcium and total alkalinity values, whereas direct moderate correlations were noted between the average coupon rates and both the average Corrater® general corrosion rates and the total iron concentrations. The average Corrater® general corrosion rates did not correlate well with the total iron values.
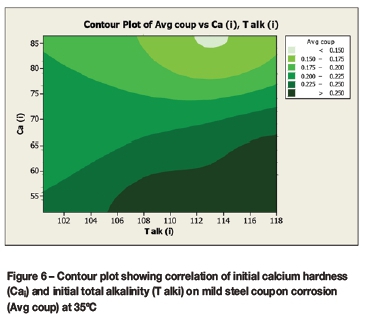
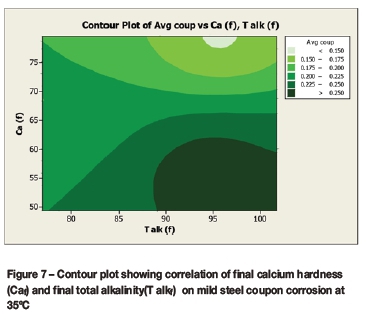
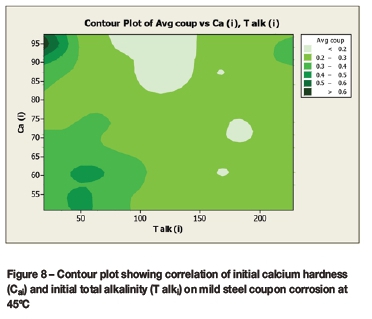
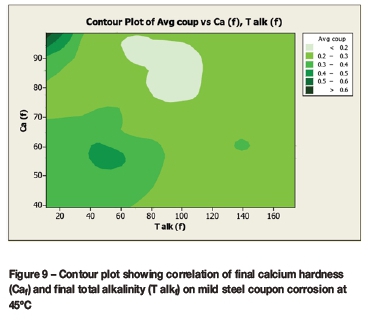
Contour plots (Figures 6 to 9) were drawn to reveal the combined effect of the calcium hardness and total alkalinity on the average coupon corrosion rate. The initial or final calcium concentrations and initial or final total alkalinity values were plotted against the average coupon rate.
A nonlinear multivariate regression analysis was conducted to predict the relationship between coupon corrosion rate and various predictors in order to determine how the response variable changes as the particular predictor variables change. This was done without taking into account the impact of the 10°C temperature difference (refer to Equation [10]):

where Ca = mg/l calcium as Ca and M alk = mg/l total alkalinity as CaCO3.
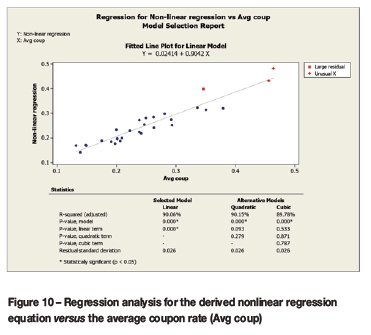
Figure 10 serves to confirm the accuracy of the empirically derived nonlinear regression equation by comparing it to the laboratory coupon corrosion data. An R2adjusted value of 90.06% was obtained. The graph also indicates where large residuals and an unusual result occurred, explicitly at the upper section of curve.
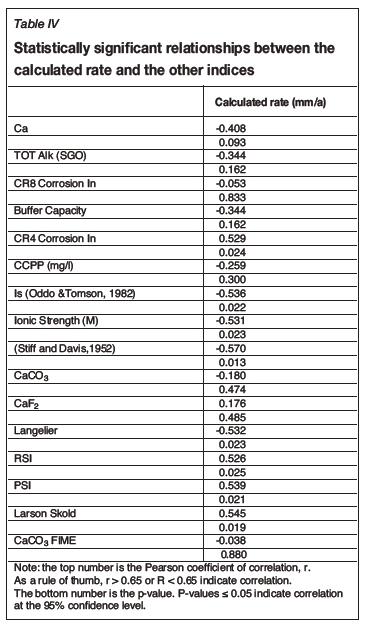
The empirically derived equation was then compared statistically against the predictive indices discussed in the literature survey. This was performed by using the test solution target values and the comparison performed at both 35°C and 45°C. The results of the comparison are given in Table IV and shown by the scatter plot correlations in Figure 11. The statistical analysis indicated that the calculated rate had the statistically significant moderately strong relationships at a 95% confidence level shown in Table V.
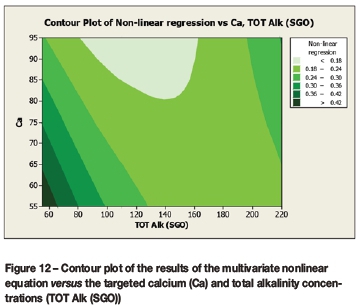
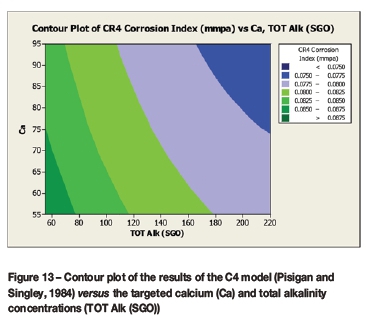
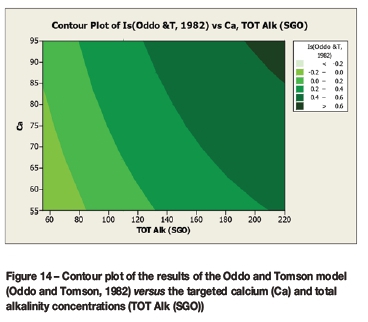
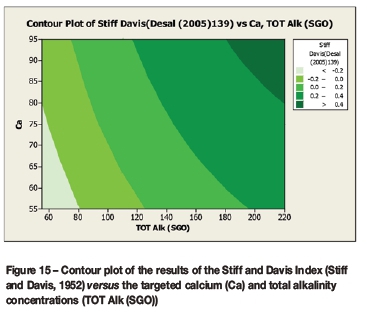
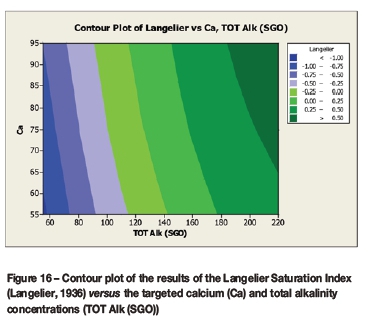
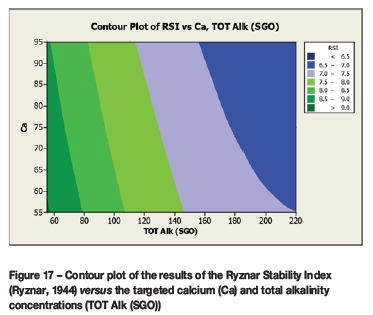
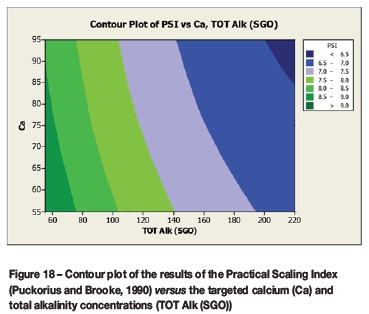
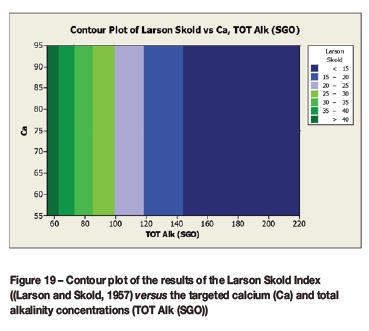
A contour plot (Figure 12) of the derived multivariate nonlinear regression equation (Equation [10]) was included to facilitate a visual comparison with the contour plots of the laboratory coupon corrosion data (Figures 6-9). Contour plots (Figures 12-19) of statistically significant indices taken from the literature, as per Table V, were also included for further comparisons.
Discussion
In order to first determine the correlation between the two coupon positions in the test vessel it was necessary to compare their results by means of a paired t-test. The paired t-test for the mean of coupon 1 versus the mean of coupon 2 showed that the two coupon positions were statistically different at a 95% confidence level. The two coupon positions did, however, demonstrate similar trends, as apparent in Figure 3; hence the average coupon rate was adopted as the result for each test.
A comparison of the plots of the average coupon rate against either the average Corrater® readings or the test solution total iron concentrations (Figure 4) demonstrated moderate direct correlations. The strength and direction of these correlations therefore supported the use of the average coupon rate for the continued corrosion studies. There was, however, a substantial discrepancy between the coupon-based rates and the Corrater® readings, with the latter indicating rates that were approximately 54 times higher. The findings of this investigation were addressed by Van der Merwe and Palazzo (2015), and similar concerns over the lack of correlation between linear polarization resistance probe measurements and coupon immersion tests have also recently been investigated by Wu et al. (2015).
Figure 5 reflects the impact of a 10°C difference in temperature, where the higher temperature produced higher corrosion rates at the lower targeted calcium hardness values of 50 and 62.5 mg/l (as Ca). At the higher calcium hardness values both temperatures resulted in similar corrosion rates. Figure 5 depicts the impact of different total alkalinities. It is apparent that higher alkalinity resulted in lower coupon corrosion rates, with the exception of the increased corrosion evident for the points corresponding to the combination of a high target calcium hardness (above 75 mg/l as Ca) and high target alkalinity (165 mg/l as CaCO3).
The contour plots (Figures 6 and 7) for the average coupon rate versus calcium and total alkalinity for the corrosion tests performed at 35°C demonstrated:
> Lowest corrosion rates at high calcium (>70 mg/l as Ca) and high total alkalinity (>90 mg/l as CaCO3)
> Highest corrosion rates at high total alkalinity (>90 mg/l as CaCO3) and low calcium (<60 mg/l as Ca).
The contour plots (Figures 8 and 9) for the average coupon rate versus calcium and total alkalinity for the corrosion tests performed at 45°C demonstrated:
> Lowest corrosion rates at:
• High calcium (80-100 mg/l as Ca) and moderately high total alkalinity (65-110 mg/l as CaCO3)
• Moderate calcium (60-80 mg/l as Ca) and moderate total alkalinity (150-200 mg/l as CaCO3
> Highest corrosion rates at low total alkalinity (<50 mg/l as CaCO3) and either low calcium (<50 mg/l as Ca) or high calcium (>85 mg/l as Ca).
The regions of either low or high corrosivity are similar for both the lower temperature of 35°C and higher temperature of 45°C.
The empirically derived nonlinear regression equation, based on only the solution's initial calcium and initial total alkalinity, was confirmed to account for 90.06% of the variations in the average corrosion coupon data.
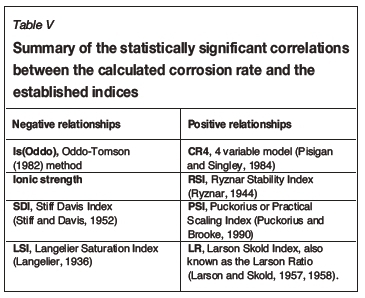
Statistically significant moderately strong relationships, at a 95% confidence level, were evident between the derived nonlinear regression equation and the various established indices, namely: LSI, Langelier Saturation Index (Langelier, 1936), RSI, Ryznar Stability Index (Ryznar, 1944), LR, Larson Skold Index also known as the Larson Ratio (Larson and Skold, 1957, 1958), SDI, Stiff Davis Index (Stiff and Davis, 1952), Is (Oddo), Oddo-Tomson (1982) method, ionic strength, CR4, four-variable model (Pisigan and Singley, 1984), and PSI, Puckorius, or Practical Scaling Index (Puckorius and Brooke, 1990).
A comparison of the contour plot of the new model versus those of other indices, for the set of target values considered revealed some subtle differences between them. One of the more obvious differences was the impact of the calcium concentration on the corrosivity, as evident by the relatively steeper diagonal contour lines for some of the indices, particularly in the new model, LSI, RSI, and PSI (Figures 12, 16, 17, and 18, respectively). As per the literature, it appears that a number of the authors included calcium in their empirically derived predictive models: LSI, RSI, SDI, and CCPP. The same can be said of pH for the LSI, RSI, PSI, SDI, and Is indices. Linear regression analysis of the correlation between the average coupon corrosion rates and the various predictors confirmed the role of the initial pH and the initial calcium concentration.
Conclusion
Although the average coupon rate, the total iron concentrations, and the Corrater® general corrosion rate readings appeared closely related, it was possible to find statistically significant linear correlations, at a 95% confidence level, only between the average coupon rate and total iron concentration as well as the average coupon rate and the Corrater® general corrosion readings.
It was also confirmed that raising the calcium hardness and/or total alkalinity within the range of chemistries explored for the application of the brackish water in a cooling system does reduce mild steel corrosion. It did, however, become apparent that calcium carbonate saturation or supersaturation can lead to precipitation, resulting in reduced levels of calcium and alkalinity which in turn leads to increased corrosion rates.
The empirically derived equation was at best capable of only moderately strong correlations with any of the numerous calcium-carbonate-based models found in the literature. A comparison of the formulae of the statistically significant eight indices and a comparison to the remaining six non-statistically significant and weakly correlated indices revealed that the latter six were linearly related to either the calcium concentration or total alkalinity, whereas the former eight indices are a function of either the log or the inverse of either the calcium concentration and/or total alkalinity. The newly proposed empirically derived nonlinear regression model differes from both sets of indices in that it is based on a quadratic equation incorporating both the calcium concentration as Ca2+ and total alkalinity in mg/l as CaCO3.
As stated in the introduction, it would be grossly inaccurate to base the calculation of the corrosivity of brackish water solely on its calcium concentration, total alkalinity, and temperature without giving any consideration to the many other factors or conditions prevailing in a typical industrial system. What is, however, apparent from the study, since it is based only on changes in the calcium hardness and total alkalinity, is that the empirically derived model may prove more accurate than most of the existing commonly found indices at estimating the corrosivity of brackish water, of similar characteristics to the chemistry explored, on mild steel between 35 and 45°C.
References
AWWARF and DVGW-TZW. 1996. Internal Corrosion of Water Distribution Systems. 2nd edn. American Water Works Association, Denver, CO. pp. 29-70. [ Links ]
Dye, J.F. 1958. Correlation of the two principle methods of calculating the three kinds of alkalinity. Journal of the American Water Works Association, vol. 50, no. 6. pp. 801-820. [ Links ]
Feigenbaum, C., Gal-Or, L., and Yahalom, J. 1978. Scale protection criteria in natural waters. Corrosion, vol. 34, no. 4. pp. 133-137. [ Links ]
Imran, S.A., Dietz, J.D., Mutoti, G., Taylor, J.S., and Randall, A.A. 2005a. Modified Larsons ratio incorporating temperature, water age, and electroneutrality effects on red water release. Canadian Journal of Environmental Engineering, vol. 131, no. 11. pp. 1514-1520. [ Links ]
Imran, S.A., Dietz, J.D., Mutoti, G., Taylor, J.S., Randall, A.A., and Cooper, C.D. (2005b). Red water release in drinking water distribution systems. Journal of the American Water Works Association, vol. 97, no. 9. pp. 93-100. [ Links ]
Langelier, W.F. 1936. The analytical control of anti-corrosion water treatment. Journal of the American Water Works Association, vol. 28, no. 10. pp. 1500-1521. [ Links ]
Larson, T.E. and Skold, R.V. 1957. Corrosion and tuberculation of cast iron. Journal of the American Water Works Association, vol. 49, no. 10. pp. 1294-1302. [ Links ]
Larson, T.E. and Skold, R.V. 1958. Laboratory studies relating mineral water quality of water to corrosion of steel and cast iron. Corrosion, vol. 14. pp. 285-288. [ Links ]
Larson, T.E. and Sollo Jr., F.W. 1967. Loss in water main carrying capacity. Journal of the American Water Works Association, vol. 59, no. 12. pp. 1565-1572. [ Links ]
Merrill, D.T. and Sanks, R.L. 1978. Corrosion control by deposition of CaCO3 films: Part 3, a practical approach for plant operators. Journal of the American Water Works Association, vol. 70, no. 1. pp. 12-18. [ Links ]
Millette, J.R., Hammonds, A.F., Pansing, F.J., Hansen, C.E., and Clark, P.J. 1980. Aggressive water: assessing the extent of the problem. Journal of the American Water Works Association, vol. 72, no. 5. pp. 262-266. [ Links ]
Oddo, J.E. and Tomson, M.B. 1982. Simplified calculation of CaCO3 saturation at high temperatures and pressures in brine solutions. Journal of Petroleum Technology, July. pp. 1583-1590. [ Links ]
Piron, D.L., Desjardins, R., Briere, F., and Ismael, M. 1986. Corrosion rate of cast iron and copper pipe by drinking water. Corrosion Monitoring in Industrial Plants Using Nondestructive Testing and Electrochemical Methods, ASTM STP 908. Morgan, G.C. and Labine, P. (eds). American Society for Testing and Materials, Philadelphia. [ Links ]
Pisigan Jr., R.A. and Singley, J.E. 1987. Influence of buffer capacity, chlorine residual, and flow rate on corrosion of mild steel and copper. Journal of the American Water Works Association, vol. 79, no. 2. pp. 62-70. [ Links ]
Pisigan, R.A. and Singley, J. E. 1984. Evaluation of the corrosivity using the Langelier Index and relative corrosion rate models. Material Performance, vol. 24, no. 4. pp. 26-36. [ Links ]
Puckorius, P.R. and Brooke, J.M. 1991. A new practical index for calcium carbonate scale prediction in cooling tower systems. Corrosion, vol. 47, no. 4. pp. 280-284. [ Links ]
Rossum, J.R. and Merrill, D.T. 1983. An evaluation of the calcium carbonate saturation indexes. Journal of the American Water Works Association, vol. 75, no. 2. pp. 95-100. [ Links ]
Ryznar, J.W. 1944. A new index for determining the amount of calcium carbonate scale formed by a water. Journal of the American Water Works Association, vol. 36, no. 4. pp. 472-475. [ Links ]
Schock, M.R. 1984. Temperature and ionic strength corrections to the Langelier Index revisited. Journal of the American Water Works Association, vol. 76, no. 8. pp. 72-76. [ Links ]
Singley, J.E. 1981. The search for a corrosion index. Journal of the American Water Works Association, vol. 73, no. 11. pp. 579-582. [ Links ]
Stiff, Jr., H.A. and Davis, L.E. 1952. A method for predicting the tendency of oil field water to deposit calcium carbonate. Petroleom Transactions of AIME, vol. 195. p. 213. [ Links ]
Stumm, W. 1960. Investigation of the corrosive behavior of waters. Journal of the American Society of Civil Engineers, Sanitary Engineering Division, vol. 86, no. SA6. pp. 27-45. [ Links ]
Van der Merwe, J.W., and Palazzo, A. 2015. Investigating the correlation between linear polarization resistance corrosion monitoring probe readings and immersion test results for typical cooling water conditions. Journal of the Southern African Institute of Mining and Metallurgy, vol. 115, no. 3. pp. 173-178. [ Links ]
White, R.T. and Higginson, A. 1985. Factors affecting the corrosivity of underground minewaters. Proceedings of Mintek 50: International Conference on Mineral Science and Technology, Sandton, South Africa. [ Links ]
Wu, J.W, Bai, D., Baker, A.P., Li, Z.H., and Liu, X.B. 2015. Electrochemical techniques correlation study of on-line corrosion monitoring probes. Material Corrosion, vol. 66, no. 2. pp. 143-151. [ Links ]
Paper received July 2014
Revised paper received Aug. 2015














