Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.115 n.11 Johannesburg Nov. 2015
http://dx.doi.org/10.17159/2411-9717/2015/v115n11a15
PAPERS OF GENERAL INTEREST
Classification of roof strata and calculation of powered support loads in shallow coal seams of China
X. Liu; G. Song; X. Li
School of Resources and Safety Engineering, China University of Mining and Technology, Beijing, China
SYNOPSIS
According to the overlying rock strength and thickness of 10 shallow coal seams in China, the strata are classified into four types: weak and laminated strata (hereinafter referred to as WL), weak and massive strata (WM), strong and laminated strata (SL), and strong and massive strata (SM). The four types of strata, together with longwall panel height (M), panel length (L), and seam depth (H) are factors that influence the loads on hydraulic power supports. Principal component analysis was used to study the seven influencing factors. It turns out that seam depth (H) is multicollinear with WL, WM, SL, and SM. Thus the enumerated seven factors are divided into two models. In Model 1, six factors; panel height, panel length, and layer thickness of the four type strata are involved. In Model 2, three factors; panel height, panel length, and seam depth are included. Using multivariate regression analysis, two equations to calculate loads on supports are obtained for each model. The equations were applied to shallow coal seams. The equation of Model 1 is more accurate than that of Model 2, but Model 2 could be further used in deep coal seams. The equations were coded through VB programming to simplify the calculation.
Keywords: shallow coal seam; panel length; mining height; seam depth; principal component analysis
Introduction
To ensure coal production in the long term, the focus of coal mining has been gradually shifted to the western areas of China in recent years due to rich coal resources in this region. Most of the coal seams in this area are shallow but the support loads are abnormally high. In these circumstances, the chock loads estimating methods used in the past do not work. If the rated working resistance of a support is larger than needed, the shield is unable to fully perform, while a lower working resistance would lead to accidents like shield crushing or even casualties. This problem is frequently found in shallow coal seams such as Shenfu-Dongsheng, Yulin, Tuha, Lingwu etc. (Zhang, 2011). Thus, to ensure safety and efficiency during mining, the estimation of support loads and selection of supports are of great significance.
Many investigators have carried out research in this field, and the concepts of typical shallow seam and sub-shallow seam have been developed (Singh et al., 2008; Huang, 2002). Generally, a shallow coal seam is 150 m or less in depth and the ratio of overlying rock layer thickness to the thickness of the zone of collapse is less than 1. Theories of short voussoir beam and step beam were developed based on geometric features and structures of broken roof rocks. According to these theories, the collapsed zone is classified into two zones; the caved zone and fractured zone, instead of typically three zones (caved zone, fractured zone, and continuous subsidence zone over gob) in medium-deep or deep coal seams. The pressure on powered supports can be calculated by Equation [1].

where γ is the average density of the overlying rocks, and H is the seam depth.
These investigations have put paid to the notion that the mine pressure in shallow coal seams is low. However, some of the investigations of mine pressure in shallow coal seams still focus only on the characteristics of strata behaviour. Estimation of support loads is based on empirical formulae and should be investigated in more detail. In the paper, the factors that affect mine pressure are analysed by principal component analysis and equations to calculate support loads are obtained, which might be helpful during the calculation of support capacity and selection of a support system.
Overlying strata classification
Strata classification
Strata are complex and differ in terms of homogeneity, thickness, and strength, and hence behave differently during failure. Investigators have established many models and hypotheses to interpret mine pressure behaviour during mining. The hypotheses of strata structure mainly involve the thickness and strength of strata. To analyse the failures of strata and the source of mine pressure, strata structures are always simplified as arch, beam, plate, shell, or a combination of these (Zhang and Hou, 2007; Hou, 2008; Huang, Zhang, and Dong, 2009). Tan (2007) investigated the elastic modulus and thickness of strata, and derived Equation [2] to describe the separation of strata.

where E1and m1are the elastic modulus and thickness of the lower stratum, and E2and m2are the elastic modulus and thickness the upper stratum. Qian proposed Voussoir Beam Theory and Key Strata Theory based on a series of studies (Qian and She, 2003). He concluded that the loads over the stratum can be calculated by Equation [3].
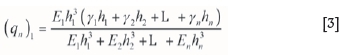
where (qn)1 is the stress offered to the stratum by the superjacent strata; hnare the thicknesses of the coal measure strata layers; ynand Enare strata layer density and elasticity modulus, respectively. Thus, different layers and composite layers (layer thickness and strength) would generate different values of mine pressure.
Based on the previous investigation, it is necessary to classify roof strata according to their strength and layer thickness. Specifically, the ratio of strata strength to coal strength and ratio of layer thickness to coal seam layer thickness are used to classify roof strata in this paper, because strata structures seem related to coal layer thickness. It is important to note that in this paper 'strong' rock is considered harder than coal, while 'weak' rock is weaker than coal. In this way, overlying strata are classified into four types: weak and laminated strata (WL), weak and massive strata (WM), strong and laminated strata (SL), and strong and massive strata (SM). Table I describes the classification and criteria in detail.
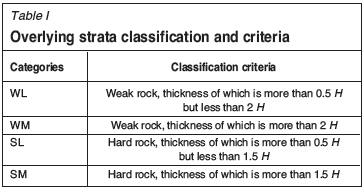
This criterion is simple and can be widely applied. The depth of the coal seam is the sum of the four type roof layer thicknesses.
Characteristics of four different roof structures
During mining, the splitting and caving characteristics of the roof rocks would be different due to the differences between the four types of roof structures. Because of its greater thickness and strength, the SM type is more likely to be the key stratum and keep stable during panel advances. SM would carry the loads imposed by superjacent strata. Hence, separations between superjacent strata are rarely found but are more likely to be encountered among strata that are below SM strata.
WL strata, in contrast, are unable to generate a load-bearing structure or to keep stable. The splitting of the key stratum would usually lead to caving of WL strata above and the weight of WL strata would be applied to strata below.
WM strata normally have abundant primary fissures. The properties of WM and SL strata are intermediate between those of WM and SL strata.
Previous investigations assumed that mine pressure does not simply increase linearly with increasing depth, and that it can be calculated by Equation [1]. However, this method is imprecise and is not widely applicable. In this paper, all the strata over the coal bed layer are considered. Studies have been conducted in 10 shallow highly mechanized longwall panels at collieries in China. The support load is deemed to be the dependent variable, and factors that influence support loads are considered as independent variables. Principal component analysis is used to analyse these factors and multiple regression analysis is then used to obtain formulae to calculate support loads.
The shallow seam panels are listed below. Table II gives more detail.
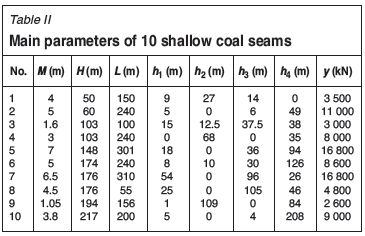
No. 1: Panel 1203 in Daliuta Coal Mine
No. 2: Panel 222201 in Yang'iacun Coal Mine
No. 3: Panel 22201 in Guoerzhuang Coal Mine
No. 4: Panel 42108 in Liangshuijing Coal Min,
No. 5: Panel 22303 in Bulianta Coal Mine
No. 6: Panel 51102 in Shangwan Coal Mine
No. 7: Panel 52304 in Daliuta Coal Mine
No. 8: Panel 1201 in Dayuan Coal Mine
No. 9: Panel 2708 in Yangcun Coal Mine
No. 10: Panel 11501 in Yushujing Coal Mine.
Principal component analysis of support working resistance
Factors influencing support resistance
Loads on the strata are always in a state of dynamic change during mining cycles. The values are influenced by many factors, viz. mining height, coal bed depth, panel length, support type, panel advance speed, goaf management etc. Normally, more factors would make the model more accurate, while on the other hand making the model much more complicated. To keep the model feasible and simple, the influencing factors should be the most important ones or the closest related to the dependent variable (here the support resistance). Thus the number of these factors should be controlled at the same time (Huang, 2005; Wang, Wang, and Lingmei, 2008). Principal component analysis is a statistical approach that simplifies various indexes to fewer, more comprehensive indexes (Wang, Wang, and Lingmei, 2008; Ren and Yu, 2011).
There are numerous factors affecting support working resistance. Here, seven factors are included. They are:
(1) Mining height (M)
(2) Depth (H)
(3) Panel length (L)
(4) Thickness of WL layers (h1)
(5) Thickness of WM layers (h2)
(6) Thickness of SL layers (h3)
(7) Thickness of SM layers (h4).
The support rated resistance y (kN) is selected as the dependent variable. After analysing the geological column and mining conditions of the 10 selected panels, the roof strata of coal mines are classified and are shown in Table II. Principal component analysis and multiple linear regression are used to obtain the relationship between support resistance y (kN) and the seven influencing factors (M, H, L, h1, h2, h3, h4).
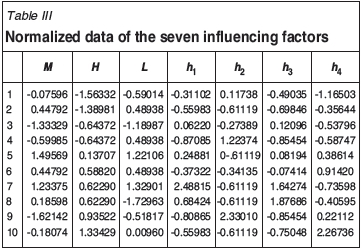
Independent variables standardization
The units of variables listed in Table II are the same (metres). However, the values of the variables vary from 0 to 310. The difference between the value ranges of the seven variables is significant, which would make principal component analysis difficult. Thus it is necessary to standardize the independent variables. Z-score is used to normalize values of the seven influencing factors. Tables III and IV describe the normalized statistics and correlation coefficient matrix, respectively.
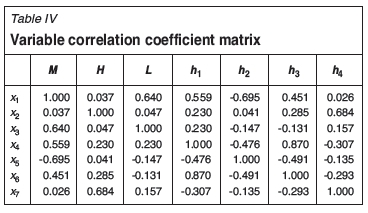
Eigenvalues and variance contribution
Equation [4] is used to calculate eigenvalues. These eigenvalues are sorted by their values in descending order (λ1/λ2/λ3/λ4/λ5/λ6/λ7). Table V lists eigenvalues and variance contribution of the correlation matrix.
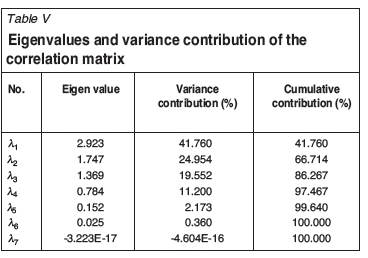
According to the principle of principal component extraction, eigenvalues can reflect the relative influence and importance of the components (Xia and Huang, 2007; Sahu, Mahapatra, and Panigrahi, 2009; Basilevsky, 1994). Components are considered to have insignificant explanatory power or are less important if their eigenvalues are less than 1. The first three components of Table V whose eigenvalues are larger than 1 are therefore selected, and their cumulative contribution sums to 87.7%. The three components can therefore represent all the components enumerated.
Selecting variables
Table VI lists the variable component matrix. These coefficients imply the relative weights of variables. The larger the coefficient (absolute value), more important this variable would be.
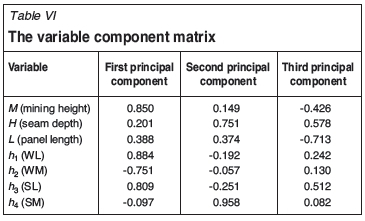
It can be seen from Table VI that mining height, WL, WM, and SL have the largest first principal components, which means these four variables have the greatest influence on this first principal component; seam depth and SM are largest at the second principal component; and panel length is largest at the third principal component.
The three principal components might include information of seven indexes, which indicates that the selected seven indexes are essential in determining support load density.
Multiple regression analysis on support resistance
Multicollinearity analysis of factors influencing support resistance
Generally, the variables are independent of each other. In some cases, dependency does exist among two or more variables. This is what multicollinearity means. To delete unnecessary variables, IBM SPSS Statistics 19.0 is used to analyze the multicollinearity of the seven selected influencing factors. Support resistance in Table II is considered the dependent variable (y), while the remainder are independent variables. Table VII shows the results of the collinearity analysis.

The coal seam depth is the sum of four roof strata type thicknesses; that is,

In Table VII, tolerance of seam depth is zero, which is less than 0.1 (tolerance limit). Meanwhile its VIF is far greater than 10. This is because seam depth (H) is multicollinear with WL, WM, SL, and SM. Thus two models are built. The first model includes six variables: mining height, panel length, WL, WM, SL, and SM. The second model includes three factors: mining height, panel length, and seam depth. Table VIII describes the two models.
Derivation of multiple linear regression equation
The objective functions of both Model 1 and Model 2 are resistance of the support system (y). Through multiple regression analysis, regression equations are obtained (Equations [6] and [7]). Table IX lists the goodness of fit.
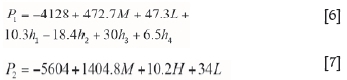
where P1and P2 are the estimated loads on supports in model 1 and model 2, respectively.
It can be seen from Table IX that the determination coefficient (R2) of Model 1 is 0.949, and 0.925 for Model 2. The adjusted R2 values are 0.848 and 0.888, respectively. This indicates that the two models have a high fitting degree. Specifically, Model 1 has a higher fitting degree than Model 2.
Residual analysis of the regression equation
The values of the variables in Table II are entered into Equations [6] and [7] to test the established regression equations of the two models, which are described in Table X.
The standard errors in Table X represent the precision of the regression equation. The residuals of panel no. 1 and no. 6 are extraordinarily large, indicating that support resistance in these two panels should be improved. In fact, panel no. 1 (Panel 1203 in Daliuta Coal Mine) is 150 m in length, 4 m in height, and 53 m deep. The selected type of support system in this panel is YZ3500-23/45. During mining, pillars of the supports were broken and water and sand inrush were found in the panel. This is because the capacity of powered supports was too low. Similarly, rib spalling was frequent during mining in panel no. 6 (Panel 41102 in Shangwan Coal Mine). The capacity of the supports should be improved. The no. 3 mine's working resistance of support calculated by model 2 is only 1090 kN, which is obviously less than the calculated value in model 1, 2637 kN, and actual value of 3000 kN. This demonstrates that model 2 is more reliable than model 1.
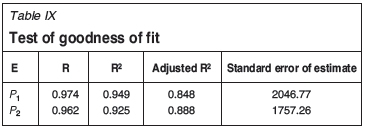
Roof control problems are rarely found in the other 8 panels, and the relative tolerances are acceptable. The selected sample data may not be overwhelming, so a normal P-P plot of regression standardized residual is used to evaluate normality of a smaller data-set.
In Figure 1, the scatter increases approximately linearly. After standardization, all the values of standardized residuals are less than unity. No extreme values or outliers are found, indicating that the data is steady.
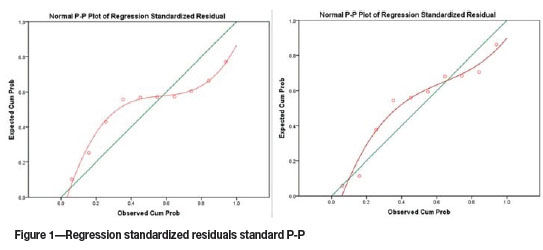
Figure 2 compares the support resistance and calculated values by Equations [1] and [2]. The three lines share the same variation trend and the differences between them are insignificant, indicating that the equations are relatively reliable. Equation [1] is more precise than Equation [2]. Through the equations, it is also found that mining height (M) and panel length (L) are more important to the support capacity, compared with WL, SL, and SM.
Applications of support load calculation equations
Equations [1] and [2] are based on, and applicable to, shallow coal seams. The equations were also tested on medium deep and deep coal seams (Panel 10217 of Tashan coal mine and Panel 1105 of Zhaogu coal mine). The supports in the panels are ZZS7000-1.8/3.7 and ZY18000/30/65D, respectively. Table XI shows the parameters of the panels and support loads calculated by the equations.
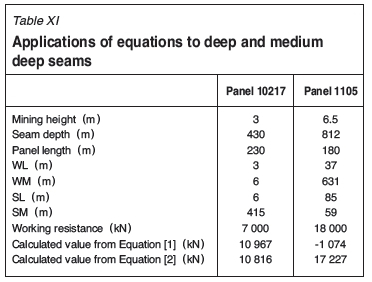
For deep and medium deep coal seams, a significant difference can be found between support resistance and calculated support loads. The calculated values from Equation [1] are 10 967 kN for Panel 10217 and -1074 kN for Panel 1105. Compared with the corresponding real support resistance (7 000 and 18 000 kN), the differences are tremendous. Therefore Equation [1] is not applicable for deep coal seams. In contrast, the calculated value from Equation [2] for Panel 10217 is larger than the real resistance, and that calculated for Panel 1105 is slightly different from the real value. Thus Equation [2] is more applicable and reliable in deep, medium deep, and shallow coal seams.
VB programming is used to make the calculation simple (Figure 3). It should be noted that Equation [1] is more accurate but applicable only for shallow coal seams. For seams deeper than 400 m, Equation [2] should be used.
For Equation [2], Figure 4 describes the relationships between support loads, panel length, and seam depth at mining heights of 2 m, 4 m, and 6 m. The panel length (x-coordinate) varies from 50 to 300 m, and seam depth (y-coordinate) varies from 50 to 220 m.
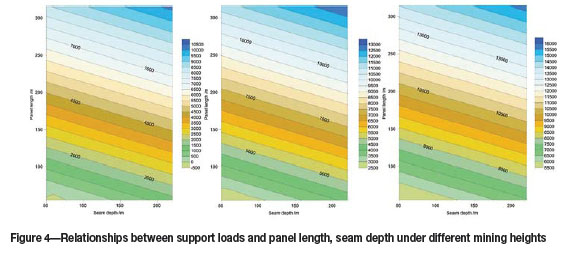
From Figure 4, it can be easily seen that the maximum support load increases from 10 000 kN for a mining height of 2 m (Figure 4a) to 16 000 kN at 6 m (Figure 4c). Support loads also increase with increasing panel length and seam depth, but the influence of panel length is more significant.
The methods shown in Figures 3 and 4 can be used to calculate support loads easily and quickly.
Conclusions
(1) Coal measure roof strata are classified into four types; weak and laminated (WL), weak and massive (WM), strong and laminated (SL), and strong and massive (SM), based on the relationship between the strength, thickness of roof strata, and thickness of coal layer
(2) Principal component analysis and multiple regression analysis were used to derive the support loads calculation equations for shallow coal seams. The equations were tested by residual analysis and normal PP plot
(3) Equation [1] is more accurate, but Equation [2] is more widely applicable. Through programming and graphical analysis, support loads can be easily calculated.
Acknowledgements
This investigation was funded by the National Basic Research Program of China (973 Program) (2013CB227903) and Project (U1361209) supported by National Natural Science Foundation of China.
References
Basilevsky, A. 1994. Statistical Factor Analysis and Related Methods. Wiley, Canada. [ Links ]
Hou, Z. 2008. Concept of both short voussoir beam and step beam in shallow seam and voussoir beam theory. Journal of China Coal Society, vol. 11. pp. 3-6. [ Links ]
Huang, Q., Zhang, P., and Dong, A. 2009. Mathematical model of "arch beam" of thick sandy soil layer movement in shallow seam. Rock and Soil Mechanics, vol. 9. pp. 181-185. [ Links ]
Huang, Q. 2002. Ground pressure behavior and definition of shallow seams. Chinese Journal of Rock Mechanics and Engineering, vol. 8. pp. 68-71. [ Links ]
Huang, Q. 2005. Studies on load-transmitting factor of thick sandy soil layer on key roof stratum in shallow seam mining. Chinese Journal of Geotechnical Engineering, vol. 6. pp. 67-71. [ Links ]
Qian, M. and Shi, P. 2003. Ground pressure and strata control. China University of Mining and Technology Press, Xuzhou. [ Links ]
Ren, X. and Yu, X. 2011. Multivariable Statistics. China Statistical Publishing House, Beijing. [ Links ]
Sahu, H.B., Mahapatra, S.S., and Panigrahi, D.C. 2009. An empirical approach for classification of coal seams with respect to the spontaneous heating susceptibility of Indian coals. International Journal of Coal Geology, vol. 80. pp. 175-180. [ Links ]
Singh, R., Mandal, P.K., Singh, A.K., Kumar, R., Maiti, J., and Ghosh, A.K. 2008. Upshot of strata movement during underground mining of a thick coal seam below hilly terrain. International Journal of Rock Mechanics and Mining Sciences, vol. 45. pp. 29-46. [ Links ]
Tan, Y. 2007. Ground pressure and strata control. China Coal Industry Publishing House, Beijing. [ Links ]
Wang, H., Wang, L., and Lingmei, G.E. 2008. Application of principal component analysis and BP neural network in the rate of coal oxygen consumption prediction. Journal of China Coal Society, vol. 8. pp. 82-87. [ Links ]
Xia, X. and Huang, Q. 2007. Analyses of the factors on top coal caving capability in steep seam. Journal of Hunan University of Science and Technology (Natural Science Edition), vol. 1. pp. 9-12 (in Chinese). [ Links ]
Zhang, X. and Hou, Z. 2007. Numerical simulation of over burden three zones formining operation with thick over burden and less depth. Coal Science and Technology, vol. 2. pp. 97-100. [ Links ]
Zhang, Z. 2011. Study on influence law of dynamic strata pressure in the shallow coal seams face under hilly and gully terrain. China university of Mining and Technology, Xuzhou. [ Links ]
Paper received Nov. 2014
Revised paper received Aug. 2015














