Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.111 n.6 Johannesburg Jun. 2011
TRANSACTION PAPERS
A mathematical model of laser surface heat-cooling treatment for medium carbon steel
I. FedotovI; T. FedotovaII, S.L. PityanaII; K. LabuschangeII; M. ShatalovIII,I; J.H. PotgieterIV
IDepartment of Mathematics and Statistics, Tshwane University of Technology, South Africa
IIDepartment of Chemical and Metallurgical Engineering, Tshwane University of Technology, South Africa
IIINational Laser Centre, Council for Scientific and Industrial Research, South Africa
IIIManufacturing and Material Sciences, Council for Scientific and Industrial Research, South Africa
IVSchool of Chemical and Metallurgical Engineering, University of the Witwatersrand, South Africa
SYNOPSIS
One of the most effective methods of metal surface heat treatment is through laser hardening. In most cases, laser parameters are determined experimentally, which is expensive and time-consuming. A mathematical model for the surface heat treatment process will allow a significant decrease in costs, and reduce the time required for optimization. In the present work, the authors present a mathematical model for laser heat treatment with forced cooling which can be applied to medium carbon steel. The model is based on a three-dimensional heat transfer equation using Green's function. The model allows one to calculate the temperature of the treated steel at different depths below the surface with and without cooling, for set values of the laser power and travelling speed, when the heat transfer coefficient is a known constant. It also takes variations in the radiation adsorption coefficient on the metal surface and laser beam spot size into account. The model was illustrated by comparing calculated and experimental temperature profiles of mild carbon steel with 0.5% C with and without cooling. A reasonably good agreement was achieved between experimental and predicted values to ensure that a high enough austenizing temperature with short enough cooling time was reached for direct martensite formation. It also predicted the depth of treatment accurately. The incorporation of cooling in the model substantially improves previous models based on heat transfer only. It delivers a tool that can with a reasonable accuracy predict the depth of surface heat treatment and cooling time required from operational parameters, such as laser power, speed of motion, and distance between laser and cooling source, that can be controlled in the work set-up. This can eliminate trial and error efforts and result in significant time and cost savings.
Keywords: Laser, surface treatment, martensite transformation, carbon steel, heat treatment.
Introduction
The main purpose of heat treating medium carbon steels is to increase their hardness, and subsequent wear resistance, through the formation of martensite in the steel. In simple terms, the process involves heating a metal to above its austenite transformation temperature (typically 800-900ºC), which dissolves precipitated carbides in the lattice structure to form a homogenous austenite structure. Martensite can then be formed when the laser heat treated steel is immediately cooled to avoid isothermal conversion of austenite into ferrite or carbide phases. For this purpose, a high temperature gradient during cooling is required. Martensite formation usually occurs as a result of two reactions, one which produces lenticular martensite, and the other, stacked martensite. The latter is characterized by a relatively high dislocation density and therefore increased hardness. In order to obtain this desired phase in the metallic component, one must achieve a fast direct austenite to martensite conversion.
In laser surface hardening, the metal surface to be hardened is heated by a highpower laser beam until it reaches a critical transformation temperature, which is normally well below its melting temperature. This is followed by rapid self-quenching, where the surrounding bulk material acts as a heat sink. The microstructures formed during the laser heat treatment depend on the alloy composition, temperature, and cooling rate1. This complex behaviour can be described and explained by conventional continuous cooling transformation (CCT) or time-temperaturetransformation (TTT) diagrams2. This is illustrated in the appropriate diagram for a steel equivalent to the mild carbon one used in this model development and discussion, and which is shown later.
Empirical experimentation with laser surface heat treatments can be costly and time-consuming. It would therefore be advantageous to use an applicable model to predict the desired treatment time, power, and temperature gradient for the required phase transformation. The transfer of heat (conduction) into material has been modelled by various researchers. Carslaw and Jeager3 were among the pioneers to mathematically model heat transfer, while Tichonov and Samarsky4 also did work in this field. Carslaw and Jeager's3 model was later refined by Ashby and Easterling5. Schuocker6 developed earlier work to calculate the temperature at any time or depth during surface heating by simulating one-dimensional heat flow. Recent modelling of heat transfer in metallic materials by Lee and Allbright7 also accounted for energy absorption during phase changes, while Abington Consultants8 developed a commercial package for this purpose.
A major disadvantage of previously reported work was that none of these models are three dimensional, or take account of cooling. It was therefore decided to investigate the development of such an improved model for medium carbon steel heat treated by a Nd:YAG high power laser. This work presents a mathematical model of laser treatment with cooling, based on a three-dimensional heat equation using Green's function. It illustrates that the combination of the laser-heating method and synchronous cooling can improve the microstructure of the heated metal via rapid quenching of austenite to directly formed martensite. This model shows that the hardenability of AISI 1055- steel is critically dependent on the cooling rates that must be achieved for direct martensite formation.
Experimental set-up
In this work, a Rofin DY 440 Nd:YAG laser was used for surface hardening. The laser was integrated with a five axis computer-controlled KUKA robot arm. The laser beam was conveyed by a 600 µm optic fibre. The experimental setup was equipped with a pyrometer, which was mounted in such a way that its detector was focused at the incident defocused laser beam on the surface of the component. The defocused laser beam was 8 mm in diameter. In these experiments the sensitivity of the pyrometer was examined by varying its pointing spot size in such a way that it was half, equal, and twice the size of the defocused laser beam. The laser hardening process was carried out under a nitrogen gas atmosphere. The gas was discharged by a specially designed nozzle fitted onto the laser head. The nozzle was placed about 20 mm behind the incident laser beam. The gas acted both as a coolant and to prevent oxidation of the component. The laser power was set at 1 kW. The beam travel speed was varied from 0.3 to 0.5 m/min.
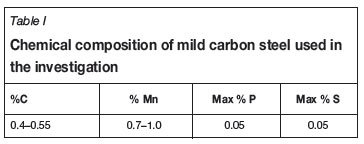
The laser hardened material was a 5 mm thick Bennox® plate produced by ArcelorMittal. The chemical composition is shown in Table I. After laser hardening treatment, transverse sections were cut, ground, and polished for metallurgical examination. Sections were etched with a 2% Nital solution to reveal the microstructure of the hardened case using optical microscopy. Hardness profiles were made perpendicular to the specimen surface on transverse sections, using a 0.3 kg load on a micro-Vickers hardness tester.
Development of the model
Mathematical model for laser treatment with cooling
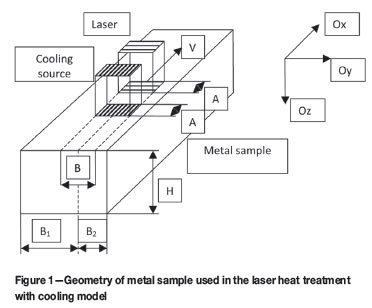
Figure 1 shows the general geometry of the laser-heating and nitrogen-cooling process. In the present mathematical model, the laser beam and cooling source are of a rectangular form, with uniform energy distribution (calculation of other geometrical forms and energy distribution laws in the sources can be obtained in the same way). It is assumed that the heat treatment of a metal sample is performed by a single path of the laser beam and cooling source with constant speed V in the direction of axis Ox (Figure 1). It is further assumed that the metal sample under thermal treatment is a rectangular rod with infinite length in the direction of heat source movement and a finite size of the cross-section.
The mathematical model for the metal laser-hardening is based on a 3-D heat transfer equation with constant coefficients which are not temperature dependent, as shown in Equation [1]. The laser influence is taken into account by introducing a corresponding non-homogenous term on the right-hand side of Equation [1]. This term depends on the power, speed, and coordinates of the moving heat source. Metal cooling is described by introducing a cooling source moving in the same direction and speed as the laser beam, but separated by means of a fixed special shift. The dependence of temperature 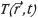 on space coordinates
on space coordinates 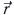 =[x,y,z]T and time t is described by the heat transfer equation:
=[x,y,z]T and time t is described by the heat transfer equation:

where -∞ < x < ∞, -B1 < y < B2, 0 < z < H
| κ | - | thermal diffusivity coefficient |
| λ | - | heat transfer coefficient |
Q1(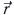 ,t ) ,t ) | - | rate of laser beam specific power to the volume unit, Q2(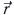 ,t ) - rate of cooling source specific power to the volume unit. ,t ) - rate of cooling source specific power to the volume unit. |
If α = radiation absorption coefficient on the metal surface, then:
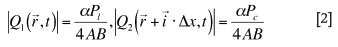
It is accepted in the proposed model that there is no heat exchange with the environment on the beam flat surfaces, i.e. there is no convection and radiation. This implies boundary conditions of the second kind:
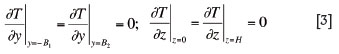
The boundary conditions of the third kind are more natural from the physical point of view. These boundary conditions were described and studied in detail in earlier work9. However, since in this study the cooling is done mainly by forced cooling with nitrogen gas, the specific kind of boundary conditions is not critical. The initial temperature of the rod is assumed to be equal to zero.
Generally speaking, the boundary conditions stated in Equation [3] are not realistic, because the cooling happens partly because of convective exchange with the surrounding medium. However, in this case, where a powerful source of cooling was introduced, one can ignore this convective exchange, thus justifying the choice of boundary conditions. The method of solving the heat transfer equation, is based on Green's function G(|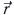 -
-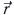 '|,t-t'). This method was used previously by other authors10,11:
'|,t-t'). This method was used previously by other authors10,11:
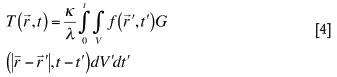
where
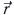 '= [x', y', z']T,
'= [x', y', z']T,
dV' = dx'dy'dz' = element of volume treated.
The equation converges rapidly at small time steps3.
Green's function is a product of three functions according to the space variables:
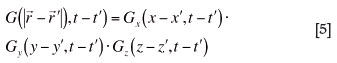
By varying the direction of the heat source's movement (x), the function Gx(x-x',t-t') has a standard Gaussian form with one member caused by the absence of boundary conditions of this variable:
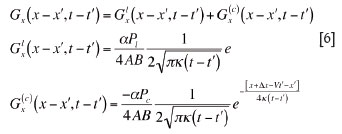
Using the two other variables, Green's function can be constructed with two equivalent methods, i.e the Fourier method and the point source method.
The point source method would be the better choice owing to the quick convergence of a series with a short timetransition process, which is a significant factor for the problem under consideration.
In this case Green's function would take the following form:
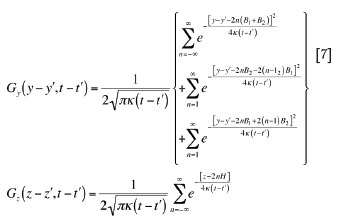
Green's function obtained using the Fourier method leads to a form different in appearance from the one in Equations [5] to [7], but is equivalent to it. It should be noted that the Fourier method is preferred for large values of time (long treatment periods).
Solution of the problem
The following set of equations can then be developed to describe the heat treatment-cooling problem and to find a solution by solving it:
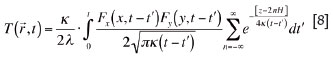
where

with erf(u)=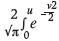 dv where the equation is an error function.
dv where the equation is an error function.
Based on the mathematical model of a metal sample heat treated with cooling, an algorithm of the task solution and a computer program were developed, which make it possible to determine the dependence of the temperature distribution on time at any point of the sample.
Results and discussion
Application of the model
Consider an example of the heat treatment of an AISI-1055 steel surface. It is assumed that the martensite structure must be formed in the surface layer and should not be less than 1 mm thick. From the isothermal diagram of steel transformation, it can be seen that the prerequisite for this is a temperature of 1200ºC at the depth of 1 mm. Under these conditions, the metal obtains an austenitic structure. If the metal is then quickly cooled to a temperature lower than 600ºC (in a time of no longer than 2 seconds), the metal obtains a martensitic structure. No unwanted ferrite and carbide phases would form when this method of heat treatment is applied.
The temperature profile during the heat treatment process was calculated using the values of the constants summarized in Table II.

Figures 2 to 4 demonstrate temperature profiles in point x = 50 mm, y = 0 mm at different values of the depth z below the material's surface. Figure 2 shows the change of temperature in the material with the laser treatment time without cooling, at depths of z = 0 mm, z = 0.5 mm, z = 1 mm and z = 1.5 mm below the surface inside the material structure.
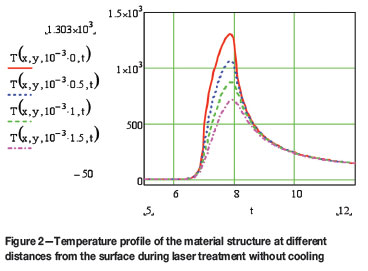
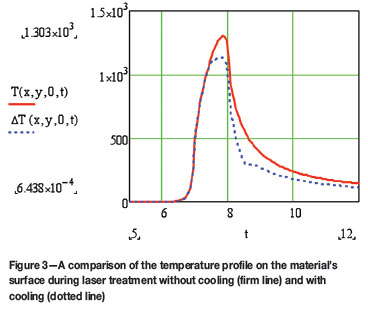
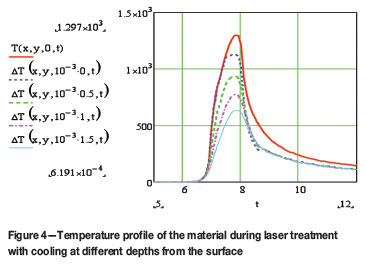
Figure 3 provides a comparison of the temperature profile of the metal sample's surface (z = 0) during laser treatment without cooling and with cooling.
Figure 4 shows the change of temperature in the laser treated material with time, at depths of z = 0 mm, z = 0.5 mm, z = 1 mm and z = 1.5 mm from the surface while simultaneously applying cooling with nitrogen gas.
Comparison of experimental values and mathematical model
A medium carbon steel with a carbon content of 0.5% was used for the validation of the theoretical model with the experimental observations. The surface of the steel was laser heated to 1200ºC, and then immediately cooled with nitrogen gas. The laser system used for heat treatment was the Nd:YAG laser described in the experimental section. The choice of nitrogen cooling was prompted by the necessity to avoid the 'nose' of the CCT diagram so as to prevent the conversion of austenite into unwanted ferrite and carbide phases. This enables one to achieve a direct austenite to martensite conversion, as is illustrated in Figure 512.
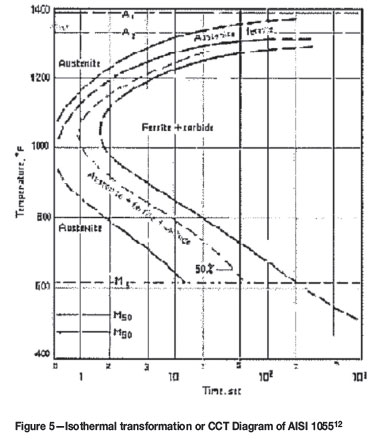
Figure 6 shows a comparison of calculated and experimentally determined temperature profiles of the material without cooling with nitrogen gas. The calculated and experimentally measured temperature profiles obtained when the cooling gas was introduced are shown in Figure 7. It is evident that the introduction of the source of cooling causes a considerable decrease in the time that is required for the transition of the metal sample from austenite into the martensite phase.
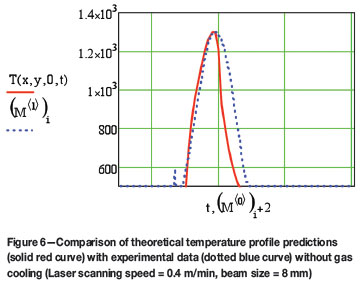
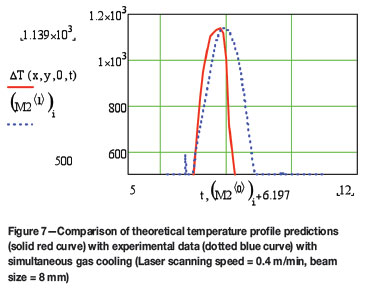
The difference between the theoretical predictions of the ultimate temperature achieved and cooling speed compared with the experimental results can be explained by a finite dimension of the pyrocam spot size. In the experiment, the temperature was averaged over the size of the spot (diameter 4-16 mm), which was several orders of magnitude of the metal grain sizes (which are typically 50-60 µm). In contrast, the theoretical model describes the temperature changes at a point. Due to the fact that the real phase transformations occur in the dimensions of the metal grains, this can be regarded as a 'mathematical point' compared to the size of the pyrocam spot.
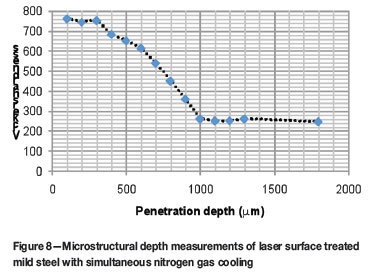
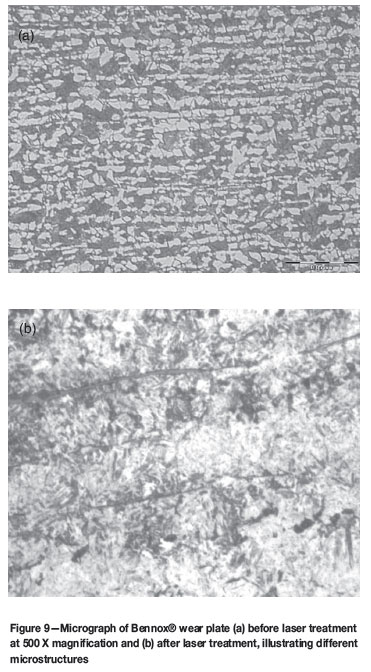
Hence the theoretical model characterizes the process of transformation more objectively. Figures 6 and 7 both indicate a reasonable degree of agreement between the experimental and modelled values. Although the data in Figure 7 predicts a high enough austenizing temperature with a short enough cooling time for martensite formation, the validity of the theoretical model would really be confirmed only if the measured surface hardness was indeed substantially more than that of the bulk material. Experimental values of the measured hardness of the laser treated surface at a number of points indicated an average value of 750 HV, while the hardness of the bulk material was only 250 HV. Figure 8 indicates that this was indeed the case, and also that the surface treatment occurred to a depth of 1 mm, as was intended. Furthermore, the micrographs in Figure 9 clearly indicate that there is a difference in the surface microstructure of the material before and after laser surface treatment.
Conclusions
A three-dimensional mathematical model based on Green's function was developed, which took both the laser heating and the synchronous cooling of the work piece into account. This is a substantial improvement on previous models, which only accounted for the heat transfer. It shows that the time of the transition process and the ultimate temperature reached during heat treatment can be calculated from the following input:
the laser heat source power
the source of cooling power
speed of the heat source's motion along the sample being heat treated
the geometry of the laser the source and source of the cooling spots
the distance between the laser source and the source of cooling
the steel grade of the sample under treatment.
The model offers substantial time and cost saving advantages in comparison with a trial and error process. The validity of the model was verified by experimental temperature measurements and the ultimate hardness and microstructure achieved in the material under investigation.
References
1. KUILBOER, R.B., KIRNER, P.K., MEIJER, J., RUND, M., and SCHNEIDER, M.F. Laser beam transformation hardening: transferability of machining parameters. A report on a co-operative work in STĆE'. Annals of the CIRP, vol. 43, no. 2, 1994, pp. 585-592. [ Links ]
2. SKVARENIA, S. and SHIN, Y.C. Predictive modelling and experimental results for laser surface hardening of AISI 1536 steel with complex geometric features by high power diode laser. Surface & Coatings Technology, vol. 201, 2006, pp. 2256-2269. [ Links ]
3. CARSLAW, H.S. and JAEGER, J.C. Conduction of Heat in Solids. Oxford University Press, 2nd Edition, UK. 1959. [ Links ]
4. TIKHONOV, A.N. and SAMARSKY, A.A. Equations of Mathematical Physics. Dover, New York, USA. 1990 [ Links ]
5. ASHBY, M.F. and EASTERLING, K.E. The transformation hardening of steel surfaces by laser beams: hypo eutectoid steels. Acta Metallurgica, vol. 32, no. 11, 1984, pp. 1935-1948 [ Links ]
6. SCHUOCKER, D. Handbook of the Eurolaser Academy, vol. 2. Chapman Hall, Cambridge, UK., 1998. [ Links ]
7. LEE, S.H. and ALLBRIGHT, C.E. Thermal sensitivity analysis by use of an analytic solution for laser surface treatment. Journal of Physics D: Applied Physics, vol. 35, 2002, pp. 710-715. [ Links ]
8. ABINGTON CONSULTANTS. [CD-ROM] Thermal Source Optimiser, rev. 1.21, 2004. <www.abingtonconsultants.co.uk > [ Links ].
9. LEUNG, M. Phase-change heat transfer in laser transformation hardening by moving Gaussian rectangular heat source. Journal of Physics D: Applied Physics, vol. 34, 2001, pp. 3434-3441. [ Links ]
10. MAIER, C., SCHAAF, P., AND GONSER, U. Calculation of the temperature profile for laser treatment of metallic samples. Material Science and Engineering, vol. A150, 1992, pp. 271-280. [ Links ]
11. MAJUMDAR, P. and XIA, H. A Green function model for the analysis of laser heating of materials. Applied Mathematical Modelling, vol. 31, 2007, pp. 1186-1200. [ Links ]
12. CHANDLER, H. Heat treater's guide. Practices and procedures for irons and steel. 2nd Edition, ASM International, 36-76, 2000, pp. 196-197. [ Links ]
Paper received Jun. 2009; revised paper received Nov. 2010.
© The Southern African Institute of Mining and Metallurgy, 2011. SA ISSN 0038-223X/3.00 + 0.00.














