Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.33 n.2 Pretoria Jul. 2022
http://dx.doi.org/10.7166/33-2-2651
CASE STUDIES
Increasing warehouse throughput through the development of a dynamic class-based storage assignment algorithm
S.E. McInerneyI; V.S.S. YadavalliII, *
IDepartment of Industrial and Systems Engineering, University of Pretoria, South Africa
IIThe author was enrolled for a BEng degree in the Department of Industrial and Systems Engineering, University of Pretoria, South Africa
ABSTRACT
This study investigates the problems faced by an agricultural wholesaler arising from an inefficient random storage assignment policy. Research was conducted on warehouse operations and storage policies. The ABC classification technique was used to create a class-based storage assignment policy. This policy was then input into an algorithm that packs products according to how frequently they are ordered. The aim of the algorithm is to store fast-moving products closest to the shipping area. If this is done, the order picking times would decrease by an average of 3 hours 20 mins per day. This would increase the warehouse's throughput and profitability.
OPSOMMING
Hierdie studie ondersoek die probleme ervaar deur 'n landbou groothandelaar as gevolg van 'n ondoeltreffende toevaksgebaseerde stoorbeleid. Navorsing is gedoen oor pakhuisbedrywighede en stoorbeleide. Die ABC-klassifikasie tegniek is gebruik om 'n klasgebaseerde stoorbeleid op te stel. Hierdie beleid is toe ingevoer in 'n algoritme wat produkte verpak volgens hoe gereeld die produkte bestel word. Die doel van die algoritme is om produkte wat vinnig beweeg naaste aan die versendingsarea te stoor. As dit gedoen word, sal die bestellingopteltye verminder met 'n gemiddelde tyd van 3 ure en 20 minute per dag. Dit sal die deurset en winsgewendheid van die pakhuis verhoog.
1 INTRODUCTION
Order picking is the retrieval of products from their warehouse storage locations to fulfil customer orders [1]. It is one of the most essential and most expensive warehouse operations [2]. The location of products within the warehouse affects the distance travelled during the order picking process as well as the time taken to pick orders. The travel distance and time influence the efficiency of the order picking operation. To decrease operating costs and increase the number of orders fulfilled per day, products need to be stored in the best available locations.
This project was carried out for FarmCorp SA (a fictitious name), a large-scale wholesaler and distributor of agricultural products in Southern Africa. FarmCorp SA operates a warehouse in Centurion that stores over 14 000 different products, with an average of 190 000 individual products flowing through the warehouse daily. The warehouse faces a storage location assignment problem (SLAP). This problem stems from the warehouse's random storage assignment policy, which allocates fast-moving products to higher racks from which a forklift is required to collect them. If every order required additional picking time, fewer orders would be completed per day, and as a result customers would wait longer to receive their orders.
These factors contribute to longer order-picking times and reduce the warehouse's throughput. Quick order fulfilment is a primary component of customer satisfaction; thus long order-picking times lead to customer dissatisfaction. The aim of this project was to increase warehouse throughput by developing a dynamic class-based storage assignment algorithm that stores fast-moving products on lower shelves and closer to the shipping area. This can be achieved through the implementation of an ABC class-based storage policy.
2 RESEARCH PROBLEM
FarmCorp SA's Centurion warehouse experiences several problems with its order-picking process owing to its current storage policy. Time is wasted when pickers (the employees responsible for completing orders) are required to search for randomly stored products. Stock stored on high-level shelves requires a forklift for it to be retrieved. Currently, 39 per cent of frequently picked stock is located on high-level shelves, lengthening the time it takes to pick these products. In addition, fast-moving products are often stored far from the shipping area, increasing the distance travelled by pickers.
The warehouse is currently operating at 62 per cent above its overall capacity. As a result, excess products are being stored in the pathways between aisles. This creates obstructions that limit the routes available for pickers and forklifts to use, increasing the distance travelled when picking orders.
Similar products are often stored in different locations because adjacent bins are unavailable. In addition, the computer system does not reroute pickers to secondary bins when the default bin is empty. This leads to pickers incorrectly reporting that products are out of stock. A storage policy that allocates products to default and secondary bins in closer proximity would result in fewer unnecessary restocks and order delays.
At present, an average of 4 900 transactions are picked each day. This is 600 transactions below the target value of 5 500. Reducing the time taken to pick an order would increase the number of transactions picked per day. This increase would have the potential to meet or exceed the target.
3 LITERATURE REVIEW
Storage operation and potential storage policies were investigated.
3.1 Storage operation
'Storing' refers to the activities surrounding the transportation of incoming inventory from the unloading area to specific storage locations in the warehouse and holding it there until it is required [3]. Storage policies specify the location of products within the warehouse [1]. An effective storage policy aims:
1. To minimise the time taken and distance travelled during the order-picking process;
2. To minimise storage costs; and
3. To increase warehouse efficiency [4].
Five main storage assignment policies are described in the literature: random, closest-open, dedicated, full turnover, and class-based.
3.2 Storage policies
A random storage policy places incoming inventory arbitrarily into any empty storage bin. Such a policy is only effective when supported by a computer-based system. Product locations must be accurately recorded in a reliable inventory management system. If not, products become impossible to locate during the order-picking process.
The random storage policy is popular, thanks to its ease of implementation and ability to adapt in line with demand fluctuations [5]. However, the lack of defined storage locations results in disorganisation, poor use of product information, and increased order-picking times in large warehouses (such as FarmCorp SA's Centurion warehouse) [6].
A closest-open storage policy emerges when pickers are responsible for the random allocation of products. The closest-open storage policy places incoming inventory into the nearest empty storage bin. As a result, products become clustered around the receiving area and dispersed towards the back of the warehouse [7].
Dedicated storage policies allocate products to fixed storage locations. When a product is out of stock, its designated storage location will remain empty. However, pickers become familiar with the product storage layout and can locate products quicker [7].
The full-turnover storage allocation policy is a form of dedicated storage in which products are allocated to storage locations based on turnover. Products with a high turnover are located close to the shipping area, while products with a low turnover are placed furthest from the shipping area [8]. Product turnover rates fluctuate, thus requiring frequent stock relocation [5].
The dedicated and closest-open storage policies are the extremes on the storage policy spectrum [5]. The performance of these two policies has been compared in many studies. The results find that the closest-open storage policy is the best suited for high space-utilisation warehouses, whereas the dedicated storage policy is best suited for low space-utilisation warehouses [9].
The class-based storage policy is a combination of the dedicated and closest-open policies. It is commonly implemented in practice because it combines the advantages of both policies [5]. The class-based storage policy divides products into classes based on predetermined criteria. Specific classes are then allocated to dedicated areas of the warehouse. Within these areas, the products are placed randomly, following the logic of the closest-open policy. The class-based storage policy is easy to implement, simple to manage, and flexible in responding to demand changes, and it decreases order-picking times [5]. The best performing class criteria are the ABC classification, family grouping, and actual sales combinations criteria
3.3 ABC class-based storage policy
A common and effective class criterion is the ABC classification [10]. This variation of the class-based storage policy splits products into three classes, A, B, and C. Products are sorted within these classes according to some specific factor (commonly a product characteristic that influences its optimal storage location). Such factors include the unit demand for the product, annual sales, product size, or product weight [11].
The ABC classification technique sorts the products into classes proportionally according to the specified factor - for example, the A-class contains 80 per cent of the products, the B-class contains 15 per cent, and the C-class the final five per cent. Products in the A-class are allocated to the preferred storage locations, the B-class products to the next best locations, and the C-class products to the remaining locations. Further adaptations to the ABC classification are presented in the literature, such as adding additional letter classes (D-class, E-class, etc.) [2].
3.4 ABC class-based storage policy with family grouping
The family grouping class criterion stores similar products together. Products are grouped according to their characteristics or product departments. This grouping assists the pickers when locating and collecting products in the order-picking process.
Unfortunately, products can belong to multiple families, creating confusion when grouping products. In addition, products in the same 'family' are often those of competitors, and are substituted for one another and thus are not commonly purchased together [12].
3.5 ABC class-based storage policy with actual sales combinations
The actual sales combinations class criterion is a variation of family grouping, in which combinations of products that are commonly sold together are grouped into families. This class criterion assigns products together, based on their product affinity - that is, a measure of the likelihood that a customer will buy a product, given that they have purchased a different product [13]. Products that are commonly purchased together are stored in proximity. The actual sales combinations class-based policy decreases order-picking travel time [10]; however, it is difficult to implement in practice [13].
3.6 Number of classes
The efficiency and performance of a warehouse is influenced by the warehouse layout [5]. The location of the input and output (receiving and shipping) terminals of the warehouse affects the optimal storage locations of products [8].
Yu, De Koster and Guo [8] researched the advantages of expanding the number of classes in a class-based storage policy. They discovered that, in practice, "a trade-off exists between the number of classes and the order picking time" [8]. The relationship between the number of classes and the order-picking time creates a dish-shaped function, shown in Figure 1, where n* represents the optimal number of classes. Two significant conclusions are deduced from the function in Figure 1.
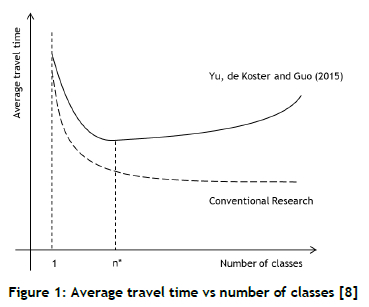
First, an optimal number of classes (n*) exists. According to [8], this number is generally less than six. Second, the gradient of the function around n* is flat. meaning that any small variation in the number of classes around this point (n*) will not have a noticeable effect on the order-picking times. The recommended number of classes is between three and eight.
3.7 Layout of classes
Once products have been sorted into classes, the question arises as to how classes should be allocated to areas within the warehouse [14]. Five class layouts are found in the literature: L-shaped, diagonal, within-aisle, across-aisle, and perimeter. The layouts are illustrated in Figure 2.

An L-shaped layout is best suited to warehouses where packing and picking activities occur separately. However, if packing and picking activities occur simultaneously, then "the within-aisle layout generates the best performance, irrespective of the number of product classes" [5]. Packing and picking activities occur simultaneously at FarmCorp SA; thus a within-aisle layout would be the best to use.
3.8 The effect of optimal product location
Optimal storage assignment:
1. Decreases aisle congestion and warehouse over-capacity;
2. Decreases order-picking time;
3. Decreases order fulfilment lead time;
4. Increases the number of daily orders fulfilled; and
5. Improves overall warehouse performance [15].
The optimal allocation of products to storage locations improves warehouse operations and increases warehouse throughput [16]. Thus this project aimed to increase the throughput and overall efficiency of FarmCorp SA's Centurion warehouse by developing a dynamic class-based storage assignment algorithm.
4 MODEL DEVELOPMENT
Three models are developed, based on the variations of the class-based storage policy presented in the literature. The three models are then input into a packing algorithm that assigns products to available bins within the warehouse. The three models are then evaluated against each other and compared with the current policy.
4.1 Warehouse layout
The warehouse contains over 25 600 storage bins, which are stored on shelves. There are five bin sizes: pigeonhole, small, medium, half bin, and normal-sized. The shelf arrangement naturally divides the warehouse into distinct sections, referred to as zones. The warehouse layout is shown in Figure 3. Zone 4 is on a mezzanine level above Zone 3. Zone 6 is a bulk storage area along the outside wall, adjacent to Zone 2. Zone 6 is therefore referred to as external storage. Zone 1 is equipped to store flammable products, and Zones 3, 4, 5, and 7 are equipped to store high-value stock.
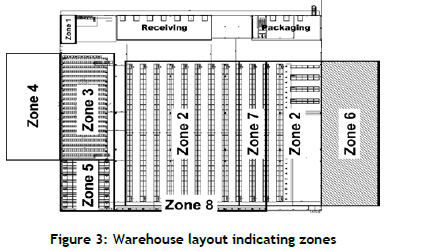
The shelves in each zone vary in height, depending on the number of levels. The shelf levels are labelled alphabetically, with level A being closest to the ground. Levels A and B are referred to as low-level shelves; and from Level C upwards, the levels are referred to as high-level shelves. Products stored on high-level shelves require a forklift for them to be picked.
4.2 Alternative models
Data on the products to be stored in the warehouse and data on the previous year's order picking transactions and sales orders are used to develop the three alternative models. The models rank the products according to how frequently they are picked. The highest ranked product is packed in the optimally placed bin.
The first alternative model is based on the ABC class-based storage policy. The selected ABC analysis criterion is the frequency with which a product is picked. This criterion was selected because the aim of the project was to minimise the time taken by the order-picking process. The frequency of picks was calculated as the number of hits a product received in a year. The term 'hits' refers to the number of times a picker picked a certain type of product. The products with an accumulated hits (a percentage) value of between 0 per cent and 80 per cent are assigned to the A-class, products with an accumulated hits (%) value of between 80 per cent and 95 per cent are assigned to the B-class, and products with an accumulated hits (%) value of between 95 per cent and 100 per cent are assigned to the C-class. The products that do not appear in the picking dataset have no forecasted demand (hits). These products are assigned to the X-class, and are considered obsolete. The A-class products are assigned to bins first, followed by the B-class products and then the C-class products.
The second alternative model allocates products to classes based on their product department and ABC class. This model places products from the same department close to each other, with the most frequently sold products from each department being placed on the lower shelves. This is done by calculating the total number of hits per department. The departments are then sorted in descending order of total hits. An ABC analysis is performed per category, similar to the first model. Products are then binned, beginning with the A-class items of the department with the greatest total hits, and ending with the X-class items from the department with the fewest total hits.
The third alternative model combines the ABC class-based storage policy with product affinity - that is, a measure of how often products are picked together. This alternative places commonly sold products together in pairs, with the most frequently picked pairs being placed closest to the shipping area. The product affinity is determined using market basket analysis - a time-consuming and complex task to do manually. It requires the formation of an n x n matrix, where n is the number of products sold in the previous year. The FarmCorp SA picking dataset contains over 14 000 products. The resulting matrix would be very large, making the calculation impossible to do manually. Thus PivotPoint, an add-on extension to Microsoft Excel, is used to perform the analysis. This software calculates the number of transactions in which products are sold together in pairs, using the 2019 and 2020 sales datasets. The product pairs are then ranked in descending order of combined hits. Products that show no affinity are then added to the ranking in descending order of individual hits.
4.3 IM classes
Once the products have been ranked in order of packing preference, the bins are ranked by location. The class-based storage policy is a combination of dedicated and random storage, by which product classes are allocated to specific areas in the warehouse and then randomly assigned to bins within that area. To aid in the allocation of product classes to these areas, the warehouse is divided into IM classes. An IM class has two parameters: the zone and the general shelf location. For example, Z2*GL indicates that the product is to be stored in Zone 2 in the general low section (shelf levels A or B). The desirability of a bin's location depends on two factors: its proximity to the floor, and its proximity to the shipping area. The IM classes are therefore ranked according to their location in relation to the shipping area.
4.4 Assumptions
Certain assumptions are made about the inputs of the allocation models and algorithm. These assumptions include the quantity of stock stored in low-level bins and the stock packing quantity.
'The quantity of stock stored in low-level bins' refers to the number of low-level bins used per product. If only one bin's worth of demand for a product were stored in low-level bins and the remaining demand were stored in the higher levels, a greater number of different products could be stored in low-level bins. However, this would result in more product replenishment. The alternative would be to store more than one bin's worth of demand for a product in low-level bins. This would result in less frequent product replenishment, but fewer different products would be stored in low-level bins. Thus there would be a tradeoff between the number of products stored in low-level bins and the frequency of product replenishment. The developed models and the algorithm will assume that only one bin's worth of demand per product is stored in the low-level bins. The aim of the algorithm is to increase the order-picking throughput by minimising the number of picks from high-level shelves. If this were to be accomplished, fewer forklifts would be required in the order-picking process, and that additional forklifts could be assigned to the replenishment process. Thus the trade-off would be justified.
The stock packing quantity is the quantity of each product that must be stored in the warehouse. Several options are available to determine this value. The current stock level or the forecasted demand quantity are two possibilities. In addition, the maximum, minimum, or average value of the current stock level and forecasted demand quantity could be used. The product master dataset does not contain both a current stock level and the forecasted demand for all the products. Thus it is assumed that the stock-packing quantity is equal to the maximum value between the forecasted demand and the current stock level for each product.
4.5 Packing algorithm
The purpose of the algorithm is to assign products to bins according to the class-based storage policy. Each alternative model is input into the algorithm. For each alternative model, the algorithm begins by assigning each product class to various IM classes, according to the IM class rankings. The algorithm then allocates products to bins within the assigned IM classes. The algorithm is developed using R software.
The algorithm receives data on the bins, ranked according to IM class, and data on the products to be stored, divided into product classes and ranked according to the selected storage model. The algorithm begins by packing the flammable products in Zone 1 (the flammable products have a limited number of storage locations). These products are sorted by descending order of product hits. The quantity of each flammable product to be stored in the Zone 1 bins is calculated by dividing the volume of a Zone 1 bin by the volume of the product. One bin's worth of each product is packed into low-level bins. This is done to ensure that all of the flammable product types are easily accessible.
The input assumptions specify that one bin's worth of stock per product may be stored in a low-level bin. Thus the algorithm populates all the bins in the low levels of the IM classes first. The number of bins available per IM class is calculated, and a product ID is assigned to each available bin. This process starts by assigning the highest-ranking product to the highest-ranking bin, and iterating until all the bins in the IM class have been assigned products.
Most products require more than one bin to store their required stock level. Since only one bin's worth of stock is being stored in low-level bins, the remaining quantity of each product must be stored in high-level bins. To ease the replenishment process, the excess quantity to be stored on high shelves is assigned a new IM class in the general high area of the same zone. The remaining products are then allocated in order of rank to the IM classes (which are also ranked).
The packing algorithm outputs a list of the bins assigned to each product as well as the products that are not packed.
5 MODEL COMPARISON
The three models were compared using data simulation in Excel. The results of the comparison were used to determine which model should be selected as the suggested solution. The data simulation involves calculations on the output data generated by the packing algorithm. This analysis uses data on the order picking process, obtained from the picking dataset. Each product type that is picked constitutes one pick transaction; and so an order might require multiple pick transactions. For each transaction, the date, the product ID, the quantity picked, the responsible picker, and the bin ID are recorded in the picking dataset. To perform the data simulation, the picking dataset was adapted to include the bin IDs for the products that were picked according to each of the alternative models. This adaptation reflects the bin from which each product would be picked if the alternative model were implemented. The results of the simulation are shown in Table 1. The alternative models will only be considered for the final solution if they fulfil all four of the technical criteria. Model 3 does not assign all the non-obsolete products to a bin. Thus, model 3 does not satisfy all the technical criteria and cannot be selected as the final solution. Models 1 and 2 satisfy all four of the technical criteria, and so can be considered for the final solution. Model 1 decreases warehouse capacity by 18 per cent more than model 2. In addition, model 1 results in 4 825 more available bins than model 2, and allows for seven more daily transactions on average. Therefore, model 1 performs the best, and so will be used to develop the final solution.
From the results in Table 1 it is deduced that the ABC class-based storage policy performs the best and should be chosen as the algorithm input.
6 MODEL VALIDATION
The selected model was validated to determine whether the ABC class-based storage assignment policy reduces order-picking time. Two simulation models were built: the first model illustrates the current storage allocation policy, and the second illustrates the policy developed in the suggested solution. Both models simulate the previous year's picking transactions to replicate the real-life warehouse operations. A simulation model tests the solution without the need to implement it physically. The simulation models were built using FlexSim software.
The pick transactions of ten days were simulated: the three busiest days (the days with the most picks), four average days, and the three slowest days (days with the fewest picks). The pick transactions for these ten days were extracted from the original and adapted picking datasets and input into the simulation. The simulation collected statistics on the order picking times, including the waiting times for a picker or forklift and the picker and forklift utilisations. These statistics were used to compare the presented solution with the current policy to validate the solution.
Table 2 and Table 3 show the output statistics from the simulation model of the current storage policy and the suggested storage policy respectively.
Table 4 analyses the differences between the results of the two simulation models. This table demonstrates that the implementation of the suggested storage policy would shorten the daily order-picking time by 3 hours and 20 minutes on average. In addition, an average of 32.4 seconds would be saved on each pick transaction. These time reductions would allow more orders to be picked per day, improving the efficiency of the order-picking process.
The suggested storage policy stores more frequently picked products on the low-level shelves. This results in fewer products requiring forklifts for them to be picked. This is evident in the decreased waiting time for forklifts between the current storage policy and the suggested storage policy. The suggested policy reduces the forklift waiting time by 3 minutes and 17 seconds per product on average.
7 CONCLUSION
7.1 Managerial implications
The implementation of the suggested storage assignment policy would require the entire warehouse to be repacked. The Centurion warehouse operates from Monday to Friday; Saturdays are used for replenishment and maintenance. Thus it is recommended that the warehouse be repacked in sections on Saturdays to avoid any major downtime for repacking. The replenishment and packing processes each have four dedicated employees responsible for these tasks. The pickers could be given overtime to work on Saturday to help with reshuffling the warehouse, which should occur in phases in order of the ranked IM classes, beginning with 'Z2*GL'. Once this has been done, the order picking times could be measured to validate that the reshuffle yields the predicted improvements in practice. In addition, the warehouse managers will need to implement strict control measures over the receiving and packing processes, to ensure that incoming stock is being placed in the correct updated storage locations and to prevent having to repack these products later. This entire process will require temporary onsite storage for displaced stock, which FarmCorp SA already has.
After the initial reshuffle, the dynamic algorithm will automatically update the products' storage locations according to any changes in product demand when bins become available. This means that an entire warehouse reshuffle will only be required initially. The demand for FarmCorp SA products is dynamic and follows seasonal demand, which affects the rate at which products are sold.
The biggest demand changes occur between summer and winter. Thus it is recommended that the algorithm be run at least every six months. However, the time period between uses could be changed at FarmCorp SA's discretion.
7.2 Recommendations
One limitation of the project was the lack of financial data. Future adaptations of this project could apply a two-part criteria ABC classification, based on the frequency of picks and the product profit margin.
The algorithm does solve the current storage assignment problem. However, to ensure that the solution is sustainable, the company should also investigate a cost monitoring or warehouse management system to improve the financial control of inventory. In addition, the warehouse's housekeeping practices must be improved, and not allow stock to be stored outside of designated zones. Implementing these changes, along with the improved storage system, would prevent the warehouse from reverting to its current practices. Furthermore, the company should consider discontinuing the least profitable or obsolete lines and extending its warehouse space.
7.3 Further applications and theoretical contributions
This case study was an application of inventory management theory. It addressed two theoretical concepts: how to determine the optimal storage location of products in a warehouse, and the effect of optimal storage location. It has proved that there is a correlation between the correct storage location of products and the efficiency of a warehouse's order-picking process. Therefore, in theory a company should increase its throughput and consequently its profitability by optimising its storage policy.
The algorithm has widespread application, and is not limited to distribution warehouses. The dynamic packing algorithm could be applied to both production and cross-dock warehouses. The algorithm logic could also be adapted for application in a grocery store, clothing store, library, parking garage, or any similar setting. Thus the algorithm could be used to improve efficiency in any storage related system.
In conclusion, the results of the data simulation and validation indicate that the dynamic storage allocation algorithm presented here reduces the number of picks from high-level shelves, groups similar products together, reduces warehouse overcapacity, eliminates obsolete stock, and reduces the order-picking activity time. The suggested storage policy allows for an increase in the daily orders being picked, and thereby improves the warehouse's throughput and operational efficiency, achieving the project's aim. The solution is therefore worth implementing to solve FarmCorp SA's storage location assignment problem.
REFERENCES
[1] Petersen, C. 1999. The impact of routing and storage policies on warehouse efficiency. International Journal of Operations & Production Management, 19(10), pp.1053-1064. [ Links ]
[2] Gagliardi, J., Renaud, J. and Ruiz, A. 2007. A simulation model to improve warehouse operations. In: Winter simulation conference. Quebec: Faculte des sciences de I'administration & CIRRELT Université Laval, pp.1-4. [ Links ]
[3] Ahmed, D. 2020. 5 basics warehouse activities you should focus to improve. [Online]. Available at: http://www.scmdojo.com/warehouse-activities/ [Accessed 29 May 2021]. [ Links ]
[4] Bevilacqua, M., Emanuele, F. and Antomarioni, S. 2019. Lean principles for organizing items in an automated storage and retrieval system: An association rule mining-based approach. Management and Production Engineering Review, 10(1), pp.29-36. [ Links ]
[5] Bahrami, B., Piri, H. and Aghezzaf, E.H. 2019. Class-based storage location assignment: An overview of the literature. In 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), Prague, Czech Republic, pp.390-397. [ Links ]
[6] Quintanilla, S., Pérez, Á., Ballestín, F. and Lino, P. 2015. Heuristic algorithms for a storage location assignment problem in a chaotic warehouse. Engineering Optimization, 47(10), pp.14051422. [ Links ]
[7] Le-Duc, T. and De Koster, R. 2005. Travel distance estimation and storage zone optimization in a 2-block class-based storage strategy warehouse. International Journal of Production Research, 43(17), pp.3561-3581. [ Links ]
[8] Yu, Y., De Koster, R. and Guo, X. 2015. Class-based storage with a finite number of items: Using more classes is not always better. Production and Operations Management, 24(8), pp.1235-1247. [ Links ]
[9] Gu, J., Goetschalckx, M. and McGinnis, L. 2010. Solving the forward-reserve allocation problem in warehouse order picking systems. Journal of the Operational Research Society, 61 (6), pp.1013-1021. [ Links ]
[10] Li, J., Moghaddam, M. and Nof, S. 2015. Dynamic storage assignment with product affinity and ABC classification - a case study. The International Journal of Advanced Manufacturing Technology, 84(9-12), pp.2179-2194. [ Links ]
[11] Lorenc, A. and Lerher, T., 2019. Effectiveness of product storage policy according to classification criteria and warehouse size. FME Transactions, 47(1), pp.142-150. [ Links ]
[12] Muller, M. 2019. Essentials of inventory management. New York: HarperCollins Leadership. [ Links ]
[13] Baer, D. and Chakraborty, G. 2013. Product affinity segmentation using the doughnut clustering approach. In Proceedings of the SAS Global Forum 2013 Conference, Cary, NC. [ Links ]
[14] Cardin, O., Castagna, P., Sari, Z. and Meghelli, N. 2012. Performance evaluation of in-deep class storage for flow-rack AS/RS. International Journal of Production Research, 50(23), pp.6775-6791. [ Links ]
[15] Da Silva, D., de Vasconcelos, N. and Cavalcante, C. 2015. Multicriteria decision model to support the assignment of storage location of products in a warehouse. Mathematical Problems in Engineering, 2015, pp.1-8. [ Links ]
Submitted by authors 21 Oct 2021
Accepted for publication 25 Apr 2022
Available online 29 Jul 2022
ORCID® identifiers
S.E. McInerney: 0000-0002-4238-0094
V.S.S. Yadavalli: 0000-0002-3035-8906
* Corresponding author: sarma.yadavalli@up.ac.za














