Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.33 n.2 Pretoria Jul. 2022
http://dx.doi.org/10.7166/33-2-2527
GENERAL ARTICLES
Inventory management concepts and implementations: a systematic review
J.B. MunyakaI, *; V.S.S. YadavalliII
ICEAT - Urban and Regional Planning Community, ENAC -School of Architecture, Civil and Environmental Engineering, Swiss Federal Institute of Technology Lausanne, Switzerland
IIDepartment of Industrial and Systems Engineering, University of Pretoria, South Africa
ABSTRACT
Inventory is a central management function. It is a cornerstone of supply chain management and logistics in the material management system. Depending on the organisational objectives, inventories in warehouses may be needed to fulfil customer or humanitarian demands. Controlling inventory is critical to operational success and organisational performance. This research reviews inventory management concepts and implementations in the face of increasingly demanding human need. Demand is a critical variable in the inventory control system, and its characteristics affect inventory treatment. Important demand characteristics include its level of certainty, which could be deterministic (i.e., known with certainty) or stochastic/Bayesian (i.e., known but uncertain), and its structural dependency (i.e., independent or dependent). This review considers the deterministic independent and dependent natures of demand and their respective impact on inventory management in operations.
OPSOMMING
Voorraad is 'n sentrale bestuursfunksie. Dit is die hoeksteen van voorsieningskettingbestuur en -logistiek in materiaalbestuurstelsels. Afhangende van die doelwitte van die organisasie, mag voorraad in pakhuise nodig wees om aan klante of humanitére eise te voldoen. Die beheer van voorraad is van kritieke belang vir operasionele sukses en organisatoriese prestasie. Hierdie navorsing hersien voorraadbestuurskonsepte en die implementering daarvan te midde van toenemende veeleisende menslike nood. Aanvraag is 'n kritieke veranderlike in die voorraadbeheerstelsel en die kenmerke daarvan beinvloed voorraadbehandeling. Belangrike aanvraag kenmerke sluit in die vlak van sekerheid, wat deterministies (d.w.s. met sekerheid bekend) of stochasties/Bayesian (d.w.s. bekend, maar onseker) kan wees, en die strukturele afhanklikheid daarvan (d.w.s. onafhanklik of afhanklik). Hierdie oorsig oorweeg die deterministiese onafhanklike en afhanklike aard van aanvraag en hul impak op voorraadbestuur in bedrywighede.
1 INTRODUCTION
Inventory (stock) management is a critical operation in manufacturing and supply chain processes. The manufacturing process uses raw materials and work-in-process goods to create finished products that are stored as inventory or sold, some of which may also be used in follow-up operations. Inventory is the most important asset held by many organisations, representing as much as half of the company's expenses, or even half of the total capital investment. In addition, according to the Science Direct publication website (accessed in 2020) [48], the past two decades have seen an increase in inventory management research interest. As shown in Figure 1, the publication of articles on inventory management has seen an increase of over 525 per cent, with the number of published articles increasing from 2 544 in 1998 to 13 381 in 2020.

Inventory management models are applied in nearly all operations. The scope in the literature spans fields such as manufacturing, medicine, humanitarian aid, environmental science, engineering, agriculture, and even energy. By filtering Science Direct's search for publications on inventory management, and taking into account both open access journals and journals to which only subscribers have access, it was found that the most frequently discussed topic in inventory management is environmental science, followed by engineering, energy, and others (Figure 2). Given the increasing impact of climate change, environmental science has created the need for re-engineering, thus increasing the demand for stock management.
Figure 2 shows the range of areas affected by stock management. The crucial challenge for an organisation is often to have a balanced demand supply that minimises inventory costs and increases the satisfaction of the target beneficiaries. As stated by Nemtajela and Mbohwa [85], proper inventory management ensures a good balance between minimising the total cost of inventory and maintaining the desired customer satisfaction level.
The rise of online retailers such as Amazon or Alibaba over the past three decades has shown the growing importance of proper inventory management. In addition, there were situations in the past when poorly managed stocks caused companies such as Solectron to lose billions of dollars. This paper undertakes a systematic review of a number of stock management concepts and their contribution to the topics outlined in Figure 2 and to future research.
2 LITERATURE REVIEW
The concepts of inventory management date back to the early days of humanity. The practice of inventory has modernised and evolved over the last 100 years, with new tools and technologies being used to support the process. For instance, in ancient times, traders counted and tallied items that were sold each day - until the Egyptians and the Greeks developed more accurate inventory record management and accounting systems, in contrast to the inaccurate and inefficient practice of hand-written notes and hunches. Over the years, progress has been made in inventory management practices. These advances have led to further cost reduction and improved customer satisfaction.
What is inventory? According to Render et al. [96], inventory is a stored resource used to satisfy a demand, current and future. Similarly, Vrat [123] defines inventory as component parts, raw materials, WIP (work-in-process), or finished products held at a specific location (a warehouse) in the supply chain. Both authors, as well as Plinere and Borisov [92], listed inventory types that included the following: 1) raw materials, work-in-process, transit, finished goods, buffer (safety stocks), decoupling (contingencies stock), anticipation (speculation inventory), and cycle (business's standing inventory), etc. These inventories differ from one organisational sector to another. For example, in humanitarian relief supply chains, the difference between life and death depends, among many other things, on decoupling stocks, whereas, in the wholesale trade, buffer stocks or even transit stocks can prevent the organisation from losing its valuable reputation. Figure 3 shows the three types of inventories commonly used in manufacturing:
Inventory management is viewed as a central function in the inventory management system [79], [94], [3]. For Khobragade et al. [61], inventory management, also known as materials management, is identified as the organisation, securing, storage, and distribution of the right materials, of the right quality, in the right quantity, in the right place and at the right time, in order to coordinate and organise the creative movement in an integrated way within a mechanical project. Inventory management involves maintaining some stock levels at a minimised cost while improving the value-adding measures of customer satisfaction, which are useful measures of organisational performance [85], [43], [41], [105]. According to Christopher [27], an organisation with a good inventory management system is able to establish good policies and controls that monitor the level of inventory and determine what levels to maintain, when the inventory should be replenished, and the size of the order. Inventory levels for finished goods are viewed as a direct function of demand [96]. In the event of a higher demand in the supply chain, the inventory level decreases proportionally.
There are factors that influence inventory management practices. Prominent among these are organisational and human factors, financial constraints, and, more recently, the increasing rate of technology adoption [3]. Financially, 'inventory' is considered the biggest and most important asset of an organisation, which - according to Render et al. [96] - constitutes up to about 50% of the total capital investment of the company's assets. In humanitarian operations, inventory not only represents a significant financial asset, but also has a direct impact on saving lives. In the industrial sector, firms with goods inventory management practices are able to increase their overall profit margins, and so increase their level of production capital, and overall customer satisfaction [33], [92]. The flowchart in Figure 4 details the basic stages in an inventory management system.

Ivanov et al. [54] consider the trade-off between service level and cost as one of the most important financial decisions in inventory management. Other important financial decisions include how much to order and how much physical inventory to hold in a warehouse in anticipation of a sudden increase in demand, to avoid delays in supply chains. It is also worth including the management of unused stock and the costs associated with holding physical stock in a warehouse as an important financial decision.
Another important factor influencing inventory management practices, apart from the financial, is technology. Although technology has largely influenced inventory management positively, Ahmad and Mohamed Zabri [2] believe that, since its introduction, technology has exposed the human impact on the day-to-day handling of inventory. In Table 1, Rushton et al. [98] compare different technological applications with different daily human processing of inventory activities. With a similar number of activities (3,000,000), Table 1 shows the error occurrence rate in processing activities using inventory management applications. The results show that the less daily human handling of stocks there is, the fewer the errors.
The study conducted by Ayad [7] examined the influence of human factors in inventory management practices by assessing different stores from the same company, each run by a store manager. The aim of the exercise was to identify human variables within the store manager's control. Findings from the study revealed that the diversity of store types and the variety of departmental operations resulted in different outcomes within the same organisation. Furthermore, analysis of Ayad's [7] findings showed that human factor variations were the result of their useful knowledge, leadership ability, or critical thinking. Another study was conducted by Strohhecker and Grobler [107] that focused on inventory managers' physiological traits; their findings identified the following four traits: personality, knowledge, intelligence, and interests. The authors also investigated the impacts of these traits on their performance, specifically during a dynamically complex inventory management task [107]. The findings showed the 'intelligence' trait to be the sturdiest predictor of inventory routine, while 'interest' in social matters led to worse inventory performance and higher costs. Using technology in inventory control is not a novelty; but a good number of organisations still avoid using technology for economic (financial) and expertise (human) reasons. Many inventory management technology applications offer efficiency - but they come at a cost.
Other factors influencing inventory management practices are related to forecasting decisions. Rajeev [94] discussed the 'rule of the thumb' decision, which resulted in less purchasing, use of a computer, variable lead-times, less attention to forecasting, training, and development, and random ordering of material [2]. Bala [9] showed that using sophisticated computerised systems for forecasting improves the profitability of an inventory management system.
3 ROLES, INVENTORY MODELS, AND THE DEMAND VARIABLE
3.1 Role of inventory
Since the primary role of inventory management is to maintain a desired stock level of defined products or items [119], the role of inventory in operations management cannot be overemphasised. History has shown that organisations that have neglected or failed to consider the importance of inventory management have lived to regret it. According to Tanthatemee and Phruksaphanrat [114], inventory management helps to improve customer service and to cope with demand uncertainty. Demand uncertainty is a potential challenge that results in high inventory levels and high carrying costs, which can lead to higher prices and low customer satisfaction, and thus a less profitable business.
3.2 Inventory models and the demand variable
The main decisions affecting demand in an inventory management problem are a) when to purchase (creation of a purchase order), and b) how much to purchase (lot size) [82]. Resolving both problems in a decision-making process requires the development of inventory models and techniques [96]. These two decision-making problems connect the inventory model's objective function with a number of decision variables (e.g., lot size and re-order point). It also links up with several inventory-related cost parameters and situational variables, such as a) the demand nature and level (including its level of certainty); b) the lead time (including its level of certainty); c) extant constraints (if any); d) quantity discounts or inflationary trends; and e) other relevant issues.
Demand is regarded as a critical variable in inventory management. Accurately forecasting the market or the level of demand helps to make the correct inventory decisions that optimise sales and profits. Based on the level of certainty of demand, two types of inventory model are usually developed: (1) deterministic demand models, and (2) stochastic (Bayesian) demand models.
3.2.1 Deterministic demand model (demand known with certainty)
In the deterministic model, inventory operations are determined on the basis of a known (certain) demand. A deterministic model produces the same output because of certainty about the factors, conditions and parameters involved, which are clearly stated at the start. Among the parameters is demand. According to Antic et al. [4], deterministic demand is represented as a sales forecast for each product per month. The deterministic demand model aims to minimise the overall costs related to production time, setup time, and overtime, and those associated with inventory, such as ordering costs, carrying costs, and stock-out costs (overstocks and shortages).
The deterministic demand model may have two types of demand: independent and dependent. It is crucial in an inventory control system to understand the difference between those two demand types as the starting point for an inventory policy. Independent demand is the demand for finished products such as cars or books, and may involve some level of uncertainty as well; while dependent demand focuses on component parts or sub-assemblies such as box console sub-assemblies for Toyota cars, and is usually considered certain once the end item on which it depends is known. Figure 5 illustrates the nature of both kinds of demand.

In an independent demand environment, the demand for an item does not depend on the demand of another item (see Figure 5). For example, finished goods items do not depend on other items because the focus is on item sale, order processing, or sales forecast. The independent demand for inventory is founded on confirmed forecasts, customer orders, estimation, and past history.
However, unlike independent demand, dependent demand for an item depends on the demand for another item. For instance, raw material and component stocks are dependent on the demand for finished goods. Raw materials and other manufacturing components, for instance, are converted to finished goods through systems such as material resources planning (MRP), distribution resources planning (DRP), or enterprise resource planning (ERP).
3.2.2 Stochastic (or Bayesian) model (demand known without certainty)
In a stochastic (probabilistic or Bayesian) model, inventory decisions are made in the light of uncertainty (demand and/or lead time). According to Antic et al. [4], stochastic demand is generated as a random variation of sales forecast within a range of about 20 per cent. For Nemtajela and Mbohwa [85], the uncertainty in demand is the result of factors such as changes in purchase orders and unpredictable events. Furthermore, Tanthatemee and Phruksaphanrat [114] believe that uncertain inventory demand is the result of changes to orders, the random capacity of suppliers, or unpredictable events. Sil [103] listed three types of stochastic model:
a) Single period: mainly concerns fashion products, perishable products, products with a short life cycle, or even seasonal products. The single period is a one-off decision (how much to order).
b) Multiple period: concerns goods whose demand is recurrent but varies from period to period; inventory systems with periodic revisions. The multi-period stochastic model is a periodic decision (what quantity to order in each period).
c) Continuous time: related to goods with recurring demand but with variable inter-arrival time between customer orders; inventory systems with continuous revisions. The continuous period stochastic model is a continuous decision (continuously deciding how much to order).
4 INDEPENDENT DEMAND INVENTORY MODELS
The main objective of an inventory management is to minimise operational costs. Minimising cost in independent demand inventory models consists of the following functions:
• optimisation of fast-moving stock to avoid stock-out (understocking)
• proper definition of safety stock (involving ordering point to prevent any risk of premature depletion of inventory)
• reduction in excessive inventory (overstocking)
Among the most significant inventory-related costs in a decision support system are: 1) ordering cost, 2) carrying or holding cost, 3) goods purchase cost, 4) stockouts and shortages cost, and 5) storing cost. According to Vrat [123], Inventory carrying (holding) costs, cost of shortage and stockout, and ordering costs are the three types of inventory-related cost that are primarily associated with inventory decision-making models. Independent demand inventory is composed of two main types of models: a) single-period (perishable) inventory models, and b) multi-period inventory models, as shown in Table 2.
4.1 Single-period (perishable) inventory model or the newsboy problem
A single-period inventory model is one that is applied by organisations that order perishable or one-time items. Such models require the order to be of the right quantity, fearing overstocks and waste as soon as the product has passed its perishable or expiry date. The same rule applies to seasonal items or any item that is no longer of value after the time it is required. A single-period inventory model does not include only perishable items, but also a wide variety of items such as style items, spare parts, or special season items. As items become obsolete at the end of the cycle, decision-makers face challenges such as managing the demand for single or multiple items. The key differences between a single-period (perishable) inventory model and a multi-period inventory model are listed in Table 2 below.
In addition to the above differences, a single-period inventory model requires that orders for items be placed before the start of the period, and replenishment cannot be done during the period. Furthermore, the stock remaining at the end of the period is considered obsolete and so is eliminated from the inventory; and its value is deducted from the profit of another order at the beginning of a new period. When the order is larger than the demand, the extra items ordered are counted as lost.
Research into the single-period inventory model is essential for businesses as well as for humanitarian aid organisations, as determining the exact number of perishable or seasonal items an organisation needs maximises the productivity expected from that particular organisation and reduces waste. In a humanitarian environment, little research has been conducted on disaster inventory systems that focus on perishable or seasonal items, particularly in the aftermath of a disaster. Among the few notable researchers are Yadavalli et al. [127]. Their analysis proposed a continuous review disaster inventory model with a doubly substitutable perishable item. Using an emergency situation, they proposed to replace an out-of-stock item with a similar item available in the inventory, thus avoiding a long waiting time and favouring instant replenishment. For example, a particular blood type that is not available in the blood bank at the time of application or that is past its expiry date may be replaced by an acceptable and available universal type.
Researchers on the newsboy (Single-period [perishable]) inventory model also called the Christmas tree problem, particularly deal with (1) single perishable items (see, for example, [56], [88], [57], [10], [40]) and (2) multi perishable items (see, for example, [90], [126], [34], [12]). According to Satyendra et al. [99], a newsboy must achieve a stock decision quantity that maximises the expected profit while minimising the expected loss under stochastic demand conditions (see the first statement in Table 2).
4.1.1 Single perishable item problem
According to Joy and Jose [55], a perishable product is one whose value decreases over a given period. Perishable items make inventory management more challenging, as they affect the inventory, service, and re-order levels. Some examples of perishable item are vegetables, fruit, baked products, and fashion items. The deterioration or loss of value of perishable products can be explained by their short life (fruit and vegetables), changes in trends (fashion items), etc. The application of the perishable inventory model is broad, and needs to be assessed on a case-by-case basis. Since the first study on perishables by Whitin [124], models have been developed that take into account perishable aspects such as items on display, the freshness of items, and price dependency [39]. Avinadav et al. [5] developed a single perishable item model that optimises the price, order quantity, and replenishment periods of a perishable item with price- and time-dependent demand. Taleizadeh et al. [112] studied discounted inventory models, focusing on the customer decision as a key factor, while Liu [73] studied a perishable inventory model with product lifetime incorporated into it. Under specific assumptions, single perishable item models are developed.
4.1.2 Multi perishable Items problem
A multi perishable items problem was initially solved by Hodges and Moore [47] using stochastic demand competing for a number of limited resources. Authors who have been solving problems related to multi-constraint or multi-item single period inventory intend to maximise the probability of targeted profits [103], [68]. In addition, an approach to solving the multi perishable items inventory model with constraints was developed by Ben-Daya and Raouf [12], considering both financial and space constraints, with items demand following a uniform probability distribution function. Further studies were conducted by Layek et al. [69] that targeted the investigation of a two-fold solution space with constraints for a multi perishable item problem. Rahimi et al. [93] introduced a two-stage stochastic mixed integer non-linear programming (MINLP) model that assists companies that are considering discount policies. With regard to the multi-product single-period inventory problem, Bhattacharya [14] and Kar et al. [59] developed a multi-item inventory model for items that are deteriorating. With Kar et al. [59], the main focus was on multi perishable items with constraints in the storage space available and the level of investment. A multi-item inventory model for items that are deteriorating was further studied by Tayal et al. [115], targeting an acceptable shortage level and the product expiration date.
Kumar et al. [65] presented a multi-item, multi-constraint problem with stochastic demands for different types of item. The model also considered the replenishment time, constraints in storage space, and the level of stock-out associated with the cost of understocking and overstocking per unit shortage, and surplus inventory. The notation used in the Kumar et al. [65] model is as follows:
r Set of retailers (1 to R).
p Set of products (1 to P).
x A random variable representing the demand.
frp(x) Probability density-function of demand of product 'p' at retail outlet 'r'.
USp Understocking cost of product 'p' (Rs. per unit).
0SP Overstocking cost of product 'p' (Rs. per unit).
Capr Storage capacity at retail outlet V (units).
Supp Available supply of product 'p' (units).
Erp Expected cost of product 'p' at retail outlet 'r' when supply quantity is Qrp.
µrp Mean demand for product 'p' at retailer 'r'.
σrp Standard deviation of product 'p' at retailer 'r'.
zrp() Standard normal deviation of product 'p' at retailer 'r'.
ΦrpQ Cumulative density function of product 'p' at retailer 'r'.
ΦrpQ Probability density function of product 'p' at retailer 'r'.
The model's objective was to minimise (Z{) the total expected cost of all products associated with understocking and overstocking in all the retail outlets. The model is presented next. Minimise (Qrp)
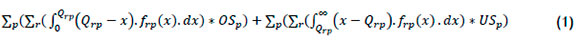
Subject to
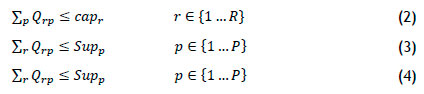
Equation (2) deals with retail outlets' storage capacity constraint, while Equation (3) makes sure that the product supply is not exceeded by delivery. Finally, Equation (4) is the non-negativity constraint. Kumar et al. 's [64] model is most applicable in the distribution of high-quality perishable foods chain.
4.2 Multi-period deterministic inventory models
A multi-period inventory model is a lot-sizing model that optimises the procurement of both single and multiple products, with cases of both a particular supplier and multiple suppliers, and from one period to another. A multi-period inventory model further involves the option of focusing on the economies of scale in the procurement process instead of accruing inventory costs from one period to the next [97]. Lot sizing, both static and dynamic, involves determining the number of items required during a manufacturing process. A multi-period inventory model has two variations:
• Fixed order quantity systems (Q model): a fixed order is placed each time the minimum stock level (re-ordering point) is reached.
• Fixed time period models (P model): orders are placed at allocated times, with the amount of inventory being determined in the aftermath of a review of the stock levels.
Figure 6 below compares both types of multi-period inventory model for further understanding:
4.2.1 Fixed-order quantity models (Q model)
A fixed-size ordering system is a pre-defined standard inventory system of a quantity of items that gradually decreases from the maximum level (Q) to the minimum level (Zero), until it reaches the ROP (re-order point), and then a new order of size EOQ (economic order quantity) is placed.
Fixed-order quantity models generally deal with certain demands; therefore, a new order of a fixed size is lodged as soon as the stock reaches the ROP (Figure 6). However, schedule orders can be scheduled to arrive at an increased lead time (L), introducing uncertainty to the demand and the system. In such cases, the precise demand throughout the lead time (ROP in the EOQ) becomes unknown. Barros et al. [11] listed a variety of uncertainty and risk factors associated with the procurement process (Table 3):
To avoid stockouts, extra stock, called safety stock, is kept on hand (Figure 7). Safety stock prevents stockouts in case the demand is higher than expected.

Figure 8 focuses on a stock level that will trigger re-ordering, while in Figure 7, although there is a re-order point, a safety stock (minimum stock) is applied. Table 4 below lists relevant publications discussing the application of the fixed-order quantity model.

4.2.2 Fixed-time period model (P model)
Maintaining an optimal stock is a challenge faced by all organisations. Unlike in the fixed-order quantity system (Q model) in which orders are only placed after the item has reached the determined re-order point (ROP), in a fixed-time period model (P model), each item's stock position is reviewed periodically, as shown in Figure 9 below. When a stock level of a given item is determined, the decision to place an order is made, taking into account the following elements: 1) the customer's request for the item in question, and 2) the adequacy of the current stock level of the item in the supporting chain or production operation until the next revision.

Using diverse service levels, Mahfuz et al. [76] applied the fixed-time period model while conducting a study in a services environment from 2004 to 2006. The study found that applying the P model saved an average cost for the services that ranged between 65 and 80 per cent of inventory investment, with a 98 to 100 per cent service level being provided. The capital raised through savings gives organisations a competitive advantage, as it can be used to purchase new technologies such as those for stock counting and stock location within the system.
According to Huang et al. [50], the fixed-time period ordering is conducted at a fixed and predetermined interval with some assumption such as 1) a variable demand, 2) a regular Lead time, 3) an ordering to restock the system to its full capacity, 4) non fixed ordered quantity, while the order timing is fixed, 5) the ordered quantity is much lower than the safety levels.
Following the above assumptions of Huang et al. [50], Equation (Eq 5, 6, 7 and 8) was generated below:

where
d is the average demand,
t is the fixed interval for re-order,
L is the lead time,
σd is the standard deviation of demand and
Za Is the standard normal Table

5 DEPENDENT DEMAND INVENTORY MODELS
Unlike independent demand inventory models, in which the demand for one item is independent of the demand for other items, in dependent demand inventory models, items are interconnected. Therefore, the demand for one item is directly dependent on the demand for another item. In an engine assembly plant, for example, the demand for the console, tyres, engine, etc. depends on the demand for a car. To manage the manufacturing process of finished products in the case of dependent demand for raw materials and other components, material resource planning (MRP) is mainly used. This management tool is applied with the help of models or applications such as just-in-time (JIT) and Kanban. In addition to MRP, enterprise resource planning (ERP) software is used to integrate all the departmental functions of organisations into one system. Software such as Oracle, SAP, and Microsoft Dynamics are also used in distribution resource planning (DRP) situations.
The association between independent demand and dependent demand is shown in a bill of material. The dependent demand is derived from the independent demand, and helps to find the quantities ordered for the dependent demand. For example, determining the quantity of finished products, such as automobiles, that are expected to be sold (independent demand) can help to determine the dependent quantities of components, such as wheels, tyres, and braking systems, that are needed to complete the production of the automobiles. For one car produced, for example, four wheels, two windscreen wipers, and two headlights are needed, among other components.
5.1 Material resources (requirements) planning (MRP)
The order quantities for dependent demand are found through the material requirements planning (MRP) system. MRP takes into account of the quantities of the required components, as well as the time needed to produce and receive them. Moustakis [80] defines MRP as a time-phased priority planning technique for computing the material requirement and scheduling supply to meet the allocated item demand [52]. This planning technique is a computer-based production as well as inventory control system that ensures a better customer order response. According to Heizer and Render [46], some areas where MRP implementation are useful include the following: (1) production scheduling, (2) quicker response to market variations, (3) improved adherence, (4) enhanced labour and facilities utilisation, and (5) control of inventory levels. Furthermore, as a starting point for further actions, MRP is dependent on the sales forecast for finished goods. Handling raw materials is far more challenging than handling finished goods, as it involves the analysis and coordination of delivery capacity, logistical processes, lead time, transportation, warehousing, and scheduling, before their final supply to the production shop floor. Raw materials administration also involves the periodic review of inventory holding and inventory tally and audit, followed by a comprehensive analysis report, leading to good financial management decisions.
A successfully implemented MRP system is able, simultaneously: (1) to ensure that the required materials (including components and other items needed for production) are available and meet customer delivery targets; (2) to ensure that inventory levels are kept as low as possible, and (3) to plan manufacturing and purchasing activities and delivery schedules.
The MRP system has three main inputs that help the system to function: (1) the master production schedule (MPS); (2) the bill of material (BOM), also known as product structure records; and (3) inventory status records. The MPS indicates the quantity of finished goods desired and the expected time of receipt of the delivery, including the necessary safety stock. The BOM consists of data on each material or process required to produce that material. The information included in the BOM includes the type of raw materials (parts and components), the item number, and the description and quantity per assembly and sub-assemblies needed to manufacture an item. Finally, the stock status file also has the role of maintaining the integrity of the record by recording and maintaining information about all of the items in stock, including stock on hand and scheduled receipts.
5.1.1 MRP applications in a material structure tree
MRP is used for both single and multiple items. Its application to a single material is illustrated in the following example. '10 units of A' means that 10 units of material A are needed, while '20 units of B' means that 20 units of material B are needed. This illustration shows that one unit represents one material for A and B respectively. But MRP is also successfully applied to multiple materials with two or more complex BOMs. For example, when 10 units of material A are to be produced within seven weeks, material A requires seven units of material B and five units of product C, while material C requires 10 units of material D and eight units of material E. In addition, item B requires three units of item D and eight units of item C; and item B requires three units of item E. From the BOM, the material structure tree is developed (as in Figure 10 below), and the stock items to be produced at each level have been calculated, the demand for B, C, D, and E being dependent on the demand for A (10 units). The demands for items B, C, D, and E were calculated as follows: Req(B)=10 x 7 = 70 units; Req(C)=10 x 5 = 50 units; Req(D) = 50 x 10 = 500 units; Req(E)= (8 x 50) + (3 x 70) = 610 units.

The material structure tree in Figure 10 has three levels, defined as follows: Level 0, Level 1, Level 2; the 'parent' elements being A, B and C, while the 'component' elements are B, C, D, E. It can be seen that elements B and C are both components and parents.
5.1.2 An outline of the MRP process
After constructing the material structure tree as in Figure 10, a schedule needs to be constructed that reveals: 1) the schedule of items ordered from suppliers in case there is no stock available, and 2) the schedule of production of the final items in order to satisfy the customer's demand for the finished products in time.
Five scheduling steps are used to determine the schedule in an MRP process. The schedules used for the production of the required material A in seven weeks, as shown in Table 5, are as given below:
(1) Gross material requirements plan
The raw material requirements plan is the step in the schedule that determines when a material is needed and when its production is required to meet the customer's demand for finished goods. A key aspect of establishing or constructing gross material requirements is determining the lead times. Using the above example of producing 10 items of A, assume that the lead time for item A is one week, for item B two weeks, for item C two weeks, and for items D and E one week each, while for parent item B it is two weeks. Since the lead time of parent item A is one week (level 0), items B and C must be available at the end of the sixth week. Since the lead time of item B is two weeks, it must be released for production at the end of the third week. Similarly, item C and its units must be released for production at the end of the third week. Finally, items D and E and their units from parent item C are to be released to production at the end of the second week, while item E from parent item B is released to production at the end of the first week.
(2) Net material requirements plan.
The net material requirements plan is constructed in a similar way to the gross requirements plan. As with the gross requirements plan, the scheduling work starts with parent A and is scheduled backwards (from week 7) to the last components, as shown in the material structure tree in Figure 9. Determining the lead times for each item is another critical aspect in the calculation of the net material requirements plan. Using the same data for A, B, C, D, and E as shown in the material structure tree, the net material requirement plans are also calculated using the available inventory. As shown in Table 5, the net requirements balance the quantity needed to meet the demand (the gross requirement).
The on-hand inventory is the number of inventory items available to a store, ready for production and shipment. In an MRP process, the on-hand inventory is the parent materials and components available before the next batch of materials is received. Looking at the material structure tree and its number of materials in Figure 9, it is assumed that material A has two units of stock, materials B and C have 10 units of stock, material D has 20 units of stock, material E has 15 units of components for material C and 20 units of components for material B. The stock on hand has a direct impact on the net material requirement and the receipt of the planned order, as it is the value subtracted from the gross material requirement plan.
For item A, with a gross requirement of 10 units and an assumed available stock of two units, the net requirement and planned order receipt are both eight units, as shown in Table 5. Table 5 also shows that the net requirements and the planned incoming order are planned for week 7.
(3) Planned-order receipt.
The planned receipt of order, also known as the planned receipt, is the projected quantity of planned material receipt based on the net material requirement. For example, item A in Table 5 has a net material requirement of 40 units, so the planned receipt is estimated to be the same quantity - 40 units.
(4) Planned-order release.
In contrast to the previous stages of the schedule, planning delivery schedules, as shown in Table 5, take into account the lead times of each material, starting with zero level materials (A) up to level 2 materials (D, E). With 40 units of item A cleared and staggered in time in the seventh week of production, and considering that item A has a lead time of one week, the planned order release for item A is therefore 40 units that are scheduled in the sixth week of production. The process continues until all materials are broken down
5.1.3 Just-in-time (JIT)
Just-in-time (JIT) is a famous Japanese concept of material planning, initially used by Japanese manufacturing companies before spreading worldwide. According to Vrat [123], JIT (or the zero-inventory system) is an idealised concept of inventory management in which a supply is delivered just-in-time, whatever material is required, wherever it is required, whenever a maximum supply is needed, and without keeping any stock on hand. In terms of material resource planning, the just-in-time concept allows companies to manage their warehouses with greater efficiency, avoiding inventories, shortages, or replenishment orders.
5.2 Enterprise resources planning (ERP)
An ERP is an integrated software that includes a set of functional modules (production, human resources, sales, finance, etc.) and incorporates all the departmental functions of organisations into one system, meeting the needs of all of the departments [15].
An ERP system, when implemented, can improve departmental performance and increase productivity. According to Bhamangol et al. [13], ERP improves access to and the accuracy and timeliness of information. It improves workflow, reduces dependence on paper trails, improves knowledge sharing, enhances control, and automates all processes by integrating and coordinating the flow of information across departments. ERP systems that are implemented in software such as Oracle, SAP, SYSPRO, or Microsoft Dynamics help large organisations to manage the large amount of data they process. Table 6 below lists the advantages of ERP systems.
5.3 Distribution resources planning (DRP)
Enns and Suwanruji [36] defined distribution requirement planning (DRP) as a time-based replenishment approach with revised inventory status and periodically generated shipping plans. The main objective of the distribution system is to provide maximum service to the customer. The concepts and logic used in the DRP system are similar to those used in the material requirements planning system, with the notable difference that DRP focuses on the distribution of remote goods rather than on the flow of parts (materials, components) within a warehouse or operating facility. Figure 11 illustrates the flow of DRP materials from the factory to the retailer and then to the end user.

In a DRP, the retailer's demand is treated as an independent demand because it is closely related to the end user, while the factory's demand (upstream) is treated as a dependent demand with a time logic that is used to anticipate needs. DRP has many benefits, including better service to customers and reduced inventory [36]. In addition, DRP for material flow is compatible with other supply chain systems [36].
6 CONCLUSION
A systematic review of inventory management concepts was discussed in this article. The study showed a growing level of interest in this process of supply chain management. With the increasing range of problems related to climate change, environmental science has been among the sectors with the most interest in stockpile management. The article reviews the literature on the deterministic demand model, highlighting the implementation of independent and dependent demand in a real situation. In the independent demand models, decision variables were developed based on the demand, type of products, cost/profit, time, ordering opportunity, and selling season. In contrast to independent demand inventory models, in which the demand for one material is independent of the demand for other materials, in dependent demand inventory models the materials are interconnected. In implementation, to manage the manufacturing process of finished products in a case of dependent demand for raw materials and other components, material resource planning (MRP) is mainly used. Enterprise resource planning (ERP) software integrates all of the departmental functions of organisations into one system. Examples of well-known ERP systems have been listed. On the other hand, like the material requirements planning system, the concepts and logic used in the DRP system focus on the distribution of goods at a distance rather than on the flow of parts (materials, components) within a warehouse or operating facility. This systematic review provides the research community with the tools to implement an inventory management project.
REFERENCES
[1] Abimanyu, Wawan, H. and Erry, R. 2019. Analysis of inventory management using methodology ROP (reorder point) to minimize DOI (days of inventory). International Journal of Innovative Science and Research Technology, 4(7), pp. 313-317. [ Links ]
[2] Ahmad, K. and Zabri, S.M. 2016. Inventory management practices among Malaysian micro retailing enterprises. A Journal of the Academy of Business and Retail Management (ABRM), 11 (1): pp. 103-115. [ Links ]
[3] Ahmad, K., Mohamed Zabri, S. and Mohamed, M.I.P. 2014. Inventory management practices among small and medium-sized retails enterprises. Proceeding of the 3rd International Conference on Technology Management, Business and Entrepreneurship, Melaka, Malaysia, pp. 344-350. [ Links ]
[4] Antic, S., Djordjevic M.L. and Lisec, A. 2022. Dynamic discrete inventory control model with deterministic and stochastic demand in pharmaceutical distribution. Applied Science, 12(3), 1536. https://doi.org/10.3390/app12031536. [ Links ]
[5] Avinadav, T., Herbon, A. and Spiegel, U. 2013. Optimal inventory policy for a perishable item with demand function sensitive to price and time. International Journal of Production Economics, 144(2), pp. 497-506. [ Links ]
[6] Axsáter, S. and Rosling, K. 1994. Multi-level production-inventory control: Material requirements planning or reorder point policies? European Journal of Operational Research, 75(2), pp. 405-412. [ Links ]
[7] Ayad, A. 2008. Optimizing inventory and store results in big box retail environment. International Journal of Retail & Distribution Management, 36(3), pp. 180-191. [ Links ]
[8] Baily, P., Farmer, D., Crocker, B., Jessop, D. and Jones, D. 2015. Procurement: Principles and management. 11th ed. https://www.pearson.com/uk/educators/higher-education-educators/program/Baily-Procurement-Principles-Management-11th-Edition/PGM1095617.html [ Links ]
[9] Bala, P.K. 2012. Improving inventory performance with clustering-based demand forecasts. Journal of Modelling in Management, 7(1), pp. 23-37. [ Links ]
[10] Baron, O., Berman, O. and Perry, D. 2010. Continuous review inventory models for perishable items ordered in batches. Mathematical Methods of Operations Research, 72(1), pp. 217-247. [ Links ]
[11] Barros, J., Cortez, P. and Carvalho, M.S. 2021. A systematic literature review about dimensioning safety stock under uncertainties and risks in the procurement process. Operations Research Perspectives, 8(1), pp. 1-25. http://dx.doi.org/10.1016Zj.orp.2021.100192. [ Links ]
[12] Ben-Daya, M. and Raouf, A. 1993. On the constrained multi-item single-period inventory problem. International Journal of Operation and Productions Management, 13(1), pp. 104-112. [ Links ]
[13] Bhamangol, B., Nandavadekar, V. and Khilari, S. 2011. Enterprise resource planning (ERP) System in Higher Education, A Literature Review. International Journal of Management Research and Development, 1(1), pp. 1-7. [ Links ]
[14] Bhattacharya, D.K. 2005. Production, manufacturing and logistics on multi-item inventory. European Journal of Operational Research, 162(1), pp. 786-791. [ Links ]
[15] Botta-Genoulaz, V. and Millet, P.A. 2006. An investigation into the use of ERP systems in the service sector. International Journal of Production Economics, 99(1), pp. 202-221. [ Links ]
[16] Bradley, J.R. and Robinson, L.W. 2005. Improved base-stock approximations for independent stochastic lead times with order crossover. Manufacturing & Service Operations Management, 7(4), pp. 319-329. [ Links ]
[17] Carvalho, J.C., Guedes, A.P., Arantes, A.J.M., Martins, A.L., Póvoa, A.P.B., Luís C.A. et al. (eds). 2017. Logística e Gestão da Cadeia de Abastecimento, 2nd ed. Lisbon: Edições Sílabo. [ Links ]
[18] Chandra, S. 2017. An inventory model with ramp type demand, time varying holding cost and price discount on backorders. Uncertain Supply Chain Management, 5(1), pp. 52-58. [ Links ]
[19] Chang, C.T., Teng, J.T. and Chern, M.S. 2010. Optimal manufacturer's replenishment policies for deteriorating items in a supply chain with up-stream and down-stream trade credits. International Journal of Production Economics, 127(1), pp. 197-202. [ Links ]
[20] Chatfield, D.C. and Pritchard, A.M. 2018. Crossover aware base stock decisions for service-driven systems. Transportation Research Part E: Logistics and Transportation Review, 114(1), pp. 312-330. [ Links ]
[21] Chen I.J. 2001. Planning for ERP systems: analysis and future trend. Business Process Management Journal, 7(5), pp. 374-386. [ Links ]
[22] Chen, C.H., Teng, J.T. and Skouri, K. 2013. Economic production quantity models for deteriorating items with up-stream full trade credit and down-stream partial trade credit. International Journal of Production Economics, 155(1), pp. 302-309. [ Links ]
[23] Chen, H. and Li, P. 2015. Optimization of (R, Q) policies for several inventory systems using the guaranteed service approach. Computers & Industrial Engineering, 80(1), pp. 261-273. [ Links ]
[24] Ho, C.F., Tai, Y.M. and Chi, Y.P. 2005. A structural approach to measuring uncertainty in supply chains. International Journal of Electronic Commerce, 9(3), pp. 91-114. [ Links ]
[25] Choi, T.M., Govindan, K., Li, X. and Li, Y. 2017. Innovative supply chain optimization models with multiple uncertainty factors. Annals of Operations Research, 257(1-2), pp. 1-14. [ Links ]
[26] Chopra, S. and Meindl, P. 2016. Supply chain management: Strategy, planning, and operation. Pearson Education, 6th-Edition. https://www.pearson.com/us/higher-education/program/Chopra-Supply-Chain-Management-Strategy-Planning-and-Operation-6th-Edition/PGM178843.html [ Links ]
[27] Christopher M. 2005. Logistics and supply chain management: Creating value-adding networks. Pearson Education, 4th Edition. https://www.pearson.com/uk/educators/higher-education-educators/product/Christopher-Logistics-Supply-Chain-Management-creating-value-adding-networks-3rd-Edition/9780273681762.html [ Links ]
[28] Chung, K.J. and Huang, Y.F. 2003. The optimal cycle time for EPQ inventory model under permissible delay in payments. International Journal of Production Economics, 84(3), pp. 307-318. [ Links ]
[29] Chung, W.W., Hua Tan, K., Lenny Koh, S., Law, C.C. and Ngai, E.W. 2007. An investigation of the relationships between organizational factors, business process improvement, and ERP success. Benchmarking: An International Journal, 14(3), pp. 387-406. [ Links ]
[30] Coculescu, C. 2017. Comparative evaluation of parametric optimization methods. Journal of Economic Computation and Economic Cybernetics Studies and Research, 41 (1 ), pp. 196-203 [ Links ]
[31] Di Nardo, M., Clericuzio, M., Murino, T. and Sepe, C. 2020. An economic order quantity stochastic dynamic optimization model in a logistic 4.0 environment. Sustainability, 12(1), 4075. [ Links ]
[32] Disney, S.M., Farasyn, I., Lambrecht, M., Towill, D.R. and De Velde, W.V. 2006. Taming the bullwhip effect whilst watching customer service in a single supply chain echelon. European Journal of Operational Research, 173(1), pp. 151-172. [ Links ]
[33] Dobler, K. and Burt, H. 1996. Purchasing and Supply Management: Text and Cases. 6th edition. McGraw-Hill, 963. [ Links ]
[34] Dutta, P. and Chakraborty, R.A.R. 2006. An inventory model for single-period products with reordering opportunities under fuzzy demand. Computers and Mathematics with Applications, 53(1), pp. 1502-1517. [ Links ]
[35] Edrawsoft. 2020. Inventory management process flowchart. Available from: https://www.edrawsoft.com/inventory-management-flowchart.html (Accessed May 2021). [ Links ]
[36] Enns, S.T. and Suwanruji, P. 2000. Distribution planning and control: An experimental comparison of DRP and order point replenishment strategies. In Conference Proceedings of the Academy of Business and Administrative Sciences, 2000, Prague, Czech Republic. [ Links ]
[37] Fadlalla, A. and Amani, F. 2015. A keyword-based organizing framework for ERP intellectual contributions. Journal of Enterprise Information Management, 28(5), pp. 637-657. [ Links ]
[38] Feng, H., Li, J. and Zhao, D. 2013. Retailer's optimal replenishment and payment policies in the EPQ model under cash discount and two-level trade credit policy. Applied Mathematical Modelling, 37(1), pp. 3322-3339. [ Links ]
[39] Feng, L., Chan, Y.L. and Cardenas-Barron, L.E. 2017. Pricing and lot-sizing policies for perishable goods when the demand depends on selling price, displayed stocks and expiration date. International Journal of Production Economics, 185(1), pp. 11-20. [ Links ]
[40] Gürler, U. and Ôzkaya, B.Y. 2008. Analysis of (s, S) policy for perishables with a random shelf life. IIE Transactions, 410(1), pp. 759-781. [ Links ]
[41] Hamisi, S. 2011 . Challenges and opportunities of Tanzanian SMEs in adapting supply chain management. African Journal of Business Management, 5 (4), pp. 1266-1276. Available online at http://www.academicjournals.org/AJBM [ Links ]
[42] Hasan, M.D., Rakibul, Y.D., Tutul, C.R. and Yi, F. 2020. Inventory management with online payment and preorder discounts. Industrial Management and Data Systems, 120(1), pp. 2001-2023. [ Links ]
[43] Hatten, T.S. 2012. Principles of small business management, 5th edn. New York: South-West Cengage. [ Links ]
[44] Hayya, J.C., Harrison, T.P. and Chatfield, D.C. 2009. A solution for the intractable inventory model when both demand and lead time are stochastic. International Journal of Production Economics, 122(2), pp. 595-605. [ Links ]
[45] He, B., Huang, H. and Yuan, K. 2015. The comparison of two procurement strategies in the presence of supply disruption. Computers & Industrial Engineering, 85(1), pp. 296-305. [ Links ]
[46] Heizer, J. & Render, B. and Munson, C. 2011. Material Requirements Planning (MRP) and ERP. Operations Management: Sustainability and Supply Chain Management, Twelfth Edition. Chapter 14, pp. 578-589. [ Links ]
[47] Hodges, S.D. and Moore, P.G. 1970. The product-mix problem under stochastic seasonal demand. Management Science, 17(2), pp. 107-114. [ Links ]
[48] Statistics of ScienceDirect data on Inventory Management. Available from: https://www.sciencedirect.com/search?qs=inventory%20management (Accessed May 2021). [ Links ]
[49] Hu, F. & Liu, D. 2010. Optimal replenishment policy for the EPQ model with permissible delay in payments and allowable shortages. Applied Mathematical Modelling, 34(10), pp. 3108-3117. [ Links ]
[50] Huang, J.C., Wu, T.J., Chiu, Y.C. and Lu, C. 2017. Improvement of inventory control and forecast according to activity-based classifications: T company as an example. AIP Conference Proceedings, 1836, 020014; https://doi.org/10.1063/L4981954 [ Links ]
[51] Huang, Y.F. 2007. Optimal retailer's replenishment decisions in the EPQ model under two levels of trade credit policy. European Journal of Operational Research, 176(3), pp. 1577-1591. [ Links ]
[52] lasya, A. and Handayati, Y. 2015. Material requirement planning analysis in micro, small and medium enterprise. Case study: Grooveline - An apparel outsourcing company final project. Journal of Business and Management, 4(3), pp. 317-329. [ Links ]
[53] Inform IT (2014). Operations Management Defined. Inform IT, books, ebooks and digital learning, Pearson. https://www.informit.com/articles/article.aspx?p=2167438&seqNum=7 (Accessed 2 April 2021). [ Links ]
[54] Ivanov, S.H., Webster, C. and Berezina, K. 2017. Adoption of robots and service automation by tourism and hospitality companies. Paper presented at the INVTUR Conference, 17-19 May 2017, Aveiro, Portugal. [ Links ]
[55] Joy, J. and Jose, K.P. 2020. A discrete time perishable inventory model with positive lead time. Malaya Journal of Matematik, 5(1), pp. 39-44. https://doi.org/10.26637/MJM0S20/0008 [ Links ]
[56] Kalpakam, S. and Arivarignan, G. 1988. A continuous review perishable inventory model. Statistics, 19(1), pp. 389-398. [ Links ]
[57] Kalpakam, S. and Sapna, K.P. 1996. An (s, S) perishable system with arbitrarily distributed lead times. Operation Research, 33(1), pp. 1-19. [ Links ]
[58] Kalpic, D. and Fertalj, K. 2004. ERP Software Evaluation and Comparative Analysis. CIT Journal of Computing and Information Technology, 12(3), pp. 195-209. https://doi.org/10.2498/cit.2004.03.02 [ Links ]
[59] Kar, S., Roy, T.K and Maiti, M. 2006. Multi-item fuzzy inventory model for deteriorating items with finite time-horizon and time-dependent demand. Yugoslav Journal of Operations Research, 16(2), pp. 161-176. [ Links ]
[60] Karande, S.H., Jain, V. and Ghatule, A.P. 2012. ERP implementation: Critical success factors for Indian universities and higher educational institutions. Pragyaan Journal of Information Technology, 10(2), pp. 24-29. [ Links ]
[61] Khobragade, P., Selokar, R., Maraskolhe, R. and Talmale, M. 2018. Research paper on inventory management system. International Research Journal of Engineering and Technology (IRJET), 5(4): pp. 252-254. www.irjet.net. [ Links ]
[62] Kisaka, J.F. 2006. The theory of power and conflict in channels of distribution. Journal of Marketing, 48(3), pp. 9-29. [ Links ]
[63] Kreng, V.B. & Tan, S.J. 2011. Optimal replenishment decision in an EPQ model with defective items under supply chain trade credit policy. Expert Systems with Applications, 38(8), pp. 9888-9899. [ Links ]
[64] Kumar, R. 2016. Economic order quantity model (EOQ). Global Journal of Finance and Economic Management, 5(1), pp. 1-5. [ Links ]
[65] Kumar, S., Rao, V.V. and Tirupati, D. 2003. Multiple products, multiple constraints, single period inventory problem: A hierarchical solution procedure. Available from: https://www.researchgate.net/publication/5113525 (accessed on the 16 March 2021) [ Links ]
[66] Lambert, D.M., Stock, J.R. and Ellram, L.M. 1998. Fundamentals of logistics management. 1st ed. Irwin McGraw-Hill Higher Education; p. 622. [ Links ]
[67] Latha, K.F., Mary, G.K.M. and Uthayakumar, R. 2021. Two echelon economic lot sizing problems with geometric shipment policy backorder price discount and optimal investment to reduce ordering cost. OPSEARCH, 12(1), pp. 1-31. [ Links ]
[68] Lau, H. 1980. Some extensions of Ismail-Louderback's stochastic CVP model under optimizing. Decision Sciences,11(3), pp. 557-561. [ Links ]
[69] Layek, A.M., Montanari, R. and Morales, L.C. 2004. Exact, approximate, and generic iterative models for the multi-product newsboy problem with budget constraint. International Journal of Production and Economics, 91(1), pp. 189-198. [ Links ]
[70] Liao, J.J. 2007. On an EPQ model for deteriorating items under permissible delay in payments. Applied Mathematical Modelling, 31(3), pp. 393-403. [ Links ]
[71] Limansyah, T., Dharma, L. and Ign, S. 2020. Economic order quantity model with deterioration factor and all-units discount. Journal of Physics: Conference Series, 1490(1), 012052. [ Links ]
[72] Lin, Y.J., Ouyang, L.Y. and Dang, Y.F. 2012. A joint optimal ordering and delivery policy for an integrated supplier-retailer inventory model with trade credit and defective items. Applied Mathematics and Computation, 218(14), pp. 7498-7514. [ Links ]
[73] Liu, L. 1990. (s;S) continuous review models for inventory with random life times. Operations Research Letters, 9(3), pp. 161-167. [ Links ]
[74] Lou, K.R. and Wang, L. 2013. Optimal lot-sizing policy for a manufacturer with defective items in a supply chain with up-stream and down-stream trade credits. Computers & Industrial Engineering, 66(1), pp. 1125-1130. [ Links ]
[75] Mahata, G.C. 2012. An EPQ-based inventory model for exponentially deteriorating items under retailer partial trade credit policy in supply chain. Expert Systems with Applications, 39(3), pp. 3537-3550. [ Links ]
[76] Mahfuz, M.H., Shahrul, I.M. and Islam, M.A. 2009. Application of fixed time period model for optimizing inventory level: A case study in a pharmaceutical company. Engineering e-Transaction, 3(2), pp 67-73, Available online at http://ejum.fsktm.um.edu.my [ Links ]
[77] Manna, A.K., Md, A., Ali, A.S. and Asoke, K.B. 2021. Optimization of a deteriorated two-warehouse inventory problem with all-unit discount and shortages via tournament differential evolution. Applied Soft Computing, 107(1), 107388. [ Links ]
[78] Mbaknol, (2015). Types of Inventory System (Q and P Models). https://www.mbaknol.com/operations-management/types-of-inventory-system-q-and-p-models/ [ Links ]
[79] Mohanty, R.P. 1985. Inventory problems under multiple constraints: Some studies. Engineering Costs and Production Economics, 9(1), pp. 355-361. [ Links ]
[80] Moustakis, V. 2000. Material requirement planning: Dissemination of innovation and knowledge management techniques. Report produced for the EC funded project INNOREGIO, Greece. [ Links ]
[81] Myerson, P.A. 2017. Lean and Technology: Working Hand in Hand to Enable and Energize Your Global Supply Chain. https://www.oreilly.com/library/view/lean-and-technology/9780134291581/ch14.html [ Links ]
[82] Naddor, E. 1966. Dimensions in operations research. Operations Research, 14(3), pp. 508-514. [ Links ]
[83] Nanaware, M.R. and Saharkar, U.R. 2017. Inventory management technique in construction. International Journal of Engineering Sciences & Research, 6(9), pp. 225-230. [ Links ]
[84] Nash, K.S. 2000. Companies don't learn from previous IT snafus. Computerworld, 16(21 ), pp. 32-33. [ Links ]
[85] Nemtajela, N. and Mbohwa, C. 2017. Relationship between inventory management and uncertain demand for fast moving consumer goods organizations. 14th Global Conference on Sustainable Manufacturing, GCSM, 3-5 October 2016, Stellenbosch, South Africa. Procedia Manufacturing, 8(1), pp. 699-706. [ Links ]
[86] Nenni, M.E. and Schiraldi, M.M. 2013. Validating virtual safety stock effectiveness through simulation. International Journal of Engineering Business Management, 5(41): pp. 1-8. www.intechopen.com [ Links ]
[87] Ouyang, L.Y. and Chang, C.T. 2013. Optimal production lot with imperfect production process under permissible delay in payments and complete backlogging. International Journal of Production Economics, 144(2), pp. 610-617. [ Links ]
[88] Parlar, M., Perry, D. and Stadje, W. 2011. FIFO versus LIFO issuing policies for stochastic perishable inventory systems. Methodology and Computing in Applied Probability, 13(1), pp. 405-417. [ Links ]
[89] Parr, A. and Shanks, G. 2000. Journal of Information Technology, 15(4), pp. 289-303. [ Links ]
[90] Patel, R.C. 1986. A note on inventory reorder point determination. Journal of Accounting Education, 4(2), pp. 131-140. [ Links ]
[91] Perlman, Y. and Levner, I. 2014. Perishable inventory management in healthcare. Journal of Service Science and Management, 7(1), pp. 11-17. doi:10.4236/jssm.2014.71002. [ Links ]
[92] Plinere, D. and Borisov, A. 2015. Case study on inventory management improvement. Information Technology and Management Science, 8(1): pp. 91-96. doi:10.1515/itms-2015-0014. [ Links ]
[93] Rahimi, M., Ghezavatia, V. and Asadib, F. 2019. A stochastic risk-averse sustainable supply chain network design problem with quantity discount considering multiple sources of uncertainty. Computers & Industrial Engineering, 130(1), pp. 430-449. [ Links ]
[94] Rajeev, N. 2008. Inventory management in small and medium enterprises: A study of machine tool enterprises in Bangalore. Management Research News, 31(9), pp. 659-669. doi:10.1108/01409170810898554 [ Links ]
[95] Reina, A., Nyoman, P.I. and Budi, S. 2014. Managing uncertainty through supply chain flexibility: Reactive vs proactive approaches. Production & Manufacturing Research, 2(1 ), pp. 50-70. [ Links ]
[96] Render, B. Stair, R.M. and Hanna, M.E. 2016. Quantitative analysis for management, 9th ed. Pearson Prentice Hall. https://www.pearson.com/us/higher-education/program/Render-Quantitative-Analysis-for-Management-with-CD-9th-Edition/PGM304065.html (Accessed in12 March 2021) [ Links ]
[97] Rezaei, J. and Davoodi, M. 2008. A deterministic, multi-item inventory model with supplier selection and imperfect quality. Applied Mathematical Modelling, 32(1), pp. 2106-2116. [ Links ]
[98] Rushton, A., Oxley, J. and Croucher, P. 2006. The handbook of logistics and distribution management, 3rd ed. London: Kogan Page. [ Links ]
[99] Satyendra, K., Venkata R.V. and Devanath, T. 2003. Multiple products, multiple constraints, single period inventory problem: A Hierarchical solution procedure, No WP2003-11-03, IIMA Working Papers, Indian Institute of Management Ahmedabad, Research and Publication Department, https://EconPapers.repec.org/RePEc:iim:iimawp:wp01787. [ Links ]
[100] Schmidt, M., Hartmann, W. and Nyhuis, P. 2012. Simulation based comparison of safety-stock calculation methods. CIRP Journal of Manufacturing Science and Technology, 61(1), pp. 403-406. [ Links ]
[101] Shah, N.H., and Monika, K.N. 2018. Inventory policies for price-sensitive stock-dependent demand and quantity discounts. International Journal of Mathematical, Engineering and Management Sciences, 3(1), pp. 245-257. [ Links ]
[102] Shaikh, A.A., Al-Amin, K., Gobinda, C.P. and loannis, K. 2019. Price discount facility in an EOQ model for deteriorating items with stock-dependent demand and partial backlogging. International Transactions in Operational Research, 26(1), pp. 1365-1395. [ Links ]
[103] Shih, W. 1979. A general decision model for cost-volume-profit analysis under uncertainty. Accounting Review, 54(4), pp. 687-706. [ Links ]
[104] Sil. 2009. Stochastic demand models. Available at: https://jmsbdssa.files.wordpress.com/2009/11/newsvendor-models.pdf (Accessed 1 April 2021) [ Links ]
[105] Sople, V.V. 2010. Logistics management: the supply chain imperative. Delhi: Dorling Kindersley (India) / Pearson Education. [ Links ]
[106] Srivastav, A. and Agrawal, S. 2018. On a single item single stage mixture inventory models with independent stochastic lead times. Operations Research, 20 (4): pp. 1-39. [ Links ]
[107] Strohhecker, J. and Grobler, A. 2013. Do personal traits influence inventory management performance? The case of intelligence, personality, interest and knowledge. International Journal of Production Economics, 142(1), pp. 37-50. [ Links ]
[108] Su, C. H. 2012. Optimal replenishment policy for an integrated inventory system with defective items and allowable shortage under trade credit. International Journal of Production Economics, 139(1), pp. 247-256. [ Links ]
[109] Sunil, C. & Peter, M. 2016. Supply chain management: Strategy, planning, and operation. 6th Edition. Pearson Education publisher. https://www.pearson.com/us/higher-education/program/Chopra-Supply-Chain-Management-Strategy-Planning-and-Operation-6th-Edition/PGM178843.html (Accessed 20 March 2021). [ Links ]
[110] Taleizadeh, A.A., Cárdenas-Barrón, L.E., Biabani, J. and Nikousokhan, R. 2012. Multi products single machine EPQ model with immediate rework process. International Journal of Industrial Engineering Computations, 3(2), pp. 93-102. [ Links ]
[111] Taleizadeh, A.A., Jalali-Naini, S.G.H., Wee, H.M. and Kuo, T.C. 2013. An imperfect, multi product production system with rework. Scientia Iranica, 20(3), pp. 811-823. [ Links ]
[112] Taleizadeh, A.A., Mohammadi, B., Cardenas-Barron, L.E. and Samimi, H. 2013. An EOQ model for perishable product with special scale and shortage. International Journal of Production Economics, 145(1), pp. 318-338. [ Links ]
[113] Taleizadeh, A.A., Najafi, A.A. and Niaki, S.T.A. 2010. Multi product EPQ model with scrapped items and limited production capacity. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 17(1), pp. 58-69. [ Links ]
[114] Tanthatemee, T. and Phruksaphanrat, B. 2012. Fuzzy inventory control system for uncertain demand and supply. Proceedings of the international Multi conference of Engineers and Computer Scientists 11 (1), IMECS 2012, March 14-16, Hong Kong. [ Links ]
[115] Tayal, S., Singh, S.R. and Sharma, R. 2014. An inventory model for deteriorating items with seasonal products and an option of an alternative market. Uncertain Supply Chain Management, 3(1), pp. 69-86. [ Links ]
[116] Taylor Ill, B.W. (2010). The Introduction to management Science. 8th Edition. Chapter 16, Inventory Management. https://jeryfrl.files.wordpress.com/2013/04/ch16-inventory-management.pdf (Accessed 8 June 2022). [ Links ]
[117] Teng, J.T. and Chang, C.H.T. 2009. Optimal manufacturer's replenishment policies in the EPQ model under two levels of trade credit policy. European Journal of Operational Research, 195(2), pp. 358-363. [ Links ]
[118] Tinani, K.S. and Kandpal, D.H. 2017. Literature review on supply uncertainty problems: Yield uncertainty and supply disruption. Journal of the Indian Society for Probability and Statistics, 18(2), pp. 89-109. [ Links ]
[119] Toomey, J.W. 1996. The role of inventory management. In MRP II. Chapman & Hall Materials Management/Logistics Series. Boston, MA: Springer. https://doi.org/10.1007/978-1-4615-4117-2_2 [ Links ]
[120] Ucharia, S.V. and Kumar, P. 2017. To study the inventory management system at organization level. International Journal of Engineering Science and Computing, 7(8), pp. 14503-14506. [ Links ]
[121] Ullah, A., Baharun, R.B., Nor, K.M., Siddique, M. and Sami, A. 2018. Enterprise resource planning (ERP) systems and user performance. International Journal of Applied Decision Sciences, 11(3): pp. 297-322. [ Links ]
[122] Umry, T.F. and Singgih, M.L. 2019. Inventory management and reorder point (ROP) strategy using ABC analysis methods in textile manufacture. IPTEK Journal of Proceedings, doi: 10.12962/j23546026.y2019i5.6188 [ Links ]
[123] Vrat, P. 2014. Basic Concepts in Inventory Management. Springer Texts in Business and Economics, in: Materials Management, edition 127, chapter 2, pp. 21-36, Springer. [ Links ]
[124] Whitin, T.M. 1957. Theory of inventory management. Princeton, NJ: Princeton University Press. [ Links ]
[125] Wu, Q., Fang, A., & Gao, H. 2010. A study on inventory cost reduction based on economic order quantity model. 2010 International Conference on Logistics Systems and Intelligent Management (ICLSIM), 3 (1), pp. 1341-1343. [ Links ]
[126] Yadavalli, V.S.S., Van Wyk, E. and Udayabaskaran, S. 2015. A temporo-spatial model for optimal positioning of humanitarian inventories for disaster relief management. Applied Mathematics & Information Sciences an International Journal, 9 (3), pp. 1205-1211. http://dx.doi.org/10.12785/amis. [ Links ]
[127] Yadavalli, V.S.S., Sundar, D.K. and Udayabaskaran, S. 2016. Two substitutable perishable product disaster inventory systems. Annals of Operations Research, 233(1 ), pp. 517-534. Doi:10.1007/10479-014-1783-3 [ Links ]
[128] Zhen, H., Lee, C.K.M. and Linda, Z. 2018. Procurement risk management under uncertainty: A review. Industrial Management & Data Systems, 118(7), pp. 1547-1574. [ Links ]
[129] Zhou, Y. 2012. The bi-ramp type demand and price discount inventory model for deteriorating items. World Congress on Intelligent Control and Automation (WCICA), Beijing, China, pp. 3298-3304. [ Links ]
Submitted by authors 12 May 2021
Accepted for publication 25 Apr 2022
Available online 29 Jul 2022
ORCID® identifiers
J.B. Munyaka: 0000-0001-9452-8225
V.S.S. Yadavalli: 0000-0002-3035-8906
* Corresponding author baraka.munyaka@epfl.ch














