Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.32 n.1 Pretoria May. 2021
http://dx.doi.org/10.7166/32-1-2459
CASE STUDIES
Supplier segmentation: a case study of Mozambican cassava farmers
N.S. Matshabaphala#; J. Grobler*
Department of Industrial Engineering, Stellenbosch University, South Africa. N.S. Matshabaphala: https://orcid.org/0000-0002-0349-8882; J. Grobler: https://orcid.org/0000-0002-1868-0759
ABSTRACT
Over 3 000 Mozambican smallholder farmers supply cassava to Company XYZ. XYZ needs an effective supplier segmentation method to gain insight into how it should direct its resources for the greatest impact. This paper describes the application of the /(-means algorithm, agglomerative hierarchical clustering, and a self-organising map with ward clustering to segment these cassava suppliers. The insights gained from the cluster analysis are then used to provide recommendations and suggest suitable intervention strategies to manage each segment of suppliers. The proposed method offers users the basis of a supplier segmentation system that is more robust than commonly used qualitative supplier segmentation models.
OPSOMMING
Meer as 3 000 kleinboere in Mosambiek lewer kassawe aan Maatskappy XYZ. XYZ benodig 'n effektiewe verskaffersegmenteringsmetode om insig te bekom oor hoe sy hulpbronne aangewend moet word om die grootste impak te maak. Hierdie artikel beskryf die toepassing van die ( -gemiddelde groepering algoritme, agglomeratiewe hiërargiese groepering en selforganiserende kaarte met wykgroepering om hierdie kassawe boere te segmenteer. Die insigte wat uit die groepontleding verkry is, is gebruik om aanbevelings te maak en geskikte intervensiestrategieë voor te stel om elke segment van verskaffers te bestuur. Die voorgestelde metode bied gebruikers die basis van n verskaffersegmenteringsstelsel wat meer doeltreffend is in vergelyking met algemeen gebruikte kwalitatiewe verskaffer-segmenteringsmodelle.
1 INTRODUCTION
Although an organisation generally accumulates many suppliers in the course of doing business, some of these suppliers are of little or no importance to the organisation beyond fulfilling a simple order transaction, while other suppliers play a strategic role in its success. The decision to invest in supplier relationships is a major step for an organisation, especially because the value gained from interacting in a supply network rests on the principle of prioritising the right suppliers. The segmentation of suppliers plays a significant role in assessing suppliers and determining appropriate relationships that an oganisation should have with its suppliers [1], [2].
Clustering has been used in many contexts by researchers in many disciplines, but it has not received much attention in supplier segmentation, where grouping suppliers based on their similarities can enhance the effectiveness of supplier relationship management [3], [4], [5]. An opportunity exists, therefore, for research into the use of clustering for supplier segmentation.
Cassava is an important crop that contributes to Mozambique's overall gross domestic product (GDP). In 2016, agriculture accounted for roughly 18% of GDP, and cassava production's direct share of agricultural output by value was more than one-quarter of the 18%. For this reason, cassava production plays a significant role in the country's social and economic growth, particularly in vulnerable rural populations [6], [7], [8].
In this paper, three techniques are applied to cluster Mozambican cassava suppliers. Over 3 000 smallholder farmers supply cassava to a for-profit social enterprise called Company XYZ. XYZ needs an effective supplier segmentation method to gain insight into how it should direct its resources for the greatest impact. The k-means algorithm, agglomerative hierarchical clustering (AHC), and self-organising maps (SOM) with ward clustering were applied to XYZ's purchasing data. The performance of the algorithms was evaluated and compared using intra-cluster and inter-cluster distances, and the best-performing algorithm, in the context of the case study, was selected. The SOM method with ward clustering outperformed the k-means and AHC, and its results were used to conduct a detailed cluster analysis. The insights gained from the cluster analysis were used to provide recommendations and suitable intervention strategies to manage each segment of suppliers.
This paper is considered significant since, to the best of the authors' knowledge, this study is the first application of clustering to segment cassava suppliers.
The rest of the paper is organised as follows. Section 2 introduces background on clustering techniques and supplier relationship management. In Section 3, the proposed techniques are applied to the selected case study. Section 4 conducts cluster analysis on the results and make recommendations from insight gained from the analysis. Finally, the conclusion, recommendations, and future research avenues are discussed in Section 5.
2 BACKGROUND
Various background concepts are crucial to understanding the context of this work. Clustering and supplier relationship management are introduced in this section.
2.1 Clustering
The cross-industry standard process for data mining (CRISP-DM) [9] is a highly recommended reference model that can be used to structure a data science project [10]. The CRISP-DM comprises six stages, shown in Figure 1.
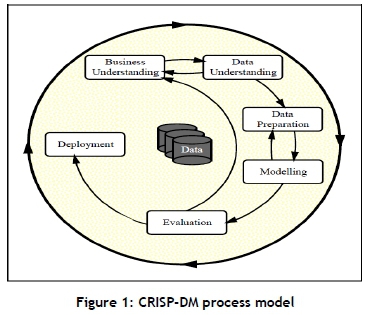
The primary goal in the business understanding phase is to understand the business problem that the organisation wants to solve. The data understanding phase starts with initial data collection, and proceeds with data exploration [11], [12], [13]. The data preparation phase covers tasks such as data cleaning, feature selection, and data transformation, all of which aims to construct the final dataset that is used in data modelling [14], [15].
In the modelling phase, the selected clustering techniques are applied to the dataset. Clustering is the process of identifying natural groupings within multidimensional data based on a similarity measure. A common way to measure the similarity between two instances, x and y, is to measure the distance between the instances in a feature space. After obtaining results from each clustering technique, the results need to be evaluated thoroughly [16], [17]. Internal validation assessment, which measures the performance of clustering, is often based on the two criteria: compactness and separation [10], [12]. Intra-cluster distance is used to measure compactness, and inter-cluster distance measures separation. Last, the deployment phase focuses on the successful integration of the results into the processes in an organisation [12], [18].
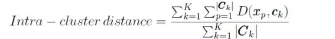
where Κ is the number of clusters, D is a measure of similarity, xpis an instance, ck is the kthcluster's centroid, and |Ckl is the number of instances in cluster Ck.
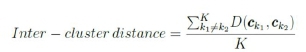
where Ck1and ck2 are cluster centres of different clusters.
Sections 2.1.1, 2.1.2, and 2.1.3 provide descriptions of the three clustering algorithms that are applied in this paper.
2.1.1 The k-means algorithm
The k-means algorithm is one of the most well-studied clustering algorithms; and it is computationally attractive because of its linear time and space complexity, which makes it suitable for very large datasets [19]. The steps for computing the k-means algorithm begin by defining the objective function that the algorithm needs to optimise. The selected objective function, SSE, is computed as [18], [20]:
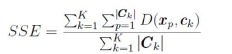
After computing the objective function, the following steps in the algorithm are applied [21], [22]:
1. Specify the number of clusters (K).
2. Select initial centroids randomly, based on the number of clusters specified.
3. Assign each instance to the cluster with the closest centroid. The centroids are updated incrementally after each assignment of an instance to a cluster. The closest centroid to an instance is the one with the smallest value with regard to the distance measure applied.
4. When all objects have been assigned, recalculate the positions of the K centroids. Centroids are recalculated as the average vector over all the data points that belong to that centroid.
5. Repeat steps 2 to 4 with the updated means until a defined convergence criterion is met.
The silhouette coefficient (SC) is a method that can be used to determine the optimal value of K. The SC is bounded between -1 and +1, where values close to +1 are an indication of good clusters. SC is defined as [23]:
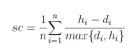
where η is the total number of instances, di is the average distance between point / and all other points in its own cluster, and hi is the minimum of the average dissimilarities between i and points in other clusters.
In the k-means algorithm, the initialisation of centroids has a direct impact on the final results. Random initialisation is commonly used in the k-means initialisation step [4], [24], [25]. Another option is to choose the initial centres more systematically by applying the k-means++ algorithm initialisation method [26].
Despite being a popular method for performing clustering across different disciplines, users have noted some significant drawbacks of k-means. The k-means is sensitive to noise and outliers. Another drawback is that k-means requires the user to specify the number of clusters (K) in advance [20], [27].
2.1.2 Agglomerative hierarchical clustering
An AHC algorithm first assigns each instance to its own cluster before merging the instances that have the closest similarity to each other into larger clusters [4], [28]. Common methods used to measure similarities between clusters in AHC include the single linkage and complete linkage methods. The equations below show the computation of the single linkage and complete linkage methods [4]:
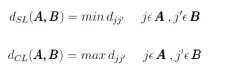
where dSL(A,B) is the single linkage distance and dcL(A,B) is the complete linkage distance between cluster A and B. djj'is the distance between instances j and j'.
The following steps are followed when applying the AHC algorithm [4]:
1. Start with K clusters, where each cluster consists of one data point.
2. Find the most similar pair of clusters using similarity measures and combine the pair of clusters to form a new cluster.
3. Update the proximity matrix by computing the distances between the new cluster and the other clusters.
4. Repeat steps 2 and 3 until defined convergence criteria are met. Generally, the algorithm is stopped when all clusters are merged.
The AHC algorithms are considered to be more robust and versatile than the k-means algorithm, as AHC is less impacted by missing values in a dataset. Another advantage is that the number of clusters does not need to be specified in advance, and they are independent of the initialisation phase. However, a common criticism is that AHC is computationally expensive; thus AHC is not suitable for very large datasets [22], [28].
2.1.3 Self-organising map
The SOM is a multidimensional scaling method that represents high-dimensional instances with codebook vectors that can be visualised in an output space that is usually a two-dimensional grid [22], [29].
The main advantage of SOM is the easy visualisation and interpretation of clusters formed by the maps. SOM is also more robust, and does not suffer from problems presented by missing values and outliers in a dataset [18], [24].
One of the shortfalls of the SOM method is that it is sensitive to the initialisation phase, and may generate suboptimal clusters if the initial weights are not chosen properly. Moreover, its performance is affected by user-dependent parameters such as the size of the map and the neighbourhood function [18], [21]. The parameters that the user needs to specify when using SOM is the size of the map, the learning rate (η), and the neighbourhood function. According to Vesanto [30], the default number of neurons should be specified in advance using the formula 5 * Vn, where n is the number of training instances.
In the initialisation phase, the codebook vectors can be initialised by assigning random values to each weight [30], [31]. The learning rate (η) determines the extent to which the weights are adjusted during each iteration [29]. The neighbourhood function is a function of the distance between the coordinates of the neurons. The initial spread of neighbouring neurons (σ) is the width of the kernel [29], [32].
The most popular choice for a neighbourhood function is to use a Gaussian kernel, as computed in the equation below [29], [32]:
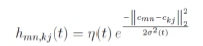
where coordinates cmin, ckj e R2 and mn are the coordinates of the winning neuron.
The quantisation error (QE) is one of the most common measures used as an indication of map accuracy. QE is computed from the average distance of the instance x to the weight vector of the winning neuron (wmn(t)) [33]. A SOM with lower average error is considered to be more accurate [31]. The formula for calculating QE is defined as [34]:
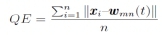
where n is the number of instances used to train the map.
The SOM algorithm is summarised in the following steps [18], [32]:
1. Randomly initialise the codebook vectors (wk(0)).
2. Initialise the learning rate (η(0)) and the neighbourhood function (hmn,kj(0)).
3. Find the winning neuron for each input instance xi. The winning neuron is the unit whose codebook vector has the highest similarity to the input pattern.
4. Use competitive learning to train the codebook vectors such that all neurons within the neighbourhood of the winning neuron move towards xi:
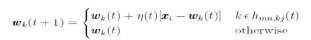
where Wk(t) is the kth codebook vector at time t.
5. Linearly decrease η(t) and reduce hmn,kj(t).
6. Repeat steps 3 to 5 until the specified convergence criteria are satisfied.
One way to determine clusters is by using the ward distance measure to decide which clusters should be merged. The distance measure is defined as [29]:
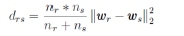
where r and s are cluster indices, nrand nsare the number of instances within the clusters, and wrand ws are the centroid vectors of these clusters (i.e., the average of all the codebook vectors within the cluster).
The two clusters are merged if their distance drs is the smallest. For the newly formed cluster (q),
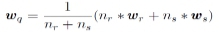
and
2.2 Supplier relationship management
The number of suppliers that an organisation has to deal with has grown rapidly over the years, and organisations are increasingly relying on their suppliers to reduce operational costs, improve quality, and develop new products faster than their competitors. Organisations are using supplier relationship management (SRM) to find new ways to involve key suppliers who can help them gain a competitive edge [35], [36]. SRM consist of three focus areas: the organisation's key requirements, the level of importance of each supplier, and possible interventions to manage each supplier [36]. These focus areas are discussed in sections 2.2.1, 2.2.2, and 2.2.3.
2.2.1 Defining requirements for suppliers
A VIPER model is generally used to determine an organisation's requirements from its supply base. VIPER is an acronym representing the key elements - value, innovation, performance improvements, effectiveness of operations, and risk - that are used when defining the requirements of an organisation [36]. The value element represents additional benefits beyond the traditional list of standard benefits that are possible through working with suppliers, and innovation focuses on factors that enable businesses to evolve continuously. The third element, performance improvements, requires an organisation to monitor the performance of its supply base according to the service level agreement. Effectiveness of operations focuses on factors that enable an organisation's operations to run smoothly and effectively. Last, risk focuses on instances where a failure in the supply chain can present a significant risk to an organisation [36], [37].
2.2.2 Supplier segmentation
Supplier segmentation is generally used by organisations selectively to allocate their resources to the suppliers from whom it expects to generate the highest return [38]. Supplier segmentation is defined as a process whereby suppliers are divided into distinct groups according to their perceived importance to an organisation [5], [39].
The organisation's key requirements from its supply base inform the development of criteria that are used in assessing suppliers [40]. The supplier potential matrix (SPM) is one of the approaches for defining criteria that is used to measure suppliers. The SPM consists of an extensive list of attributes categorised under two dimensions, referred to as supplier capabilities and supplier willingness [41]. Capabilities mostly focus on a supplier's skills, and willingness focuses on a supplier's motivation to collaborate with an organisation [37], [42], [43]. Another approach is to define criteria based on five key areas: risk, alignment, current importance, future importance, and difficulty of replacing suppliers [36].
Once a set of criteria has been selected, each supplier is rated against each criterion. The key challenge is that the scoring process produces separate scores for each criterion [44], [45]. Generally, mathematical models are used to aggregate the suppliers' scores according to all the criteria that are met. The aggregated score of each supplier is then used in the segmentation process, in which suppliers are grouped together based on their aggregated score [36], [46].
It is important to note that SPM has some limitations. First, the method is inevitably exposed to subjective bias, as it primarily relies on the input made by the organisation's decision-makers as the only means to rate suppliers. In order to reduce the possibility of systematic bias, these judgements should be supplemented by insights obtained from objective data such as past transactions with suppliers. Furthermore, the SPM method is practical only for organisations with a relatively small number of suppliers.
2.2.3 Supplier Intervention strategies
After suppliers are placed in different clusters based on their scores, the organisation needs to determine specific interventions it should have with their supply base in order to achieve its strategic goals. The interventions depend on the risk involved in the supplier relationship, the potential gain from a supplier relationship, and the degree of business impact.
3 APPLICATION OF CRISP-DM TO THE MOZAMBICAN CASSAVA SUPPLIER SEGMENTATION CASE STUDY
This section explains how the CRISP-DM reference model was applied in the clustering project using purchasing data from Company XYZ.
3.1 Business understanding
The organisation requires an efficient approach to segment its over 3 000 farmers into logical categories based on their similarities, to define the type of relationship it should have with each group. The organisation aims to use the results to define different intervention and development strategies for each cluster in order to achieve its strategic goals.
Using a VIPER model, the company defined the following key requirements from its supply base:
• Supply risk: The no. of purchases feature is used to measure supply risk. The feature measures the number of times a farmer has supplied cassava in the period of analysis.
• Effectiveness of operations: Farmers who deliver roots using their own transport enhance the effectiveness of operations, which is measured using the amount paid for using own transport feature.
• Performance improvements: The performance of farmers is measured by their yields using the quantity of cassava purchased and average starch content features.
• Innovation and value: The organisation decided first to focus on core requirements, and not engage in any innovative or value-enhancing initiatives with its supply base.
3.2 Data understanding
The historical purchasing data about cassava that was received from the organisation contained purchasing details for transactions dated between February 2018 and April 2020 (Table 1).
For each feature, a data quality report was generated containing measures such as count of missing values, minimum, maximum,1st and 3rd quartile, mean, median, mode, and standard deviation. The relationships between pairs of features were examined using a scatterplot matrix (splom) for continuous features and stacked bar graphs for categorical features.
3.3 Data preparation
The latitude of plot, longitude of plot, and starch content features were the only ones that contained missing values. An imputation approach was used to replace the missing values.
Two datasets were constructed to be used in the data modelling phase. In the first dataset (DS1), only outliers that resulted from invalid data were removed. In the second dataset (DS2), outliers were removed using a clamp transformation method. This method clamps all values beyond specified upper and lower thresholds. In the data exploration phase, the cassava quantity and cassava cost features obtained a perfect positive correlation. As a result, the cassava quantity feature was removed from the dataset. Furthermore, the latitude of plot and longitude of plot features were removed from the dataset, as they provided similar information to that of the location of plots feature. Moreover, the information provided by the field worker feature had a direct link with the location of factory feature. Thus the fieldworker feature was removed.
All clustering algorithms used in this study were distance-metric based; thus, the dataset needed to be standardised. The MinMaxScaler normalisation method was applied to all features to ensure that there were no features that dominated others owing to a significant difference in range. Moreover, the categorical and binary features were transformed into numerical values using the one-hot encoding method. In order to have one record per farmer, purchases made by each farmer were aggregated accordingly. The transport cost and cassava cost features were summed to one value per farmer. For the starch content feature, an average value for all the farmer's transactions was used. Furthermore, a new feature called no. of purchases was added to count the number of transactions for each farmer.
3.4 Modelling and evaluation
The three clustering techniques were implemented and are evaluated in this section.
3.4.1 K-means
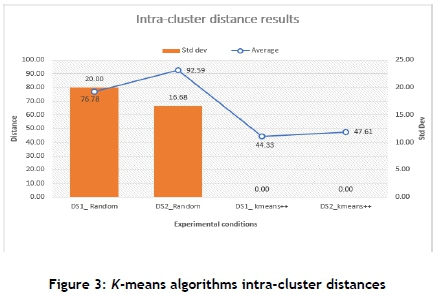
In implementing the k-means algorithm, the optimal number of clusters (K) was obtained using the silhouette coefficient (SC). The centroids were initialised using the random and k-means++ initialisation methods, and the algorithm was executed for 30 independent simulation runs for each set of experimental conditions. Figure 2 and Figure 3 respectively show the inter-cluster and intra-cluster results that were obtained.

For the k-means algorithm and the SOM, the sets of 30 performance metric values of the four experimental conditions were compared using Mann-Whitney U tests at 95% significance. If the first set of experimental conditions statistically significantly outperformed the second set of experimental conditions, a win was granted for the first set of experimental conditions. A draw was recorded if no statistical difference could be observed. If the second set of experimental conditions outperformed the first set of experimental conditions, a loss was recorded against the first set of experimental conditions.
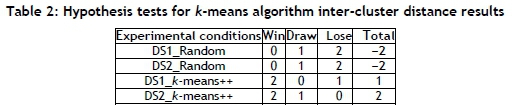
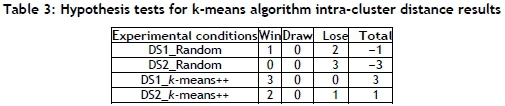
For instance, if the results for DS1_Random compared with other experimental conditions are recorded as 0-1-2, as shown in Table 2, it means that DS1_Random was granted zero wins, one draw, and two losses. Table 2 indicates that DS2_k-means++ obtained the best results in inter-cluster measure, and DS1_k-means++ obtained the best results in intra-cluster distance, as shown in Table 3.
3.4.2 Agglomerative hierarchical clustering
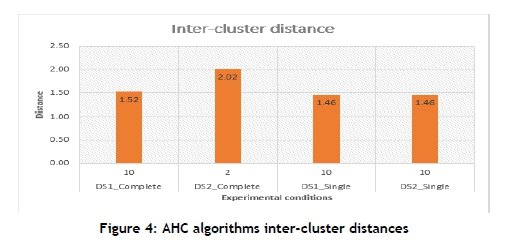
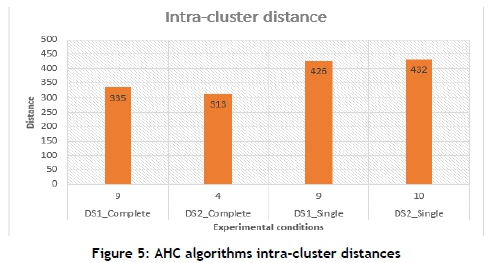
The AHC algorithm was run for all possible values of K, which are 2 to 10 clusters as specified by the organisation's requirements. The two datasets, DS1 and DS2, were trained using the complete linkage and single linkage methods to measure similarities between objects. The best inter- and intra-cluster distance was selected for each set of experimental conditions as shown in Figures 4 and 5. The highest inter-cluster distance was achieved by DS2_Complete at K=2. The AHC algorithm achieved the lowest intra-cluster distance at K=4 by DS2_Complete.
3.4.3 Self-organising map
In the SOM implementation, the size of the output map was calculated to be 17 by 17 dimensions. The random initialisation method was applied to initialise the weight vectors. Two methods were used for training, the random and batch training methods. To obtain clusters, the ward clustering method was applied to the SOM results. The optimal number of clusters (K) was selected using the silhouette coefficient (SC).
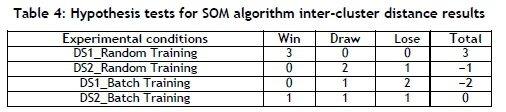
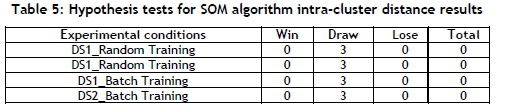
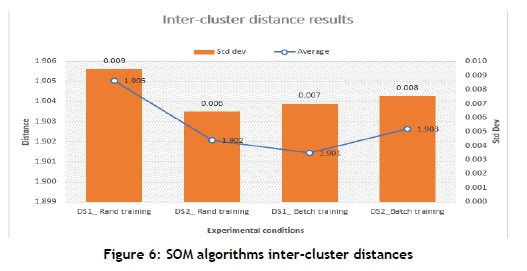
Figures 6 and 7 respectively show the inter-cluster and intra-cluster results obtained from the 30 runs, while Table 4 and Table 5 respectively indicate inter- and intra-cluster distance performances for SOM. The inter-cluster results show that DS1_Random Training outperformed other experimental conditions. The intra-cluster measure shows that there was no significant difference in the performance of each set of experimental conditions. Consequently, DS1_Random Training was selected.
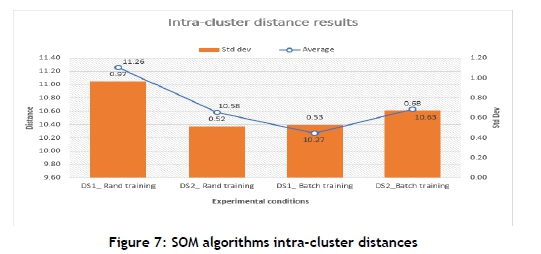
4 CLUSTER ANALYSIS AND RECOMMENDATIONS
In this section, the results obtained are analysed, and the insights gained from the analysis are used to make recommendations to the organisation.
4.1 Cluster analysis of SOM results
The SOM was selected as the best-performing technique, as it obtained the best results with respect to both the inter-cluster and the intra-cluster distances. The SOM obtained the best results using DS1_Random Training at K=10. The SOM was implemented in two phases. The first phase was to train the SOM and obtain the codebook vectors, and the second phase was to cluster the SOM results using ward clustering.
The first clustering results showed that the algorithm had clustered farmers based solely on the location of plots, overlooking other features that also form part of the organisation's clustering criteria. In order to address this issue, the location of plot feature was removed from the dataset, and the adjusted dataset was trained using a SOM.
After removing the feature from the dataset, the question arose whether SOM would still be the best algorithm. As a result, all the experiments were rerun. For each algorithm, the set of experimental conditions that obtained the best results was selected, and the SOM again outperformed the k-means algorithm and AHC. The best results for SOM was obtained by DS1_Random Training.
Sections 4.1.1, 4.1.2, and 4.1.3 evaluate the cluster analysis results based on the three defined criteria: supply risk, effectiveness of operations, and performance improvement.
4.1.1 Criterion 1: Supply risk
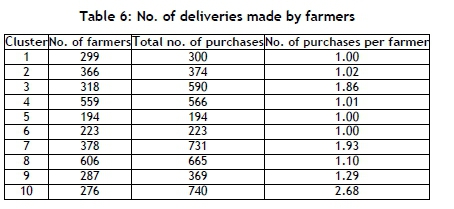
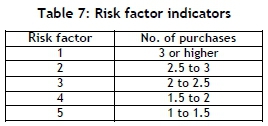
Table 6 shows the total number of purchases per cluster and the average number of purchases per farmer. The results were evaluated using the performance indicator outlined in Table 7. Throughout this section, a score of 1 is low and 5 is high.
4.1.2 Criterion 2: Effectiveness of operations
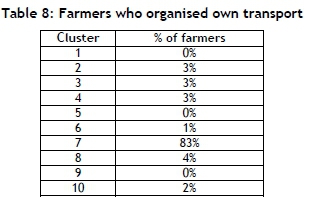
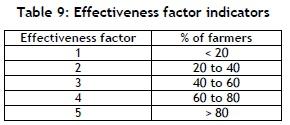
Table 8 shows a percentage of farmers who delivered cassava using their own transport per cluster. The results were evaluated using the performance indicator outlined in Table 9.
4.1.3 Criterion 3: Performance improvements
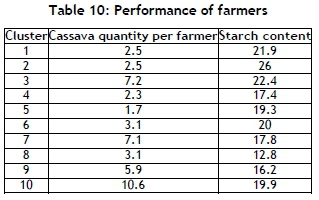
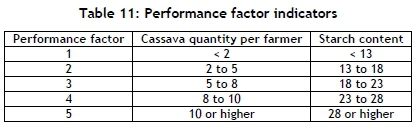
The performance was measured using the cassava quantity and starch content features. Table 10 shows the average amount of cassava delivered per farmer. The results were evaluated using the performance indicator outlined in Table 11.
4.2 Deployment and recommendations
The cluster analysis showed that certain clusters are similar and can be managed using the same intervention strategy. As a result, the total number of strategies to manage the ten clusters have been summarised in the four intervention strategies that are explained below:
• Inform and observe: For clusters 5 and 8, the organisation informs the farmers about its growth strategy and its requirements. Then the organisation monitors farmers' progress to determine whether they have the willingness and the potential to grow.
• Educate: This strategy applies to clusters 1, 2, 4, 6, and 9, and the key objective of this strategy is to improve yields substantially. The organisation should carry out a massive campaign to mentor smallholder farmers, and the focus should be primarily on improving their capacity to produce high-quality fresh roots consistently.
• Develop: For clusters 3 and 7, farmers should be encouraged to organise themselves as associations to facilitate access to fundamental farming inputs from the organisation and its partners. The organisation should also consider signing a service level agreement with each association that is formed.
• Invest: For cluster 10, the organisation should assist farmers with financing to support their growth into becoming commercial farmers.
5 CONCLUSION
The purpose of this investigation was to investigate the use of different clustering algorithms to segment Mozambican cassava suppliers. Three clustering algorithms were investigated. Purchasing information from farmers who have supplied cassava to two cassava processing plants in Mozambique was used as basis for the analysis.
The SOM with ward clustering was shown to outperform the other two algorithms. The algorithm produced 10 clusters, which were further analysed. Finally, four intervention strategies - inform and observe, educate, develop, and invest - were devised to assist XYZ in their quest for improved SRM.
Future research opportunities exist in undertaking more in-depth cluster analysis and the development of further SRM initiatives, and in extending the scope of this study to include yield (quantity and quality) prediction of cassava.
REFERENCES
[1] Lambert, D.M. 2008. Supply chain management: Processes, partnerships, performance. Supply Chain Management Institute. Sarasota, Florida. [ Links ]
[2] Omurca, S.I. 2013. An intelligent supplier evaluation, selection and development system. Applied Soft Computing, 13, pp. 690-697. [ Links ]
[3] Tuma, M. & Decker, R. 2013. Finite mixture models in market segmentation: A review and suggestions for best practices. Electronic Journal of Business Research Methods, 11, pp. 1 -13. [ Links ]
[4] Xu, R. & Wunsch, D.C. 2005. Survey of clustering algorithms. IEEE Transactions on Neural Networks, 16, pp. 645678. [ Links ]
[5] Brown, A.J. 2017. Development of a supplier segmentation method for increased resilience and robustness: A study using agent based modeling and simulation, PhD thesis. University of Kentucky, Lexington. [ Links ]
[6] Costa, C. & Delgado, C. 2019. The cassava value chain in Mozambique. Jobs Working Paper No. 31. Washington, DC: World Bank. [ Links ]
[7] Salvador, E.M., Steenkamp, V. & McCrindle, C.M.E. 2014. Production, consumption and nutritional value of cassava (Manihot esculenta, Crantz) in Mozambique: An overview. Journal of Agriculture Biotechnology and Sustainable Development, 6, pp. 29-38. [ Links ]
[8] Zvinavashe, E., Elbersen, H.W., Slingerland, M., Kolijn, S. & Sanders, J.P.M. 2011. Cassava for food and energy: Exploring potential benefits of processing of cassava into cassava flour and bioenergy at farmstead and community levels in rural Mozambique. Biofuels, Bioproducts and Biorefining, 5, pp. 151 -164. [ Links ]
[9] Chapman, P. 1999.The CRISP-DM user guide. In 4th CRISP-DM SIG Workshop in Brussels. NCR Systems Engineering, Copenhagen. [ Links ]
[10] Marbán, Ó., Mariscal, G. & Segovia, J. 2009. A data mining & knowledge discovery process model. Data mining and knowledge discovery in real life applications. Ponce, J & Karahoca, A. I-Tech, Vienna, Austria. [ Links ]
[11] Kelleher, J.D.B., Mac Namee, B. & D'Arcy, A. 2015. Fundamentals of machine learning for predictive data analytics: Algorithms, worked examples, and case studies. MIT Press, Boston. [ Links ]
[12] Wirth, R. & Hipp, J. 2000. CRISP-DM: Towards a standard process model for data mining. In Proceedings of the 4th International Conference on the Practical Applications of Knowledge Discovery and Data Mining, London, April 2000. [ Links ]
[13] Garcia, S., Ramirez-Gallego, S., Luengo, J., Benitez, J.M. & Herrera, F. 2016. Big data preprocessing: Methods and prospects. Big Data Analytics, 1, pp. 9-19. [ Links ]
[14] Kotsiantis, S.B., Kanellopoulos, D. & Pintelas, P.E. 2006. Data preprocessing for supervised learning. International Journal of Computer Science, 1, pp. 111 -117. [ Links ]
[15] Idri, A., Benhar, H., Fernández-Alemán, J.L. & Kadi, I. 2018. A systematic map of medical data preprocessing in knowledge discovery. Computer Methods and Programs in Biomedicine, 162, pp. 69-85. [ Links ]
[16] Sargent, R.G. 2000. Verification, validation and accreditation of simulation models. In IEEE Winter Simulation Conference Proceedings, , pp. 50-59. IEEE, Orlando, FL, USA. December 2000. [ Links ]
[17] Huang, M., Lin, W., Chen, C., Ke, S., Tsai, C. & Eberle, W. 2016. Data preprocessing issues for incomplete medical datasets. Expert Systems, 33, pp. 432-438. [ Links ]
[18] Omran, M.G.H., Engelbrecht, A.P. & Salman, A. 2007. An overview of clustering methods. Intelligent Data Analysis, 6, pp. 583-605. [ Links ]
[19] Wang, S., Chaovalitwongse, W. & Babuska, R. 2012. Machine learning algorithms in bipedal robot control. IEEE Transactions on Systems, 42, pp. 728-743. [ Links ]
[20] Jain, A.K. 2010. Data clustering: 50 years beyond K-means. Pattern Recognition Letters, 31, pp. 651-666. [ Links ]
[21] Jain, A.K., Murty, M.N. & Flynn, P.J. 1999. Data clustering: A review. ACM Computing Surveys (CSUR), 31, pp. 264-323. [ Links ]
[22] Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O.P., Tiwari, A., Er, M.J., Ding, W. & Lin, C. 2017. A review of clustering techniques and developments. Neurocomputing, 267, pp. 664-681. [ Links ]
[23] Liu, Y., Li, Z., Xiong, H., Gao, X. & Wu, J. 2010. Understanding of internal clustering validation measures. In IEEE International Conference on Data Mining. December 2010. Sydney, NSW, Australia. [ Links ]
[24] Bação, F., Lobo, V. & Painho, M. 2005. Self-organizing maps as substitutes for k-means clustering. in Computer Science, 3516, pp. 476-483. [ Links ]
[25] Shirkhorshidi, A.S., Aghabozorgi, S., Wah, T.Y. & Herawan, T. 2014. Big data clustering: A review. In Computational Science and Its Applications, 8583, pp. 707-720. June 2014. Guimaraes, Portugal. [ Links ]
[26] Bahmani, B., Moseley, B., Vattani, A., Kumar, R. & Vassilvitskii, S. 2012. Scalable k-means++. arXiv preprint, 5, pp. 622-633. [ Links ]
[27] Dey, A. 2016. Machine learning algorithms: A review. International Journal of Computer Science and Information Technologies, 7, pp. 1174-1179. [ Links ]
[28] Joshi, A. & Kaur, R. 2013. A review: Comparative study of various clustering techniques in data mining. International Journal of Advanced Research in Computer Science and Software Engineering, 3, pp. 1 -12. [ Links ]
[29] Engelbrecht, A.P. 2007. Computational intelligence: An introduction. John Wiley & Sons. West Sussex, England. [ Links ]
[30] Vesanto, J. 2005. SOM implementation in SOM toolbox. Available online: http://www.cis.hut.fi/projects/somtoolbox/documentation/somalg.shtml. [ Links ]
[31] Gorricha, J.M.L. 2015. Exploratory data analysis using self-organising maps defined in up to three dimensions. PhD Thesis. Universidade NOVA de Lisboa, Lisbon, Portugal. [ Links ]
[32] Bullinaria, J.A. 2010. Self organizing maps: algorithms and applications. The University of Birmingham Neural Computation Course Lectures. University of Birmingham. Lecture notes. [ Links ]
[33] Liu, Y. & Weisberg, R.H. 2011. A review of self-organizing map applications in meteorology and oceanography. Self-Organizing Maps: Applications and Novel Algorithm Design,1, pp. 253-272. [ Links ]
[34] Natita, W., Wiboonsak, W. & Dusadee, S. 2016. Appropriate learning rate and neighborhood function of self- organizing map (SOM) for specific humidity pattern classification over Southern Thailand. International Journal of Modeling and Optimization, 6, pp. 61 -89. [ Links ]
[35] Park, J., Shin, K., Chang, T.-W. & Park, J. 2010. An integrative framework for supplier relationship management. Industrial Management & Data Systems, 110, pp. 495-515. [ Links ]
[36] O'Brien, J. 2018. Supplier relationship management: Unlocking the hidden value in your supply base. Kogan Page Publishers, London, UK. [ Links ]
[37] Vänttinen, S. 2018. Supplier segmentation from the perspective of internal knowledge-sharing: A case study in the retailing business. Master;s Thesis. Hanken School of Economics, Helsinki, Finland. [ Links ]
[38] Rezaei, J., Wang, J. & Tavasszy, L. 2015. Linking supplier development to supplier segmentation using best worst method. Expert Systems with Applications, 42, pp. 9152-9164. [ Links ]
[39] Day, M., Magnan, G.M. & Moeller, M.M. 2010. Evaluating the bases of supplier segmentation: A review and taxonomy. Industrial Marketing Management, 39, pp. 625-639. [ Links ]
[40] Kraljic, P. 1983. Purchasing must become supply management. Harvard Business Review, 61, pp. 109-117. [ Links ]
[41] Rezaei, J. & Ortt, R. 2013. Multi-criteria supplier segmentation using a fuzzy preference relations based AHP. European Journal of Operational Research, 225, pp. 75-84. [ Links ]
[42] Hudnurkar, M., Rathod, U. & Jakhar, S.K. 2016. Multi-criteria decision framework for supplier classification in collaborative supply chains: Buyer's perspective. International Journal of Productivity and Performance Management, 65, pp. 622-640. [ Links ]
[43] Segura, M. & Maroto, C. 2017. A multiple criteria supplier segmentation using outranking and value function methods, Expert Systems with Applications, vol. 69, p. 87-100, 2017. [ Links ]
[44] Rezaei, J. & Ortt, J.R. 2012. A multi-variable approach to supplier segmentation, International Journal of Production Research, vol. 50, p. 4593-4611. [ Links ]
[45] Rezaei, J. & Ortt, J.R. 2013. Supplier segmentation using fuzzy logic. Industrial Marketing Management, 42, pp. 507-517. [ Links ]
[46] Rezaei, J. & Ortt, J.R. 2011. Two multi-criteria approaches to supplier segmentation. In IFIP International Conference on Advances in Production Management Systems. pp. 317-325. Springer, Berlin, Heidelberg. September 2011. [ Links ]
[47] Haggblade, S., Djurfeldt, A.A., Nyirenda, D.B., Lodin, J.B., Brimer, L., Chiona, M., Chitundu, M., Chiwona-Karltun, L., Cuambe, C. & Dolislager, M. 2012. Cassava commercialization in Southeastern Africa. Journal of Agribusiness in Developing and Emerging Economies, 2, pp. 4-40. [ Links ]
Submitted by authors 2 Nov 2020
Accepted for publication 18 Jan 2021
Available online 28 May 2021
# Author was enrolled for an M Eng (Industrial Engineering) in the Department of Industrial Engineering, Stellenbosch University, South Africa
* Corresponding author: jacominegrobler@sun.ac.za














