Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.30 n.1 Pretoria May. 2019
http://dx.doi.org/10.7166/30-1-1849
GENERAL ARTICLES
Design and implementation of deadlock control for automated manufacturing systems
H. KaidI*; A. Al-AhmariI; A.M. El-TamimiI; E. Abouel NasrI, II; Z. LiIII
ICollege of Engineering, Industrial Engineering Department, King Saud University, Riyadh 11421, Saudi Arabia
IIMechanical Engineering Department, Helwan University, Cairo, Egypt
IIISchool of Electro-Mechanical Engineering, Xidian University, No. 2 South Taibai Road, Xi'an 710071, China
ABSTRACT
Petri nets are robust mathematical tools for the modelling, handling, and control of deadlock problems in automated manufacturing systems (AMSs). Several methods have been proposed to prevent deadlocks in AMSs. However, it is important to convert the controlled system represented by Petri nets into the program of a programmable logic controller (PLC) for the implementation of automation tasks. This study proposes a methodology based on Petri nets for deadlock prevention, and generates PLC codes for an AMS. In the suggested methodology, a Petri net model of an uncontrolled system is built, and the controlled Petri net model is developed using a deadlock-prevention method. The controlled Petri net model is then transformed into an automation-controlled Petri net model, which is further converted into a controlled token-passing logic model. The controlled token-passing logic model is utilised to generate the ladder diagrams for the AMS under consideration. The proposed methodology was tested using a real-world AMS at King Saud University labs. It provides an effective method for PLC implementation from a controlled system model represented by Petri nets.
OPSOMMING
Petri-nette is robuuste wiskundige instrumente wat gebruik word om dooiepunt probleme in geoutomatiseerde vervaardigingstelsels (AMSe) te modelleer, hanteer en te beheer. Verskeie metodes is al voorgestel om dooiepunte in AMSe te verhoed, maar dit is belangrik om die beheerde stelsel deur die Petri-nette voorgestel om te skakel na die rekenaarkode van 'n programmeerbare logiese beheerder (PLC) sodat dit geïmplementeer kan word. 'n Metodologie gegrond op Petri-nette vir dooiepunt voorkoming word voorgehou en genereer PLC rekenaarkode vir AMSe. In die voorgestelde metodologie word n Petri-netmodel van n onbeheerde stelsel geskep en die beheerde Petri-netmodel is dan ontwikkel met die dooiepuntvoorkomingsmetode. Die beheerde Petri-net model word dan getransformeer tot 'n outomasiebeheerde Petri-netmodel wat dan verder omskep word in n beheerde kenteken-aanstuur logiese model. Hierdie model word dan gebruik om leerdiagramme vir die AMS te genereer. Dié metodologie is getoets in 'n reële wêreld AMS by die King Saudi Universiteit se laboratoriums. Dit verskaf n effektiewe metode vir PLC implementering van n beheerde stelsel wat deur Petri-nette voorgestel word.
1 INTRODUCTION
An automated manufacturing system (AMS) is a conglomeration of robots, machine tools, fixtures, and buffers. Different types of products enter the manufacturing system at separate points of time; the system can process these parts based on a specified sequence of operations and resource sharing. The sharing of resources leads to the occurrence of deadlock states in an AMS through its operation, in which the local or global system is incapacitated Li et al. [1], Li et al. [2], El-Tamimi et al. [3], and Chen et al. [4]. Thus there is a need for an effective deadlock-control algorithm to ensure that these deadlocks do not occur in an automated manufacturing system. Petri nets are a mathematical and major graphical tool that is suitable for modelling, analysing, and controlling deadlocks in AMSs. Petri nets are used to describe the characteristics and behaviour of an AMS, such as synchronisation, conflict, and sequences. In addition, they could be used to provide behavioural properties - for example, boundedness and liveness Chen et al. [5].
In the last three decades, there has been a deluge of deadlock-control algorithms, based on Petri nets that were developed for deadlock prevention in AMSs Ezpeleta et al. [6], Huang et al. [7], Uzam and Zhou [8], Li and Zhou [9], Huang et al. [10], Uzam and Zhou [11], Li et al. [12], Huang [13], Li et al. [14], Li and Zhou [15], Chao [16], Chen and Li [17], Li et al. [18], Chen et al. [19], Chen et al. [20], Qin et al. [21], Li et al. [22], Li and Zhao [23], Chen et al. [24], and Uzam et al. [25]. Most of the deadlock-control policies have been proposed via the structural analysis of Petri nets Chao [26, 27] or reachability graph analysis of Petri nets Uzam and Zhou [8], Ghaffari et al. [28], Uzam [29], and Nasr et al. [28]. Deadlock-control algorithms (policies) based on reachability graph analysis can usually become a maximally permissive liveness-enforcing supervisor; but the former can lead to a sub-optimally controlled system, and the monitor number in a sub-optimal supervisor depends on the Petri net size Lautenbach [31]. The latter may encounter a problem of explosion state, since listing a portion or all of the reachable markings is necessary.
The control policies to prevent deadlocks in an AMS lead to a controlled system described by a Petri net. However, the results obtained in the supervisory control literature are mostly related to the theoretic studies as opposed to practical (implementation) studies. After designing a controller (supervisor), it is a need to have an automatic ways for the generation of control code from the controller to test the applicability of the deadlock prevention methods for real world systems and determining which methods are suitable for these systems that can definitely lead to the maximal permissiveness, structural complexity, and computational complexity. It is necessary to convert a controlled Petri net system representation into a programmable logic controller (PLC) implementation to evaluate the applicability of deadlock control methods to the execution of automation tasks. PLCs have appeared as a robust tool in the fulfillment of automation operations in industrial production systems. Ladder diagrams (LDs) are the most popular language used to program a PLC. The main problem with LDs is that programming is done heuristically. In simple manufacturing systems, it is not difficult to develop PLC programs with these methods. Nevertheless, when multiple systems are considered, the problem is magnified. Indeed, it is difficult to find ladder logic programs when the manufacturing system is single and has multiproduct types that are implemented using heuristic approaches Venkatesh et al. [32, 33]. To overcome this problem, Petri nets can be used to provide a successful solution for the conceptual design, and the heuristic design is replaced by the transformation of Petri nets into LDs, which is introduced in Satoh et al. [34], Jafari and Boucher [35], Burns and Bidanda [36], and Uzam et al. [37]. In Jones et al. [38], a token-passing logic (TPL) technique has been introduced that provides options to involve counters, flags, and timers. This technique is used in the transformation of an automation Petri Net (APN) into LDs. Moreover, the same technique has been used to handle the timed-transition Petri nets Uzam et al. [39], timed place Petri nets Uzam et al. [39] and Uzam et al. [40], and colored Petri nets Uzam et al. [39].
This paper proposes a methodology based on Petri nets for deadlock prevention, and generates PLC codes (ladder diagrams) for an AMS to elucidate the weaknesses or disadvantages of the existing methods in the literature. In addition, the contributions of this research are clearly emphasised. The rest of the paper is structured as follows. Section 2 introduces Petri nets. The proposed methodology is described in Section 3. A real-world AMS case study is presented in Section 4. Finally, the conclusions and future research are given in Section 5.
2 BASICS OF PETRI NETS
A place/transition net or Petri net N [12, 19, 30] is a quadruple (P, T, F, W), where P is a non-empty and finite set of places, and T is a non-empty and finite set of transitions. Elements in P υ T are called nodes with P υ T*0 and P Ո T=0. P and T are graphically described by circles and bars respectively. F e (P χ T) υ (T χ P) is the set of directed arcs (with arrows) that join the places with transitions, and vice versa. W: (P χ T) u(T P χ T) IN is a mapping that allocates a weight to an arc, where IN = {0, 1, 2, ...}. N is called an ordinary or unweighted net if V (p, t) εF((t, p)eF), W(p, t) = 1 (W(t, p) = 1), denoted as N = (P, T, F). N is called a weighted net if there is an arc between p and t with W(p, t) >1 or W(t, p) >1. If there is no arc between a place p and a transition t, we have W(p, t) = W(t, p) = 0.
Assume that a net N = (P, T, F, W) and node a ε P υ T, *a = {b ε P υ T | (b, a) ε F} is called the preset of node a, while a* = {b ε P υ T|(a, b) ε F} is called the post-set of node a. A marking M of N is a mapping M: P - IN. (N, M0) is a marked net or a net system, denoted as PN = (P, T, F, W, Mo), where Mo is an initial marking. For a Petri net modelling an AMS, Mo indicates the various raw parts that are to be simultaneously processed in an AMS, and the initial capacity configuration of resources such as robots and machines. A transition t ε T is enabled at marking M if Vp ε 't, M(p) > W(p, t), which is indicated as M[t>. If a transition t fires, it withdraws W(p, t) tokens from each place pc*t, and stores W(t, p) tokens in each place p εt*. Thus it reaches a new marking M', indicated as M[t>M', where M'(p) = M(p) - W(p, t) + W(t, p). A Petri net is pure or self-loop free if Va, b ε P υ T, W(b, a) = 0 and W(a, b) > 0. Incidence matrix [N] is an integer matrix of a net N, which consists of | T| columns and |P| rows with [N](p, t) = W(t, p) -W(p, t).
Suppose (N, Mo) is a net with N = (P, T, F, W). It can be said that a transition t εT is live if for all M εΗ^, Mo), 3 M εR(N, M), there exists a firing sequence such that M[t]M'. A transition is in a deadlock state at Mo if 3 t ε T, Mo[t> holds. M is said to be reachable from M if there is a firable finite transition sequence δ = tit2t3. . . t„, and markings M1, M2, M3, . . ., and Mn-3such that M[t1] M1[t2)M2[t3)M2. . . Mn-i[tn] Mi that is represented as M[δ]M', satisfying the state equation M = M + [N] 5, where 5 : T - IN is a mapping from T to the number of appearances of t in δ, and called a firing count vector or a Parikh vector. The reachable set of markings from M in N is called the reachability set of a net (N, M), and is indicated as R(N, M). Petri net N with an initial marking Mo is said to be /(-bounded if V M εR(N, Mo), M(p) < k (k e IN). Petri net N is said to be safe if all its places are safe, each place p does not have more than one token.
P-vectors (place vectors) and T-vectors (transition vectors) are column vectors. A P-vector I: P - Z catalogued by P is said to be a place invariant or P-invariant if I * 0 and IT. [N] = 0T, and a T-vector J: T - Z catalogued by T is said to be a transition invariant or T-invariant if J * 0 and [N].J = 0, where Zis the set of integers. When each element of I is non-negative, the place invariant I is called a place semiflow or P-semiflow. Assume that I is a P-invariant of a net with (N, Mo) and M is a reachable marking from the initial marking Mo. Then ITM = ITMo. Let MIM = {p \I(p) * 0} be the support of P-invariant I. The supports of P-invariant I are classified into three types: (1) ||I ||+ is the positive support of P-invariant I with ||I||+= {p\I(p) > 0}. (2) | is the negative support of P-invariant I with = {p \I(p) < 0}. (3) I is a minimal P-invariant if is not a superset of the
support of any other one and its components are mutually prime. Let li be the coefficients of P-invariant I if V pi εP, li = I(p). Since regular (ordinary and weighted) Petri nets do not handle both actuators and sensors, an extended Petri net has been developed to handle both actuators and sensors Uzam et al. [37] and Uzam et al. [39], which is called an automation Petri net (APN). An APN is an octuple (P, T, F, In, En, X, Q, Mo), where P, T, F, and Mo are explained above. In is an inhibitor arc, graphically represented by an arc with a small circle (not an arrow). An inhibitor arc connects an input place p to a transition t, and the transition t is enabled if the input place p has tokens that are less than the inhibitor arc weight In(p, t). En is an enabling arc represented by an arc with an empty arrow. An enabling arc connects an input place p to a transition t. The transition t is enabled if the input place p has tokens whose number is at least equal to the enabling arc weight En(p, t). X = {xi, X2, .., Xm} is the set of firing conditions associated with the transitions, which can be known as external events - for example, sensor readings. Q = {qi, qj, .., qn} is the actions set, which can be allocated to the places. Q may represent more than one action in any place. In the APN, the movement of tokens between their places represents the behaviour of an APN, which is achieved via the firing of the transitions that are enabled.
3 THE PROPOSED METHODOLOGY
The proposed methodology is based on a deadlock-prevention method proposed by Ezpeleta et al. [6]. Figure 1 illustrates the steps of the proposed methodology, which are described as follows:
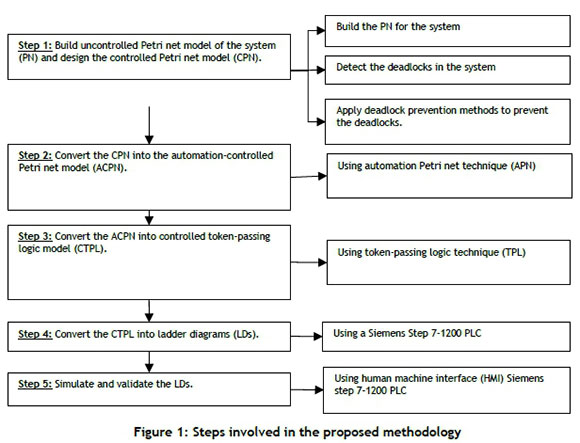
3.1 Step 1: Build the Petri net model of the uncontrolled system, and obtain the controlled Petri net model
In this step, a deadlock-prevention method based on strict minimal siphons (SMSs) is adopted to design a controlled Petri net model. This method is adopted from Ezpeleta et al. [6]. A siphon in a net N is defined as a set of places S = {pi, . . . , pk}. A substantial characteristic of a siphon is that, at a given marking, once a siphon is emptied it remains emptied at any subsequent marking reachable from the given marking.
Definition 1. Let N be a net. A place set S C P, S Φ 0, satisfying 'S C S', is said to be a siphon. When a siphon does not include other siphons, it is said to be a minimal siphon. A minimal siphon S is said to be strict if 'S ÇS '.
Siphons play an essential part in the Petri net liveness examination, particularly in an unweighted Petri net. When a siphon 5 at a marking in a Petri net is unmarked, there are no enabled transitions in 5', and all the transitions associated with 5 cannot be fired. Therefore, the transitions are in a deadlock state, leading to the absence of liveness in the system. In Ezpeleta et al. [6], a monitor or control place is added to each SMS to fulfill the liveness of a Petri net. The proposed policy is simple and guarantees success. However, it leads to a more complex Petri-net-controlled system than the original Petri net model, since the number of added control places is equal to that of the SMSs in the target Petri net model, and the added arcs are more than those of the added control places. The strict minimal siphon control based on the complementary set of a siphon is used to create the monitors. A complementary set [S] of a siphon S is the set of operation places that are the holders of the resources in S but that do not belong to S. Moreover, [S]u S is the P-invariant support that indicates the places of operations in [S] that will contend for the resources in S with the places of operations belonging to 5. S will be unmarked when all tokens in S flow into [S]. Before constructing the control algorithm, we state the following notations that will be used. S represents a strict minimal siphon that cannot include the place p semiflow support (i.e., siphons that can be unmarked). Assuming that S is a siphon, we have S = Sa u Sr, Sr = S Ո Pr, Sa =S \ Sr, where Sadenotes the places of operations and Sr denotes the places of resources. [S] indicates the following set of state places: [S]=(UreSRH(r))\SA, where H(r) = fp\p εPA,p e ||/r||+\{r}} indicates the P-invariant positive support I, Vi,je{1,2,...,n},i*j, Η(η)ՈΗ(η)=0. Assume that [S] is a set of complements of S: design and add a monitor for [S], and the initial marking of the monitor can be computed as Moa(VS) = Mo(S)-1. According to the strict minimal siphon concept, the developed deadlock prevention algorithm proposed by Ezpeleta et al. [6] is shown in Table 1.

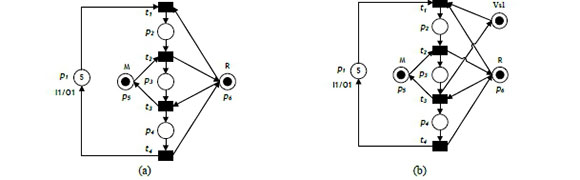
To demonstrate the above algorithm, consider the Petri net model illustrated in Figure 2(a). The model comprises of a single robot R, which holds a part at a time; one machine M, which processes a part at a time; one loading buffer and an unloading buffer (O1). One part type is processed in the manufacturing system (PA). The robot reaches the loading buffer, grips, and loads PA to the M. If M finishes its operation, the robot reaches the machine, grips, and unloads the part to the unloading buffer. The Petri net model comprises four transitions and six places. The places can be described as the following set partition: P0= {pi}, Pr = {p5, p6}, and Pa = {p2, p3, p4}, where P°, Pr , and Pa are the input, resources, and operation places respectively. The model has five reachable markings and four minimal siphons, one of which is a strict minimal siphon. Its augmented siphon is S = {p4, p5, pe}- Table 2 shows the required monitor using the adopted algorithm. Figure 2(b) displays the controlled Petri net model.

3.2 Step 2: Convert the controlled Petri net model (CPN) into the automation-controlled Petri net model (ACPN).
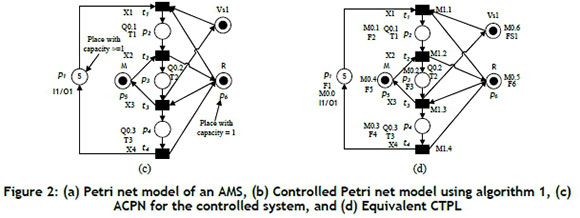
In this step, the automation-controlled Petri net model that proposed by Uzam et al. [37] and Jones et al. [38] is used to convert the CPN into ACPN to determine the firing conditions X, actions Q, and the capacity of the places. For example, consider the CPN model presented in Figure 2(b), where the firing conditions X1, X2, and X3 are assigned to tj, t2, and t3 respectively. Moreover, actions Q0.1, Q0.2, and Q0.3 are assigned to robot loading operation (P2), machine operation p), and robot unloading operation (p4) respectively. Time delays T1 (3 seconds), T2 (4 seconds), and T3 (3 seconds) are assigned to robot loading operation, machine operation, and robot unloading operation respectively. Finally, places pj, ps, pe, and Vs1 have 5, 1, 1, and 1 tokens capacities respectively. Figure 2(c) displays the automation-controlled Petri net model of this example.
3.3 Step 3: Convert the automation-controlled Petri net model (ACPN) into a controlled token-passing logic model (CTPL).
In this step, a token-passing logic technique that proposed by Jones et al. [38] is used to facilitate the direct transformation of an automation Petri net into a control logic, which can be achieved with a ladder diagram program. Each place in an ACPN corresponds to a place in a CTPL. The simulated movement of tokens at each place in the CTPL is accomplished by deploying memory words (16 bits) at each one; each place has at least a related memory word in TPL, where the capacity of each place is at least 1. If the stored value of a memory word of a place in the TPL is at least 1 and the firing condition X of a transition that related to that place becomes enabled, then the memory word at the input and output places might be respectively decreased and increased. Note that the flags can be used instead of memory bits Jones et al. [38]. Figure 2(d) illustrates the equivalent CTPL for the ACPN of the numerical example.
3.4 Step 4: Convert the CTPL model into ladder diagrams (LDs).
In this step, the conversion of the CTPL model to ladder diagrams is proposed in Uzam et al. [37]. The conversion is achieved by using a SIEMENS Step 7-1200 PLC. First, we have proposed a general methodology to carry out the conversion from a CTPL into LDs, which is shown by considering the following structures: initial markings (states), firing transition CTPL, CTPL without action, CTPL with action, CTPL with conflict, CTPL with inhibitor and enabling arcs, CTPL with weighted arc, and timed-place CTPL.
Initial markings (states): An initial marking describes the initial state of the manufacturing system resources, input buffers, and control places before starting, and needs to be inserted into the beginning of the LD to guarantee correct operation. To insert an initial marking into an LD at the first rungs of the LD, consider the CTPL model illustrated in Figure 3(a), where the firing conditions X1 and X2 are assigned to tj and t2 respectively. Moreover, flags F1 and F2 are assigned to resource operation (pj) and resource state (P2) respectively. F1 and F2 are denoted as coils where, if the token numbers in F1 and F2 are more than zero, the coils case is set (F1 and F2 =1); else the case is reset (F1 and F2 =0). When the firing conditions X1 or X2 fire, F2 will be decreased or increased by 1 token respectively. To convert this into LD, counter up and down is used to simulate the case of F2, where the present value of the counter is 1. When the firing conditions X1 and X2 are satisfied for t1 and t2, the counter value is decreased and increased by 1 respectively. Therefore, if the current counter value is more than or equal to the value at the PV, then a signal state '1' is assigned to F2; otherwise a signal state '0' is assigned to F2. Figure 3(b) illustrates the LD for the CTPL displayed in Figure 3(a).
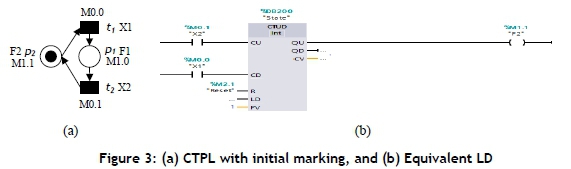
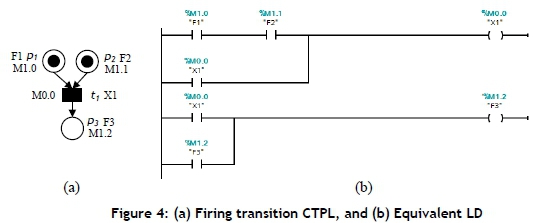
Firing transition CTPL: The transition indicates the start or end event of any operation. To represent transition events in LDs, consider the CTPL model shown in Figure 4(a), where flags F1 and F2 are assigned to pj and p2 respectively, and firing condition Xj is assigned to an immediate transition tj. When the firing condition Xj is satisfied (all the input places F1 and F2 have non-zero tokens), the transition is enabled to fire. To represent this via an LD, Xj is denoted as a coil, where, if F1 and F2 have a signal state '1' or Xj has a signal state '1', the coil case is set (Xj =1); otherwise the case is reset (Xj =0). Figure 4(b) shows the LD for the TPL value in Figure 4(a). The initial marking is not presented in the LD.
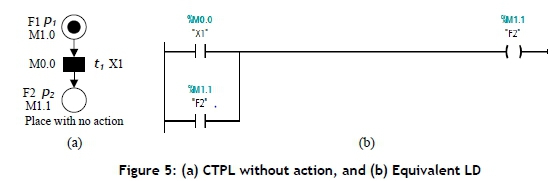
CTPL without Action: Consider the CTPL model shown in Figure 5(a). A place with no action is assigned to p2. To represent a place with no action in LD, p2 is represented as a flag F2 where, if the transition Xj fires, it withdraws a token from the input place F1 and deposits a token to the output place F2. F2 is denoted as coil if the number of tokens at F2 is at least 1, and the coil case is set (F2 =1); otherwise it is reset (F2 =0). To convert this into LDs, coil F2 has a signal state '1' if Xj has a signal state '1' or F2 has a signal state '1'; otherwise a signal state '0' is assigned to F2. Figure 5(b) shows the LD for the CTPL displayed in Figure 5(a). The initial marking is not presented in the LD.
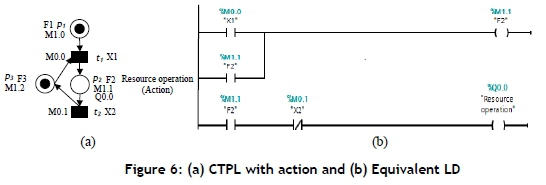
CTPL with Action: A CTPL is shown in Figure 6(a). An action Q0.0 is assigned to place p2. This action occurs only if the token number at p2 is at least 1. To represent an action in LDs, F2 is represented as a coil, where, if the transition Xj fires and transition X2 is not enabled to fire, the coil case is set (F2 =1); else it is reset (F2 =0). The action of resource operation is represented as a coil, where, if the memory state of F2 has a signal state '1', the action case is set; if the signal state is '0' at F2, the action is reset. Figure 6(b) displays the LD for the CTPL illustrated in Figure 6(a). The initial marking is not presented in the LD.
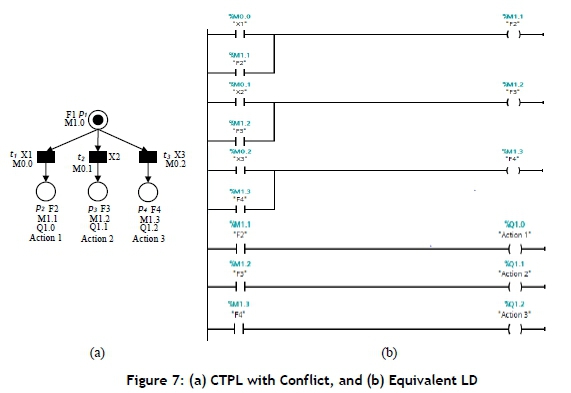
CTPL with Conflict: Conflict occurs in a Petri net when there is an input place that has more than one output transition. To resolve the conflict case, a priority is assigned to each of the transitions by selecting which transition is to be permitted to fire; this selection often depends on a priority scheme. Consider the CTPL model shown in Figure 7(a). If there is one token in place pj and firing conditions Xj, X2, and X3 appear simultaneously, the conflict can be found. In LDs, the conflict can be resolved by deciding the order of priorities for the conflicting transitions, where the PLC automatically scans from left to right, top to bottom; the output place that is mentioned will fire first, followed by others. Thus it can be seen from Figure 7(b) that transition tj of TPL has priority over transitions t2 and t3, and transition t2 has priority over transition t3. Figure 7(b) shows the LD for the CTPL shown in Figure 7(a). The initial marking is not presented in the LD.
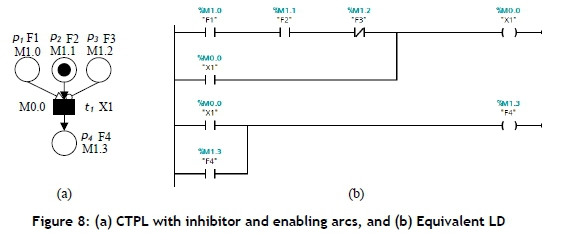
CTPL with inhibitor and enabling arcs: In Figure 8(a), the inhibitor and enabling arcs in a CTPL are illustrated. The places p1, p2, and p3 are connected to a transition t1, where p1 has an enabling arc En (p2, t1), and p3has an inhibitor arc In (p2, t1). Places p1, p2, p3, and p4are represented as flags F1, F2, F3, and F4 respectively. The transition t1 (X1) can be fired when the token number in each of the input places p1 and p2 is at least 1 and p3 has no token. Thus the firing condition X1 appears. If a transition t1 fires, i t withdraws a token from p2 and stores a token in output place p4. Note that the markings of places p1 and p3 do not change. To convert this into LD, F1, F2, and F3 are denoted as coils; if F1 and F2 have at least 1 token, the coils case is set (F1 and F2 =1); otherwise it is reset (F1 and F2 =0). Moreover, if F3 has no token, the coil case is set (F3 =1); otherwise it is reset (F3 =0). The coil F4 has a signal state '1' if X1 has a signal state '1' or F4 has a signal state '1'; otherwise a signal state '0' is assigned to F4. Figure 8(b) shows the LD for the CTPL shown in Figure 8(a). Note that the initial state is not presented in the LD.
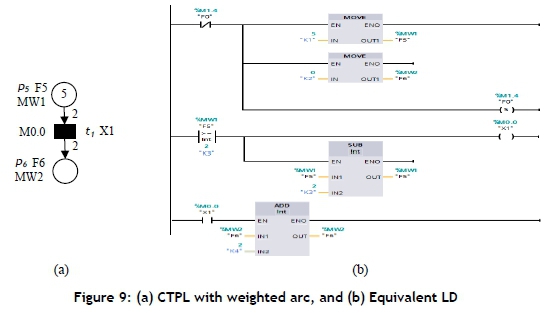
CTPL with a weighted arc: The CTPL with a weighted arc is displayed in Figure 9(a). The transition t1 is fired if the token number at the input place p1 is more than or equal to the arc weight 2 and the firing condition X1 appears. If a transition t1 fires, it withdraws two tokens from p1 and deposits two tokens in output place p2. Flags F5 and F6 are assigned to p1 and p2 respectively. Firing condition X1 is assigned to an immediate transition t1. To convert the CTPL into an LD, if a transition t1 is fired, it will withdraw two tokens from F1 and place two tokens in the F2. This can be achieved by reducing the value of F5 by 2, using a subtraction instruction (SUB) and increasing the value of F6 by 2, using an addition instruction (ADD). Figure 9(b) shows the LD for the CTPL displayed in Figure 9(a). The initial marking is considered in the LD.
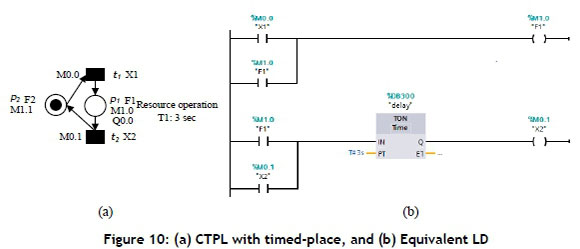
Timed-place CTPL: In Figure 10(a), the timed-place CTPL is illustrated. The places p1 and p2 are denoted as the operation and state of resources respectively. Places p1 and p2 are represented as flags F1 and F2 respectively. The resource operation takes 3 seconds to complete. If this time has elapsed, effectively the transition t2 will be fired. To convert the CTPL into LD, an ON-delay timer is used to represent the time delay for transition t2 to be fired. If the flag F1 is set, action Q0.0 is activated, and it will take 3 seconds to complete. If the time has elapsed, effectively transition t2 is fired; thus F1 is reset and action Q0.0 is deactivated. Figure 10(b) shows the LD for the CTPL displayed in Figure 10(a). The initial state is not presented in the LD.
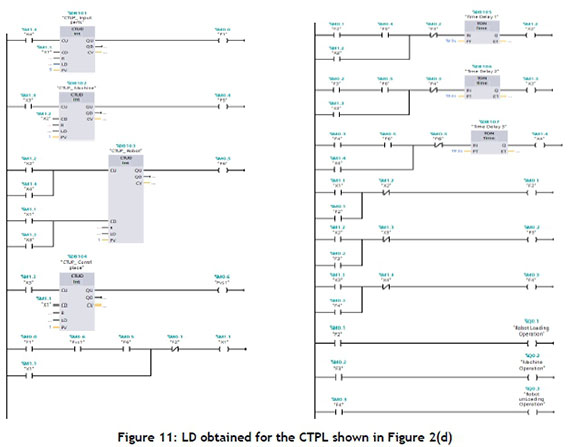
Based on the above conversions, the LD obtained for the CTPL, shown in Figure 2(d), is given in Figure 11. The LD can be described as follows. Rungs 1 to 4 indicate the set and reset of the input buffer, resources available states, and control place, which are F1, F5, F6, and FS1 respectively. Moreover, rungs 5 to 8 represent the enabling rules and firing conditions of transitions and time delays of resource operations (X1, X2, X3, X4) respectively. Similarly, rungs 9 to 11 represent the memory states of resource operations (F2, F3, F4) respectively. Finally, rungs 12 to 14 denote the actions of resources (F2, F3, F4) respectively.
4 MANUFACTURING SYSTEM CASE STUDY
4.1 Description of the system and Petri net model
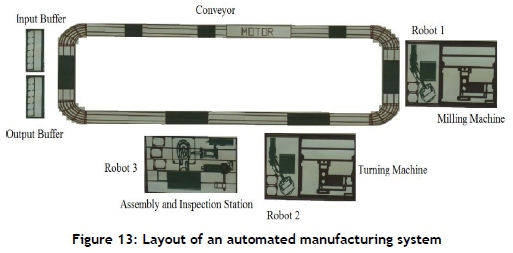
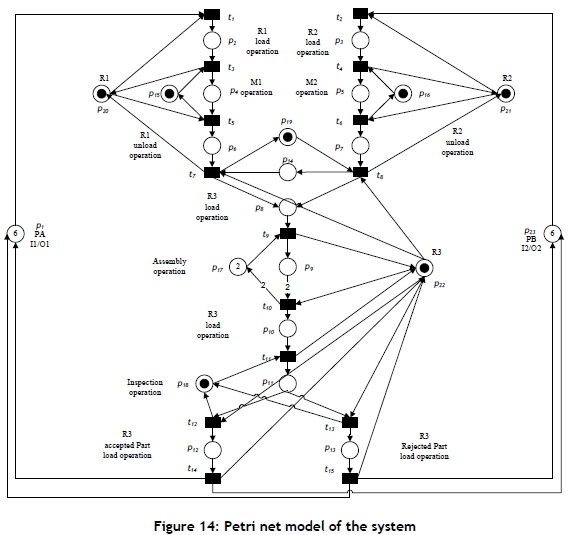
The AMS used in this case paper is illustrated in Figure 12. The scheme of the system is shown in Figure 13. This system is located in King Saud University (Computer Integrated Manufacturing [CIM] lab). There are machining stations M1 (milling machine) and M2 (turning machine), assembly and inspection stations, input and output buffer, conveyor for transporting the parts among machines and stations, and three robots R1-R3. Each machine (robot) processes (holds) one part at the same time. Two part types A and B are produced in the system under consideration. Both parts A and B have similar routing (M1 then M2) and are subsequently assembled in an assembly station; the assembled part is inspected at an inspection station; and then the final product leaves the manufacturing cell. In this case study, robots work in a mutually exclusive manner: R1 loads/unloads part A on M1 from the conveyor, R2 loads/unloads part B into M2 from the conveyor, and R3 loads/unloads parts A and B onto the assembly and inspection stations from the conveyor. The Petri net model is illustrated in Figure 14. The properties of the developed Petri net models are obtained using an integrated net analyser (INA). It has been found that the system is not live (deadlock).

4.2 Controlled system for case study
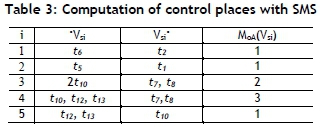
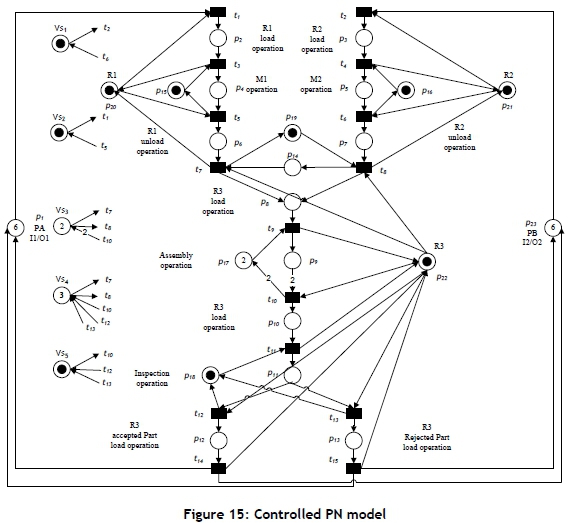
The suggested deadlock-prevention algorithm was applied to this case study. The system model has five strict minimal siphons that can be empty, which are S1={p7,p16,p21}, S2={p6,p15,p20}, Ss={Pio,P12,P13'Pi7'P22}' s4={Pi2,P13,P17,P1ß,P22}, and S5={p8,p12,p13,p18,P22}- Each siphon requires a control place to make the siphon controlled. Table 3 displays the required control places using the algorithm from Ezpeleta et al. [6]. Figure 15 shows the controlled Petri net model after addition of the control places.
4.3 APN model for the controlled system
The obtained controlled system lacks identification and recognition of the two part types at the milling machine, turning machine, and assembly station. To solve this problem, four sensors are added to the conveyor. Sensor 1 (a proximity sensor) and sensor 2 (an infrared reflective sensor) are added to recognise parts A and B in the milling and turning machines respectively. After machining the two parts, they can be recognised at the assembly station. Therefore, sensor 3 (a proximity sensor) and sensor 4 (an infrared reflective sensor) are added to detect parts A and B respectively in the assembly station. An APN model designed for the controlled system using the algorithm from Ezpeleta et al. [6] is shown in Figure 16. In the APN model, there are 34 places (Vs1, Vs2, -, Vs5, pi, p3, P29) and 17 transitions (X1, X2, X17). The model consists of eight resources: the conveyor, robot 1, robot 2, milling machine, turning machine, robot 3, assembly station, and inspection station. Initially, the conveyor is off, and the remaining resources are idle. In the conveyor, places p28 and p29 represent the conveyor off and on states respectively. In robot 1, places p2, pe, and p20 describe the loading operation, unloading operation, and idle/busy states of robot 1 respectively. A time delay of 3 s is assigned to each operation that is required for the robot 1 operations. In robot 2, places p3, p7, and p2j represent the loading operation, unloading operation, and idle/busy states of robot 1 respectively. A time delay of 3 s is assigned to each operation that is required for the robot 2 operations. In robot 3, places p8«, p10, p12, p13, and p22 represent the loading operation, unloading operation, unloading operation, unloading operation, and idle/busy states of robot 3 respectively. A time delay of 3 s is assigned to each operation that is required for the robot 3 operations. Further, in the milling machine, places p4 and p15 denote the milling operation and idle/busy states of the milling machine respectively. A time delay of 4 s is assigned to each operation that is required for the milling operations. The same situation for the turning machine, assembly, and inspection stations: places p5, p9, and p11 represent the operations and places p16, p17, and p18 denote the idle/busy states respectively. Times delays of 5 s, 6 s, and 4 s respectively are assigned to each operation that is required for the operations. Places p14, p19, p24, and p25 are used to represent the sensors 3, 4, 1, and 2 respectively. Place p1 denotes part A and part B on the conveyor coming toward the milling and turning operations, while places p26and p27denote an accepted assembled part and rejected assembled part respectively. Places p28 and P29 describe the off and on states of the conveyor motor respectively. Finally, places Vs1, Vs2, Vs3, Vs4, and Vs5 are used to represent the obtained controllers. The transitions are characterised as follows: If there is a part A at the milling area and sensor 1 detects it (with I0.0), and Vs2 has one token, then R1 is starting (X1) to pick it up and is trying to upload M1. When the loading time has elapsed, M1 begins to mill part A (X3). When the milling time has ended, R1 begins to unload part A from M1 to the conveyor (X5). If there is a part B at the turning area and sensor 2 detects it (with I0.1), and Vs1 has one token, then R2 is starting (X2) to pick it up and is trying to upload M2. When the loading time has elapsed, M2 begins to turn part B (X4). When the turning time has elapsed, R2 begins to unload part B from M2 to conveyor (X6). If there are parts A and part B at the assembly area, sensor 3 detects part A (with I0.2), sensor 4 detects part B (with I0.3), and Vs3 and Vs4 have more than one token; then R3 is starting to pick up two parts A (X7) and B (X8) and is trying to upload the assembly station. When the loading time has elapsed for each part, M2 begins to assemble two parts (X9). When the assembly time has elapsed, R3 begins to unload an assembled part from the assembly station to the inspection station (X10). When the unload time has elapsed, the inspection station begins to check an assembled part (X11). If an assembled part is accepted, R3 begins to unload an accepted part from the inspection station to an accepted sink (X12). Otherwise, R3 begins to unload a rejected part from the inspection station to a rejected sink (X13).
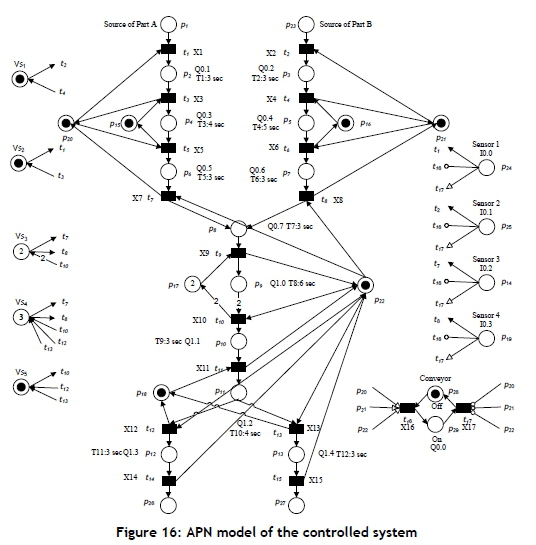
Spec. 1. The motor of the conveyor is switched on through transition t16, and appears if there are no parts A and B on the milling, turning, or assembly areas and R1, R2, or R3 are empty. This is realised by adding inhibitor arcs from places P24, P25, P14, and P19 to transitions t16, In (p24, t16) = 1, In (P25, t16) = 1, In (pu, t16) = 1, and In (P19, t16) = 1 respectively. Moreover, by adding enabling arcs from places P20, P21, and P22 to transitions t16, En (P20, t16) = 1, En (P21, t16) = 1, and En (P22, t16) = 1 respectively, the operation of the conveyor is achieved with one token in place P29, and is realised by an action Q0.0. The motor of the conveyor is switched off through transition t17, and appears when there are parts A and B on the milling, turning, or assembly areas and R1, R2, or R3 are empty.
This is realised by adding enabling arcs from places p24, p25, p14, and pi9to transitions t16, En (p24, t16) = i, En (p25, t16) = i, En (p14, t16) = 1, and En (p19, t16u) = i respectively. Moreover, inhibitor arcs are added from places p20, p2i, and p22to transitions tie, In (p20, t16) = i, In (p2i, t16) = i, and In (p22, tie) = i respectively.
Spec. 2. R1 (loading operation) is switched on through transition ti if there is a part A in the M1 area - i.e., M (p24) = 1, R1 is idle - i.e., M (p20) = i, Vs2 has one token - i.e., M (Vs2) = i, and there is no operation in M1 - i.e. M (p4) = 0. R1 (Loading operation) is achieved with one token in place p2, and is realised by a level action (Q0.1). R1 (Loading operation) is switched off through transition t3, and appears when the presence of part A in the M1 machine is detected. When the loading time in R1 has elapsed, the M1 operation is switched on through transition t3, and appears when M1 is idle - i.e., M (pis) = i; the M1 operation is achieved with a token in place p4, and is realised by a level action (Q0.3). R1 (unloading operation) is switched on through transition ts if the M1 operation time has elapsed and R1 is idle - i.e., M (p20) = 1. R1 (unloading operation) is achieved with a token in place p6, and is realised by a level action (Q0.5). R1 (unloading operation) is switched off when the unloading time has elapsed.
Spec. 3. R2 (loading operation) is switched on through transition t2 if there is a part B in the M2 area - i.e., M (p25) = 1, R2 is idle - i.e., M (p21) = i, Vs1 has one token - i.e., M (Vs1) = i, and no operation in M2 - i.e., M (ps) = 0. R2 (Loading operation) is achieved with a token in place p3, and is realised by a level action (Q0.2). R1 (Loading operation) is switched off through transition t4, and appears when the presence of part B in the M2 machine is detected. When the loading time in R2 has elapsed, the M2 operation is switched on through transition t4, and appears when M2 is idle - i.e., M (pie) = i; the M2 operation is achieved with a token in place p5, and is realised by a level action (Q0.4). R2 (unloading operation) is switched on through transition te if the M2 operation time has elapsed and R2 is idle - i.e., M (p21) = 1. R1 (unloading operation) is achieved with a token in place p7, and is realised by a level action (Q0.6). R2 (unloading operation) is switched off when the unloading time has elapsed.
Spec. 4. R3 (loading operation) is switched on through transitions t7 or tg, and appears if R3 is idle - i.e., M(p22) = i, Vs3 and VS4have more than one token - i.e., M(Vs3) > 1 and M(Vsa) s 1 respectively, no assembly operation - i.e., M(pg) = 0, and there is a part A or a part B in the assembly area - i.e., M(p14) = i or M(p19) = i respectively. R3 (loading operation) is achieved with a token in place pg, and is realised by a level action (Q0.7). R3 (loading operation) is switched off through transition tg, and occurs when the presence of parts A and B in the assembly station is detected. If the R3 loading time has then elapsed and the assembly station is idle - i.e., M (p17) = i, the assembly operation is switched on through transition t9. Therefore, the assembly operation is achieved with a token in place p9, and is realised by a level action (Q1.0). The assembly operation is switched off through transition t10, and appears when the assembly time has elapsed. R3 (unloading operation) is switched on through transition t10, and appears when the assembly operation time has elapsed and R3 is idle - i.e., M (p22) = i. R3 (unloading operation) is achieved with a token in place p10, and is realised by a level action (Q1.1). R3 (unloading operation) is switched off through transition t11, when the unloading time has elapsed.
Spec. 5. The inspection operation is switched on through transition tii, and appears when the inspection station is idle - i.e., M (p18) = i. The inspection operation is achieved with a token in place p11, and is realised by a level action (Q1.2). The inspection operation is switched off through transition t12 (accepted assembled part) or t13 (rejected assembled part), and appears when the inspection time has elapsed.
Spec. 6. R3 (unloading operation) is switched on through transition t12 (accepted assembled part) or t13 (rejected assembled part), and appears when there is an assembled part in the inspection station, and R3 is idle - i.e., M (p22) = 1. R3 (unloading operation) is achieved with a token in place p12 or p13, and is realised by a level action Q1.3 or Q1.4 respectively. R3 (loading operation) is switched off through transitions t14 or t15, and appears when the unloading time has elapsed.
Spec. 7. To record the number of accepted and rejected assembled parts, places p26 and p27 are used respectively. When transitions t14 and t15 fire, the token number in these places is increased. Thus the token numbers in these places denote the number of accepted and rejected assembled parts respectively in the manufacturing system.
4.4 TPL for the APN Model
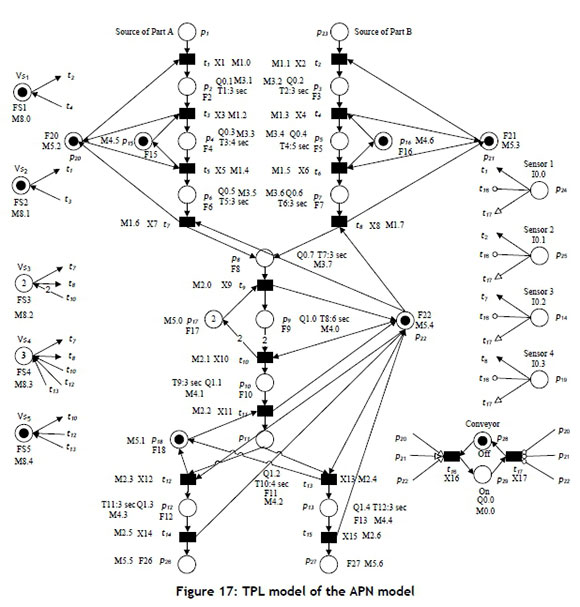
The TPL methodology introduced in section 3 is used to convert the APN model into an LD for implementation on a PLC. Specifically, an APN model can be converted into TPL by assigning memory bits (Mx.x) to places and transitions. An ON-delay timer is associated with timed places to realise the timing requirements. Moreover, output bits (Qx.x) are assigned to the operation places to describe actions at places. Sensor readings are represented by input registers (Ix.x). A designed TPL model for the APN model using Algorithm 1 is illustrated in Figure 17. In the TPL model, flags (FS1, FS2, FS5, F2, F3,..., F29) are assigned to the places (VSi, VS2, .., VS5, pi, p3, .., P29) respectively. Moreover, memory bits (M8.0, M8.1, M8.4, M3.1, M3.2, M3.7, M4.0, M4.1, M4.4, M4.5, M4.6, M5.0, M5.1, M5.2, M5.3, M5.4, M5.5, M5.6) are assigned to the places (Vs1, Vs2, -, Vs5, pi, p3, .··, Ps, p9, p10, .., P13, p15, p16, p17, p18, p20, p21, p22, p26, p27) respectively. Likewise, memory bits (M1.0, M1.1, M1.7, M2.0, M2.1, M2.6,) are assigned to the firing conditions (X1, X2, X8, X9, X10, -, X15) respectively. Input registers (I0.0, I0.1, I0.3, I0.4) are assigned to the sensor places (p24, p25, pi4, pi9) respectively. Finally, output bits (Q0.0, Q0.1, Q0.2, ... Q0.7, Q1.0, Q1.1, Q1.4) are assigned to the places (p29, p2, p3, -, ps, p9, p10, -, p13) respectively.
4.5 LD for the TPL Model
The TPL model using Algorithm 1 is converted directly into the LD code for implementation. The obtained LD code, as shown in Figure 18, is constructed as follows: rungs 1 to 12 indicate the set and reset of control places and resources available states, which are FS1, FS2, FS3, FS4, FS5, M1, M2, assembly station, inspection station, R1, R2, and R3 respectively. Moreover, rungs 12 to 26 represent the firing conditions and time delays of resource operations (Xi, X2, .., X«) respectively. Similarly, rungs 27 to 38 represent the memory states of resource operations (F2, F3, -, F13) respectively. Rungs 39 and 40 imply memory states of accepted assembled parts and rejected assembled parts respectively. Rungs 41 and 42 represent memory states of switches start and end respectively, which are used in the validation LD step for starting and stopping the system during the simulation. To display whether the output of the inspection station is accepting or rejecting the assembled part, rungs 43 and 44 represent memory states of the accepted and rejected assembled parts via the inspection station respectively. A problem that may occur in the system model is that the assembled part may comprise the same two parts (two part As or two part Bs). To avoid this problem, rungs 45 to 48 are designed. For recording the number of accepted assembled parts and rejected assembled parts in the collection sinks, rungs 49 and 50 respectively are used. When the system is switched on, all resources are idle, and all sensors have value 0; the conveyor motor (action Q0.0) must be in operation and can be realised by rungs 51 and 52. Finally, rungs 53 to 64 represent the actions of resource operations (F2, F3, -, F13) respectively.
4.6 Validation of LD
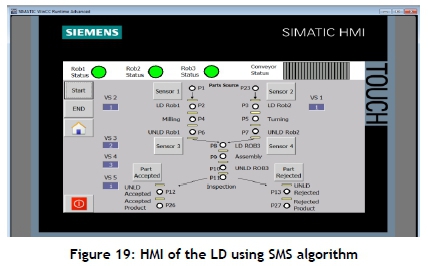
Validation of the obtained LD is carried out to test the applicability, drawbacks, and strengths of the suggested deadlock-control method. A human-machine interface (HMI) is used to introduce a visual representation of a control system and provide real-time data acquisition on its LCD screen. A combination HMI-PLC plays a significant role in the design of a truly lean automation solution, providing many benefits throughout the life cycle of machine automation. To validate the suggested LD using HMI, other components that are pivotal to the operation of a manufacturing control system are considered, in addition to the on/off buttons and various input/output sensors that monitor the arrived parts. Subsequently, a decision is taken about the PLC that will get the data from the input/output sensors and convert the data into logical combinations. Programming of the HMI includes assigning tags to screen elements. A tag is a connection or link between an address in the PLC and a screen element of the HMI. Figure 19 shows the HMI window that is designed for the selected system to validate the obtained LD, as illustrated in Figure 18. Controller simulation is carried out to check the response between the LD and the HMI programs. The simulation results show that the suggested AMS controller is applicable and correct. In addition, the HMI program is proportionate with a real-time view of the system model, locates faults rapidly, and enables the reduction in the troubleshooting time for faults.
5 CONCLUSIONS
The paper presents a methodology based on Petri nets, including deadlock-prevention methods and converting the methods into PLC codes (ladder diagrams). A real-time application of AMS is used to demonstrate the proposed methodology, which can be implemented in a wide range of discrete event manufacturing systems. Moreover, the proposed methodology is appropriate for multiproduct manufacturing systems, and provides an effective PLC implementation. In addition to model and control an AMS using multi-step look-ahead control policies Gu et al. [41] and state-tree structure Gu et al. [42], the research could be extended in several ways:
1. In this paper, it is assumed that the machines, robots, motors, actuators, and sensors are working without failures. Unreliable resources or fault occurrences are common in real-world systems. Therefore, the extension of this research could involve fault tolerance and a supervisor under dynamic control specifications of the system design.
2. Most of the developed deadlock-control methods have been designed for pure Petri nets (not involving self-loops, inhibitor arcs, or enabling arcs) and might not lead to optimally controlled systems. Nevertheless, deadlock-control methods with non-pure Petri nets might exist that might lead to optimally controlled systems. However, mathematically representing a non-pure Petri net is difficult, and requires significant research effort.
ACKNOWLEDGMENT
The authors would like to thank Deanship of scientific research for funding and supporting this research through the initiative of DSR Graduate Students Research Support (GSR), King Saud University.
REFERENCES
[1] Li, Z., Zhou, M. and Wu, N. 2008. A survey and comparison of Petri net-based deadlock prevention policies for flexible manufacturing systems. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 38(2), pp. 173-188. [ Links ]
[2] Li, Z., Wu, N. and Zhou, M. 2012. Deadlock control of automated manufacturing systems based on Petri nets - A literature review. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 42(4), pp. 437-462. [ Links ]
[3] El-Tamimi, M., Nasr, E.A., Al-Ahmari, A., Kaid, H. and Li, Z. 2015. Evaluation of Deadlock Control Designs in Automated Manufacturing Systems, International Conference on Industrial Engineering and Operations Management, [ Links ]
[4] Chen, Y., Li, Z., Barkaoui, K. and Giua, A. 2015. On the enforcement of a class of nonlinear constraints on Petri nets. Automatica, 55, pp. 116-124. [ Links ]
[5] Chen, Y., Li, Z., Khalgui, M. and Mosbahi, O. 2011. Design of a maximally permissive liveness-enforcing Petri net supervisor for flexible manufacturing systems. IEEE Transactions on Automation Science and Engineering, 8(2), pp. 374-393. [ Links ]
[6] Ezpeleta, J., Colom, J.M. and Martinez, J. 1995. A Petri net based deadlock prevention policy for flexible manufacturing systems. IEEE Transactions on Robotics and Automation, 11(2), pp. 173-184. [ Links ]
[7] Huang, Y., Jeng, M., Xie, X., and Chung, S. 2001. A deadlock prevention policy for flexible manufacturing systems using siphons, IEEE International Conference on Robotics and Automation. Proceedings 2001 ICRA, 1, pp. 541-546. [ Links ]
[8] Uzam, M. and Zhou, M. 2004. Iterative synthesis of Petri net based deadlock prevention policy for flexible manufacturing systems, IEEE International Conference on Systems, Man and Cybernetics, 5, pp. 4260-4265. [ Links ]
[9] Li, Z. and Zhou, M. 2004. Elementary siphons of Petri nets and their application to deadlock prevention in flexible manufacturing systems. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 34(1), pp. 38-51. [ Links ]
[10] Huang, Y., Jeng, M., Xie, X., and Chung, D. 2006. Siphon-based deadlock prevention policy for flexible manufacturing systems, IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 36(6), pp. 1248-1256. [ Links ]
[11] Uzam, M. and Zhou, M. 2007. An iterative synthesis approach to Petri net-based deadlock prevention policy for flexible manufacturing systems, IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 37(3), pp. 362-371. [ Links ]
[12] Li, Z. W., Hu, H. S., and Wang, A. R. 2007. Design of liveness-enforcing supervisors for flexible manufacturing systems using Petri nets, IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 37(4), pp. 517-526. [ Links ]
[13] Huang, Y. 2007. Design of deadlock prevention supervisors using Petri nets, The International Journal of Advanced Manufacturing Technology, 35(3-4), pp. 349-362. [ Links ]
[14] Li, Z., Zhou, M., and Jeng, M. 2008. A maximally permissive deadlock prevention policy for FMS based on Petri net siphon control and the theory of regions, IEEE Transactions on Automation Science and Engineering, 5(1), pp. 182-188. [ Links ]
[15] Li, Z. and Zhou, M. 2008. Control of elementary and dependent siphons in Petri nets and their application, IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 38(1), pp. 133-148. [ Links ]
[16] Chao, D.Y. 2010. Fewer monitors and more efficient controllability for deadlock control in S3PGR2 (systems of simple sequential processes with general resource requirements), The Computer Journal, 53(10), pp. 1783-1798. [ Links ]
[17] Chen, Y. and Li, Z. 2011. Design of a maximally permissive liveness-enforcing supervisor with a compressed supervisory structure for flexible manufacturing systems, Automatica, 47(5), pp. 1028-1034. [ Links ]
[18] Li, S.Y., Li, Z.W., and Hu, H.S. 2011. Siphon extraction for deadlock control in flexible manufacturing systems by using Petri nets, International Journal of Computer Integrated Manufacturing, 24(8), pp. 710725. [ Links ]
[19] Chen, Y., Li, Z., and Barkaoui, K. 2014. Maximally permissive liveness-enforcing supervisor with lowest implementation cost for flexible manufacturing systems, Information Sciences, 256, pp. 74-90. [ Links ]
[20] Chen, Y., Li, Z., and Zhou, M. 2014. Optimal supervisory control of flexible manufacturing systems by Petri nets: A set classification approach, IEEE Transactions on Automation Science and Engineering, 11(2), pp. 549-563. [ Links ]
[21] Qin, M., Li, Z., and Al-Ahmari, A. M. 2015. Elementary siphon based control policy for flexible manufacturing systems with partial observability and controllability of transitions, Asian Journal of Control, 17(1), pp. 327-342. [ Links ]
[22] Li, Z., Liu, G., Hanisch, H.-M., and Zhou, M. 2012. Deadlock prevention based on structure reuse of Petri net supervisors for flexible manufacturing systems, IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 42(1), pp. 178-191. [ Links ]
[23] Li, Z. and Zhao, M. 2008. On controllability of dependent siphons for deadlock prevention in generalized Petri nets, IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 38(2), pp. 369-384. [ Links ]
[24] Chen, Y., Li, Z., Barkaoui, K., and Uzam, M. 2014. New Petri net structure and its application to optimal supervisory control: Interval inhibitor arcs, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 44(10), pp. 1384-1400. [ Links ]
[25] Uzam, M., Li, Z., Gelen, G., and Zakariyya, R. S. 2016. A divide-and-conquer-method for the synthesis of liveness enforcing supervisors for flexible manufacturing systems, Journal of Intelligent Manufacturing, 27(5), pp. 1111-1129. [ Links ]
[26] Chao, D. Y. 2009. Direct minimal empty siphon computation using MIP, The International Journal of Advanced Manufacturing Technology, 45(3-4), pp. 397-405. [ Links ]
[27] Chao, D. Y. 2011. Improvement of sub-optimal siphon- and FBM-based control model of a well-known S3PR, IEEE Transactions on Automation Science and Engineering, 8(2), pp. 404-411. [ Links ]
[28] Ghaffari, A., Rezg, N., and Xie, X. 2003. Design of a live and maximally permissive Petri net controller using the theory of regions, IEEE Transactions on Robotics and Automation, 19(1), pp. 137-141. [ Links ]
[29] Uzam, M. 2004. The use of the Petri net reduction approach for an optimal deadlock prevention policy for flexible manufacturing systems, The International Journal of Advanced Manufacturing Technology, 23(3-4), pp. 204-219. [ Links ]
[30] Nasr, E. A., El-Tamimi, A. M., Al-Ahmari, A., and Kaid, H. 2015. Comparison and evaluation of deadlock prevention methods for different size automated manufacturing systems, Mathematical Problems in Engineering, 501, pp. 1-19. [ Links ]
[31] Lautenbach, K. 1987. Linear algebraic calculation of deadlocks and traps, in Concurrency and nets, first ed. US: Springer, pp. 315-336. [ Links ]
[32] Venkatesh, K., Zhou, M., and Caudill, R. J. 1994. Comparing ladder logic diagrams and Petri nets for sequence controller design through a discrete manufacturing system, IEEE Transactions on Industrial Electronics, 41(6), pp. 611-619. [ Links ]
[33] Venkatesh, K., Zhou, M., and Caudill, R. 1994. Evaluating the complexity of Petri nets and ladder logic diagrams for sequence controllers design in flexible automation, IEEE Symposium on Emerging Technologies and Factory Automation, pp. 428-435. [ Links ]
[34] Satoh, T., Oshima, H., Nose, K., and Kumswai, S. 1992. Automatic generation system of ladder list program by Petri net, IEEE International Workshop on Emerging Technologies and Factory Automation, pp. 128-133. [ Links ]
[35] Jafari, M. A. and Boucher, T. O. 1994. A rule-based system for generating a ladder logic control program from a high-level systems model, Journal of Intelligent Manufacturing, 5(2), pp. 103-120. [ Links ]
[36] Burns, G. L. and Bidanda, B. 1994. The use of hierarchical Petri nets for the automatic generation of ladder logic programs, Proc. of ESD IPC, 94, pp. 169-179. [ Links ]
[37] Uzam, M. and Jones, A. 1998. Discrete event control system design using automation Petri nets and their ladder diagram implementation, The International Journal of Advanced Manufacturing Technology, 14(10), pp. 716-728. [ Links ]
[38] Jones, A., Uzam, M., and Ajlouni, N. 1996. Design of discrete event control systems for programmable logic controllers using T-timed Petri nets, Proceedings of the 1996 IEEE International Symposium on Computer-Aided Control System Design, pp. 212-217. [ Links ]
[39] Uzam, M., Jones, A., and Ajlouni, N. 1996. Conversion of Petri net controllers for manufacturing systems into ladder logic diagrams, Proceedings of the 1996 IEEE International Symposium on Emerging Technologies and Factory Automation, 2, pp. 649-655. [ Links ]
[40] Uzam, M. and Jones, A. 1996. Towards a unified methodology for converting coloured Petri net controllers into ladder logic using TPLL: Part I - Methodology. Proceedings of International Workshop on Discrete Event Systems, Edinburgh, UK, pp. 178-183. [ Links ]
[41] Gu, C., Li, Z. W., Wu, N. Q., Khalgui, M., Qu, T., and Al-Ahmari A. 2018 Improved multi-step look-ahead control policies for automated manufacturing systems. IEEE Access, 6(1), pp. 68824-68838. [ Links ]
[42] Gu, C., Wang, X., and Li, Z. W. 2019. Synthesis of supervisory control with partial observation on normal state tree structures. IEEE Transactions on Automation Science and Engineering, 16(2), pp. 984-997. [ Links ]
Submitted by authors 5 Oct 2017
Accepted for publication 28 Jan 2019
Available online 29 May 2019
* Corresponding author. yemenhussam@yahoo.com