GENERAL ARTICLES

 

Improving the operations performance of a chemotherapy clinic: A two-phase approach

 

 

A.A. Alabdulkarim^*

Mechanical and Industrial Engineering Dept., Majmaah University, Saudi Arabia

 

 

---

ABSTRACT

The increasing number of cancer patients, coupled with the development and use of new, efficient medications, has increased the demand for cancer service care. Outpatient chemotherapy clinics (OCCs) are complex facilities, due to the large variability in treatment durations resulting from different cancer types and chemotherapy protocols under limited resources. In this paper we address the operations planning problem encountered by OCCs, of optimally assigning the first days of treatment for a set of new patients in tandem with the presence of existing patients. We propose a two-phase approach to optimise the start days of a set of new patients. In the first stage, a system dynamics (SD) simulation model, adapted from the literature, is used to find the critical days for the new patients - i.e., the upper bounds by which patients must begin treatment. The optimal start days are then determined using a new mixed-integer programming (MIP) model. The results show that the optimal start days can be effectively prioritised and evaluated using simulation and mathematical programming.

---

OPSOMMING

Die toenemende aantal kankerpasiënte, gepaardgaande met die ontwikkeling en gebruik van nuwe, doeltreffende medisyne, het die vraag vir kankerversorging verhoog. Buitepasiënt chemoterapie-klinieke is ingewikkelde fasiliteite as gevolg van die wye verskeidenheid van kanker tipes en behandelingsprotokolle wat onderhewig is aan beperkte hulpbronne. Hierdie artikel adresseer die bedryfsbeplanningprobleem wat deur hierdie klinieke ervaar word. Hierdie probleem sluit in die optimale toedienning van die aanvanklike behandeling aan nuwe pasiënte in tandem met die teenwoordigheid van bestaande pasiënte. 'n Tweeledige benadering is voorgestel om die begindae van 'n groep nuwe pasiënte se behandeling te optimiseer. In die eerste stadium word 'n sisteemdinamika simulasiemodel, wat uit bestaande literatuur aangepas is, gebruik om die kritiese dae vir die nuwe pasiënte te bepaal, met ander woorde die laaste geleentheid wanneer 'n nuwe pasiënt met behandeling moet begin. Die optimale begindae word dan bepaal met 'n gemengde heelgetalprogrammeringsmodel. Die resultate toon dat die optimale begindae effektief geprioritiseer en evalueer kan word deur middel van simulasie en wiskundige programmering.

---

 

 

1 INTRODUCTION

Cancer is one of the leading causes of morbidity and mortality worldwide [1]. In 2012, the number of new cases reported was 14.1 million; and this figure is expected to reach 24 million in 2035 [2]. In the United States (US), for example, about 1.7 million cancer incidences were diagnosed in 2014, and cancer accounts for almost one of every four deaths [3]. Consequently, the demand for oncology services has been rising; again, in the US, the demand for oncology services is projected to increase by 45 per cent by 2030 [4]. On the positive side of the ledger, the number of cancer survivors has been increasing, along with the patients' life expectancies. In particular, in 2014 there were 14.5 million cancer survivors, compared with just three million in 1971 [2]. Therefore, many countries dedicate significant budgets to treat cancer and face its burden on their economies. In 2010, cancer cost the US about $290 billion; this number is expected to reach $458 billion in 2030 [2].

Cancer is usually treated using surgery, radiotherapy, chemotherapy, hormonal therapy, immunotherapy, and/or other methods. This paper addresses chemotherapy, since it is one of the most widely used and most effective treatment methods. The overall aim of chemotherapy is to eliminate cancerous cells under patient-driven constraints, such as the drug concentration and toxicity currently in the patient's body. This aim is achieved by infusing drug(s) into the patient's body in prescribed amounts at pre-specified times. However, chemotherapy affects normal cells as well, and this complicates the treatment mission. Chemotherapy is typically planned and prescribed according to specified protocols. Every protocol includes the drug type(s), dosages, number of doses, and times between doses. As a result of the complexity of these treatment factors, oncologists may need to test, adjust, or even cancel a patient's prescribed treatment plan.

For the treatment planning problem, system dynamics (SD) modelling can be used as a decision-support tool for oncologists to enable them to test multiple scenarios of treatment plans to approve the most effective one. SD can also help to highlight the impact (i.e., the robustness) of any deviation from the prescribed treatment plans, as the study of Heshmat and Eltawil [5] suggests. In this paper, we applied the SD model of Heshmat and Eltawil [5] to different test scenarios of patients requiring treatment at an outpatient chemotherapy clinic (OCC) over a specified planning horizon. The SD model abstracts the chemotherapy treatment regimen and can be efficiently applied at the strategic level of chemotherapy by setting and testing various treatment scenarios and protocols before execution. Therefore, the SD model gives stakeholders the ability to obtain managerial insights into OCCs. Optimising any SD model (and simulation models in general) is often challenging. To do so, we develop a MIP model to assign new patients to their optimum start-of-treatment days. The remainder of the paper is devoted to the implementation and evaluation of our SD/MIP two-stage approach. The discussion is organised as follows. Section 2 gives a literature review concerning the problem. Section 3 describes the developed MIP model. Section 4 elaborates on the SD model. In Section 5, the results are demonstrated, and conclusions are presented in Section 6.

 

2 LITERATURE REVIEW

The review paper [6] concluded that research into OCC planning is limited but growing, and should be expanded. In fact, relatively few studies addressing OCCs can be found in the literature, compared with those dedicated to general outpatient clinics. Mazier, Billaut, and Tournamille [7] studied the drug preparation problem in OCCs to minimise the treatment delay. Santibahez et al. [8] proposed a simulation-based optimisation model to assign new patients to start days to minimise the nursing workload. Sadki, Xie, and Chauvin [9] developed a MIP model to plan the working times of oncologists in an oncology center. Woodall et al. [10] proposed a MIP model to produce weekly and monthly schedules for nurses. Liang and Turkcan [11] developed a multi-objective mathematical programming model to solve the nurse assignment problem in OCCs. Turkcan, Zeng, and Lawley [12] developed a two-stage MIP model to solve various operations planning and scheduling problems in OCCs, but the authors did not discuss methods to suggest the earliest/optimal start days for new patients. Heshmat and Eltawil [13] also proposed that all new patients have an equal priority to start their treatment on the first day. However, in real-life scenarios, patients differ in their status, and of course, some patients ought to have priority over others. Sevinc, Sanli, and Goker [14] proposed a two-phase algorithm to solve the chemotherapy scheduling problem to assign patients to minimise their overall wait times. Condotta and Shakhlevich [15] discussed a multilevel model to determine the appointment days for patients to minimise their overall wait times and the nurses' workloads. Liang et al. [16] applied discrete-event simulation to evaluate operational performance at an OCC. Baril et al. [17] applied simulation to model the direct and indirect activities of nurses in an OCC for the purposes of enhanced reengineering.

 

3 THE PROPOSED MODEL FOR THE PLANNING PROBLEM

This section aims to develop the operations planning model that assigns new patients to their optimum treatment-start days to minimise both patient treatment delay and completion times in the clinic. The developed model is based on the model of Heshmat and Eltawil [13]. The model notation is listed in Table 2, and the mathematical model follows that.

 

Table 1 - Click here

 

 

The objective function (1) is developed to minimise the treatment delay of a set of new patients, and the total completion time for the treatments. Any delay of the treatment is constrained by the parameter tf, which represents the critical time beyond which the patient should not be delayed. This parameter is estimated in the next section for a set of new patients. According to the first portion of the weighted sum objective function, the first treatment day ought to be decided as early as possible. However, OCCs have fixed working times. The second portion is designated to minimise the makespan of all the treatments. The set of constraints (2) assigns a set of new patients to their start days. The set of constraints (3) ensures that the working times of the nurses are consistent with their allowed working time. Equation (4) calculates the total completion time of all the treatments (for both new and existing patients); it can only be regarded as approximate because the appointment times are not determined in the planning stage. The set of constraints (5) ensures that the completion time of the OCC is bounded by its working time.

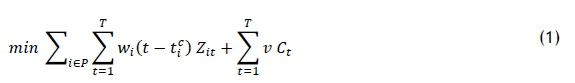
Subject to

 

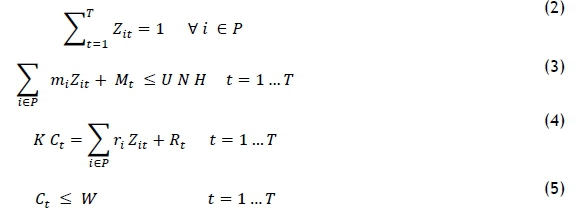
4 DESCRIPTION OF THE SD MODEL

In this section we describe the SD model developed by Heshmat and Eltawil [5]. Figure 1 depicts the SD model that is used to test the usefulness of chemotherapy protocols. First, the drug dose is infused according to a protocol while the cancer is increasing. As long as the drug dose is infused, the concentration rate increases. As the drug concentration increases, the concentration rate decreases; this can be fulfilled by modifying the drug infusion doses. The tumor is reduced when the drug concentration increases. The impairment decreases when the number of cancerous cells decreases. The treatment efficacy is reduced by increasing the impairment. A causal loop diagram is quite effective to examine a complicated causal relationship among variables and clarify feedback loops. On the other hand, there are some disadvantages; for example, SD cannot differentiate between inflow and outflow, nor the cumulative effect as the difference between them. Stocks, as a source of accumulation in a system, distinguish the state of the given system and supply it with inertia and memory. Similarities between stocks and flows and some chemotherapy variables are considered in the model (Figure 1). The drug growth in the patient's body is similar to a stock. This is mirrored in the two variables, drug accumulation and toxicity. Similarly, the number of cancerous cells is a dynamic variable that varies with time, while drug concentration rate, toxicity rate, tumor growth, and tumor decrease are similar to flows.

 

5 RESULTS

This section is dedicated to presenting the results after solving the two models. First, the critical times of treatment delays are estimated for a set of new patients. The runs are done according to the oncology protocols; thus, every run is for a specific patient with his/her features. After that, the set of new patients is assigned to the starting days by solving the developed MIP model.

5.1 Estimating t^c_i

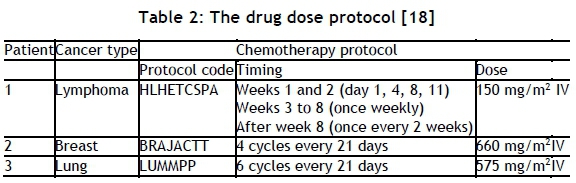
This section is dedicated to estimating the critical starting day for each member in the set of new patients. We use real chemotherapy protocols for a set of three new patients with different types of cancer, as shown in Table 2.

The results from the SD model are shown in Figures 2 to 4 for the three patients. It is clear that treatment efficacy is affected by the treatment delay. However, the degree of deviation is different from one patient to another due to the initial conditions and the drug and patient parameters. Therefore we defined the critical starting day of a patient as the day on which the treatment efficacy begins to worsen. Accordingly, if for patients 1, 2, and 3 is the 2nd, 8th, and 10^th day respectively.

5.2 The optimal starting days

After estimating the critical days for the new patients, the optimal starting days of the three patients are computed in this section. This is accomplished by solving the MIP model, which is presented in section 2 above. The model is solved using CPLEX solver for the parameters shown in Table 3.

The results in Figure 5 show that patients 1, 2, and 3 should come to the clinic on the second, third, and fifth days respectively of the planning horizon. This result can be taken as a reference in the decision about the actual schedule of patients in OCCs to minimise the patient treatment delay, considering the variability in patient clinical status.

 

6 CONCLUSION

This paper has presented a novel approach to predicting the critical starting days for a set of new patients with cancer to prepare to optimise their starting chemotherapy treatments. The approach consists of two stages: in the first stage, the critical days are estimated using a system dynamics model from the literature; and in the second stage, the optimal starting days are computed. This approach can be implemented in outpatient chemotherapy clinics to minimise patient treatment delay and the completion of the treatment, taking into account the variability in patient status. In the future we shall test the developed approach against actual clinical data.

 

REFERENCES

[1] WHO. 2014. Cancer key facts. [Online]. Available: http://www.who.int/mediacentre/factsheets/fs297/en/        [ Links ]

[2] AACR. 2014. Cancer progress report. [Online]. Available: http://www.cancerprogressreport.org/2014/Documents/        [ Links ]

[3] ACS. 2015. Cancer statistics. [Online]. Available: http://www.acsjournals.com/view/0/index.html        [ Links ]

[4] APHA. 2016. Home. [Online]. Available: https://apha.confex.com/apha/142am/webprogram/Paper303082.html        [ Links ]

[5] Heshmat, M. & Eltawil, A. 2018. A system dynamics-based decision support model for chemotherapy planning, Journal of Simulation, pp. 1-12.         [ Links ]

[6] Lame, G., Jouini, O. & Stal-Le Cardinal, J. 2016. Outpatient chemotherapy planning: A literature review with insights from a case study, IIE Transactions on Healthcare Systems Engineering, 6(3), pp. 127-139.         [ Links ]

[7] Mazier, A., Billaut, J.-C. & Tournamille, J.-F. 2010. Scheduling preparation of doses for a chemotherapy service, Annals of Operations Research, 178(1), pp. 145-154.         [ Links ]

[8] Santibanez, P., Aristizabal, R., Puterman, M.L., Chow, V.S., Huang, W., Kollmannsberger, C. & Tyldesley, S. 2012. Operations research methods improve chemotherapy patient appointment scheduling, Joint Commission Journal on Quality and Patient Safety, 38(12), pp. 541-553.         [ Links ]

[9] Sadki, A., Xie, X. & Chauvin, F. 2013. Planning oncologists of ambulatory care units, Decision Support Systems, 55(2), pp. 640-649.         [ Links ]

[10] Woodall, J.C., Gosselin, T., Boswell, A., Murr, M. & Denton, B.T. 2013. Improving patient access to chemotherapy treatment at Duke Cancer Institute. Interfaces, 43(5), pp. 449-461.         [ Links ]

[11] Liang, B. & Turkcan, A. 2016. Acuity-based nurse assignment and patient scheduling in oncology clinics. Health Care Management Science, 19(3), pp. 207- 226.         [ Links ]

[12] Turkcan, A., Zeng, B. & Lawley, M. 2012. Chemotherapy operations planning and scheduling. IIE Transactions on Healthcare Systems Engineering, 2(1), pp. 31-49.         [ Links ]

[13] Heshmat, M. & Eltawil, A. 2017. A new approach to solve operations planning problems of the outpatient chemotherapy process. 4th International Conference on Control, Decision and Information Technologies (CoDIT), pp. 0544 - 0549.         [ Links ]

[14] Sevinc, S., Sanli, U.A. & Goker, E. 2013. Algorithms for scheduling of chemotherapy plans. Computers in Biology and Medicine, 43(12), pp. 2103- 2109.         [ Links ]

[15] Condotta, A. & Shakhlevich, N. 2014. Scheduling patient appointments via multilevel template: A case study in chemotherapy. Operations Research for Health Care, 3(3), pp. 129-144.         [ Links ]

[16] Liang, B., Turkcan, A., Ceyhan, M.E. & Stuart, K. 2015. Improvement of chemotherapy patient flow and scheduling in an outpatient oncology clinic. International Journal of Production Research, 53(24), pp. 7177-7190.         [ Links ]

[17] Baril, C., Gascon, V., Miller, J. & Bounhol, C. 2017. The importance of considering resources tasks when modeling healthcare services with discrete event simulation: An approach using work sampling method. Journal of Simulation, 11(2), pp. 103-114.         [ Links ]

[18] BC. 2016. Health professionals. [Online]. Available: http://www.bccancer.bc.ca/health-professionals/professionalresources/chemotherapy-protocols/lymphoma-myeloma        [ Links ]

 

 

Submitted by authors 12 Mar 2018
Accepted for publication 16 Aug 2018
Available online 10 Dec 2018

 

 

* Corresponding author a.alabdulkarim@mu.edu.sa