SPECIAL EDITION

 

Warm-start heuristics for solving the passive optical network planning problem

 

 

R. Luies^{I, *}; S.E. Terblanche^I; M.J. Grobler^II

^IDepartment of Industrial Engineering, North-West University, South Africa
^IIDepartment of Computer Engineering, North-West University, South Africa

 

 

---

ABSTRACT

The use of automated network planning systems is crucial for reducing the deployment cost and planning time of passive optical telecommunication networks. Mixed integer linear programming is well suited for the purpose of modelling passive optical networks; however, excessive computing times for solving large-scale problem instances render these approaches impractical. In this paper, an arc-based, a path-based, and a composite integer linear programming formulation of the passive optical network planning problem are considered. A reduction in computing times and peak memory usage is obtained by applying multiple heuristics as warmstarts to these problem formulations. Finally, the computational results presented in this paper are based on real-world Geographic Information System data - more specifically, a neighbourhood in Potchefstroom, South Africa.

---

OPSOMMING

Die gebruik van geoutomatiseerde netwerkbeplanningstelsels is noodsaaklik om die ontplooiingskostes en beplanningstyd van passiewe optiese telekommunikasienetwerke te verminder. Alhoewel gemengde heeltallige lineêre programmering benaderings geskik is vir die modellering van passiewe optiese netwerke, die rekenaarvereistes ten opsigte van verwerkingstyd veroorsaak dat hierdie benaderings onprakties is. In hierdie artikel word 'n skakelgebaseerde, 'n padgebaseerde en 'n saamgestelde lineêre programmering benadering voorgestel. Die resultate toon dat n verbetering in verwerkingstyd asook geheue gebruik is moontlik deur die gebruik van heuristiek wat begin oplossings genereer vir die voorgestelde probleem formulerings. Die resultate in hierdie artikel is gebaseer op werklike Geografiese Inligtingstelsel data, spesifiek data van n woonbuurt in Potchefstroom, Suid-Afrika.

---

 

 

1 INTRODUCTION

Global consumer internet protocol traffic is expected to reach 233 EB per month in 2021 [1]. The increase in bandwidth demand requires that internet service providers deploy access networks that are able to keep up with the increase in bandwidth usage. Asymmetric digital subscriber line (ADSL) technology is widely used in South Africa currently, and is on average slower than fibre-to-the-home (FTTH) [2]. The obvious solution is to move away from ADSL and towards passive optical networks (PONs); but this requires extensive network planning.

The complexities involved in the design of a PON necessitate the use of automated network design tools. Apart from the choice of splitter types and splitter locations, a cost-efficient topology design is essential. There are several approaches in the literature to designing cost-efficient PONs, but there is typically a trade-off between the use of heuristics and exact solution approaches. The former is typically more computationally efficient without any solution quality guarantees, whereas the latter has the attractive feature of providing proven optimal solutions that may, however, be at the expense of computing times and memory usage.

Integer linear programming (ILP) is well suited for the purpose of modelling passive optical networks; however, being an exact solution approach, it may result in excessive computing times when solving large-scale problems. In this paper, a combination of heuristics and ILP approaches is presented in order to speed up computing times and allow for better memory use. The computational results presented in this paper employ warm-start solutions (partial initial solutions) obtained from the heuristics in Luies, Grobler and Terblanche [3] as starting solutions for the ILP formulation presented here. Table 1 gives a brief overview of the features of these heuristics.

The paper is organised as follows. In section 2, the PON planning problem is defined, focusing on the structure of a PON. In section 3, related work on PON planning automation is given, all of which can be classified as exact, heuristics, or meta-heuristics approaches. In section 4, four different mathematical models are presented. The methodology of employing the models and heuristics is given in section 5. The results are given in section 6. The paper is concluded in section 7.

 

2 PROBLEM DEFINITION

A PON implements a point-to-multipoint architecture, in which an optical splitter serves multiple optical network units (ONUs). ONUs convert optical signals to electrical signals, and are the equipment used by the customers to connect to the network. The central office (CO) contains optical line terminals (OLTs) that control the flow of information to the ONUs. The network has two parts: the feeder network, which connects the CO with all the optical splitters; and the distribution network, which connects the ONUs to optical splitters. The structure of a typical PON is provided in Figure 1. Optical splitters cannot be used as a switch, and they broadcast the same data to multiple ONUs. The main advantage of an optical splitter is the reduction in network deployment cost. Only a single fibre from the CO to the optical splitter is needed to connect multiple ONUs. Each optical splitter can serve a predetermined number of ONUs, usually by a power of two. Multiple optical splitter types may be placed at a single location. The common split ratios are 1:8, 1:16, 1:32, and 1:64.

 

 

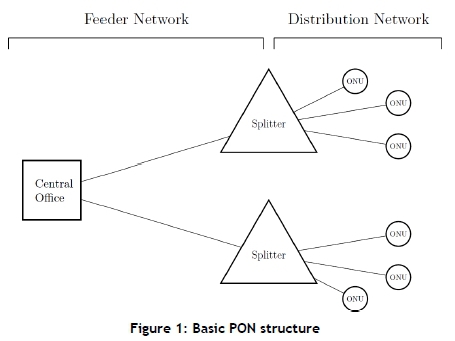
PONs have a tree structure, and the network deployment cost can be reduced by placing several fibre cables in a single trench (duct sharing). The number of optical splitters at each location, the types of optical splitters, and the layout of the fibre cables (via optical splitters) must be chosen to ensure that all ONUs are connected to the CO with minimum deployment cost.

 

3 RELATED WORK

According to [4], when more ONUs connect to the same optical fibre splitter, the more likely it is that fibre optic cables will share parts of the same path. The number of paths between an optical splitter and an ONU increases exponentially as the node density increases. When considering different paths between optical splitters and ONUs, these paths can potentially share the trenches with paths to other ONUs. A heuristic, based on a network flow formulation and presented by Van Loggerenberg, Grobler and Terblanche [5], constructs feasible solutions by limiting the number of paths to improve fibre duct sharing. A disintegration heuristic is proposed [6] in an attempt to reduce computing times by using the output of a centroid, a density-based, and a hybrid clustering algorithm. The computational results are favourable for large problem instances. Van Loggerenberg [7] employs a Benders decomposition approach to improve scalability.

Li and Shen [8] proposed a suboptimal heuristic to minimise the deployment cost of greenfield PONs through disintegration. The heuristic algorithm selects some random optical splitters as the initial solution, and improves the solution through a simulated annealing process. The algorithm is finally compared with a random-cut heuristic to show the efficiency of the algorithm.

Ouali and Poon [9] demonstrate how an ILP can be applied to automate FTTH designs by reducing the capital expenditure of telecommunication companies. The proposed model incorporates multi-hierarchical PONs, and optimal solutions could be computed for one of the so-called MediumNet datasets (two optical splitters and 94 ONUs) they considered in their study. No optimal solutions could be computed for the so-called BigNet datasets (five optical splitters and 482 ONUs).

Various approximation approaches to solving PON planning problems are suggested - for instance, simulated annealing, particle swarm optimisation, and genetic algorithms [10, 11, 12, 13].

Two greedy heuristic algorithms are presented by Luies et al. [3]. The first algorithm uses all the optical splitters at first, removing the splitter that impacts the network deployment cost the most. This process is repeated until the network deployment cost cannot decrease any further. The second algorithm estimates possible optical splitter locations by clustering the ONUs according to their geographic location, and then by connecting the optical splitter location closest to the centroid of these clusters.

 

4 MODELS

The model formulations considered in this paper are all based on the well-known multi-commodity network flow formulation [14]. In the context of PON planning, a commodity-pair is defined as a pair that contains either an optical splitter and an ONU, or an optical splitter and the CO. Four different mathematical models are presented below: an arc-flow formulation, a path-flow formulation, an aggregated arc-flow formulation, and a composite path-arc-flow model formulation. The number of paths used in the path-flow implementation is limited to only the shortest paths, which reduces computation times and memory usage at the expense of higher network deployment costs. The aggregated arc-flow formulation does not require a flow over every commodity-pair. Although the total cost is lower for the aggregated arc-flow than for the heuristic path-flow implementation, it is not trivial to determine which ONU connects to which optical splitter location. The arc-flow formulation determines which commodity-pairs use trenches, but has significantly more flow variables, which may result in higher computing times and memory usage. The models are discussed in more detail in sections 4.1 - 4.4.

4.1 Arc-flow formulation (CPARC)

The setup cost for a CO is denoted by c_c. The set U denotes the index set of all ONUs included in the network. The cost of a single ONU is c_u, with ueU. The set of splitter locations is denoted by S and the set of splitter types by Z. It is possible to place more than one type of optical splitter at a single location, which is represented by the decision variable y_i^z ε N₀, with i εS and z εΖ.

The graph representation of the PON network is facilitated by a set of edges Ε and a set of arcs A. Variables indexed by an arc (i,j) e A imply directional flow from node i to node whereas indexing with an edge e ε Ε is directionless, which is typically associated with variables associated with trenching. The trenching cost for edge e is c^T_e, and the binary decision variable x_eε (0,1} specifies whether the solution includes edge e for trenching. The set of commodities Κ includes all commodity-pairs considered in the formulation. The set K^u_s C Κ contains the distribution commodity-pairs, and the set K^s_c C Κ contains feeder commodity-pairs. The flow variable f_ijk e Z over arc (i,j) ε A for commodity k ε Κ determines the placement of a fibre cable between nodes i and j

The objective of the commodity-pair arc-flow formulation (CPARC) is to

The objective function (1 ) shows the total deployment cost of the network. The first two terms of the objective function are constant, since the ONUs are fixed for each problem instance. To ensure that each ONU is connected to exactly one optical splitter location, constraint set (2) is applied. Each ONU is a sink node with an incoming flow of one, whereas each optical splitter location is a source node with an outgoing flow N_t, which is the sum of all the flows from the ONUs connected to the splitter i. The function ф(ί) returns a set of all the nodes adjacent to node i. The flow to all other nodes should be zero in constraint set (2).

Constraint set (3) presents the feeder network. In this case, each optical splitter location is a sink node with an incoming flow equivalent to the sum of the optical splitters at that location. The CO is the source node, with an outgoing flow equal to the number of splitters used in the solution. The flow of all the other nodes should be zero.

Constraint set (4) ensures that the optical splitter locations contain valid optical splitter ratios. Constraint set (5) sets the binary decision variables x_e e {0,1} whenever there is a flow over an edge e. Since constraint set (5) is a set of big-M constraints, Δ can be any suitable large positive number.

4.2 Heuristic path-flow formulation (HPATH)

Unlike the arc-flow formulation, the number of paths used in the path-flow formulation can be limited to reduce computing times and memory usage, but unfortunately at the expense of solution quality. In this paper, only the shortest path between each commodity-pair is considered.

In order to facilitate the formulation of path variables, the index set P(k) is used to describe the set of all possible paths between the nodes of the commodity-pair k e K. The implementation of a heuristic that involves only shortest paths will imply that the set P(k) will be restricted to only a single shortest path for a commodity-pair k e K.

The variable f_pεZ denotes the flow over a path ρ ε P(k), for a commodity k e K. The total fibre cable cost for the network is the sum of all the paths used multiplied by the cost of each path c^F_p. The variables from the previous formulation that relate to the splitter locations, splitter types, and trenching decisions are re-used in the formulation below. The objective of the heuristic path-flow formulation (HPATH) is to

The objective function (6) represents the total deployment cost. The first two constant terms are the setup cost of the CO and of the ONUs. Constraint set (7) represents the constraints for the distribution network. Each constraint considers the path from all the optical splitter locations to each individual ONU via the set of commodity-pairs K^u_s(j), where j is an ONU. The sum of all the paths to the commodity-pairs that include a specific ONU should be one, since only a single ONU can be connected to an optical splitter.

Similar to the distribution network, the feeder network uses path-flow constraints. Constraint set (8) includes the path-flow constraints for the feeder network.

Constraint set (10) enables the edges included in the path p. P(k,e) retrieves any path that contains e as an element for commodity-pair k. For the big-M constraints, Δ can be any large number - e.g., |P|.

4.3 Aggregated arc-flow formulation (AARC)

The aggregated arc-flow formulation is similar to the arc-flow formulation, with the exception that the aggregated arc-flow does not consider flow over each commodity-pair separately. There are fewer flow variables in the aggregated arc-flow than in the arc-flow model; however, there is no way to know which ONU is connected to which optical splitter. As a heuristic, the solutions obtained from the aggregated arc-flow model can reveal some information about the problem, such as the optimal trenching decisions according to the binary variables x_e, and the optimal splitter locations.

The flow variables considered in the aggregated arc-flow formulation are divided into feeder flow variables ff. e LL and distribution flow variables ffj e LT, for each arc (i,j) e A.

The objective of the aggregated arc-flow formulation (AARC) is to

The objective function (11 ) shows the total deployment cost of the network, and the constraints for the feeder network are described in (12). Constraint set (13) models the flows for the distribution network, and constraint set (14) ensures that the total number of ONUs is always less than or equal to the sum of all the optical splitter capacities at a location. Finally, constraint set (15) enables any edge with a flow in any direction. For the big-M constraints, Δ is any suitable large number.

4.4 Composite arc-path formulation (APATH)

The composite formulation is a combination of the aggregated arc-flow and the path-flow formulation. One drawback of the aggregated arc-flow formulation is the loss of information on the commodities - i.e., there is no way to know which ONU is assigned to which optical splitter. Only the feeder network uses the aggregated arc-flow formulation because there is only one CO, and we know that each optical splitter in the solution connects to the CO. Determining the paths from the remaining edges is then trivial. The distribution network uses the path-flow; this allows the preservation of information of about the resulting commodity-pairs.

The objective of the arc-path-flow formulation (APATH) is to

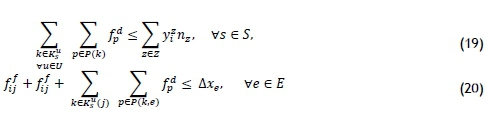
The objective function is similar to the other formulations, except that the feeder and distribution networks are shown in separate parts. The last terms in (16) show the arc-flow f_i^f_j. ε Z and path-flow f^d_pε Z variables. y^z_i ε N₀is a decision variable for the optical splitter types at each location. Constraint set (17) is the same as constraint set (12), which corresponds to the constraints for the feeder network. Constraint set (18) is the same as constraint set (7), which allows every ONU to be connected to only one optical splitter. Constraint set (19) ensures the correct optical splitter ratios. Finally, edges are enabled with big-M constraints in (20).

 

5 METHODOLOGY

For the computational results in this study, the ILP models presented above were solved by employing the greedy algorithms presented in [3] as warm-start heuristics. More specifically, the algorithm that recursively removes optical splitters (RECREM) and the clustering algorithm (KSPLIT) were considered. It should be noted, however, that the aggregated arc-flow model (AARC) only produces partial optimal solutions - that is, it only provides information on the optimal trenching decisions and on the optimal splitter locations. But this information may be used in other problem formulations to 'force' the trenching and splitter locations to take on the optimal values, thus excluding all the edge and splitter variables not present in the optimal solution. AARC may therefore be employed as a pre-processor to the other ILP problem formulations. A drawback of this approach, however, is the inability to produce optimal solutions with CPARC, if AARC is not solved to optimality when applied as a pre-processor to CPARC.

The edges and optical splitter locations determined with RECREM, KSPLIT, and AARC are used to warm-start the other ILP implementations. The path-flow implementation (HPATH) is limited to only the shortest path between each commodity pair in order to improve scalability. The pre-processed input can improve the solution quality of HPATH, since some of the edges are removed, allowing for different shortest paths than in the initial input data.

The composite arc-path model (APATH) is an attempt to combine the ability to limit the number of paths and the ability to explore multiple paths at the same time. An aggregated arc-flow is used for the feeder network. Since a single CO is used, it is trivial to determine the path between each optical splitter and the CO. It is not trivial, however, to determine the paths between ONUs and optical splitter locations, since the flows are aggregated. Thus the path-flow formulation is used for the distribution part of the PON network. The APATH should produce slightly better quality solutions than the HPATH formulation.

 

6 RESULTS

The problem instances considered in this paper are real-world instances derived from Geographic Information System data. More specifically, a digital street map of a residential area in Potchefstroom, South Africa was used to determine ONU locations and potential splitter locations. From this information, three different datasets were created: SmallNet, MedNet, and HugeNet. Each of these datasets has a different number of ONUs and splitter locations to demonstrate the scalability of the suggested approach. SmallNet has 76 edges, 24 ONUs, and six possible optical splitter locations; MedNet has 933 edges, 389 ONUs, and 62 possible optical splitter locations; and HugeNet has 1787 edges, 662 ONUs, and 124 possible optical splitter locations.

Table 2 shows the results of the different heuristics that are considered. In the case of AARC, partial solutions are obtained, and in the case of RECREM and KSPLIT, relatively low-quality feasible solutions are obtained. It is possible, of course, also to combine AARC with RECREM and KSPLIT by using the latter to generate warm-start solutions to improve the computing times of the AARC formulation. This combined approach is labelled as either AARC-RECREM or AARC-KSPLIT in the results displayed in Table 2.

 

 

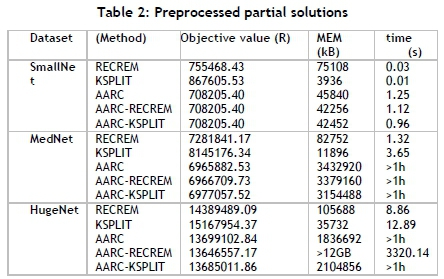
From the results in Table 2, it is observed that the KSPLIT algorithm uses the least amount of memory, but it also obtains the worst objective function values. RECREM scales better than KSPLIT for computing times, and it also produces better quality solutions. Although the peak memory usage is worse for RECREM, the reported computing times for KSPLIT are higher.

AARC produce good quality results, but lacks some information about the solution. The objective value obtained AARC is a realistic value, but there is no way of knowing with this model which optical splitter connects to which ONU. When AARC solves to optimality, the edges used and optical splitter locations are the same as in the optimal solution of CPARC. The problem is that AARC is not able to produce an optimal solution for a large dataset such as MedNet and HugeNet.

Using KSPLIT as a warm-start for AARC improves the total computation time of SmallNet, but has no significant impact on MedNet and HugeNet. With RECREM as a warm-start for AARC, there is a slight improvement in the objective function value; however, there is excessive memory usage.

Table 3 shows the results obtained for the path-flow, arc-flow, and arc-path composite models respectively. Results are also reported when these formulations are solved with warm-start solutions obtained from the heuristic approaches RECREM and KSPLIT, or with the partial solution computed by solving the AARC formulation. Recall that the solutions obtained from solving the different ILP formulations may only be considered heuristic if AARC is not solved to optimality.

 

 

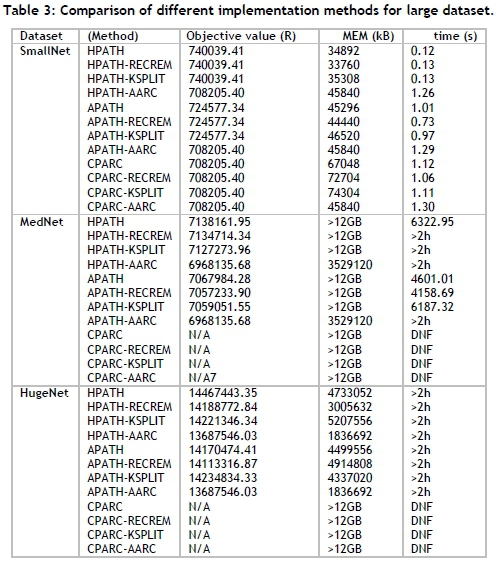
The SmallNet problem instance is used to benchmark the solution quality of each model formulation. HPATH only considers shortest paths between commodity-pairs; thus its search space is a subset of the APATH search space. APATH only considers shortest paths for the distribution network, whereas an arc-flow formulation is used for the feeder network, which leads to a larger search space than for HPATH. CPARC considers the complete search space, and is not presented as a heuristic; but it is obvious from MedNet and HugeNet that CPARC does not scale well. For the SmallNet, HPATH performed around two per cent worse when comparing its objective value with that of APATH, and ARC-PATH performed more than four per cent better than HPATH.

For SmallNet, AARC was solved to optimality, and when used as a warm-start for other models, it also resulted in the lowest possible objective function value. Since the solution obtained from AARC has fewer possible optical splitter locations and edges for the input than other models, fewer decision variables are created and memory usage is lower. Peak memory usage of APATH and HPATH with AARC used as a warm-start for MedNet was less than 4GB, which is significantly than with the other heuristics (all larger than 12GB). The combined approach of APATH and HPATH with AARC also resulted in a 1.3 per cent to 2.4 per cent improvement in solution quality. The results obtained for HugeNet also show the same trend: the peak memory usage is lower and solution quality is higher when AARC is used as a warm-start for HPATH. When AARC is used as a warm-start there is a 3.02 per cent to 5.39 per cent improvement in objective function value, compared with when other heuristics were used. Unfortunately, CPARC did not obtain a single solution for the MedNet and HugeNet problem instances, since the decision variables for CPARC are significantly more than in the other model formulations. In most cases, RECREM and KSPLIT showed little to no improvement for some instances.

 

7 CONCLUSION

The arc-flow model does not scale with an increase in the number of optical splitter locations and ONUs. The composite arc-path model and the path-flow model both show potential as heuristics, especially when they are provided with partial solutions to be used as a warm-start, which is obtained by solving the aggregated arc-flow model. In most cases, RECREM and KSPLIT did not show significant improvement, if at all, for some of the problem instances. It is clear that the partial solutions obtained from the aggregated arc-flow model provided valuable information about the problem, and may be exploited to improve the solution quality of other approaches. Using the aggregated arc-flow solutions as a warm-start also improved the scalability of the path-based formulation when employed as a heuristic.

Future work includes the exploration of multiple methods - for instance, the use of statistical learning to extract valuable information from the problem. This may be achieved by investigating the structure of PONs in an attempt to determine which edges and optical splitter locations are more likely to be used in the optimal solution.

 

REFERENCES

[1] Cisco VNI. 2017. Cisco visual networking index: Forecast and methodology 2016-2021.         [ Links ]

[2] Yu, S.-Y., Mahanti, A. and Gong, M. 2016. Benchmarking ISPs in New Zealand, in Performance Computing and Communications Conference (IPCCC), 2016 IEEE 35th International. IEEE, pp. 1-7.         [ Links ]

[3] Luies, R., Grobler, M.J. and Terblanche, S.E. 2017. Solving the passive optical network planning problem: A parallel approach, in Southern African Telecommunications and Networks Access Conference (SATNAC), 2017, pp 38-43.         [ Links ]

[4] Van Loggerenberg, S.P., Grobler, M.J. and Terblanche, S.E. 2012. Optimization of PON planning for FTTH deployment based on coverage, in Proc. Southern African Telecommun. and Netw. Access Conf. SATNAC 2012.         [ Links ]

[5] Van Loggerenberg, S.P., Grobler, M.J. and Terblanche, S.E. 2013. Solving the passive optical network with fiber duct sharing planning problem using discrete techniques, Electronic Notes in Discrete Mathematics, vol. 41, pp. 343-350 [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1571065313001145        [ Links ]

[6] Van Loggerenberg, S.P., Grobler, M.J. and Terblanche, S.E. 2015 Heuristic approach to the passive optical network with fibre duct sharing planning problem, ORiON, vol. 31, no. 2, pp. 95-110.         [ Links ]

[7] Van Loggerenberg, S.P. 2015. Optimisation of passive optical network design under demand uncertainty. PhD dissertation, North-West University, Potchefstroom.         [ Links ]

[8] Li, J. and Shen, G. 2008. Cost minimization planning for passive optical networks, in Optical Fiber Communication/National Fiber Optic Engineers Conference, 2008. IEEE, pp. 1 -3.         [ Links ]

[9] Ouali, A. and Poon, K.F. 2011. Optimal design of GPON/FTTH networks using mixed integer linear programming, in 16th European Conference on Networks and Optical Communications (NOC), 2011. IEEE, pp. 137-140.         [ Links ]

[10] Mitcsenkov, A., Bakos, P., Paksy, G. and Cinkler, T. 2013. Technology-independent topology design heuristics for point-to-multipoint optical access networks, in 17th International Conference on Optical Networking Design and Modeling (ONDM), April, pp. 298-303.         [ Links ]

[11] Lakic, B. and Hajduczenia, M. 2007. On optimized passive optical network (PON) deployment, in Second International Conference on Access Networks Workshops, August 2007, pp. 1 -8.         [ Links ]

[12] Bonsma, E., Karunatillake, N., Shipman, R., Shackleton, M. and Mortimore D. 2003. Evolving greenfield passive optical networks, BT Technology Journal, vol. 21, no. 4, pp. 44-49.         [ Links ]

[13] Kokangul, A. and Ari, A. 2011. Optimization of passive optical network planning, Applied Mathematical Modelling, vol. 35, no. 7, pp. 3345-3354.         [ Links ]

[14] Ahuja, R., Magnanti, T. and Orlin, J. Network flows: Theory, algorithms and applications, : Prentice Hall.         [ Links ]

 

 

Available online 9 Nov 2018

 

 

* Corresponding author: ruanluies@protonmail.com