GENERAL ARTICLE

 

A multi-stage optimisation method for the management of an on-demand fixture manufacturing cell for mass customisation production systems

 

 

E. Naidoo^*; J. Padayachee; G. Bright

University of KwaZulu-Natal, South Africa

 

 

---

ABSTRACT

The implementation of reconfigurable fixtures is a major facilitator of mass customisation. Traditional scheduling techniques do not consider reconfigurable fixtures comprehensively. This paper describes a multi-stage optimisation method that manages the recirculation of reconfigurable fixtures in a mass customisation production system. The method was based on an on-demand fixture manufacturing cell that served a part processing cell. The method consists of three stages: using established techniques such as k-means clustering and hierarchical clustering; and a novel mixed integer linear programming (MILP) model to optimise operation sequences. Minimisation of total idle time (and thus makespan) was used as the measure of performance.

---

OPSOMMING

Die implementering van herkonfigureerbare hegstukke is 'n belangrike fasiliteerder van massaproduksie aanpassing. Tradisionele skeduleringstegnieke oorweeg nie herkonfigureerbare hegstukke omvattend nie. Hierdie artikel beskryf 'n multi-fase optimiseringsmetode wat hersirkulering van herkonfigureerbare hegstukke in 'n massa aanpassing produksie stelsel bestuur. Die metode is gegrond op 'n op-bestelling vervaardigingsel wat gedien het as 'n komponentprosesseringsel . Die metode bestaan uit drie fases: die gebruik maak van gevestigde tegnieke soos k-gemiddeld groepering en hiërargiese groepering; en 'n nuwe gemengde heelgetal lineêre programmering model om operasionele volgordes te optimiseer. Minimering van die totale niksdoentyd (en dus totale maaktyd) is gebruik as die maatstaf van vertoning.

---

 

 

1 INTRODUCTION

The Industry 4.0 manufacturing paradigm has generated an increased research interest in mass customisation [1]. These production systems are expected to be facilitated by reconfigurable fixtures that can provide flexibility and responsiveness for customer-driven variations in product demand and type [2]. Thus these fixtures have to be treated as components of the manufacturing system that influence production performance. The use and recirculation of reconfigurable fixtures was not adequately considered by traditional scheduling techniques.

This research presents a multi-stage optimisation method that simultaneously schedules fixture reconfiguration and part processing operations. An on-demand fixture manufacturing cell and a part processing cell were developed to demonstrate the application of the method. The results showed that reconfigurable fixtures can be recirculated in a production system with improvements in fixture utilisation and the minimisation of total idle time for a just-in-time workflow policy.

The paper is structured as follows: Section 2 presents a review of the relevant literature; Section 3 describes the fixture and production system on which the method was applied; Section 4 presents the assumptions and notation of the method before the respective stages of the method are described; Section 5 presents the testing results of the method conducted on a sample problem; and the paper concludes with Section 6, with reference to future work.

 

2 LITERATURE REVIEW

2.1 Reconfigurable fixtures

Mass customisation requires that fixtures be capable of rapidly and economically adapting to customer product demands [2]. Reconfigurable fixtures have emerged as a solution to dealing with a variety of geometries for different parts undergoing the same manufacturing process [3]. These include modular, adaptive, phase-change-based, sensor-based, and chuck-based designs [4]. Modular fixture designs are popular in industry. They can adapt to customised parts when modules are attached to a fixture base in an appropriate configuration for the customised part. An example of such a fixture is the Blüco-Technik® dowel fixture, on which the fixture concept in this study was based [5].

2.2 Group technology paradigm

Group technology (GT) involves grouping similar parts into part families. This concept is exemplified in cellular manufacturing systems (CMS), where part families are processed in specialised cells [6]. Mass customisation aims to maximise the advantages of both high-volume and low-volume production, while minimising their respective disadvantages [7]. GT is a concept that partially achieves this by having separate cells (or groups of manufacturing resources) for variability, but containing similar parts (by characteristics such as size or type) in each cell to improve efficiency. CMS also provides a suitable platform on which modular fixtures can be used. The fixture base and its modules can be customised within the confines of the cell's domain, producing fixtures of greater effectiveness for the given task [6].

2.3 Scheduling studies

An investigation of scheduling techniques was conducted. Evolutionary algorithms have emerged as the state-of-the-art in scheduling studies, which comprise several job shop scheduling problems (JSSP) with modifications [8]. These include varied uses of genetic algorithms [9], ant colony optimisation [10], and particle swarm optimisation [11]. Meta-heuristics have proven to be suitable for multi-objective problems with minimal constraints [12].

The CMS paradigm state-of-the-art was reviewed. Raminfar, Zulkifli, Vasili and Hong [13] developed a dynamic deterministic integrated mathematical model to solve production planning and cell formation in CMS simultaneously. Sakhaii, Tavakkoli-Moghaddam, Bagheri and Vatani [14] developed an integrated MILP model to solve a dynamic CMS, with uncertainty for part processing times and simultaneous minimisation of multiple cost functions. Liu, Wang, Leung and Li [15] solved a cell formation and task scheduling problem in CMS with a discrete bacteria foraging optimisation algorithm.

Studies considering fixtures were investigated. Thörnblad, Strömberg, Patriksson and Almgren [16] used a time-indexed formulation for a flexible JSSP, where the availability of each type of fixture was limited. Wong, Chan and Chan [17] solved a resource constrained assembly JSSP with lot streaming using a genetic algorithm, where fixtures were recyclable and limited. Yu, Doh, Kim, Lee and Nam [18] conducted a study on a reconfigurable manufacturing system using priority rules, where an idle time penalty was enforced for unavailable recyclable fixtures.

In 2008, Bi et al. [3] mentioned that using modular fixture components efficiently in production planning was yet to be addressed. The literature review revealed that fixture management in scheduling studies was limited to standard fixtures only, with only the availability of these fixtures considered. The research undertaken here aimed to address this discrepancy by providing an exact solution approach to the problem with which future developments can be compared.

 

3 PROBLEM DESCRIPTION

3.1 The fixture design

The reconfigurable fixture employed in this study was of the modular type. It consisted of a modular base on which pin configurations were constructed, as shown in Figure 1. This was done by inserting the dowel pins (modules) into the base array in an arrangement that was appropriate for securing the part. The part considered was a two-dimensional plaque of customisable shape with a customisable design engraved on it. Figure 1 displays the pin configuration for a square-shaped part.

 

 

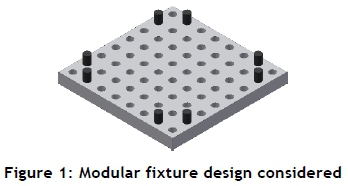
The specifications of the fixture and its configurations for this study are as follows:

• Array pattern: 8x8 holes (64 holes total) per fixture;

• Pin range: 8-16 pins per configuration.

The array pattern and pin range were constrained to these parameters for the purpose of the research demonstration. The parameters can be scaled up or down while retaining the same scheduling techniques presented in the paper.

3.2 The production system

The method presented in this paper was demonstrated on a production system consisting of two cells, as shown in Figure 2.

Figure 2 describes the workflow through the production system. The layout represented a microcosm of a mass customisation production system. The group technology paradigm was employed so that fixtures and parts were served by two dedicated cells. Cell 1 was responsible for fixture reconfigurations, and parts were processed in Cell 2. The finished part was then dispatched, while the fixture was recirculated through the system.

It can be observed from Figure 2 that the production system relies on a synchronous workflow from Cell 1 to Cell 2. Cell 1 has to be reconfiguring a fixture for the next part while the current part is being processed on the previously reconfigured fixture in Cell 2. Bottlenecking results when one cell is busy while the other cell has already completed its operation. Buffering the fixtures before Cell 2 would prevent this problem, but doing so would create a high fixture inventory with minimal fixture utilisation. A just-in-time workflow policy was evident in the system, where fixtures were moved directly from Cell 1 to Cell 2 without intermediate buffering. This promoted the lean manufacturing principles that modern manufacturing systems strive to implement [19].

3.3 Optimisation requirements

The production system, and the fixtures implemented in it, exhibited complications that had to be solved to ensure optimal management of such a system in practice. These were as follows:

• Optimally assigning parts to fixtures;

• Optimally sequencing these parts on their respective fixtures;

• Optimally scheduling the operations in Cell 1 and Cell 2 so that bottlenecking was minimised.

 

4 THE SCHEDULING METHOD

The optimisation method developed in this research consisted of three stages:

1. Clustering stage: Groups similar parts (based on pin configurations) and assigns them to the same fixture (producing fixture-part mappings). Each part group is assigned to one fixture, where the number of groups depends on the number of fixtures available. Having similar parts assigned to the same fixture minimises the extent of reconfiguration required on a single fixture, as parts vary.

2. Intracluster sequencing stage: Sequences parts in the same group (i.e., defines the manufacturing order within the group) so that the dissimilarity between successive parts is minimised. This further reduces the extent of reconfiguration required on a single fixture.

3. Final sequencing stage: Schedules pairs of fixture-part mappings in Cell 1 and Cell 2 with the objective of synchronising fixture reconfiguration and part processing times. This reduces idle time in both cells, thus improving total makespan.

4.1 Assumptions

The assumptions adopted for the development of the method were as follows:

• Fixture reconfiguration times (pij.) and part processing times (πij) are predetermined.

• There are fewer fixtures than parts: |Q|<|P|.

• The required number of fixtures are already manufactured and stored; only reconfigurations are required.

• Fixture reconfiguration operations and part processing operations occur without interruption.

• A job does not exit Cell 1 until Cell 2 is available, and Cell 1 does not start a new job until the previous job has exited the cell - i.e., just-in-time unit workflow policy.

• The fixture reconfigured in Cell 1 in time period k is used to process the part assigned to it in Cell 2 in the next time period

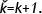
4.2 Method notation

The method notation is as follows [20]:

p; p Є P, P= [1,..,n] P is the set of parts to be processed; p is an index of the ordered set P.

q; q Є Q Q = [1,..,m] Q is the set of fixtures available; q is an index of the ordered set Q.

i; i Є l, I={1,..,m] I is the set of i, where I is a set of subsets that holds all p-q mappings between sets P and Q i denotes a subset, and is also an index of the ordered set I.

î; î Є I, I={1,..,m] î is an alternate index of the ordered set I.

j ; j Є i, i={1,.., \ i\] i is the subset of I corresponding specifically to p-q mappings on fixture

q; j is an index of the unordered subset i; j denotes a part p that is mapped to the fixture q.

; Єi, i={1,.., is an alternate index of the unordered subset i.

k; k Є K, K={1,..,n+1] K is the set of time periods in which parts or fixtures are processed or reconfigured, respectively; k is an index of the ordered set K.

k; k Є K, K={1,..,n+1J k is an alternate index of the ordered set K.

Fixture reconfiguration time; time for fixture ΐ to be reconfigured to pin configuration corresponding to from pin configuration corresponding to (implicitly) - i.e., subsequent reconfiguration for fixture is a parameter.

Part processing time; time for part p corresponding to fixture-part mapping jei to be processed; is a parameter.

X_ijk A binary decision variable; X_ijk= 1 if fixture i is reconfigured for the fixture-part mapping jei in time period k; otherwise X_ijk= 0.

A slack variable; = 1 if fixture-part mapping jЄi that was reconfigured in time period k is processed in time period k=k+1 while fixture-part mapping is synchronously being reconfigured in time period ; otherwise = 0.

A slack variable; is equal to the absolute time difference between part processing time for fixture-part mapping jei reconfigured in time period k, and fixture reconfiguration time for fixture-part mapping that is being reconfigured in time period , the idle time for every time period where two operations are synchronous.

4.3 Clustering stage (Stage 1)

The clustering stage used a binary dissimilarity measure to quantify the comparisons between pin configurations. The fixture base array was represented as an 8x8 binary matrix, corresponding to the fixture specifications listed in Section 3.1. The binary dissimilarity measure compared the matrix of one pin configuration with another on an element-wise basis. A '1' represented the presence of a pin module in that hole, and a '0' represented its absence. The binary dissimilarity measure used is shown in Equation 1:

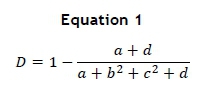
where:

a = number of positive matches (1 to 1)

b = number of positive-to-negative mismatches (1 to 0)

c = number of negative-to-positive mismatches (0 to 1)

d = number of negative matches (0 to 0)

Lloyd's algorithm was used for k-means clustering [21]. It minimised the distances (dissimilarities) of data points in a cluster from the cluster centroid. The measure was a modification of the Sokal and Michener binary similarity measure [22], but with exponential weightings used on the mismatches (b and c). Subtracting the value from 1 converted what would otherwise be a similarity measure into a dissimilarity measure. The exponents on b and c imposed a harsh penalty on any pin that had to be removed and/or replaced, which is how fixture reconfiguration times are inflated.

Dissimilarity values were calculated by comparing each pin configuration with every other one in the job list. These dissimilarity values were amalgamated into a non-metric distance matrix, since the dissimilarity values were non-Euclidean. This was undesirable, because Lloyd's algorithm relies on grouping data points that are close to each other in real space [21]. Thus non-metric multidimensional scaling (MDS) was used to scale the data into two dimensions. This was done by minimising Kruskal's normalised stress criterion for the 'Stress' equation, shown in Equation 2 [23]:

Equation 2

 

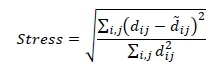
where:

d_ij = raw dissimilarity values for each pair of objects

= scaled distances in the required number of dimensions for each pair of objects

The results of the MDS procedure yielded a two-dimensional map of n data points, representative of the non-metric distance matrix. Lloyd's algorithm was used on this map to group the data points into m number of clusters, based on their closeness. This procedure produced the final result, indicating which parts were to be assigned to which fixture.

4.4 Intracluster sequencing stage (Stage 2)

The intracluster sequencing stage used agglomerative hierarchical clustering with single linkage, together with optimal leaf ordering, to sequence the part groups on their respective fixtures.

Within the paradigm of hierarchical clustering, the objects are referred to as 'leaves', sub-clusters as 'subtrees', and the final dendrogram as the 'tree' [24]. The single linkage option is for the shortest distance (or lowest dissimilarity in this case), so that subtrees were clustered to leaves or other subtrees based on the nearest individual leaves within the subtree/s [25]. This ensured that the tree was constructed on a basis of closest individual leaves, as opposed to closest subtrees.

The default order produced from the agglomerative hierarchical clustering algorithm does not necessarily represent the optimal order. For n number of leaves, there are 2ⁿ¹ possible linear orderings of the tree leaves that are consistent with the structure of the tree [24]. The optimal leaf order was then obtained by using the algorithm designed by Bar-Joseph, Gifford and Jaakkola [24]. The algorithm minimised the cumulative pairwise dissimilarity of the linear ordering. This resulted in a leaf order that was representative of the sequence in which pin configurations were to be reconfigured on the fixture assigned to the corresponding group of parts. This minimised the reconfiguration effort by minimising the number of pin removals/insertions per circulation of the fixture through the manufacturing system.

4.5 Final sequencing stage (Stage 3)

The final sequencing stage was a MILP model, solved by a branch and bound algorithm, which minimised the total idle time in the system. The model is as follows [20]:

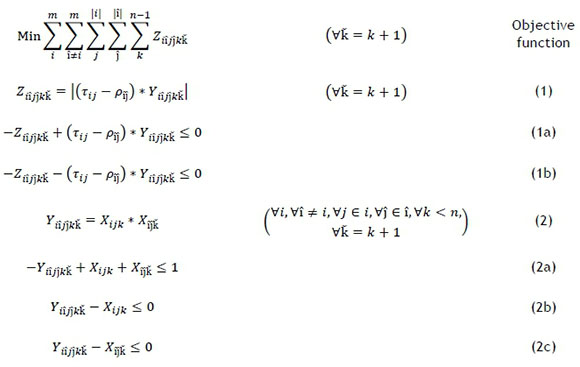
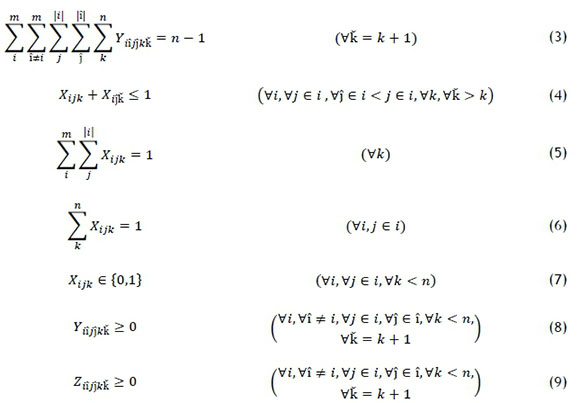
The objective function synchronises part processing and fixture reconfiguration operations by minimising total idle time. Idle time is reduced by minimising the summation of absolute time differences between the part processing time and the fixture reconfiguration time of sequential jobs. Mathematically, this is the time difference between the part processing of fixture-part mapping jЄi, reconfigured in time period k, and the fixture reconfiguration of fixture-part mapping in time period .

Constraint (1) calculates the idle time for each time period. This constraint is non-linear due to the absolute value of the time difference that is calculated. Constraints (1a) and (1b) are used instead of (1) to linearise this constraint.

Constraint (2) allows idle time to be calculated for successive reconfiguration operations (i.e., when X_ijk and 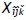equal 1). Constraints (2a) to (2c) are used instead of (2) to linearise this constraint.

Constraint (3) ensures that the number of sequential reconfiguration operations corresponds with the number of sequential time periods.

Constraint (4) imposes the intracluster manufacturing order, previously established in Stage 2, for each fixture .

Constraint (5) ensures that there is only one reconfiguration operation, corresponding with fixture-part mapping jЄi, assigned to each time period k.

Constraint (6) ensures that each reconfiguration operation, corresponding with fixture-part mapping jЄi, is assigned to a time period k only once.

Constraint (7) is a bound enforcing a binary condition on the decision variable X _ijk.

Constraints (8) and (9) are bounds enforcing non-negativity for slack variables and respectively.

 

5 RESULTS

Testing revealed that the model presented in Stage 3 was computationally expensive, and that solution times increased significantly with an increase in problem size. This was the consequence of the exact solution approach deemed necessary for the problem. A sample problem of reasonable size was created, with 12 predetermined part shapes. Figure 3 shows the pin configurations that would be required to secure the variety of part shapes.

 

 

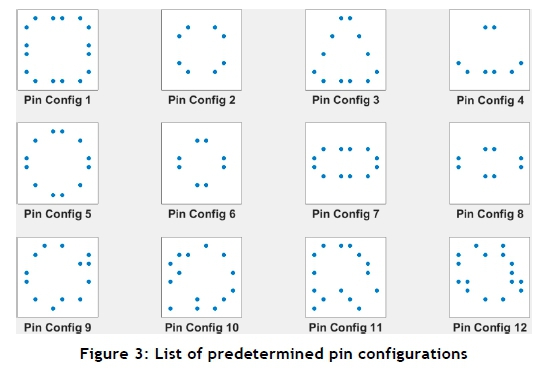
The first eight configurations are for: 1) a large square; 2) a medium square; 3) a large equilateral triangle; 4) a medium equilateral triangle; 5) a large circle; 6) a medium circle; 7) a rectangle; and 8) an oval. The last four configurations are for arbitrarily shaped parts.

The fixture reconfiguration times (p?) and part processing times (ij) for the parts that correspond to these pin configurations were each randomised within a range of 30-90 seconds to demonstrate the ability of the model to cope with data exhibiting a high variance. These parameters are summarised in Table 1. The number of fixtures available was increased from two to four for subsequent tests.

The tests were conducted using the functionalities of MATLAB® 2016a. These tests were executed on an Intel® Xeon® CPU E3-1270 v3 at 3.50GHz with 16 GB RAM on a 64-bit operating system.

5.1 Multi-dimensional scaling

The twelve-dimensional non-metric distance matrix for the sample problem was scaled to two dimensions. This was done with the non-metric MDS algorithm in MATLAB® 2016a [23], iterated 100 times. The map produced is shown on the left of Figure 4 in Section 5.2. Part numbers are shown next to their respective data points.

The goodness of scaling can be represented by the value of the final minimised stress from Equation 2. Sturrock and Rocha [23] produced an evaluation table that provides threshold values to gauge the usability of scaled data. The threshold value quoted for scaling from twelve dimensions to two dimensions was 0.183. The stress value from this test was 0.158. This was below the threshold, which implied that there was a >99 per cent chance that the results adequately represented the original data. This is summarised in Table 2. The results confirmed that the similarity of parts could be correlated to the closeness of the data points displayed in Figure 4, rendering it feasible for k-means clustering.

5.2 K-means clustering

The k-means clustering algorithm in MATLAB® 2016a [21] was used to cluster the data points to m number of clusters. The algorithm was run for 100 iterations. The k-means++ algorithm [26] was used for initialisation. The clustering results for m=4 fixtures are shown on the right of Figure 4 below. The corresponding silhouette plot is shown in Figure 5.

 

 

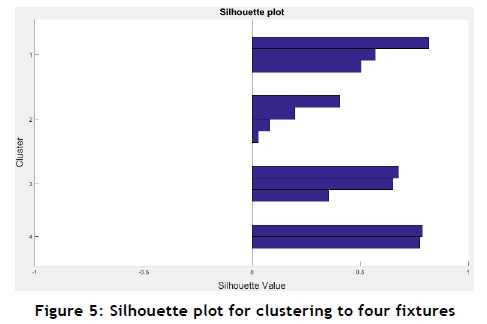
Silhouette values measure the goodness of the clusters formed. Silhouette values closer to 1 signify a definite, unambiguous cluster [25]. The results showed that good clusters were formed, implying minimal reconfiguration effort on fixtures as successive parts within a group are processed. Figure 5 displays lower silhouette values for the second cluster due to grouping of parts that were less similar to each other. This was the best of the clusters available for those parts, but slightly greater effort would be required between reconfigurations.

5.3 Intracluster order

The k-means clustering results were used, together with the non-metric distance matrix, to yield the intracluster manufacturing order for each cluster. The default order was created from the agglomerative hierarchical clustering algorithm with single linkage in MATLAB® 2016a [25]. The resultant sequence was then optimally reordered to produce the final intracluster order for implementation. The results for m=4 fixtures are summarised in Table 3.

Optimal re-ordering was useful for every case except Fixture 4 in Table 3, where there was no scope for improvement. It should be noted that the optimal order is true for both the forward and the reverse directions, as the cumulative pairwise dissimilarity traversed in either case is the same. Improvements ranged from 3.1203 per cent (for the two-fixture problem) to 14.202 per cent.

5.4 MILP model

The results from k-means clustering and optimal leaf ordering were used as the input for the MILP model. The solver used the branch and bound algorithm to solve for the exact solution. The performance is summarised in Table 4. The graph of convergence for m=4 fixtures is shown in Figure 6.

The solution time increased logistically for an increasing number of fixtures with a constant number of parts. This correlated with the logistically increasing number of nodes that were explored to reach convergence in each test. It was expected that the solution method would be computationally expensive, due to the NP-hardness of the problem and the algorithm used [27]. The parameters used to configure the MATLAB® 2016a MILP solver are summarised in Table 5.

 

6 CONCLUSION

This paper presented a multi-stage optimisation method for scheduling an on-demand fixture manufacturing cell in tandem with a part processing cell. This represented a microcosm of a mass customisation production system.

The optimisation method comprised three stages. The first stage optimally assigned parts to fixtures. The second stage optimally sequenced those parts on their respective host fixtures. The third stage was a MILP model that optimally scheduled tasks in the aforementioned cells to minimise total idle time, and thus makespan.

Scaling of the non-metric distance matrix to two dimensions produced a stress value that ensured the adequate accuracy of the two-dimensional map. The silhouette values revealed that the clusters formed in each case were suitable. The optimal re-ordering of the default single linkage dendrogram order successfully improved the intracluster sequence. The MILP model proved to converge for the data set tested, thus minimising total idle time. The branch and bound algorithm ensured that the increase in solution time occurred logarithmically for an increasing number of fixtures. Optional parameters were adjusted to improve this issue.

It can be concluded that the optimisation method presented in this research addresses the scheduling of reconfigurable fixtures in circulation with part manufacturing operations at a level not previously undertaken. This would make it useful for mass customisation production systems, where the use of reconfigurable fixtures cannot be scheduled using current approaches. Operating costs can be reduced, and tardiness penalties can be avoided. However, fully optimal scheduling can only be achieved for small problems, as the algorithm execution time does not scale polynomially.

The method could be readily edited to include batch workflow instead of unit workflow. More complicated fixture designs can also be implemented with the MILP model, as only the operation times are required. This would only require a new dissimilarity measure to be formulated and implemented. The MILP model could also be applied in other cellular manufacturing systems that use a just-in-time workflow policy, as the fundamental principle is to minimise total idle time between two cells with synchronous workflow.

The optimisation method is limited by the assumptions presented in Section 4.1, and by the technical limitations of the exact solution technique used. The optimality of the final solution is affected by the hypothesis that similar part shapes should be assigned to the same fixture, where the only variable considered is pin removals/insertions. The method does not account for the effect of modules that specialise in clamping parts in three dimensions. The clusters were formed from a scaled data set, which affects the accuracy of the data even when within stress specifications. Although good (near-optimal) solutions were found here, there is still scope for improvement. The MILP model is also limited by its inability to handle dynamic schedules, as the inputs to the model must be predetermined and static. Dynamic scheduling must be taken into account for the method to be fully applicable in an industrial environment.

Future work in this research area includes:

• A heuristic to deal with larger-sized problems faster, producing good but sub-optimal solutions;

• A more complex fixture design with a dissimilarity measure to quantify comparisons;

• The influence of manufacturing new fixtures and maintaining an optimal fixture inventory;

• Exploration of the vehicle routing problem (VRP) as a potential approach to solving both Stage 1 and Stage 2 in a single step.

 

REFERENCES

[1] Yao, X. and Lin, Y. 2016. Emerging manufacturing paradigm shifts for the incoming industrial revolution. International Journal of Advanced Manufacturing Technology, 85(5), pp. 1665-1676.         [ Links ]

[2] Smith, S., Jiao, R. and Chu, C.-H. 2013. Editorial: Advances in mass customization. Journal of Intelligent Manufacturing, 24(5), pp. 873-876.         [ Links ]

[3] Bi, Z.M., Lang, S.Y.T., Verner, M. and Orban, P. 2008. Development of reconfigurable machines. International Journal of Advanced Manufacturing Technology, 39(11-12), pp. 1227-1251.         [ Links ]

[4] Patil, A.T., Pise, S.M., Bhatwadekar, S.G. and Sangale, S.B. 2015. Various flexible fixturing systems in manufacturing - A review. International Journal of Innovative Research in Science, Engineering and Technology, 4(9), pp. 8440-8444.         [ Links ]

[5] Bi, Z.M. and Zhang, W.J. 2001. Flexible fixture design and automation: Review, issues and future directions. International Journal of Production Research, 39(13), pp. 2867-2894.         [ Links ]

[6] Groover, M.P. 2001. Group technology and cellular manufacturing, in Automation, Production Systems, and Computer-Integrated Manufacturing, 2^nd edition, Prentice-Hall, pp. 420-459.         [ Links ]

[7] Fogliatto, F.S., da Silveira, G.J.C. and Borenstein, D. 2012. The mass customization decade: An updated review of the literature. International Journal of Production Economics, 138(1), pp 14-25.         [ Links ]

[8] Gen, M. and Lin, L. 2014. Multiobjective evolutionary algorithm for manufacturing scheduling problems: State-of-the-art survey. Journal of Intelligent Manufacturing, 25(5), pp. 849-866.         [ Links ]

[9] Manikas, A. and Chang, Y. 2009. Multi-criteria sequence-dependent job shop scheduling using genetic algorithms. Computer & Industrial Engineering, 56(1), pp. 179-185.         [ Links ]

[10] Tavares Neto, R.F. and Godinho Filho, M. 2013. Literature review regarding ant colony optimization applied to scheduling problems: Guidelines for implementation and directions for future research. Engineering Applications of Artificial Intelligence, 26(1), pp. 150-161.         [ Links ]

[11] Koulinas, G., Kotsikas, L. and Anagnostopoulos, K. 2014. A particle swarm optimization based hyper-heuristic algorithm for the classic resource constrained project scheduling problem. Information Sciences, 277(1), pp. 680-693.         [ Links ]

[12] Sun, Y., Zhang, C., Gao, L. and Wang, X. 2011. Multi-objective optimization algorithms for flow shop scheduling problem: A review and prospects. International Journal of Advanced Manufacturing Technology, 55(5-8), pp. 723-739.         [ Links ]

[13] Raminfar, R., Zulkifli, N., Vasili, M. and Hong, T.S. 2012. An integrated model for production planning and cell formation in cellular manufacturing systems. Journal of Applied Mathematics, 2013(ID 487694), pp. 1-10.         [ Links ]

[14] Sakhaii, M., Tavakkoli-Moghaddam, R., Bagheri, M. and Vatani, B. 2016. A robust optimization approach for an integrated dynamic cellular manufacturing system and production planning with unreliable machines. Applied Mathematical Modelling, 40(1), pp. 169-191.         [ Links ]

[15] Liu, C., Wang, J., Leung, J.Y.-T. and Li, K. 2016. Solving cell formation and task scheduling in cellular manufacturing system by discrete bacteria foraging algorithm., International Journal of Production Research, 54(3), pp. 923-944.         [ Links ]

[16] Thörnblad, K., Strömberg, A.-B., Patriksson, M. and Almgren, T. 2013. Scheduling optimization of a real flexible job shop including side constraints regarding maintenance, fixtures, and night shifts. Department of Mathematical Sciences, Division of Mathematics, Chalmers University of Technology and University of Gothenburg.         [ Links ]

[17] Wong, T.C, Chan, F.T.S. and Chan, L.Y. 2009. A resource-constrained assembly job shop scheduling problem with lot streaming technique. Computers & Industrial Engineering, 57(3), pp. 983-995.         [ Links ]

[18] Yu, J.-M., Doh, H.-H., Kim, J.-S., Lee, D.-H. and Nam, S.-H. 2012. Scheduling for a reconfigurable manufacturing system with multiple process plans and limited pallets/fixtures. International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 6(2), pp. 232-237.         [ Links ]

[19] Groover, M.P. 2001. Chapter 27: Lean production and agile manufacturing, in Automation, Production Systems, and Computer-Integrated Manufacturing, 2^nd Edition, Prentice-Hall, pp. 832-845.         [ Links ]

[20] Naidoo, E., Padayachee, J., Bright, G. 2017. Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for Mass Customisation Production Systems - Model Formulation, Presentation and Validation. Proceedings of the 14^th International Conference on Informatics in Control, Automation and Robotics, 1(1), pp. 17-24.         [ Links ]

[21] Lloyd, S.P. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory, 28(2), pp. 129-137.         [ Links ]

[22] Choi, S.-S., Cha, S.-H. and Tappert, C.C. 2010. A survey of binary similarity and distance measures. Journal of Systemics, Cybernetics & Informatics, 8(1), pp. 43-48.         [ Links ]

[23] Sturrock, K. and Rocha, J. 2000. A multidimensional scaling stress evaluation table. Field Methods, 12(1), pp. 49-60.         [ Links ]

[24] Bar-Joseph, Z., Gifford, D.K. and Jaakkola, T.S. 2001. Fast optimal leaf ordering for hierarchical clustering. Bioinformatics, 17(1), pp. S22-S29.         [ Links ]

[25] Rokach, L. 2010. Chapter 14: A survey of clustering algorithms, in Data Mining and Knowledge Discovery Handbook, 2^nd edition, Springer, pp. 269-298.         [ Links ]

[26] Arthur, D. and Vassilvitskii, S. 2007. K-means++: The advantages of careful seeding. Proceedings of the 18^th annual ACM-SIAM symposium on discrete algorithms (SODA), pp. 1027-1035.         [ Links ]

[27] Ibaraki, T. 1977. On the computational efficiency of branch-and-bound algorithms. Journal of the Operations Research Society of Japan, 20(1), pp. 16-35.         [ Links ]

 

 

Submitted by authors 23 Aug 2017
Accepted for publication 17 May 2018
Available online 31 Aug 2018

 

 

* Corresponding author: 212539072@stu.ukzn.ac.za