Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.29 n.2 Pretoria Aug. 2018
http://dx.doi.org/10.7166/29-2-1968
FEATURE ARTICLE
The value of money and the flaw-of-averages
P.S. Kruger*
Department of Industrial and Systems Engineering, University of Pretoria, South Africa
ABSTRACT
Given the state of uncertainty in the world, decision analysis and decision-making under conditions of uncertainty are becoming more important. However, any rational decision-making requires a criterion on which to base the decision - which implies the availability of a value system. This paper will provide a short introduction to the basic principles of some value systems and related concepts such as the value of money, the flaw-of-averages, interest and discount rates, utility theory, and decision analysis. It will employ a Monte Carlo simulation approach to investigate the possible influence of the flaw-of-averages on interest calculations, net present value calculations, and decision trees. It will show that, under certain circumstances, the flaw-of-averages might be present and significant.
OPSOMMING
Besluitanalise en besluitneming onder toestande van onsekerheid word meer belangrik gegee die heersende toestand van onsekerheid in die wêreld. Enige rasionele besluitneming benodig 'n kriterium waarop die besluit gebasseer kan word. Dit impliseer die beskikbaarheid van 'n waardestelsel. Hierdie publikasie sal 'n kort inleiding verskaf tot die basiese beginsels van sommige waardestelsels en verbandhoudende konsepte soos die waarde van geld, die gemors-van-gemiddeldes, rente- en verdiskonteringskoerse, utiliteitsteorie, en besluitanalise. Dit sal gebruik maak van 'n Monte Carlo simulasie benadering om die moontlike invloed van die gemors-van-gemiddeldes op renteberekeninge, huidige waarde berekeninge, en besluitbome te ondersoek. Dit sal aantoon dat, onder sekere omstandighede, die gemors-van-gemiddeldes betekenisvol teenwoordig mag wees.
1 INTRODUCTION AND BACKGROUND
Neither a borrower nor a lender be,
For loan oft loses both itself and friend,
And borrowing dulls the edge of husbandry.
"The Tragedy of Hamlet, Prince of Denmark", Act 1 Scene 3, by William Shakespeare
The purpose of this section is to provide a short introduction to some of the principles of selected concepts that will be used in sections 2 and 3. The reader with intimate knowledge of, for example, the value of money, the flaw-of-averages, the time and utility value of money, and decision analysis, may skip this section without loss of continuity.
Unless otherwise stated, all Monte Carlo simulation experiments in this paper have been conducted with a sample size of 10,000 replications, and all statistical inferences have been conducted at a five per cent level of significance.
Table 1 provides a summary of all the symbols and variables that will be used.
1.1 The value of money
Nowadays people know the price of everything and the value of nothing. "The Picture of Dorian Gray" by Oscar Wilde
The concept of money has been part of everyday life for millennia. It has developed, for example, from the use of gold coins, with intrinsic value to the present-day paper money with no intrinsic value at all. It is nevertheless the absolute core of any economic activity. The value of money might be defined as the purchasing power of the money [1], which is determined by the demand and the supply of money, like the prices of all other economic goods and services. This value might be influenced by numerous other factors such as interest rates, inflation rates, exchange rates, the state of an economy, business confidence, the political, social and financial stability in a country, and many more.
1.2 The flaw-of-averages
The best argument against democracy is a five-minute conversation with the average voter. Winston Leonard Spencer Churchill
The flaw-of-averages is a phenomenon that is well-known to mathematicians. Ignoring it, and only using averages, might have the result that the calculations performed with a model and the decisions based on it were wrong [4]. In its simplest form, it states that the convex transformation of a mean is less than or equal to the mean after convex transformation. In the context of probability theory, it is generally stated in the following form: If X is a random variable with expected value E(X) and the function F(X) is convex, then
F(E(X)) ≤ E(F(X))
where F(E(X)) is the function of the expected value and E(F(X)) is the expected value of the function [4]. This is often known as the flaw-of-averages (FoA) [5].
All that is required for the possible existence of the FoA is for a model or system to have a nonlinear input-output transformation function, and for at least one of the model input variables to be subjected to uncertainty [4].
1.3 The expected value of money
Fear of harm ought to be proportional not merely to the gravity of the harm, but also to the probability of the event.
"Logic and the Art of Thinking". An unknown co-author, possibly Blaise Pascal
The expected value (EV) is a concept used extensively in decision analysis as a criterion for decisionmaking, and was formulated independently by Blaise Pascal and Pierre de Fermat [6]. The EV of an alternative subjected to uncertainty may be computed by multiplying each possible outcome (gain or return) by the number of ways in which it can occur, and then dividing the sum of these products by the total number of cases [6]. It therefore attempts to incorporate both probability and return in one concept. However, the use of the EV might lead to erroneous decisions. This was first pointed out by Nicolaus Bernoulli, and became known as the St Petersburg aradox [6], which might be briefly described as follows [6, 7]:
"A game of chance for a single player consists of the tossing of an unbiased two-sided coin. If a head appears, the gambler receives two Rand and the coin is tossed again. If heads appears again, the gambler receives four Rand. This process is repeated until tails appears, at which time the game is terminated and the gambler may take his money. The question is: How much should the gambler be willing to pay for the privilege of playing this game?"
The expected value (EV) may be calculated as follows:
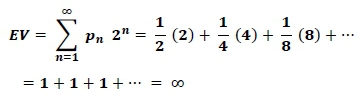
with pn being the probability for a head to occur on toss n (assumed to be ½ in this case), and n the number of tosses.
If the gambler is a true expected value decision-maker, they should be willing to pay almost any very large amount to play the game. However, no right-minded gambler or decision-maker will be willing to do this. It seems as if something else is playing a role in this decision process that is not included in the concept of an expected value.
In 1738 Daniel Bernoulli, the brother of Nicolaus, published an influential paper titled Exposition of a New Theory on the Measurement of Risk, with the central theme that "the value of an item must not be based on its price, but rather on the utility that it yields" [6]. Daniel argued further that "any decision relating to risk involves two distinct and yet inseparable elements: the objective facts and the subjective view about the desirability of what is to be gained or lost" [6]. He argued that the expected value considers only the facts resulting in the St Petersburg paradox [6]. Since then numerous attempts have been made to resolve the St Petersburg paradox [8], but Daniel Bernoulli's arguments resulted in the development of what became known as utility theory [7]. Utility theory and related concepts such as a utility function, the attitude towards risk, diminishing marginal utility, and the influence of wealth on decision-making have developed into some of the important concepts in economics and finances, and will be discussed in more detail in section 1.5.
1.4 The time value of money
Take no usury or interest from him; but fear your God, that your brother may live with you. You shall not lend him your money for usury, nor lend him your food at a profit.
The Bible, Leviticus 25:36-37
Charging interest on loans or receiving interest on investments has been common practice for many years, but has been condemned by many cultures. However, the concept of interest is a vital part of any economic and financial system. For long periods in the past, the basic interest rate was considered as virtually constant; but in more recent times the interest rate has displayed more volatility, as shown in Figure 1 (obtained from the World Bank data base [9]). This might be the result of the increasing political, social, economic, and financial uncertainty experienced throughout the world [10]. The data shown in Figure 1 might contain some systematic variation but also some randomness. The data displays a typical time series characteristic; and it was decided to use an auto-regressive-moving-average (ARMA or Box-Jenkins) modelling approach [11, 12] to isolate and evaluate the random component. A piece-wise linear function was fitted to the data (or, equivalently, the calculation of first order derivatives) and used to transform the data into a stationary process, as required by the ARMA-modelling process [11, 12]; it is shown in Figure 2. The autocorrelation function of the data set is shown in Figure 3. The auto-correlation function shows a diminishing sine wave pattern; and, based on this, a second-order autocorrelation model (AR(2)) was fitted to the data [11], enabling the estimation of the noise-term by calculating the residuals, as shown in Figure 4.
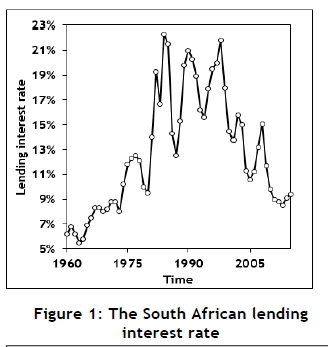
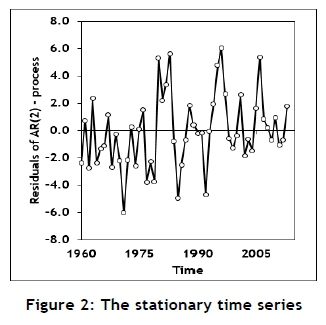
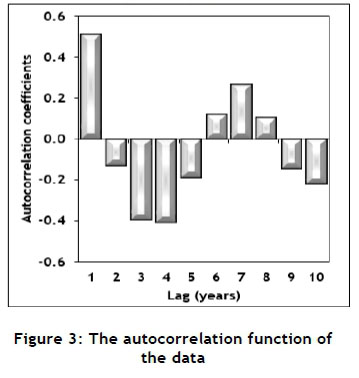
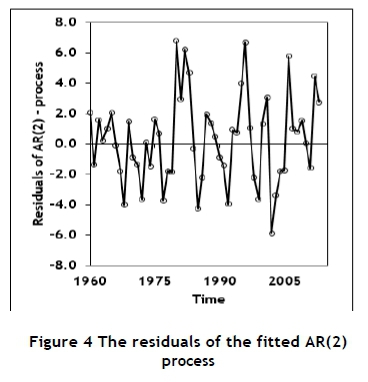
The mean of the residuals is zero, as can be expected; but it has a standard deviation of about three percentage points, indicating a significant random component.
This estimate of the random component might suffer from several inadequacies. For example, it might overestimate the random component, since some systematic errors might still be included. Furthermore, it might underestimate the true random component, since the Reserve Bank uses its control over the prime rate to limit the volatility of the interest rate. The use of instruments such as various commissions and services charges levied by financial institutions might further inflate the nominal interest rate. The data shown in Figure 1 is an annual average. This averaging might cause some smoothing that might hide some of the variance inherent in the interest rate. Nevertheless, it seems as if the interest rate might contain a significant random component; and it might be appropriate to consider it as a random variable, or at least as a variable containing a significant random component. This is important, since the interest rate is often one of the principle input variables of financial systems, and its stochastic characteristics might cause the effect of the flaw-of-averages to be present. This possibility will be investigated in section 2 for the calculation of compound interest and net present value.
1.5 The utility value of money
The utility resulting from any small increase in wealth will be inversely proportionate to the quantity of goods previously possessed. Wealth is anything that can contribute to the adequate satisfaction of any sort of want. "Exposition of a New Theory on the Measurement of Risk" by Daniel Bernoulli
Utility theory was only properly formulated by John von Neumann and Oskar Morgenstern as part of their development of game theory in the late 1940s [3], and might be summarised as shown in Figure 5. Consider a simple decision-making problem consisting of only two possible decisions with outcomes X1 and X2, and associated probabilities of occurrence of P1 and P2 respectively. The expected value (EV) might be calculated, as well as the expected utility (EU) given a utility function U(X). Using the value of the EU and the inverse function U'(X), the certainty equivalent (CE) might be calculated.
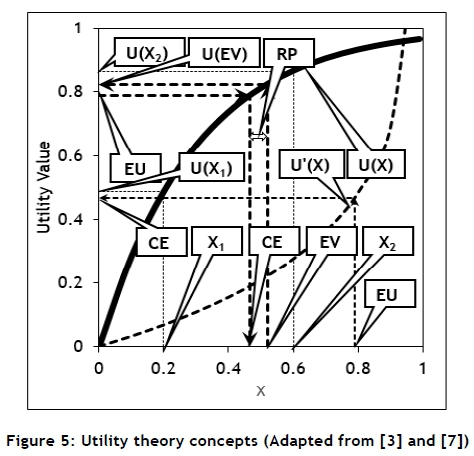
The EV and the EU might be used for purposes of decicion-making, and the CE and the risk premium (RP) provide estimates of the decision-maker's attitude towards risk. Proper definitions of these concepts are available elsewhere [3, 7]. Tables 2, 3, and 4 provide an illustration of the calculations required and the output obtained for a hypothetical example.
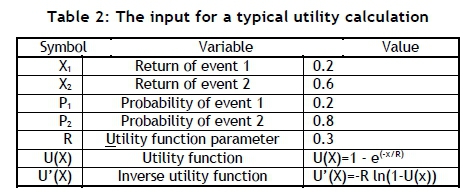

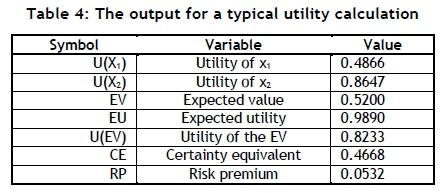
The exponential expression chosen to model the utility function is used often because of its flexibility in modelling various utility functions adequately, and the availability of the inverse function in a closed mathematical format.
More detailed definitions and discussions of the important concepts of utility theory, such as the certainty equivalent, can be found elsewhere in the literature [3, 7]
1.6 Decision trees
Object to be beloved and played with. Better than a dog anyhow Charms of music and female chit-chat Not forced to visit relatives and bend in every trifle If many children forced to gain one's bread
Marry, Marry, Marry. Q.E.D.
Part of Charles Robert Darwin's list on the relative
advantages and disadvantages of marriage
A decision tree [13, 3] is one of the important techniques available as support for decision-making under conditions of uncertainty. The concept is straight forward, and is best illustrated by an example, albeit a somewhat facetious one. Consider the dilemma faced by Charles Robert Darwin about whether he should commit to marriage or not. He might have constructed his problem as a decision tree - as shown in Figure 6, which illustrates most of the concepts and structures found in a typical decision tree. The decision tree indicates that, if Darwin is an expected value decisionmaker, he should get married to his rich first cousin, Emma Wedgwood, as soon as possible. They were married for 43 years til Charles' death in 1882, and the union produced 10 children. The possible effect of the flaw-of-averages on decisions based on decision tree analysis will be discussed in section 3.
2 COMPOUND INTEREST, NET PRESENT VALUE, AND THE FLAW-OF-AVERAGES
The power of compound interest is the most powerful force in the universe.
Attributed to Albert Einstein
2.1 Compound interest
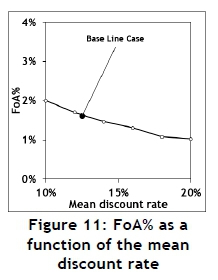
In section 1.2 it was mentioned that, for the flaw-of-averages (FoA) to be present, at least one of the input variables should be subjected to uncertainty, and this variable should be transformed by a non-linear relationship. The following equation, used for calculating compound interest, shows that F is a linear function of P. Furthermore, n and t are constants in a specific situation. However, as shown in section 1.4, the interest rate, i might be a random variable, while F is a non-linear function of i, and therefore the FoA might be present. A Monte Carlo model was designed as a base line case with parameter values and results, as shown In Table 5. A symmetric triangular distribution was assumed for the interest rate, since there is no better information available to the contrary; and the triangular distribution is often used under such circumstances [14]. The parameter values chosen are like those obtained for the World Bank data shown in Figure 1 of section 1.4.
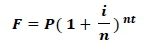
With: F, the final value,
P, the principle (assumed to be one),
i, the annual interest rate,
n, the annual compound frequency (assumed to be 12) and
t, the transaction time (years).
The Monte Carlo model was designed and used to execute a few experiments to investigate the sensitivity of the output to the input. These results are summarised in Figures 7, 8, and 9.
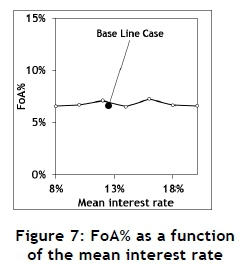
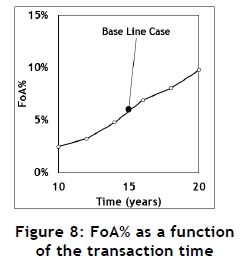
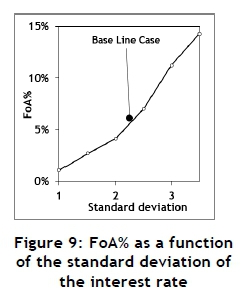
The mean does not show a significant influence on the FoA; but both the transaction time and the standard deviation of the interest rate have a significant influence. This confirms the results obtained and published elsewhere [4].
If the FoA is ignored, it might result in incorrect decisions. Consider two hypothetical investments, A and B. The parameter values for these examples are summarised in Table 6, and the results are summarised in Figure 10.
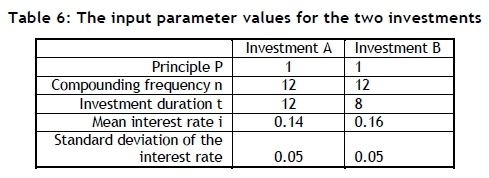
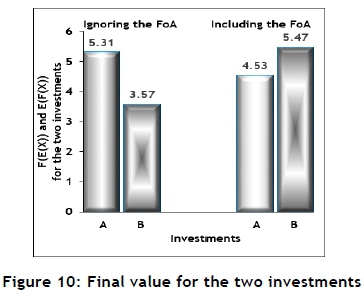
Figure 10 shows that investment A is better than investment B for some combinations of the values of the assumed standard deviations of the two interest rates, but that investment B is better than A for other combinations. Furthermore, the typical risk profiles shown in Figure 11 indicates that, although one investment might be the better one, there might be a higher risk associated with it. This is the result of the differences in the assumed values for the standard deviations of the investments. However, the FoA might not be so important in the case of compound interest. A typical financial institution usually has control, within limits, of the interest it charges or offering, and might compensate for the effects of the FOA, whether wittingly or not. Various other instruments, such as financing fees, might also be used for this purpose.
2.2 Net present value
Do not dwell in the past, do not dream of the future,
concentrate the mind on the present moment.
The Buddha
The net present value (NPV) is in many ways the mirror image of simple interest, and does have some disadvantages [15]; but it is one of the best-known and most widely used available measures for choosing between two projects and incorporating the time value of money [15]. The NPV may be calculated using the following formula:
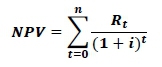
with: NPV, the net present value,
Rt, the cash flow at time t,
i, the discount rate,
t, the time of a cash flow and
n, the total number of time periods.
This formula shows that the NPV is a linear function of Rt and a non-linear function of i and t. However, t is usually a constant in a specific situation, and will be treated as a parameter. It will be assumed that the interest rate, i, is a random variable (see section 1.4).
A Monte Carlo model was designed as a base line case with parameter values and results, as shown in Table 7. A symmetric triangular distribution was assumed for the discount rate.
The Monte Carlo model was used to execute a few experiments to investigate the sensitivity of the output to the input. These results are summarised in Figures 11, 12, and 13.
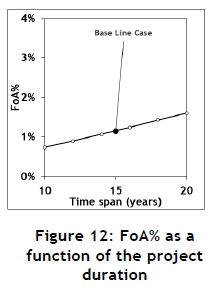
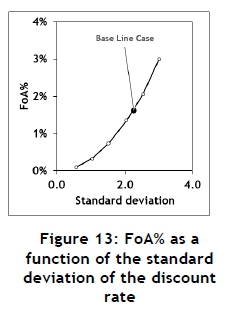
The mean of the discount rate and the project duration do show a small influence on the FoA%, but the standard deviation of the discount rate has a significant influence. If the FoA is ignored, it might result in erroneous decisions. Consider two hypothetical projects, 1 and 2. The parameter values for these examples are summarised in Table 8, and the results are summarised in Figure 14.
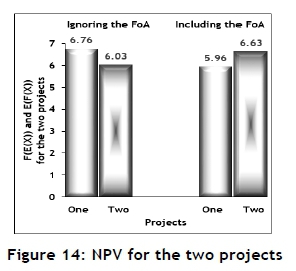
Conclusions and remarks similar to those made in section 2.1 about the compound interest are appropriate for the net present value (see section 2.1).
3 DECISION ANALYSIS AND THE FLAW-OF-AVERAGES
There's a time and a place
For you to make your mark and show your face
There's a place in time
When you must step outside the line
"A time and place" by Mike and the Mechanics
The branch of operations research concerned with decision-making under conditions of uncertainty is known as decision theory [3, 7, 16], and one of the best-known techniques for supporting decision theory is known as decision trees [3, 7, 13). The basic principles of decision tree were briefly discussed in section 1.6. The idea of a decision tree was probably first used by Blaise Pascal in the formulation of his famous wager [6], which might be stated as:
God is, or he is not. Which way should we incline?
Figure 6 of section 1.6 might be used to define a basic building block from which most decision trees constructed. Such a basic building block is shown in Figure 15. The symbols, variable definitions, and variable values that will be used are shown in Table 9 and Figure 15. The decision tree shown in Figure 15 will be used as a base line case.
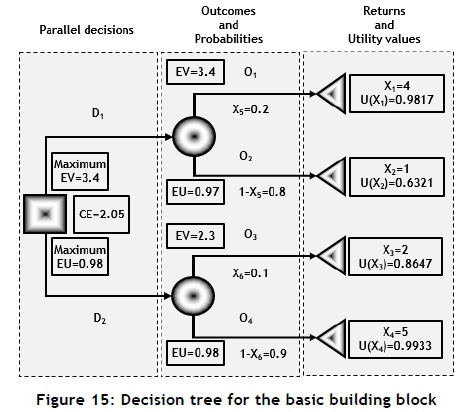
From Figure 15, decision D1 is the best if the EV is used, but decision D2 is the best, based on the EU. However, the existence of this event is dependent on the shape of the assumed utility function. A Monte Carlo simulation model was designed and executed for the basic building block. The results are summarised in Table 10, indicating that the FoA% for the EV, the EU, and the CE are all significant.
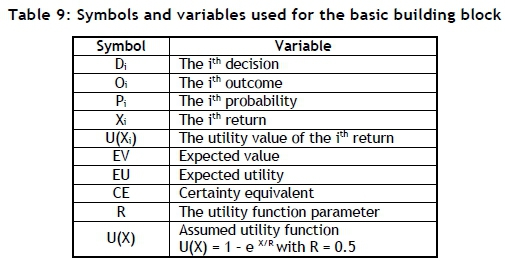
The Monte Carlo model was also used to conduct several experiments for values of the input variables close to the values for the equivalent variable values of the basic building block. The results are shown in Figures 16 and 17 as Tornado and Spider sensitive plots respectively. Both Figures 17 and 18 indicate that the EV is not sensitive to the value of the assumed utility function parameter. This value determines the shape of the utility function, which does not have an influence on the EV. The value of the utility function parameter will therefore not be included in the following sensitivity analysis.
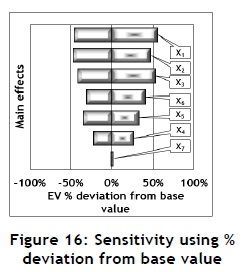
However, this kind of sensitivity analysis - that is, changing one input variable value at a time while keeping the values of all the other input variables constant - might suffer from some drawbacks, such as not being able to identify any two-factor interactions. A significant two-factor interaction might indicate that the sensitivity of the output for the value of a specific input variable might not only depend on the specific value of that input, but might also be influenced by the value of another input variable. This problem might be resolved by using the principles of experimental design [11, 17].
An appropriate six-factor fractional factorial design was identified [17]. The characteristics of this design are summarised in Table 11 [17].
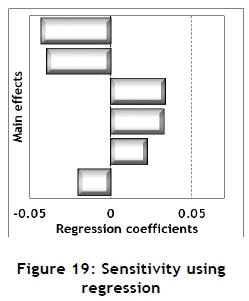
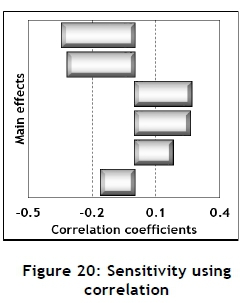
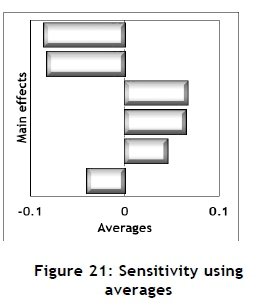
The 32 experiments, each of sample size of 10,000, were conducted using the Monte Carlo simulation model. These results may be used to conduct sensitivity analysis for the main effects. Several such measures are available, and are shown in Figures 19, 20, and 21.
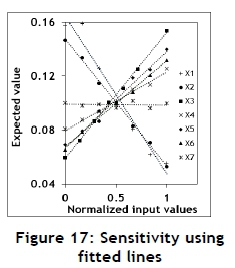
Regression coefficients may be obtained by fitting a regression equation using the results from the Monte Carlo experiments for the main effects as follows:
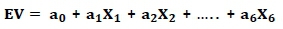
with Xi, for i=1 to 6 the main effects
ai, for i=0 to 6 the regression coefficients
The values of the regression coefficients are shown in Figure 19.
Secondly, correlation coefficients may be calculated from the Monte Carlo results for the main effects relative to the EV; these are shown in Figure 20. Thirdly, the main effects may be estimated by calculating the averages of the high value minus the average of the low value [17], as shown in Figure 21.
The approximate patterns provided by these different approaches are very much the same.
The results of the Monte Carlo experiments might also be used to fit a regression equation that includes both the main effects and the two-factor interactions, as follows:
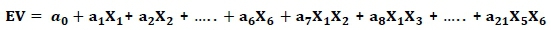
with Xi, i=1 to 6 the main effects (variables),
XiXj, i=1 to 5 and j=2 to 6 the two factor interactions and
ai, i=0 to 21 the regression coefficients.
The regression coefficients and P-values are shown in Table 12, which indicates that two of the main effects are non-significant. However, one of the two-factor interactions is significant. The presence of a significant two-factor interaction implies that the results from this section cannot be assumed, without further investigation, to be applicable to all decision trees. Therefore, every decision tree should be investigated on its own for the presence and severity of the FoA.
4 SUMMARY AND CONCLUSIONS
If a man will begin with certainties, he shall end in doubts; but if he will be content to begin with doubts, he shall end in certainties.
Francis Bacon
One of the main insights provided by this paper is the important contribution of uncertainty, typically manifested as the standard deviation of one of the input variables of a model, on the existence and severity of the flaw-of-averages. The crucial role played by the standard deviation in many aspects of statistical modelling is well-known.
This paper investigated the possible existence and severity of the flaw-of-averages (FoA) in three well-known and widely used industrial engineering models: compound interest, net present value, and decision trees. It was determined that the FoA is significant in all three of these situations, albeit under certain circumstances. The FoA might play a significant role in numerous other widely used models - for example, any inventory control model such as vendor problem subjected to uncertainty, will probably display the FoA [4]. Therefore, it might be prudent to consider the use of a Monte Carlo simulation model to evaluate the effect of the flaw-of-averages in any situation where a significant uncertainty of one or more of the input variables is present or suspected.
REFERENCES
[1] Sennholz, H.F. 1996. The value of money. Foundation for Economic Education. Available from: https://fee.org/articles/. Last accessed July 2017. [ Links ]
[2] Dayan, P. 2008. The role of value systems in decision making. Gatsby Computer Neuroscience Unit, UCL, London. Available from: http://mitpress.universitypressscholarship.com/view/10.7551/mitpress/9 780262195805.001.0001/upso-9780262195805-chapter-3. Last accessed July 2017. [ Links ]
[3] Winston, W.L. 1994. Operations research: Applications and research. Duxbury Press. [ Links ]
[4] Kruger, P.S. and Yadavalli, V.S.S. 2016. Probability management and the flaw-of averages. The South African Journal of Industrial Engineering, 27(4), pp 1-17. [ Links ]
[5] Savage, S.L. 2003. Decision making with insight. Thomson Brooks Cole. [ Links ]
[6] Bernstein, P.L. 1998. Against the gods: The remarkable story of risk. John Wiley & Sons, New York. [ Links ]
[7] Clemen, R.T. and Reilly, T. 2001. Making hard decisions with decision tools. Duxbury Press. [ Links ]
[8] Garcia, J.A. 2013. A bit about the St. Petersburg paradox. Available from: www.math.tamu.edu/-david.larson/garcia13.pdf. Last accessed September 2017. [ Links ]
[9] The World Bank Group. 2017. Lending interest rate (%) - South Africa. Available from: http://data.worldbank.org/indicator/FR.INR.LEND?locations=ZA. Last accessed July 2017. [ Links ]
[10] Jeffries, S. 2016. Welcome to the new age of uncertainty. The Guardian. Available from: https://www.theguardian.com/world/2016/jul/26/. Last accessed July 2017. [ Links ]
[11] Montgomery, D.C. and Johnson, A.J. 1976. Forecasting and time series analysis. McGraw-Hill. [ Links ]
[12] Box, G.E.P., Jenkins, G.M. and Reinsel, G.C. 2013. Time series analysis. John Wiley & Sons, Inc., Hoboken, NJ. [ Links ]
[13] Olivas, R. 2007. Decision trees primer. Available from: http://www.public.asu.edu/-kirkwood/DAStuff/decisiontrees/index.html. Last accessed June 2017. [ Links ]
[14] Kelton, W.D., Sadowski, R.P. and Sadowski, D.A. 1998. Simulation with Arena. McGraw-Hill. [ Links ]
[15] De Neuville, R. and Scoltes, S. 2002. Real options for engineering systems. MIT Press. Available from: http://ardent.mit.edu/real_options/RO_current_lectures. Last accessed July 2017. [ Links ]
[16] Arsham, H. 2015. Tools for decision analysis: Analysis of risky decisions. Available from: http://home.ubalt.edu/ntsbarsh/Business-stat/opre/partIX.htm. Last accessed July 2017. [ Links ]
[17] National Institute of Standards and Technology, US Department of Commerce. 2003. NIST/SEMATECH e-handbook of statistical methods. Available from: http://www.itl.nist.gov/div898/handbook/pri/section3/pri3347.htm. Last accessed July 2017. [ Links ]
Submitted by authors 13 Apr 2018
Accepted for publication 13 Jun 2018
Available online 31 Aug 2018
* Corresponding author: paul.kruger12@outlook.com














