Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.29 no.1 Pretoria 2018
http://dx.doi.org/10.7166/29-1-1898
GENERAL ARTICLE
A two-stage greedy heuristic for a flowshop scheduling problem under time-of-use electricity tariffs
A.E. Pilerood; M. Heydari*; M.M. Mazdeh
Department of Industrial Engineering, Iran University of Science and Technology, Islamic Republic of Iran
ABSTRACT
This paper studies a two-machine flowshop scheduling problem under time-dependent electricity tariffs, in which electricity prices may vary from time to time throughout the day. The main issue is to assign a set of jobs to available time slots with different electricity prices to minimise the total resource cost required for processing the jobs. The main contribution of this work is two-fold. First, a new continuous-time mixed-integer linear programming (MILP) model is proposed for the problem. Second, a two-stage greedy heuristic is developed. A computational experiment on randomly generated instances demonstrates that the greedy algorithm can improve the objective function by almost 40 percent. The algorithm can be applied by production managers to scheduling jobs in a flowshop under time-of-use (TOU) electricity tariffs to save electricity costs.
OPSOMMING
Hierdie artikel bestudeer 'n vloei skeduleringsprobleem met twee masjiene wat onderhewig is aan tydafhanklike elektrisiteitstariewe. Die tarief mag varieer van tyd-tot-tyd deur die loop van die dag. Die hoof probleem is die toekenning van werk aan beskikbare tydgleuwe met verskillende tariewe met die doel om die totale hulpbronkoste te minimeer. Hierdie artikel se hoofbydrae is tweeledig. Eerstens word 'n nuwe kontinue tyd gemengde heeltal lineêre programmering model voorgestel. Tweedens word 'n tweevlakkige suinige heuristiek ontwikkel. 'n Rekenaarsimulasie met lukraak gegenereerde insette demonstreer dat die algoritme die koste met byna 40 persent kan verminder. Die algoritme kan deur produksiebestuurders toegepas word om take in n vloei-werkswinkel wat onderhewig is aan elektrisiteitstarief veranderinge te skeduleer met die doel om kostes te verminder.
1 INTRODUCTION
Energy has been the subject of many researches in recent years. In fact, rapid economic development in various countries has led to the unbridled use of energy sources in different parts of the world; therefore, energy shortages became a bottleneck in the development of many countries. Electricity tariffs and international non-renewable energy costs are increasing at a rapid rate. These trends highlight the need for competitive, energy-intensive industries to reduce their energy costs [1].
Management of energy consumption in the manufacturing sector will be realised with two approaches: a hard approach, and a soft one. In the first approach, energy consumption could be managed by changing and using modern and efficient machinery and other hardware-related techniques. However, in the software approach, management principles can be used to reduce energy consumption and create sustainable production. Demand-side management is one of the soft approaches that can be used by energy suppliers. The aim of this approach is to transfer energy consumption from peak to non-peak hours to reduce the cost of generating energy, in addition to enabling the public to use the produced energy. One of the most common methods is time-based pricing policies. In this policy, called time-of-use (TOU) tariffs, the cost of electricity consumption varies throughout the day, and as a result, consumers are urged to manage their demand for energy consumption. For example, in Iran, the cost of electricity consumption varies according to different periods of the day [2]. Figure 1 shows the relationship between hours and the low-load, medium-load, and peak-load of the electricity distribution system for a typical home in the first six months of the year. The electricity tariff varies in each of these situations.
In Iran, approximately 13 percent of the manufacturing sectors use electricity as their main source of energy, and more than 80 percent of the energy is consumed by production lines.
On the other hand, one of the common workshop environments is a flowshop, in which a number of jobs require different operations at different stages. Each operation at any stage requires a specific time for each job. The basic point in a flowshop is that each job should pass each stage in a oneway and forward-flow sequential order. Determining an appropriate sequence and schedule for doing jobs in a flowshop can reduce various costs in the system. This paper is among the few that address the theoretical discussions of scheduling-related optimisation with time-dependent costs in a flowshop environment.
This research addresses the problem of job scheduling in a two-machine flowshop to minimise energy costs, where the tariff of electricity follows a TOU policy. The main challenge is to allocate operations to the empty time intervals in the flowshop so that the amount of energy required to process the jobs is minimised. This paper is important from two perspectives. First, a continuous-time mixed-integer linear mathematical model is presented for determining optimal task scheduling. Second, a two-step greedy heuristic algorithm is presented to solve high-level problems. The algorithm can be applied by production managers to schedule jobs on a two-machine flowshop under TOU electricity tariffs to save electricity costs.
2 LITERATURE REVIEW
The paper by Nilsson and Söderström [3] is among the earliest research with a particular focus on time-dependent costs. In their research, different concepts of time-dependent costs of energy are discussed, and they state that the energy costs can be reduced in the planning of industrial enterprises production by considering the peak time of energy consumption and changing the production schedule. Castro, Harjunkoski and Grossmann [4] addressed the role of time-dependent scheduling with regard to variable hourly energy costs, and provided a variety of algorithms for optimal scheduling of the factory production plan in continuous production planning. According to their claim, time-dependent scheduling can be used to reduce the energy costs for factories by up to 20 percent. Wan and Qi [5] examined the varied cost of task execution in different timeslots (i.e., slotcost) and filled the gap in the study of these subjects in the scheduling literature. In their general model, each time interval k can have a cost of πk. They did not discuss the energy-related costs specifically, but stated that TOU could be a specific application of their research. They then examined the combination of different objective functions of single-machine scheduling with this time-dependent cost, and proved that general hybrid problems, such as the combination of total flow time with time-dependent costs, or total tardiness with time-dependent costs, are categorised as NP-hard problems.
Another study of scheduling jobs with time-dependent costs was done by Moon, Shin and Park [6]. They defined a scheduling problem for parallel machines, taking into account time-dependent and machine-dependent electricity costs. The research tries to find the best scheduling by offering a meta-heuristic algorithm based on a genetic algorithm to minimise energy costs and the maximum time of completion - i.e., makespan. In fact, by inserting idle time at costly times, they tried to find optimal scheduling; but since inserting the idle time of machines can lead to a longer completion time for tasks, they attempted a trade-off between these two functions.
Shrouf, Ordieres-Meré, García-Sánchez and Ortega-Mier [7] investigated a single-machine scheduling problem for time-dependent energy costs. In this research, a machine can be defined by three states: processing, idle, and off. Each of these three states has a different energy consumption, and energy costs change overnight and hourly. The results of this research determine which jobs should be done and in which order, and how the machine transits between the different states. The aim of this research is to minimise the total cost of energy. After providing a mathematical model, a meta-heuristic algorithm based on a genetic algorithm is proposed, due to the difficulty of the problem.
Fang, Uhan, Zhao and Sutherland [8] studied a single-machine scheduling problem in which each task has a different processing time and energy consumption. The main aim of this study was to achieve the best scheduling of jobs to minimise the total cost of energy, where the energy costs are time-dependent.
Another study, by Zhang, Zhao, Fang and Sutherland [9], is in the area of flowshop scheduling to minimise the two objective functions of energy cost and CO2 emission, and in which energy costs follow the time-dependency model. In their problem, every job has a processing time and a certain amount of energy consumption per machine. According to their assumption, replacing tasks from the peak time of energy consumption to a non-peak time can increase CO2 production while reducing energy costs (because coal power stations can be used instead of gas). Consequently, the paper aims to find a Pareto front of energy costs and CO2 emissions. In order to solve the problem, the researchers presented time-indexed integer programming.
Che, Zeng and Lyu [10] presented a mathematical model and a greedy heuristic algorithm to find the best scheduling of jobs in a single-machine environment. In their study, each job for processing had a certain processing time with an accompanying amount of required energy. Consequently, finding a schedule to minimise the costs of processing the entire job was realised by the proposed mathematical model, which assumed a TOU pricing policy for energy. The authors presented a greedy heuristic algorithm to achieve fairly good answers. Ding, Song, Zhang, Chiong and Wu [11] investigated a similar problem to that studied by Che et al. [10], but in the environment of parallel machines. The aim of that was to find the optimal scheduling to achieve the lowest total energy cost of the system, with the makespan no less than a threshold determined by the user. To solve this problem, they proposed two approaches. In the first approach, the problem was modelled by mathematical programming in the form of a time-interval-based mixed integer linear program. In the second approach, the problem was redefined by the Dantiz-Wolfe decomposition technique, and a heuristic algorithm of column generation was proposed to solve it.
3 PROBLEM DEFINITION AND MATHEMATICAL MODEL
We are studying a two-machine flowshop problem with a given set J=(1,2,..., n) of two-operation jobs that are available to be processed at time zero. Each job requires the first operation to be on machine 1 and the second operation on machine 2. At any time, each machine can process one job at most; and each job can be processed on one machine at most. Once the processing of a job on a machine has started, it must be completed without interruption. Also, each job must be processed in the same order on every machine. Let pj,1 and pj,2 be the processing times of job j on machines 1 and 2 respectively.
On the other hand, the processing of jobs consumes energy resources and incurs corresponding resource costs - i.e., electricity costs. Let qj,1 and qj,2 be the resource demand for the first and the second operations of job j respectively. The resource price varies in time horizon and obeys the TOU tariffs. A set of P, consisting of K time periods, is used to formulate the time-dependent pricing scheme. Period k is characterised by its starting time tk, duration ak, and resource price fk. The main aim of the problem is to assign the jobs to the available cost periods with different resource prices in the time horizon [0,T] to minimise the total resource cost required for processing them. In fact, when an inserted idle time schedule is permitted, the solution is to determine the start time and the completion time of each operation. The single machine version of this problem has been proven to be strongly NP-hard [8].
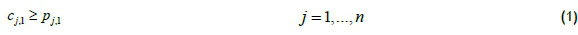
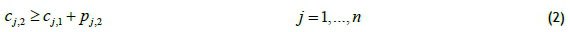
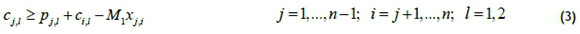
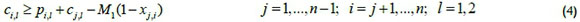
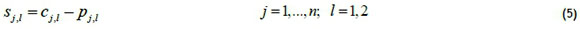
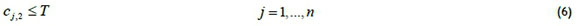
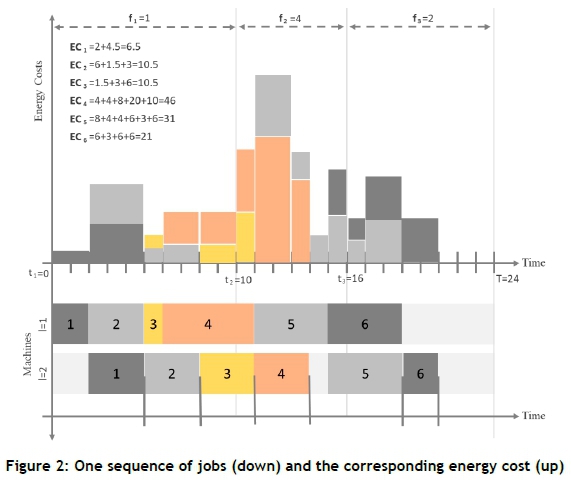
To clarify the problem, let's consider a small example with six jobs and three cost periods. Suppose each job has a specific processing time and energy demand on each machine, based on Table 1. Table 2 gives the TOU tariffs throughout a day. Figure 2 shows one sequence of jobs and their corresponding energy cost (EC).
It is worth mentioning that T is seen as the upper bound for the makespan of the problem because, if some sequences with a completion time later than T exist, they will not be feasible. So T is a parameter that is defined by the decision-maker. In this paper, T is a number more than the upper bound of the makespan. Kim [12] developed a procedure to generate a sequence with the maximum makespan, which we show as Q,. Then in our problem it is assumed that T>Cu, which implies that a feasible schedule always exists.
To develop a mixed integer mathematical model, two types of variables are needed. The first type will be used to sequence jobs and determine a feasible schedule, while the latter will be used to calculate the total energy costs (TEC).
To define a feasible schedule, an approach inspired by Manne [13] is suggested, based on whether a job occurs before others. Let Xj,i be a binary variable equal to one, if job j precedes job i in the sequence (not necessarily immediately before it), and zero otherwise. Also let sj,l and cy be the start time and completion time of each job j on the lth machine respectively. Finally, the constant M1 used in the formulation represents a large positive number. Then constraints (1-6) can be used to sequence jobs in a two-machine flowshop and also determine the start and completion time of each operation.
It should be noted that an operation might be processed in more than one cost period because either its processing time is sufficiently greater than the duration of a period, or it is processed across two or more adjacent periods. For this reason, three cases can be distinguished to calculate the energy cost of operations. The first is when an operation is completely processed within a cost period. The second happens when an operation is processed in two adjacent cost periods. Finally, the third happens when an operation is completed within more than two cost periods. Figure 3 shows an example of each of these cases.
To calculate the energy costs of each job, two types of binary variables are defined: Sj,k,l (a binary variable), which is equal to 1 if job j starts its lth operation at time period k; and Fj,k,l, which is equal to 1 when job j completes its lth operation at time period k. yj,k,l shows how much time of each operation lth of job j is processed at time period k. Also, tk, ak, and fk are starting time, duration, and resource cost of each cost period respectively. Finally, for simplicity, tK+i is considered as T, while K is the total number of cost periods.
To accelerate the speed of solvers, it can be useful to define a value for M1=T+max(pj,l) and M2=T.
With the notation given above, the investigated problem can be formulated as the following MILP model:
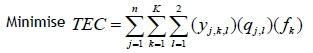
Subject to:
(1-6)












Constraints (7-10) calculate the amount of time each operation occupies at different cost periods. Constraints (11-13) deal with assigning the binary variable of Sj,k,l, and similarly, constraints (14-16) calculate Fj,k,l, which shows if an operation is completed in a period.
Some studies in the literature use a discrete-time formulation for scheduling problems under time-dependent costs. With discrete-time formulation, the number of binary variables can be large due to the division of the time horizon. In this work, a continuous-time formulation is proposed. The proposed MILP can find optimum solutions for small size instances, while heuristic algorithms are suggested to solve larger size instances.
4 GREEDY HEURISTIC ALGORITHM
In this section, a two-stage greedy heuristic algorithm is proposed to solve high-level problems. The logic of this algorithm is to allocate tasks and operations to cost intervals, so that in each stage the lowest cost is realised. The first stage of this algorithm is to allocate operations to the boundaries of the cost intervals. The second stage of the algorithm will allocate the remaining tasks to the cost intervals.
Before investigating the algorithm, it is necessary to provide a series of definitions.
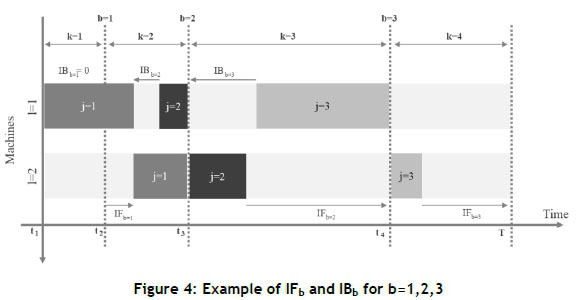
Definition one. Boundaries set (B): Boundary is a part of the time that a cost interval varies from its own adjacent cost interval. The set B represents all the boundaries of the problem, which is B={1,2,...,K-1}. Also, the time of the boundary is b ε B is tb+1. Figure 4 shows a planning horizon with four cost intervals and three boundaries.
Definition two. ∆qj: The difference between the resource demands of job j on the first machine and those on the second machine. In fact, ∆qj=qj,1-qj,2.
Definition three. ∆fb: Indicates the difference between the resource cost of a cost interval and that of the previous cost interval, which is calculated for each boundary as ∆fb=fb+1-fb>
Definition four. q'j: Shows an average value for the resource demand, which is calculated as the weighted average of the resource demands of each job on both machines. It is calculated as the following equation:

Definition five. IFb: Indicates the amount of idle time on the second machine if we move from the boundary b ε B to go forward in time. Indeed, it represents the amount of idle time on the second machine after the boundary b ε B . If we assume that a new operation begins at the time of the boundary tb+1, then that operation can continue its activity until either it reaches another operation, or it reaches the end of the programming horizon. Figure 4 shows the value IFb for b=1,2,3.
Definition six. IBb: The amount of idle time on the first machine shows for the roll-back movement at the time of the border b є B . Figure 4 shows the value IBb for b=1,2,3.
Definition seven. 1h,k: By considering an initial sequence of operations, h,k indicates the amount of idle time between the first idle time on the first machine in the cost interval k ε P and the next operation on the first machine or the end of the programming horizon, whichever comes first. Figure 5 shows the value 1h,k for different cost intervals.
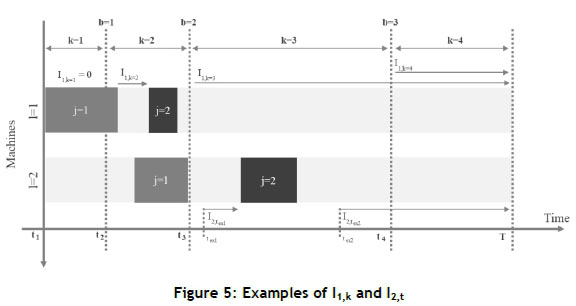
Definition eight. I2,t: Indicates the amount of empty time on the second machine from any desired time t forward to the next operation on the second machine or the end of the programming horizon, whichever comes first. Figure 5 shows the value I2,t(ex1) and I2,t(ex2) for two imaginary time points of ex1 and ex2 as examples.
Definition nine. Feasible partial sequence (π): A partial job sequence - a sequence that does not necessarily consist of all the jobs - will be called feasible if it has the following conditions:
1) The time of completion of the last job on the second machine is not greater than T; 2) The operations on each machine do not have any overlap, and each machine at any moment processes only one task; 3) The sequence of jobs on the first machine is equal to the sequence of jobs on the second machine. Consequently, the total cost of resources for jobs of feasible partial sequence can be easily calculated.
Definition ten. Adjustment function: This function will modify the partial sequences so that they are feasible. This function transforms the infeasible partial sequence by pushing the overlapped jobs forward in time in order for the partial sequence to be feasible. The output of this function is of two types:
1) If it can be arranged by replacing tasks forward, the total resource cost of the partial sequence will be calculated and reported.
2) A FALSE value will be reported if it fails to reach a feasible sequence by pushing tasks forward.
Figure 6 shows an example of how the initial infeasible partial sequence will be made feasible by pushing tasks forward in time, if the new job number 4 is placed after the first job.
The first stage of the proposed algorithm is to allocate tasks with the highest ∆qj to boundaries with the highest Afb. In the second stage of the algorithm, the remaining jobs will be seen as a continuous pack of jobs with a new resource demand of q'j. Therefore, the jobs that have a higher q'j will be allocated to the idle times of each cost interval, and an interval that has the least cost will be considered as the starting time of the job. This procedure will be continued until all jobs are scheduled. The algorithm pseudo-codes of the first and second stages are presented below. The description of the basic operators used in the pseudo-codes is: Set cardinality |A|, which returns the number of elements within the set A; Set difference A-B denotes the difference between sets A and B, returning set A with all members in B removed from A.
Although the answer is not optimal, the result obtained from implementing this algorithm can be viewed as acceptable. It can also be used as a foundation for implementing a more complex meta-heuristic that may yield a closer configuration to the optimal solution.
5 THE RESULTS OF IMPLEMENTING THE ALGORITHM
The processing time per operation, and the number of resources required of each operation on each machine respectively, are generated from the discrete uniform random distribution with a range of 1 to 10 and a range of 1 to 5 respectively. Then, based on the proposed approach by [12], the upper limit is calculated for the maximum completion time of jobs, and is considered to be equivalent to the T parameter. Then the programming horizon is divided into an equal number of cost intervals, and the resource cost per interval is generated based on the discrete uniform random distribution in the range of 1 to 5. This algorithm is coded by Matlab 2012. To investigate the proposed heuristic algorithm's performance, the algorithm is implemented on a wide range of problems. The algorithm's performance quality for small size problems is compared with the optimum value obtained from the implementation of the mathematical model. The suggested mathematical model is solved by CPLEX, and the results are reported at Table 3. Table 3 shows the result of error from the optimal value for small-size instances. For each class of problems, 10 samples are generated, and the average error of the heuristic algorithm is compared with the optimum value.
For large-size problems, the algorithm's performance is compared with two general dispatching rules, the sequence resulting from the Johnson rule and the sequence resulting from the highest resource demand (HRD) rule - i.e., jobs are sorted based on the non-decreasing order of q'. When applied to a sequence, these rules will result in a Johnson sequence and an HRD sequence respectively.
For each class of problems, 50 instances are generated. Table 4 shows the result of a comparison between the total resource costs of the sequences derived from the two dispatching rules. The average improvement rates show the average improvement of the objective function while the heuristic algorithm is applied.
6 CONCLUSION
This paper examined a two-machine flowshop scheduling under a time-of-use (TOU) tariff situation. The main objective of the study was to find a scheduling that minimises the total resource costs, although electricity prices may vary from time to time throughout a day. A new continuous-time mixed-integer linear programming (MILP) model was proposed for the problem, which could be solved using CPLEX to find an optimal solution for small-sized problems. To solve problems in large instances, a two-stage greedy heuristic was developed. The logic of this algorithm was to allocate tasks and operations to cost intervals, so that the lowest cost is realised in each stage. The first stage of this algorithm was to allocate operations to the boundaries of the cost intervals. The second stage of the algorithm allocates the remaining tasks to the cost intervals. A computational experiment on randomly-generated instances demonstrates that the greedy algorithm can improve the objective function by almost 40 percent. As for future research, it would be worthwhile to study other objective functions beside total energy costs, considering a multi-objective approach to solve the problem.
REFERENCES
[1] Goosen, P., Swanepoel, J. A., & Du Plessis, J. N. (2016). The need for a comprehensive energy management information system for industries. South African Journal of Industrial Engineering, 27(3), 111. URL: http://www.scielo.org.za/scielo.php?pid=S2224-78902016000300002&script=sci_arttext&tlng=en [ Links ]
[2] http://bahaye_bargh.tavanir. org.ir/ [ Links ]
[3] Nilsson, K., & Söderström, M. (1993). Industrial applications of production planning with optimal electricity demand. Applied eEnergy, 46(2), 181-192. URL: http://www.sciencedirect.com/science/article/pii/030626199390067Y [ Links ]
[4] Castro, P. M., Harjunkoski, I., & Grossmann, I. E. (2009). New continuous-time scheduling formulation for continuous plants under variable electricity cost. Industrial & eEngineering cChemistry Rresearch, 48(14), 6701-6714.URL: http://pubs.acs.org/doi/abs/10.1021/ie900073k [ Links ]
[5] Wan, G. & Qi, X. 2010. Scheduling with variable time slot costs. Naval Research Logistics, 57(2), 159-171. URL: http://onlinelibrary.wiley.com/doi/10.1002/nav.20393/full [ Links ]
[6] Moon, J.Y., Shin, K. & Park, J. 2013. Optimization of production scheduling with time-dependent and machine-dependent electricity cost for industrial energy efficiency. The International Journal of Advanced Manufacturing Technology, 68(1-4), 523-535. URL: https://link.springer.com/article/10.1007/s00170-013-4749-8 [ Links ]
[7] Shrouf, F., Ordieres-Meré, J., García-Sánchez, A. & Ortega-Mier, M. 2014. Optimizing the production scheduling of a single machine to minimize total energy consumption costs. Journal of Cleaner Production, 67, 197-207. URL: http://www.sciencedirect.com/science/article/pii/S0959652613008780 [ Links ]
[8] Fang, K., Uhan, N.A., Zhao, F. & Sutherland, J.W. 2016. Scheduling on a single machine under time-of-use electricity tariffs. Annals of Operations Research, 238(1-2), 199-227. URL: https://link.springer.com/article/10.1007/s10479-015-2003-5 [ Links ]
[9] Zhang, H., Zhao, F., Fang, K. & Sutherland, J.W. 2014. Energy-conscious flow shop scheduling under time-of-use electricity tariffs. CIRP Annals - Manufacturing Technology, 63(1), 37-40. URL: http://www.sciencedirect.com/science/article/pii/S0007850614000146 [ Links ]
[10] Che, A., Zeng, Y. & Lyu, K. 2016. An efficient greedy insertion heuristic for energy-conscious single machine scheduling problem under time-of-use electricity tariffs. Journal of Cleaner Production, 129, 565577. URL: http://www.sciencedirect.com/science/article/pii/S0959652616302359 [ Links ]
[11] Ding, J.Y., Song, S., Zhang, R., Chiong, R. & Wu, C. 2016. Parallel machine scheduling under time-of-use electricity prices: New models and optimization approaches. IEEE Transactions on Automation Science and Engineering, 13(2), 1138-1154. URL: http://ieeexplore.ieee.org/abstract/document/7349258/ [ Links ]
[12] Kim, Y.D. 1993. A new branch and bound algorithm for minimizing mean tardiness in two-machine flowshops. Computers & Operations Research, 20(4), 391-401. URL: http://www.sciencedirect.com/science/article/pii/030505489390083U [ Links ]
[13] Manne, A.S. 1960. On the job-shop scheduling problem. Operations Research, 8(2), 219-223. URL: https://pubsonline.informs.org/doi/abs/10.1287/opre.8.2.219 [ Links ]
Submitted by authors 6 Jan 2018
Accepted for publication 2 May 2018
Available online 31 /May 2018
* Corresponding author Mheydari@iust.ac.ir














