Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.29 no.1 Pretoria 2018
http://dx.doi.org/10.7166/29-1-1784
GENERAL ARTICLE
An inventory classification approach combining expert systems, clustering, and fuzzy logic with the ABC method, and an application
A. AktepeI, *; S. ErsozI; A.K. TurkerI; N. BarisciII; A. DalgicI
IKirikkale University, Faculty of Engineering, Department of Industrial Engineering, Yahsihan, Kirikkale, Turkey
IIGazi University, Faculty of Engineering, Department of Computer Engineering, Teknikokullar Ankara, Turkey
ABSTRACT
The classification of inventories requires using several criteria to control different functions of inventory management. In this study, a new classification algorithm, called the FNS (functional, normal, and small) algorithm, is developed that combines classical ABC classification with a new grouping strategy. In the algorithm, handling frequency, lead time, contract manufacturing process, and specialty are used as input criteria, and the outputs are new classes for the inventories. The algorithm is applied in a large company operating in the defence industry. The main problem in the company is not being able to manage and track inventories effectively. The company has previously used the Pareto analysis approach, but this no longer met the company's inventory management needs. In our study, the ABC classification method is enriched and combined with the proposed FNS algorithm to create nine different classes for inventories. To achieve this, the classical ABC classification method is integrated with expert systems, clustering, and fuzzy logic methods. Now, inventories can be classified in more detail, and useful counting strategies can be created. The classification system developed is currently being used by the company, and is integrated into its enterprise resources planning (ERP) system.
OPSOMMING
Die rangskikking van inventarisse maak gebruik van verskeie kriteria om verskillende aspekte van inventarisbestuur te beheer. In hierdie artikel word 'n nuwe rangskikking algoritme ontwikkel wat die klassieke ABC-klassifikasie met 'n nuwe groeperingstrategie kombineer. Die hanteringsfrekwensie, leityd, kontrakvervaardiging-proses en spesialiteit word as insetkriteria gebruik. Die uitsette is die nuwe klassoorte vir die inventarisse. Die algoritme is in 'n groot maatskappy, wat in die verdedigingsektor handel, toegepas. Die maatskappy se bestaande inventarisbestuurstelsel voldoen nie meer aan hul behoefte nie. Die bestaande stelsel het voorheen van die Pareto-analise benadering gebruik gemaak. Die voorgestelde algoritme skep nege verskillende klasse vir inventarisse. Om dit te bewerkstellig word die klassieke ABC-klassifikasie metode geïntegreer met ekspertstelsels, bondelvorming, en wasigheidsleer-metodes. Nou kan inventarisse in meer detail geklassifiseer word en nuttige voorraadopname-strategieë kan geskep word. Die voorgestelde algoritme word deur die maatskappy gebruik en is in hul hulpbron-bestuurstelsel geïntegreer.
1 INTRODUCTION
Inventories are not only physical objects, they are also important investments for companies. They consist of raw materials, semi-manufactured goods on production lines, final products, and even auxiliary materials. Production without any failure, best service to the customer, and maximising the profitability of businesses cannot be imagined without an efficient inventory management. Inventories that tie up the cash capital of businesses have key functions for satisfying customer demand. However, these turn into an advantage through efficient inventory control and management [1]. In today's economy, with the continuous increase in competition, the importance of efficient inventory management increases daily; but this is only possible with well-implemented inventory policies and accurate decisions. Companies that reduce their costs in this way, and provide the best service in the shortest time for their customers, will have competitive advantage. It is crucial for a company to understand inventory management concepts and build an efficient inventory management system [2]. Inventories need to be classified by focusing on several criteria to manage the different functions of the inventories. Classification increases the efficiency and ease of use of inventory management. With the help of recently developed technologies, companies have begun to use more efficient methods to classify their inventories. The financial value of the inventories is not a sufficient criterion for versatile classification. For this reason, different criteria, such as availability and lead time, should also be used for inventory classification.
As a contribution to the literature in this field, an algorithm is offered in this study to make classification more efficient by taking more than one criterion into consideration. In the eight-step FNS algorithm developed in this study, classification of the inventories is carried out by using different criteria such as handling frequency, lead time, contract manufacturing, and specialty. The first assignment is conducted using expert system decision rules. The second assignment is carried out using a clustering algorithm. In the third, two groups, created with the first and second assignments, are intersected. The final groups are created by joining these two groups. Where the parts could not be assigned to any group, the final assignment is realised with the help of fuzzy rules. Applying the algorithm is carried out in a large company that is in a key position in the defence industry. Following the application, the results are discussed in detail.
2 LITERATURE REVIEW
A single criterion, the financial value of the inventory, has dominated inventory classification for a long time in the literature. However, with increasing competition, it is understood that additional criteria must be considered for more efficient classifications [3, 12, 14]. As a supporting example, Ramanathan [3] developed a new approach for the ABC inventory classification with multiple criteria. In his study, a linear programming model, based on data enveloped analysis (DEA), was developed for the classification problem. This model focuses on m numbered inventory units and j numbered criteria. The aim of the model is to calculate inventory scores by appointing the optimum weights for each inventory unit. This model is solved for each inventory unit, and a score is calculated for each part. In Ramanathan's study, 47 inventory units were analysed in terms of average unit cost, annual usage, critical factor, and lead time. The results of the study are compared with the classical ABC analysis.
In another study carried out by Zhou and Fan [4], an improved version of the Ramanathan model ('R model') was proposed ('ZF model'). This study argues that a unit that has a high value in an important criterion can be placed in class A. For this purpose, in addition to the optimum inventory score calculated by the R model, a worst inventory score is also calculated for each unit, in contrast to the R model. As a result, the weighted average of both scores is obtained. The results have been compared with the results of the R model.
Soylu [5] developed another approach using the Tchebycheff distance measure approach for inventory classification problems. He used the advantage of the Tchebycheff measure to create efficient solutions that are not convex in particular. Seperate Tchebycheff distance functions for each inventory unit were calculated, and several weights were acribed accordingly.
Özdemir and Özveri [6] carried out a multi-criteria ABC analysis in an electrical generator manufacturing company. They combined the classical ABC analysis with the analytical hierarchy process (AHP) method. Seventy different products were evaluated, using five criteria. These criteria were price, demand, delivery time, criticality, and substitution rate. It was observed that results produced by the AHP method were better in terms of costs. Chen, Li, Levy, Hipel & Kilgour [7] used a simple cluster theory to classify inventory units. They proposed a new classification approach, carrying out an application for 47 different inventory units with multiple criteria. In another study, a weighting method was developed for different classification sequences [8].
In a study by Chen [9], both the ZF model and the R model are resolved for the inventory units. In the R model, there is an inventory with m items, which are classified as A, B, or C based on n criteria. yij is the performance score of the jth item, and wij is the weight of the ith criterion for the jth item. To aggregate the performance of an item in terms of multiple criteria into a single score for inventory classification, Ramanathan [3] proposed a weighted linear optimisation model - the R model. As noted earlier, Chen [9] improved the R model by developing the ZF model. The difference between the two models is that the ZF model makes each item select a set of weights least favourable to itself for performance aggregation. In Chen's [9] study, inventory scores were calculated seperately for both of the models. In the second step, an ABC sequence was obtained by using normalised values of performance scores. The aim of the study was to prevent the units from being appointed to the wrong classes using the interaction values between the two models. The application was carried out for the 47 units used in both models, and the results were compared. In another study, the particle optimisation method was applied to the inventory classification problem, and a flexible classification algorithm was developed [10].
Çakir and Canbolat [11] developed a fuzzy AHP-based inventory sequence system, in which the fuzzy AHP method was applied to actual inventory data. First, linguistic comparisons of decision-makers was carried out. The prioritisation method of Mikhailov [18] was applied to these data, and an analysis was conducted with a web-based system. Using this method, a flexible and consistent classification system was suggested in which decision-makers are able to use their linguistic expressions for each unit. In the study of Rezaei and Dowlatshahi [12], an easy, efficient, and practical method was developed for multi-criteria problems.
After the famous study of Zadeh [13], fuzzy sets were used for various decision-making problems. For example, Chu, Liang & Liao [14] developed an ABC analysis approach with fuzzy sets. In their study, a new approach, called 'fuzzy-ABC', was proposed. This new method, which is also easy to apply, includes expert views for the classification process. The method developed in the study was applied with a data set of 60 different parts and three different criteria. The membership function value of each unit was calculated using a fuzzy method. Bhattacharya, Sarkarz & Mukherjeez [15] used the TOPSIS (technique for order preference by similarity to ideal solution) method to classify the inventory units. In this method, the shortest distance is calculated by using weighted distances to both ideal and negative ideal solutions of the alternatives. In their study, a multi-criteria ABC analysis was conducted with the TOPSIS method. From the studies of Kampen, Akkerman & Donk [19] and Praveen, Jay & Venkataram [20], readers can find the literature reviews of different algorithms used for inventory classification.
3 ALGORITHM DEVELOPED IN THIS STUDY
In this study, expert systems and k-means clustering algorithms are used to classify the inventory units using multiple criteria. First, the inventory units are classified in accordance with expert system decision rules. Then a k-means clustering algorithm is used to create the second assignment. If the expert systems and k-means clustering algorithms become insufficient for grouping some parts, a fuzzy rule-based method is developed to make the final assignment. Each part is thus assigned to the final groups.
Classification of inventories with multiple criteria enables us to produce more sensitive results. In this study, we create a new grouping method called the 'FNS algorithm'. FNS is an abbreviation for functional, normal, and small. Group F (functional) includes the inventory units that are functional for the warehouse. Group N (normal) includes inventory units that are described as normal; in other words, they are less critical parts than those in group F. Inventory units in group S (small) are ordinary parts that have low importance. In the FNS algorithm, the handling frequency (C1), lead time (C2), contract manufacturing process duration (C3), and specialty criteria (C4) are used. We also integrate the FNS model results with the classical ABC inventory classification method, thus integrating non-financial and financial criteria. The flow chart of the developed algorithm is shown in Figure 1.
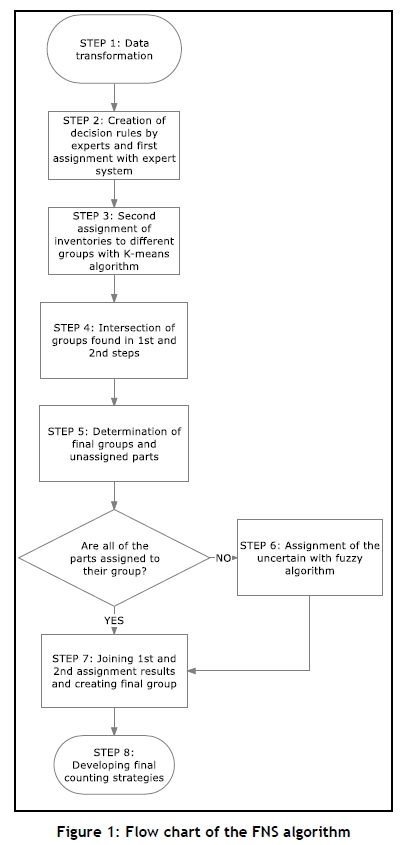
The steps of the FNS algorithm are described below:
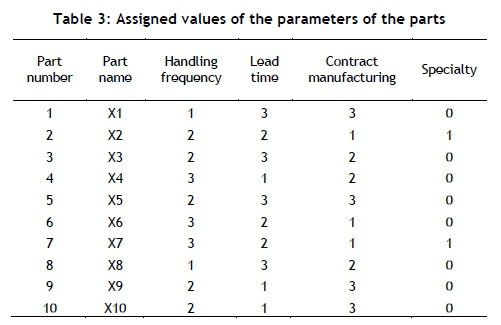
Step 1: Data transformation is carried out to create labels for the data of the criteria (handling frequency (C1), lead time (C2), contract manufacturing process duration (C3), and specialty (C4)). The application data are transformed as follows:
-
Criterion 1 - Handling frequency: Parts needing 20 days or fewer for handling frequency are numbered 1, those needing 21 -40 days' handling frequency are assigned a value of 2, and those needing 41 -100 days' handling frequency are assigned a value of 3.
-
Criterion 2 - Lead time: Parts needing 20 days or fewer for lead time are assigned a value of 1, those with a 21 -40 days' lead time are assigned 2, and those with 41 -100 days' lead time are assigned 3.
-
Criterion 3 - Contract manufacturing: Contract manufacturing is the activity of having some products produced by different companies for various reasons. With this criterion, such units are taken into account as well. Parts with 20 days of contract manufacturing time are assigned 1, those with 21 -40 days of contract manufacturing time are assigned 2, and those with 41-100 days of contract manufacturing time are assigned 3.
-
Criterion 4 - Specialty: Special parts are units that are difficult to supply for some economic or political reason. Under this criterion, crucial (special) units are assigned a value of 1, and others are assigned 0.
Step 2: Inventories are assigned to Groups F, N, or S according to the expert decision rules on handling frequency (C1), lead time (C2), contract manufacturing process duration (C3), and specialty criteria (C4). In this step, experts create the decision rules for assigning the inventory units.
Step 3: The k-means algorithm is created with criteria C1, C2, C3, and C4. To create three different groups, k is determined as 3 in the k-means algorithm.
The k-means clustering technique is one of the most widely-used. K is the parameter that specifies in advance how many clusters are being sought. K points are then chosen at random as cluster centres. All instances are assigned to their closest cluster centre according to the ordinary Euclidean distance metric. Next, the centroid or mean of the instances in each cluster is calculated; this is the 'means' part. These centroids are taken to be the new centre values for their respective clusters. Finally, the whole process is repeated with the new cluster centres. Iteration continues until the same points are assigned to each cluster in consecutive rounds, at which stage the cluster centres have stabilised and will remain the same forever [22].
SPSS [16] software is used to develop the k-means algorithm.
Step 4: New groups are created by intersecting the two different assignments found in Steps 2 and 3. Three different groups were created in the first step, and three in the second step. When we intersect them, nine (3x3) different combinations are obtained (FF, FN, FS, NF, NN, NS, SF, SN, and SS).
-
FF, NN, and SS are the final groups, because in both the expert system and the k-means algorithm, the same group is determined.
-
However, FN, FS, NF, NS, SF, and SN are not final groups because the labels found by the expert system and by clustering are different.
Step 5: An initial filter is applied in this step: If a part is assigned to group F by both the expert system and the k-means algorithm (F and F: FF), the final group of this part is determined as F; similarly, (N and N: NN) is determined as N, and (S and S: SS) is determined as S. Other parts that cannot be assigned to the final group in this step are transferred to Step 6.
Step 6: A fuzzy rule-based algorithm is used in this step for parts that are not assigned to the final group at Step 4. Using fuzzy logic enables us to determine the final groups of unspecific parts (FN, FS, NF, NS, SF, and SN).
Step 7: First, classical ABC analysis is implemented for all parts. Each part is assigned to A, B, or C class. This result is then combined with the results of the FNS algorithm for each part. The final group for a part is determined by intersecting the classical ABC method and the FNS algorithm. Thus the final group of a part may now be FA, FB, FC, NA, NB, NC, SA, SB, or SC.
Step 8: In this last step, new counting scenarios are developed for all the parts that are assigned to their final groups. After classifying the inventories, we develop a counting method. This is an important requirement, because there are various types of inventories in a company, and companies have difficulty tracking a wide variety of product types. Company policy also requires that inventories be counted at the end of each period, so a practical and useful counting method is necessary. Alternative scenarios are therefore developed for counting the inventories.
In order to measure the efficiency of the suggested algorithm, an application is carried out in a company that operates in the defence sector. In the next section we describe this application.
4 APPLICATION
In the classical ABC approach, a classification is performed by using price per unit multiplied by quantity. However, in the FNS method, the following criteria are used:
-
Handling frequency (C1): Frequency of using parts in production.
-
Lead time (C2): Time between order and arrival date.
-
Contract manufacturing process duration (C3): Time between sending date for contract manufacturing processes and arrival date.
-
Specialty (C4): Supply of the part is difficult for special parts.
In Table 1, the explanations of the criteria used in the FNS algorithm are discussed.
Table 2 shows the data used for the application of the FNS algorithm. Data are collected for nearly one thousand parts with the help of the store manager and production engineer. Here, we display a sample of the data and the results for ten different parts.
Application of Step 1. Data transformation: In order to use the data in the SPSS [16] and MATLAB [17] software, data transformation is required. Table 3 is the transformed version of Table 2, as explained above in Step 1.
Application of Step 2: An expert team consisting of two professors, one store manager, and two industrial engineers have produced the decision rules for the expert assignment. An initial assignment is carried out in this step. The decision rules created by the experts are shown in Table 4, including an explanation using the first rule.
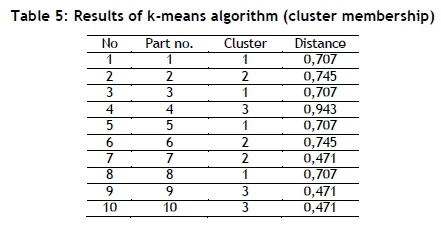
Application of Step 3: In this step, the k-means clustering algorithm is applied as a second grouping strategy. SPSS software, making use of random initialisation, is used to build this algorithm. Ten reruns are performed, and the maximum iteration is determined as 300. As a result of the application, three different groups are created, as shown in Table 5. Cluster 1 represents group S, cluster 2 represents group N, and cluster 3 represents group F.
Application of Step 4: In this step, the results of Steps 2 and 3 are combined. In Table 6, the assignment results of Steps 2 and 3 and their combination are shown.
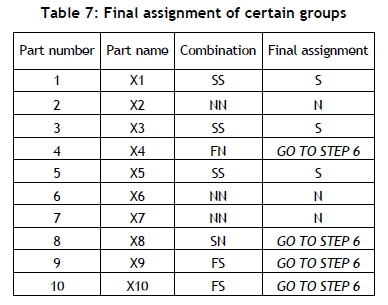
Application of Step 5: The final assignment of some parts is performed in this step, as shown in Table 7. Some parts cannot be assigned to their final group. (The first assignment by the expert system is different from the assignment result of the clustering algorithm.) To determine the final group for these kinds of parts, assignments are carried out at Step 6 with a fuzzy algorithm.
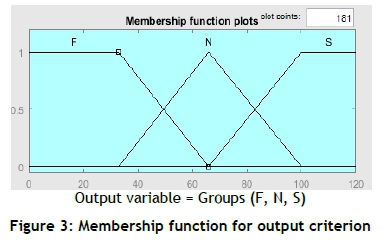
Application of Step 6: For parts that could not be assigned to their final group at Step 5, a fuzzy rule-based algorithm is developed. The algorithm for unassigned parts is developed with the fuzzy logic designer module of Matlab R2016a. Inputs to the module are the C1, C2, C3, and C4 criteria, and outputs are the final groups. Membership functions for each input criterion are shown in Figure 2. Handling frequency (C1) is divided into three sets (low, medium, high); lead time (C2) is divided into three sets (low, medium, high); contract manufacturing process time (C3) is divided into three sets (low, medium, high); and specialty (C4) is divided into two sets (yes, no). The membership function for the output is shown in Figure 3, and the interface of the Mamdani type fuzzy assignment algorithm [21] is shown in Figure 4.
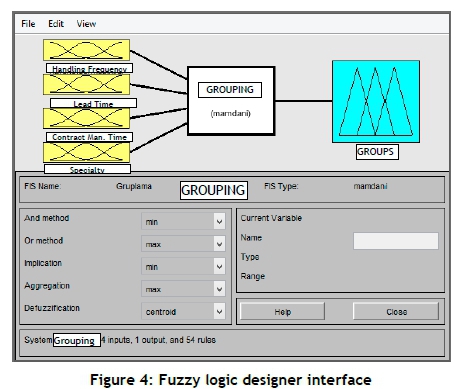
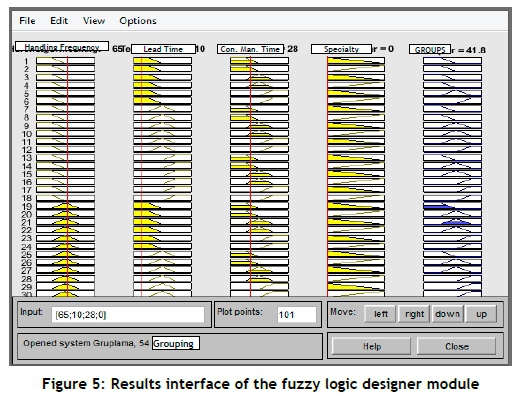
In the rules section of the module, there is an interface where the best appointment is carried out. Figure 5 shows the results of the fuzzy assignment algorithm with one example. For each part, a final score is calculated with the input criteria values, rules (3X3X3X2=54 rules), and the centroid defuzzification method, which is given in Equation 1.
In Equation 1, μ ε (ζ) is membership degree, z is fuzzy set, and z* is defuzzified output.
For example, if handling frequency = 65, lead time = 10, contract manufacturing time = 28, and specialty = 0, then the Group is found at 41.8 and this value is inside Group N.
The final groups of some remaining parts assigned at Step 5 are shown in Table 8.

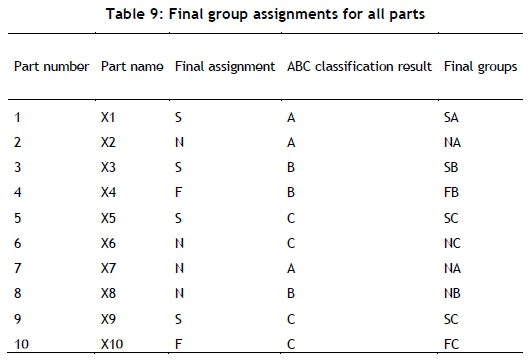
Application of Step 7: After completing all the final assignments of parts, the final groups are obtained by joining the result of the FNS algorithm with the classical ABC analysis. The final groups are shown in Table 9.
Application of Step 8: In this last step, counting strategies have been developed according to the final groups found in Step 6. The objective here is to indicate the primary inventory units in the counting process. We determine practical and useful counting strategies by producing different scenarios that are better than the company's current counting strategy. (The company currently has difficulty counting and tracking different kinds of inventories.) With our approach, the inventory manager can pick one of the counting strategies developed and discussed below. The company can use one of the six different scenarios in Table 10, according to its primary counting purpose. Counting hundreds of various types of inventories was a big problem for the company, not least because it was very time-consuming. This problem is now solved with the help of the counting strategies developed as a result of the FNS algorithm.
-
Scenario 1: According to this counting strategy, functional units are counted first. The categories are as follows:
I. Category= {FA, FB},
II. Category = {FC, NA, NB, SA},
III. Category = {NC, SB, SC}.
-
Scenario 2: According to this counting strategy, overcosting units are counted first. The categories are as follows:
I. Category = {FA, FB, NA},
II. Category = {FC, NB, SA},
III. Category = {NC, SB, SC}.
-
Scenario 3: According to this counting strategy, inventory units belonging to the FA group are first.
The categories are as follows:
I. Category = {FA},
II. Category = {FB, FC, NA},
III. Category = {NB, NC, SA, SB, SC}.
-
Scenario 4: According to this counting strategy, the number of categories is increased. The categories are as follows:
I. Category = {FA},
II. Category = {FB, NA},
III. Category = {FC, NB, SA},
IV. Category = {NC, SB, SC}.
-
Scenario 5: According to this counting strategy, the first category includes inventory units in the FA group. The FB and FC inventory groups are assigned to sub-categories. Similarly, parts belonging to the NA group are assigned to sub-categories.
The categories are as follows:
I. Category = {FA},
II. Category = {FB, NA},
III. Category = {FC, NB},
IV. Category = {NC, SA},
V. Category = {SB, SC}.
-
Scenario 6: According to this counting strategy, the FA inventory group is counted on its own. The FB and FC groups are appointed to the sub-clusters.
The categories are as follows:
I. Category = {FA},
II. Category = {FB, FC, NA},
III. Category = {NB, NC, SA, SB, SC}.
The comparison of our approach with the approach formerly used in the company is shown in Table 11.
5 CONCLUSION
There are many studies of the classical ABC inventory classification method in the literature. Inventory classification methods with more than one criterion were subsequently developed, contributing to the classical ABC inventory classification method. In this study, the FNS algorithm, which is proposed as a contribution to inventory classification methods with more than one criterion, is developed. In addition, an inventory counting strategy is developed and an application is carried out. The algorithm developed in this study offers a new perspective to the literature by integrating expert systems, k-means, and fuzzy logic algorithms.
There are many advantages of the FNS algorithm. These are:
-
The inventory stock-out problem is solved with efficient tracking. The inventory management system becomes more controllable and inspectable.
-
Disruptions in production due to inability to follow inventories effectively are decreased.
-
Inventories are not classified only according to their monetary value. This brings some advantages, such as being able to seperate critical inventories that are significant for production but whose monetary value is low.
-
With the help of the classification and counting algorithm, the time required for inventory control is decreased. Control time is used more effectively by classifying parts within the framework of system requirements.
With the FNS algorithm, inventories are grouped according to multiple criteria. This is then combined with the ABC classification, thus taking both non-financial and financial criteria into account.
A major problem in many companies is that they are not able to manage and track inventories, and a pareto analysis approach cannot meet all a company's needs for this. In our study, the ABC classification method is enriched and combined with the proposed FNS algorithm to create nine different classes (FA, FB, FC, NA, NB, NC, SA, SB, SC) for inventories. In addition, we develop counting strategies for inventories.
Another contribution of the algorithm is its flexibility, which is its ability to choose one of the six different counting strategies. This enables the inventory manager to pick a strategy according to the priorities in different situations.
The classification system developed in this study is currently being used by a company that is a major player in the defence industry. It can be a reference for inventory classification for most companies that have a high diversity of part types; and the FNS algorithm can equally be applied to other sectors with different data sets.
REFERENCES
[1] Çitak, Ş. 2013. Bir Elektronik Firmasinda Çok Ölçütlü Stok Siniflandirma. Ankara: Gazi Üniversitesi, Fen Bilimleri Enstitüsü [ Links ].
[2] Kara, Ö. 2014. isletmelerde Stok Yönetimi. Istanbul: Okan Üniversitesi, Sosyal Bilimler Enstitüsü [ Links ].
[3] Ramanathan, R. 2006. ABC inventory classification with multiple-criteria using weighted linear optimization, Computers & Operations Research, 33, 695-700. [ Links ]
[4] Zhou, P. & Fan, L. 2007. A note on multi-criteria ABC inventory classification using weighted linear optimization, European Journal of Operational Research, 182, 1488-1491. [ Links ]
[5] Soylu, B. 2008. Çok Kriterli ABC Stok Siniflandirma Problemi Için Tchebycheff Ölcüsü Temelli Yaklasim, Yöneylem Arastirmasi ve Endüstri Mühendisligi, 28. Istanbul: Ulusal Kongresi Bildiriler Kitabi, Galatasaray Üniversitesi. [ Links ]
[6] Özdemir, A. & Özveri, O. 2004. Çok Kriterli Envanter Siniflandirmasinda Analitik Hiyerarsi Süreci Analizinin Uygulanmasi, D.E.Ü.I.I.B.F. Dergisi, 19(2), 137-154. [ Links ]
[7] Chen Y., Li K.W., Levy J., Hipel K.W. & Kilgour D.M. (2006) Rough-Set Multiple-Criteria ABC Analysis. In: Greco S. et al. (eds) Rough Sets and Current Trends in Computing. RSCTC 2006. Lecture Notes in Computer Science, vol 4259. Springer, Berlin, Heidelberg. [ Links ]
[8] Hadi-Vencheh, A. 2010. An improvement to multiple criteria ABC inventory classification, European Journal of Operational Research, 201, 962-965. [ Links ]
[9] Chen, J.X. 2011. Peer-estimation for multiple criteria ABC inventory classification, Computers & Operations Research, 38, 1784-1791. [ Links ]
[10] Tsai, C.Y. & Szu-Wei, Y. 2008. A multiple objective particle swarm optimization approach for inventory classification, International Journal of Production Economics, 114, 656-666. [ Links ]
[11] Cakir, O. & Canbolat, M.S. 2008. A web-based decision support system for multi-criteria inventory classification using fuzzy AHP methodology, Expert Systems with Applications, 35, 1367-1378. [ Links ]
[12] Rezaei, J. & Dowlatshahi, S. 2010. A rule-based multi-criteria approach to inventory classification, International Journal of Production Research, 48 (23), 7107-7126. [ Links ]
[13] Zadeh, L.A. 1983. The role of fuzzy logic in the management of uncertainty in expert systems, Fuzzy Sets and Systems, 11, 199-227. [ Links ]
[14] Chu, C.W., Liang, G.S. & Liao, G.T. 2008. Controlling inventory by combining ABC analysis and fuzzy classification, Computers & Industrial Engineering, 55, 841-851. [ Links ]
[15] Bhattacharya, A., Sarkarz, B. & Mukherjeez, S.K. 2007. Distance-based consensus method for ABC analysis, International Journal of Production Research, 45(15), 3405-3420. [ Links ]
[16] SPSS Statistical Analysis Software. 2017. http://www-03.ibm.com/software/products/tr/spss-stats-base. (Date of access: 15.03.2017). [ Links ]
[17] MATLAB Software. 2017. https://www.mathworks.com/products/matlab.html. (Date of access: 10.02.2017) [ Links ]
[18] Mikhailov, L. 2003. Deriving priorities from fuzzy pairwise comparison judgements, Fuzzy Sets and Systems, 134(3), 365-385. [ Links ]
[19] Kampen, T.J., Akkerman, R. & Donk, D.P. 2012. SKU classification: A literature review and conceptual framework, International Journal of Operations and Production Management, 32(7), 850-876. [ Links ]
[20] Praveen, M., Jay, B.S. & Venkataram, R. 2016. Techniques for inventory classification: A review, International Journal for Research, Applied Science & Engineering Technology, 4(10), 508-518. [ Links ]
[21] Mamdani, E.H. 1977. Application of fuzzy logic to approximate reasoning using linguistic synthesis, IEEE Transactions on Computers, 26(12), 1182-1191. [ Links ]
[22] Witten, H.I. & Frank, E. 2005. Data mining: Practical machine learning tools and techniques. San Francisco, USA: Morgan Kaufmann Publishers. [ Links ]
Submitted by authors 2 Jun 2017
Accepted for publication 2 Mar 2018
Available online 31 May 2018
* Corresponding author aaktepe@gmail.com














