Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.28 n.2 Pretoria Aug. 2017
http://dx.doi.org/10.7166/28-2-1732
GENERAL ARTICLES
Single- and multi-objective ranking and selection procedures in simulation: A historical review
Department of Industrial Engineering, Stellenbosch University, South Africa
ABSTRACT
Ranking and selection (R&S) procedures form an important research field in computer simulation and its applications. In simulation, one usually has to select the best from a number of scenarios or alternative designs. Often, the simulated processes have a stochastic nature, which means that, to distinguish alternatives, they must exhibit significant statistical differences. R&S procedures assist the decision-maker with the selection of the best alternative with high confidence. This paper reviews past and current R&S procedures. The review traces back to the 1950s, when the first R&S procedure was proposed, and discusses the various R&S procedures proposed since then to the present day, presenting a cursory view of the research in the area. The review includes studies in both the single-objective and the multi-objective domains. It presents the research trend, discusses specific issues, and gives recommendations for future research in both domains.
OPSOMMING
Rangorde- en keuseprosedures (R&K) vorm 'n belangrike navorsingsveld in rekenaarsimulasie en -toepassings. Simulasiestudies vereis gewoonlik dat die beste kandidaat van 'n aantal scenarios of alternatiewe ontwerpe gekies moet word. Die gesimuleerde prosesse is gewoonlik van 'n stogastiese aard, en hulle moet statisties-beduidend verskil ten einde onderskeid te kan tref. R&K prosedures ondersteun die besluitnemer om die beste alternatief met groot vertroue te kies. Hierdie artikel verskaf 'n resensie van vroeë en huidige R&K prosedures. Die ondersoek strek terug tot in die 1950s toe die eerste R&K prosedures voorgestel is, en bespreek die verskeie R&K prosedures wat sedertdien ontwikkel is, terwyl 'n oorsigtelike blik op die navorsingsveld gegee word. Die resensie sluit studies in beide enkel- en multidoelwitdomein in. Dit bespreek navorsingsneigings en spesifieke kwessies, en maak voorstelle vir verdere navorsing in beide domeins.
1 INTRODUCTION
Computer simulation is a powerful and essential tool in modern society to improve the operation of current systems and business practices. It contributes to the efficient management of processes and systems - the main focus of many industrial engineers - by providing a what-if analysis. In operating a system, one often faces a situation where the following question arises: If some changes were made to the current parameter settings (or decision variables)1 in the operation of the system, what would happen? Would they result in a better performance of the system or not? It is usually not easy to estimate the effect of the changes because the system is often complex and exhibits a stochastic nature. Simulation helps decision-makers in such cases by simulating the real system and providing the estimates of system performance measures. One can compare the performance of the simulated system (with the changed parameter settings) to that of the real system (with the current parameter settings) to reach a better decision.
The question can be easily extended to involve several parameter settings, or system designs: suppose there were k different system designs, which of the k designs would give the best result in terms of the performance measure? There have been consistent efforts among scholars in simulation and statistics to answer this kind of question, which has formed an important subfield of research in simulation application: ranking and selection (R&S). Ranking and selection procedures provide the decision-makers with a series of actions to take in order to select the best among a number of estimated system performances with high confidence.
Ranking and selection procedures are distinguished from general simulation optimisation algorithms, in that they are applied to find the best system from a small, limited number of system designs, and that they are dedicated to guarantee a certain statistical significance in doing so. R&S procedures form part of the larger domain of simulation optimisation, which includes algorithms and techniques to solve problems with large solution spaces. (See Amaran et al. [1]Error! Reference source not found. for the more general topic of simulation optimisation.)
This paper reviews past and current R&S procedures from a historical point of view. The review begins in the 1950s, when the first R&S procedure was proposed by Bechhofer [2], and discusses various R&S procedures proposed since then to the present day. We attempt to provide a general view of the research area by reviewing different approaches applied in R&S procedures, and by studying how the procedures have been developed over the years. We believe that the concise yet informative review in this paper will help simulation practitioners to acknowledge the existence of various R&S procedures and to understand the differences in their approaches, purposes, strengths, and limitations. Our research includes both single-objective and multi-objective R&S procedures.
2 REVIEW OF SINGLE-OBJECTIVE RANKING AND SELECTION PROCEDURES
There are two basic approaches in single-objective R&S procedures (or simply 'R&S procedures', as usually a single performance measure is assumed unless explicitly stated): the indifference-zone (IZ) procedures and the optimal computing budget allocation (OCBA) procedures. These are discussed in the next two subsections.
2.1 The indifference-zone procedures
Indifference-zone (IZ) procedures guarantee, with a probability of at least P*, that the system design ultimately selected is the best when its true mean is at least δ* better than the true mean of the second-best system design [3]. The smallest difference that the decision-maker considers worth detecting is chosen as δ* > 0. We assume there are k different system designs, and let Xijdenote the jth independent observation from system design i. It is assumed that Xij~ N(μi, σi2) with μiand δi unknown. Now, without loss of generality, suppose that the true means of the system designs are indexed as μ1> μ2> . . . > μkso that system design k (which is unknown) is the best system design in the minimisation problem. Because the true means μi(i = 1, ... , k) are unknown, they are to be estimated from observation Xj (i = 1, ... , k). Under this formulation, the IZ procedures identify the smallest sample size (or the number of simulation replications) Nifor each system i, (i = 1, ... , k), to guarantee the probability of correct selection:
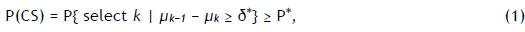
where 1/k < P* < 1. If there are system designs whose means are within δ* of the best, then the decision-maker is indifferent about which of these is selected, leading to the term 'indifference-zone formulation' [4]. In this case, the IZ procedures select one of these solutions with a probability of at least P*.
The concept is illustrated in Figure 1. Suppose we simulate three designs of a system, and the performance indicator follows the three distributions labelled 'I', 'II', and 'III'. System design I 'seems' to be 'close' to system design II, and if the decision maker chose 8* beforehand, such that δ* > δ1, then it can be concluded that system designs I and II do not differ statistically significantly, and they are for practical purposes the same. The different distributions observed (I and II) are due to in-sample variation. System design III, on the other hand, 'seems' to differ 'largely' from system designs I and II. The differences are due to cross-sample variation, which means that system design III is worse than system designs I and II if the objective is to be minimised. The decision-maker can now choose between system designs I or II, based on practical and financial considerations.
The initial work based on the IZ approach is shown in Bechhofer [2]. His work was motivated by "some deficiencies" of analysis of variance (ANOVA), one of the most popular statistical techniques in those days (and perhaps these days as well). ANOVA tests whether there is a significant difference among the means of k populations, often to identify the effects of k different treatments. In many instances, however, the interest of the experimenters would be to rank the treatments so that they can select the best treatment, or a few best treatments. Bechhofer [2] presents a procedure for ranking means of k normal populations with known variances as a solution to this kind of problem. His work became the origin of the many R&S procedures that followed, having established not only the concept of indifference-zone δ* but also that of the probability of correct selection P(CS).
Bechhofer's procedure is a single-stage procedure that is applied to limited cases - i.e., ranking problems with populations of known variances. Dudewicz [5] proved that no procedure that has only a single-stage of sampling can satisfy the requirement of (1) when the variances are unknown. For a procedure to deal with the cases with unknown variances, at least two stages of sampling are required, of which the first stage sampling is to estimate the unknown variances for each population, and the later stage(s) of sampling are to obtain more accurate estimates of the true means.
Dudewicz and Dalal's two-stage procedure [6], called Procedure Pe, was the first that assumed unknown variances to appear in the literature. The procedure takes an initial sample of size n0from each population (this is the first stage of sampling), calculates the sample variances sj2for each system i, and identifies the required sample size Nibased on the value of si2, δ* and a critical value h, which plays a crucial role in the proof of the required P*. In the second stage of sampling, the procedure takes the remaining Ni - n0observations and indicates the best system based on the total Njobservations. The drawback of Procedure Pe is that it uses weighted sample means 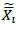 t(defined in Equation 4.5 in [6], p.37), which is harder to understand than the simple overall sample means
t(defined in Equation 4.5 in [6], p.37), which is harder to understand than the simple overall sample means  . It seems that Dudewicz and Dalal would have liked to develop a procedure that used the overall sample means
. It seems that Dudewicz and Dalal would have liked to develop a procedure that used the overall sample means 
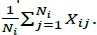 , which is intuitively appealing, but that they failed to prove that such a procedure guaranteed the desired confidence P*.
, which is intuitively appealing, but that they failed to prove that such a procedure guaranteed the desired confidence P*.
A few years later, Rinott [7] achieved the task, resulting in the development of Procedure Pr*. Procedure Pr* uses the overall sample means 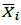 t and guarantees P* in selecting the best among k normal populations with unknown variances. Actually, it has almost the same structure as Procedure Pe, except for the definition of the critical value h and the use of the overall sample means Rinotts's procedure is considered to be one of the most important works in early R&S research, and became the touchstone of the IZ procedures that followed. Many IZ procedures that were developed after this have been based on Rinott's procedure, with the goal of improving it. The focus was to reduce the sample size N, to achieve the same confidence level P*. (See, for example, [8], [9], Error! Reference source not found., Error! Reference source not found. and Error! Reference source not found.. )
t and guarantees P* in selecting the best among k normal populations with unknown variances. Actually, it has almost the same structure as Procedure Pe, except for the definition of the critical value h and the use of the overall sample means Rinotts's procedure is considered to be one of the most important works in early R&S research, and became the touchstone of the IZ procedures that followed. Many IZ procedures that were developed after this have been based on Rinott's procedure, with the goal of improving it. The focus was to reduce the sample size N, to achieve the same confidence level P*. (See, for example, [8], [9], Error! Reference source not found., Error! Reference source not found. and Error! Reference source not found.. )
Kim and Nelson [13] described their very efficient procedure to reduce the required sample size Ni to guarantee P*. They proposed a procedure (called the KN procedure) that is different from the above-mentioned two-stage procedures based on Rinott's procedure, in the sense that it is fully sequential - i.e., it takes as many stages as required. In the KN procedure, n0 samples are taken initially for each system i, and after that, inferior systems are eliminated at each stage and a single observation from each system i that is still in play is taken in the next stage. The procedure continues until there remains only one system, which is concluded to be the best system, or until the predesignated number of observations is reached. The screening rule, which decides which system should be eliminated at each stage, is designed to guarantee the required confidence level P*. The experimental results show that the fully sequential procedure is far superior to Rinott's procedure, and therefore needs significantly less computational effort to guarantee the same level of P*. The KN procedure is the most advanced form of the IZ procedures, and is widely used in practice, having been incorporated into many commercial simulation software programs.
The IZ procedures assume the least favourable configuration (LFC) - that is:

for a minimisation problem when the means of k populations are indexed as μ1, > μ2 > ... > μk. Obviously, of all possible situations that satisfy μ1> μ2 > ... > μk and the IZ condition of μk-1 - μk > δ, the above-mentioned condition (2) is the worst case to define the best system k (the smallest mean μkin this case), and thus the least favourable configuration. In the IZ approach, the required confidence P* is often guaranteed by showing that the probability of correct selection under the LFC equals P*- that is, P(CS) > Plfc(CS) = P*. Therefore, the IZ procedures are conservative in their confirmation of P*.
2.2 The optimal computing budget allocation procedures
In R&S, optimal computing budget allocation (OCBA) presents another approach. Chen et al. [14] proposed OCBA procedures, which do not guarantee P* or involve the indifference-zone concept δ*, but aim at maximising the probability of correct selection P(CS) given a limited computing budget. A preselected limited computing budget - i.e., the total number of simulation replications - is allocated across system designs to maximise the P(CS). The problem can be formulated as

where Niis the number of simulation replications allocated to system design i while T is the limited total computing budget. A big concern in solving (3) is how to approximate P(CS), since there is usually no mathematically closed form of it. One solution is proposed by Chen [15], who used an approximation of P(CS) with a Bayesian model, by which an asymptotic solution to the approximation is obtained. Suppose we have to rank and select from k competing system designs whose performances are depicted by random variables with means μi, μ2, ... , μk, and finite variances σ12, σ22, Ok2. We let design b be the best design based on the sample mean, Nithe number of simulation replications allocated to design i, and δb,i= μi- μb. Chen et al. [14] showed that the following relationship between Niand Nj,

asymptotically maximises the approximated P(CS). The number of simulation replications for the best design is given as

The result in (4) shows that system designs with larger variances are allocated more replications (to obtain more accurate estimates). Also, more replications are allocated to system designs whose performance is closer to that of the best system design, which is reasonable as more replications are generally needed to distinguish smaller differences. However, when the difference between two systems is so small that the decision-maker is indifferent to either of them, the OCBA procedure becomes very inefficient, allocating a large amount of the simulation budget to some system designs to distinguish the small, insignificant difference.
There are many variants of OCBA that consider correlated sampling [16]; non-normal distributions [17]; different objective functions [18]; subset selection [19]; complete ranking [20]; and constraints [21]. Lee et al. [22] provided a comprehensive review of these OCBA procedures.
3 REVIEW OF MULTI-OBJECTIVE RANKING AND SELECTION PROCEDURES
When two or more performance measures or objectives are concerned in selecting the best among k populations, we call them 'multi-objective ranking and selection' (MORS) problems. This section introduces MORS procedures that have appeared in the literature so far. There are not many of them, but they are too important to ignore.
In the multi-objective context, one needs to determine how to define the best system designs when multiple (usually conflicting) performance measures are considered. Most modern approaches employ the concept of Pareto optimality for this purpose. In this concept, instead of a single best solution, a set of solutions that is not dominated by any other feasible solutions is defined to form a Pareto optimal set. We first informally discuss Pareto optimality. (See [23] for a formal definition of Pareto optimality.)
Consider the deterministic bi-objective Schaffer function No. 1, defined as [24]:

It is easy to see, on inspection, that 0 < x < 2. If x = 0, then f1(x) = 0 and f2(x) = 4; but if x = 2, then f1(x) = 4 and f2(x) = 0. The values in [0,4] form the Pareto set of this problem. The set can be visualised as illustrated in Figure 2.

Now suppose that we studied a stochastic problem with simulation, and that six system designs were considered. The estimations for f1(x) and f2(x) were observed with n0independent replications per design. The results are shown in Figure 3, together with a few important concepts.
First, consider the rightmost point, labelled 'A'. Here, the estimations for this design are f1(x)= 2.2 and f2(x) = 0.48. Second, note that for each estimation, a distribution per objective is associated with it, as shown for point 'A' only. Now consider the two points within the square: the question here is, are they statistically significantly different or not? They also have distributions representing them in both dimensions, and these distributions might significantly overlap. The question raised must be answered while accounting for both objectives (two in this case). In a problem with p objectives, the task becomes even more complicated.
With this background, we can proceed to discuss the indifference-zone, the optimal budget allocation, and alternative approaches in the multi-objective ranking and selection domain.
3.1 The multivariate indifference-zone approach
There were attempts in the 1980s to solve MORS problems using a multivariate concept [25], [26]. This line of research can be seen as an extension of the indifference-zone procedures to the multi-objective domain by dealing with the multiple objectives (say p objectives) of a system with a p-variate normal population. Let πi be a p-variate normal population with mean vector μi and positive definite covariance matrix Σi, i.e. πi~ Np(μi, Σi) (i = 1, ... , k). This approach aims at developing a procedure that selects the best population out of the k populations (π1, ... , πk) when the means of all p variates of the k populations are considered that guarantees the desired confidence P*.
In this multivariate approach, the concept of the Pareto optimality is not employed. Instead, an experimenter-specified function g is introduced to define the best in the multi-variate context. The function is defined with a range space {1, 2, ... , k} such that

if and only if the experimenter, out of π1, π2, ..., πk, would prefer πjwith μi as the best. A few more concepts are introduced, based on the experimenter-specified function g, such as M = (μi, μ2, ... , μk) (the set of true mean vectors), Pj(preference sets), and dB(M) (the distance from M to the boundary of the preference set it belongs to), in order to establish a probability requirement similar to (1) as follows:

That is, the procedure guarantees at least P* of choosing the true best population g(M), whenever the mean vector M is at least Euclidean distance δ* from mean vectors where other populations are best.
Dudewicz and Taneja [25] initially proposed a multivariate procedure that achieves the requirement (7), which is essentially the multivariate version of Procedure Pe of Dudewicz and Dalal [6]. It was later improved by Hyakutake [26], to make it more efficient and easier to use in practice. This line of research, however, is not found further in the literature, probably due to the fact that the procedures do not employ the Pareto optimality concept. The MORS problems were left untouched for a decade until the advent of the famous multi-objective optimal computing budget (MOCBA) procedure.
3.2 The multi-objective optimal computing budget allocation procedure
The multi-objective optimal computing budget allocation (MOCBA) procedure has been undoubtedly the most popular method in MORS since it was first proposed by Lee et al. [27] - until now. It is the multi-objective version of optimal computing budget allocation (OCBA) procedures discussed in Section 2.2. In essence, the MOCBA procedure allocates the limited simulation budget (the number of simulation replications) among k systems, so that the probability of incorrect selection is minimised. Two types of error are associated with the probability of incorrect selection: a Type I error and a Type II error. According to Lee et al. [28], a Type I error occurs when at least one truly dominated system design is observed as being non-dominated, while a Type II error occurs when at least one truly non-dominated system design is observed as dominated by other system designs. In simple terms, this means that one might incorrectly include a system design in the estimated Pareto set while it is inferior to at least one of the other members of the set (Type I error), or one might incorrectly exclude a system design from the estimated Pareto set when it should be a member of the set (Type II error). In the MOCBA procedure, these two types of error are approximated, and then bounded by two upper bounds ub1 and ub2respectively. To minimise ub1, the optimisation model is defined as

where Niis the number of simulation replications allocated to system design i and T denotes the simulation budget - i.e., the total number of simulation replications available. The MOCBA procedure provides an asymptotic allocation rule, which is proved to be an optimal solution to the above simulation model as T →∞. The allocation rule itself is not discussed here for the purpose of simplicity. Interested readers are referred to [28].
3.3 The new attempts at multi-objective ranking and selection
The MOCBA procedure is extremely complicated and very difficult to apply, but has nevertheless been widely used because it is virtually the only method applicable in MORS. Very recently a few new attempts have been made to develop simpler MORS procedures.
Feldman et al. [29] and Hunter and Feldman [30] discuss ideas that have the same approach in principle - one in the multi-objective context, the other in the bi-objective context. The research is at an early stage, with the ultimate goal of developing an asymptotic simulation budget allocation rule in a multi-objective context. They claim, therefore, that the method is a direct competitor to the MOCBA procedure. They mean to achieve the goal by adopting the concept of the SCORE (sampling criteria for optimisation using rate estimators) allocation rule [31], which is a simulation budget allocation rule for constrained simulation optimisation problems.
Branke and Zhang [32] have proposed another MORS procedure: the myopic multi-objective budget allocation (M-MOBA). It is a very simple yet efficient MORS method, which looks one step ahead (thus 'myopic') at each iteration. Suppose that nisamples have been allocated to system design i (i = 1, ... , k) up to the current iteration, and now the algorithm is about to allocate τ more samples. The M-MOBA procedure investigates which system design i would have the biggest probability of changing the current Pareto set if all τ new samples were allocated to system design i and none were allocated to the rest. It allocates the τ samples to the system design with the highest probability. The principle is that, if additional samples allocated to system design i do not lead to a change in the current Pareto set, then, in the myopic sense, they do not have any value. However, if the additional samples cause a change to the current Pareto set, then this information is assumed to be helpful. The system design i is then simulated with the additional samples, bringing an improvement to the current Pareto set.
Research work on MORS is relatively new, and we believe that there are still many opportunities for refinement, improvement, and new development.
4 CONCLUSION
In this paper we reminded the simulation practitioner of the development of R&S procedures. Since simulation studies are usually concerned with what-if analyses, they must be able to distinguish good system designs, especially when stochastic designs are simulated. Systems designs might seem to differ numerically, but the important question for the simulation practitioner is: Which of the system designs differ statistically significantly from the others? Once this question has been answered, only then can one or more alternatives be proposed to the final decision-makers (e.g., financial officers, senior engineering management, directors). Ranking and selection (R&S) procedures not only answer this question, but also extend the scope of simulation applications from the traditional what-if analysis (as a tool to improve the current operations of the system) to the level of optimisation (i.e., finding the best solution for the current system among a number of possible solutions).
This paper provides a general view of the R&S research area by reviewing past and current R&S procedures from a historical point of view. The (single-objective) R&S research begins with the indifference-zone procedures in the 1950s, which set the major trend until the early 2000s, when the optimal computing budget allocation (OCBA) procedures took over. In multi-objective ranking and selection (MORS), the multivariate approach appeared briefly in the 1980s, followed by the multi-objective optimal computing budget allocation (MOCBA) procedure, which has clearly been the predominant method since it was first introduced in 2004. Very recently, however, new attempts have been made to develop simpler MORS methods than the MOCBA procedure - an encouraging and desirable development.
REFERENCES
[1] Amaran, S., Sahinidis, N.V., Sharda, B. and Bury, S.J. 2014. Simulation optimization: A review of algorithms and applications, 4OR, 12(4), pp. 301-333. [ Links ]
[2] Bechhofer, R.E. 1954. A single-sample multiple decision procedure for ranking means of normal populations with known variances, The Annals of Mathematical Statistics, pp. 16-39. [ Links ]
[3] Kim, S.H. and Nelson, B.L. 2007. Recent advances in ranking and selection, Proceedings of the 39th conference on Winter Simulation: 40 years! The best is yet to come, pp. 162-172. [ Links ]
[4] Kim, S.H. and Nelson, B.L. 2006. Selecting the best system, Handbooks in Operations Research and Management Science, 13, pp. 501 -534. [ Links ]
[5] Dudewicz, E. 1971. Nonexistence of a single-sample selection procedure whose P(CS) is independent of variances, South African Statistical Journal, 5(1), pp. 37-39. [ Links ]
[6] Dudewicz, E.J. and Dalal, S.R. 1975. Allocation of observations in ranking and selection with unequal variances, Sankhya: The Indian Journal of Statistics, Series B, pp. 28-78. [ Links ]
[7] Rinott, Y. 1978. On two-stage selection procedures and related probability- inequalities, Communications in Statistics - Theory and Methods, 7(8), pp. 799-811. [ Links ]
[8] Nelson, B.L., Swann, J., Goldsman, D. and Song, W. 2001. Simple procedures for selecting the best simulated system when the number of alternatives is large, Operations Research, 49(6), pp. 950-963. [ Links ]
[9] Chick, S.E. and Inoue, K. 2001. New two-stage and sequential procedures for selecting the best simulated system, Operations Research, 49(5), pp. 732-743. [ Links ]
[10] Chen, E.J. and Kelton, W.D. 2005. Sequential selection procedures: Using sample means to improve efficiency, European Journal of Operational Research, 166(1), pp. 133-153. [ Links ]
[11] Hong, L.J. and Nelson, B.L. 2005. The tradeoff between sampling and switching: New sequential procedures for indifference-zone selection, IIE Transactions, 37(7), pp. 623-634. [ Links ]
[12] Wang, H. and Kim, S.H. 2013. Reducing the conservativeness of fully sequential indifference-zone procedures. IEEE Transactions on Automatic Control, 58(6), pp.1613-1619. [ Links ]
[13] Kim, S.H. and Nelson, B.L. 2001. A fully sequential procedure for indifference-zone selection in simulation, ACM Transactions on Modeling and Computer Simulation (TOMACS), 11(3), pp. 251-273. [ Links ]
[14] Chen, C.H., Lin, J., Yucesan, E. and Chick, S.E. 2000. Simulation budget allocation for further enhancing the efficiency of ordinal optimization, Discrete Event Dynamic Systems, 10(3), pp. 251-270. [ Links ]
[15] Chen, C.H. 1996. A lower bound for the correct subset-selection probability and its application to discrete-event system simulations, IEEE Transactions on Automatic Control, 41(8), pp. 1227-1231. [ Links ]
[16] Fu, M.C., Hu, J.Q., Chen, C.H. and Xiong, X. 2007. Simulation allocation for determining the best design in the presence of correlated sampling, INFORMS Journal on Computing, 19(1), pp. 101-111. [ Links ]
[17] Glynn, P. and Juneja, S. 2004. A large deviations perspective on ordinal optimization, Proceedings of the 2004 Winter Simulation Conference, 1, pp. 577-585. [ Links ]
[18] He, D., Chick, S.E. and Chen, C.H. 2007. Opportunity cost and OCBA selection procedures in ordinal optimization for a fixed number of alternative systems, IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 37(5), pp. 951-961. [ Links ]
[19] Chen, C.H., He, D., Fu, M. and Lee, L.H. 2008. Efficient simulation budget allocation for selecting an optimal subset, INFORMS Journal on Computing, 20(4), pp. 579-595. [ Links ]
[20] Xiao, H., Lee, L.H. and Ng, K.M. 2014. Optimal computing budget allocation for complete ranking, IEEE Transactions on Automation Science and Engineering, 11(2), pp. 516-524. [ Links ]
[21] Lee, L.H., Pujowidianto, N., Li, L.W., Chen, C., Yap, C.M. 2012. Approximate simulation budget allocation for selecting the best design in the presence of stochastic constraints, IEEE Transactions on Automatic Control, 57(11), pp. 2940-2945. [ Links ]
[22] Lee, L.H., Chen, C., Chew, E.P., Li, J., Pujowidianto, N.A. and Zhang, S. 2010. A review of optimal computing budget allocation algorithms for simulation optimization problems, International Journal of Operations Research, 7(2), pp. 19-31. [ Links ]
[23] Coello Coello, C.A.C. 2009. Evolutionary multi-objective optimization: Some current research trends and topics that remain to be explored, Frontiers of Computer Science in China, 3(1), pp. 18-30. [ Links ]
[24] Coello Coello, C., Lamont, G.B. and Van Veldhuizen, D.A. 2007. Evolutionary algorithms for solving multi-objective problems (2nd ed.). Springer, New York. [ Links ]
[25] Dudewicz, E.J. and Taneja, V.S. 1981. A multivariate solution of the multi-variate ranking and selection problem, Communications in Statistics - Theory and Methods, 10(18), pp. 1849-1868. [ Links ]
[26] Hyakutake, H. 1988. A general treatment for selecting the best of several multi- variate normal populations, Sequential Analysis, 7(3), pp. 243-258. [ Links ]
[27] Lee, L.H., Chew, E.P., Teng, S. and Goldsman, D. 2004. Optimal computing budget allocation for multi-objective simulation models, Proceedings of the 2004 Winter Simulation Conference, 1, pp. 586-594. [ Links ]
[28] Lee, L.H., Chew, E.P., Teng, S. and Goldsman, D. 2010. Finding the non-dominated Pareto set for multi-objective simulation models, IIE Transactions, 42(9), pp. 656-674. [ Links ]
[29] Feldman, G., Hunter, S.R. and Pasupathy, R. 2015. Multi-objective simulation optimization on finite sets: Optimal allocation via scalarization, Proceedings of the 2015 Winter Simulation Conference, pp. 3610-3621. [ Links ]
[30] Hunter, S.R. and Feldman, G. 2015. Optimal sampling laws for bi-objective simulation optimization on finite sets, Proceedings of the 2015 Winter Simulation Conference, pp. 3749-3757. [ Links ]
[31] Pasupathy, R., Hunter, S.R., Pujowidianto, N.A., Lee, L.H. and Chen, C.H. 2014. Stochastically constrained ranking and selection via SCORE, ACM Transactions on Modeling and Computer Simulation (TOMACS), 25(1), pp. 1-26. [ Links ]
[32] Branke, J. and Zhang, W. 2015. A new myopic sequential sampling algorithm for multi-objective problems, Proceedings of the 2015 Winter Simulation Conference, pp. 3589-3598. [ Links ]
Submitted by authors 13 Mar 2017
Accepted for publication 3 May 2017
Available online 31 Aug 2017
* Corresponding author: jb2@sun.ac.za
# Author was registered for a PhD (Industrial Engineering) in the Department of Industrial Engineering, Stellenbosch University, South Africa
1 Various terms are used in simulation to indicate parameter settings of the system: system designs, systems, designs, scenarios, and/or alternatives. The term population is also used in the same context in statistics.














