Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.28 no.2 Pretoria Ago. 2017
http://dx.doi.org/10.7166/28-2-1753
FEATURE ARTICLES
The power of one: Benford's law
P.S. Kruger*; V.S.S. Yadavalli
Department of Industrial and Systems Engineering, University of Pretoria, South Africa
ABSTRACT
The concept of Benford's law, also known as the first-digit phenomenon, has been known to mathematicians since 1881. It is counter-intuitive, difficult to explain in simple terms, and has suffered from being described variously as 'a numerical aberration', 'an oddity', 'a mystery' - but also as 'a mathematical gem'. However, it has developed into a recognised statistical technique with several practical applications, of which the most notable is as a fraud detection mechanism in forensic accounting. This paper will briefly discuss and demonstrate the special numerical characteristics of Benford's law. It will attempt to investigate the law's possible application to the detection of data manipulation and data tampering that might exist in papers published in engineering and scientific journals. Firstly, it will be applied to an investigation of the so-called Fisher-Mendel controversy. Secondly, Benford's analysis will be applied to six recently published papers selected from the South African Journal of Industrial Engineering.
OPSOMMING
Die konsep van Benford se wet, ook bekend as die eerste-syfer-fenomeen, is bekend aan wiskundiges sedert 1881. Dit is teen-intuïtief, moeilik om te verduidelik op 'n eenvoudige wyse, en gaan gebuk onder verskeie beskrywings soos ''n numeriese afwyking', ''n koddigheid', ''n misterie', maar ook as ''n wiskundige juweel'. Dit het nietemin ontwikkel in 'n erkende statistiese tegniek met vele praktiese toepassings, waarvan die gebruik as 'n bedrog betrappingsmeganisme in forensiese rekeningkunde noemenswaardig is. Hierdie artikel sal die spesiale numeriese karakteristieke van Benford se wet bespreek en demonstreer. Dit sal die wet se moontlike gebruik om datamanipulering en -vervalsing wat mag bestaan in ingenieurs- en wetenskaplike publikasies te identifiseer. Eerstens sal dit toegepas word om die sogenaamde Fisher-Mendel kontroversie te ondersoek. Tweedens sal dit gebruik word om ses artikels wat onlangs gepubliseer is in die Suid-Afrikaanse Tydskrif vir Bedryfsingenieurwese aan 'n Benford analise te onderwerp.
From The power of one by Bryce Courtenay
1 INTRODUCTION
We are drowning in information but starved for knowledge. John Naisbitt
Numbers are an inescapable part of everyday life, and terms such as data processing, data capture, database, data mart, data warehouse, data mining, data farming, metadata, and even big data, have become almost household words. Numbers are used for many purposes such as counting, measuring, reporting, accounting, mathematics, labelling, ordering, and coding. Technology, especially computer technology, has caused an explosion in the amount of readily available - but sometimes unorganised - data. The challenge is to change the almost overwhelming amount of available data and numbers into information and insight. This is in many ways the main purpose of descriptive statistics - that is, to provide tools to analyse, model, and identify the possible existence of usable patterns in a data set. However, the identification and isolation of such patterns can often be difficult without special computational tools or extraordinary perception. This can be demonstrated by what occurred during a meeting in 1919 between the two great numerical mathematicians Srinivasa Ramanujan and G.H. Hardy [1]. The following anecdote has been recounted by Hardy on several occasions: Once, in a taxi from London on his way to visit Ramanujan in hospital, Hardy noticed the taxi's number, 1729. He must have thought about it a little because he entered the room where Ramanujan lay in bed and, with scarcely a hello, blurted out his disappointment with the number. It was, he declared, "rather a dull number", adding that he hoped that it was not a bad omen. "No, Hardy," said Ramanujan, "it is a very interesting number. It is the smallest number expressible as the sum of two [positive] cubes in two different ways" [1]. These numbers became known as 'taxicab-numbers', and since 1919 only six such numbers have been identified. The largest and most recent was discovered in 2008, and contains 23 digits. Unfortunately, most humans do not possess the extraordinary mathematical vision and insight of Ramanujan, and so must rely on the proper application of the available statistical techniques. One such technique is known as Benford's law, or the first-digit phenomenon. This paper will attempt to discuss and illustrate the characteristics and application of Benford's law.
2 BENFORD'S LAW
In fact, 'the law is an ass'. From Revenge for honour by George Chapman
Benford's law is well-known among mathematicians, statisticians, and accountants, and recently several articles have appeared, including in the popular media [1 - 9]. However, it is often perceived as no more than an interesting mathematical oddity. Given the number and variety of data sets that might conform to Benford's law, it is somewhat surprising that there are not many more applications, apart from forensic accounting. Some possible applications have been mentioned or suggested, such as analysing election results, digital signal processing, digital analysis of data integrity, information technology auditing, accounts receivable, credit card transactions, loan data, stock prices, purchase orders, and inventory [1, 5, 9, 10]. However, Benford's law remains an enigma, and continues to defy attempts at an easy derivation [10].
2.1 The basic principles of Benford's law
There are three types of lies: lies, damned lies, and statistics. Benjamin Disraeli
Consider the generation of 1000 random numbers between 1 and 1000, using a reliable pseudo-random number generator. If the first significant digit of each random number is isolated and classified as one of the numbers 1 to 9 and counted, common sense and intuition would indicate that each number between 1 and 9 should appear with approximately the same probability or relative frequency. This is true, as indicated by Figure 1. However, if 10 such random number streams are generated, multiplied by each other, and subjected to the same numerical manipulation, the relative frequency histogram shown in Figure 2 is the result. This is certainly not the rectangular distribution shown in Figure 1, and is known as Benford's law, or the first-digit phenomenon [1-9]. Furthermore, if the 10 random numbers are added rather than multiplied, the relative frequency histogram shown in Figure 3 is the result. This distribution seems to be close to a normal distribution, and is probably caused by the central limit theorem - which might be an indication that Benford's law is similar to that theorem [11]. The number 10 was chosen after preliminary experiments had shown that this is adequate to show the emerging patterns clearly.

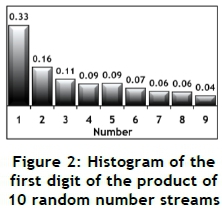
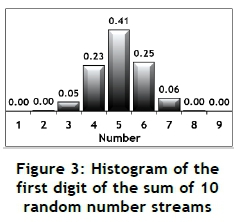
Simply stated, Benford's law claims that for many, but not all, data sets with a natural origin, including the results from mathematical operations, might produce relative frequencies for the first digit where the occurrence of the smaller numbers is higher than that of the larger numbers [8].
2.2 The background to Benford's law
Those who do not remember the past are condemned to repeat it. George Santayana
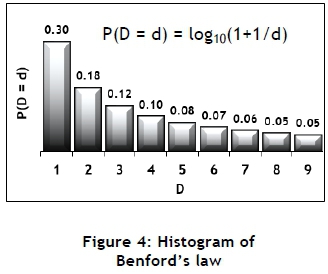
In 1881 the astronomer Simon Newcomb noticed that some of the pages in his book of logarithmic tables were much more worn and dirty than the other pages. Furthermore, the numbers appearing in these pages tended to start with '1'. He published a paper to report on his observations [12], but this paper was largely ignored and forgotten. In 1938 the physicist Frank Benford rediscovered this phenomenon, and published a paper that referred to it as the "law of anomalous numbers" [2]. In this paper, Benford investigated 20 datasets from a variety of sources and origins - for example, the surface area of rivers, the size of the population in cities, numbers appearing in the Reader's Digest, and the results obtained from mathematical operations such as power functions [2]. Neither Newcomb nor Benford explained the phenomenon, but both suggested that the resultant distribution might be of a logarithmic type. It was only in 1995 that a statistical derivation of Benford's law was published [11], showing that the distribution of the first digit was indeed a logarithmic series distribution given by the following expression:
P(D = d) = Log10(1+1/d)
The variable D is the first digit having values equal to d = 1, 2 .... 9
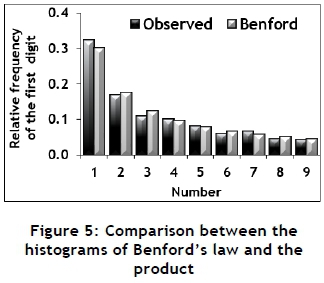
The histogram of this distribution is shown in Figure 4. Throughout the rest of this paper, this distribution provides the frequencies that are expected when Benford's law is considered applicable. Figure 5 shows the comparison between the histograms of the product of 10 random numbers and Benford's law. Tables 1 and 2 show the results of statistical tests performed for both the product and the sum of 10 random digits. These tests will be described in section 2.3. It seems as if multiplication operations provide a good conformance with Benford's law, but not addition. One of the main applications of Benford's law is in forensic accounting [3, 4, 6], where it is used to detect possible fraud. However, financial statements often contain a significant number of addition operations. This apparent contradiction is typical of Benford's law, since it often displays exceptions that are difficult to explain.
2.3 Evaluating the conformance to Benford's law
Get your data first, then you can distort them at your leisure.
Attributed to Mark Twain (Samuel Langhorne Clemens)
The graphical evidence of conformance provided by Figure 5 might be significant, compelling, and even dominating. However, several statistical tests known as the goodness-of-fit or lack-of-fit tests [14], and techniques based on so-called fit indexes [14-17], are available for supporting the graphical evidence. Apart from the graphical evidence, only three such techniques will be used in this paper.
The chi-square goodness-of-fit test is one of the best-known and most widely-used goodness-of-fit tests, although it does suffer from some limitations [13]. It is sensitive to sample size and outliers, and does not provide much evidence for the strength of the fit - although the magnitude of the P-value might be useful. The chi-square tests will be conducted using the following hypothesis statement:
Null hypothesis H0: The fit between the observed and expected frequencies is good
Alternative hypothesis Ha: The fit is poor
The root mean square error (RMSE) fit index [14-17] is considered as one of the best indexes of its kind [16] and is easier to understand and evaluate than the chi-square test. Furthermore, it may be used to evaluate the strength of the fit and is useful for comparing different data sets.
Both the chi-square test and the RMSE-fit index evaluate the fit between the observed and expected frequencies in its entirety. A hypotheses test for the difference in proportions may be used to evaluate the difference in each pair of relative frequencies separately [13]. This may proof valuable in determining which pair of relative frequencies contributes the most to the possible failure of the chi-square test and/or the RMSE-fit index. Furthermore. It may provide a suitable starting point for any further investigation that may be considered. The tests for the difference in proportions will be conducted using the following hypothesis statement:
Null hypothesis H0: p1= p2The fit between the observed and expected frequencies is good
Alternative hypothesis Ha: p1 ≠ p2The fit is poor
where p1and p2are the observed and expected relative frequencies respectively.
For most statistical hypothesis tests, it is necessary to define a level of significance, the value of which might be open to debate. The great Swiss mathematician, Jacob Bernoulli, who could be considered the initiator of the concept of statistical inference, referred to the level of significance as "the level of moral certainty" [18]. Bernoulli professed to be unsure what an acceptable value for the level of moral certainty should be and, given his background in the law, suggested: "It would be useful if the magistrates set up fixed limits for moral certainty" [18]. He derives his definition of probability from previous work by Gottfried Wilhelm Leibniz, and concluded: "Probability is a degree of certainty" [18] - and that is what a level of significance is. This supports the notion that an appropriate value for a probability might be subject to the situation, personal judgment, and risk preference. A value of the level of confidence of 0.05 was chosen for the purposes of this paper, as it is the most widely-used and widely-accepted value, and will be used to evaluate the P-values (as shown in Table 3). However, rejecting a hypothesis based on a level of significance of 0.05 might be unnecessarily conservative in the case of Benford's law. Based on several references from the literature [14-17], the cut-off criterion for the value of the RSME-fit index that will be used in this paper is shown in Table 3.
It seems to be difficult to decide on an adequate sample size for Benford. The consensus in the literature [15] seems to be that a sample size of at least 50 to 100 might be required for Benford'd law to be observed - if it does exist - but that a sample size of 500 or more might be preferred for proper analysis.
Table 4 shows a set of possible guidelines for deciding whether or not a data set might be expected to conform to Benford's law [14-17].
2.4 The characteristics of Benford's law
Figures don't lie, but liars do figure. Possibly Mark Twain
The results obtained from applying a Benford test on a data set should be interpreted with care and insight. The results from a Benford test should never be used as an absolute proof or disproof of the presence of Benford's law - nor, for example, the possible existence of data tampering. It can at best be used to provide an indication of whether further investigation of the data set might be appropriate. Special care should be taken in interpreting the results from typical statistical goodness-of-fit tests. These tests are sensitive to small samples, and are usually designed either to reject or not reject a hypothesis at a high level of confidence that might not be required for the effective application of Benford analysis.
Traditionally, Benford's law is applicable to data sets from natural and accounting origins. However, there are some indications that it might also be applicable to data generated as the consequence of mathematical operations (see Tables 5 and 6). For this reason, it is in part the purpose of this paper to investigate the possibility that the data typically published as part of engineering and scientific papers might also conform to Benford's law.
Tables 5 and 6 shows the results from experiments performed by applying Benford analysis to a selection of typical data sets. The purpose of these experiments is to demonstrate the characteristics of Benford's law, and to serve as motivation for some remarks about the characteristics of Benford's law. The second-to-last column shows the relative frequencies observed from the data set in comparison with the relative frequencies of the Benford distribution. The last column contains the final decision of the authors, based on the available evidence.
Data set A, the Fibonacci numbers, is a series with a high value for the first order auto-correlation coefficient, which might indicate that the numbers are not independent, and that the series has no dimensions, does not result from a natural process, and contains only additive operations; and yet it is almost a perfect fit for Benford's law. Data set A is a good example of an apparently inexplicable exception to the suggested guidelines provided in Table 4.
Data set B, the prime numbers, and data set C, the square root, are both a poor fit to Benford's law; but, for no obvious reason, data set D, the factorials, does provide a good fit; and the same is true for data set E, the power function. The good fit provided by data set E, the power function, is important, since many natural systems and processes, such as the size of craters on the moon and the height of solar flares, follow a power function. This might provide some reason that so many data sets from natural processes tend to conform to Benford's law.
The Benford distribution is discrete; but some continuous processes, such as exponential growth, also conform to Benford's law. As an example, data set F was obtained from the calculation of compound interest, which does provide a good fit.
Further examples of the exceptions to Benford's law arfe provided by data sets G and H. Values from an exponential distribution provide a good fit, but not values from a normal distribution.
Data sets I, cost data, and J, population data, are typical examples of data sets that should conform to Benford's law. However, the fit for data set J is not very good. The reason for this might be the fact that the available data does not contain populations of less than 1500, thus causing a lower limit.
The exceptions to Benford's law are difficult to explain without further research.
3 APPLICATIONS OF BENFORD'S LAW
The world looks neater from the precincts of MIT on the river Charles than from the hurly-burly of Wall Street by the Hudson. Fischer Black.
Two typical possible applications of Benford's law will be investigated and discussed in this section: the Fisher-Mendel controversy, and papers selected from the South African Journal of Industrial Engineering. The main purpose is to determine whether data extracted from these documents conforms to Benford's law; and the authors should therefore be absolved from any possible data manipulation or data tampering.
3.1 The Fisher-Mendel controversy
Numbers don't lie, sir. Politics, poetry, promises - those are lies! Numbers are as close as we get to the handwriting of God.
Hermann Gottlieb
Gregor Johann Mendel gained posthumous recognition as the founder of the modern science of genetics, primarily because of his paper, published in 1865, dealing with his numerous experiments with peas [19]. However, Ronald Aylmer Fisher, probably one of the most accomplished and respected statisticians of the 20th century, analysed Mendel's data; and in a paper published in 1936, he concluded that "the data of most, if not all, of the experiments have been falsified so as to agree closely with Mendel's expectations" [20].
This accusation gave rise to a controversy, known as the Mendel-Fisher controversy, which in some ways is still raging. Several attempts have been made to resolve the controversy [21]. A compromise conclusion was reached, essentially saying that Fisher was probably correct from a purely statistical point of view, although he might have been over-conscientious and conservative [21]. At the same time, there is no conclusive evidence that Mendel - the scientist, Augustinian friar, and abbot of St Thomas' Abbey - was guilty of data tampering. It should be mentioned that Fisher did not question Mendel's conclusions, but said only that "the data is too good to be true" [20,21], and admitted that, if there were any data falsification, it might be due to an over-zealous assistant of Mendel who might have been aware of what was expected, and possibly performed some selective sampling to please the friar [21]. In the late 1950s, Fisher was also involved in another dispute, the so-called cancer controversy [22], when he doubted that smoking cigarettes caused lung cancer, claiming that his analysis did not provide conclusive proof of the existence of a relationship between smoking and lung cancer. It has been suggested that, in this case, Fisher might have been guilty of selective sampling [23]. It is conceivable that Fisher was not aware of Benford's law when he wrote his paper on the Mendel data, since Benford had published his paper only two years later. It seems appropriate, therefore, to subject Mendel's data to a Benford analysis.
For this purpose, Mendel's original paper [19] was obtained and a data set extracted. The extraction process involved some data filtering - for example, all of the data consisting of ratios was omitted. Such a process of selective sampling should be performed with extreme care, since it can easily introduce statistical bias. The results of this analysis are shown in Table 7 and Figure 6, and seem to vindicate the already-mentioned conciliatory conclusions recently reached [20,21]. Regarding Figure 6, the frequency of interval 5 seems too low and the frequency of interval 6 seems to be too large. This might indicate selective or biased sampling, and could serve as the starting point of any further investigation. Furthermore, intervals 5 and 6 contribute 63 per cent of the total chi-square statistic, providing a possible reason that the chi-square test resulted in a rejection of the nulhypothesis.
3.2 Benford analysis of papers selected from the South African Journal of Industrial Engineering
Data is like garbage. Youd better know what you are going to do with it before you collect it. Mark Twain
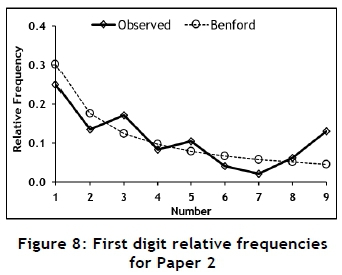
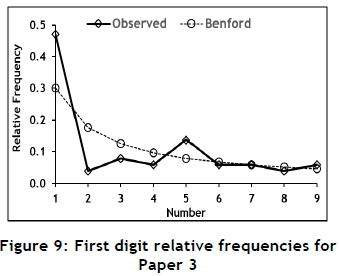
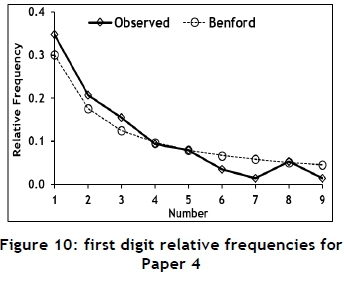
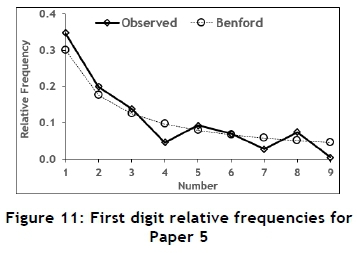
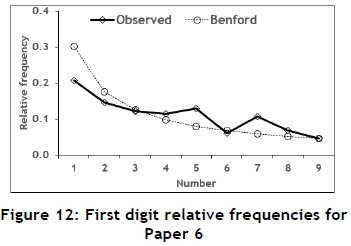
To investigate the use of Benford's law to identify possible data tampering in papers published in typical engineering journals, six papers from recent issues of the South African Journal of Industrial Engineering were selected. These papers were not randomly selected, but rather because of the amount of useable data they contained. The six papers were each subjected to a Benford analysis; the results are summarised in Tables 8, 9, 10, 11, 12, and 13 and in Figures 7, 8, 9, 10, 11, and 12.
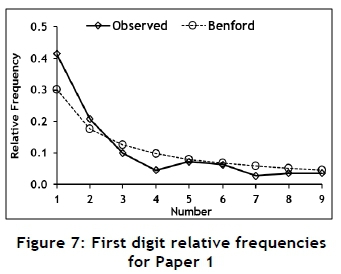
The data set for Paper 1 passes all the tests, and therefore can be considered as conforming to Benford's law.
The data set for Paper 2 fails the chi-square and two of the proportion tests, but none of the other. The proportion test for digit 9 indicates that this relative frequency might be an outlier, and might be the reason that the data set fails the chi-square test, since this test is sensitive to outliers. Further investigation showed that the data set for Paper 2 contains several probability values greater than 0.9, which might be the cause of the outlier and thus the failure of the chi-square test. Since it is known that probabilities do not necessarily conform to Benford's law, these values can be considered for removal from the data set; but this should be done with trepidation. Given the available information and the preceding arguments, Paper 2 can be considered to conform to Benford's law.
The fit of Papers 4 and 5 is not very good, but might suffer from the same problem regarding outliers as that discussed in the case of Paper 2; but it is still considered to conform to Benflord's law.
Paper 6 seems to conform to Benford's law in all respects.
Furthermore, the graphical evidence points to a consistent tendency towards conformance with Benford's law for all the papers.
There are several reasons that typical data from engineering and scientific papers might not conform to Benford's law. This could include small sample sizes, upper limits, and limited data ranges for variables such as probabilities, indexes and ratios, dependent data, data from different types, sources and origins, etc. These factors might cause further investigation to be considered, although it might not be necessary.
For the sake of transparency - and to heed the advice of Robert Louis Stevenson, among others: "There is so much good in the worst of us, and so much bad in the best of us, that it hardly behooves any of us to talk about the rest of us" - it should be revealed that the authors of this paper are the authors of Paper 1, and that the main author of this paper is also the co-author of Paper 2. Furthermore, it should be admitted that paper 6 is this very paper. The titles and authors of the other papers will remain anonymous.
Given all the evidence, it is the authors' considered opinion that, "on the balance of probabilities", the authors of the six papers investigated can be found "not guilty, beyond a reasonable doubt" of any data tampering or unethical behaviour!
4 COMMENTS, CAVEATS, AND CONCLUSIONS
I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind.
Lord Kelvin (William Thomson)
Some other interesting characteristics of Benford's law have not been mentioned - for example [8]: Benford's law is related to Ziph's law, known to linguists and used to study the frequency of words in a manuscript. Benford's law can be generalised beyond the first digit. However, the distribution of the n-th digit, as n increases, rapidly approaches a uniform distribution. A Benford data set is scale invariant - that is, it can be multiplied by a constant, and will still retain the Benford characteristics. An extension of Benford's law can be used to predict the distribution of first digits in other bases besides the decimal.
It has been stated that "the widely-known phenomenon called Benford's law continues to defy attempts at an easy derivation" [10]. In that sense, "most experts seem to agree that the ubiquity of Benford's law, especially in real-life data, remains mysterious" [10]. This characteristic of Benford's law complicates the decision about whether a data set should, or should not, conform to Benford's law. Benford's law is by no means perfect - as is the case with most other statistical tests - but it does provide another alternative, and a valuable way of performing certain kinds of statistical analysis, when applicable.
Statistical inference is an invaluable tool for effective decision-making, but should be interpreted with care. It should not be applied blindly, and some room should be left for the consideration of good judgment, common sense, and even intuition based on experience and knowledge. In this respect, the validity and value of graphical evidence, such as a graph of relative frequencies, should not be under-estimated.
This paper has showed that Benford analysis can be applied to the investigation of the data published as part of engineering or scientific papers. However, considering the implementation of such an approach, similar to computerised testing for plagiarism, can be difficult to implement in practice.
Given the explosion in data availability, there is a need for effective scanning mechanisms to identify the possible existence of aberrations and anomalies in large data sets. Benford's law might be useful in this kind of digital profiling. Furthermore, it seems as if the possible use of the results of a Benford analysis to serve as a kind of process signature has not been investigated. This could be useful, for example, in condition monitoring types of applications.
The available statistical and graphical evidence provides enough reason to declare that both Gregor Johann Mendel and the authors of the selected papers published in the Journal should be exonerated from any professional misconduct.
REFERENCES
There are more things in heaven and earth, Horatio, than are dreamt of in your philosophy.
From Hamlet: Prince of Denmark by William Shakespeare
References to many publications dealing with Benford's law are available [24]. However, for the sake of brevity, only those publications that have been referenced or are the most significant or informative to this paper are included in the list of references below.
[1] Weisstein, E.W. 2016. Hardy-Ramanujan number. MathWorld: A Wolfram Web Resource, available from http://mathworld.wolfram.com/Hardy-RamanujanNumber.html [Accessed January 2017]. [ Links ]
[2] Benford, F. 1938. The law of anomalous numbers. Proceedings of the American philosophical society, pp.551-572. [ Links ]
[3] Durtschi, W.L. & Pacini, C. 2004. The effective use of Benford's law to assist in detecting fraud in accounting data. Journal of Forensic Accounting, (V). [ Links ]
[4] Goldacre, B. 2011. Benford's Law: Using stats to bust an entire nation for naughtiness. The Guardian, Saturday 17 September 2011, available from http://www.badscience.net/2011/09/benfords [Accessed January 2017]. [ Links ]
[5] Hill, D.P. 1998. The first-digit phenomenon. American Scientist, July-August 1998. [ Links ]
[6] McGinty, J.C. 2014. Accountants increasingly use data analysis to catch fraud. The Wall Street Journal, available from http://www.wsj.com/articles/accountants-increasingly-use-data-analysis-to-catch-fraud-14 [Accessed January 2017]. [ Links ]
[7] Wales, J. & Sanger, L. 2016. Benford's Law. Wikimedia Foundation, Wikipedia Encyclopaedia, available from https://en.wikipedia.org/wiki/Benford%27s_law [Accessed January 2017]. [ Links ]
[8] Nigrini, M.J. 1999. I've got your number. Journal of Accountancy, May 1, 1999. [ Links ]
[9] Singleton, T.W. 2011. Understanding and applying Benford's law. ISACA Journal, (3), available from www.isaca.org/Journal/archives/2011/Volume-3/Pages/Understanding-and-Applying-Benfords-Law.aspx [Accessed January 2017]. [ Links ]
[10] Berger, A. and Hill, T.P. 2011. Benford's law strikes back: no simple explanation in sight for mathematical gem. The Mathematical Intelligencer, 33(1), pp.85-91. [ Links ]
[11] Hill, T.P. 1995. A statistical derivation of the significant-digit law. Statistical Science, (10). [ Links ]
[12] Newcomb, S. 1881. Note on the frequency of use of the different digits in natural numbers. American Journal of Mathematics, (4). [ Links ]
[13] Montgomery, D.C. & Runger, G.C. 2011. Applied statistics and probability for engineers. John Wiley & Sons. [ Links ]
[14] Cangur, S. & Ercan, I. 2015. Comparison of model fit indices used in structural equation modeling under multivariate normality. Journal of Modern Applied Statistical Methods, (14). [ Links ]
[15] Kenny, D.A. 2015. Measuring model fit, available from http://davidakenny.net/cm/fit.htm [Accessed January 2017]. [ Links ]
[16] Pike, D.P. 2008. Testing for the Benford property. School of Mathematical Sciences, Rochester Institute of Technology, available from www.researchgate.net/publication/251693892_Testing_for_the_Benford_Property, [Accessed January 2017]. [ Links ]
[17] Tanaka, J.S. 1993. Some clarifications and recommendations on fit indices. Testing structural equation models. Newbury Park, available from http://web.pdx.edu/~newsomj/semclass/ho_fit.doc [Accessed January 2017]. [ Links ]
[18] Bernstein, P.L. 1996. Against the gods: The remarkable story of risk. John Wiley & Sons. [ Links ]
[19] Mendel, G. 1865. Experiments in plant hybridization (1865). Available from http://www.mendelweb.org/Mendel.html [Accessed January 2017]. [ Links ]
[20] Franklin, A. 2008. Ending the Mendel-Fisher controversy. University of Pittsburgh Press. [ Links ]
[21] Pires, A.M. & Branco, J.A. 2010. A statistical model to explain the Mendel-Fisher controversy. Statistical Science, (25). [ Links ]
[22] Fisher, R.A. 1958. Cigarettes, cancer and statistics. Centen Rev (2). [ Links ]
[23] Stolley, P.D. 1991. When genius errs: R.A. Fisher and the lung cancer controversy. American Journal of Epidemiology, (133). [ Links ]
[24] Hürlimann, W. (ed.). 2006. Benford's law from 1881 to 2006: A bibliography. Available from arxiv.org/pdf/math [Accessed January 2017]. [ Links ]
Submitted by authors 28 Mar 2017
Accepted for publication 4 Jul 2017
Available online 31 Aug 2017
* Corresponding author: paul.kruger12@outlook.com














