Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.26 no.3 Pretoria Nov. 2015
http://dx.doi.org/10.7166/26-3-1208
CASE STUDIES
A two-phased multi-criteria decision-making approach for selecting the best smartphone
A. YildizI; E.U. ErgulII
IVacuity of Technology, Department of Automotive Engineering Amasya University, Turkey aytac.yildiz@amasya.edu.tr
IIFaculty of Technology, Department of Electrical and Electronics Engineering Amasya University, Turkey engin.ergul@amasya.edu.tr
ABSTRACT
In the last 20 years, rapid and significant developments have occurred in communication and information technologies. In parallel with these developments, the importance of smartphones has increased. In addition, many smartphone manufacturers have launched and continue to launch a number of new models with many features. People who want to buy a new smartphone have difficulties selecting the best smartphone among the numerous models available on the technology markets. Therefore, smartphone selection has become a complex multi-criteria decision-making (MCDM) problem for people. Hence, decision-making processes will be facilitated by using MCDM methods, and these will provide the most appropriate decision. In this paper, the best smartphone among the 28 alternatives determined by the person who will buy them are selected by using three main criteria and 17 sub-criteria with the help of a two-phased MCDM approach. In the first phase, 28 smartphone alternatives are ranked using the analytic network process (ANP). In the second phase, a model that includes the best four alternatives of ANP is created. Afterwards, the best smartphone is selected using the generalised Choquet integral (GCI) method according to this model. Finally, the findings and the results are given.
OPSOMMING
Gedurende die afgelope twintig jaar het daar vinnige en noemenswaardige ontwikkeling in die kommunikasie en informasie tegnologie geskied. In parallel hiermee het die belangrikheid van slimtelefone toegeneem. Daarmee saam stel slimtelefoon-vervaardigers gereeld nuwe modelle met nuwe funksies vry. Dit is dus moeilik vir 'n potensiële kliënt om die beste seleksie uit die groot verskeidenheid tot hul beskikking te maak. Slimtelefoonseleksie is 'n ingewikkelde multi-kriteria besluitnemingsprobleem. Die besluitnemingsproses word dus gefasiliteer deur gebruik te maak van multi-kriteria besluitnemingsmetodes. Hierdie artikel bepaal die beste slimtelefoon vanuit agt-en-twintig alternatiewe deur gebruik te maak van drie hoof kriteria en sewentien subkriteria met die hulp van 'n twee-ledige multi-kriteria besluitnemingsbenadering. Eerstens word die agt-en-twintig alternatiewe met behulp van die analitiese netwerk proses gerangskik en daaruit word 'n model, wat uit die vier beste alternatiewe bestaan, geskep. Laastens word die beste slimtelefoon gekies deur die veralgemeende Choquet integraal metode op die model toe te pas.
1 INTRODUCTION
87 per cent of the world's population (approximately 6.8 billion people) are mobile phone subscribers. According to a report by the International Telecommunication Union (ITU) [1], although the usage and commonness of communication technologies has increased, communication costs have decreased.
Nevertheless, the interest in mobile communication is increasing. In parallel to this interest, mobile phone manufacturers have produced many different models. Because of the fast circulation in mobile phone models, mobile phone users have decision-making difficulties when purchasing the most suitable phone model. Also, new generation mobile phones are not only used for communication, but also for many different purposes such as internet access, computer, camera, calculator, etc. Customers therefore want to choose the most suitable smartphones by taking into account many qualitative and quantitative criteria. Quantitative criteria include, for example, pixel density, camera resolution, random access memory (RAM) size, battery power, talk time, standby time, built-in memory, weight, thickness, screen size, processor type, number of processors, and cost; and qualitative criteria include durability, ease of use, aesthetics, and brand.
Multi-criteria decision-making (MCDM) methods are used for the solution of problems - such as selecting the best smartphone - that are affected by many criteria. Decision problems vary depending on the status of the solution and the methods used. If there are many conflicting criteria, the problem is known as an MCDM problem. MCDM is a process of determining the most suitable or best solution according to the selected criteria [2]. Because the criteria generally conflict with each other, there is no single solution that satisfies all criteria simultaneously. Thus, the solution is a set of non-inferior solutions, or a compromise solution according to the decision-maker's preferences [3]. The advantage of MCDM methods is that they evaluate the large number of criteria and alternatives together [4].
MCDM methods are used to select the best alternative from a finite number of alternatives in problems that have multiple conflicting objectives. In MCDM methods, criteria information is processed to get the best result. There are some common steps in MCDM methods. These include the following, first, evaluation criteria are determined; then the alternatives are generated; the alternatives are evaluated according to the criteria; an MCDM method is applied; the alternatives are ranked from the best to the worst; and lastly, if this solution is not satisfactory, new data is collected and all the steps are repeated.
Many MCDM approaches have been proposed in the literature. Some of these include the simple additive weighting (SAW), weighted product method (WPM), the technique for order preference by similarity to ideal solution (TOPSIS), and the analytic hierarchy process (AHP) [5].
Because many criteria are relevant in the process of purchasing a smartphone, this is an MCDM problem. Some studies of this problem are summarised here. For example, Isiklar and Buyukozkan [6] use two MCDM methods to evaluate the mobile phone options according to the preference orders of users. They use AHP to determine the relative weights of evaluation criteria and apply TOPSIS to rank the mobile phone alternatives [6]. Chen et al. [7] apply an AHP-based mechanism to develop an effective web-based recommendation system; their system contains rank-based analysis and an equal weight-based system. Bayraktar et al. [8] use a data envelopment analysis (DEA) approach to analyse and compare customer satisfaction and loyalty to mobile phone brands in an emerging technology market in Turkey. They construct a European customer satisfaction index (ECSI) model for input and output indicators of their DEA model, and, according to 251 mobile phone users, they select the most efficient mobile phone brand [8]. Akyene [9] uses entropy and TOPSIS for mobile phone selection. Hu and Liao [10] use AHP to analyse the consumer purchase evaluation factors of smartphones. They classify the main functions of smartphones into five categories; according to their results, the most important factor that affects consumers' choice is the hardware and software specifications [10]. Hu et al. [11] propose a smartphone improvement for promoting the product value to satisfy the customers' needs with a hybrid MCDM model. They combine a decision-making trial and evaluation laboratory (DEMATEL)-based analytic network process (ANP) and vise kriterijumska optimizacija i kompromisno resenje (VIKOR) to reduce the gaps corresponding with each criterion in their study [11]. Erinci and Sulak [12] use AHP for smartphone selection; they take into consideration both objective criteria and fuzzy subjective criteria.
In this paper, a two-phased MCDM approach is used to select the best smartphone out of 28 alternatives. In the first stage, ANP is used to rank the alternatives according to the criteria. Then, the generalised choquet integral (GCI) is used to rank the best four alternatives determined by the ANP algorithm. After that, the best smartphone is selected.
The rest of the paper is organised as follows. In Section 2, MCDM methods used in this study are briefly described. The application of ANP and GCI to the smartphone selection problem is given in Section 3. Overall findings and discussion are given in Section 4. Finally, overall conclusions are given in Section 5.
2 MCDM METHODS USED IN THIS STUDY
In this study, two popular MCDM methods, the analytic network process (ANP) and the generalised choquet integral (GCI) methods, are used and combined for the selection of smartphones.
ANP is an important method for analysing and solving multi-criteria decision-making problems. It uses all the factors and criteria for making the best decision, as well as inner and outer dependencies.
As in ANP, GCI is quite successful in decision-making problems that have uncertainty and interaction between decision criteria. The combination of ANP and GCI facilitates the selection processes and increases their effectiveness. The sensitivity of the results obtained by ANP and GCI are increased by taking into consideration the dependencies within and between the criteria. Also, it shows which criteria are important in ANP and the performance values of all criteria and sub-criteria in GCI for all alternatives separately, thereby making the selection process much easier.
For these reasons, ANP and GCI were used together in this paper. Decision-making in this selection problem can be done more sensitively by using this two-staged selection approach.
The main purpose of the study is to use GCI to select the best smartphone. Due to the large number of smartphone alternatives, however, it was decided to reduce the alternatives to eliminate the disadvantages of the implementation of the method. ANP is used because it ranks the alternatives by taking into account the relationships between the criteria. Afterwards, the best four alternatives ranked by ANP are re-evaluated using GCI, and the best smartphone is selected. The flowchart of the two-phased approach used in the best smartphone selection is depicted in Figure 1. Brief descriptions of these methods are given below.
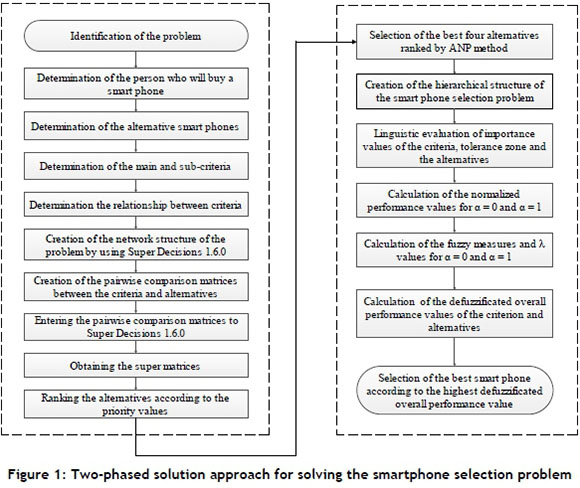
2.1 Analytic network process (ANP)
The analytic hierarchy process AHP [13] is the most frequently-used method in solving MCDM problems. In this method, the problem is constructed in a linear top-to-bottom form as a hierarchy, and the elements in each level are independent from each other [14]. On the other hand, many problems cannot be constructed hierarchically. Thus, to eliminate this problem, Saaty [15] proposed ANP, a general form of the AHP. AHP is easier to apply than the ANP method; but, although the ANP has many weight calculation processes, it also has some useful features. One of the significant features is the pair-wise comparison process. Also, the qualitative values are transformed into quantitative values in the ANP.
Similarly to the AHP, the performance of the weights of criteria and the scores of alternatives in the ANP are assessed indirectly from pair-wise comparison judgments [14]. ANP uses complex interrelationships among decision levels [16]. ANP evaluates all the relationships by taking into consideration all interactions, interdependences, and feedbacks in a decision-making problem. ANP is a useful method for solving complicated decision-making problems. This method not only enables pair-wise comparisons of the sub-criteria under the main criteria, but also provides independent comparisons for all interacted subcriteria. A graphical comparison of the AHP and ANP methods is shown in Figure 2.
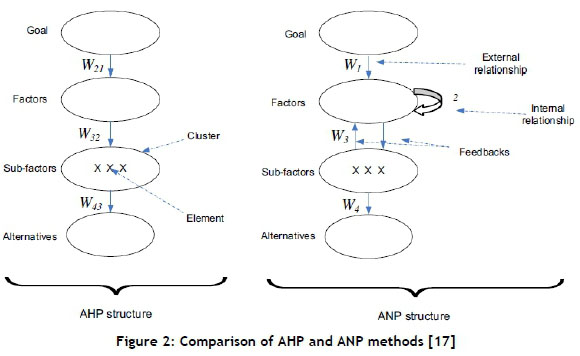
All interactions and feedbacks within the clusters are called 'inner dependencies', whereas interactions and feedbacks between the clusters are called 'outer dependencies'. In such circumstances, a complicated analysis is necessary to figure out the weights of all components. The ANP method is useful for getting more accurate and effective results in complex decision-making problems, due to involving relationships among sub-criteria under each cluster and interactions among different criteria [17].
The steps of ANP can be summarised as follows [15]:
Step 1. The identification of the problem and the establishment of the model: The problem, objectives, main criteria, sub-criteria, and alternatives are identified.
Step 2. Determination of the relationship between criteria: Internal and external dependencies and feedbacks are identified by determining interactions between main criteria and sub-criteria.
Step 3. Creation of the pair-wise comparison between the criteria and alternatives: The group of decision-makers makes the pair-wise comparison by using the priority values.
Step 4. Making consistency analysis of comparison matrices: To determine the consistency of comparisons, a consistency ratio (CR) is calculated for each matrix after the comparison matrices are configured. If the value of CR is lower than 0.10, it can be said that the comparisons are consistent. If the value of CR is higher than 0.10, there is an inconsistency, and the decision-maker must revise the pair-wise comparisons.
Step 5. Creation of the super matrices: To obtain the global priorities in a model that contains the interdependent effects, local priority vectors are written as maximum to the column of the super matrix. Super matrix is a sectional matrix, and each matrix section shows the relationship between two criteria in a model. The long-term relative effects on each criterion are determined by taking the power of the super matrix. The (2n+1) power of the super matrix is taken to equalise the importance weight in a point, where n is a randomly-selected large number and the obtained new matrix is called 'limit super matrix'.
Step 6. The selection of the best alternative: The importance weights of the criteria and alternatives are determined by using the limit super matrices. The alternative that has the highest importance weight is determined as the best alternative in the selection problem. The criterion that has the highest importance weight is determined as the most important criterion in the weighting problem.
The various applications of ANP in MCDM problems can be found in the literature. Some of these studies are summarised below.
Sarkis and Talluri [18] used ANP in the selection and evaluation of the best supplier. Shyur and Shih [19] applied a model that uses ANP and TOPSIS together for supplier selection. Gencer and Gurpinar [20] applied ANP to select the supplier in the electronics sector. Liao et al. [21] used ANP to select the optimal programme suppliers for Taiwan TV channels. Kuo and Lin [22] used an approach that combines ANP and DEA for supplier selection. Vujanovic et al. [23] combined DEMATEL and ANP for the evaluation of vehicle fleet maintenance management indicators. Kilic et al. [24] used a combination of ANP and the preference ranking organisation method for enrichment evaluations (PROMETHEE) methods to select the best enterprise resource planning (ERP) for small- and medium-sized enterprises (SMEs). Neumüller et al. [25] used ANP in distribution centre selection.
2.2 Generalised choquet integral (GCI)
The weighted average and other averages, such as arithmetic average, are used if the criteria in the decision-making problem are independent from each other. The criteria and sub-criteria are weighted when there is an interaction between the criteria [26]. Therefore, the Choquet integral is more useful when there are uncertainties and interactions between the criteria [27].
The Choquet integral, a numeric-based approach, is represented by intervals [28-32]. A Choquet integral is an extension of the standard fuzzy integral [33]. The Choquet and Sugeno integrals are used as aggregation operators. The Choquet integral [34] is the generalisation of the weighted average method, the ordered weighted average (OWA) operator, and the max-min operator [31]. The importance of a criterion and interactions between criteria are represented in a Choquet integral. The generalised Choquet integral proposed in Auephanwiriyahul et al. [33], in which measurable evidence is represented in terms of intervals, whereas fuzzy measures are real numbers, is an extension of the standard Choquet integral. In the generalised version of the Choquet integral, measurements are done by using intervals instead of real numbers [31,35]. Some studies with the Choquet integral method are summarised below.
Yayla et al. [36] used GCI in subcontractor selection. Yayla and Yildiz [37] used GCI in the selection of white good brands. Ming-Lang et al. [35] used ANP and the Choquet integral in optimal supplier selection. Tsai and Lu [31] used the Choquet integral to evaluate the service quality of an e-store. Demirel et al. [38] used the Choquet integral in the selection of a warehouse location.
The steps of the GCI are given as below [31,38]:
Step 1. Given criterion i, linguistic preferences of respondents for the degree of importance, perceived importance levels of alternative smartphones, and tolerance zone are surveyed.
Step 2. The parameters are created as corresponding to j, main criteria (j=1,2,...,m); i, sub-criteria based on the main criteria (i=1,2,...,nj), and t decision-maker (t=1,2,3,...,k); for the i criteria; 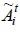 degree of importance,
degree of importance, perceived smartphone performance, and
perceived smartphone performance, and  expected smartphone performance tolerance zone.
expected smartphone performance tolerance zone.
Step 3. The average values of 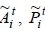 and
and 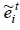 are calculated by Equation 1.
are calculated by Equation 1.
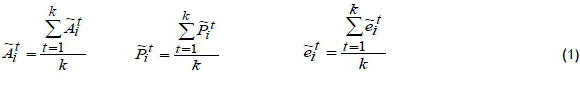
Step 4. 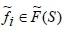 is a fuzzy function, and its effect on both criteria on smartphone performance is normalised by Equation 2.
is a fuzzy function, and its effect on both criteria on smartphone performance is normalised by Equation 2.

Here, all the fuzzy-valued 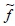 function groups become
function groups become 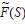 . For
. For 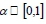 ;
; 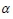 -level cuts of
-level cuts of

Step 5. The performance of a smartphone is found by using Equation 4 considering the sub-criteria j.

Here, expressions are valid for i=1,2,...,nj . To calculate smartphone performance, there is a need for λ and fuzzy measures g(A(i)). Here, fuzzy values gand λ can be solved by using Equations 5-7 below.
expressions are valid for i=1,2,...,nj . To calculate smartphone performance, there is a need for λ and fuzzy measures g(A(i)). Here, fuzzy values gand λ can be solved by using Equations 5-7 below.
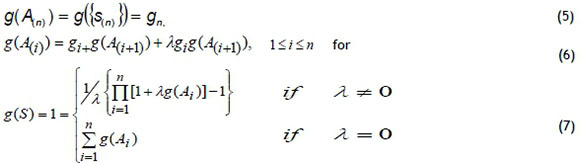
Choquet integral function, f : S - [0,1],0 < f (s(i)) < f (s(2)) < ...f (s(n)) < l, f (s(o)) = Ο and
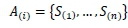 are expressed below.
are expressed below.
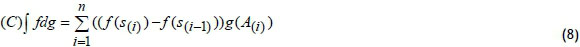
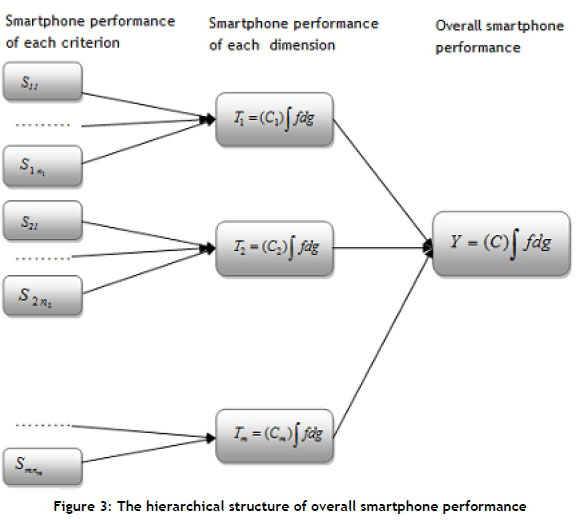
Total smartphone performance obtained from all the sub-criteria is reduced to a fuzzy Y number by the application of the Choquet integral two-step hierarchical process.
Step 6. If the  (x) is accepted as the member of
(x) is accepted as the member of 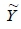 , by using Equation 8, fuzzy number
, by using Equation 8, fuzzy number 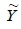 can be simplified to Y absolute value and alternative smartphones' simplified total performance compared, and the alternative with the highest defuzzified total performance value will be chosen as the best alternative.
can be simplified to Y absolute value and alternative smartphones' simplified total performance compared, and the alternative with the highest defuzzified total performance value will be chosen as the best alternative.

For ease of understanding, these GCI steps are presented in Figure 3.
3 APPLICATION OF THE METHODS
In this study, a two-phased approach containing ANP and GCI is used to solve the best smartphone selection problem. For this reason, first, 28 alternative smartphones are determined by the person who wants to buy a smartphone and by two experts who have in-depth information about the smartphones (decision-making team) as a result of an investigation of the relevant websites and the technology markets. The criteria taken into consideration when purchasing a smartphone are analysed, and then the 17 most important criteria to which the customers pay attention are determined. These 17 criteria are divided into groups according to the opinion of the decision-makers, under three main criteria: technical specifications (e.g., pixel density, RAM, camera, built-in memory, battery power, talk time, standby time, processor type, and operating system), physical properties (e.g., weight, thickness, durability, and screen size), and user-related features (e.g., ease of use, aesthetic, brand, and cost). Quantitative values of 11 of these criteria found from the web pages of the smartphone brands are shown in Table 1. Since processor (CPU) type and operating system criteria are transformed to quantitative values by the experts, they are also given in Table 1. Out of the criteria in Table 1, some qualitative criteria - such as durability, ease of use, aesthetics, and brand - are added to the criteria.
In this phase, 28 alternative smartphones are ranked by the ANP based on the priority values. First, the pair-wise comparisons are done by taking into consideration the internal dependencies, the external dependencies, and the feedbacks depending on the alternatives and the criteria. According to the pair-wise comparisons, the network structure shown in Figure 4 is constructed using Super Decisions 1.6.0.
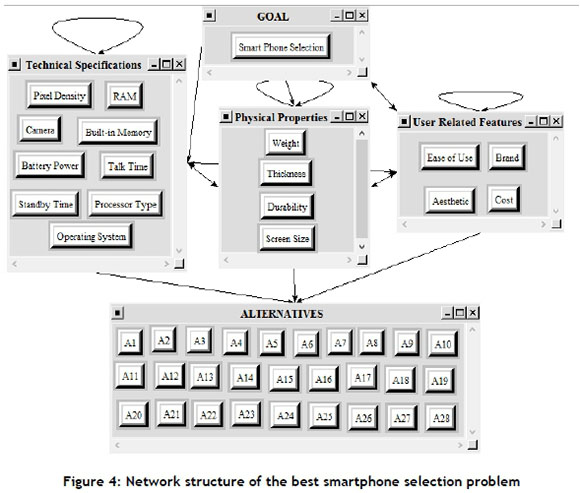
The Super Decisions software implements the ANP for decision-making with dependence and feedback developed by Dr Thomas Saaty. Written by the ANP team that works for the Creative Decisions Foundation, Super Decisions is decision-making software based on AHP and ANP [39].
After the construction of the network structure, the pair-wise comparison matrices are constructed by taking into consideration the opinions of the decision-making team.
According to the purpose, the construction of the pair-wise comparison matrices, the following are compared pair-wise with each other:
• Main criteria;
• Sub-criteria for each main criterion;
• Alternatives depending on each sub-criterion; and
• Sub-criteria related to each other.
The linguistic evaluations of the decision-making team for these pair-wise comparisons are made according to Table 2.

When evaluated, the pair-wise comparison matrices of the quantitative criteria, which is the data presented in Table 1, is transformed into the linguistic terms by the decision-making team with the help of some mathematical transformations. The pair-wise comparison matrices are filed according to these expressions. In the evaluation of the pair-wise comparison matrices of the qualitative criteria, the linguistic terms in Table 2 are used in line with the general agreement of the decision-making team.
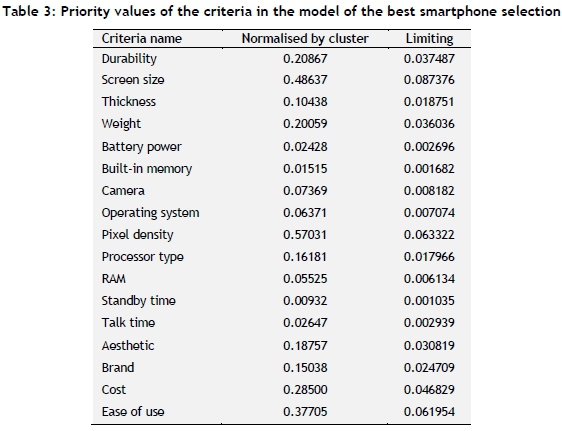
Linguistic evaluation values obtained after filling the pair-wise comparison matrices are transferred to the Super Decisions software according to the network structure shown in Figure 4. After transferring data to Super Decisions, the unweighted supermatrix, weighted supermatrix, and limit matrix are obtained. After obtaining the super matrices, the priority values of sub-criteria are obtained by using the 'Priorities' menu of the program; these values are given in Table 3. As can be seen there, for the model of the smartphone selection, the preference order of the most important five sub-criteria is screen size, pixel density, ease of use, RAM, and cost.
After the criteria weights are obtained from the priority values, the priority values of each smartphone alternatives are obtained by using the 'Synthesise' menu of the program, and preference order is obtained by using the 'Full Report' menu of the program. These values are given in Table 4.
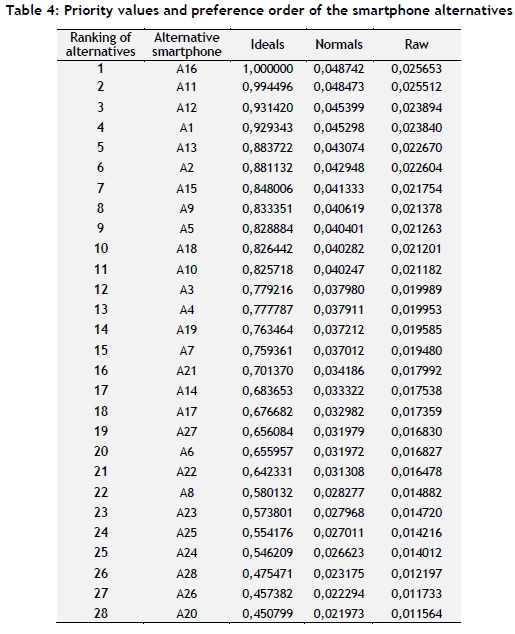
As can be seen from Table 4, Sony Xperia Z3 (A16) is the first choice with a 0.0487 priority value. Other than the alternatives, Samsung Galaxy Note 4 (A11) is the second choice with a 0.0484 priority value; the HTC One M8 (A12) is the third choice with a 0.0453 priority value; iPhone 6 Plus (A1) is the fourth choice with a 0.0452 priority value; and Asus Zenfone 6 (A28) is the last choice with a 0.0231 priority value. After the priority values and preference order of the smartphone alternatives are obtained, the first four smartphones in the second phase are evaluated in line with the general agreement of the decision-making team.
3.2 Phase II: The application of GCI to the smartphone selection
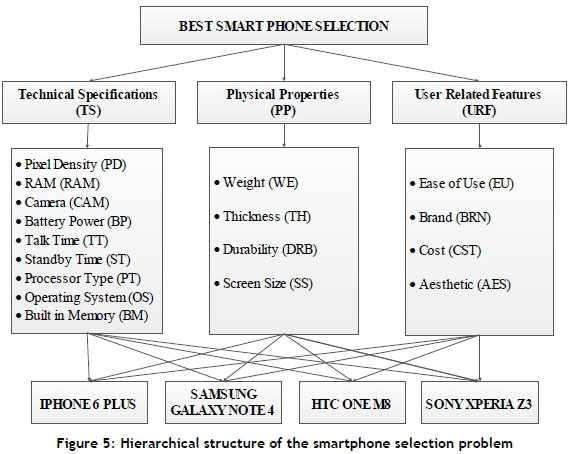
In this phase, the generalised Choquet integral is used to select the best smartphone out of the best four smartphones ranked by ANP according to the priority values. In this phase, the hierarchical structure of the smartphone selection problem is created. This structure is shown in Figure 5. Figure 5 includes the selection criteria and the four alternative smartphones determined by ANP.
The step-by-step application of GCI to the best smartphone selection problem is given below.
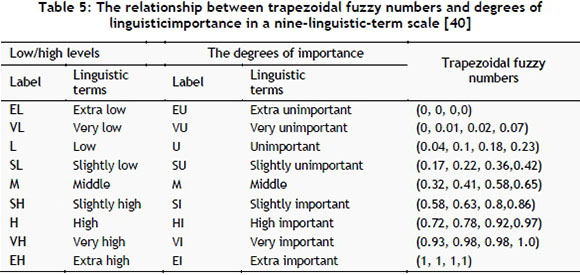
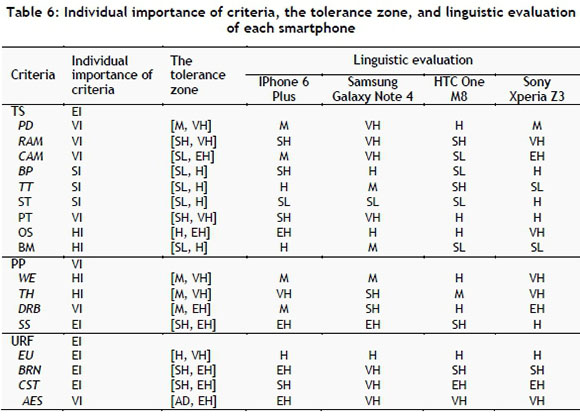
Step 1. Quantitative values are transformed into linguistic terms by using some mathematical operations as applied in the ANP in Table 1. Individual importance values of the smartphone selection criteria, expected tolerance interval of smartphone performance, and perceived performance of smartphones are evaluated by using the linguistic terms given in Table 5. Qualitative criteria not included in Table 1 are evaluated directly by the decision-making team according to the linguistic terms in Table 5. These evaluations are given in Table 6.
Step 2. Individual importance values of criteria are expressed as 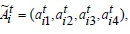 perceived performance of alternative smartphones is expressed as
perceived performance of alternative smartphones is expressed as 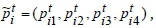 ,, and tolerance zone of expected performance of smartphones is expressed as
,, and tolerance zone of expected performance of smartphones is expressed as 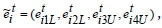 by taking into account the decision-making team and all the criteria. Here,
by taking into account the decision-making team and all the criteria. Here, 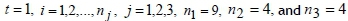 . The transformed form of the trapezoidal fuzzy numbers of Table 6 is given in Table 7.
. The transformed form of the trapezoidal fuzzy numbers of Table 6 is given in Table 7.
Step 3. Because the shared evaluation of the person who buys the smartphone and two decision-makers is taken into account, this step is not used here.
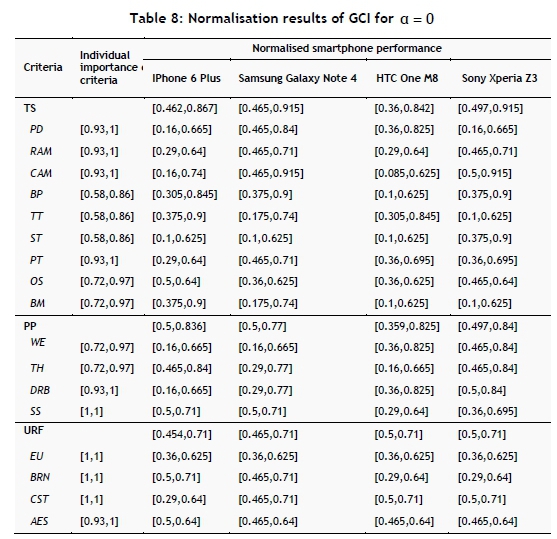
Step 4. The performance values of alternative smartphones are normalised by using Equation 3. For example, the normalised performance differences of smartphones for the Pixel Density (PD) sub-criterion of the technical specifications' main criteria (for a = 0 ) are calculated as:
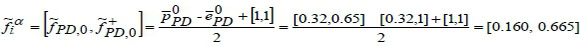
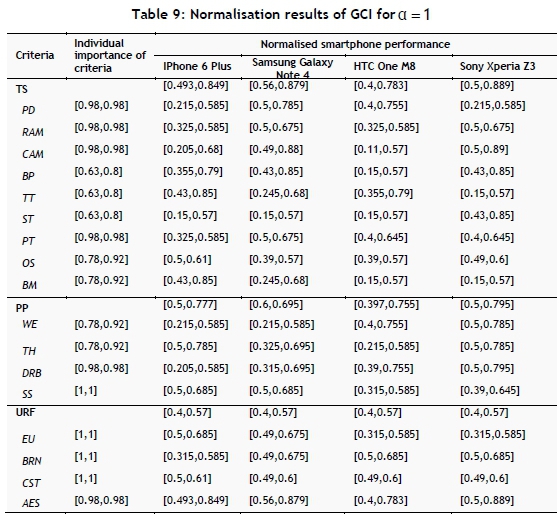
The same operations are repeated for the other sub-criteria and main criteria. The obtained normalised smartphone performances are given in Table 8 for a = 0 and Table 9 for a = 1.
Step 5. The calculations given below are applied to all the sub-criteria by taking into consideration the sub-criteria for calculating the smartphone performance of the main criteria. For example, the smartphone performance of the technical specifications' main criteria is calculated below. fjß values are ordered first in these calculations as:
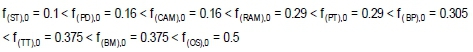
The importance values corresponding to these values are found as:
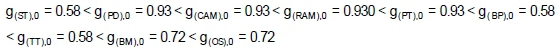
By using Equation 7:
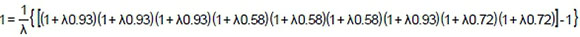
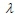 is found.
is found.
For α = 0 , by using Equations 5 6, fuzzy measures are obtained as:
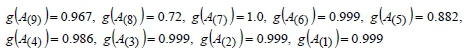
The same calculations are done for all criteria, both a = 0 and a = l . Then the performance values of the smartphones are calculated by Equation 8. For example, the overall performance of 'iPhone 6 Plus' is calculated below by using the technical specifications' main criteria for a = 0 :

and also 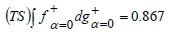 is found. Consequently
is found. Consequently 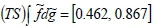 = [0.462,0.867] is obtained. The same calculations are done for the other criteria for a = 0 and a = l . Step 6. Similarly to Steps 4 and 5, alternative smartphone performances are calculated by using the two-phased sum process of GCI, and they are defuzzified using Equation 9. As an example, the defuzzified performance value of 'iPhone 6 Plus' is calculated as:
= [0.462,0.867] is obtained. The same calculations are done for the other criteria for a = 0 and a = l . Step 6. Similarly to Steps 4 and 5, alternative smartphone performances are calculated by using the two-phased sum process of GCI, and they are defuzzified using Equation 9. As an example, the defuzzified performance value of 'iPhone 6 Plus' is calculated as:
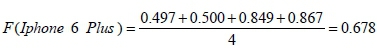
Similarly, defuzzified values of the main criteria and sub-criteria for all alternatives are calculated; these values are given in Table 10.
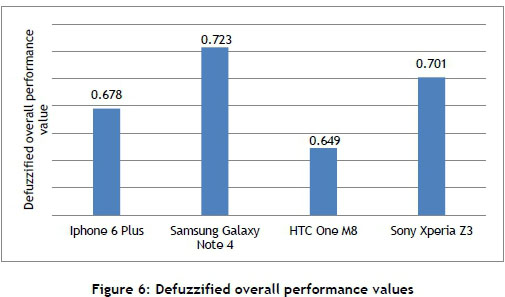
According to these values, 'Samsung Galaxy Note 4' is determined to be the best smartphone because it has the highest defuzzified performance values (0.723). The second best alternative is 'Sony Xperia Z3', the third best alternative is 'iPhone 6 Plus', and the last alternative is 'HTC One M8'.
4 FINDINGS AND DISCUSSION
In this paper, a two-phased MCDM approach is used to solve the best smartphone selection problem. In the first phase, 28 chosen smartphone alternatives are reduced by using ANP. In the second phase, the best four alternatives determined by ANP are used in GCI, and the best smartphone is selected.
'Samsung Galaxy Note 4' has the highest value (0.705) according to the defuzzified performance value of the main criteria. According to the sub-criteria of the technical specifications' main criteria, the 'CAM' (Camera) criterion belongs to 'Sony Xperia Z3', which has the highest value criterion (0.701). As a result, it is indicated that the 'CAM' criterion is very important for the best smartphone selection. According to the 'physical properties', 'Sony Xperia Z3' has the highest value (0.658). According to the sub-criteria of the 'physical properties' main criterion, the 'DRB' (Durability) criterion belongs to 'Sony Xperia Z3', which has the highest value (0.659). It is indicated that the 'DRB' criterion is very important when physical properties are used in the selection of the best smartphone.
It is seen that 'HTC One M8' has the highest performance value (0.599) in the 'user related features' main criterion. 'BRN' (Brand) and 'CST' (Cost) have the highest value (0. 599) in this main criterion. This result parallels the study of Akyene (2012). Regarding this result, it can be said that 'BRN' and 'CST' are very important in the selection of the best smartphone.
Consequently, 'Samsung Galaxy Note 4' is selected as the best smartphone because it has the highest overall defuzzified performance value (0.723). In this case, according to the chosen selection criteria set out in the study, this smartphone would be more appropriate for the person who buys a smartphone. One of the advantages of GCI is that it can obtain the performance values of all main and sub-criteria by using this method. Therefore, partial preference can be made by using this method. For example, if only 'technical specifications' are important for people who buy a smartphone, they can choose 'Samsung Galaxy Note 4'. If only 'physical properties' are important for people who buy a smartphone, they can choose 'Sony Xperia Z3'. If only 'aesthetics' are important for people who buy a smartphone, they can choose 'iPhone 6 Plus'.
In ANP, the criteria consist of interdependent and interaction characteristics, so they cannot be evaluated by any additive measures. Therefore, it would be more suitable to apply a Choquet integral model to evaluate the criteria.
In order to determine the efficiency of the combination of ANP and GCI in this paper, the ANP method was run for the best four alternatives again; these results are given in Table 11. According to these results, it can be seen that the ranking of the alternatives is the same as in GCI.
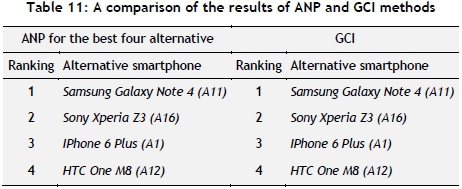
Consequently, in decision-making problems that have a lot of criteria, alternatives, and interactions, the efficiency of the ANP method decreases and the complexity of GCI increases. Therefore, reducing the number of alternatives provides an effective selection in the solution of such complex decision-making problems. In this study, the number of alternatives is reduced by using the ANP, and this new set of alternatives is evaluated using GCI, so that a more effective and accurate selection process is performed. The combination of ANP and GCI in this paper can be used in the solution of these types of decision-making problems because it can make more accurate and effective decisions.
5 CONCLUSION
Technology makes life easier, and thus it becomes indispensable for people. Many products appear on the market with rapidly-developing technology. One of these products is smartphones. The increasing speed of technological change creates a greater number and variety of smartphones. Before customers can become accustomed to the features of newly-produced smartphones on the market, the production of the top model means that customers find it difficult to determine their preferences. Today, telephones constitute a very large and important part of human life. Besides personal preferences while purchasing a smartphone, different desires and expectations emerge; and the majority of consumers prefer smartphones that include many features.
On the other hand, when the features of smartphones are increased, prices also increase in the constantly evolving smartphone market. The choice of a suitable smartphone from among many alternatives is a complicated problem, because smartphones have many kinds of core processors, RAM with gigabytes of capacity, screens with full HD resolution, fast operating systems, etc. Many different criteria affect the choice of smartphone, as is the case with other products. Thus MCDM methods will help to solve the smartphone selection problem.
In this study, a two-phased approach is used to solve the smartphone selection problem of a person who plans to buy a smartphone. The main goal of the study has been to use GCI in the selection of the best smartphone. However, it was decided to reduce the 28 alternatives in order to obtain a meaningful result; otherwise such a large range of choice would disadvantage the consumer. For this reason, ANP (an MCDM method that takes into account interactions between the criteria) was selected to reduce the number of alternatives.
Thus 28 smartphone alternatives were first ranked by using ANP, and then the best four alternatives were determined. A new selection model was constructed using the same criteria, and the best smartphone was selected by using GCI. In combination, ANP and GCI help the consumer to make a more accurate selection because they take into account the interactions between the criteria.
This study is important because it is the first work in the literature that combines the ANP and GCI methods in choosing the best smartphone. In addition, this is the first study that applies the generalised Choquet integral to select the best smartphone. In future work, ANP and fuzzy TOPSIS will be used together to solve this problem, and the results will be compared. Moreover, the features that people seek in a smartphone can be added to the selection model by using the fuzzy QFD method.
REFERENCES
[1] Measuring the information society. International Telecommunication Union (ITU) Annual Report 2012, ISBN 978-92-61-14071-7. [ Links ]
[2] Bazzazi, A., Osanloo, M. and Karimi, B. 2011. Deriving preference order of open pit mines equipment through MADM methods: Application of modified VIKOR method. Expert Systems with Applications, 38, pp. 2550-2556. [ Links ]
[3] Sayadi, M.K., Heydari, M. and Shahanaghi, K. 2009. Extension of VIKOR method for decision making problem with interval numbers. Applied Mathematical Modelling, 33, pp. 2257-2262. [ Links ]
[4] Chatterjee, P., Athawale, V.M. and Chakraborty, S. 2010. Selection of industrial robots using compromise ranking and outranking methods. Robotics and Computer-Integrated Manufacturing, 26(5), pp. 483-489. [ Links ]
[5] Chan, F.T.S. and Prakash, A. 2012. Maintenance policy selection in manufacturing firms using the fuzzy MCDM approach. International Journal of Production Research, 50(23), pp. 7044-7056. [ Links ]
[6] Isiklar G. and Buyukozkan G. 2007. Using a multi-criteria decision making approach to evaluate mobile phone alternatives. Computer Standards & Interfaces, 29, pp. 265-274. [ Links ]
[7] Chen, D.N., Hu P.J.H., Kuo Y.R. and Liang, T.P. 2010. A web-based personalized recommendation system for mobile phone selection: Design, implementation, and evaluation. Expert Systems with Applications, 37, pp. 8201-8210. [ Links ]
[8] Bayraktar, E., Tatoglu, E., Turkyilmaz, A., Delen D. and Zaim, S. 2012. Measuring the efficiency of customer satisfaction and loyalty for mobile phone brands with DEA. Expert Systems with Applications, 39, pp. 99-106. [ Links ]
[9] Akyene T. 2012. Cell phone evaluation base on entropy and TOPSIS. Interdisciplinary Journal of Research in Business, 1(12), pp. 9-15. [ Links ]
[10] Hu, Y.C. and Liao, Y.L. 2013. Utilizing analytic hierarchy process to analyze consumers' purchase evaluation factors of smartphones. World Academy of Science, Engineering and Technology, 7, pp. 1050-1055. [ Links ]
[11] Hu, S.K., Lu, M.T. and Tzeng, G.H. 2014. Exploring smart phone improvements based on a hybrid MCDM Model. Expert Systems with Applications, 41, pp. 4401-4413. [ Links ]
[12] Erinci, F. and Sulak, H. 2014. Analytic hierarchy process with smartphone selection.The Journal of Faculty of Economics and Administrative Sciences, 19(4), pp. 225-239. [ Links ]
[13] Saaty, T.L. 1980. The analytic hierarchy process. New York: McGraw-Hill. [ Links ]
[14] Pang, B. and Bai, S. 2013. An integrated fuzzy synthetic evaluation approach for supplier selection based on analytic network process. Journal of Intelligent Manufacturing, 24, pp. 163-174. [ Links ]
[15] Saaty, T.L. 1996. Decision making with dependence and feedback: The analytic network process. Pittsburgh: RWS Publications. [ Links ]
[16] Liang, X., Sun, X., Shu G., Sun, K., Wang, X. and Wang, X. 2013. Using the Analytic Network Process (ANP) to determine method of waste energy recovery from engine. Energy Conversion and Management, 66, pp. 304-311. [ Links ]
[17] Zaim, S., Sevkli, M., Akdag, H.C., Demirel, O.F., Yayla, A.Y. and Delen, D. 2014. Use of ANP weighted crisp and fuzzy QFD for product development. Expert Systems with Applications, 41, pp. 4464-4474. [ Links ]
[18] Sarkis, J. and Talluri, S. 2002. A model for strategic supplier selection. The Journal of Supply Chain Management, Winter, pp. 18-28. [ Links ]
[19] Shyur, H.J. and Shih, H.S. 2006. A hybrid MCDM model for strategic vendor selection. Mathematical and Computer Modelling, 44, pp. 749-761. [ Links ]
[20] Geneer, C. and Gurpinar, D. 2007. Analytic network process in supplier selection: A case study in an electronic firm. Applied Mathematical Modelling, 31(11), pp. 2475-2486. [ Links ]
[21] Liao, S.K., Chang, K.L. and Tseng, T.W. 2010. Optimal selection of program suppliers for TV companies using an Analytic Network Process (ANP) approach. Asia-Pacific Journal of Operational Research, 27(6), pp. 753-767. [ Links ]
[22] Kuo, R.J. and Lin, Y.J. 2012. Supplier selection using analytic network process and data envelopment analysis. International Journal of Production Research, 50(11), pp. 2852-2863. [ Links ]
[23] Vujanovic, D., Momcilovic, V., Bojovic, N. and Papic, V. 2012. Evaluation of vehicle fleet maintenance management indicators by application of DEMATEL and ANP. Expert Systems with Applications, 39, pp. 10552-10563. [ Links ]
[24] Kilic, H.S., Zaim, S. and Delen, D. 2015. Selecting the best ERP System for SMEs using a combination of ANP and PROMETHEE methods. Expert Systems with Applications, 42, pp. 2343-2352. [ Links ]
[25] Neumüller, C., Kellner, F., Gupta, J.N.D. and Lasch, R. 2015. Integrating three-dimensional sustainability in distribution centre selection: The process analysis method-based analytic network process. International Journal of Production Research, 53(2), pp. 409-434. [ Links ]
[26] Grabisch, M. and Roubens, M. 2000. Application of the Choquet integral in multicriteria decision making. In: Grabisch, M., Murofushi, T. and Sugeno, M. (eds.) Studies in fuzziness. Heidelberg: Physica Verlag, pp. 348-374. [ Links ]
[27] Grabisch, M. and Labreuche, C. 2008. A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid. 4OR: A Quarterly Journal of Operations Research, 6(1), pp. 1-44. [ Links ]
[28] Choquet, G. 1954. Theory of capacities. Annales de l'Institut Fourier (Grenoble), 5, pp. 131-295. [ Links ]
[29] Murofushi, T. and Sugeno, M. 1989. An interpretation of fuzzy measures and the Choquet integral as an integral with respect to a fuzzy measure. Fuzzy Sets and Systems, 29(2), pp. 201-227. [ Links ]
[30] Chiang, J.H. 2000. Aggregating membership values by a Choquet-fuzzy-integral based operator. Fuzzy Sets and Systems, 114(3), pp. 367-375. [ Links ]
[31] Tsai, H.H. and Lu, I.Y. 2006. The evaluation of service quality using generalized Choquet integral. Information Sciences, 176, pp. 640-663. [ Links ]
[32] Tan, C.Q. and Chen, X.H. 2011. Induced Intuitionistic Fuzzy Choquet integral operator for multicriteria decision making. International Journal of Intelligent Systems, 26(7), pp. 659-686. [ Links ]
[33] Auephanwiriyahul, S., Keller, J.M. and Gader, P.D. 2002. Generalized Choquet fuzzy integral fusion. Inf. Fusion, 3, pp. 69-85. [ Links ]
[34] Sugeno, M. 1974. Theory of fuzzy integrals and its applications. PhD Thesis, Tokyo Institute of Technology, Tokyo. [ Links ]
[35] Ming-Lang, T., Chiang, J.H. and Lan, L.W. 2009. Selection of optimal supplier in supply chain management strategy with analytic network process and Choquet integral. Computers & Industrial Engineering, 57, pp. 330-340. [ Links ]
[36] Yayla, A.Y., Yildiz, A. and Yildiz, K. 2013. A generalized Choquet integral algorithm for subcontractor selection in textile industry - A case study for Turkey. Fibres & Textiles in Eastern Europe, 6(102), pp. 16-21. [ Links ]
[37] Yayla, A.Y. and and Yildiz, A. 2013. Fuzzy ANP based MCDM methodology for a family automobile purchasing decision. South African Journal of Industrial Engineering, 24(2), pp. 167-180. [ Links ]
[38] Demirel, T., Demirel, N.C. and Kahraman, C. 2010. Multi-criteria warehouse location selection using Choquet integral. Expert Systems with Applications, 37, pp. 3943-3952. [ Links ]
[39] Saaty, T.S. 2001. The Analytic Network Process: Decision making with dependence and feedback. RWS Publication. [ Links ]
[40] Delgado, M., Herrera, F., Herrera-Viedma, E. and Martinez, L. 1998. Combining numerical and linguistic information in group decision making. Information Sciences, 107, pp. 177-194. [ Links ]
* Corresponding author














