GENERAL ARTICLES

 

Modelling production uncertainties using the adaptive neuro-fuzzy inference system

 

 

A. Azizi^I; A.Y. bin Ali^II; L.W. Ping^II

^IFaculty of Manufacturing Engineering University of Malaysia, Pahang, Malaysia Amirazizi@ump.edu.my
^IIFaculty of Mechanical Engineering University of Science, Malaysia. Meamir@eng.usm.my, Meloh@eng.usm.my

 

 

---

ABSTRACT

Production throughput measures the performance and behaviour of a production system. Production throughput modelling is complex because of uncertainties in the production line. This study examined the potential application of the adaptive neuro-fuzzy inference system (ANFIS) to modelling the throughput of production under five significant production uncertainties: scrap, setup time, break time, demand, and lead time of manufacturing. The effects of these uncertainties on the production of floor tiles were studied by performing 104 observations on the production uncertainties over 104 weeks, based on a weekly production plan in a tile manufacturing industry. The results of the ANFIS model were compared with the multiple linear regression (MLR) model. The results showed that the ANFIS model was capable of forecasting production throughput under uncertainty with higher accuracy than was the MLR model, indicated by an R-squared of 98 per cent.

---

OPSOMMING

Produksie deurset meet die vertoning en gedrag van 'n produksiesisteem. Produksie deurset modellering is ingewikkeld as gevolg van die onsekerhede in die produksielyn. Hierdie studie ondersoek die toepassing van die aanpasbare neuro-wasige afleidingsisteem om die deurset van produksie onderhewe aan vyf noemenswaardige produksie onsekerhede, naamlik skroot, opstel tyd, breek tyd, aanvraag en die vervaardiging leityd. Die effek van hierdie onsekerhede op die vervaardiging van vloerteëls is ondersoek deur 104 weeklikse observasies op die produksie onsekerhede oor 'n tydperk van 104 weke te neem. Die resultate van die model is vergelyk met 'n meervoudige lineêre regressie model. Die resultate toon dat die aanpasbare neuro-wasige afleidingsisteem in staat was om produksie deurset onderhewe aan onsekerheid te voorspel met 'n hoër akkuraatheid as die meervoudige lineêre regressie model. Dit word aangedui met 'n bepaalheidskoëffisient van 98 persent.

---

 

 

1 INTRODUCTION

Throughput of production refers to the volume, output, or rate of production for a process over a specific period of time. Throughput is an important measure of production system performance. Modelling production throughput is complex in today's dynamic production systems because of uncertainties in the production line. The production uncertainties relate to changes in demand and disturbances on production shop floors, such as machine breakdowns and random manufacturing lead times. Handling production uncertainties and modelling the production throughput will achieve a more systematic production by approaching a more reliable and robust manufacturing system. Modelling and planning under uncertainty is one of the most important open problems in optimisation [1]. Thus manufacturing industries must find a robust approach that handles uncertainties quickly and effectively in order to survive global competition driven by customer-designed products [2]. Mula et al. [3] showed how those models that consider uncertainty in the production system can make better planning decisions than those models that do not reflect the uncertainty. However, current theories for handling and evaluating uncertainty in production planning and control are still being debated, because they are dependent on the time factor [1, 4].

In most production systems, the production throughput cannot be accurately estimated because of production uncertainties such as machine breakdown time and scrap. In make-to-stock production systems, such as the push-type system, the manufacturers try only to produce, without considering demands. However, since the exact number of demands is not certain, inaccurate estimation of production throughput leads to stock out or excess inventory. In make-to-order production environments, the demand orders are expected to be produced without considering randomness in the lead time of the manufacturing or the breakdown time of machines. These conditions create the critical issue, which is to meet the customers' demands by the due date with the right quantities. When a decision is based on an inaccurate estimate, industries are forced to bear the production risk. The time lost in the setup, breakdown of equipment, and scrap increases the manufacturing lead time. Furthermore, the availability of machines may vary due to the break time. Demand also changes from time to time due to fluctuations. So making decisions about production, where fluctuations are considered, has become more and more complex. In this regard, the tile industry has been attempting to develop a new model that can answer customer orders in a timely manner under production uncertainties. Many strategies and policies have been proposed to address the fluctuations and disruptions in the production line. However, most of these methods are unsustainable due to the existence of the uncertain variables reviewed and detailed in Section 2 below. The complexity of the estimation of the production throughput under uncertain conditions becomes even greater if the manufacturing environments involve multi-stage production and multiple products. In the area of tile production, production sequencing and the scheduling of tiles have been studied to achieve effective setup time by recognising families of tile products with the same designs using an analytical solution [5]; but this solution needs a steady-state production situation, whereas the real production system is not that. In this study, more uncertainties of production line are considered for throughput modelling using the adaptive neuro-fuzzy inference system (ANFIS).

 

2 UNCERTAIN VARIABLES OF PRODUCTION

Uncertainty has usually been measured by observing its values at different time periods. Uncertain variables, also called stochastic or random changes, involve breakdown time, scrap, and processing time, according to Wazed et al. [6]. Van Donk and Van der Vaart [7] distinguished three main types of uncertainty in manufacturing: uncertainty of the item throughput, mixed uncertainty of a component, and delivery uncertainty. Koh and Gunasekaran [8] presented significant uncertainty parameters in manufacturing environments with reference to demand changes, lead time variations, and resource break. Saad and Gindy [9] categorised the uncertainty variables within the production facilities, previously identified by Atwater and Chakravorty [10] into internal and external disturbances. Internal disturbances include machines, tools/fixtures, transport, and operators. External disturbances include product variety, priority, throughput, quality, wrong time, and parts for the supplier. Koh and Saad [11] categorised manufacturing uncertainty parameters into process yield loss, quality variation, process lead time, and scraps.

Subrahmanyam et al. [12] classified uncertainty variables of the production system into cancelled or rushed orders, operation time's variability, and equipment breakdowns. Das and Abdel-Malek [13] grouped four uncertainty factors into product mix, sales quantities, order delivery time, and design changes. Koh and Saad [14] recognised that the planned setup time is usually exceeded because of a changeover time increment that affects the delivery performance of products. Wazed et al. [6] compiled setup time with other uncertain factors through different sources such as uncertainties in lead time, operation yield, demand, machine breakdown, and product quantity.

 

3 CURRENT METHODS TO TACKLE UNCERTAINTY

Zimmermann [4] defined 'uncertainty modelling' as a genuine modelling decision, in which any of the existing uncertainty theories might need to be applied, or a 'wait-and-see' approach should be adopted. Artificial intelligence approaches and machine learning techniques deal with uncertainty in manufacturing management through modelling quantitative information [15]. For example, the Petri net technique is used to relocate operations in order to use shop floor resources in the presence of machine breakdown uncertainty [16]. Li et al. [17] applied the artificial neural network (ANN) to estimate makespan, and later combined this with a genetic algorithm to improve the accuracy of makespan. In another study, ANN was employed to predict the raw material of tile, especially in a study of the quality characteristics of the granule [18]. The ANN model was then compared with a multiple linear regression model to show its higher efficiency using three statistical comparison criteria, which are root mean square error (RMSE), mean relative error (MRE), and the coefficient of determination (R²).

The stochastic optimisation method was introduced by Mulvey et al. [19] to deal explicitly with uncertainty, and to make decisions that are less sensitive to the variations in input data. Stochastic programming on demand uncertainty has been the most popular trend recently in the production planning for manufacturing industries [20-22]. Petkov and Maranas [23] formulated a stochastic model under demand uncertainty - the levels of which were probability specified. Hood et al. [24] presented a method that used stochastic integer programming to meet demand uncertainty. Their efforts involve the simple enumeration of a few discrete cases to handle uncertainty in demand. Li et al. [25] pointed out that the degree of uncertainty and complexity is very high in a re-manufacturing system.

Wazed et al. [26] proposed a few simulation models using WITNESS software to analyse the various effects of two main uncertainty variables: machine breakdown and lead time. They concluded that machine breakdown has a greater effect on production throughput, whereas lead time uncertainty has a greater influence on cycle time. Later, Wazed et al. [27] considered a production system under machine breakdown and quality variation. They examined the effect of common processes on the throughput and cycle time using the same simulation software (WITNESS). They found that the variation in the level of common processes in the system has a significant effect on production throughput and cycle time. Using simulation methodology, Brennan and Gupta [28] examined the performance of a manufacturing environment under demand and lead time uncertainties. The effects of the use of different lot-sizing rules were also considered. These uncertainties were eventually addressed using appropriate lot-sizing rules. Minifie and Davis [29] developed a simulation model to examine the interaction effects of demand and supply uncertainties. These uncertainties were modelled for changes in lot-size, timing, planned orders, and policy fence on several system performance measures such as late deliveries, number of setup times, ending inventory levels, and component shortages. System performance was concluded to be significantly affected by demand changes and supply uncertainties. Emran et al. [30] examined the impact of uncertainty in operational release planning on total duration using Monte Carlo simulation. They concluded that every uncertain factor individually increases makespan; and for any combination of uncertainty factors, impact is bigger than the addition of their individual impacts.

In dynamic environments that involve more than one type of uncertain factor, the analytical approach is replaced by an expert system methodology such as fuzzy logic. Pai et al. [31] proposed an application of fuzzy logic to deal with problems of capacity uncertainty. This capacity uncertainty was extracted from fuzzy rules and uncertain input data that was presented by fuzzy number and conditional if-then rules. Fuzzy programming was applied for planning production in a multi-site environment under uncertain capacities and demands by Sakawa et al. [32]. Petrovic et al. [33] applied fuzzy modelling in studying customer demand and external supply uncertainties to assess the impact on the supply chain performance. Chen and Lee [34] presented a fuzzy approach to maximising the satisfaction level of multiple objectives in a supply chain under uncertain demands and prices. Bral and Gardner [35] presented a fuzzy method to determine production process availability by considering process failures and machine breakdown. Gorkemli and Ulusoy [36] proposed a fuzzy-Bayesian method to determine the reliability and availability of a production system in which exponential distributions for breakdown and repair times of machines were chosen. The method was used to quantify uncertainties in the production environment.

The first study that proposed a neuro-fuzzy regression algorithm to develop a forecasting model of weekly manufacturing lead time estimation, considering the breakdown time indicator in an actual assembly shop - a producer of heavy electric motors - was done by Asadzadeh et al. [37]. The input data were the sum of failure times, the sum of repair times, and the sum of processing times, and were collected for 70 weeks with 70 observations. The results show that the developed model is able to forecast by 94.70 per cent R².

 

4 METHODOLOGY

The reason for using the artificial neural network (ANN) with the fuzzy inference system (FIS) is that neural networks do not make any assumption about the probability distribution functions of data [38]. ANFIS is applied to estimate the parameters of significant variables in order to examine the effects of these parameters on the production throughput. The ANFIS model categorises the input space into fuzzy subspaces and maps the output using a set of linear functions. ANFIS is a fuzzy mapping algorithm based on the Tagaki-Sugeno-Kang fuzzy inference system [39,40]. ANFIS has been successfully used to map the input-output relationship based on available data sets [41]. The system acquires its adaptability by using a hybrid learning method that combines back propagation and least mean square optimisation algorithms. The ANFIS model output matches the system output with a minimum RMSE. Using a learning process, ANFIS can determine the mapping relation between inputs and output data sets in order to identify the optimal distribution of membership functions; the relation involves a premise and a consequent part [42]. ANFIS, which was developed by Jang [43], is a universal approximate that incorporates Sugeno-type fuzzy inference systems into adaptive neural networks. ANFIS uses the power of two patterns - artificial neural networks and fuzzy logic - in a single framework.

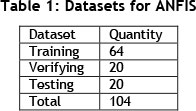
This study involves five sets of data for five input variables including breakdown time, demand, setup time, lead time of manufacturing, scrap, and one set of data for the output variable, which is production throughput. Following McLachlan et al.[44], we randomly generated ten different sample sets (from the 104 collected observations) in an Excel 2007 spreadsheet for both the output and input variables to assign for training, testing, and verifying. This was to make sure that the majority of data sets were trained. Further statistical analysis was performed to calculate the training error (average loss over the training samples) and to evaluate the overfitting condition that occurs when the model is trained too much. Overfitting occurs when the mapping between the input and the output data has lost its generalisation capability to fit any data on which it was not trained [45]. Therefore, the dataset with the lowest training error and no over-fitting is categorised into three groups according to Jang [43], including 64 observations assigned for training, 20 for testing, and 20 for verifying, as presented in Table 1. The training process maps the relationship between the input and output datasets to determine the optimal distribution of membership functions. The training set was assigned to build the ANFIS model. The verifying data set was used to ensure that the trained model is a suitable representation of the target system, and to avoid over-fitting of the system to the training data set.

 

 

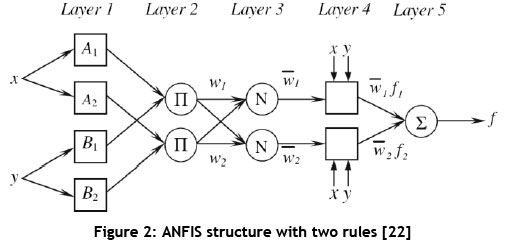
There are five layers to develop ANFIS model. Clustering is the first stage of fuzzification in the FIS. The input uncertainties were fuzzified after all numerical values of the input uncertain variables had been loaded. Cluster membership probabilities reflect uncertainty where a given individual value can be assigned to any given cluster. The propagation of each uncertainty was broken down into the different clusters of fuzzy to see the behaviour of uncertainties on the production throughput. Clustering included the selection of type, number, and linguistic value of membership function. Subtractive clustering proposed by Chiu [46] is applied because it finds out the optimum cluster centres (optimal parameters of membership functions) and consequently the optimum fuzzy model [47]. It calculates a measure of the likelihood of each data point as the cluster centre based on the density of surrounding data points. The algorithm selects the data point with the highest potential as the first cluster centre. Subsequently, all data points in the vicinity of the first cluster centre (as determined by radii) will be removed in order to determine the next cluster centre. Finally, this process is iterated until all of the data is within the radii of a cluster centre.

The next stage is to train the inputs to minimise the RMSE and to adjust the shape of the membership functions. The hybrid learning algorithm was used to develop the ANFIS model. This algorithm consisted of back propagation for the input parameters associated with input membership functions, and least-squares estimation for the parameters associated with output membership functions. The training process using the hybrid learning algorithm adjusted the premise parameters, the consequent parameters, and the training error plot. This study includes five inputs and one output, and is clustered into three clusters. As the presentation of the training process for our model is long and may become complicated, we generally show the estimation procedure of ANFIS using only two inputs and one output, with two rules for easy understanding them, in Figures 1 and 2 [22].

 

 

 

 

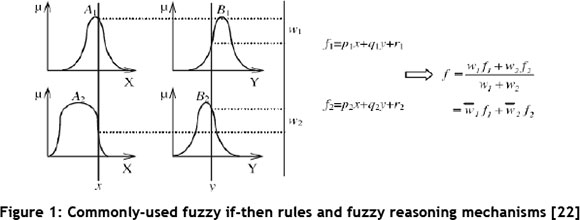
Where

x, y: Inputs,

fi: Output , i= 1, 2,

Wi: Weight , i= 1, 2,

A and B: Linguistic labels.

For a first-order Sugeno fuzzy model, a common rule set with two fuzzy if-then rules in (1) and (2) is assumed according to [43].

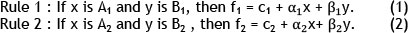
Where

f₁: first order polynomial, the output of rule 1,

f₂: second order polynomial, the output of rule 2,

a_i and β_i: Coefficients of inputs, i= 1, 2,

c_i: Constant parameters, i= 1, 2.

Layer 1: Input node layer

The first layer presents the output of each uncertainty.

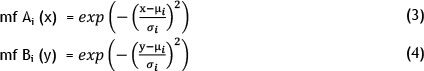
where

mf = membership function,

μ, σ = premise parameters that change the shape of the membership functions.

Layer 2: Rule nodes (inference layer or rule layer)

The weight of each cluster is found in layer 2.

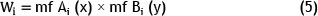
where

W_i= weight of cluster i.

Layer 3: Normalised layer (average nodes layer)

In layer 3, the defuzzification method is performed through the weighted average, which is denoted by W_i.

Layer 4: Consequent nodes layer (aggregation layer)

In layer 4, W_iis multiplied by the output of the mf i.

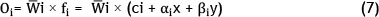
Layer 5: Total output layer

In layer 5, the overall output of the training process is obtained by summation of all outputs of clusters.

The learning process stops when a maximum number of training iterations (epochs) is achieved - which in this study is 200 epochs. The best ANFIS model is selected using the fuzzy logic toolbox in MATLAB software version 2008 [48], based on a lower RMSE for both the training and the verifying data sets, in which the RMSE is under control and is not increasing [49,50].

 

5 RESULTS

Three if-then rules were extracted using the subtractive clustering algorithm. These rules were described by production experts with 'AND' as the logical operation to represent the different levels of production throughput based on different cluster relations of the uncertain variables, as presented in Table 2. Linguistic values were also defined with respect to the number of membership functions (clusters) to determine the quality of membership functions. Three linguistic values were defined for each uncertainty by production experts. The qualities of these linguistic values were low, medium, and high respectively.

 

 

The parameters of each uncertain variable, including the mean and standard deviation, were estimated using the back propagation method, as shown in Table 3.

 

 

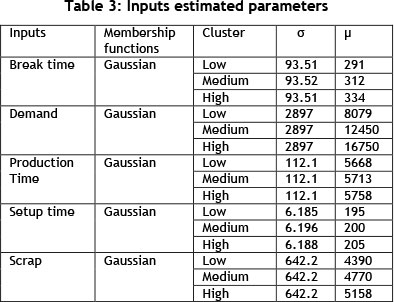
Table 4 presents the estimated coefficients of the Sugeno linear functions using the leastsquares method.

 

 

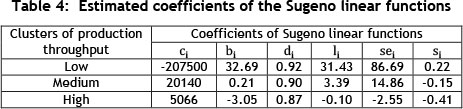
The Sugeno linear functions are formulated for all three clusters, shown in (9) to (11).

Where

P = Production throughput,

B = Break time,

D = Demand,

L = Lead time of manufacturing,

Se = Setup time,

S = Scrap.

Table 5 summarises the estimated coefficients of the multiple linear regression (MLR) function using the least-squares method by Minitab Software, version 16.

 

 

The MLR model is presented in equation (12) based on the estimated coefficients shown in Table 5.

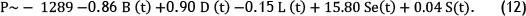
R-squared has been successfully used in forecasting models by many authors [51-53]. This comparison criterion measures the goodness of model fit and the model performance. R-squared evaluates how much variability in actual values is explained by the model. Thus it is a suitable criterion to compare the performances of two different models with the same uncertain variables. R-squared is also appropriate for different units of variables because it is unitless. R-squared is calculated via equation (13).

Table 6 presents the accuracy of the MLR and ANFIS models using R-squared.

 

 

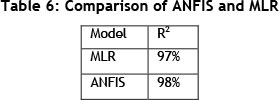
The results demonstrated that the ANFIS inference is an alternative option that is capable of forecasting with a slightly higher accuracy than the commonly-used MLR model.

 

6 CONCLUSION AND FURTHER RESEARCH

An adaptive neuro-fuzzy inference system for modelling production throughput has been developed using a real data set collected from the tile manufacturing industry. The ANFIS model enables accurate prediction, compared with the MLR model. The results of ANFIS have shown that neuro-fuzzy systems are as robust as MLR for dealing with production uncertainties. It might be applied as a reliable method in uncertain manufacturing environments because of its flexibility and adaptability. Further studies can be achieved by including more input variables, and by examining the ANFIS approach in another dynamic manufacturing industry.

 

REFERENCES

[1] Horner, P. 1999. Planning under uncertainty, OR/MS Today, 26.         [ Links ]

[2] Gunasekaran, A. 1998. Agile manufacturing: Enablers and an implementation framework, International Journal of Production Research, 36(5), pp 1223-1247.         [ Links ]

[3] Mula J., Poler R., Garcia-Sabater J.P. & Lario, F.C. 2006. Models for production planning under uncertainty: A review, Int. J. Production Economics, 103, pp 271-285.         [ Links ]

[4] Zimmermann, H.J. 2006. Intelligent manufacturing management, StudFuzz, 201, pp 383-400.         [ Links ]

[5] Andres, C., Albarracin, J.M., Torino, G., Vicens, E. & Garcia-Sabater, J.P. 2005. Group technology in a hybrid flowshop environment: A case study, European Journal of Operational Research, 167, pp 181-272.         [ Links ]

[6] Wazed, M.A., Ahmed, S. & Nukman, Y. 2009. Uncertainty factors in real manufacturing environment, Australian Journal of Basic and Applied Sciences, 3(2), pp 342-351.         [ Links ]

[7] Van Donk, D.P. & Van der Vaart, T. 2005. A case of shared resources, uncertainty and supply chain integration in the process industry, International Journal of Production Economics, 96(1), pp 97-108.         [ Links ]

[8] Koh, S.C.L. & Gunasekaran A. 2006. A knowledge management approach for managing uncertainty in manufacturing, Industrial Management and Data Systems, 106(4), pp 439-459.         [ Links ]

[9] Saad, S.M. & Gindy, N.N. 1998. Handling internal and external disturbances in responsive manufacturing environments, International Journal of Production Planning and Control, 9(8), pp 760-770.         [ Links ]

[10] Atwater, J.B. & Chakravorty, S.S. 1994. Does protective capacity assist managers in competing along time-based dimensions?, Production and Inventory Management Journal, 35, pp 53-59.         [ Links ]

[11] Koh, S.C.L. & Saad, S.M. 2002. Development of a business model for diagnosing uncertainty in ERP environments, International Journal of Production Research, 40(13), pp 3015-3039.         [ Links ]

[12] Subrahmanyam, S., Pekny, J.F. & Reklaitis, G.V. 1994. Design of batch chemical plants under market uncertainty, Industrial and Engineering Chemistry Research, 33, pp 2688-2701.         [ Links ]

[13] Das, S.K. & Abdel-Malek, L. 2003. Modelling the flexibility of order quantities and lead-times in supply chains, International Journal of Production Economics, 85(2), pp 171-181.         [ Links ]

[14] Wazed, M.A., Ahmed, S. & Nukman, Y. 2009. Uncertainty factors in real manufacturing environment, Australian Journal of Basic and Applied Sciences, 3(2), pp 342-351.         [ Links ]

[15] Monostori, L. 2003. AI and machine learning techniques for managing complexity, changes and uncertainties in manufacturing, Engineering Applications of Artificial Intelligence, 16, pp 277291.         [ Links ]

[16] Ounnar, F. & Ladet, P. 2004. Consideration of machine breakdown in the control of flexible production systems, International Journal of Computer Integrated Manufacturing, 17(1), pp. 6982.         [ Links ]

[17] Li, S., Li, Y., Liu, Y. & Xu, Y. 2007. A GA-based NN approach for makespan estimation, Applied Mathematics and Computation, 185, pp 1003-1014.         [ Links ]

[18] Neshat, N., Mahlooji, H. & Kazemi, A. 2011. An enhanced neural network model for predictive control of granule quality characteristics, Scientia Iranica, 18(3), pp 722-730.         [ Links ]

[19] Mulvey, J.M., Vanderbei, R.J. & Zenios, S.A. 1995. Robust optimization of large-scale systems, Oper. Res., 43(2), pp 264-281.         [ Links ]

[20] Chou, Y.C. & Hong, I.H. 2000. A methodology for product mix planning in semiconductor foundry manufacturing, IEEE Transactions on Semiconductor Manufacturing, 13, 278-285.         [ Links ]

[21] Christie, R. & Wu, D. 2002. Semiconductor capacity planning: Stochastic modeling and computational studies, IIE Transactions, 34, pp 131-143.         [ Links ]

[22] Catay, B., Erenguc, S.S. & Vakharia, A.J. 2003. Tool capacity planning in semiconductor manufacturing, Computers and Operations Research, 30, pp 1349-1366.         [ Links ]

[23] Petkov, S.B. & Maranas, C.D. 1997. Multiperiod planning and scheduling of multiproduct batch plants under demand uncertainty, Industrial and Engineering Chemistry Research, 36, pp 48644881.         [ Links ]

[24] Hood, S.J., Bermon, S. & Barahona, F. 2003. Capacity planning under demand uncertainty for semiconductor manufacturing, IEEE transaction on Semiconductor Manufacturing, 16(2), pp 273280.         [ Links ]

[25] Li, C., Liu, F., Cao, H. & Wang Q. 2009. A stochastic dynamic programming based model for uncertain production planning of re-manufacturing system, International Journal of Production Research, 47(13), pp 3657-3668.         [ Links ]

[26] Wazed, M.A., Ahmed, S. & Nukman, Y. 2009. Impacts of common components on production system in an uncertain environment, Sci. Res. Essays, 4, pp 1505-1517.         [ Links ]

[27] Wazed, M.A., Ahmed, S. & Nukman, Y. 2010. Impacts of common processes in multistage production system under machine breakdown and quality uncertainties, African Journal of Business Management, 4(6), pp 979-986.         [ Links ]

[28] Brennan, L. & Gupta, S.M. 1993. A structured analysis of material requirements planning systems under combined demand and supply uncertainty, International Journal of Production Research, 31(7), pp 1689-1707.         [ Links ]

[29] Minifie, J.R. & Davis, R.A. 1990. Interaction effects on MRP nervousness, International Journal of Production Research, 28(1), pp 173-183.         [ Links ]

[30] Emran, A., Kapur P., Pfahl D. & Ruhe, G. 2010. Studying the impact of uncertainty in operational release planning - An integrated method and its initial evaluation, Information and Software Technology, 52, pp 446-461.         [ Links ]

[31] Pai, P-F., Chang, P.T., Wang, S-S. & Lin, K-P. 2004. A fuzzy logic-based approach in capacity-planning problems, International Advanced Manufacturing Technology, 23, pp 806-811.         [ Links ]

[32] Sakawa, M., Nishizaki, I. & Uemura, Y., 2001. Fuzzy programming and profit and cost allocation for a production and transportation problem, European Journal of Operational Research, 131, pp 1-15.         [ Links ]

[33] Petrovic, D., Roy, R. & Petrovic, R. 1998. Modeling and simulation of a supply chain in an uncertain environment, European Journal of Operational Research, 109(2), pp 299-309.         [ Links ]

[34] Chen, C. & Lee, W. 2004. Multi-objective optimization of multi-echelon supply chain networks with uncertain product demands and prices, Computers and Chemical Engineering, 28, pp 11311144.         [ Links ]

[35] Bral, A. & Gardner, L. 2002. Availability modeling for the application of manufacturing equipment, Proceedings Annual Reliability and Maintainability Symposium, pp 411-416.         [ Links ]

[36] Gorkemli, L. & Ulusoy, S.K. 2010. Fuzzy-Bayesian reliability and availability analysis of production systems, Computers and industrial engineering, 59(4), pp 690-696.         [ Links ]

[37] Asadzadeh, S., Azadeh, A. & Ziaeifar, A. 2011. A neuro-fuzzy-regression algorithm for improved prediction of manufacturing lead time with machine breakdowns, Concurrent Engineering, 19(4), pp 269-281.         [ Links ]

[38] Castellano, G. & Fanelli, A.M. 2000. Variable selection using neural-network models, Neurocomputing, 31, pp 1-13.         [ Links ]

[39] Jang, J.S.R., Sun, C.T. & Mizutani, E. 1997. Neuro-fuzzy and soft computing - A computational approach to learning and machine intelligence, New Jersey: Prentice Hall.         [ Links ]

[40] Loukas, Y.L. 2001. Adaptive neuro-fuzzy inference system: An instant and architecture-free predictor for improved QSAR studies, Journal of Med. Chem., 44(17), pp 2772-2783.         [ Links ]

[41] Gallo, S., Murino, T. & Santillo, L.C. 1999. Time manufacturing prediction: Preprocess model in neuro fuzzy expert system, CD Proceedings of European Symposium on Intelligent Techniques, Greece, p 11.         [ Links ]

[42] Ying, L.C. & Pan, M.C. 2008. Using adaptive network based fuzzy inference system to forecast regional electricity loads, Energy Conversion and Management, 49(2), pp 205-211.         [ Links ]

[43] Jang, J-S.R. 1993. ANFIS: Adaptive-network-based fuzzy inference system, IEEE Transactions on Systems, Man and Cybernetics, 23(3), pp 665-685.         [ Links ]

[44] McLachlan, G. J., Do, Kim-Anh, Ambroise, C. 2004. Analyzing microarray gene expression data. John Wiley and Sons. New Jersey. USA.         [ Links ]

[45] Bishop, C.M. 1995. Neural networks for pattern recognition, New York, USA: Oxford University Press.         [ Links ]

[46] Chiu, S.L. 1994. Fuzzy model identification based on cluster estimation, Journal of intelligent and Fuzzy systems, 2(3), pp 267-278.         [ Links ]

[47] Lohani, A., Goel, N. & Bhatia, K. 2006. Takagi-Sugeno fuzzy inference system for modeling stage-discharge relationship, Journal of Hydrology, 331, pp 146-160.         [ Links ]

[48] Beale, H. & Demuth, H.B. 2001. Fuzzy systems toolbox for use with MATLAB, 1st ed.,Massachusetts: International Thomson Publishing.         [ Links ]

[49] El-Shafie, A., Taha, M.R. & Noureldin, A.. 2007. A neuro-fuzzy model for inflow forecasting of the Nile River at Aswan High Dam, Water Resources Management, 21(3), pp 533-556.         [ Links ]

[50] Mousavi, S.J., Ponnambalam, K. & Karray, F. 2007. Inferring operating rules for reservoir operations using fuzzy regression and ANFIS, Fuzzy Sets and Systems, 158(10), pp 1064-1082.         [ Links ]

[51] Aburto, L. & Weber, R. 2007. Improved supply chain management based on hybrid demand forecasts, Applied Soft Computing, 7(1), pp 136-144.         [ Links ]

[52] Chien, C.F., Hsu, C.Y. & Hsiao, C.W. 2012. Manufacturing intelligence to forecast and reduce semiconductor cycle time, Journal of Intelligent Manufacturing, 23(6), pp 2281 -2294.         [ Links ]

[53] Zheng, F. & Zhong, S. 2011. Time series forecasting using a hybrid RBF neural network and AR model based on binomial smoothing, World Academy of Science, Engineering and Technology, 75, pp 1471-1475.         [ Links ]

 

 

* Corresponding author