Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.25 n.2 Pretoria Aug. 2014
GENERAL ARTICLES
Development of a Stereolithography (STL) input and Computer Numerical Control (CNC) output algorithm for an entry-level 3-D printer1
A.C. BrownI, *; D. de BeerII; P. ConradieIII
IVaal University of Technology South Africa. andrewb@vut.ac.za
IINorth West University South Africa Deon.De Bee r@nwu.ac.za,
IIIVaal University of Technology South Africa. pieterc@vut.ac.za
ABSTRACT
This paper presents a prototype Stereolithography (STL) file format slicing and tool-path generation algorithm, which serves as a data front-end for a Rapid Prototyping (RP) entry-level three-dimensional (3-D) printer. Used mainly in Additive Manufacturing (AM), 3-D printers are devices that apply plastic, ceramic, and metal, layer by layer, in all three dimensions on a flat surface (X, Y, and Z axis). 3-D printers, unfortunately, cannot print an object without a special algorithm that is required to create the Computer Numerical Control (CNC) instructions for printing. An STL algorithm therefore forms a critical component for Layered Manufacturing (LM), also referred to as RP. The purpose of this study was to develop an algorithm that is capable of processing and slicing an STL file or multiple files, resulting in a tool-path, and finally compiling a CNC file for an entry-level 3D printer. The prototype algorithm was implemented for an entry-level 3-D printer that utilises the Fused Deposition Modelling (FDM) process or Solid Freeform Fabrication (SFF) process; an AM technology. Following an experimental method, the full data flow path for the prototype algorithm was developed, starting with STL data files, and then processing the STL data file into a G-code file format by slicing the model and creating a tool-path. This layering method is used by most 3-D printers to turn a 2-D object into a 3-D object. The STL algorithm developed in this study presents innovative opportunities for LM, since it allows engineers and architects to transform their ideas easily into a solid model in a fast, simple, and cheap way. This is accomplished by allowing STL models to be sliced rapidly, effectively, and without error, and finally to be processed and prepared into a G-code print file.
OPSOMMING
'n Prototipe stereolitografie (STL) dokument ontvou en instrumenttrajek generasie algoritme vir 'n intreevlak driedimensionele drukker word in dié studie bekendgestel. Driedimensionele drukkers word hoofsaaklik in toevoegingsvervaardiging gebruik deur lae plastiek, keramiek of metaal in al drie rigtings (x, y en z) op 'n plat oppervlak te deponeer. Rekenaar numeriese beheer word egter benodig om die driedimensionele drukker te begelei. Die STL algoritme vorm dus 'n integrale deel vir laag-op-laag vervaardiging. Die doel van hierdie studie is om 'n algoritme te ontwikkel wat die vermoë het om een of meer STL dokumente te prosesseer en te ontvou en 'n gepaste instrumenttrajek te formuleer en daaruit beheerinstruksies vir die drukker te genereer. Die STL lêer is geprosesseer tot 'n G-kode lêer deur middel van die algoritme. Die ontwikkelde algoritme hou innoverende geleenthede in vir laag-op-laag vervaardiging, aangesien dit aan ingenieurs en argitekte toelaat om vinnig en maklik hul idees in driedimensionele soliede voorwerpe te omskep. Dit is moontlik deur die STL modelle vinnig en sonder foute te ontvou en te prosesseer tot 'n G-kode beheerlêer.
1 INTRODUCTION
In recent years, three-dimensional (3-D) printing, also known as Additive Manufacturing (AM), Solid Freeform Fabrication (SFF), Layered Manufacturing (LM), or Rapid Prototyping (RP), has been identified as an innovative manufacturing technology of functional parts that involves slicing a 3-D model into two-dimensional (2-D) layers, which are then reproduced physically, layer-by-layer, to create the prototype. The 3-D model is first modelled in a Computer-Aided-Design (CAD) system, producing a Stereolithography (STL) file - a tessellated (triangulated) surface model. STL is synonymous to the tessellated standard triangular language model. Even though many other formats have been created for RP, none has been universally adopted in the same way as STL by the various makers of CAD packages [1]. The STL file is then processed by a slicing procedure that results in the creation of a tool-path from the slice's information. The information produced by the slicing process is saved as Computer Numerical Control (CNC) instructions that are used by a 3-D printer to produce the prototype. G-code is the term used to describe a text file that contains commands to run a CNC machine.
The issue of slicing plays a crucial role in the AM process. Several researchers have developed and presented papers that focus on slicing algorithms. Tata et al. [8] discussed an adaptive slicing algorithm that can vary the slice thickness depending on the geometry of the object to be prototyped, in an attempt to minimise layering error and improve surface quality.
Jin et al. [2] developed an adaptive tool-path generation algorithm that aimed to optimise both the surface quality and fabrication efficiency in RP systems. The algorithm can generate contour tool-paths for the boundary of each RP sliced layer to reduce the surface errors of the model, and zigzag tool-paths for the internal area of the layer to speed up the fabrication process.
The objectives of this research are:
- Read the STL file/s and determine their orientation.
- Slicing. This is the process of transferring an STL file to a series of layers. The result of the slicing process is the tool-path, also known as machine path.
- Tool-path generation. The tool-path is the movement of the 3-D printers' extrusion nozzle head during the printing process to fill the interior (fill) of each layer.
- G-code file. This is the CNC file containing all the slicing and tool-path information. It is also the input file, containing all the commands for the entry-level 3-D printer.
This research focuses on the development of an STL slicing and tool-path generation algorithm for an entry-level 3-D printer. The major technical challenges in the RP process are the slicing approach and tool-path generation technique.
The organisation of this paper is as follows: In section 2, a literature review of the structure of the proposed slicing and tool-path generation algorithm is provided, and previous work conducted by other researchers is summarised. Section 3 describes the research methodology of the experiment and discusses sections of the adopted algorithm. Section 4 presents the preliminary research results obtained from the research experiment. Section 6, the conclusion, discusses the implications for research and practice.
2 RELATED WORK
In 2011, Professor Deon De Beer, Executive Director of the Technology Transfer and Innovation (TTI) Centre and Directorate at the Vaal University of Technology (VUT), developed and launched the first South African IDEA 2 PRODUCT (i2p) lab, with the objective of empowering clients (students, staff, and the wider community) to develop their ideas into physical prototypes. The i2p lab has a dual purpose, starting with the generation, refinement, and improvement of the initial idea, and ending in a physical prototype. A client will thus experience both value-added services with respect to the initial idea, and relevant skills enhancement.
The i2p lab is still in its initial design stages, but it already consists of 20 AM platforms. The printers consist of the RAPMAN, BFB 3000, and the fairly new 3-D printer called the UP!. These 3-D printers have two things in common: the FDM technology, and the ability to input a 3-D model and fabricate a prototype.
The STL file format is the most widely-accepted file format in the RP industry. The reasons for its popularity are its simplicity and its ease of file generation without involving very complicated CAD software [3]. Different build orientations for a CAD model will affect the surface quality, the build time, the complexity of the support structure, and the total number of slice layers. The build orientation is usually determined based on the height and surface quality requirement of the STL model [2].
The slicing process is very important in LM. It greatly influences the surface roughness form, error preparation time, and actual machine build time. Slicing is the process of transferring an STL file to a series of layers. This procedure, for FDM machines using LM technology, involves vector generation by intersecting an XY plane at a particular height to create the model layers (slices). The result of the slicing process is the tool-path, also known as a machine path. Currently, the developed slicing processes can be divided into uniform slicing and adaptive slicing. In uniform slicing, the distance between two consecutive layers is the same, while in adaptive slicing the distance between two layers varies depending on the surface curvatures of the CAD model. Most of the RP systems use uniform slicing, while research is still being done to explore adaptive slicing [2]. Pandey et al. [6] proposed a slicing procedure for Fused Deposition Modelling based on real-time edge profiles of a deposited layer.
The work by Chang [4] slices a 3-D model designed in PowerSHARE into N sections with the aid of a special macro. The resulting section at each Z level consists of curves such as lines, conic arcs, and Bezier spans. These entities that form a contour are then coded and saved into a custom, pre-defined file for generating a tool-path by using computer-aided manufacturing software presented by the same company, PowerSHARE [5].
The tool-path creation procedure requires information from the slicing method to generate the information required for the G-code file. Normally this procedure is conducted by reading entire facets into the computer's memory; then the facets are sliced and generated vectors are sorted. This method demands a considerable amount of computer memory, and encounters difficulties in processing very large and complex STL files, thus affecting the final physical models' quality and build time. Hayasi and Asiabanpour [5] proposed a new tool-path generation algorithm that solves the computer bottleneck in tool-path generation for very large STL files. Tata et al. [8] demonstrated that the productivity of the LM processes can be significantly improved by upgrading the slicing software.
Various types of tool-path patterns and algorithms have been developed. These include contour, zigzag (also known as crisscross), spiral, and partition patterns with different considerations of the build time, surface quality, warpage, cost, stiffness, and strength of RP prototypes.
3 METHODOLOGY
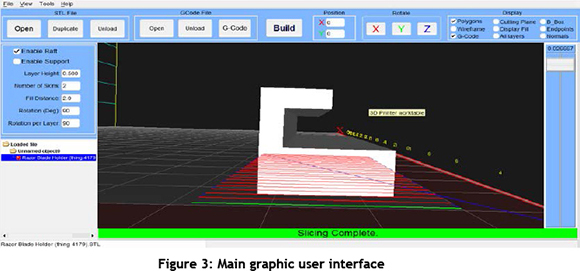
The research presented in this paper has been implemented using the C++ programming language on an OpenGL CASCADE platform. The OpenGL platform is an open-source CAD kernel system that includes C++ components for 3-D surface and solid modelling, visualisation, and rapid application development. The OpenGL library can return either filled polygons or polygons' oriented boundary contours, which are appropriate inputs for 3D printing and FDM. The OpenGL functions were used to gain access to STL files and for display purposes. A user interface form facilitated the data entries (e.g., layer thickness, fill distance, cutting plane, 3-D printer's minimum and maximum X, Y, and Z speed, extrusion rate, and raft options). Figure 1 illustrates the user interface form. The Fast Light Toolkit (FLTK), which is also an open source, cross-platform Graphical User Interface library written in C++, is used to create the user interface of the algorithm for flexibility with multiple operating systems.
The goal of the algorithm is to create a G-code file for an AM entry-level 3-D printer. The G-code section of the algorithm uses the standard G-code instructions (presented in Table 1), but it is not limited to only these variables; more G-code variables can be added. It is called a 'G-code' because the lines of code that control the 3-D printer start with a G command such as G1, G21, etc. Each command has a different function. CNC also consists of M codes that control other aspects of the machine, and F codes that control the 3-D printers' extruder speed.

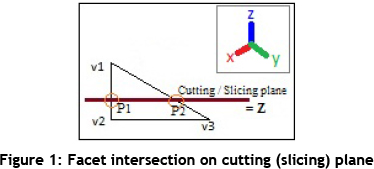
The following is a brief description of how G-code is generated by the algorithm. The first step is reading an STL file or multiple STL files. The STL model is made up of discrete triangles. The algorithm uses the orientation of a triangle to determine which side of the triangle represents the inside of the object to be created, and which side borders empty space. This concept of 'vertex order dictating' is important, and is used throughout the algorithm. When a slice is made at some height (Z step value), the algorithm checks every triangle in the STL model to verify that it intersects the cutting plane. If a triangle intersects the cutting plane, two of the vectors of the triangle will have one end above the cutting plane and one end below. The algorithm simply calculates where those vectors intersect the plane, and those vertices become part of the output as polygons. Since the two vertices come from the same triangle, they are linked.
If a facet does intersect the cutting plane, two of the vertices of the facet will have one end above the cutting plane and the opposite or other end below the cutting plane (see Figure 1). This particular positioning relationship between the cutting plane and the corresponding facet is denoted as:
((V1 > Z) & ((V2 < Z) & (V3 < Z))
There are other cases of facet intersections. According to the cutting plane's z-axis value, Z, there are ten kinds of different positional relationships between the cutting plane and the corresponding facet (F), as shown in Figure 2 and listed below:
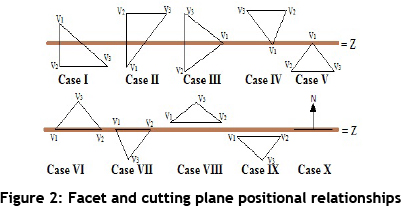
I. (V1 > Z) & ((V2 < Z) & (V3 <Z))
II. (V1 < Z) & ((V2 > Z) & (V3 > Z))
III. V1 = Z & ((V2 < Z) & (V3 > Z))
IV. V1 = Z & ((V2 > Z) & (V3 > Z))
V. V1 = Z & ((V2 < Z) & (V3 < Z))
VI. ((V1 = Z) & (V2 = Z)) & (V3 > Z)
VII. ((V1 = Z) & (V2 = Z)) & (V3 < Z)
VIII. ((V1 > Z) & (V2 > Z) & (V3 > Z))
IX. ((V1 < Z) & (V2 < Z) & (V3 < Z))
X. ((V1 = Z) & (V2 = Z) & (V3 = Z))
In Case I, none of the facet's (F) vertices contact the cutting plane, but one of the vertices (v1) is on the opposite side of the cutting plane when viewed from the y-axis or the x-axis. This creates two intersection points, point 1 (p1) and point 2 (p2), as displayed in Figure 1. These vertices' points become part of the output as polygons or line groupings that form a closed loop, which represents a layer of the STL model. The dot product of two vectors, also known as the scalar product, is a number obtained by performing a specific procedure on the vector components. The dot product is required to calculate the angle between the two vectors that intersect the cutting plane, thus determining the location of the facet's intersection with the cutting plane.
Case II is identical to Case I; the only difference is the location of the F's vertices, but the same concept is applicable. In Case III, one of the F's vertices contacts the cutting plane. The other intersection point must be determined using the common equation of a straight line, also known as the 'slope-intercept form':
y = mx + c (1)
This is called the slope-intercept form because 'm' is the slope and 'c' is the y-axis intercept. Also in Case III, the z values of the intersection points are both recorded. This coding allows the algorithm to recognise the acquired line data in other parts of the code. In Case IV, the F contacts the cutting plane at a single point, which results in unnecessary information for the rest of the code. The same applies for Case V, which also results in redundant information, since the F also touches the cutting plane at only one point.
In Case VII, the F contacts the cutting plane with its two vertices, which are directly on the cutting plane, and these two points are the intersection locations. The recorded information is the values of these vertices and the z value of the other vertex, which is used to determine whether to keep or delete the data.
In Case VIII and Case IX, the F does not intersect the cutting plane, so the algorithm ignores these facets and proceeds to the next value of the cutting plane on the z-axis. In Case X, F is parallel to either the base or the summit, and there is no need to calculate the intersection points because all the vertices of the F symbolise the intersection points. The outputs of the F intersection point discovery algorithm are all the pairs of intersection points that are situated on the cutting plane. These pairs of vertices are linked because they come from the same F. Once all of the facets have been checked or flagged, the resulting points represent lines that are sorted in a start-to-end fashion to create polygons.
At this point, polygons that represent a particular layer have been identified. Since the 3-D printer extruder head has a thickness, and we cannot just randomly fill in this geometry with a perfect layer of extrusion material, it is almost impossible to fill in the layer exactly. Instead, the goal is to generate a path that gives us the best possible fill to fit this set of polygons. The algorithm does not fill the inside of a model with solid material, since this uses more material and creates a heavier object that is not actually any more useful or stronger than one with a lot of empty spaces inside. The in-fill of an object's interior is produced by creating parallel lines at a certain angle. These lines are then rotated in successive layers.
If the 3-D printer extruder head followed the outer edge of the created polygon (Polygon 1) during the fabrication process, half the material would end up outside the polygon, resulting in an object larger than the STL model. To compensate for the width of the extruded material, we shrink the polygons so that we end up with another polygon (Polygon 2) that is slightly smaller than our target. If the extruder follows our polygon (Polygon 2), then the outer edge of the extruded material will match the edge of the original target polygon, and we shall create an object of the correct size. This tracing of the outside of the polygon is called a wall (or shell, or skin). If we want multiple skin layers, we shrink the polygons again, this time by the full thickness of the extruded material, instead of half, and the extruder can follow that polygon for an additional wall.
The shrinking algorithm of polygons works by selecting each vertex of the polygon and moving it inward, depending on the width of the print material (filament): Acrylonitrile Butadiene Styrene (ABS) or Polylactic Acid (PLA). The two adjacent vertices are used to decide where the point should be moved. If the vertex is pointing out of the polygon, the point needs to be moved inward more than the amount being shrunk, and the angle of the adjoining edges is used to find that point. The outside ('fill') polygons are shrunk and the inside ('hole') polygon is enlarged by a certain size.
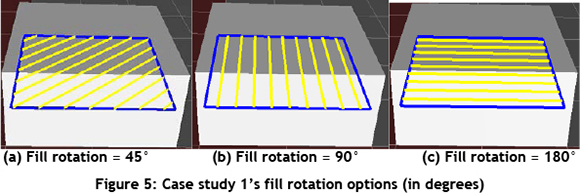
After the generation of the skin or wall polygons, the fill polygons must be created. Crisscross or zigzag lines are used to fill the inside of a layer. The crisscross lines can be changed by selecting the angle of the lines. Basically, the whole plane is filled with parallel lines, and then the print material is extruded along any of those lines that are within the fill polygons. For every layer or slice, the fill distance is always the same, and the direction of the crisscross lines is changed by a fixed angle between successive layers (see Figure 5) .A number of STL files have been tested for feasibility studies, and they have proved that the reliability of the developed algorithm issatisfactory.
4 PRELIMINARY RESULTS AND DISCUSSION
The data and results obtained are described in the following section. The main user interface for displaying the STL files, settings, and options for G-code generation is shown in Figure 3.
The main graphic user interface (GUI) of the system is very important. It must be user-friendly and easy to understand. Providing the user with options for viewing the models to be printed is a priority. There are several benefits for visualising a print job:
- Positioning STL models in the desired orientations.
- Positioning models economically: avoiding, as much as possible, voids in the job volume not occupied by models. The algorithm automatically separates objects by 5 mm.
- Positioning models so that they do not intersect each other.
- Changing options and settings for the G-code file, such as extruder speed, layer height, print material width, fill distance, rotation per layer, and so on.
- Previewing generated G-code before fabrication.
Two case studies were presented and successfully tested with the algorithm. The properties of these STL files are shown in Table 2. Several other STL files were tested and successfully printed from the generated G-code files.

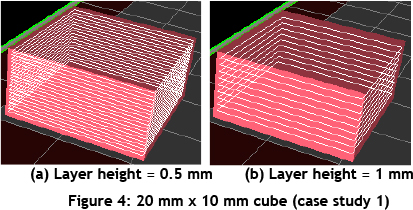
The comparison of layer heights is shown in Figure 4. The layer height is the step value of the selected layer height (the Z-step increment value). The rotation of the fill lines is shown in Figure 5. The rotation options are not limited to these, but a user can select between 0° and 180°. A sample of the G-code generated by the algorithm for case study 1 is shown in Figure 6.
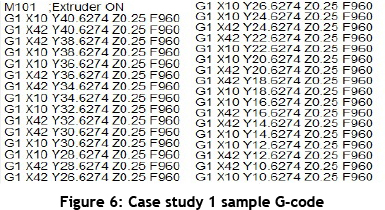

Even though the generated G-codes are saved into one file with the ".gcode" extension, the algorithm output can be demonstrated layer by layer. The processing time for parts is determined by the selected options (i.e., the processing time for a model with a layer height of 0.235mm will take more time than the same model with a layer height of 0.5mm). The schematic illustration of the sample G-code obtained from case study 1 is shown in Figure 6, and the G-code from case study 2 is shown in Figure 8.
The following parts have been successfully printed with the G-code generated by the algorithm and the BFB 3000 entry-level 3-D printer, using ABS plastic material:

5 CONCLUSION
This paper proposed a slicing and tool-path generation algorithm for STL files, with the goal of creating a G-code machine path file. The proposed algorithm's objectives were to read STL files and slice them into layers, and then finally generate a G-code file for an entry-level 3-D printer. The algorithm reported in this paper has been successfully tested on several STL files. This algorithm is customised for entry-level 3-D printers, utilising the FDM technology or SFF. The use of screenshots in this research provides a clear view of how the slicing plane thickness, fill distance, and orientation can affect the generated G-code file, which ultimately influences the build time and quality of the final fabricated prototype.
The results should be interpreted with caution because of the following limitations of our research. The generated G-code file has not been tested using multiple entry-level 3-D printers, but has been successfully tested with the BFB 3000 3-D printer. Multiple STL models with different settings were also successfully printed from this generated G-code file.
Future work can be done to improve the algorithm. To meet the demand for increasingly intricate and detailed prototypes, it is necessary to include a computational technique in the generation of support geometry. The inclusion of a support structure for STL files with overhangs is necessary as parts become more complex. A time estimate is also necessary to know how long a slicing job will take, instead of relying on a progress bar. Since the research has proven that the slice layer's thickness will influence the final slicing total time and the physical build time, it is necessary to know the time estimate of a slicing job. The new STL file format that contains colour information could also be adapted into the algorithm for future research.
REFERENCES
[1] Fadel, G.M. & Kirschman, C. 1996. Accuracy issues in CAD to RP translations. Rapid Prototyping Journal, 2(2), pp. 4-17. [ Links ]
[2] Jin, G.Q., Li, W.D., Tsai, C.F. & Wang, L.H. 2011. Adaptive tool-path generation of rapid prototyping for complex product models. Journal of Manufacturing Systems, 30, pp. 154-164. [ Links ]
[3] Choi, S.H. & Kwok, K.T. 2002. A tolerant slicing algorithm for layered manufacturing. Rapid Prototyping Journal, 8, pp. 161-179. [ Links ]
[4] Chang, C.C. 2004. Direct slicing and G-code contour. International Journal of Advanced Manufacturing Technologies, 23, pp. 358-365. [ Links ]
[5] Hayasi, M.T. & Asiabanpour, B. 2009. Machine path generation using direct slicing from design- y-feature solid model for rapid prototyping. The International Journal of Advanced Manufacturing Technology, 45, pp. 170-180. [ Links ]
[6] Pandey, P.M., Reddy, N.V. & Dhande, S.G. 2003. Real time adaptive slicing for fused deposition modeling. International Journal of Machine Tools & Manufacture, 43, pp. 61-71. [ Links ]
[7] Rock, S.J. & Wozny, M.J. 1991. A flexible format for solid freeform fabrication. Proceedings from the Solid Freeform Fabrication Symposium. Austin: The University of Texas, pp. 1-12. [ Links ]
[8] Tata, K., Fadel, G., Bagchi, A. & Aziz, N. 1998. Efficient slicing for layered manufacturing. apid Prototyping Journal, 4(4), pp. 151-67. [ Links ]
* Corresponding author
1 This article is an extended version of an article presented at the 2012 RAPDASA conference














