Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.3 Pretoria Nov. 2013
GENERAL ARTICLES
Optimisation of make-to-order production for multiple-line production
Chien-Chung Lee
Department of Business Administration. Aletheia University, Taiwan, R.O.C. mark8924@gmail.com
ABSTRACT
This work considers the make-to-order production of multiple-line production considering the production rate, production time interval, production yield, holding cost, manufacturing cost, set-up cost, the penalty cost of shortage, and constrained delivery deadline. Based on the research motivation of efficient and fast decisions, this paper constructs a mathematical model for achieving the maximum total profit, and selects the particle swarm optimisation (PSO) as the approach to a solution due to its simplicity and rapid convergence. The proposed model can be categorised as a nonlinear programming (NLP) model, and can also function as a decision-making tool for real-time analyses of multiple-line production planning. A numerical example is then followed to describe and analyse the results. Actually, this study is a computerised tool to deal with the production planning of make-to-order production by constrained delivery deadlines. This research can provide not only an efficient but also a fast referenced decision for an enterprise to face fast-changing business environments, and it can solve other cases easily by changing only its input parameters.
OPSOMMING
Die navorsing handel oor multi-lyn vervaardiging wat bedryf moet word vir 'n gegewe produksietempo, produksietyd, opbrengs, houkoste, vervaardigingskoste, voorbereidingskoste, tekortkoste en afleweringstyd. Die sisteemmodel het ten doel maksimering van wins deur gemaklik gebruik te maak van die metode van swermoptimisering. Die model is nie-lineêr, gebruikersvriendelik en wyd aanpasbaar via verandering van parameters.
1 INTRODUCTION
Yu and Zheng [1] state that a decision support system (DSS) is a computerised tool that may help the decision-maker make quick and precise decisions. A DSS not only possesses the characteristics of real-time decision support, but also helps the decision-maker to make efficient decisions concerning resources. In addition, a DSS mainly applies the strong capabilities of computers for computation and data storage to conduct optimisation planning. That is why computerised planning can play an important role in dealing with current diverse production planning problems. For order-based insight into production, the total profit should be considered. The selling price, the manufacturing cost, the set-up cost, the holding cost, as well as the penalty cost if incomplete products are delivered, would all be considered.
Hailian and Xiongqing [2] state that the manufacturing cost would be a significant factor to be considered. Several studies are focused on manufacturing cost, such as that of Klansek and Kravanja [3]. They present the self-manufacturing cost estimation, which is defined as the sum of the material, the power consumption, and the labour costs. Shehab and Abdalla [4] aim to develop an intelligent knowledge-based system that creates an environment to help inexperienced users to estimate the manufacturing cost of a product at the conceptual design stage of the product life cycle. In addition, Ouyang and Lin [5] develop an integrated framework for feature-based manufacturing cost estimation at an early design stage. One of the evaluation and optimisation criteria for machining processes is the manufacturing cost [4].
Allahverdi and Soroush [6] argue that scheduling with set-up times or set-up costs plays a crucial role in modern manufacturing and service environments, where reliable products/services are to be delivered on time. Set-up cost and delivery on time are important issues. Ohta and Nakatani [7] describe how meeting due dates, 'delivery on time', is the most important goal of scheduling if a due date for each job has been promised to the customer. The competitive advantage of an enterprise will decrease and lose its market share if an enterprise does not comply with the order deadline to satisfy the customer's need. So meeting the order delivery deadline would be an important factor.
As far as set-up costs are concerned, the major benefits of reducing set-up costs include reduced expenses, increased competitiveness, and increased profitability [6]. Flynn [8] demonstrates that scheduling with set-up times/costs increases the output capacity in cellular manufacturing environments. Wortman [9] underlines the importance of the problem by effectively managing the manufacturing capacity. And Darwish [10] describes how the classic economic production quantity (EPQ) model is generalised by considering a relationship between the set-up cost and the production run length. Thus the dependency between set-up cost and run length can be relevant [10]. A factory must be able to manufacture a continually increasing variety of customised products; so attention must be paid to the need for a new production scheduling method to reduce set-up costs [11]. Although this problem is found in the electronics industry, the contributing conditions are common to many industries [11]. Moreover, Takahashi et al. [12] state that the set-up cost should be considered in the total cost.
Other important costs, such as the holding and penalty costs, would also be considered in the total cost [13]. The cost of holding inventory is traditionally assumed to increase linearly with a rate equal to a percentage of the product value [14,15]. The following studies that discuss holding cost were considered:
a. Wee and Iyer [16] provide an optimal holding cost allocation scheme that leads to the maximum possible service rate for both a pooled and a split system [16].
b. Wahab and Jaber [17] discuss the economic production quantity (EPQ) model for items with imperfect quality when different holding costs for good and defective items respectively are considered [17].
c. Corbacioglu and van der Laan [18] analyse a two-product system, show how the correct holding cost rates deviate from the traditional valuation methodology, and demonstrate the impact on operational performance.
d. Ohta and Nakatani [7] consider the job-shop scheduling problem of minimising the total holding cost subject to there being no delayed jobs.
For the studies of penalty costs, Liu and Li [19] discuss the quadratic assignment problem with penalty costs taken into consideration. Kosuch and Lisser [20] solve a particular stochastic version of the restricted shortest path problem, where the penalty is considered. Estevez-Fernandez [21] considers the penalty functions when there are delays. Chan et al. [22] revisit the study of Bansal et al. [23] to describe the penalty if delay occurs. Thus the penalty cost issue draws much attention.
Because a wide range of complex optimisation problems occur that traditional derivative-based optimisation techniques cannot handle, particle swarm optimisation (PSO), a population-based evolutionary technique, was developed [24,25,26]. There are a number of optimisation techniques; however, PSO has recently attracted more research attention due to its algorithmic simplicity and rapid convergence compared with traditional evolutionary computation techniques [24,25,26].
PSO is one of the modern heuristic optimisation techniques. It was developed by Eberhart and Kennedy in 1995, using the social analogy of swarm behaviour in populations of natural organisms, such as a flock of birds or a school of fish [24,25,26]. Advancements in the PSO development over the last decade have made it one of the most promising approaches for nonlinear optimisation problems, and particularly for a wide range of real-world problems [24,25,27,28]. Most of the applications of PSO have been concentrated on solving continuous optimisation problems, but studies of discrete optimisation problems are relatively few. So PSO has rarely been applied in production and operations management (POM) optimisation problems [29]. Liao et al. [30] developed a PSO algorithm for the flow shop scheduling problem where it is a discrete optimisation problem. There have been several successful studies recently that focus on discrete problems with the modified PSO algorithms introduced to those problems [28].
Nearchou [29] applied PSO to the simple assembly line balancing problem (SALBP), a well-known NP-hard POM problem. This is the first work concerning the application of PSO on assembly line balancing problems ALBPs. Nima Hamta et al. [31] extended the first work on SALBP to address multi-objective (MO) optimisation of a single-model ALBP. Jin et al. [27] proposed the importance of randomness in PSO, and then gave a PSO variant without randomness to show that the traditional PSO cannot work without randomness.
PSO can be widely applied in image and video analysis, design and restructuring of electricity networks, control, antenna design, electronics and electromagnetics, and so on [31]. A new approach to solve the generation scheduling (GS) problem is presented, and the PsO method is suggested to apply to the GS problem [32]. PSO can also be applied to two complex and time-consuming nuclear engineering problems [26].
Lastly, the production yield is regarded as an important factor in considering production planning [33,34,35,36] because a high production yield will result in a small cost loss. This work considers an order of multiple-line production in which various production rates and production time intervals, the production yield, the holding cost, the manufacturing cost, the production set-up cost, and the penalty cost of shortage, are considered. We also consider that the manufacturing cost, holding cost, and set-up cost are increased by the production time interval for each production line. The unit penalty cost of shortage increases by the quantity of shortage, to satisfy real-world situations. This paper constructs a mathematical model, categorised as a nonlinear programming (NLP) model, to achieve the maximum total profit, and selects PSO as the approach to a solution due to its simplicity and rapid convergence. The proposed work is a computerised decision-making tool to deal with the make-to-order production planning of multiple-line production with constrained delivery deadlines. This model not only can provide an efficient and a fast referenced decision for an enterprise to face the fast-changing business environment, it can also function as a decision-making tool for real-time analysis of production.
2 ASSUMPTIONS AND NOTATIONS
The assumptions and notations of this study are as follows.
2.1 Assumptions
The conditions that were assumed for this study are:
1. The production lines and labour can be transferred and adjusted at any time without any restriction.
2. The set-up cost includes the replacement cost and the necessary cost of equipment. Therefore, when the production changes from the current product to another, the setup cost of the new product should be considered. In addition, the same product has similar set-up cost in the same plant.
3. The production line is completely balanced in this study.
4. MTO (make-to-order) production is considered.
5. The materials arrive at the beginning of each production interval, and the slacks are considered as inventory at the end of the interval.
2.2 Notations
i: the code of production line where i=1,2,3...,/
p: the sales price per finished product unit.
T: the production time limitation.
Ri:: the production rate of the i-th production line.
H: the holding cost per unit product per unit time.
C: the manufacturing cost per unit product per unit time.
Ti: the production time interval of the i-th production line.
S(Ti): the set-up cost function of the i-th production line, where S(Ti) is an increasing function of Ti.
y;: the yield rate of the production line, where y; is a variable and can be estimated in advance.
pen(M): the penalty cost function of the business enterprise, where pen(M) is an increasing function of M, and M means the quantity that is short of the demand quantity.
3 MODEL DEVELOPMENT
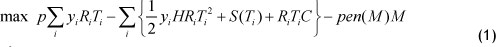
where:

Equation (1) describes the maximisation of the production profit of an enterprise that considers the yield rate shown in the first term; the holding cost, production set-up cost, and manufacturing cost in the second term; and penalty cost in the last term.
Equation (2) presents production constraints that show that the slack quantity of product is equal to the difference between order quantity and production quantity: Σi yi Ri Ti Equation (3) states that the production time of each production line should be less than or equal to the production time limitation T.
Equation (4) shows the non-negative constraint.
Combining Eq. (1) to (4), the proposed model is a nonlinear programming problem (NLP).
PSO has been applied in this work because of its algorithmic simplicity and rapid convergence, compared with traditional evolutionary computation techniques. PSO is a population-based stochastic algorithm for optimisation problems in an n-dimensional continuous space. In PSO, M particles cooperate to search for the global optimum in the n-dimensional search space. They are randomly generated, and update their solution through the generations. In each generation, the particle changes its velocity by considering the particle's best memory, called pbest, and the group's best memory, called gbest. The algorithm of PSO is presented in the following.
Step 1: The M solutions (called particles) for n-dimensional space are randomly generated.
Step 2: According to the searching space, a fitness function is defined, and the fitness value of the particle is evaluated with the function.
Step 3: The new velocity of the particle is modified according to the best positions of the particle and the swarm (pbest and gbest).
Step 4: The new velocities and positions of the particles for the next generation are determined according to the following:
vik+1 = vik + c1 x rand(.) x (pbesti - sik)+c2 x rand(.) x (gbest - sik)
sik+1 = sik + vik+1
in which vik and vik represent the velocities of the particle i and the kth and k + 1th generation respectively. pbestt represents the best position of the particle i. gbest represents the best position of the swarm, and S represents the new position of the particle i.
Step 5: If the search satisfies the termination condition then it stops; otherwise it returns to step 2.
4 EXAMPLE AND ANALYSIS
4.1 Numerical example
An enterprise accepts an order with a quantity of 40,000 (Q=40,000) and contracts the exact delivery deadline and selling price (p=650 dollars). A plant estimates that it will take 1,200 hours to manufacture the order. This manufacturing plant owns five production lines, and each production line has its production rate Ri, and average yield rate yi, which are listed in Table 1. The holding cost is 0.009 dollars per hour per unit product, and the manufacturing cost is five dollars per hour per unit product. The set-up cost and penalty cost functions are listed in Table 2.

Applying PSO as the searching method, the optimal solution is presented as follows: the optimal profit is 25,223,320 dollars; the optimal production time is T1=T3=0 hours, T4=T5=1200 hours, and T2=562.9 hours; the acceptable completed product quantity is around 40,000; the contribution (profit) per unit input working hour is 8,513.05 dollars; and the usage of resource capacity achieves 0.4938 (shown in Table 3).
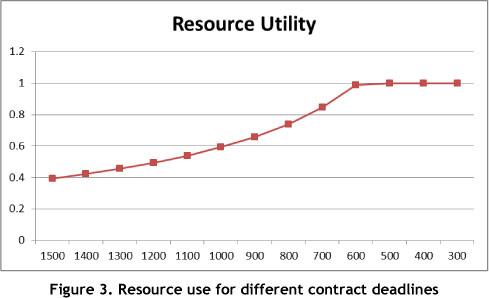
From the usage of resource capacity of 0.4938, it follows that more than 50 per cent of resources are unoccupied, and we may try to reduce the manufacturing time from 1,200 hours to 600 hours.
Consider that the manufacturing time is only 600 hours. From Table 3, it can be found that the total profit changes to 25,070,755 dollars. Only T4=562.9 hours. The other production lines reached their upper time limit of 600 hours. The acceptable complete product quantity is also around 40,000. The contribution (profit) per unit input working hour is 8,461.56 dollars, and the usage of resource capacity is 0.9876.
Furthermore, this paper tries to reduce the manufacturing time again (shown in Table 3). It reveals that when the manufacturing time decreases to 500 hours or below, the usage of resource capacity reaches 100 per cent. That means that all the available resources are used, and shortages occur.
From Figure 1, it follows that the profit would reduce fast if the contract deadline is less than 600 hours. Besides, Table 3 shows that the production times of the five production lines all reached their upper limit when the contract deadline was less than 600 hours. Actually, when the contract deadline equals 600 hours, the contract quantity can still be completed because the 4-th production line still has some available time. It is obvious that the contract deadline should be negotiated to be greater than 600 hours.

4.2 Analysis and discussion
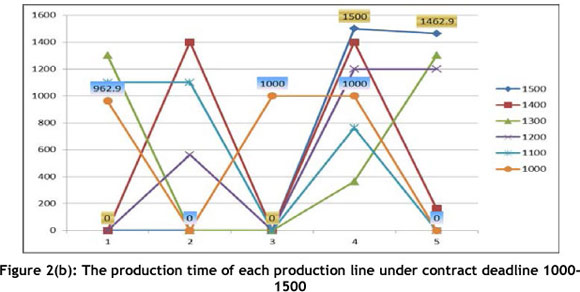
To discuss the situation of the contract deadline, we consider 1,000 hours. It proposes the idea that it is not necessary to use all five production lines when the near-optimal solution is achieved. If the cost of setting one more production line would surpass the cost of holding more products, the solution is to hold more products instead of setting more production lines to work. Figures 2(a) and (b) and Table 3 present such a case. The higher the contract deadline, the less the production lines work because of attention to optimal profit (holding more products instead of setting more lines, because the set-up costs of one more line would exceed the cost of holding more products).
Traditionally, a plant will average the workload of all its production lines because it seems a good way to assign the workload. From the proposed numerical case, based on the considerations of work balance, the production time of each production line is assigned to be 592 (Q/yi/Ri/n) hours, where n means the number of production lines; and it will result in a profit of 25,033,547 dollars. However, a profit (delivery deadline=1000) of 25,239,618 dollars is achieved with the proposed PSO approach, and this only sets up three production lines (shown in Table 3). Such an assignment not only results in greater profit (206,071 dollars), but also saves more space and more equipment, which can be used for other contracts or purposes. Although two production lines are unused, the reserved production capacity can allow a plant to consider dedicating more production resources to other production plans.
Combining Figures 1 and 3 shows that, once the resource utilisation reaches its upper limit (the production limit is 600 hours), a smaller profit is achieved. This is because the production capability is exhausted and some demand cannot be met, thus incurring penalty costs.
A sensitivity analysis of the contract deadline between 510 and 600 was conducted, and is shown in Table 4. Table 4 strongly supports the result that the contract deadline should be more than 600 hours.

When considering the case where the contract deadline is 1,000 hours, the resource price shows -12.67 dollars per unit hour if the contract deadline moves up to 1,010 hours. Conversely, the resource price is 5.36 dollars if the contract deadline decreases to 990 hours. This phenomenon can be explained by the shortage quantity: the shortages are all zero, irrespective of whether the contract deadline is more or less than 1,000 hours. So increasing the contract deadline would cause the resource to become exhausted, and thus a unit resource added would detect negative profit improvement (shown in Table 5). The result is that the resource price (profit improvement divided by resource increment) becomes negative. On the other hand, decreasing the contract deadline would cause the resource usage rate to increase, and therefore the resource price would become positive. Now, we simulate the contract deadline at 600 hours. The simulated results reveal that the shortage of 175 (shown in Table 4) would occur if the contract deadline went down to 590 hours; although the resource usage rate goes up, the resource price shows a huge negative value (shown in Table 4) because of the existence of 175 shortage items - that is, because the penalty is significant. In addition, increasing the contract deadline would cause the resource to become exhausted, and that is why the resource price goes into the negative; -81.06 dollars per unit hour.
5 CONCLUSIONS
This work considers an order of multiple production lines, taking into account different production rates and production time intervals, the production yield, the holding cost, the manufacturing cost, the production set-up cost, and the penalty cost of shortage.
This study makes two main contributions:
First, this work develops a mathematical model under the concept of production management to solve real-world situations, such as multiple-line production, different production time intervals for each production line, and so on. Because of the complexity of the real-world considerations, the proposed model is regarded as an NLP problem, which means that the proposed model is hard to solve. Fortunately, the PSO approach can be applied as a solution method, due to its simplicity and rapid convergence. Actually, the proposed model is a computerised model that deals with the production planning of an order for multiple-line production with constrained delivery deadlines. This model can provide an efficient but fast referenced decision for an enterprise in a fast-changing business environment.
Second, the proposed model and solution method can be the decision reference of an enterprise, but can also satisfy the customers' needs, because this research was carried out to solve the real-world problem of production planning.
A plant commonly organises its workload to balance all production lines; however, the optimum solution of the proposed case obtained by PSO shows that setting up only some production lines can result in greater profit if the contract deadline is more than sufficient.
The repeated characteristics of the proposed work make this study a valuable decision support tool because of the application of PSO. Other enterprises can easily duplicate this study to solve problems by following the proposed model, merely changing its input parameters.
Future focused research is recommended to develop a more flexible model, such as random yield rate and flexible production rate, to deal with the situations of different production rates of each production line, sudden changing of production capacity, sudden-inserting orders, and so on. It is also strongly suggested that multi-itemised production be further investigated. In summary, this study can offer a good and valuable tool to perform the production planning of a contract order for an enterprise with multiple production lines, considering different order quantities, various production time intervals, the production yield, the holding cost, the manufacturing cost, the production set-up cost, and the penalty cost of shortage.
REFERENCES
[1] Yu, D. & Zheng, S. 2011. Towards adaptive decision support systems: A service-oriented approach. Advances in Information Sciences and Service Sciences, 3(7), 26-34. [ Links ]
[2] Hailian, Y. & Xiongqing, Y. 2010. Integration of manufacturing cost into structural optimization of composite wings. Chinese Journal of Aeronautics, 23, 670-676. [ Links ]
[3] Klansek, U. & Kravanja, S. 2006. Cost estimation, optimization and competitiveness of different composite floor systems - Part 1: Self-manufacturing cost estimation of composite and steel structures. Journal of Constructional Steel Research, 62, 434-448. [ Links ]
[4] Shehab, E.M. & Abdalla, H.S. 2001. Manufacturing cost modelling for concurrent product development. Robotics and Computer Integrated Manufacturing, 17, 341-353. [ Links ]
[5] Ouyang, C. & Lin, T.S. 1997. Developing an integrated framework for feature-based manufacturing cost estimation. International Journal of Advance Manufacturing Technology, 13(9), 618-629. [ Links ]
[6] Allahverdi, A. & Soroush, H.M. 2008. The significance of reducing setup times/setup costs. European Journal of Operational Research, 187, 978-984. [ Links ]
[7] Ohta, H. & Nakatani, T. 2006. A heuristic job-shop scheduling algorithm to minimize the total holding cost of completed and in-process products subject to no tardy jobs. International Journal of Production Economics, 101, 19-29. [ Links ]
[8] Flynn, B.B. 1987. The effects of setup time on output capacity in cellular manufacturing. International Journal of Production Research, 25, 1761-1772. [ Links ]
[9] Wortman, D.B. 1992. Managing capacity: Getting the most from your firm's assets. Industrial Engineering, 24, 47-49. [ Links ]
[10] Darwish, M.A. 2008. EPQ models with varying setup cost. International Journal of Production Economics, 113, 297-306. [ Links ]
[11] Monkman, S.K., Morrice, D.J. & Bard, J.F. 2008. A production scheduling heuristic for an electronics manufacturer with sequence-dependent setup costs. European Journal of Operational Research, 187, 1100-1114. [ Links ]
[12] Takahashi, K., Aoi, T., Hirotani, D. & Morikawa, K. 2011. Inventory control in a two-echelon dual-channel supply chain with setup of production and delivery. International Journal of Production Economics, 133, 403-415. [ Links ]
[13] Wang, Y.C. & Cheng, W.T. 2008. A sensitivity analysis of solving joint replenishment problems using the RAND method under inaccurate holding cost estimates and demand forecasts. Computers & Industrial Engineering, 55, 243-252. [ Links ]
[14] Ayomoh, M.K.O., Oladeji, O. & Oke, S.A. 2004. Investing the dynamics of an inventory system in the manufacturing sector: A case study. South African Journal of Industrial Engineering, 15(1), 19-30. [ Links ]
[15] Berling, P. 2008. Holding cost determination: An activity-based cost approach. International Journal of Production Economics, 112, 829-840. [ Links ]
[16] Wee, K.E. & Iyer, A. 2011. Consolidating or non-consolidating queues: A game theoretic queueing model with holding costs. Operations Research Letters, 39, 4-10. [ Links ]
[17] Wahab, M.I.M. & Jaber, M.Y. 2010. Economic order quantity model for items with imperfect quality, different holding costs, and learning effects: A note. Computers & Industrial Engineering, 58, 186-190. [ Links ]
[18] Corbacioglu, U. & van der Laan, E.A. 2007. Setting the holding cost rates in a two-product system with remanufacturing. International Journal of Production Economics, 109, 185-194. [ Links ]
[19] Liu, L. & Li, Y. 2006. The fuzzy quadratic assignment problem with penalty: New models and genetic algorithm. Applied Mathematics and Computation, 174, 1229-1244. [ Links ]
[20] Kosuch, S. & Lisser, A. 2010. Stochastic shortest path problem with delay excess penalty. Electronic Notes in Discrete Mathematics, 36, 511-518. [ Links ]
[21] Estevez-Fernandez, A. 2012. A game theoretical approach to sharing penalties and rewards in projects. European Journal of Operational Research, 216, 647-657. [ Links ]
[22] Chan, S.H., Lam, T.W. & Lee, L.K. 2013. Scheduling for weighted flow time and energy with rejection penalty. Theoretical Computer Science, 470, 93-104. [ Links ]
[23] Bansal, N., Blum, A., Chawla, S. & Dhamdhere, K. 2003. Scheduling for flow-time with admission control. ESA Proc., 43-54. [ Links ]
[24] Lu, H., Sriyanyong, P., Song, Y.H. & Dillon, T. 2010. Experimental study of a new hybrid PSO with mutation for economic dispatch with non-smooth cost function. Electrical Power and Energy Systems, 32, 921-935. [ Links ]
[25] Qin, J., Li, X. & Yin, Y. 2012. An algorithmic framework of discrete particle swarm optimization. Applied Soft Computing, 12, 1125-1130. [ Links ]
[26] Waintraub, M., Schirru, R., & Pereira, C. M. 2009. Multiprocessor modeling of parallel particle swarm optimization applied to nuclear engineering problems. Progress in Nuclear Energy, 51, 680-688. [ Links ]
[27] Jin, X., Liang, Y., Tian, D. & Zhuang, F. 2013. Particle swarm optimization using dimension selection methods. Applied Mathematics and Computation, 29, 5185-5197. [ Links ]
[28] Zhang, W.B. & Zhu, G.Y. 2011. Comparison and application of four versions of particle swarm optimization algorithms in the sequence optimization. Expert Systems with Applications, 38, 8858-8864. [ Links ]
[29] Nearchou, A.C. 2011. Maximizing production rate and workload smoothing in assembly lines using particle swarm optimization. International Journal of Production Economics, 129, 242-250. [ Links ]
[30] Liao, C.J., Tseng, C.T. & Luarn, P. 2007. A discrete version of particle swarm optimization for flowshop scheduling problems. Computers & Operations Research, 34, 3099-3111. [ Links ]
[31] Nima Hamta, S.M.T., Fatemi Ghomi, F., Jolai, M. & Shirazi, A. 2013. A hybrid PSO algorithm for a multi-objective assembly line balancing problem with flexible operation times, sequence-dependent setup times and learning effect. International Journal of Production Economics, 141, 99-111. [ Links ]
[32] Siahkali, H. & Vakilian, M. 2009. Electricity generation scheduling with large-scale wind farms using particle swarm optimization. Electric Power Systems Research, 79, 826-836. [ Links ]
[33] Benson, R.F., Conningham, S.P. & Leachman, R.C. 1995. Benchmarking manufacturing performance in the semiconductor industry. Production and Operations Management, 38(3), 201-216. [ Links ]
[34] Gering, M. 1999. Activity based costing and performance improvement. Management Accounting, 24-25. [ Links ]
[35] Kane, V.E. 1986. Process capability indices. Journal of Quality Technology, 18(1), 41-52. [ Links ]
[36] Meyersdorf, D. & Yang, T. 1997. Cycle time reduction for semiconductor wafer fabrication facilities. Advanced Semiconductor Manufacturing Conference and Workshop, IEEE/SEMI, 418-423. [ Links ]