Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.3 Pretoria Nov. 2013
GENERAL ARTICLES
Quantitative methods required for implementing PAS 55 or the ISO 55000 series for asset management
J.R. MinnaarI, *; W. BassonII; P.J. VlokIII
IDepartment of Industrial Engineering. Stellenbosch, South Africa. 15678067@sun.ac.za
IIDepartment of Industrial Engineering. Stellenbosch, South Africa. 15647277@sun.ac.za
IIIDepartment of Industrial Engineering. Stellenbosch, South Africa. pjvlok@sun.ac.za
ABSTRACT
Asset management is an important part of any organisation, as it allows them to extract value from their assets. The publicly-available specification for asset management (PAS 55) outlines what a standardised asset management system should consist of. The newly-proposed series of standards from the International Organizations for Standardization (the ISO 55000 series) also aims to provide a standardised framework for an asset management system. Both of these documents, however, only tell organisations what should be done, not how to do it. This article provides an introductory overview of numerical tools that an organisation can use when implementing an asset management system, and provides resources for further reading.
OPSOMMING
Batebestuur is 'n belangrike aspek van enige organisasie. Batebestuur laat organisasies toe om waarde uit hul bates te ontgin. PAS 55 (die publieke spesifikasie van die Britse Standaarde Instituut) verskaf 'n gestandaardiseerde raamwerk vir die implementering van 'n batebestuurstelsel. Die Internasionale Organisasie vir Standaardisering (ISO) is ook besig om 'n stel internasionale standaarde te publiseer wat verder poog om batebestuurstelsels te standardiseer. Beide hierdie dokumente beskryf egter slegs wat gedoen moet word, nie hoe dit gedoen moet word nie. Hierdie artikel gee 'n oorsig van beskikbare numeriese metodes wat organisasies kan gebruik wanneer 'n batebestuurstelsel geïmplementeer word.
1 INTRODUCTION
Assets allow organisations to achieve strategic objectives and meet stakeholder needs. Managing these assets optimally has become crucial for organisations to stay competitive in today's global market. Responding to calls from the industry for a consistent, standardised specification when implementing asset management plans and procedures, the Institute for Asset Management worked with the British Standards Institution [1] to publish PAS 55, the first publicly-available specification for the optimised management of physical assets. The International Standards Organization (ISO) [2,3,4] is currently circulating, for review, a new draft series of international standards (the ISO 5500 series), based on PAS 55. The ISO 55000 series will be available in March 2014.
The key benefit of PAS 55 and the proposed ISO 55000 series of international standards is that they both provide a minimum set of requirements for an effective asset management system, but allow the organisation itself to determine how best it should be implemented to suit their needs. A mature asset management system that adheres to these minimum requirements allows for consistent decision-making on activities that impact asset-related risks, performance, and cost profiles. This implies that management should be equipped to make objective, predictable, and consistent decisions that involve trade-offs between short- and lon-term effects, and optimal combinations of interrelated and conflicting benefits. PAS 55 requires that an organisation's strategy "clearly state the approach and principal methods by which assets and asset systems will be managed" (PAS 55, Section 4.2. (g), p. 7). ISO 55001 also specifically requires that "the method for decision-making and prioritizing of the activities and resources to achieve its asset management plan(s) and objectives shall be documented" (ISO 55001, Section 6.2.2, p. 4). ISO 55000 further requires that the organisation "shall retain appropriate documented information as evidence of the results of monitoring, measurement, analysis and evaluation" (ISO 55001, Section 9.1, p. 9). As mentioned, PAS 55 and the ISO 55000 series only tell the user what to do, not how to do it. Organisations are thus left to determine (and document) appropriate tools and methodologies for decision-making themselves.
One category of specifications that is common to both PAS 55 and ISO 55000 is related to quantitative justification for decisions that are implemented. Quantitative decision-making is a remarkably under-researched area in asset management, and so this article attempts to identify quantitative specifications and corresponding numerical methods that will enable an organisation to adhere to the requirements set out in PAS 55 and in the ISO 55000 series. Section 2 gives background information on PAS 55 and the ISO 55000 series, and Section 3 highlights the requirements in PAS 55 and the ISO 55000 series where numerical methods are needed. For convenient reference, Section 4 gives a short description of each of the numerical methods that can be used. Section 5 gives a numerical illustration of how some of these methods relate to each other, and how each can benefit an organisation.
Since PAS 55 and the ISO 55000 series are the foundations of this article, knowledge of these documents is key to gaining maximum benefit from this article. It is recommended that a copy of each document is kept on hand while studying this article.
2 BACKGROUND ON PAS 55 AND THE ISO 55000 SERIES OF INTERNATIONAL STANDARDS
PAS 55 consists of seven sections: (1) general requirements, (2) asset management policy, (3) asset management strategy, objectives, and plans, (4) asset management enablers and controls, (5) implementation of asset management plan(s), (6) performance assessment, and (7) improvement and management review.
PAS 55 requires that an organisation continually endeavour to improve its assets and asset management plan(s) or procedure(s). An organisation should be aware of new technology and knowledge associated with asset management. The first part of Section 4 in the PAS 55 document thus sets out basic requirements for an organisation to meet when implementing asset management plan(s) and procedure(s). According to PAS 55, "the organisation shall establish, document, implement, maintain and continually improve an asset management system in accordance with the requirements of this PAS" (Section 4.6.5.2, p. 18).
The importance of a well-managed asset management system is emphasised throughout the PAS 55 document. It requires the use of measurable objectives, as well as monitoring and measuring the performance of the system. Section 4.6 focuses entirely on performance assessment and improvement, and Section 4.6.1 (e) specifically requires "both qualitative and quantitative measures".
The proposed ISO 55000 series of international standards builds on these principles, but attempts to make it more universally applicable. It consists of three international standards: ISO 55000 provides an overview, principles, and the terminology of asset management; ISO 55001 specifies requirements for an asset management system; and ISO 55002 provides guidelines for the application of ISO 55001.
The requirements of ISO 55001 are divided into seven categories: organisational context, leadership, planning, support, operation, performance operation, and improvement.
The next section identifies six areas where numerical methods are needed. These areas stretch over one or more of the sections used in PAS 55 or in the ISO 55000 series.
3 SPECIFICATIONS REQUIRING THE AID OF QUANTITATIVE METHODS
The six areas of concern identified are data analysis, life cycle management, asset criticality, risk management, statistical failure analysis, and sustainable development. These six areas are defined in turn, and sections in PAS 55 and the ISO series are specified that require the use of numerical methods to establish asset management techniques. The application of the numerical methods is briefly described in relation to the six areas.
3.1 Data analysis
Data analysis is a broad term that describes the processing of data, with the goal of deriving useful information to support decision-making. Although PAS 55 implies the need for data and data analysis, ISO 55000 explicitly calls for data-driven decision-making processes (ISO 55000, 2.4.2, b, 1). This requirement is derived from one of the founding principles of asset management, which states that "asset management turns the organizational strategic intent into decisions and actions on assets to realize their value" (ISO 55000, 2.4.2, b). This implies that data analysis is central to asset management.
Data analysis encompasses many techniques. In its simplest form it takes the shape of descriptive statistics. By merely calculating the mean (measure of central tendency), the minimum and maximum values, and the standard deviation (measures of variability), management should be able to make more informed decisions. Descriptive statistics allow management to gain insight quickly into what their assets need to achieve (e.g. how many products a machine must be able to produce to meet customer demand). Descriptive statistics also provide a simple method for measuring asset management performance against objectives, and allow management to identify opportunities for improvement.
Descriptive statistics also form part of the more comprehensive exploratory data analysis (EDA) method described by Tukey [5]. EDA emphasises easy-to-understand summaries and the visual representation of data to serve as a basis for further data collection, analysis, and appropriate tool selection.
The same basic principles of EDA can be combined with fields in computer science to perform data mining. This important step in discovering knowledge in large databases has several applications that are extremely relevant for asset management. Fayyad et al. [6] list a few common applications for data mining that can greatly aid organisations looking to implement PAS 55 or ISO 55000. These applications range from simple summarising of data to discovering underlying patterns.
Asset management plan(s) and procedure(s) can only be as reliable as the data being used as input. A well-constructed data analysis could provide valuable information, therefore, to implement a successful asset management plan. Data analysis is fundamental to most of the numerical methods mentioned in this article, and is thus presented as a useful starting point for most numerical methods.
3.2 Life cycle management
Life cycle management is essential to the process of asset management. Both PAS 55 and ISO 55001 require an organisation to set up a life cycle management plan. The plan should consider the complete life cycle of the asset, from acquisition, to utilisation, to maintenance, and finally to the disposal of the asset. A popular term for the process is 'from cradle to grave'. The life cycle management plan should also include the risk associated with the specific asset and the consequences of this risk.
Sections 4.3.1(d), 4.3.3, 4.4.7.2(c), 4.4.7.3(f), 4.4.7.4(f), and 4.5.1 in PAS 55 set the requirements for life cycle management. In the ISO 55000 series, Section 2.4.4.2 in ISO 55000 states that the preferred methods for managing assets should be stipulated as part of the strategic approach to decision-making. This is also made a requirement in Section 6.2.2 in ISO 55001. In the guidelines for the application of ISO 55001 (ISO 55002), several references are made to life cycle management (Sections 6.1.2, 6.2.2.4, 7.5.1, and 7.5.2), most of which deal with the financial consequences of an asset over its entire life. Life cycle management should support cost-effective decision-making.
Perhaps one of the simplest ways to improve strategic decision-making of assets with longterm financial consequences is to incorporate life cycle costing (LCC). By calculating the net present value of all the expected costs of an asset over its lifetime, an organisation will be able to determine whether an expensive machine with low cost maintenance is a better option than a low cost machine with high maintenance cost. Barringer [7] provides a more in-depth summary of LCC. There are several other numerical methods - discussed in the next paragraph - that organisations can use for more advanced life cycle management.
Markov chains show how random variables change over time, and how they can be used to determine the different states of the asset during its life cycle. The resulting model can then be used to determine the costs associated with the life cycle. Stump [8] gives a good example of how Markov chains can be implemented in a life cycle cost analysis. Markov chains are further discussed in Section 4.1 below. Multiple-objective optimisation (MOO), discussed in Section 4.2, is used when more than one objective needs to be satisfied. This is applicable when different activities in the life cycle of the asset need to be considered. A cost-benefit analysis weighs the cost and benefits of the different life cycle activities. More details about a cost-benefit analysis are given in Section 4.3. The economic order quantity (Section 4.4) determines the size of the inventory lot and helps to determine the life cycle cost of the asset. Simulation is used to represent real-world situations, and could represent the entire life cycle of the asset. Examples of simulation and specific software packages to be used are discussed in Section 4.5.
3.3 Asset criticality
During the implementation of an asset management plan in an organisation, it is important to establish the critical assets and asset systems. PAS 55 defines critical assets/asset systems as "assets and/or asset systems that are identified as having the greatest potential to impact on the achievement of the organisational strategic plan".
PAS 55 also states that an organisation shall establish, implement, and maintain plan(s) that not only identify the critical assets, but also determine how the organisation responds to emergency situations concerning critical assets. Likewise, the ISO 55000 series requires that a strategic approach determine the criticality of assets and asset systems, and weight them appropriately when making decisions.
Sections 4.3.1 (e), (f), and (g) and Section 4.3.4 in PAS 55 set the requirements relating to asset criticality. The guidelines for implementing ISO 55001 (ISO 55002) provide additional information about how asset criticality should be incorporated into an asset management system in Sections 6.1.2, 6.2.2.2, 7.1, 7.2, and 7.6.
A criticality analysis forms part of the failure mode and effect analysis (FMEA), and determines the severity of a failure. It is described in Section 4.6. The FMEa is a qualitative analysis that is used to identify the failure modes and their causes and effects. The Monte Carlo method, described in Section 4.7, provides different outcomes for a specific action, and can help to determine the critical asset. The cost-benefit analysis can again be used. Finally, network models represent objects and their relationships, and can determine the objects or assets that have the most important function in the organisation. They are discussed further in Section 4.8. Simulation could be used to optimise processes in an organisation and to determine assets critical to the system. Simulation is also a powerful tool that can be used to identify potential bottlenecks in various scenarios, showing not only the critical assets and asset systems, but also their sensitivity to change.
3.4 Risk Management
A large section in PAS 55 is dedicated to risk management. Organisations implementing either PAS 55 or ISO 55001 should be able to describe their asset-related risks, and how this risk profile changes over time. Risk management is defined by both PAS 55 and the ISO 55000 series as "coordinated activities to direct and control an organisation with regard to risk".
PAS 55 requires that the organisation's asset management policy and risk management framework support each other. The asset management plan(s) shall consider all asset-related risks, and shall optimise and prioritise the different risks (as mentioned in PAS 55).
PAS 55 sets the requirements for risk management in Sections 4.2 (d), 4.3.1 (e), 4.3.2 (h), 4.3.3, 4.3.4 (a) and (c), 4.4.1 (g), and 4.4.7. "Actions to address risks and opportunities" in ISO 55001 Section 6.1 details all the requirements for managing risk.
A quantitative risk assessment is done to determine the magnitude and probability of the loss. A variety of numerical methods can be used to conduct the risk assessment. Multiple-objective optimisation (MOO) and the Monte Carlo method can also be used for risk management; both help to determine the consequences of a risk and the most adverse risk. Forecasting models, as mentioned in more detail in Section 4.9, attempt to predict the unpredictable future by using past data, and can be used to predict changing circumstances and possible risks associated with specific events. Decision trees and utility theory can also be used when decisions need to be made under uncertainty when specific probabilities are available. This is discussed in Section 4.10.
3.5 Statistical failure analysis
The process of determining when machinery will fail helps to determine the life cycle of the assets and how to manage the asset efficiently. PAS 55 clearly states that an organisation shall establish, implement, and maintain process(es) and/or procedure(s) to analyse past performance, monitor current performance, and predict the future performance of the asset.
Statistical failure analysis can also play an important part in improving stakeholder confidence. Being able to predict, within a certain confidence interval, when something will fail is crucial for achieving a reliable and predictable operating state. The ISO 55000 series puts a strong emphasis on continual improvement and preventative action. Requirements for these are given in Section 10 of ISO 55001. PAS 55 also identifies key areas where failure analysis is needed in Sections 4.6.1 (a) and (d), 4.6.2 (a), (b), and (c), and 4.4.7.3 (a).
Important methods that can be used to facilitate failure analysis incorporate the log-linear and power law point processes (both discussed in Section 4.11), as well as the Weibull distribution (discussed in Section 4.12). These methods are used to determine metrics such as MTBF (mean time between failures), MTTF (mean time to failure), MFOP (maintenance free operating period), and FIT (failure in time). Simulation can be used to simulate processes in an organisation to determine when assets will fail.
3.6 Sustainable development
PAS 55 distinguishes between being sustainable and sustainable development as mentioned below:
Sustainable: "achieving or retaining an optimum compromise between performance, costs and risks over the asset's life cycle, whilst avoiding adverse long-term impacts to the organisation from short-term decisions"
Sustainable development: "enduring, balanced approach to economic activity, environmental responsibility and social progress"
Sustainable development is a long-term commitment by an organisation, and is an important part of asset management, as mentioned in PAS 55 Section 4.2 (g): "The policy shall clearly state the principles to be applied, such as the organisation's approach to health and safety or sustainable development."
Recently, sustainability and sustainable development have received much attention from all types of organisations. The world is rapidly changing, and organisations are becoming more aware of the impact they have on the environment. Many regulations have been implemented to support and promote sustainable development. Because asset management is also a growing field, it is important to consider these regulations when implementing asset management plan(s) and procedure(s). The ISO 55000 series also mentions that the asset management system should follow a long-term sustainable approach.
Important methods that can be used to facilitate sustainable development incorporate life cycle management and the methods associated with life cycle management mentioned previously: network models and geographic integrated systems (GIS). GIS is a tool that helps to comprehend geography, and aids the process of decision-making. GIS helps organisations to plan efficient asset use while considering resources and the environment. ESRI [9] discusses the relationship between GIS and sustainable development, and is further described in Section 4.13.
4 ANALYSIS OF NUMERICAL METHODS APPLICABLE TO ASSET MANAGEMENT
4.1 Markov chains
Markov chains are a type of stochastic process that involves the study of how a random variable changes over time. Winston [10] defines a stochastic process and Markov chains thus:
Stochastic process
"A stochastic process is a collection of random variables that is often used to represent evolution of a random value or system over time."
Markov chains
"A Markov chain is a random, memoryless process. It is a mathematical system that transitions from one state to another with the next state depending only on the current state and not the preceding events. The number of states could be finite or countable."
A discrete-time stochastic process is a Markov chain if, for t = 0, 1, 2, ... and all states,
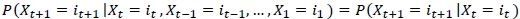
Markov chains can be used to calculate the probability of whether a machine will be broken or repaired at a future date, depending on the probabilities of whether the machine is currently working or broken.
4.2 Multiple-objective optimisation
Multiple-objective optimisation (MOO) is the simultaneous optimisation of a mathematical optimisation problem involving more than one objective. MOO is a multiple criteria decision-making technique that generates more than one solution to the problem. The decision-maker needs to decide which objectives are most important. Different MOO methods are discussed by Marler et al. [11].
MOO can be used when two objectives such as low maintenance cost and high machine efficiency need to be satisfied. The best solution is chosen depending on other constraints, such as the budget of the organisation.
4.3 Cost-benefit analysis (CBA)
A cost-benefit analysis compares the costs and benefits of a project to determine whether the project is a good and feasible investment. A basis is established for comparing different projects to determine whether the benefits outweigh the costs, and if so, by how much.
Willmott et al. [12] consider four types of losses that affect the cost-benefit analysis: equipment, transformation, material, and management.
An example of asset management is to compare the costs and benefits of fixing a broken machine or of buying a new one. The benefits are usually also shown in terms of monetary value.
The cost of fixing a broken machine can be compared with the cost of buying a new machine. Benefits can include the efficiency of the new or fixed machine, insurance costs, and operating costs. The cost associated with each option is compared with the other, and the best option is chosen.
4.4 Economic order quantity (EOQ)
Economic order quantity determines the optimal number of units that need to be ordered to keep the total inventory holding cost and ordering cost to a minimum. It is discussed by Mohammad et al. [13].
Specific assumptions need to be made to be able to conduct the analysis. The ordering cost is constant, the rate of demand is known and spread evenly throughout the year, the lead time is fixed, the purchase price of the item is constant (i.e. no discount is available), the replenishment is made instantaneously, the whole batch is delivered at once, and only one product is involved.
The following equations are used to facilitate the analysis:
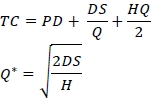
TC total cost
Q order quantity
Q* optimal order quantity
P purchase unit price
D annual demand quantity
S fixed cost per order
H annual holding cost per unit
4.5 Simulation
Simulation is a powerful management science technique that is widely used to imitate the operation of a real-world process or system over time. Simulation is used to solve complex, real-world problems, and is mostly done with software packages (as described by James [14]) that include Simio, Arena, and ProModel. Simulation can be used for most optimisation problems, but it requires training and can be costly.
4.6 Criticality analysis (CA)
Criticality analysis is performed to determine the severity of the consequences of a failure. According to Taylor et al. [15], a criticality analysis can take a qualitative or quantitative approach, depending on the available data. The criticality analysis forms part of the failure mode, effect, and criticality analysis (FMECA). The quantitative criticality analysis is more applicable to numerical decision-making, and will be discussed in detail.
A worksheet is created (as described by Taylor et al. [15]) to aid the quantitative criticality analysis. The worksheet is used to identify and compare the different failure modes. The purpose of this worksheet is to identify and rank potential failure modes, causes, and effects. A combination of the severity and frequency of failures is used to rank and identify critical assets. The probability of failure is also classified into five levels, as discussed by Taylor et al. [15].
4.7 Monte Carlo simulation
Monte Carlo simulation is a computerised mathematical technique used to aid decision-making. The Monte Carlo simulation accounts for risk, and provides a range of possible outcomes and probabilities for a specific choice of action. It is discussed by Benbow et al. [16]. The use of random numbers and probability distributions in each iteration of calculations makes Monte Carlo simulations ideal for instances when decisions need to be made under uncertainty. Monte Carlo simulation can, for example, be used to determine the optimal time to conduct maintenance on a machine.
4.8 Network models
Asset management rarely deals with assets or asset systems in isolation. Network models can be used to account for the (often complex) relationships between assets. A network consists of nodes and arcs. A node is a set point that can represent an asset or an asset state, and an arc is used to connect the different nodes and represent a possible direction of motion. Four specific network models are described by Winston [10]:
1. Shortest-path problems
2. Maximum-flow problems
3. CPM-PERT project-scheduling models
4. Minimum-spanning tree problems
Network models are also applicable when maintenance costs increase and the trade-in price of the old machine decreases as the age of a machine increases. The price of a new machine should also be included. The goal is then to minimise the net cost incurred for a predetermined time period. It is then possible to determine when it would be best to trade the machine in for a new one.
4.9 Forecasting models
Forecasting methods attempt to predict the future values of variables by drawing on past data to establish the relationship between the dependent variable and one or more independent variables. Four forecasting models should be considered: the moving-average forecasting method, simple exponential smoothing, Holt's method (exponential smoothing with a trend), and Winter's method (exponential smoothing with seasonality). For a detailed description and examples on forecasting, refer to Winston [10].
4.9.1 Moving-average forecasting methods
The moving average calculates the average of the last N observations.
ft,1 = average of the last N observations
ft,l = average of xt, xt_l, xt_2, ..., Xt-N+1
The value of N is determined by calculating the mean absolute deviation (MAD) and the forecast error.
et (forecast error) = xt - (forecast error xt)
MAD is calculated by averaging the absolute values of all e't.
4.9.2 Simple exponential smoothing
Simple exponential smoothing is used when a time series fluctuates about a base level.
The key exponential smoothing equation is
Aτ = αχτ + (1 - α)At-1
where
Aτ - smoothed average over a time series after observing xt
α- smoothing constant (0 < α< 1)
A0 is chosen as the observed value for the period immediately preceding period 1.
The forecast error is calculated with
et = xt-At-1
and from here the following equation is obtained:
At = At-1 + α(xt - At-1) = At-1 + αet
4.9.3 Holt's method: Exponential smoothing with trend
Holt's method is primarily used when a linear trend is observed without seasonality. Three equations are important when using Holt's method:
Lt = αxt + (1 -α)(Lt-1 + Tt-1)
Tt = β(Lt-Lt-1)+ (1 -β)Tt-1)
and finally
ft,k = Lt + kTt
Lt- estimate of the base level
Tt- estimate of the per-period trend
α and β - smoothing constants between 0 and 1
4.9.4 Winter's method: Exponential smoothing with seasonality
Winter's method is used when a trend and seasonality is observed. Four equations are important when using Winter's method.
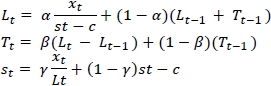
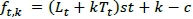
Lt and Tt have the same meanings as in Holt's method, and c is the number of periods in the length of the seasonal pattern; st is an estimate of a seasonal multiplicative factor for month t obtained after observing xt.
Forecasting can be used to predict machine failures if enough past failure data is available.
4.10 Utility theory and decision trees
Winston [10] describes utility theory and decision trees as methods to aid decision-making under uncertainty. Utility represents a preference of one event over another. The utility theory is defined by an action, the probability of that action occurring, and the reward received if the action occurs. The Von Neumann-Morgenstern concept is a popular aid in decision-making. This concept involves a lottery that is represented by a tree, as seen in Figure 1.
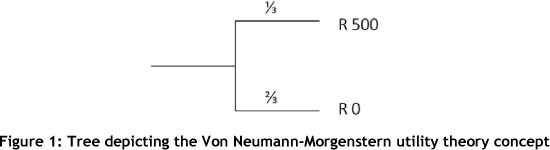
The utility theory makes it possible to decide between two lotteries by using a simple calculation:
L - ρA + (1 -ρ)β
For many possible options, a more general equation is identified:
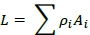
Decision trees are used to determine the optimal solution for large complex decision problems. Decision trees follow the same concept as the utility theory by making use of probabilities, actions, and rewards (as seen in Figure 1). Decision trees are, however, divided into decision forks and event forks. Decision forks represent a point in time where a decision needs to be made, and event forks show where outside forces determine the outcome of the event.
4.11 Log-linear and power law methods
The log-linear and power law methods are two formats of the non-homogeneous Poisson process (NHPP) as discussed by Vlok [18]. These methods are a good representation of repairable systems.
Both methods make use of a series of equations that include specific parameters that need to be calculated. These equations can determine the expected number of failures between two instances, the mean time between failure (MTBF), reliability of the system, the confidence band, the residual life estimation, and the long-term cost optimisation.
Parameter estimation for repairable systems can be calculated with the least-square parameter or the maximum likelihood method.
It is important to remember that the limitations of these failure analysis techniques lie in the assumptions made, and not in the techniques themselves.
Other metrics that can also be used are MTBF, MTTF (mean time to failure), MFOP (maintenance free operating period), and FIT (failure in time). Stanley [19] gives a detailed description of these metrics.
Both of these methods (log-linear and power law) can be used to calculate the expected arrival time of the next failure when the inter-arrival times of previous failures have been recorded.
4.12 Weibull distribution
The Weibull distribution is widely used, due to its flexibility in providing good models for small sample sizes, as well as a broad variety of data sets, as noted by Dodson [20].
The Weibull distribution can be used to analyse non-repairable systems. According to Vlok [18], the Weibull distribution can be used when neither the order of events nor the specific machine responsible for these events is of importance.
The Weibull distribution can also be used to predict the residual life of a specific unit, as well as the confidence levels around the predicted residual life.
Furthermore, the Weibull distribution can be used to predict the long-term cost of a specific unit, and can lead to the optimisation of the long-term cost.
4.13 Geographic information system (GIS)
Geographic information system (GIS) is the integration of cartography, statistical analysis, and database technology. It is an information system that captures, integrates, stores, manipulates, analyses, shares, manages, and displays geographic information to support decision-making (as discussed by ESRI [9]). GIS results in a number of benefits, including:
1. cost saving and increased efficiency;
2. better decision-making;
3. improved communication;
4. better record keeping; and
GIS can be used to set up a database to locate all the organisation's assets in order to manage them.
4.14 Pareto principle
The Pareto principle is also known as the 80-20 rule. It states that 80% of the effects come from 20% of the causes. The Pareto principle is related to the Pareto efficiency. The Pareto principle can be applied to optimisation efforts and to occupational health and safety, to aid the process of hazard prioritisation. Gryna et al. [21] give more detail on the Pareto principle.
The Pareto priority index (PPI) helps to evaluate each project. A high value suggests high priority. The PPI is defined as follow:
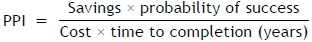
5 NUMERICAL ILLUSTRATION
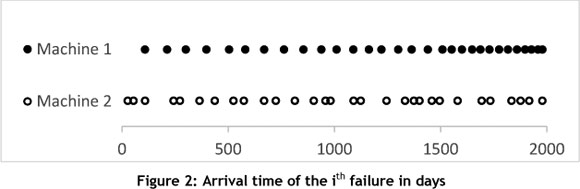
This section makes use of an example to illustrate the benefits of the methods discussed above. A useful first step is to do a quick criticality analysis of the organisation's assets (Section 3.1). If sufficient data is not available, this can be achieved by consulting experts and experienced operators. Suppose the criticality analysis identified Machine 1 and Machine 2 as the most critical assets. The inter-arrival time between failures (measured in days) was recorded for each machine as shown below:
Because these machines are critical to the organisation, it is important to know when they will fail - or, preferably when to intervene preventatively to avoid costly, unexpected failure. Some of the techniques described in the previous section will be used to analyse the data. The simplest form of analysis is to calculate the mean, which in this case gives the MTBF, a commonly-used benchmark of the frequency of machine failures (see Section 3.1 for simpler descriptors of data). For this example, the MTBF is exactly the same (66 days) for both machines over their lifetime of six years.
This simple calculation is a first indication of how frequently to expect failures or how frequently to do preventative maintenance. Unfortunately, this is also the extent of analyses performed by some organisations. They calculate MTBF and then base their maintenance schedule on this number. This is a mistake. As can be seen in Figure 2 above, MTBF does not present the whole picture: Machine 1's failure rate clearly increases over time, while Machine 2's failure rate is seemingly random.
If all that is required is a rough estimate of how many times a machine will fail in its lifetime, then MTBF is a good estimate. The number of failures can then also be multiplied by the cost of repairing a machine, to get an estimate of the life cycle cost. If, for example, it costs R15,000 to repair Machine 1 and R20,000 to repair Machine 2, and both machines have a MTBF of 66, the total cost of maintenance (ignoring the time-value of money) will be R990,000 and R1,320,000 respectively. This estimate allows an organisation to determine where best to spend resources. In this case it would be logical to focus maintenance activities on Machine 2, as it is the more costly of the two.
To decrease the number of times that Machine 2 fails, and thus to reduce costs, it is necessary to model the inter-arrival times of failure to predict better when it will fail, and thus when to perform preventative maintenance. A popular choice for reliability modelling is the Weibull distribution (see Section 4.12, Weibull distribution). The Weibull shape parameter for Machine 2's inter-arrival time between failures was determined to be 2.3 and the scale parameter 74.9.
Assume that an organisation decided only to calculate MTBF and used it to decide that preventative maintenance should be performed five days before the machine's expected failure; thus every 61 days. According to the model described above, the probability of Machine 2 surviving for 61 days is 53.5 per cent. If we assume that preventative maintenance costs R2,500 and takes two hours, and that the time to replace a broken machine is eight hours and costs R20,000, then the expected long-term maintenance cost for this strategy is R10,635. The same model can be used to calculate an optimal preventative maintenance strategy that will minimise this long-term cost. For Machine 2, the optimal preventative maintenance interval is 29 days, resulting in a long-term cost of R4,350.
As shown above, a more in-depth analysis can save an organisation a lot of money. But this does not mean an in-depth analysis of every machine is required, as this can be very time-consuming and costly. Figure 2 shows that Machine 1 has a predictable trend. This can be exploited to reduce the effort of analysis by applying a simple forecasting model, as described in Section 4.9. If there are several machines of the same make as Machines 1 and 2, care must be taken to include the relationships when analysing the system. When machines work in series, for instance, one machine breaking might damage the machine next to it. To overcome these complexities, it is recommended to make use of a network model (Section 4.8) or simulation (Section 4.5). When it is not just the cost that must be reduced, multi-objective optimisation might also be required.
6 SUMMARY AND CONCLUSION
This article describes an analysis of the requirements stipulated in PAS 55 and the ISO 55000 series where quantitative analysis and numerical methods are needed. It also identifies methods that can address the specifications, and provides basic summaries of the methods for convenience.
Asset management practitioners often shy away from the complexity of numerical analysis, but with the momentum that PAS 55 has gained over the last few years, and the keen anticipation of ISO 55000, the asset management community will be compelled to incorporate quantitative analysis as part of its trade.
The research in this article suggests that the tools and methods required to address the quantitative specifications in PAS 55 and the ISO 55000 series exist. It is left to the current generation of asset managers to incorporate these tools and methods into their field as part of standard operating procedure.
REFERENCES
[1] British Standards Institution 2008. Part 1: Specification for the optimized management of physical assets. PAS 55: Asset Management. [ Links ]
[2] International Standards Organization 2013. ISO 55000: Asset management - Overview, principles and terminology. [ Links ]
[3] International Standards Organization 2013. ISO 55001: Asset management - Requirements [ Links ]
[4] International Standards Organization 2013. ISO 55002: Asset management - Guidelines on the application of ISO 55001 [ Links ]
[5] Tukey, J. 1977. Exploratory data analysis. Reading, MA, 231. [Online]. Available: http://xa.yimg.com/kq/groups/16412409/1159714453/name/ExploratoryDataAnalysis.pdf. [Accessed on 11 February 2013]. [ Links ]
[6] Fayyad, U., Piatetsky-Shapiro, G. & Smyth, P. 1996. From data mining to knowledge discovery in databases. AI magazine, 17, 37 [Online]. Available: http://www.aaai.org/ojs/index.php/aimagazine/article/viewArticle/1230. [Accessed on 11 February 2013]. [ Links ]
[7] Barringer, H. 2003. A life cycle cost summary. In International Conference of Maintenance [Online]. Available: http://www.barringer1.com/pdf/LifecycleCostSummary.pdf. [Accessed on 11 February 2013]. [ Links ]
[8] Stump, E.J. 1988. An application of Markov chains to life-cycle cost analysis. Engineering Costs and Production Economics [Online] Available: http://www.tandfonline.com/doi/abs/10.1080/10157891.1987.10472807. [Accessed on 11 February 2013]. [ Links ]
[9] ESRI. 2007. GIS for sustainable development. [Online] Available: http://www.esri.com/library/bestpractices/sustainable-development.pdf. [Accessed on 11 February 2013] [ Links ]
[10] Winston, W.L. 2004. Operations research: Applications and algorithms. Brooks/Cole, Cengage Learning. [ Links ]
[11] Marler, R. & Arora, J. 2004. Survey of multi-objective optimization methods for engineering. [Online]. Available: http://www.cse.ohio-state.edu/-parent/classes/788/Au10/OptimizationPapers/MultiObjective/journal_survey.pdf. [Accessed 12 February 2013]. [ Links ]
[12] Willmott, P. & McCarthy, D. 2001. Total productive maintenance TPM - A route to world-class performance. Butterworth-Heinemann. [ Links ]
[13] Jaber, M.Y. & Bonney, M. 1999. The economic manufacture/order quantity EMQ/EOQ and the earning curve: Past, present, and future. International Journal of Production Economics., Vol. 59, pp 93-94 [ Links ]
[14] Bekker, J. 2012. Short notes on aspects of discrete-event simulation., Presented as part of Simulation 414, Industrial Engineering, University of Stellenbosch [ Links ]
[15] Dyadem Press. 2003. Guidelines for failure mode and effects analysis for automotive, aerospace and general manufacturing industries. Taylor & Francis . [ Links ]
[16] Benbow, D.W. & Broome, H.W. 2008. The certified reliability engineer handbook. ASQ Quality Press. [ Links ]
[17] Gerstner, T. & Griebel, M. 2008. Encyclopedia of quantitative finance. Wiley. [ Links ]
[18] Vlok, P.J. 2012. Introduction to elementary statistical analysis of failure time data: Long term cost optimization and residual life estimation., Published as part of the Quality Management 444 course presented at the Department of Industrial Engineering, University of Stellenbosch. [ Links ]
[19] Stanley, S. 2011. MTBF, MTTR, MTTF & FIT: Explanation of terms. Tech. Rep., IMC Networks. [Online]. Available: http://www.imcnetworks.com/Assets/DocSupport/WP-MTBF-0311.pdf. [Accessed 12 February 2013]. [ Links ]
[20] Dodson, B. 2006. The Weibull analysis handbook. Quality Press. [ Links ]
[21] Gryna, F.M., Chua, R.C.H. & DeFeo, J.A. 2005. Juran's quality planning and analysis for enterprise quality. McGraw-Hill. [ Links ]
* Corresponding author














