Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.3 Pretoria Nov. 2013
GENERAL ARTICLES
The robust min-max newsvendor problem with balking under a service level constraint
Taesu CheongI; Kysang KwonII
IDepartment of Industrial and Systems Engineering. National University of Singapore, Singapore. isects@nus.edu.sg
IIOptimization & Analytics Lab. SK Innovation, Seoul, South Korea. kskwon@sk.com
ABSTRACT
In this paper we study an extension of a classic newsvendor model with balking under a service-level constraint. We also relax the assumption that the demand distribution is fully available to a decision-maker; we assume that only the mean and variance of the demand distribution are known, and discuss the procedure for determining the optimal order quantity for the concomitant model. We further extend our base model to two different cases: (i) when the fixed ordering cost is included, and (ii) when yield is uncertain. We illustrate the solution procedures for each case with numerical examples. Moreover, we discuss the performance and robustness of the approach through randomly generated test instances, and perform a numerical sensitivity analysis to evaluate the impact of the changes of a targeted fill-rate and variances of a demand distribution.
OPSOMMING
Die navorsing handel oor uitbreiding van die klassieke koerantverkoopsmodel met weiering teen die agtergrond van 'n diensrandvoorwaarde en bekende gemiddelde en variansie van vraag. Die bogenoemde uitbreiding sluit ook as alternatief die bestelkoste vir onsekere vraag in. Die modelprestasie word gedemonstreer via 'n reeks van syfervoorbeelde.
1 INTRODUCTION
The newsvendor model has served as one of the fundamental models in stochastic inventory control problems [17], and has been used in numerous applications including production/inventory control, supply chain coordinations, option pricing and contract, and yield management. A comprehensive literature survey of the model can be found in Khouja [8] and Petruzzi & Dada [16].
It is well known that newsvendor-type problems can easily be solved when the full demand distribution is available, and that they have an elegant solution structure called the critical fractile solution [17]. However, in practice it is often found that there may be weak or no justification that demand should follow a certain distribution. Thus a robust min-max (or distribution-free) approach for the newsvendor model, pioneered by Scarf [18], has been proposed, and various forms of extensions have been discussed in the extant literature [1,5,6,9,11,13]. It allows us to make a decision about the worst case distribution when only the mean and variance information for demand can readily be captured or estimated from the data. This is indeed a risk-averse approach [15].
In this paper we specifically consider a robust min-max approach for an extension of the newsvendor model with customer balking and a service-level constraint. It is often observed that demand for a product can be influenced by product availability on the shelf. For example, customers may not purchase items if the inventory on the shelf is below a certain level. We often observe such customer behaviour in our daily life, especially for perishable products such as dairy products, fruits, or vegetables in grocery stores. If there are few items left on the shelf, customers are reluctant to buy them, possibly thinking that the products might not be in as good shape as they should to be, might no longer be fresh, or might be close to their expiry date. This is referred to as 'balking' [14]. Thus, in this study, if the inventory level drops below a threshold K, we assume that customers may balk with probability 1 - γ, and so demand is deflated by γ.
Moon & Choi [11] and Liao et al. [9] are the researchers who are most relevant to this study. Moon & Choi [11] provide the optimal order quantity that minimises the expected cost against the worst possible distribution of the demand with mean µ and variance σ2 with balking. However, they disregard the impact of lost sales, which is typically captured by the shortage cost in a newsvendor setting. Most of all, the phenomenon of customer balking exacerbates the magnitude of lost sales. It is thus reasonable and important to incorporate this aspect to reflect customer balking effects better. Liao et al. [9] examine a simple extension of the model in Moon & Choi [11] by also incorporating a linear lost-sales penalty cost in the profit function. However, the main concern about this extension is that, in many cases, the lost sales penalty is difficult to estimate in practice, since it includes intangible factors such as loss of goodwill or customers. In order to handle the lost sales effect in a tractable manner, we incorporate the notion of service level (or fill-rate) into the decision framework, and so our model is more viable in practice than the earlier models in the literature.
The main contribution of this work is that we incorporate the service level constraint for considering the lost-sales effect due to the understocking of items and customer balking, and we provide a practical guide to the interdependence of retail shelf management and associated inventory control in the broader sense. As Liao et al. [9] point out, the previous distribution-free newsvendor model with balking neglected this aspect, despite the significance of lost sales. They therefore attempt to consider this aspect with the explicit lost-sales penalty term in the profit function - although they admit that the penalty cost is hardly ever estimated in practice. In this paper we aim to discuss the optimal ordering policy for the robust min-max single-period model with balking under a fill-rate constraint, to improve the practicality of the concomitant model. Furthermore, we present two extensions of the base model: one including a fixed ordering cost, and the other assuming yield uncertainty. We note that, in the shipment of perishable goods, the amount that perishes during storage and transit in the United States is 10 to 15 per cent of perishable freight tonnage [10]. The percentages are even higher in countries that do not have a sufficiently developed cold chain infrastructure [3]. Thus the extension for yield uncertainty also readily captures the aspect in which the exact random shrinkage distribution during a shipment is almost never estimated. (Many items in a grocery store are perishable and are subject to freight shrinkage during a shipment.) We then evaluate the performance of the concomitant robust min-max model with a set of randomly generated instances, and discuss the conditions under which the robust min-max approach presented in this paper can be recommended for use by practitioners in the retail industry.
The remainder of this paper is organised as follows. Section 2 presents the base model with balking and a service level constraint, using cases where the exact demand distribution is either available or is not available. Sections 3 and 4 discuss the extensions of the base model in Section 2: the fixed ordering cost case and the random yield case respectively. Section 5 presents computational experiments for evaluating the performance and checking the robustness of distribution-free models. We conclude the discussion in Section 6.
2 BASE MODEL
We mainly adopt the notation presented in Moon and Choi [11] (listed in Table 1):
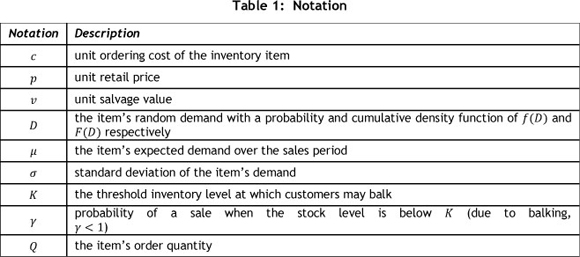
Then the expected profit function πF(Q) can be expressed as
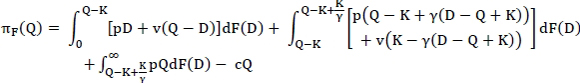
which has explicit dependence on the demand distribution F(D) with mean µ and variance σ2. As presented in the equation above, there are three possible cases, depending on the demand realisation:
a. 0 < D < Q - K : the resulting inventory level after the demand is met is still above the threshold K, and so no change occurs in the sales rate.
b. Q - K < D < Q - K + K/γ: the stock level becomes less than the threshold K, and so the amount of Ď = (Q - K) + γ(D - (Q - K)) is the realised demand size, and the amount of Q - Ď = K - γ(D - Q + K) will be salvaged at the end of the selling season.
c. Q - K + K/γ < D: all the ordered items must be sold out; so a shortage of items occurs with the amount of D - (Q - K + K/γ).
As mentioned earlier, we introduce the service level constraint in our decision model. Service level or fill-rate β is defined as β = 1 - Expected lost sales/Expected total demand, which is the average fraction of demand that is satisfied immediately from stock on the shelf [12]. Let ξ be the desired service level, and the decision-maker determines the optimal order quantity under the constraint β ≥ ξ. We note that, in the concomitant model, the expected lost sales equal ∫∞q-K+K/γ(D - (Q - K + K/γ))dF(D), and so the fill-rate β(Q), which is a function of an order quantity Q, is given as β(Q) = 1 - (∫∞q-K+K/γ(D - (Q - K + K/γ))dF(D)/µ) ≥ξ.
Under the assumption that the demand distribution F(·) is fully available to the decisionmaker, the optimal order quantity Q*F is determined as follows:
Q*F = arg maxQ {πF(Q): ∫∞Q-K+k/γ(D - (Q - K + K/γ))dF(D) < (1 - ξ)µ}.
We note that πF(Q) can be rewritten as
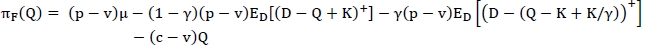
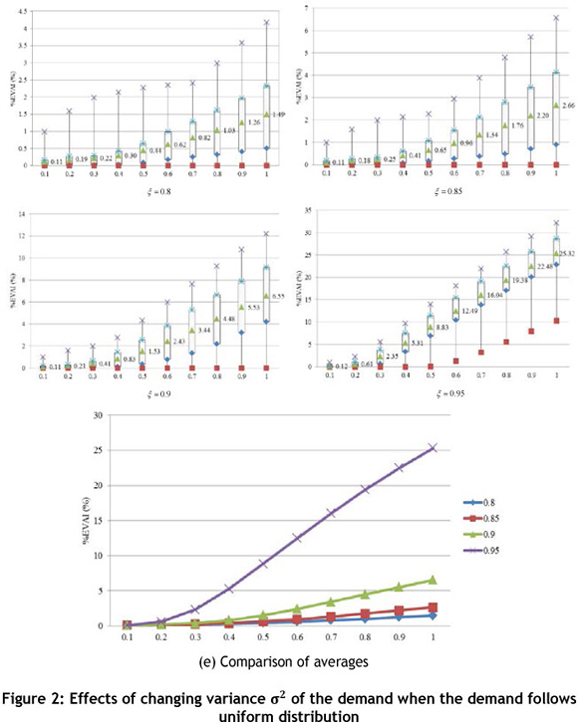
where (a)+ = max{a,0}. Let
CF(Q) = (1 - γ)(p - v)Ed[(D - Q + K)+] + γ(p - v)Ed [(D - (Q - K + K/γ))+] + (c - v)Q so that πF(Q) = (p - v)µ - CF(Q). Note that maximising πF(Q) is equivalent to minimising CF (Q), and it can easily be verified that CF (Q) is convex in Q (by evaluating the second-order derivative of CF(Q) with respect to Q).
Similarly, the fill-rate constraint can be also expressed as
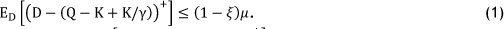
Let SLF(Q) = Ed [(D - (Q - K + K/γ))+] - (1 - ξ)µ. It can also easily be shown that SLF(Q) is convex in Q so that the feasible solution set ΩF = {Q ≥ 0:SLF(Q) < 0} is convex.
Consequently, if the demand distribution information F(·) is available, the optimal order quantity QF is determined by solving the constrained convex optimisation problem minQєΩFCF (Q). We now discuss how to determine the optimal order quantity Q*F when the exact demand distribution information is known. Since CF (Q) is convex in Q, as mentioned earlier, we examine the first-order condition:†
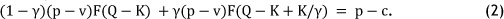
† Let H(Q) = ED [{D - h(Q))+] = ∫∞h(Q)(D - h(Q))dF (D) where h(Q) is a function of Q. Then dh(Q)/dQ = - dh(Q)/dQ [1-F(h(Q))].
Let QF be Q satisfying Equation (2). If SLF(Q'F) < 0 (or Q'F є ΩF), then Q*F = Q'F. Otherwise the optimal order quantity must be a boundary point in ΩF. It can be shown that the fill-rate β, which is a function of Q, strictly increases in Q. Then the conditions that (i) CF (Q) is convex in Q and (ii) 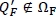 imply that Q*F should satisfy the fill-rate constraint with equality (i.e. SLF(Q*F) = 0). Algorithm 1 summarises the discussion above.
imply that Q*F should satisfy the fill-rate constraint with equality (i.e. SLF(Q*F) = 0). Algorithm 1 summarises the discussion above.

So far we have discussed the newsvendor model with balking and a service level constraint under the full demand distribution information. We now present the corresponding robust min-max model in which there is no assumption about the demand distribution apart from the mean µ and variance σ2. Let Г(µ, σ) be the set of all possible demand distributions with mean µ and variance σ2. In the robust min-max model, we derive an upper-bound function C(Q) such that 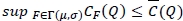 for all Q ≥ 0, and the following lemma provides the theoretical basis for the derivation of the upper bound function:
for all Q ≥ 0, and the following lemma provides the theoretical basis for the derivation of the upper bound function:
Lemma 1. Let g(Q) be a random variable, which is a function of Q and independent of D, E[g(Q)] be the expectation of g(Q), and Var[g(Q)] be the variance of g(Q).
a. Then,
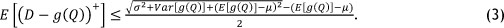
b. Suppose that g(Q) is a constant (i.e. E[g(Q)] = g(Q) and Var[g(Q)] = 0). Then, for any g(Q), there is always a demand random variable D whose distribution is FD ЄГ(µ, σ) where the upper bound (right-hand side of Equation (3)) is tight.
Proof. See Appendix A.
Thus, (i) when  , and (ii) when
, and (ii) when 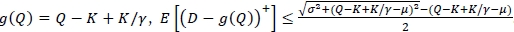 . Based on the results, a possible candidate of
. Based on the results, a possible candidate of 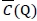 is
is
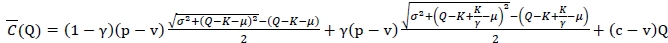 . The first and second derivatives of
. The first and second derivatives of 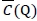 in Q are
in Q are
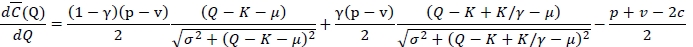
and
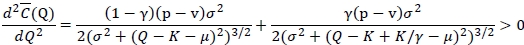
respectively by using the Leibniz rule. Since 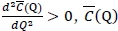 is convex in Q.
is convex in Q.
We next consider the fill-rate constraint when there is no assumption about the demand distribution. Due to the result from Lemma 1,
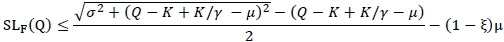
and let 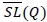 be the function of the right-hand-side of the inequality above. We identify the constraint
be the function of the right-hand-side of the inequality above. We identify the constraint 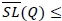 as the distribution-free fill-rate constraint. We note that Lemma 1(ii) implies that there is a demand distribution F satisfying
as the distribution-free fill-rate constraint. We note that Lemma 1(ii) implies that there is a demand distribution F satisfying 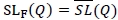 . Since it can be verified that
. Since it can be verified that 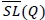 is also convex in Q, the set
is also convex in Q, the set 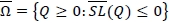 is convex, and moreover
is convex, and moreover 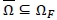 for all F Є Г (µ,σ) due to the relation
for all F Є Г (µ,σ) due to the relation 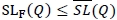 .
.
Therefore, the robust min-max model is to determine Q that minimises the upper bound function 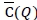 over the set
over the set 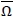 , say,
, say, 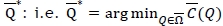 . Note that
. Note that 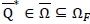 for all F Є Г(µ,σ). We now discuss how
for all F Є Г(µ,σ). We now discuss how 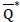 can be determined, and we can apply the same argument that we made for the case where the exact demand distribution is known because both
can be determined, and we can apply the same argument that we made for the case where the exact demand distribution is known because both 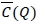 and
and 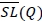 are convex in Q. Thus we present the simple solution procedure to determine
are convex in Q. Thus we present the simple solution procedure to determine 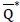 for this robust min-max model in Algorithm 2.
for this robust min-max model in Algorithm 2.

We note that Moon & Choi [11] suggested the notion of the expected value of additional information (EVAI) to measure the additional value of acquiring the exact demand distribution. In this case, the expected marginal value of knowing the exact demand distribution relative to the lack of distribution information can be expressed as EVAI = 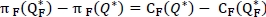 , and we introduce
, and we introduce 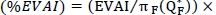 100 (%), which is the percentage loss due to the lack of demand distribution information, to evaluate the performance of the robust min-max approach.
100 (%), which is the percentage loss due to the lack of demand distribution information, to evaluate the performance of the robust min-max approach.
Example 1. For the illustration, we assume that the mean and the standard deviation of the demand are µ = 800 and σ = 150 respectively. The demand deflation threshold and the corresponding deflation rate are K = 200 and γ = 0.8 respectively. The cost parameters are as follows: the unit ordering cost is c = $35, the unit retail price is ρ = $60, and the unit salvage value is v = $15. Lastly, let the target fill-rate be ξ = 0.85. Suppose that the demand distribution is given as U(540,1060), whose mean and standard deviation are 800 and 150 respectively. The optimal order quantity Q*Ffor the distribution is approximately 829; on the other hand, the optimal quantity 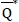 for the robust min-max model is close to 804. Since CF(Q*F) ≈ $19319.764 and
for the robust min-max model is close to 804. Since CF(Q*F) ≈ $19319.764 and 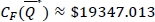 , (EVAI) is $27.249 and (%EVAI) ≈ 0.141(%), indicating that the loss due to the lack of demand information is insignificant. We now increase the fill-rate to ξ = 0.95. Then
, (EVAI) is $27.249 and (%EVAI) ≈ 0.141(%), indicating that the loss due to the lack of demand information is insignificant. We now increase the fill-rate to ξ = 0.95. Then 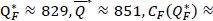 $19319.764, and
$19319.764, and 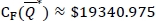 . Thus (EVAI) = $21.211 and (%EVAI) ≈ 0.109(%). We note that, as the desired service level ξ is increased from 0.85 to 0.95, the order quantity obtained from the first-order condition of the model having full demand information still satisfies the corresponding fill-rate constraint (i.e. Equation (1)), and thus Q*F remains at the same value, 829. On the other hand, the order quantity satisfying the first-order condition of the robust min-max model eventually violates the distribution-free fill-rate constraint, and so
. Thus (EVAI) = $21.211 and (%EVAI) ≈ 0.109(%). We note that, as the desired service level ξ is increased from 0.85 to 0.95, the order quantity obtained from the first-order condition of the model having full demand information still satisfies the corresponding fill-rate constraint (i.e. Equation (1)), and thus Q*F remains at the same value, 829. On the other hand, the order quantity satisfying the first-order condition of the robust min-max model eventually violates the distribution-free fill-rate constraint, and so 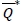 is changed from 804 to 851. In this example, (%EVAI) decreases when ξ is increased from 0.85 to 0.95, and we note that this is not a typical pattern. Depending on the parameter values, the changes in (%EVAI) may not have any consistent pattern as ξ, increases; however, as presented in Section 5, (%EVAI) generally increases in ξ.
is changed from 804 to 851. In this example, (%EVAI) decreases when ξ is increased from 0.85 to 0.95, and we note that this is not a typical pattern. Depending on the parameter values, the changes in (%EVAI) may not have any consistent pattern as ξ, increases; however, as presented in Section 5, (%EVAI) generally increases in ξ.
3 THE FIXED ORDERING COST CASE
We now discuss an extension of the base model given in Section 2. Suppose (i) that whenever the retailer procures any positive number of items (i.e. Q > 0), a fixed cost A is charged; and (ii) that the retailer owns an inventory I ≥ 0 initially where possessing the initial inventory is irrelevant to any cost. It is well known that the classic newsvendor model with a fixed ordering cost follows the so-called (s,S) inventory replenishment policy [4]. However, it will be shown that the extension we examine in this section does not follow the (s,S) policy because of the fill-rate constraint.
Let S be the inventory level after receiving an order (i.e. S = I + Q). Then the expected total profit function under the exact demand information πF(1)(S) is expressed as
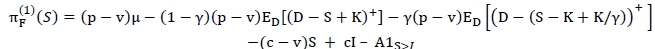
with the fill-rate constraint Ed [(D - (S - K + K/γ))+] < (1 - ξ)µ where 1α is an indicator function. The corresponding robust min-max optimisation model is 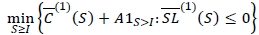
where
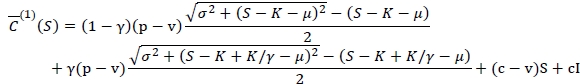
and
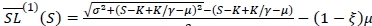
Let 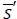 be the minimiser of the robust min-max expected cost function
be the minimiser of the robust min-max expected cost function 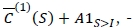 that is,
that is,  satisfies the following first-order condition:
satisfies the following first-order condition:
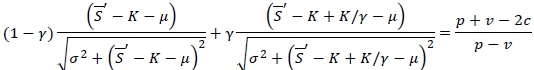
due to the convexity of 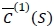 . In addition, there is a unique
. In addition, there is a unique 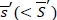 satisfying the equation
satisfying the equation 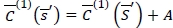 .
.
The fact that 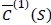 is strictly convex and is not bounded from above ensures the existence of such an
is strictly convex and is not bounded from above ensures the existence of such an 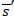 . We also note that
. We also note that 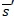 corresponds to the reorder point in a (s, S) policy, and without the fill-rate constraint, the pair
corresponds to the reorder point in a (s, S) policy, and without the fill-rate constraint, the pair 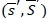 forms such a policy, because the retailer places an order up to
forms such a policy, because the retailer places an order up to 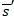 only when
only when 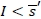 due to the fact that
due to the fact that 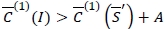 for
for 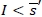 , and
, and 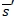 is the break-even point.
is the break-even point.
We now discuss how to determine the optimal order quantity 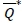 for this robust min-max model. Let
for this robust min-max model. Let 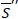 be a S satisfying the distribution-free fill-rate constraint with equality, or
be a S satisfying the distribution-free fill-rate constraint with equality, or 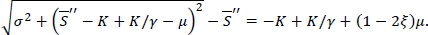
We note that the fill-rate constraint 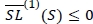 is equivalent to
is equivalent to
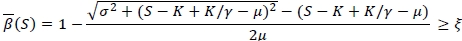
and it can be easily verified that the distribution-free fill-rate function 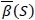 is increasing in S. Thus we can interpret
is increasing in S. Thus we can interpret 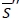 as the minimum inventory level required for the targeted service level in the expected sense. Given
as the minimum inventory level required for the targeted service level in the expected sense. Given 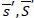 , and
, and 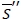 , we can consider the following three cases:
, we can consider the following three cases:
a. If 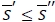 , both
, both 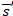 and
and 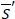 satisfy the fill-rate constraint due to the property of
satisfy the fill-rate constraint due to the property of 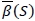 , and so the model becomes an unconstrained optimisation problem. The optimal order quantity is determined according to the
, and so the model becomes an unconstrained optimisation problem. The optimal order quantity is determined according to the 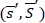 policy:
policy:
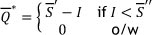
b. If 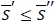 , the inventory level after receiving an order should be equal to
, the inventory level after receiving an order should be equal to 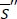 due to the convexity of the objective function
due to the convexity of the objective function 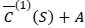 . Thus
. Thus 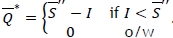 .
.
c. Otherwise, the inventory level after receiving an order should be at least greater than or equal to 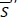 . If
. If 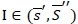 , the order needs to be placed up to
, the order needs to be placed up to 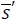 because
because 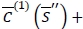
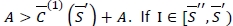 , it is unnecessary to place an order because
, it is unnecessary to place an order because  is convex and
is convex and 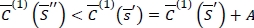 . This suggests the following ordering policy:
. This suggests the following ordering policy: 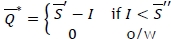
Algorithm 3 summarises the procedure for determining the optimal order quantity for the robust min-max model with a fixed ordering cost.

Example 2. Using the parameter values in Example 1, we assume that the fixed ordering cost is A = $600. Then, if 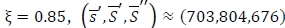 . Since
. Since 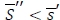 , the optimal policy for this robust min-max model is (804 -I) if I < 703, and 0 otherwise. If we increase the value of ξ from 0.85 to 0.9,
, the optimal policy for this robust min-max model is (804 -I) if I < 703, and 0 otherwise. If we increase the value of ξ from 0.85 to 0.9, 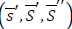 is changed into (703,804,740), and so the optimal policy becomes (804 -I) if I < 740, and 0 otherwise. Lastly, if
is changed into (703,804,740), and so the optimal policy becomes (804 -I) if I < 740, and 0 otherwise. Lastly, if 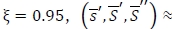 (703,804,851). Since
(703,804,851). Since  , the optimal policy in this case is (851 - I) if I < 851, and 0 otherwise.
, the optimal policy in this case is (851 - I) if I < 851, and 0 otherwise.
4 THE RANDOM YIELD CASE
In this section we consider the case in which the ordered or produced quantity Q is not perfect. This type of problem is in the class of random yield models [19]. We especially assume the multiplicative random yield model that appears frequently in the literature [2,7]. We note that Jung & Lee [6] present a robust newsvendor model with balking and random yield; however, unlike ours, their model assumes that the yield distribution follows a binomial distribution. Let ρ be a random variable with support on (0,1] whose probability (cumulative) density function is y(ρ) (Y(ρ)). In addition, we denote µρ and σ2ρ as the expectation and variance of the random variable ρ respectively. We assume that ρ is independent of the order quantity Q and of the demand D. In this random yield case, it is assumed that out of Q items, only ρQ can be sellable or in a good shape. Then the expected profit function πF(2)(Q) can be expressed as
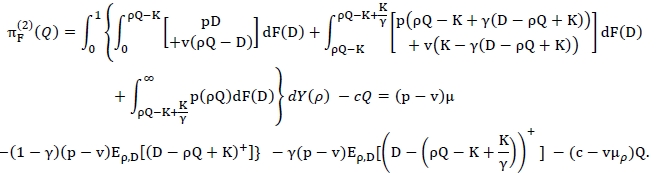
Let
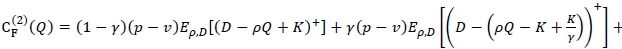
(c - υµρ)Q, and it is clear that maximising πF(2)(Q) is equivalent to minimising CF(2)(Q). Like the previous cases, the fill-rate β(Q) is given as 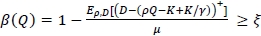 . Under the assumption that the exact demand and yield distributions are available, the optimal order quantity Q*F is
. Under the assumption that the exact demand and yield distributions are available, the optimal order quantity Q*F is
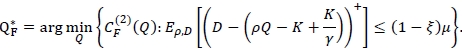
We now discuss the robust min-max approach where the exact distributions for both demand D and yield p are not available. Due to Lemma 1, by letting g(Q) = ρQ + κ where κ is a constant so that E[g(Q)] = µρQ + κ and Var[g(Q)] = (σρQ)2, we can obtain:
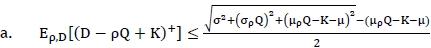 , and
, and
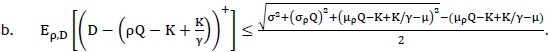
By applying the results above, the objective function for the corresponding robust min-max model, 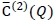 , is derived as
, is derived as
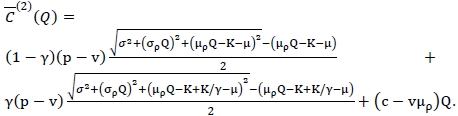
Similarly, the distribution-free fill-rate constraint for the random yield case becomes 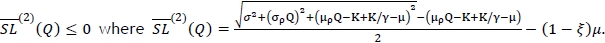 . Therefore the corresponding robust min-max decision model with random yield reduces to
. Therefore the corresponding robust min-max decision model with random yield reduces to 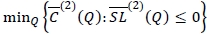 .
.
Since it can be shown that 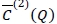 is convex in Q, we set the first derivative of
is convex in Q, we set the first derivative of  with respect to Q equal to zero, which leads to
with respect to Q equal to zero, which leads to
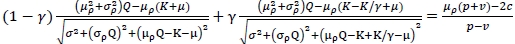
And let 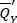 be Q satisfying the first-order condition above. If
be Q satisfying the first-order condition above. If 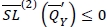 holds, then
holds, then 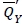 is the optimal order quantity for the robust min-max model with random yield. Otherwise, in a similar way to the base model case
is the optimal order quantity for the robust min-max model with random yield. Otherwise, in a similar way to the base model case 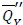 , satisfying the fill-rate constraint with equality (i.e.
, satisfying the fill-rate constraint with equality (i.e. 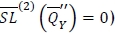 is the optimal solution for the model. Thus we can summarise a simple procedure to seek the optimal order quantity
is the optimal solution for the model. Thus we can summarise a simple procedure to seek the optimal order quantity 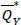 for the robust min-max model with random yield as presented in Algorithm 4.
for the robust min-max model with random yield as presented in Algorithm 4.

Example 3. In order to illustrate the random yield extension, we use the parameter values in Example 1. We additionally assume that µρ = 0.9 and σρ = 0.1. If 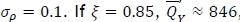 , and it satisfies
, and it satisfies 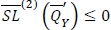 , then, according to Algorithm 4, the optimal order quantity is
, then, according to Algorithm 4, the optimal order quantity is 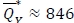 . However, if ξ = 0.95, the fill-rate constraint is violated, and so, from Step 2 in Algorithm 4,
. However, if ξ = 0.95, the fill-rate constraint is violated, and so, from Step 2 in Algorithm 4, 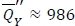 , which is the optimal order quantity in this case. We note that the order quantities under perfect yield assumptions in Example 1 are 804 if ξ = 0.85, and 851 if ξ = 0.95. Due to the the random yield effect of produced or ordered quantity, the order quantity increases, and its increasing rate seems higher as the targeted fill-rate increases.
, which is the optimal order quantity in this case. We note that the order quantities under perfect yield assumptions in Example 1 are 804 if ξ = 0.85, and 851 if ξ = 0.95. Due to the the random yield effect of produced or ordered quantity, the order quantity increases, and its increasing rate seems higher as the targeted fill-rate increases.
5 COMPUTATIONAL RESULTS: PERFORMANCE OF THE ROBUST MIN-MAX APPROACH
We have performed extensive computational experiments to evaluate the performance and robustness of this distribution-free approach. For the experiments, 1,000 problem instances are randomly generated, and all the parameters for each instance are drawn from the uniform distributions specified in Table 2. We take some parameter values from Moon & Choi [11].

For each instance, we evaluate three different distributions (i.e. normal, uniform, and triangle distributions), and compare them with results from the robust min-max approach. We note that the information on the mode of a triangle distribution is additionally required, and it is drawn from U(750,900). In addition, for a given instance, we evaluate (%EVAI) for four different levels of the desired fill-rate ξ as {0.8,0.85,0.9,0.95}.
Figure 1 presents the box plots of the ratio (%EVAI) from the 1,000 randomly-generated instances for each distributional form while varying the value of ξ in order to see the effect of the desired service level on the performance of the robust min-max approach. Appendix B provides the closed-form formulas for the cumulative density function P(D < κ) and E[(D - k)+] for each distributional form, which are essential to calculate CF(Q). We note that we replaced median with the sample average in the box plots. The results indicate (i) that the percentage gap (%EVAI) is less than 3 per cent on average for all the targeted service levels, and (ii) that when the targeted fill-rate ξ is less than or equal to 0.9 (90 per cent), the maximum value of (%EVAI) remains less than 3 per cent. However, we can observe that both the variability and the average of (%EVAI) increase significantly at ξ = 0.95, compared with the cases for ξ< 0.9, and its maximum reaches to 10-12 per cent. For ξ< 0.95, it turns out that its application to the normal distribution results in better performance than in the other distributions. Furthermore, these computational results partly provide justification for the use of the robust min-max approach if (i) the desired fill-rate is less than 90 per cent, and (ii) it is difficult to estimate the form of a demand distribution function, but the information of mean and variance is readily available or can be estimated. When the targeted fill-rate is 95 per cent, the performance of the robust min-max approach becomes degraded, and it seems that the degradation would be exacerbated for a fairly high fill-rate (close to 1). However, use of the robust min-max approach could still be recommended (at least for the cases we examined in this experiment), since the 75-percentile of (%EVAI) from the set of problem instances is still below 4 per cent. Therefore the robust min-max approach is likely to work well or to be acceptable in most cases. However, the increased mean and variance of (%EVAI) for the min-max model, compared with the base model, could mainly be because the optimal solutions for the robust min-max model are likely to lie on the constraint boundary of the distribution-free fill-rate constraint for a high ξ, and even more conservative decisions of the robust min-max model could be made when the service level is high
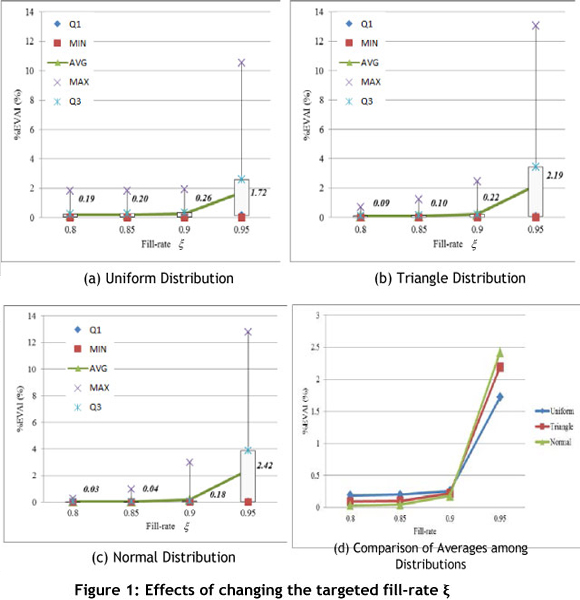
We now investigate how the change in variance of the demand affects the performance of the robust min-max approach depending on the targeted fill-rate ξ. Let ω be the coefficient of variation (i.e., ω = σ/µ). We note that, in the previous numerical experiment, we restricted the value of ω to between 0.1 and 0.5 (refer to Table 2). In order to see the effect of changes in the variance of demand for the uniform distribution, we choose 1,000 random instances in the same way as the previous experiments. For each value of ξє {0.8,0,85,0.9,0.95}, we vary the value of ω from 0.1 to 1.0 by a 0.1 increment, and calculate (%EVAI) as shown in Figure 2.
As seen in Figure 2, the variance of demand has a significant impact on the performance of the robust min-max approach, and the impact increases as the desired service level increases. In general, the variability and average of (%EVAI) from a set of randomly-generated problem instances increase as ω increases. For ξ equal to either 0.8 or 0.85, the robust min-max approach could still be recommended on average, even for a higher variance in demand. The robust min-max approach performs moderately well in the cases when the demand variance is low (ω < 0.4) for ξ≥ 0.9cases, and the performance degradation becomes significant when ξ is equal to 0.95. This suggests to practitioners that there may be a reason to explore the underlying true demand distribution if both the targeted fill-rate and the coefficient of variation are high enough. As mentioned earlier, decision-makers tend to make conservative decisions when they lack the exact demand distribution information for higher fill-rate cases. This often leads to a larger information gap and an increased variability of (%EVAI). In earlier works discussing robust min-max models [1,11], their numerical experiments used the value of ω less than 0.3 to conclude that the distribution-free approach is robust. Although none of these studies attempted to investigate the impact of the variance of demand on the performance of the robust min-max approach, our results could indicate that robust the min-max models in the earlier literature might be robust even in the cases where demand distributions have high variance (see the cases when the desired service level ξ is not too high). As mentioned earlier, one reason that our model is more likely to be conservative as the targeted service level increases is due to the incorporation of the fill-rate constraint, which results in a performance degradation of robust min-max approaches. In harsh conditions, the fill-rate constraint could possibly raise the value of the order quantity Q too high. However, their models have no such constraint, and we presume that the optimal order quantity obtained from the first-order condition may not be too conservative.
Lastly, we also performed numerical experiments to examine the effect of the threshold K, and found that its effect is insignificant.
6 CONCLUSION
In this paper we have investigated the robust min-max approach for the classic newsvendor model with customer balking under a service-level constraint. In the approach, we only require the first two moments of the demand distribution to determine an order quantity where the demand distributional form is hardly estimated, which in practice is usually the case. In order to control the lost-sales and customer balking effects in a tangible way, we incorporate the service rate constraint in our model, rather than include a lost-sales cost penalty, which is generally difficult to estimate in practice. We present the procedure to identify an optimal order quantity for the robust min-max model, and we extend the base model into two cases: one with a fixed ordering cost, and the other with imperfect yield. We also examine the effects of the variability of the demand and the targeted fill-rate on the information gap (%EVAI). Extensive numerical experiments indicate that the robust min-max approach generally performs well and efficiently; but we also observe that the quality of the solutions determined by the robust min-max approach is degraded for the very high targeted fill-rate, and the degradation accelerates as the fill-rate comes close to 1. Similarly, its performance becomes less robust as the coefficient of variation for the demand distribution increases for the high targeted fill-rate. Thus the distribution-free model is generally efficient and robust, especially for situations where the coefficient of variation ω < 0.4 or 0.5, and the targeted service level ξ < 0.9.
REFERENCES
[1] Alfares, H.K. & Elmorra, H.H. 2005. The distribution-free newsboy problem: Extensions to the shortage penalty case, International Journal of Production Economics, 93-94, pp. 465-477. [ Links ]
[2] Bassok, Y., Hopp, W.J. & Rohatgi, M. 2002. A simple linear heuristic for the service constrained random yield problem, IIE Transactions, 34(5), pp. 479-487. [ Links ]
[3] Bolton, J.M. & Liu, W.B. 2006. Creating an effective china cold supply chain -Current status, challenges and implementation considerations, Accenture Report, http://www.procurementleaders.com/8201/23171/ (Accessed on 19 September 2011). [ Links ]
[4] Feldman, R.M. & Valdez-Flores, C. 2010. Applied probability and stochastic processes, 2nd edition, Springer-Verlag. [ Links ]
[5] Gallego, G. & Moon, I. 1993. The distribution free newsboy problem: Review and extensions, Journal of the Operational Research Society, 44, pp. 825-834. [ Links ]
[6] Jung, U. & Lee, S. W. 2012. Robust newsvendor model with random yield and customer balking, Journal of the Korean Society for Quality Management, 40(4), pp. 441-452. [ Links ]
[7] Keren, B. 2009. The single-period inventory problem: Extension to random yield from the perspective of the supply chain, Omega, 37(4), pp. 801-810. [ Links ]
[8] Khouja, M. 1999. The single-period (news-vendor) problem: Literature review and suggestions for future research, Omega, 27, pp. 537-553. [ Links ]
[9] Liao, Y., Banerjee, A. & Yan, C. 2011. A distribution-free newsvendor model with balking and lost sales penalty, International Journal of Production Economics, 133, pp. 224-227. [ Links ]
[10] Lundquvist, J., Fraiture, C. & Molden, D. 2008. Saving water: From field to fork - Curbing losses and wastage in the food chain, SIWI Policy Brief, SIWI. [ Links ]
[11] Moon, I. & Choi, S. 1995. The distribution free newsboy problem with balking, Journal of the Operational Research Society, 46, pp. 537-542. [ Links ]
[12] Nahmias, S. 2005. Production and operation analysis, 5th edition, McGraw-Hill/Irwin. [ Links ]
[13] O'Neil, S., Zhao, X. & Sun, D. 2008. Coping with demand shocks: A distribution-free algorithm for solving newsvendor problems with limited demand information, Working paper, University of Notre Dame, Notre Dame, IN. [ Links ]
[14] Pasternack, B.A. 1990. The newsboy problem with balking, ORSA/TIMS Conference, Philadelphia. [ Links ]
[15] Perakis, G. & Roels, G. 2008. Regret in the newsvendor model with partial information, Operations Research, 56(1), pp.188-203. [ Links ]
[16] Petruzzi, N.C. & Dada, M. 1999. Pricing and the newsvendor problem: A review with extensions, Operations Research, 47, pp.183-194. [ Links ]
[17] Porteus, E. 2002. Foundations of stochastic inventory theory, Stanford University Press, CA. [ Links ]
[18] Scarf, H. 1958. A min-max solution of an inventory problem. In K. Arrow, S. Karlin, H. Scarf (eds), Studies in the mathematical theory of inventory and production, Stanford University Press, CA, pp. 201-209. [ Links ]
[19] Yano, C.A. & Lee, H.L. 1995. Lot sizing with random yields: A review. Operations Research, 43(2), pp. 311-334. [ Links ]
APPENDICES
Appendix A: Proof of Lemma 1
a. By and large, this lemma is a generalised version of all the corresponding lemmas from [5], and its proof is also based on the proofs in those lemmas. Note that
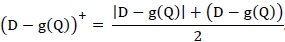
Due to Cauchy-Schwarz inequality and Jensen's inequality,
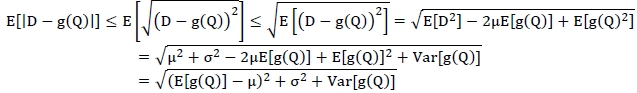
and hence
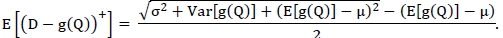
b. To show the existence of a demand random variable that yields the tight bound in Equation (3) when g(Q) is a constant, consider the following random variable D:
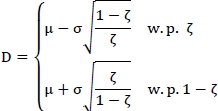
where
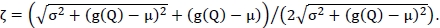
Since 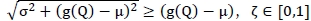 implies that D is a proper random variable unless σ = 0. Then it is straightforward to show that E[D] = µ. and Var[D] = σ2. Also, note that
implies that D is a proper random variable unless σ = 0. Then it is straightforward to show that E[D] = µ. and Var[D] = σ2. Also, note that 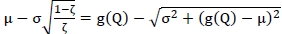 and
and 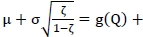
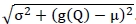 . Therefore,
. Therefore,
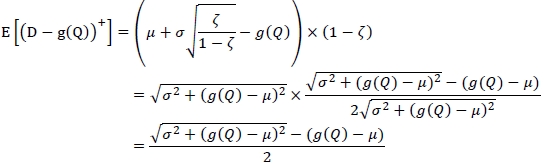
which completes the proof.
Appendix B: List of explicit expressions for F(κ) and E[(D - κ)+]

ǂ http://en.wikipedia.org/wiki/Error_function; http://www.maths.abdn.ac.uk/simigc/tch/ma2001/notes/node61.html














