Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.3 Pretoria Nov. 2013
GENERAL ARTICLES
Immune genetic algorithm for scheduling service workflows with QoS constraints in cloud computing
K. SellamiI, *; M. Ahmed-NacerII; P.F. TiakoIII; R. ChelouahIV
IApplied Mathematics Laboratory, A/Mira University of Bejaia, Algeria. Khaled.sellami@univ-bejaia.dz
IILSI Laboratory. USTHB University, Algiers. anacer@cerist.dz
IIICITR, Langston University and CITRD, Tiako University, Oklahoma, USA. pftiako@lunet.edu
IVLARIS Laboratory, EISTI, France. Chelouah.rachid@yahoo.com
ABSTRACT
Resources allocation and scheduling of service workflows is an important challenge in distributed computing. This is particularly true in a cloud computing environment, where many computer resources may be available at specified locations, as and when required. Quality-of-service (QoS) issues such as execution time and running costs must also be considered. Meeting this challenge requires that two classic computational problems be tackled. The first problem is allocating resources to each of the tasks in the composite web services or workflow. The second problem involves scheduling resources when each resource may be used by more than one task, and may be needed at different times. Existing approaches to scheduling workflows or composite web services in cloud computing focus only on reducing the constraint problem - such as the deadline constraint, or the cost constraint (bi-objective optimisation). This paper proposes a new genetic algorithm that solves a scheduling problem by considering more than two constraints (multi-objective optimisation). Experimental results demonstrate the effectiveness and scalability of the proposed algorithm.
OPSOMMING
In verdeelde rekenaarverwerking is hulpbrontoewysing en skedulering van diens werkstrome 'n belangrike uitdaging, veral in 'n wolkrekenaar omgewing waar daar baie rekenaarhulpbronne beskikbaar is op bepaalde plekke. Daarbenewens moet die kwaliteit van die diens kwessies, soos uitvoertyd en bedryfskoste, in ag geneem word. Om hierdie uitdaging suksesvol te adresseer moet twee klassieke rekenaarverwerking probleme aangepak word: eerstens, die toekenning van hulpbronne aan elk van die take in die saamgestelde webdienste of werkstrome en tweedens die skedulering van hulpbronne wanneer elke hulpbron gebruik kan word deur meer as een taak en op verskillende tye nodig mag wees. Die bestaande benaderings vir die skedulering van werkstrome of saamgestelde webdienste in wolkverwerking fokus op die vermindering van die beperkingsprobleme, soos die sperdatum of die kostebeperking. Hierdie artikel stel 'n nuwe genetiese algoritme, wat die hulpbrontoewysing en skedulering probleem deur die oorweging van meer as twee beperkings oplos, voor. Eksperimentele resultate demonstreer die doeltreffendheid en skaalbaarheid van die voorgestelde algoritme.
1 INTRODUCTION
Due to increasing interest in service-oriented architecture (SOA) and virtualisation, many organisations have chosen to expose their hardware and/or software resources over cloud computing environments. 'Cloud computing' [1] is an internet-based computing paradigm driven by economies of scale, where a pool of computation resources - usually deployed as web services - are provided on demand over the internet, in the same way that public utilities are. Unlike grid computing, which typically provides persistent and permanent use of all available IT resources, this pool of resources is generally used as a pay-per-use model where quality of service (QoS) guarantees are exploited by the infrastructure provider using customised service level agreements (SLA) [2]. Composition of web services is currently carried out by orchestration [3] - that is, a workflow that combines invocations of individual operations of the web services involved [3]. It is therefore a composition of individual operations, rather than a composition of entire web services.
There are many high performance applications in health care, finance management, the military, etc. that can be conducted as workflows and deployed over grid or cloud computing environments.
The process that maps and manages the execution of interdependent tasks of workflow on distributed resources is called 'service workflow scheduling'. This process has recently become one of the major concerns of the grid and cloud computing community [4]. Workflow scheduling in the cloud is a difficult problem. It is well known as an NP-complete problem, and the difficulty depends on the problem size. To schedule workflow tasks effectively in these cloud environments, workflow management systems require more elaborate scheduling strategies to meet QoS constraints and the precedence relationships between workflow tasks. Many heuristic and meta-heuristic based algorithms have been proposed for workflow scheduling in heterogeneous distributed system environments. Most of these have focused either on single objective optimisation [5,6] such as the execution time (makespan), or on bi-objective optimisation [7,8,9,10] of the makespan and cost, without paying attention to other QoS parameters such as reliability, resource utilisation, or energy consumption.
This paper proposes a new algorithm for scheduling composite service workflows in cloud environments. It proposes to optimise several objective functions simultaneously, depending on the requirements of the users and providers: makespan, cost, reliability, and resource utilisation. When physical resources are involved, we propose a way to monitor energy consumption. We therefore present a genetic algorithm that solves this scheduling problem.
2 PROBLEM DESCRIPTION
Inputs
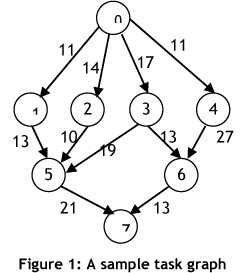
1.A set of several workflow tasks T={T1, T2,..,Tn} that have a precedence constraint, modelled by directed acyclic graphs (DAGs), where n is the number of workflow tasks. Figure 1 shows a workflow application with eight tasks. The nodes of the graph represent the tasks, while the arcs denote precedence constraints and the control/data dependencies between tasks.
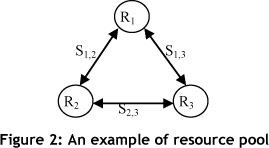
2.A set of candidate cloud resources R={R1,R2,..,Rm} (the resource pool) modelled by non-directed acyclic graphs, where m is the number of candidate cloud resources. Figure 2 shows a three-cloud resource connected at different network speeds (bandwidths).
3.A response time and price for each cloud resource.
Multi-objective problem
The general multi-objective problem is posed as follows:
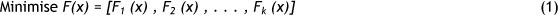
where x is a vector representing a solution, and F1 to Fk are conflicting objectives. The workflow planning problem as a multi-objective problem is characterised by the fact that it features a group of conflicting objectives that have to be optimised simultaneously. For instance, minimising execution time is often contradictory to the goal of optimising the cost of execution. Nevertheless, the goal of the problem is to find a good compromise between all optimisation goals. Therefore, in our case, the multi-objective problem has been modified to become a single-objective problem. The objectives that we could possibly want to optimise are:
1. Execution time (known as makespan): represents the duration from the user submitting a workflow to receiving the results. It consists of the workflow execution time and network transmission time, shown in Formula 2:
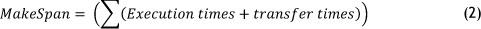
2. Cost: the cost for running a cloud workflow is defined in Formula 3. It consists of the processing cost and the data transfer costs.
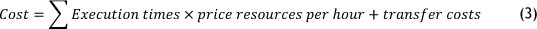
3. Reliability: represents the probability that the workflow will be executed successfully [9] to be maximised.
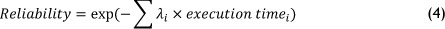
where λi is the failure rate of the physical resource. When several virtual machines (VM) are running on the same resource, we consequently assume that λVM < λresource
4. Availability (usage): represents the average time a cloud resource is not occupied during the workflow execution,
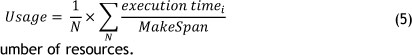
where N is the number of resources.
5. Energy consumption
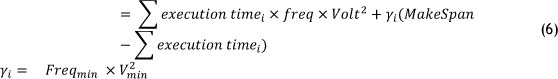
The latter equation is only applicable to non-virtual resources.
3 RELATED WORK
Many heuristics have been developed to schedule interdependent tasks in grid and cloud computing: genetic algorithms [5,7,9] and particle swarm optimisation (PSO) based algorithms [11,12]. The HEFT algorithm (heterogeneous earliest finish time) is one of the most widely-used heuristics that attempt to minimise the makespan [5]. Most of these algorithms focus on optimising either one or two objectives. However, there are new challenges for scheduling workflow applications in a cloud environment by optimising more than one or two QoS parameters, which is the concern of this paper. To date, one of the few works dealing with multi-objective planning for workflow execution on grids is that proposed by Yu et al. [13]. The authors proposed an improved NSGAII (non-sorted genetic algorithm) based scheduling method to solve the problem. Using a Pareto-based algorithm [14], this approach allows one to decide between several possible solutions, based on their advantages and disadvantages. When the budgets of users are known in advance, the use of a Pareto-based algorithm is rather slow. Our paper uses a novel aggregating-based approach to optimise for three objectives - makespan, cost, and reliability - under different constraints and environments.
4 AN IMPROVED GENETIC ALGORITHM FOR WORKFLOW SCHEDULING IN CLOUD
Fundamentally, the problem formulated in section 2 is a constrained optimisation problem. So how to achieve the best QoS for a workflow scheduling with increasing parameters is a major challenge. Genetic algorithms (GA) have been used to address this challenge in the past.
The pseudo-code of a classic genetic algorithm is shown in algorithm 1. It first creates an initial population consisting of randomly-generated solutions. After applying genetic operators (selection, crossover, and mutation) one after the other, new offspring are generated. Then the evaluation of the objective function (the fitness) of each individual in the population is conducted. The individuals with the best fitness (fittest individuals) are selected to be carried over to the next generation. These steps are repeated until the termination condition is satisfied. Typically, a GA is terminated after a certain number of iterations, or if a certain level of fitness value has been reached [15].
The construction of a genetic algorithm workflow scheduling problem can be divided into four parts [16]: (1) the definition of an appropriate structure to represent the solution; (2) the determination of the fitness function; (3) the design of genetic operators; and (4) the determination of probabilities controlling the genetic operators. A flowchart of our approach is shown in Figure 3. It consists of an iterative process performing different genetic operations on a pool of initial random solutions.
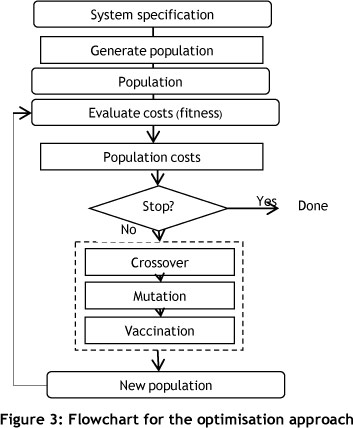
Our representations and methods are described in the following sub-sections.
4.1 Genetic encoding
Our chromosome structure must take into account the following conditions:
1-The precedence between the different tasks (or services)
2-The uniqueness of each resource time allocated for a given task
3-Tasks must be scheduled on resources able to handle them
4-The uniqueness of the execution time of each task
In our work a solution is an associative array composed of a collection of paired tasks and resources (see Figure 4). The solution array is indexed by task identifier (Ti) and the pairs containing substructures, including important parameters such as the task rank and the resource parameters (see Table 1). Using this representation, the combination of a task, its rank, a resource, and its parameters (frequency, voltage, etc.) can be considered as a gene from a genetic point of view. The term 'rank' in this representation is completely independent from the task interdependencies, and this variable is used to determine the priority between several tasks that are ready to be scheduled at the same time (see the scheduling algorithm below, and section 4.3 for details).


The genetic algorithm is granted full access to modify the parameters of the different task-resource pairs and to change the sub-elements if the simulation allows it. To do so, genetic operators such as crossover and mutations are applied to the different solutions.
4.2 Fitness function
Fitness function is a particular type of objective function that prescribes the quality of a solution (that is, a chromosome) of a GA. Choosing a proper fitness function is very important for the effectiveness and efficiency of evolutionary algorithms.
This is even more important in our case because we are using an aggregative model to define the global fitness value of a solution. In this paper we introduce a generic fitness function model that can easily be adapted to optimise any kind of numerical objective.
Objectives to optimise can be divided into two categories: the one we want to minimise (makespan, cost, energy consumption, etc), and the one we want to maximise (reliability, for instance). In both categories, the objectives have very different scales and values, making a straight comparison between them impossible. The first step we used to define our fitness function was to normalise all the objectives according to formulae (7) and (8).
Then the fitness function is evaluated by summing all the objectives and scaling the result between 0 and 100 according to formula (9), with 0 being the best value and 100 the worst. Using this method, it is possible to compute a fitness value that is representative of all objectives. However, this fitness value depends on the current pool of solutions, and therefore it cannot be compared with fitness values from other algorithms or even other iterations.
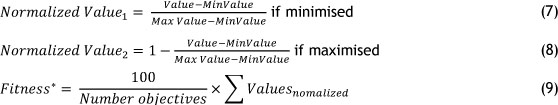
where MinValue and MaxValue are the extremes of the considered objective for the current pool of solutions. The second important part in designing the fitness function was to take constraints into consideration. To achieve this goal, we applied the penalties method to the previously computed fitness values by using formulas (10), (11), and (12).

The process of generating and evaluating a solution has two steps: first, the genetic algorithm generates the solutions and assigns each task to a resource, and provides the parameters for the substructures; and the second step is to evaluate the solutions to compute their fitness functions. To do this, a scheduler deploys the previously generated solutions that simulate the result of the proposed solution, and computes the QoS variables.
In order to evaluate the solutions, our scheduler will simulate them, based on the HEFT (heterogeneous earliest finish time) model. Tasks are scheduled according to their given resource one by one, after their parent tasks are done and all data has been transmitted. If several possible resources are ready to be scheduled, the one with the highest rank (generated by the GA) goes first.
This method of scheduling, described in the pseudo-code in Figure 5 below, ensures that the constraints between the tasks are respected, and thus avoids the algorithm having to solve a complex constraint satisfaction problem.
4.3 Genetic operators
Genetic operators are the core of a genetic algorithm. They define how to generate new solutions from the existing ones. The two genetic operators are the crossover and the mutation operators.
4.3.1 Selection and crossover
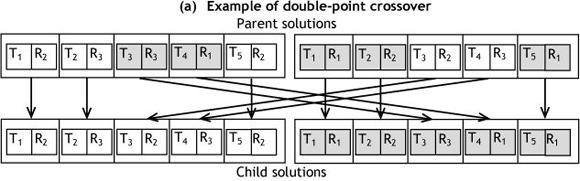
Crossover produces new individuals from the existing ones by interchanging sequences of task-resource pairs. We used the double-point crossover (see the example shown in Figure 6.a), which showed good performance for a workflow scheduling problem [7,13]. In our algorithm we choose the parent solutions in two steps:
- We reduce the initial pool of solutions by keeping only X per cent of the solutions based on their fitness value. The process consists of sorting the solutions of the pool by their fitness value using equation (12), and keeping only the X per cent best ones. Therefore we execute what is called a 'rank selection' of X per cent. X is a parameter of the algorithm, and is usually around 50 per cent.
- Then we randomly select parent solutions in the chosen pool. All solutions have an equal probability of being selected.
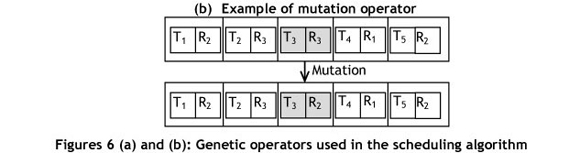
4.3.2 Mutation operator
In the mutation process, a gene of the chromosome will be mutated. The mutation probability Pm determines if the chromosome will be the subject of a mutation. Each chromosome of the population is assigned a random probability of mutation. The chromosome whose probability is lower than or equal to Pm will be the chromosome to mutate. The mutation of a gene Gi is made in one of its pairs, and will have one of the following modifications (see the example shown in Figure 6.b): the task rank will be modified; the resource associated with the task will be changed; or the resource parameters will be changed (whenever it is possible).
4.3.3 Vaccination
To ensure that all generated solutions respect the constraints that force some tasks to be executed only with appropriate resources, we use a vaccination process similar to the one described in [17]. If considered as a constraint satisfaction problem (CSP), that kind of constraint can be encoded as a gene: given a constraint like task Ta on resource Rb, an individual solution must have a gene/pair (Ta,Rb) in order to respect the constraints. Thus in our algorithm a vaccine changes one or very few positions of a member, based on the CSP of what corrects an existing solution.
After the crossover and mutation process, every solution that does not respect the constraints will be vaccinated, thus correcting the deficient genes.
In Figure 7 we show an example where the constraints are task T1 on resource R2, and task T6 on resource R1 or resource R3. In this example we are also shown a solution S1 that has its task T6 scheduled on resource R2.

Task T1 is assigned in a way that respects the constraints; however, S1 is vulnerable to (T6,R2). Consequently, the solution S1 will be randomly vaccinated by one of the genes (T6,R1) or (T6,R3) in order to be modified to fit the constraints. In the example of Figure 7, S1 is corrected by (T6,R1).
5 EXPERIMENTS
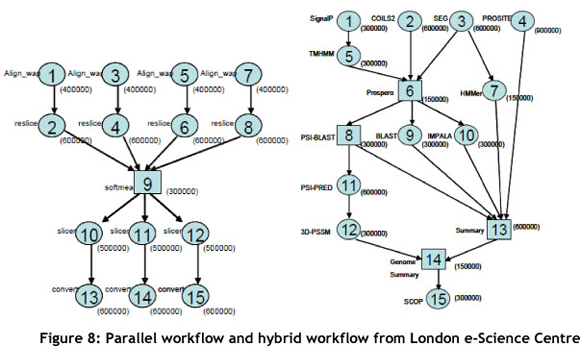
To demonstrate the robustness of the proposed genetic algorithm, we tested it on various real-life project workflows already studied by other scientists [18] (see Figure 8), including a neuroscience workflow with many parallel features [19], and a protein annotation workflow with hybrid features [20]. The experimental results presented in this document come mostly from experiments conducted on these two specific workflows. We used a simulation environment on a machine with an Intel Core2 Quad CPU Q8300 @ 2.50GHz and 3.25 GB of RAM running on MS Windows XP, and our environment was compiled with mingw32.
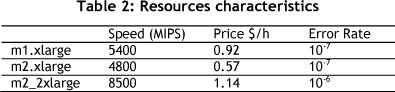
These experiments were done using the characteristics of the Amazon EC2 cloud resources [21,22]. However the error rate for Amazon EC2 resources was not provided. We therefore arbitrarily assigned error rates that correspond to computers of similar performance (cf. Table 2). For the connection speed between the resources we considered a connection speed of 100Mb/s.
For both workflows, the number indicated next to each task is the number of millions of instructions (MI) required to perform the considered task. The volumes of data transmitted between each task were randomly chosen between 32Mb and 1024Mb.
We chose these two workflows because parallel workflow and workflows with hybrid features can be scheduled with very different effectiveness results even while using the same scheduling algorithm. Therefore, to ensure that our algorithm was reliable, we used both categories of workflows.
The parameters for our immune genetic algorithm (IGA) were a population of 100 individuals, and a 0.05 probability of mutation.
5.1 Performance analysis
In our first experiments, we tried to evaluate our multi-objective results. Multi-objective optimisation being a difficult task, it is often impossible to improve a variable without degrading another one. For this reason we faced the problem of finding methods to evaluate our multi-objective results. Without reference values from other researchers for the QoS variable that we were studying with these specific resources, we defined our own evaluation protocol:
For each workflow, we processed single-objective optimisation tests on every QoS variable one by one, to get the approximate best value possible for each of them individually, and only after we had our multi-objective algorithm in the same conditions.
Using this method, we evaluated the multi-objective results of each QoS variable with the best single objective optimisation result for the same variable. These results are displayed in the next two subsections with different graphs where the multi-objectives results are evaluated between 0 and 1 - 0 being the worst possible value, and 1 the best result achieved in a single objective. We have also used HEFT algorithm results as references.
For the hybrid workflows, we ran the tests with the following constraints: tasks 2, 3, 4, and 11 had to be scheduled on resource 3. For the parallel workflows, tasks 2, 4, 14, and 15 had to be scheduled on resource 3. Following our experiment plan, we ran several simulations with different weights for the various QoS variables.
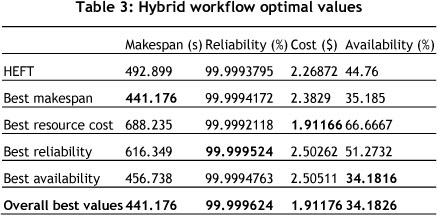
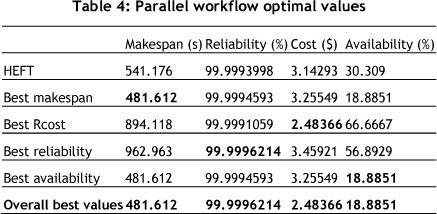
The best single optimisation results for the hybrid workflow are shown in Table 3, and those for the parallel workflow in Table 4. The results of the experiments are shown in Tables 5 and 6.
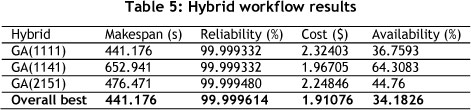
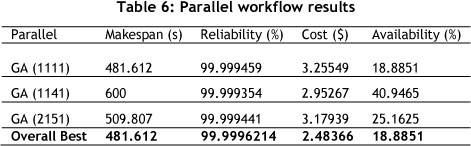
5.2 Constraint handling
The HEFT algorithm is currently one of the most widely-used algorithms to schedule workflows. However, it is a deterministic algorithm that cannot take into account parameters such as maximal price or maximal makespan requirement. Due to the popularity of this algorithm, it is mandatory to outperform it when conceiving new scheduling algorithms.
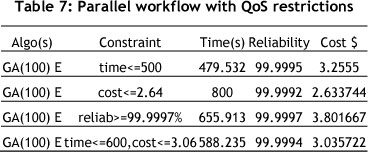
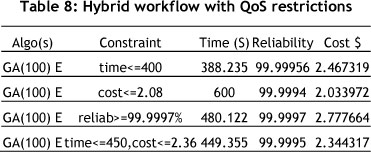
As a consequence, we ran various experiments to check that our genetic algorithm was capable of respecting constraints such as deadlines, maximum cost, and minimal reliability.
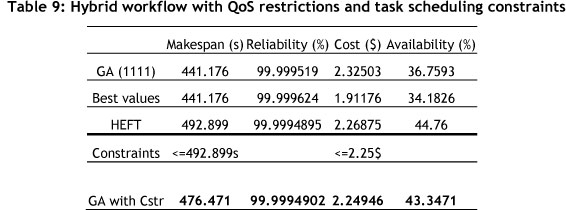
Tables 7 and 8 show the results of the experiments conducted on the parallel workflow and the hybrid workflow problems without task scheduling constraints. Table 9 and Figure 9 show the result of experiments on the hybrid workflow problems, combining both deadlines and task scheduling constraints.
5.3 Comparison with other algorithms
In another experiment, we evaluated the convergence speed of several algorithms: the aggregative genetic algorithm (GA) using our fitness function and crossover method; the NSGAII algorithm; the PAES algorithm; the HEFT algorithm; and our modified aggregative genetic algorithm using the vaccination process (IGA). We applied these four algorithms to both the hybrid and the parallel workflows, with four task scheduling constraints (for a total of 15 tasks). The outputs of the algorithms were evaluated between 0 and 1 by computing the mean value of the QoS variables, where 1 is the best value possible (all QoS variables maxed to their single objective best value) and 0 the worst value. The results were evaluated after numerous iterations of each algorithm, allowing us to plot two convergence speed graphs; one a function of the number of iterations, and the other a function of time. These results are shown in Figures 10 and 11.
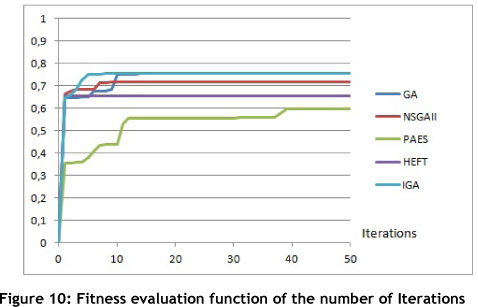
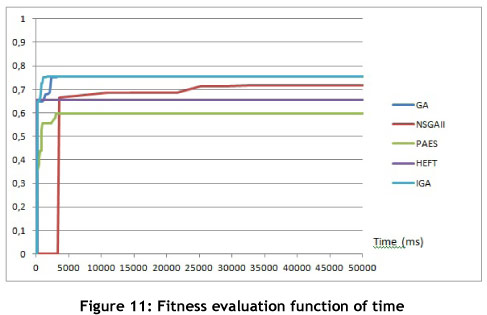
Both our GA and IGA algorithms are better than the other algorithms. While it is true that HEFT will give a result in the shortest time, and that the Pareto archived evolution strategy (PAES) [23] iterates faster, the results for fitness value favour both our algorithms, as they give better final results.
The case of the non-dominated sorting genetic algorithm (NSGAII) [24] is different. While one cannot deny that NSGAII gives results that are almost as good as those of our algorithms, and that it is possible to integrate the vaccination operator to NSGAII, this algorithm remains slower. The time needed to compute the Pareto front after each iteration is extremely long, especially with a large number of QoS variables.
6 CONCLUSION
Cloud computing is viewed as a major logical step in the evolution of the Internet as a source of remote computing services driven by economies of scale, utilising a pool of computation resources is usually deployed as composite web services and service workflows. Workflow and composite web services execution costs must therefore be considered during scheduling. Traditional scheduling research usually targets makespan as the only optimisation goal, while several isolated efforts have addressed the problem by considering, at most, two objectives. In this paper we have proposed a general framework and genetic algorithm for multi-objective scheduling of service workflows in cloud computing environments. We have presented the different objectives as multiple QoS functions including time, cost, reliability, utilisation, and energy. We have (1) proposed a new fitness function model for faster convergence, and (2) adopted an immune genetic algorithm efficiently to solve the constraint satisfaction problem linked with the task scheduling constraints. Our genetic algorithms were tested against algorithms in the literature that were previously used to solve this problem. Results for three different and widely-studied workflow applications demonstrated that the solutions generated by our algorithm are superior for user-defined constraints.
ACKNOWLEDGEMENTS
This research is supported by a research grant from the Ministry of Higher Education and Scientific Research in Algeria (CNEPRU project N° B*00620090014). The authors acknowledge the LARIS Laboratory of EISTI France, the Centre of IT Research at Langston University, and the LSI Laboratory of the USTHB University for their support. The authors also thank the anonymous referees for their valuable suggestions.
REFERENCES
[1] Foster, I., Zhao, Y., Raicu, I. & Lu, S. 2008. Cloud computing and grid computing 360-degree compared. Proceedings of the 2008 IEEE Grid Computing Environments Workshop, pp 1-10. [ Links ]
[2] Rajan, S. & Jairath, A. 2011. Cloud computing: The fifth generation of computing. International Conference on Communication Systems and Network Technologies, 15(4), Publisher: IEEE, pp 665667. [ Links ]
[3] Peltz, C. 2003. Web services orchestration and choreography. Computer, 36(10), pp 46-52. [ Links ]
[4] Yu, J., Buyya, R. & Ramamohanarao, K. 2008. Workflow scheduling algorithms for grid computing, metaheuristics for scheduling in distributed computing environments, F. Xhafa and A. Abraham (eds), ISBN: 978-3-540-69260-7, Springer, Berlin, Germany. [ Links ]
[5] Wieczorek, M., Prodan, R. & Fahringer, T. 2005. Scheduling of scientific workflows in the ASKALON grid environment, Special Issues on Scientific Workflows, ACM SIGMOD Record, 34(3), pp 56-62. [ Links ]
[6] Bajaj, R. & Agrawal, D.P. 2004. Improving scheduling of tasks in a heterogeneous environment, IEEE Transactions on Parallel and Distributed Systems, 15(2), pp 107-118. [ Links ]
[7] Yu, J. & Buyya, R. 2006. Scheduling scientific workflow applications with deadline and budget constraints using genetic algorithms, Scientific Programming, 14, pp 217-230. [ Links ]
[8] Wu, Z., Ni, Z., Gu, L. & Liu, X. 2010. A revised discrete particle swarm optimization for cloud workflow scheduling, in Proceedings of International Conference on Computational Intelligence and Security, CIS 2010. [ Links ]
[9] Wang, X., Yeo, C.S., Buyya, R. & Su, J. 2011. Optimizing the makespan and reliability for workflow applications with reputation and a look-ahead genetic algorithm, Future Generation Computer Systems, ISSN: 0167-739X, Elsevier Science, Amsterdam, The Netherlands, 27(8), pp 1124-1134. [ Links ]
[10] Mezmaz, M., Melab, N., Kessaci, Y., Lee, Y.C., Talbi, E.-G., Zomaya, A.Y. & Tuyttens, D. 2011. A parallel bi-objective hybrid metaheuristic for energy-aware scheduling for cloud computing systems, J. Parallel Distrib. Comput. 71, pp 1497-1508. [ Links ]
[11]Sellami, K., Ahmed-Nacer, M., Dris, D. & Tiako, P.F. 2013. A PSO optimization for workflow scheduling based on energy-aware in cloud computing environment, The Third International Conference on Parallel, Distributed, Grid and Cloud Computing for Engineering, PARENG 2013, in press. [ Links ]
[12] Pandey, S., Wu, L., Guru, S. & Buyya, R. 2010. A particle swarm optimization (PSO)-based heuristic for scheduling workflow applications in cloud computing environments, Proceedings of the 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, Australia. [ Links ]
[13] Yu, J., Kirley, M. & Buyya, R. 2007. Multi-objective planning for workflow execution on grids, Proceedings of the 8th IEEE/ACM International Conference on Grid Computing, IEEE Press, New York, USA. [ Links ]
[14] Zitzler, E. & Thiele, L. 1999. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach, IEEE Transactions on Evolutionary Computation, 3, pp 257-271. [ Links ]
[15] Zomaya, A.Y., Ward, C. & Macey, B. 1999. Genetic scheduling for parallel processor systems: Comparative studies and performance issues, IEEE Transactions on Parallel and Distributed Systems, 10(8), pp 795-812. [ Links ]
[16] Hou, E.S., Ansari, H.N. & Ren, H. 1994. A genetic algorithm for multiprocessor scheduling, IEEE Transactions on Parallel and Distributed Systems, 5(2), pp 113-120. [ Links ]
[17] Yongshou, D., Yuanyuan, L., Lei, W., Junling, W. & Deling, Z. 2007. Adaptive immune-genetic algorithm for global optimization to multivariable function, Journal of Systems Engineering and Electronics, 18(3), pp 655-660. [ Links ]
[18] Yu, J. & Buyya, R. 2006. A budget constrained scheduling of workflow applications on utility grids using genetic algorithms, The workshop on workflows in support of large-scale science. [ Links ]
[19] Zhao, Y., Wilde, M., Foster, I., Voeckler, J., Jordan, T., Quigg, E. & Dobson, J. 2004. Grid middleware services for virtual data discovery, composition, and integration, 2nd Workshop on Middleware for Grid Computing. [ Links ]
[20] O'Brien, A., Newhouse, S. & Darlington, J. 2004. Mapping of scientific workflow within the e-protein project to distributed resources, in UK e-Science All Hands Meeting, Nottingham. [ Links ]
[21] Amazon Elastic Compute Cloud (Amazon EC2), http://aws.amazon.com/en/ec2/ : UE (Irlande), June 2012 tarification. [ Links ]
[22] Sarda, K., Sanghrajka, S. & Sion, R. 2011. Cloud performance benchmark series: Amazon EC2 CPU speed benchmarks, Cloud Computing Center & Network Security and Applied Cryptography Lab, Stony Brook University, New York, USA. [ Links ]
[23] Knowles, J.D. & Corne, D.W. 1999. The Pareto archive evolution strategy: A new baseline algorithm for multi-objective optimization, The congress on Evolutionary Computation, pp 98-105. [ Links ]
[24] Deb, K., Agrawal, S., Pratap, A. & Meyarivan, T. 2000. A fast elitist multi-objective genetic algorithm: NSGAII, Parallel Problems Solving from Nature VI, pp 849-858. [ Links ]
*Corresponding author.