Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 no.2 Pretoria Jan. 2013
CASE STUDIES
Failure effects and resolution of modes: a novel FMEA treatise for finalizing mould designs in foundries
T.A. SelvanI, *; C. JegadheesanII; P. Ashoka VarthananIII; K.M. SenthilkumarIV
IDepartment of Mechanical Engineering Sri Krishna College of Engineering and Technology Coimbatore, Tamil Nadu, India - 641008. ta_selvan@yahoo.co.in
IIArulmigu Meenakshi College of Engineering Vadamavandal, Tamil Nadu, India - 604410. cjega1987@gmail.com
IIIDepartment of Mechanical Engineering Sri Krishna College of Engineering and Technology Coimbatore, Tamil Nadu, India - 641008. ashoka_varthanan@rediffmail.com
IVDepartment of Mechanical Engineering Sri Ranganathar Institute of Engineering and Technology Coimbatore, Tamil Nadu, India - 641111. kmscit@gmail.com
ABSTRACT
This paper proposes a novel strategy to finalize the mould design of a specific cast component through the failure analysis using case study data of a foundry. Traditional failure mode and effect analysis (FMEA) is one of the effective tools for prioritizing the possible failure modes by calculating the Risk priority Number (RPN) of a process/design. But in foundries, prioritizing the failures through the traditional FMEA produces unmatched results when RPN values are identical during preproduction trials. Hence it is very difficult to finalize moulds design of a specific cast component using traditional FMEA approach. This research paper addresses an alternate FMEA approach named FEAROM (Failure Effects And Resolution of Modes) to resolve the difficulty in finalizing the mould designs. Analytical Hierarchy Process (AHP) is used for validating the results obtained using FEAROM method. The results presented are based on an experimental study carried out for a specific component in a foundry using the sand casting method. It is found that proposed FEAROM model matches well in practice and produces quality castings.
OPSOMMING
Hierdie artikel stel 'n nuwe strategie voor om die gietvormontwerp van 'n spesifieke gietstuk te finaliseer deur 'n gevallestudie van 'n falingsanalise van 'n smeltery. Tradisionele faal-en-effek-analise is een van die effektiewe hulpmiddels om die moontlike falings te prioritiseer deur die Risiko Prioriteitsnommer van 'n proses of ontwerp te bereken. In smelterye gee die prioritisering van faalings deur die Risiko Prioriteitsnommers onvergelykbare resultate wanneer die Risiko Prioriteitsnommers identies is tydens voorproduksieproewe. Gevolglik is dit baie moeilik om gietvormontwerpe van spesifieke gietstukke te finaliseer deur van die tradisionele faal-en-effek-analise benaderings gebruik te maak. Hierdie artikel stel 'n alternatiewe faal-en-effek-analise benadering voor, genaamd FEAROM ('Failure Effects And Resolution of Modes'), om die probleme met gietvormontwerpfinalisering aan te spreek. 'n Analitiese Hiërargieproses word gebruik om die resultate, met die FEAROM benadering bepaal, te valideer. Die resultate is gegrond op 'n gevallestudie van 'n spesifieke gietstuk in 'n smeltery wat gegiet is met die sandgietmetode. Daar word gevind dat die voorgestelde FEAROM model goed ooreenstem met die praktyk en hoë gehalte gietvorms as gevolg het.
1. INTRODUCTION
In recent days, the foundries are under immense pressure to produce high quality casting at the shortest possible lead time. In order to ensure the required quality level, the foundries have to implement a continuous quality enhancement strategy during development stage of cast components. Failure prevention is an important practice to improve the quality level [1, 2, 3]. Among the various failure prevention techniques, FMEA has been used popularly in several areas during the past few decades. One such area is an equipment performance and reliability (EPR) model for measuring maintenance performance based on machine effectiveness [4].
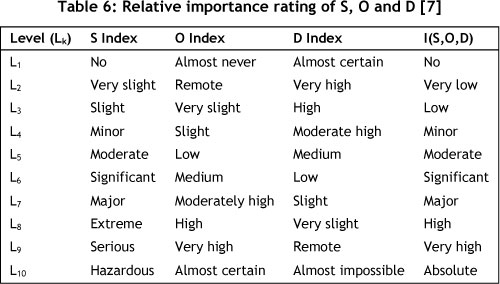
Traditional FMEA approach is based on three important indexes, viz., occurrence (O), severity (S) and detection (D) with scale levels of 1 to 10 indicated in Tables 1, 2, and 3 respectively.
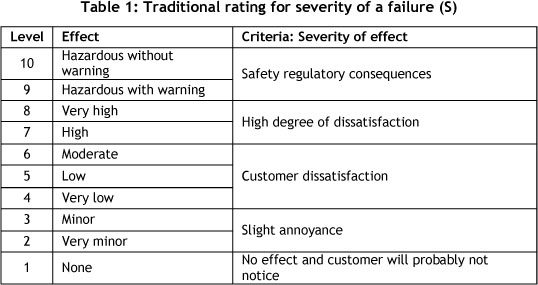
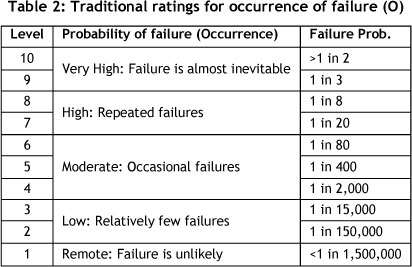
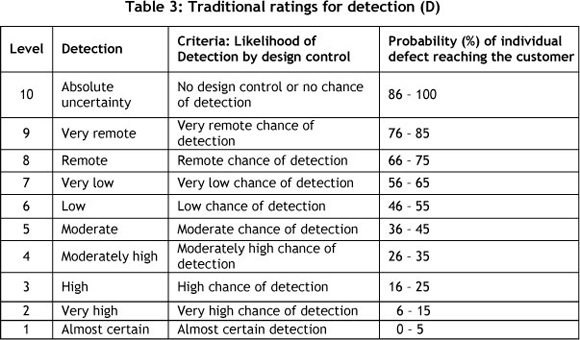
In traditional FMEA the RPN index is calculated as:

In traditional RPN evaluation, the original ordinal scale values of S, O and D is transformed into a new metric cardinal scale value. Moreover, there is pitfall in traditional FMEA due to the nature of RPN scale itself. As a product of three numbers, the RPN scale does not cover the range [1, 1000] continuously and presents a series of "holes" corresponding to prime numbers present in the range itself. Actually, 88% of the scale is empty with only 120 unique RPNs because some of the RPNs are repeating. For example, RPN 120 appears 24 times from product of S, O and D. Other extremes 1, 123, 1000 appear only once. RPNs are not continuous and heavily distributed at the bottom of the scale from 1 to 1000. The distribution of RPN present in the Table 4. This leads to series of problems in RPN interpretation. This causes problems in interpreting the meaning of the differences between different RPNs. For example, the difference between 200 and 300 the same as or less than the difference between 700 and 800 is not interpreted.
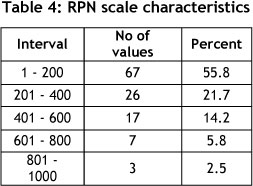
Another disadvantage associated with the traditional FMEA is that different combinations of S, O and D may produce exactly the same value of RPN. For example, consider two different events having values of (4, 6, 1) and (8, 3, 1) for S, O and D respectively. Both situations results in an RPN value of 24, but their hidden risk implications may be totally different. This may lead to either waste of resources and time or in some cases a high risk event may go unnoticed.
Furthermore the RPN scale properties lead to a series of problems in the RPN interpretation. For example, if two or more failure modes have the exact RPN, one may face difficulty in selecting which failure mode demands higher priority for corrective action. Also, the assumption is that the three failure mode indexes are all equally important. The relative importance among S, O and D is not taken into consideration. This may not be the case when considering a practical application of FMEA. In practice, different weight to the three indexes is assigned because different experts have different knowledge and judgments.
Many researchers have proposed modified versions of the FMEA approach to overcome the above difficulties associated with it. Wang et al., [5] proposed a fuzzy FMEA approaches to reduce the dependence on expert opinion in traditional FMEA. Chang et al., [6] has proposed a modified FMEA using fuzzy methods and grey theory to eliminate the pitfalls in the traditional FMEA. This could be even extended to the cases where they may possess same RPN indexes. Franceschini & Galetto [7] investigated and devised a novel method for ranking the risk priorities of failures in FMEA. The authors devised a method for managing data provided by the design team. The investigation considers each characteristic index as a fuzzy subset along with the 'tie ranking' rule when two or more failure modes have the same RPN. Further investigation of this work was extended by Sellapan & Karuppusami [8] using ANOVA. Chen & Ko [10, 11] proposed a fuzzy based approach to cope with the vague nature of product development processes for both FMEA and Quality Function Deployment (QFD) through fuzzy Linear and Nonlinear Programming models. Zhang & Chu [11] proposed the fuzzy based linear programming method as an effective solution for the calculations of fuzzy RPNs which resolves the vagueness and uncertainty existing in the evaluating process of the traditional FMEA. Hao Liu [12] proposed an extended fuzzy QFD from product planning to part deployment through a modified fuzzy k-means clustering method with fuzzy inference method for FMEA and α- cut operations to calculate the fuzzy sets in QFD.
Overall, it is obvious that many investigators proposed a modified FMEA approach to overcome the shortcomings of the traditional FMEA by combining fuzzy sets with different techniques. Other fuzzy FMEA approaches have been proposed for the RPN calculation in the literature [13, 14, 15, 16, 17]. Vast majority of fuzzy FMEA approaches employs fuzzy-if then rules for prioritization of failure modes. This requires vast amount of expert knowledge and expertise. In particular, different experts may have different knowledge and judgments. When their judgments are inconsistent, it is nearly impossible to combine or reduce rules. In general, most of these techniques are very complex and require a special function definition and technical know-how. In particular, these methods are quite complex to manage and are not always available to the designers. Hence, there is a clear need to develop a straight forward and simple fuzzy logic approach for FMEA which can take advantage of the benefits of fuzzy logic. Moreover, Wong & Lai [18] indicated in his work that most research is carried out only in Universities and suggested to make more effort to develop real world applications. Also in foundries, prioritizing the failures through the traditional FMEA produces unmatched results for finalizing mould designs when RPN values are identical during preproduction trials. These issues motivated the authors to devise a simplified but an effective fuzzy FMEA model named FEAROM (Failure Effects And Resolution Of Modes). The FEAROM methodology is developed based on the investigations of Franceschini & Galetto [7] and Sellapan & Karuppusami [8]. The new logic synthesis expression for Risk Priority Code (RPC) to change the order of priority among indexes is the basis for our work. The new logics of synthesis expresses changed composition of the operators and tie-ranking rule which is different from one that proposed by Franceschini & Galetto [7]. The new logic synthesis is appropriate to apply for finalizing mould designs in foundries.
The proposed FEAROM model eliminates the pitfalls in the traditional FMEA and helps the FMEA team to implement flexible and convenient strategy to find the most favorable mould design in preproduction trials. The approach also enables the possibility of accounting the discriminating importance of the characteristic indexes. FEAROM method is capable of dealing with information expressed on an ordered qualitative scale. An artificial numerical conversion of the scale is not necessary. The proposed FEAROM model is a fuzzy multi-criteria decision-making (MCDM) method. Hence it has been validated using a similar MCDM method called Analytical Hierarchy Process (AHP).
2. SOLUTION METHODOLOGY
The proposed FEAROM approach is discussed in detail under this section. Also, a modified AHP methodology used for validating the results of the FEAROM approach is discussed under this section.
2.1 FEAROM Methodology
Initially, the methodology uses the traditional FMEA to find the rank order of mould designs. The mould design that has the least RPN value is considered most important, next higher RPN value as second important and so on.
The FEAROM model advocates the decision making criteria to prioritize mould designs during the development stage of cast components. This method is suitable when the three index values, viz., S, O and D are considered equally important or different weights are given for each index by team members. The decision making criteria utilizes an ordered qualitative scale for data processing which have ordinal properties only. The proposed FEAROM model considers fuzzy subset to find the rank order of the mould designs in preproduction trials.
The projected FEAROM technique is proficient to deal with the circumstances when,
- The ranking scale for S, O and D is assigned different values by the team members but the indexes have the same maximum importance.
- Two or more mould designs have the same RPN.
- When three S, O, and D indexes are assumed with a different level of importance
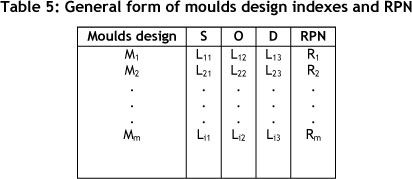
The evaluation criteria S, O and D are denoted by Kj (with j = 1, 2, 3) while the alternative mould designs during development stage are denoted by Mi (with i = 1, ...,m). The grade membership of alternatives Mi in Kj indicates the degree to which Mi satisfies the criterion specified.
The FEAROM model suggests a two step procedure:
Step 1: Calculate Risk Priority Code (RPC) [7]

where
RPC (Mi) is the Risk Priority Code for the moulds design Mi
I (Kj) is the importance associated with each criterion Kj = Lk
Lk is the kth level of the scale (refer Table 6)
Kj(Mi) = Lij (refer Table 5)
From equation (2) it is evident that the Max operation selects the largest of its arguments. If all the arguments are low, they do not affect the Max operation. Consider a criterion that has more importance, it will get an importance rating of Lk that is high on the scale. When we take Min of the importance criteria with evaluation Kj (Mi) we still get a low score. Thus, it is clear that high-importance criterion have little effect on the overall score. The formulation suggested in the equation (2) satisfies the properties of Pareto optimality. The term [Min {(I (Kj), Kj (Mi)}] indicates that 'if the criterion is important, then it has a low score'. The mould design with the most dangerous failure mode is the one with the highest RPC value.
Step 2: Calculate Critical Failure Mode (CFM)
The CFM equation given below is used for determining the least RPC value. The mould design with the lowest RPC value is chosen as per FEAROM method.

where
A is the set of failure modes of mould designs
RPC (Mi) is defined on a new 10 point ordinal scale
If two or more mould designs have the same critical failure mode, then the following equation is used for breaking the tie [8]:

Where,
N (Mi) is the number of elements in the row corresponding to Mi for which Lij < CFM (M*)
Let Lij denote the levels of S, O and D respectively corresponding to the mould designs Mi where i = 1, 2, 3... m and j = 1, 2, 3. Take 1< Lj < 10 for all i, j. Lij precisely takes the levels {1,2, 10}in some order as shown in Table 5.
The importance rating for S, O and D, is mentioned in Table 6. These values are used in FEAROM model to rate the relative importance of S, O and D.
2.2 Validation using Modified Analytic Hierarchy Process (AHP)
The familiar AHP has been used in the selection of an appropriate mould design in foundries. The outcome of AHP is used to verify and validate FEAROM model. Thomas L. Saaty (1980) was the first to develop the AHP for decision making where objective is to select the best alternative. It is based on the concept that the inconsistencies in making subjective judgments are sorted out. AHP is a multi criteria decision-making method that can be used in both subjective and objective evaluation criteria. AHP allows the systematic consideration and evaluation of multiple decision criteria. The analytic hierarchy process involves pairwise comparisons of the decision elements. The use of AHP in solving a decision problem involves the following five steps [19]:
Step 1 : Setup the decision hierarchy by breaking down the decision problem into a hierarchy of interrelated decision elements.
Step 2: Collect input data by pairwise comparison of decision elements.
Step 3: Use the eigenvalue method to estimate the relative weights of decision elements.
Step 4: Aggregate the relative weights of decision elements to arrive at a set of ratings for decision alternatives (or outcomes).
Step 5: Check for consistency using the consistency ratio (CR) is((p - n)/(n - 1))/ACl. µ is the largest positive eigen value. ACI is the average consistency index of randomly generated weights. According to Saaty, the values for ACI depended on the order (n) of the matrix and are as follows (first row is the order of the matrix; second row is the ACI value).
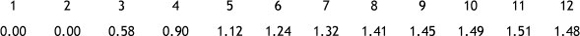
As a working rule of AHP, a CR value of 10% or less is acceptable.
The relative importance (weights) of the categories and criteria in the model for pairwise comparisons is established as follows:

where W = Weight or relative importance
Ln and Li are any two criteria.
The relative importance is W when Ln > Li and it is 1/W when Ln < Li.
Each comparison in pair is made to evaluate the importance of one factor over another relative to the criteria to be evaluated at that point. In typical analytic hierarchy studies a nine-point scale is used as explained in Table 7.
3. APPLICATION OF FEAROM THROUGH AN EXPERIMENTAL STUDY
The study was conducted in the macro foundry produces steel castings called SHREE KUMARAN ALLOYS located at Coimbatore city of India [website: http://www.shreekumaranalloys.com/]. The Gate Valve body casting with flanged ends called GTV valve body, which is being manufactured using CO2 sand casting, is considered in this work. The GTV valve body is made using cast steel A216 WCB grade. The objective of this work is to identify and finalize the appropriate mould design in order to produce high quality castings. Three different mould designs (M1, M2 and M3) of GTV valve body is considered by the industry during the preproduction trials. The corresponding patterns of the three mould designs are shown in Figures 1-3. A sample inspection-ready fettled casting, which was made using one of the moulds discussed above, is shown in figure 4.




As mentioned earlier, the aim of this work is to select the one from the three alternative mould designs, which produces high quality castings. A brain storming session is convened by the FMEA team members of the industry to assign the S, O and D values for each design. The team members and the assigned values under their supervision are shown in Table 8. The average values of the failure indexes for each mould design is considered as shown in Table 9. These values are used for selecting the best mould design using a modified novel FMEA approach named FEAROM method.
3.1 Ranking using Traditional FMEA and FEAROM Methods
In traditional FMEA, it is appropriate to consider least RPN value first, next higher RPN value second and so on for ranking the mould designs during the development stage. Hence, the traditional FMEA ranking order is 3, 1 and 2 for M1, M2 and M3 respectively [refer column six in Table 9]. It is obvious that the three characteristics indexes (S, O and D) are assumed with equal importance (L10) using traditional FMEA method. Practically, different importances are considered by team members due to various methods adopted for detecting the failure modes. This problem can be overcome using FEAROM method, as discussed below, for two cases.
Case (a): The same maximum importance (L10) is assumed for all characteristic indexes (S, 0 and D).This is similar to traditional FMEA. The importance rating is shown below.
1 (S) = L10; I (O) = L10; I (D) = L10
Step 1: The aggregated RPC index for the three mould designs M1, M2 and M3 is calculated using equation (2) [refer column seven in Table 9]:
RPC (Mi) = Max [Min (L10, L8), Min (L10, L6), Min (L10, L7)]
RPC (Mi) = Max [L8, L6, L7] = L8
RPC (M2) = Max [L8, L4, = L8
RPC (M3) = Max [L7, L5, L7] = L7
Step 2: The calculation of Critical Failure Mode (CFM) is done using equation 3:
CFM (M*) = Min [RPC (MJ, RPC (M2), RPC (M3)} MiЄA
CFM (M*) = Min {L8, L8, L7} = L7 = RPC (M3)
Based on the CFM analysis, the most preferable mould design is M3. But still a tie exists between the other two mould designs. This tie could be overcome by using the tie ranking rule mentioned in equation 4.
Tie raking rule for M1 and M2 is: T (Mi) = N (Mi) where N (Mi) is the number of times Lij < L7
Therefore, T (M1) = 1; T (M2) = 2
Since T (M1) < T (M2), M1 is the preferable mould design than M2.
Hence the rank order of mould designs is M2, M3 and M1 respectively (refer column eight in Table 9)
Case (b): In the selection of mould design, i.e., in the present context, it is essential to define different levels of importance for the three indexes S, O and D. This is because disagreed values are assigned by the FMEA team members for each index. Therefore, traditional FMEA approach based on RPN cannot be applied for mould design selection.
The FMEA team members of the industry decided to assign different levels of importance for the indexes S, O and D as given below. Generally, occurrence (O) is given the highest rating followed by severity (S). Detection (D) is given least rating. This is due to the practical considerations imposed for the CO2 sand casting method in the industry.
I (S) = L8; I (O) = L10; I (D) = L6
By applying equation (2) to (4), the results obtained are shown in columns (9) and (10) in Table 9. Further analysis of Table 9 has been described in section 4.
3.2 Validation using Modified AHP
The same mould design cases solved using FEAROM method is also attempted using the AHP. Case (a): As applied for FEAROM approach, maximum importance value 10 is considered for the three characteristics indexes S, O and D. The three mould designs Mi, M2 and M3 are considered as alternatives and the indexes S, O, and D are the evaluation criteria. The relative weight of indexes and mould designs are calculated using equation (5) and is shown in step1and step 3 respectively.
Step 1: Pairwise comparison matrix
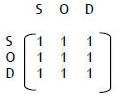
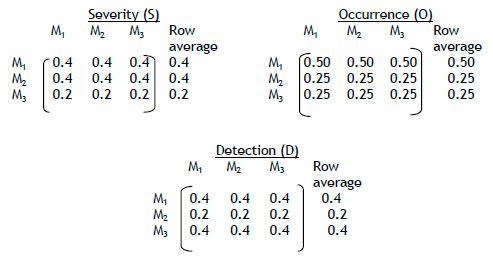
Step 2: Formation of normalized matrix
Elements value = original value (from pairwise matrix)/Total column value

The weights of various criteria are as follows:
Severity (S) = 0.33
Occurrence (O) = 0.33
Detection (D) = 0.33
Step 3: Compare the mould designs (alternatives) with respect to each criteria
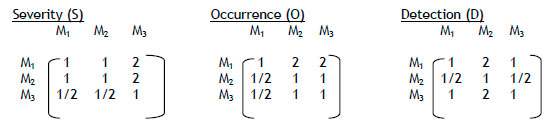
The weights are calculated as described in step 2 and the following matrices are obtained.
Step 4: Computation of weights for mould designs
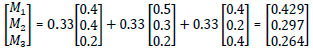
The alternative with the lowest overall priority is ranked first and so on. Mould design M3 has the least weight than the other two mould designs. The rankings are shown in Table 10.
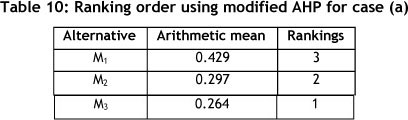
Step 5: Check for consistency
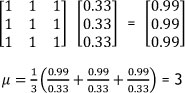
The consistency ratio (CR) 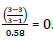 . Because CR value is less than 10%, the present matrix is consistent.
. Because CR value is less than 10%, the present matrix is consistent.
Case (c): In concurrence with FEAROM, the importance values 8, 10 and 6 are considered for the three characteristics indexes S, O and D respectively.
Step 1: Pairwise comparison matrix

Step 2: Formation of normalized matrix
Elements value = original value (from pairwise matrix)/Total column value

The weights of various criteria are as follows:
Severity (S) = 0.260
Occurrence (O) = 0.634
Detection (D) = 0.106
Step 3: The same as before
Step 4: Computation of weights for mould designs
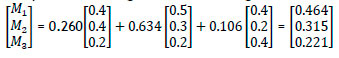
The alternative with the lowest overall priority is ranked first and so on. Mould design M3 has the least weight than the other two mould designs. The rankings are shown in Table 11.
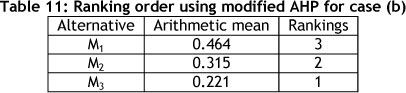
Step 5: Check for consistency

The consistency ratio (CR) is (((3.04 - 3)/2))/0.58 = 0.0345 = 3.45%. Because CR value is less than 10%, the present matrix is consistent.
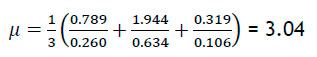
4. RESULTS AND DISCUSSIONS
As discussed in the previous sections, a modified FMEA approach termed FEAROM is applied for selecting the best mould design out of three alternatives. The detailed data related to the GTV valve sand casting given in Table 8 is used for identifying the best mould design. The best mould design is selected using FEAROM method based on the calculated RPC values (shown in Table 9). Two different cases are solved using FEAROM method. One is considering equal importance for all the three indexes (S, O and D) and the other is considering different importance ratings for S, O and D. The former case alone can be solved using the traditional FMEA approach. Traditional FMEA cannot be applied for the latter case. But the proposed FEAROM methodology can solve both the cases. FEAROM selects the mould design M3 in both the cases.
Analysis of the data in Table 9 reveals that the mould design M3 is ranked as first in both case (a) and case (b) using FEAROM model. But the mould design M2 is ranked as first using traditional FMEA method (refer Table 9) which does not match with practical result. This leads to difficulty in selecting the best mould design.
To validate the decision obtained using FEAROM method, modified AHP method is also applied to the same data set shown in Table 9. It is evident from Tables 10 and 11 that modified AHP method also selects mould design M3 for both the cases. Therefore, the outcome of the FEAROM method matches with the results of the proven AHP method. Table 12 depicts the mould design selected using the three methods, viz., traditional FMEA, FEAROM and modified AHP method.

Based on the analysis, mould design M3 is selected by the design team. Therefore, the potential failures in the mould design M3 needs to be eliminated before final approval. The FMEA design team recommended 100 x 150 mm open riser instead of 89 x 150 mm open riser in the pattern to eliminate the problem of shrinkage.
The mould design M3 is implemented and the preproduction trial of the GTV valve body is cast using the altered pattern. The post trail-production analysis is carried out and the castings obtained using M3 is found to match the acceptable standards of the customer. Hence the same was adopted by the industry for their batch production.
5. CONCLUSION
This research paper has demonstrated and substantiated the application of the novel method named FEAROM to prioritize the mould design for a GTV valve body. Two cases were solved for the considered data set. The first case equally rates the indexes S,O and D. Whereas the second case rates index O higher than index S. Index S in-turn is rated higher than index D. Traditional FMEA does not solve the second case. Also, in case of a tie in RPN, traditional FMEA could not select the best method. The proposed FEAROM method is able to overcome the above mentioned difficulties. Based on the outcome of FEAROM method mould design M3 was selected. Modified fuzzy AHP method was also applied to the same data set to verify the FEAROM outcome. Modified AHP method also indicated that mould design M3 is better for both the cases. Thus validation of FEAROM model was made. The preproduction trials were carried out using the proposed mould design M3 and the quality of the obtained castings was found to be good. Therefore, FEAROM method can be used for finalizing the mould design for similar sand casting components in future orders during their preproduction trials. The method is also very simple and straight forward and can be used for making multi-criteria decision quickly.
REFERENCES
[I] Ahmed, J.U. 1996. Modern approaches to product reliability improvement, International Journal of Quality and Reliability Management, 13, pp.27- 41. [ Links ]
[2] Dowlatshahi, S. 2001. The role of product safety and liability in concurrent engineering, Computational Industrial Engineering, 41, pp.187- 209. [ Links ]
[3] Lu, Y. 2002. Analyzing the reliability problems in concurrent fast product development processes, PhD thesis, National University, Singapore. [ Links ]
[4] Abdul Samat, H., Kamaruddin, S. & Abdul Azid, I., 2012. Integration of overall equipment effectiveness (OEE) and reliability method for measuring machine effectiveness, South African Journal of Industrial Engineering, 23(1), pp. 92-11. [ Links ]
[5] Wang, Y.M., Chin, K.S., Kwai Poon, G.K., & Yang, J.B. 2009. Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean, Expert System Applications, International Journal, 36, pp. 1195-120. [ Links ]
[6] Chang, C.L., Wei, C.C., & Lee, Y.H. 1999. Failure mode and effects analysis using fuzzy method and grey theory, Kybernetes, 28, pp.1072- 1080. [ Links ]
[7] Franceschini, F., & Galetto, M. 2001. A new approach for evaluation of risk priorities of failure modes in FMEA, International Journal of Production Research, 39, pp.2991- 3002. [ Links ]
[8] Sellapan, N. & Karuppusami, G. 2009. A New Approach for Prioritization of Failure Modes in Design FMEA using ANOVA, World academy Science, Engineering and Technology, 49, pp.524-531. [ Links ]
[9] Chen, L.H., & Ko, W.C. 2009a. Fuzzy linear programming models for new product design using QFD with FMEA, Applied Mathematics Modeling, 33, pp.633-647. [ Links ]
[10] Chen, L.H. & Ko, W.C. 2009b. Fuzzy approaches to quality function deployment for new product design, Fuzzy Sets and Systems, 160, pp.2620-2639. [ Links ]
[11] Zhang, Z. F., & Chu, X. N. 2011. Risk prioritization in failure mode and effects analysis under uncertainty. Expert Systems with Applications, 38, pp.206-214. [ Links ]
[12] Liu, H.T. 2009. The extension of fuzzy QFD: From product planning to part deployment, Expert Systems with Applications, 36, pp.11131-11144. [ Links ]
[13] Bowles, J. B. & Pelaez, C. E. 1995. Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis, Reliability engineering and system safety, 50, pp.203-213. [ Links ]
[14] Braglia, M., Frosolini, M. & Montanari, R. 2003. Fuzzy criticality assessment model for failure modes and effects analysis, International journal of Quality & Reliability Management, 20 (4), pp. 503-524. [ Links ]
[15] Garcia, P.A.A., Schirru, R., Frutuoso, P.F. & Melo, E. 2005. A Fuzzy data envelopment analysis approach for FMEA, Progress in Nuclear Energy, 46(3- 4), pp.359-373. [ Links ]
[16] Guimaraes, A.C.F., & Lapa C.M.F. 2004. Effect analysis fuzzy inference system in nuclear problems using approximate reasoning, Analysis of Nuclear Energy, 31(1), pp. 107-115. [ Links ]
[17] Pillay, A., & Wang, J. 2003. Modified failure mode and effects analysis using approximate reasoning, Reliability Engineering and System safety, 79, pp.69-85. [ Links ]
[18] Wong, B.K. & Lai, V.S. 2011. A survey of the application of fuzzy set theory in production and operations management: 1998 - 200, International Journal of Production Economics, 129, pp.157168. [ Links ]
[19] Francis, R.L., & White, J. A. 1984. Facilities Layout and Location - An analytical approach, PHI, Chapter 2, pp. 21-55. [ Links ]
* Corresponding author














