Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.2 Pretoria Jan. 2013
GENERAL ARTICLES
A study of R2R control improvement using adjustment limit to reduce frequency of control
C. C. Wang
Department of Industrial Engineering and Management Ming Chi University of Technology, Taiwan. ieccwang@mail.mcut.edu.tw
ABSTRACT
In the traditional run-to-run (R2R) control scheme, the controller provides the feedback strategy, enabling each run of process output to remain as close to the target as possible. However, in practice this process encounters bottlenecks if all the runs are started with a control parameter adjustment, as this will increase process variation in the stable process. In this paper, an improved R2R control scheme is developed to add an adjustments limitation technique to both the EWMA controller and the self-tuning controller. From the simulation, analysis of the results shows that the proposed procedure can effectively reduce the frequency of controller adjustments, without affecting the capability of the original controller. Therefore, in practical applications, the proposed control framework can be used to prevent the problem of process over-control.
OPSOMMING
In 'n lot-tot-lot beheerskema, verskaf die beheerder tradisioneel terugvoer sodat elke proseslopie so na as moontlik aan die teiken is. In die praktyk ervaar hierdie proses egter opeenhopings wanneer al die lopies begin is met 'n beheerparameter verstelling, aangesien dit prosesvariasie in 'n andersins stabiele proses veroorsaak. In hierdie artikel word 'n verbeterde lot-tot-lot beheerskema ontwikkel om 'n limiet-verstellingstegniek tot die eksponensieelgeweegde bewegende gemiddeld beheerder (EGBG) en die selfverstellende beheerder by te voeg. Die simulasieresultate toon dat die voorgestelde prosedure die frekwensie van beheerderverstellings effektief kan verminder sonder om die vermoë van die oorspronklike beheerder te affekteer. Die voorgestelde beheerraamwerk kan dus in die praktyk gebruik word om proses oorbeheer te voorkom.
1. INTRODUCTION
The manufacturing process in the semiconductor industry is highly complex because continuous production creates difficulties in quality control. In the past few years, run-to-run (R2R) control techniques have been developed and applied in numerous process controls. The R2R control methods integrate the statistical process control (SPC) and engineering process control (EPC) techniques to update the process parameters, improving the product quality of subsequent runs. SPC is an offline quality improvement technique that recognises the special cause of process variation in traditional manufacturing processes, but that is unable to make on-line adjustments, and cannot prevent critical situations in continuous semiconductor production. In 1980, certain scholars proposed combining EPC with SPC. The integrated method of EPC and SPC depends on mature measuring and control technology. Ingolfsson & Sachs [1] extended the concept of integration by proposing the application of the R2R control method to silicon wafer production processes. The results showed that the implementation of the R2R control method was beneficial for these processes. Furthermore, some scholars have suggested the R2R application for semiconductor manufacturing processes. Masatoshi & Ken [2] implemented a novel feed-forward technology for gate trim etching to obtain accurate critical dimension (CD) control for 130 nm node application-specific integrated circuit (ASIC) manufacturing. In addition, several scholars [3,4,5] applied the concept of R2R control to improve the chemical-mechanical planarisation (CMP) process. The R2R control method is based on the integration of SPC and EPC, enabling the adjustment of equipment parameters to reach the optimal process control. The design of R2R controllers is generally divided into two stages: (1) the design of experiment (DOE) is employed to construct the initial model, which is subsequently used to calculate an optimum control foundation; and (2) the R2R controller modifies parameters after each run.
In many practical applications, combining SPC and EPC is advantageous because it enables quick detection and removal of special cause variation. However, this method is difficult to use in the semiconductor manufacturing process. Integrating SPC and EPC does not completely solve the demands of actual processes. In the initial stage, unstable processes gradually stabilise after the required adjustment, and do not need excessive control. Jiang et al. [6] suggested adding an exponentially-weighted moving average (EWMA) control chart on the R2R EWMA controller to adjust the process parameters. The results show that small variations of response not only steadily control the situation, but also require fewer adjustments. However, if the processes have a high correlation (Φ>0.7), the EWMA controller will not be applicable. In this paper, the problem will be solved.
Most relevant literature focuses on the research method of R2R controllers or improvements of control algorithms based on quantitative measurements [7,8,9,10]. Recently, R2R controllers based on qualitative measurements have been proposed [11,12]. Wang & Tsung [11] considered the deep reactive ion etching process to propose a categorical controller for the R2R processes. Shang et al. [12] proposed a new improved categorical R2R controller to reduce the effect of misclassification on the process. However, the idea of using warning boundary integration to reduce control frequency has not been studied in relation to the R2R controller. In addition, in the traditional R2R control scheme, the process controller provides feedback control through the process output, affecting the approximation of each run to the target as much as possible. In practice, this control scheme is problematic: if all the runs are executed with the parameter adjustment in the stable process, the process is likely to generate the phenomenon of over-control. Dr Deming has said: "If anyone adjusts a stable process for a result that is undesirable, or for a result that is extra good, the output that follows will be worse than if he had left the process alone." Therefore, in any process, there is a danger of over-controlling the process. In this paper, the improvement control scheme will be proposed to solve the problem of over-control.
The manufacturing process can generally be divided into three stages: (1) the machining warm-up period, when the process can affect the machine equipment or raw materials leading to a large variation, thus requiring more control; (2) the stabilisation period, when the process is stable and process variation is minimal, thus making control unnecessary; (3) equipment wear resulting from the aging process, when materials usually need to be replaced or reset, and manufacturing equipment needs to be adjusted to ensure process stability. Therefore the process parameters do not require frequent adjustments from beginning to end. This study proposed a novel control procedure that integrated the adjustment limit scheme to improve self-tuning, and EWMA controllers for the single-input-single-output (SISO) process control system. When the process output exceeds the adjustment limit, the self-tuning or EWMA controller is started, which regulates the process parameter so that the next run can be close to the target value. The analysed results show that the proposed process control scheme could efficiently reduce the number of process parameter adjustments without increasing the variance of the process output.
2. METHODOLOGY
Run-to-run (R2R) process control methods are significant in the field of semiconductor manufacturing. The main objective is to use on-line model tuning to update the process so that the product quality of the next run can be close to the target. Due to the development of the R2R control in the initial stage, numerous practical examples assume that other variables remain unchanged and use a single controlled variable adjustment. Furthermore, the exponentially-weighted moving average (EWMA) controller and the self-tuning controller are the most popular R2R control methods in the semiconductor manufacturing industry. Therefore, in this paper the added adjustment limit technique is proposed to improve the EWMA controller and the self-tuning controller.
2.1 EWMA control for the single-input single-output process
The EWMA controller is a feedback control method. The controller predicts response feedback to adjust the process control parameters, and enables the process response to approach the target in the next run. The EWMA controller for the SISO process is described as follows:

where yt is the quality characteristic of the process output, a is the process offset, β is the process gain, and a and β are the unknown parameters that must be estimated from the historical data. In addition, the noise term  is assumed white, i.e
is assumed white, i.e Equation (1) can be derived as follows:
Equation (1) can be derived as follows:

The EWMA controller can only estimate and replace the interceptor. The coefficient of b is determined by the experiment in the actual process. When equation (2) was applied to the EWMA controller, the error et calculated by the real output and estimated output was:

Therefore the revised equation of EWMA becomes the following:

where λ is the predicted weight between 0 and 1. If equations (2) and (3) are combined into equation (4), then equation (4) can be derived as follows:

The EWMA controller used equation (5) to determine the estimated output by the continually revised technique. The adjusting control parameter can therefore be derived as:

where µι is the input at the time t, Τ is the target value, and the other parameters are defined as in equation (2). This feedback control rule can be rewritten as the backward difference operator and equation (5) can be revised to:
and equation (5) can be revised to:
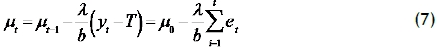
where µο = (T - a0)/b and et = yt - Τ.
2.2 Self-tuning control for the single-input single-output process
The self-tuning controller is an on-line estimating method that can provide satisfactory control performance for short run production. The unknown process parameters are continuously estimated by using the recursive estimation technique. The self-tuning (ST) is based on an idea of separating the estimation problem from the controller design problem, known as the 'separation theorem'. This controller can be designed as a proportional-integral-derivative, a generalised minimum variance, or a constrained input philosophy. Del Castillo [11] regarded the self-tuning controller as feasible for the R2R control method in the SISO system. The self-tuning model can evaluate the response trend and compensate for errors of the target value. The self-tuning model is described as follows:

where yt is the quality characteristic of the process output, a is the process offset, and β is the process gain.
If the process has a deterministic trend, then Dt = dt+Nt, where Dt is the disturbance term and d is the deterministic drifting rate per hour. Nt is the noise term in the form of an Autoregressive Integrated Moving Average (ARIMA) model. If Nt follows ARIMA (1,0,1), then  , where c is the first-order moving average (MA) coefficient, and w is the autoregressive (AR) coefficient. The noise term st is assumed to be white noise,
, where c is the first-order moving average (MA) coefficient, and w is the autoregressive (AR) coefficient. The noise term st is assumed to be white noise, 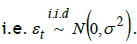
2.3 Adjustment limit scheme
This study proposed to add an adjustment boundary technique to improve the efficiency of the controller (EWMA and self-tuning). The adjustment limit is calculated by the target value and the receivable variance of the process. In practice, the target value (T) and the receivable variance of the process given by the historical data. The adjustment limits can be calculated by
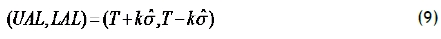
UAL is the upper adjustment limit, and LAL is the lower adjustment limit. If k is set near 0, the width of the limits would be narrow, and vice versa. The width of the adjustment limits affected the variance of responses. This study set eight different values of k (0.02, 0.025, 0.05, 0.1, 0.3, 0.5, 0.7, and 1) and follow-up was used to assess their difference. Because the only source of variance was εt,  was the variance of εt, and set
was the variance of εt, and set  = 1.
= 1.
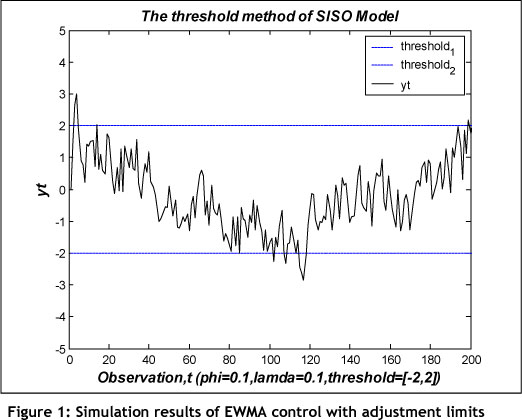
Figure 1 shows the simulation result for EWMA control with adjustment limits. The EWMA control parameters were set at Φ=0.01 and λ = 0.1, and adjustment limits were ±2. According to Figure 1, the initial stage was unstable and required control; after a period the process stabilised and no significant control was needed, and the result was stable. Therefore, as shown in Figure 1, the controller only started when the adjustment limits exceeded 200 runs. The results show that when the process variations are in the interval of the adjust limits, it means that the process is stable. The R2R controller should not begin at startup to avoid an 'over-control' problem and to avoid incurring additional costs.
The simulation technique was used to evaluate the effects of the process output by integrating adjustment limits in the R2R control. However, the approach when setting the adjustment limits was of concern, because the adjustment limit settings affect the cost of production and quality. Therefore the Mean Square Error (MSE) index was used to evaluate the control result and find reasonable adjustment limits to reduce the adjustment frequency and manufacturing costs further. The MSE is defined as follows:

where yi is the quality characteristic of the process output, yt is the target, and η is the number of runs. If the MSE is small, the variance between process responses is small, which means that the process is well-controlled.
Once the adjustment limits are integrated, the R2R controller does not adjust the process parameter on each run, thus decreasing the variance of response. To verify the effect of process variation, the F-test was used to validate the MSE of a traditional r2r control with adjustment limits incorporated into the R2R control. The F value determines the influence of the response variance in different control methods and parameter settings. The F value is defined as follows:

3. ANALYSIS AND RESULTS
This study simulated four different control strategies to compare the control results. The EWMA and self-tuning controllers were used as the baseline for comparison. The other two were used to integrate the adjustment limits on the EWMA and the self-tuning controllers, and the process parameters were only adjusted when the process response exceeded the adjustment limits. This paper simulated more than 200 different process data in the four different control strategies, using the s-plus® program. The simulated process parameters were set at α = 2.0, β=2.0, c=0.5, w=0.2, T = 0, and λ=0.1; and the auto regressive parameters were set at Φ=0.01, 0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95, and 0.99. The widths of the adjustment limits were ±0.02, ±0.025, ±0.05, ±0.1, ±0.3, ±0.5, ±0.7, and ±1, and the initial parameters of self-tuning were (ø,β,d)=(1,-1,-1). Table 1 shows the comparison of the EWMA and self-tuning control results for different autoregressive values. For the EWMA algorithm, the MSE value is increased along with the increase in the autoregressive parameters, and showed how control results occur with a lower autoregressive value.
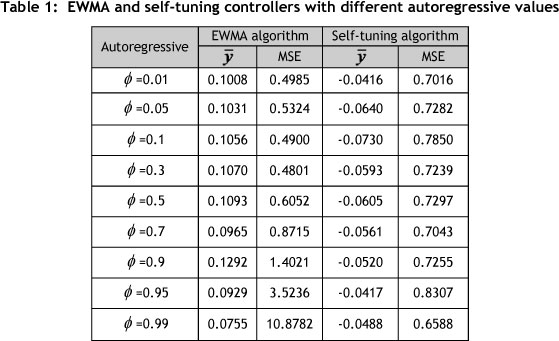
After dropping the unstable part in the initial stage, the self-tuning control produced lower MSE results than the EWMA control in the higher autoregressive process (Φ ≥0.7). Table 2 shows the comparison of the results of the EWMA and self-tuning controllers with the integrated adjustment limits for different autoregressive values. The p-value is calculated from the F-value (equation 10). If the p-value is larger than 0.05, the process response variation does not increase due to the integrated adjustment limits on the controller. From Table 2, the results show that the MSE increased significantly in the lower autoregressive process. Even when adjustment limits were integrated into the EWMA controller, the MSE still increased in the higher autoregressive process. However, when the self-tuning control integrated with the adjustment limits was used, the high and low autoregressive processes were still stable (adjustment limits <±0.5). Therefore, the simulation found that integrating the adjustment limits on the controller (EWMA controller, self-tuning controller) could reduce the control adjustment frequency without increasing the MSE value (tables 1 and 2).
In the past, the EWMA control has not been applicable in the high autoregressive (Φ>0.7) process. However, using adjustment limits on the EWMA control can overcome this bottleneck - that is, the proposed method can be applied to high autoregressive processes. In addition, if the beginning of the process response was unstable, by using the self-tuning controller after a period the process can become stable. The self-tuning controller can be used after eliminating the unstable responses to achieve the same results with the EWMA controller if the process has lower corrections (Φ<0.7). In other words, when the processes have lower autoregressive values, the EWMA and self-tuning controllers are the same as the control ability in the R2R process. However, if the process has high autoregressive values, the self-tuning control can produce a lower MSE. Therefore, according to the simulated analysis results, the self-tuning control is better than the EWMA control capability.
To explain further: using the adjustment limits that have been added to the self-tuning control can achieve the same control effect and reduce the control frequency. However, the adjustment limits could not be carelessly set up. Under the setting of the process parameters, the adjustment limits were found to mismatch by more than ± 0.1 when the auto regressive processes were extremely low(Φ<0.1) or exceedingly high (Φ>0.7), as shown in Table 2. According to the analysis results, we suggest that the adjustment limits could be set at ±0.05.
4. CONCLUSION
In semiconductor processing, chemical concentration is often used as the main parameter of process control. However, chemicals are expensive, so producers need to consider the cost of control. The adjustment limits were determined for the start of the control mechanism. From an analysis of the results, the proposed method can reduce the number of process parameter adjustments, and maintain the process in a stable state.
According to the analysis results, regardless whether the autoregressive processes were high or low, the adjustment limits should not exceed ±0.1. High adjustment limits would reduce the high frequency of controls. But this control result would have a greater MSE value for the process output. Therefore, setting suitable adjustment limits is key to the success of the proposed method.
When the adjustment limits begin, the process responses appear as a higher MSE in the initial stage, and require adjustments for each run. However, after a series of runs, the processes stabilise and adjusting each run process becomes unnecessary. Users can select historical response values to estimate the response value of the next run, and can calculate the MSE (that is, the t to t-4 run response values and the  of the t+1 run can be selected to estimate the MSE). When the MSE stabilises (MSE <1), it can begin the adjustment limits and regulate the process parameters in the next run when the predicted response is over the adjustment limit. If the MSE is unstable, the process parameters must be adjusted in each run until the MSE is acceptable.
of the t+1 run can be selected to estimate the MSE). When the MSE stabilises (MSE <1), it can begin the adjustment limits and regulate the process parameters in the next run when the predicted response is over the adjustment limit. If the MSE is unstable, the process parameters must be adjusted in each run until the MSE is acceptable.
Table 3 compares the four different control strategies for their strengths, weaknesses, and application situations. Because the self-tuning controller, when combined with adjustment limits, can reduce the frequency of controls, the cost of the production process can be controlled without increasing the MSE value. Moreover, each run was chosen to cause over-control problem which could also be effectively improved. Therefore this control scheme is suggested as the best for the R2R process, and it satisfies customer requirements. In practice, the engineer can use the results of this study in the R2R process, thus efficiently reducing process variation, controlling costs, and manufacturing high-quality products.
REFERENCES
[1] Ingolfsson, A. & Sacha, E. 1993. Stability and sensitivity of an EWMA controller, Journal of Quality Technology, 25(4), pp. 271-287. [ Links ]
[2] Masatoshi, N. & Ken, T. 2004. Advanced gate etching for accurate CD control for 130-nm node ASIC manufacturing, IEEE Transactions on Semiconductor Manufacturing, 17, pp. 281-285. [ Links ]
[3] Patel, N.S. & Jenkins, S.T. 2000. Adaptive optimization of run-to-run controllers: The EWMA example, IEEE Transactions on Semiconductor Manufacturing, 13(1), pp. 97-107. [ Links ]
[4] Guo, R.S., Chen, A. & Chen, J.J. 2000. Run-to-run control schemes for CMP process subject to deterministic drifts, Semiconductor Manufacturing Technology Workshop, pp. 251-258. [ Links ]
[5] Jen, C.H., Jiang, B.C. & Fan, S.K.S. 2004. General run-to-run (R2R) control framework using self-tuning control for multiple-input multiple-output (MIMO) processes, International Journal of Production Research, 42(20), pp. 4249-4270. [ Links ]
[6] Jiang, B.C., Wang, C.C., Jen, C.H. & Luo, L.C. 2009. Combining EWMA control chart to reduce process control frequency for run-to-run (R2R), Journal of Quality, 16(4), pp. 333-243. [ Links ]
[7] Jiang, B.C., Wang, C.C., Jen, C.H & Wu, M.Y. 2009. A run-to-Run controller using fuzzy neural network techniques for SISO process, Expert Systems with Application, 36, pp. 12044-12048. [ Links ]
[8] Jen, C.H. & Jiang, B.C. 2008. Combining on-line experiment and process control methods for changes in a dynamic model, International Journal of Production Research, 46(13), pp. 3665-3682. [ Links ]
[9] Jiang, B.C., Wang, C.C., Lu, J., Jen, C.H., & Fan, S.K. 2009. Using simulation techniques to determine optimal operational region for multi-responses problems, International Journal of Production Research, 47(12), pp. 3219-3230. [ Links ]
[10] Jen, C.H., Jiang, B.C. & Wang, C.C. 2011. Integration R2R control schemes and on-line experiment for dealing with the changes in semiconducting dynamic processes, International Journal of Production Research, 49(19), pp. 5657-5678. [ Links ]
[11] Wang, K. & Tsung, F. 2007. Run-to-run process adjustment using categorical observations, Journal of Quality Technology, 39(4), pp. 312-325. [ Links ]
[12] Shang, Y., Wang, K., & Tsung, F. 2009. An improved run-to-run process control scheme for categorical observations with misclassification errors, Quality and Reliability Engineering International, 25, pp. 397-407. [ Links ]
[13] Del Castillo, E. 1996. A multivariate self-tuning controller for run-to run process control under shift and trend disturbances, IIE Transactions, 28, pp. 1011-1021. [ Links ]














