Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Industrial Engineering
On-line version ISSN 2224-7890
Print version ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.24 n.2 Pretoria Jan. 2013
GENERAL ARTICLES
Silver, copper and aluminium coatings for micro-material handling operations
S. MatopeI, *; A.F.Van der MerweII; Y.I.RabinovichIII
IDepartment of Industrial Engineering Stellenbosch University, South Africa. smatope@sun.ac.za
IIDepartment of Industrial Engineering Stellenbosch University, South Africa. revdm@sun.ac.za
IIIParticle Engineering Research Center, University of Florida, United States of America. yrabinovich@perc.ufl.edu
ABSTRACT
Micro-material handling has challenges accompanying it because of adhesive forces, which make the picking and placing of micro-parts difficult. The adhesive forces hinder the picking of a micro-part, and once picked, they pose even a greater challenge when attempts to release a micro-part are made. Van der Waals' forces are part of the adhesive forces and are always present between interacting surfaces in a micro-material handling operation. However, Van der Waals' forces can profitably be manipulated in a micromaterial handling operation. The paper reveals how the Van der Waals' forces can be advantageously used in micro-material handling operations involving silver, copper and aluminium coatings of rms surface roughness values ranging from 0.5 nm to 2.72 nm, which are produced by the electron beam evaporation (e-beam) method. These were found to exert Van der Waals' forces ranging from 17 nN to 314 nN, which can be used for reliable micro-material handling operations.
OPSOMMING
Die hantering van materiaal op 'n mikroskaal het uitdagings wat daarmee gepaard gaan as gevolg van kleefkragte. Kleefkragte bemoeilik die optel van 'n mikro-onderdeel en, wanneer dit eers opgetel is, is daar selfs 'n groter uitdaging wanneer die part geplaas en gelos moet word. Van der Waalskragte vorm deel van die kleefkragte en is altyd teenwoordig tussen opervlaktes wat met mekaar in aanraking kom wanneer mikro-materiale gehanteer word. Van der Waalskragte kan egter voordelig gemanipuleer word in 'n mikro-materiaalhanteringsituasie. Hierdie artikel toon hoedat Van der Waalskragte voordelig gebruik kan word wanneer silwer-, koper- en aluminiumbedekkings met 'n wgk oppervlakgrofheid tussen 0.5 nm en 2.72nm, wat deur die elektronstraalverdamping (e-straal) metode geproduseer word, gehanteer moet word. Daar is gevind dat hierdie bedekkings Van der Waalskragte tussen 17nN en 314nN uitoefen. Die Van der Waalskragte kan gebruik word vir betroubare mikro-materiaalhantering.
1. INTRODUCTION
The current trend in research is towards the miniaturization of components. The engineering world market is demanding more micro-products [1, 2]. However, the handling of micro-components in the assembling of these micro-products is still a challenge. Currently mechanical grippers, electromagnetic grippers, pneumatic grippers among others are used to handle these micro-parts. However, the use of these grippers may induce residual stresses strains and charges on the handled micro-components [3]. Electrostatic force actuated grippers have been used for micro-material handling purposes by Neugebauer et al. [4] in the assembly of piezo-ceramic sensors; by Fantoni [5] in the handling of metallic cylinders; and by Hesselbach et al. [6] in the picking and placing of glass spheres. However, the electrostatic forces may leave residual charges on the handled parts and in some cases an energy supply is required [3, 7]. Lambert et al.[8] used capillary force in the handling of watch ball bearings, but oxide layers may be formed on corrosive materials. On the other hand Van der Waals' forces do not exhibit these shortcomings. Their advantages are that they do note induce residual stresses, strains, charges and they do not require an external source of power for them to function [3]. Therefore, this paper explores how Van der Waals' forces can be utilised for micro-material handling purposes using samples prepared by electron beam evaporation (e-beam) method.
According to Lambert [9], for a material handling operation to be reliable, the principal force that actuates the gripper should be maximized, and the other forces minimized. Since this paper seeks to maximize the use of Van der Waals' forces in a micro-material handling operation, the other adhesive forces should be minimized. Electrostatic force can be eliminated or reduced by using the anti-static mat [10] or Faraday's cage [11]. Surface tension can be eliminated by introducing dry nitrogen to the micro-parts or evacuating the atmosphere in which the micro-parts are lying [9]. The Van der Waals' forces may be maximized by improving the nature or characteristics of the interacting surfaces.
A simple micro-material handling operation consists of three steps: the picking, transferring and releasing steps [12, 3]. It also consists of five interactive surfaces which are: the picking place's surface, two micro-part's surface, gripper's surface, and the placement position's surface. For a reliable pick-transfer-release cycle to be realized; the micro-gripper should exert more Van der Waals' force to overcome the combined effect of the Van der Waals' force of the picking position and the weight of the micro-part; during transfer the micro-gripper should continue exerting (on the micro-part) a Van der Waals' force which is larger than the weight of the micro-part or else the micro-part would drop; and for an effective release, the combined effect of the Van der Waals' force from the release surface and the weight of the micro-part should overcome the Van der Waals' force exerted by the micro-gripper.
2. THEORETICAL FRAMEWORK ON THE DEPENDENCE OF VAN DER WAALS' FORCES ON SURFACE ROUGHNESS
Van der Waals' forces depend on parameters that include material type, geometrical configuration, and the surface roughness of the interacting micro-parts [10]. Materials have different Hamaker constants depending on their types [13]. The Hamaker constants (AH) of silver (Ag), copper (Cu), aluminium (Al), and silica (SiO2) are: AH (Ag)= 4·10-19 J, AH (Cu) = 2·10-19 J, AH(Al)= 1.5·10-19 J, AH(SiO2) = 8·10-20 J [13, 14, 15]. Hamaker constant for the Van der Waals' force or dispersion force between two different materials 1 and 2, is calculated using the combination rule given by Equation 1, derived by Israelachvili [14]:
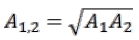
Analytical modelling of Van der Waals' forces with respect to the geometrical configuration has generally proven that a plane surface exerts more Van der Waals' forces than others because it affords more contact area [16]. Therefore, in this paper a plane surface is used for experimental purposes.
Rabinovich et al. [17, 18] have proven that Van der Waals' forces depend on surface roughness. The Van der Waals' forces are generally inversely proportional to surface roughness. The rougher the surface, the less is the exerted Van der Waals' forces. For a rough flat sample, within the framework of mono-roughness numerical model, the theoretical dispersion adhesion force (Van der Waals' force) can be calculated using Equation 2. This equation, besides taking the root-mean-square (rms) surface roughness values into consideration, also includes peak-to-peak separation distance of asperities of the surface roughness profile of a given micro-part [18]. The model of roughness, which was used to develop Equation 2 was substantiated in Refs. [18, 19]. Moreover, this equation was analyzed in Refs. [20-23] and it was shown that it gives correct results for calculating the Van der Waals' force acting between interacting surfaces whose rms values are in the nanorange.
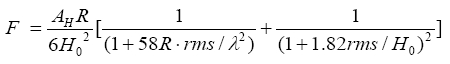
Where AH is the Hamaker constant, R is the radius of the interacting smooth sphere (or the radius of the cantilever tip of the atomic force microscope (AFM)), Ho is the shortest separation distance of the interacting samples at the contact position and is normally taken as 0.2 nm or 0.3 nm, rms is the root-mean-square surface roughness of the rough interactive surface of the micro-part, λ is the peak-to-peak distance of the asperities of the surface roughness of the given rough micro-part.
The theoretical model suggested in Refs. [17, 18], considers only one contact point between the rough interacting samples. This model was expanded by Drelich [21] by taking into account the multiple point interaction. The more precise model for adhesion force between rough solids was developed by Butt [24] and Butt et al. [25], who considered a roughness layer surrounding interacting samples for the calculation of capillary force. Butt [24] and Butt et al. [25] also considered the contribution of the dispersion force in the total adhesion force besides the capillary force.
Note that the theoretical model of [17] and [18] and Eq.2 are valid only for the rigid materials. For soft materials, as Tormoen & Drelich proved in Ref. [23], the deformation of the materials led to reduction or even elimination of the roughness effects on the adhesion force. This effect results in the development of large adhesion forces subsequent to large preloads.
In the present paper we used only the simplest model of Rabinovich et al. [17, 18] for comparison with experiment. The validity of this comparison between the theoretically calculated Van der Waals' forces and experimentally obtained values was done by the authors in [11]. The thrust of the present paper is towards the application of the silver, copper and aluminium coatings in the micro-material handling. It should be noted that this paper is based on three types of material coatings rather than two that were consider by the authors in [26].
3. MICRO-PARTS' SURFACE PREPARATION
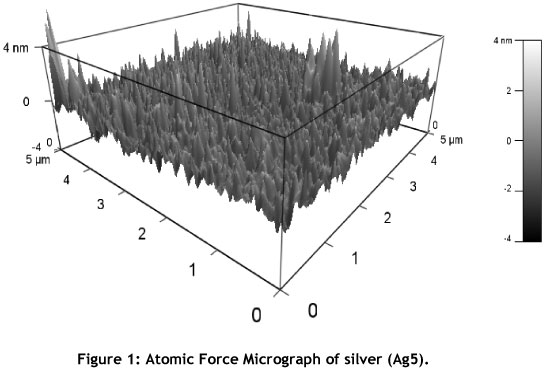
The electron beam evaporation method (e-beam) was used to prepare the samples following the same procedure whose detail is found in other works [11, 26, 27]. E-beam method involves the use of an electron beam of high energy to convert the samples from solid state to vapour state under vacuum conditions. The vapour in this case was deposited on a silicon substrate with a root mean square (rms) roughness of 0.43 nm. In this study, the vacuum pressures between 2x10-6 mbar and 3 x 10-6 mbar and deposition rates between 0.6 and 1.2 Angstroms/ second were used, same as in [11], [26] and [27]. The deposition time was either 5 or 20 minutes in each case. This method was used because it afforded the production of surfaces of relatively evenly distributed roughness, free of scratches, not hardened, not plastically deformed, without foreign inclusions and relatively homogenous in nature as shown in Figure 1 for a silver sample e-beam deposited for 5 minutes (Ag5). The Varian 3117 e-beam evaporator (machine) at iThemba laboratories was used for this operation: detailed procedure on its usage is in Ref. [27].
An Atomic Force Microscope (Asylum Research MFP3D AFM, Santa Barbara, CA) with colloid probe was used to measure the interaction forces between the e-beam deposited films and silica spheres glued on cantilevers, same as in [11] and [28]. Silica spheres (Bangs Laboratories, Inc. Fishers, IN) with radius of 2.5 Mm, and rms of surface roughness value of 0.2 nm were used. The AFM's cantilevers' type was Mikromasch NSC12 / tipless/ AlBS with stiffness, k, of 0.17 N/m and 0.27 N/m (of length 350 and 300 µm, respectively). A metallic grounded box (Faraday cage) was used to decrease or remove the effect of electrostatic force. Measurements were conducted under relative humidity of 20% as stated in [11, 29]. Silver, aluminium and copper e-beam coatings on silicon, which were deposited for 5 or 20 min, were examined. AFM probe's loading force was within 5 to 10% of adhesion force to prevent possible deformation of samples as in [11].
To produce the atomic force micrographs as shown in Figure 1, atomic force cantilevers (AC240TS, Olympus) with stiffness constant, k, of 2 N/m and with tip of radius 9±2 nm were used. These extra-sharp tips enabled the investigation of surface topography at a high resolution. The peak-to-peak distances were found to be approximately equal to 100 nm, significantly larger than the tip radius. The surface topography was obtained in contact mode as height's image as shown in Figure 1. The scan rate was 2 µΓη/s using 512 points per line. The surface roughness was calculated using standard AFM software.
4. ANALYSIS AND EVALUATION OF RESULTS
The silver, copper and aluminium coatings were found to have rms surface roughness values in the 0.5 - 2.72 nm range, while peak-to-peak distance was in the limit of 90±20 nm. The rms surface roughness of silver was in the lower range because it was smoother than the other two.
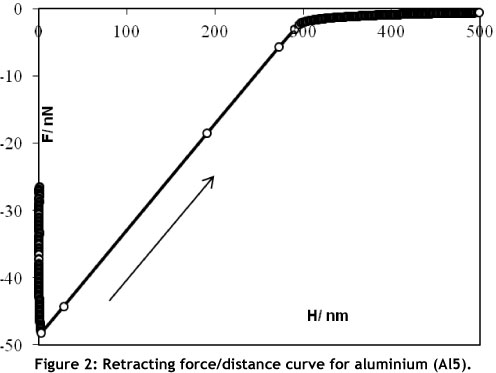
Figure 2 shows a retracting curve for aluminium e-beam deposited for 5 minutes (Al5). Retracting curve illustrates the value of the Van der Waals' adhesive forces measured when detaching the AFM silica spherical probe from the e-beam coated silicon wafer. The Van der Waals' force's value in Figure 2 is close to the statistical mean of several force measurements on the sample. The exerted Van der Waals' forces, obtained from retracting curves, for the three samples (silver, copper and aluminium) ranged from 17 nN to 314 nN.
The statistical distribution of the measured Van der Waals' forces had a standard deviation of 25% of the average force [11]. In addition to that, the possible systematic error due to calibration was about 5%. The obtained experimental values of adhesion forces were compared to theoretical values calculated with Equation 2 and were found to agree in the limit of statistical scatter [11].
The measured values of the exerted Van der Waals' forces between AFM silica sphere; and the silver, copper and aluminium e-beam prepared coatings are shown in Figure 3 as a function of the materials' surface roughness (rms). The theoretical curves, calculated with Equation 2, are also given in Figure 3 (by lines). It should be noted that Equation 2 assumes that the adhesion force involved is only Van der Waals' (dispersion) force. Since the jump-in distances (the minimum distance of approach of an AFM tip towards a target sample which results in the tip being rapidly attracted to the sample) measured on the samples by the atomic force microscope were less than 23 nm, this gave an assurance that the measured force was primarily Van der Waals' force. Other forces, for example electrostatic forces, are very strong and can cause jump-in distances of at least 300 nm.
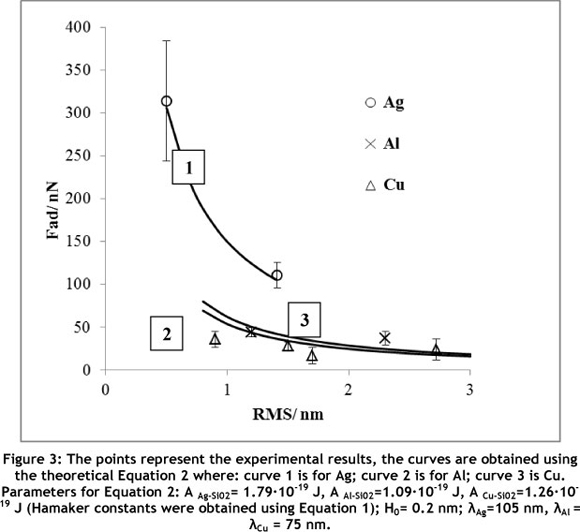
Figure 3 reveals that silver exerts the highest adhesion forces, aluminium and copper exerts lower adhesion forces. Figure 3 also shows that the Van der Waals' forces decrease as the rms surface roughness values increase. It can be noted that silver has the lowest rms surface roughness values and exerts the largest Van der Waals' forces; aluminium and copper have higher rms surface roughness values and exert smaller adhesion forces. Although the Hamaker constant of copper is a little bigger than that of aluminium, the experimental adhesion force of aluminium and copper are about the same in the limit of the statistical scatter.
Deducing from theory (Equation 2) and from experimental results (Figure 3) Van der Waals' force is directly proportional to Hamaker constant AH and decreases with increasing rms of surface roughness. Figure 3 proves the dominant role of the surface roughness in the adhesion force as compared to Hamaker constant. Actually, with reference to Equation 1; for two interacting pairs a and b: where pair a is of metal 1 (m1) with silica (si) sphere and pair b is of metal 2 (m2) with silica (si) sphere, the Hamaker constants are A12a = square root (sprt) of (Am1 Asi) and A12b= sqrt(Am2Asi ), where Am1 and Am2 are the Hamaker constants of the corresponding metals. Therefore, in turn, the ratio of the Van der Waals' force when these two pairs (a and b) interact with each other should be proportional to the ratio of the square root of (Am1/Am2). For an increase of Hamaker constant from 1.5-10-19J to 4·10-19 J (i.e. practically maximal possible range of Hamaker constants for metals) the Van der Waals' force between a metal and silica increases only by 1.63 times (the square root of 4-10-19 J /1.5-10-19 J); while an increase of rms of roughness from 0.4 to 3 nm (for the same Hamaker constant) yields an 8.65 times decrease in Van der Waals' forces when Equation 2 is used for calculations. It should be also noted that surface roughness of the micro-parts can be logically varied (for micro-part manipulation purposes using Van der Waals' forces), whilst the Hamaker constants are invariable for a given material.
Logical variation of rms of roughness of metallic samples can be performed by utilising corresponding e-beam's parameters. Relatively smooth silver (with rms of roughness within the range of 0.5- 0.7 nm) would be suited for the placement position's surface, copper with rms values within the range of 1- 1.5 nm would be appropriate for the gripper's surface and the aluminium with rms within the 2-3 nm range would be suitable for the picking position's surface. As a result, a copper gripper would pick micro-parts from an aluminium base and deposit them onto to a silver base.
It should be emphasized that in order for a micro-part to be picked the gripper should exert a higher Van der Waals' force than that exerted by the base material (on which the micropart rests). For example, if a 2.5 µm silica sphere (similar to the AFM silica spherical probe used in the measurements considered in this paper) is a micro-part to be handled, and given that its density is 2.648 g/cm3 [30], then its weight would be 1.7x10-3 nN. If the picking position is made of aluminium with rms surface roughness of 2.5 nm, the Van der Waals' force between flat aluminium and silica sphere (using Equation 2) will be 26.96 nN, which is significantly larger than the particle's weight (so weight can be ignored). Then, a micro-gripper made of copper with rms surface roughness of 1.2 nm which exerts 67.88 nN (calculated using Equation 2) could be used to pick the micro-part and release it onto a silver base with rms surface roughness of 0.5 nm which exerts 247.75 nN Van der Waals' forces (Equation 2). In these calculations, the experimentally measured peak-to-peak distance of 90 nm is used, and H0 is assumed to be equal to 0.2 nm. The force exerted by the silver is relatively larger than the other two materials which would result in a more reliable release action. Furthermore, the maximum weight of silica sphere which may be picked and placed using the Van der Waals' forces of e-beam generated surfaces discussed in this paper would be 40.92 nN, the difference between 67.88 nN (exerted by the gripper) and 26.96 nN (exerted by the picking position). This would give a silica sphere of a maximum radius of about 998 Mm (when the gravitational force per unit mass is taken as 9.81 N/kg).
5. CONCLUSIONS
The adhesive Van der Waals' forces exerted by plane coatings of silver, copper and aluminium developed on silicon substrates by e-beam method were investigated. Silver exerted the highest Van der Waals' forces because it had the smoothest surfaces of low rms surface roughness values and also had the largest Hamaker constant. It was also observed for silver that at the slightest increase in rms surface roughness value, there was a significant decrease in the exerted Van der Waals' forces. Aluminium and copper samples with smaller Hamaker constants and larger rms of roughness demonstrate smaller Van der Waals' forces than the silver samples. This gives an opportunity for the development of micro-material handling systems actuated by Van der Waals' forces. A reliable Van der Waals' force actuated micro-material handling systems requires that the micro-gripper's surface exerts more Van der Waals' force on the micro-part than the picking position's surface; and for a reliable release action the placement position's surface should exert more Van der Waals' forces on the micro-part than the micro-gripper. Experimental examination of the e-beam deposited coatings of silver, copper and aluminium revealed a wide range of the exerted Van der Waals' forces: from 17 nN to 314 nN, with silver exerting the largest forces. The relatively smooth silver samples of rms surface roughness of 0.5 nm exerted a Van der Waals' force of 248 nN making them suitable for the placement position's surface; copper samples of rms roughness of 1.2 nm exerted 68 nN making them appropriate for the gripper's surface; and aluminium samples of average rms roughness of 2.5 nm exerted a Van der Waals' force of 27 nN making them suitable for the picking position's surface. In a reliable Van der Waals' force actuated micro-material handling operation, a copper gripper would pick micro-parts from an aluminium base and deposit them onto a silver base.
ACKNOWLEDGEMENTS
Authors thank iThemba Labs in South Africa, Department of Industrial Engineering at the University of Stellenbosch at South Africa for financial support and the Particle Engineering Research Center (PERC) and the Center for Particulate and Surfactant Systems (CPaSS) at the University of Florida for the opportunity to perform experimental measurements.
REFERENCES
[1] Hesselbach, J., Wrege, J.& Raatz, A. 2007. Micro Handling Devices Supported by Electrostatic Forces. Annals of the CIRP-Manufacturing Technology, 56(1), pp 45-48. http://dx.doi.org/10.1016/j.cirp.2007.05.013 [ Links ]
[2] MINAM Position Paper. 2011. Ed: Dickerhof, M., Salomon, P., Gavillet, J.,Fillion, B., Duret, D., Ratchev, S., Zdebski, D., Gommel, U., Meyer, T., Wogerer, C., Neuy, C., Ledantec, M., Vuillermoz, P., Matthews, C., Bolt, P. & Anson, S. Paving the ground for the next generation of Micro Nano enabled Products in Europe, September 2011 pp 1-24. http://www.minamwebportal.eu/attachments/MINAM%20Position%20Paper.pdf [ Links ]
[3] Neugebauer, R., Koriath, H-J., Van der Merwe, A. F., MUller, M. & Matope, S. 2011. Study on Applicability of Adhesive Forces for Micro-material Handling in Production Technology. Proceedings of the International Conference on Industrial Engineering and Engineering Management for Sustainable Global Development, pp 55-1 to 55-12, Stellenbosch, South Africa. http://www.isem.org.za/index.php/isem/isem2011/paper/view/55/110 [ Links ]
[4] Neugebauer, R., Koriath, H.-J. & Muller, M. 2010. Planar electrostatic grippers for precise handling of piezoceramic micro-parts. Proceedings of the euspen International Conference, June 2010, Delt. http://publica.fraunhofer.de/dokumente/N-137447.html [ Links ]
[5] Fantoni, G. 2003. Assembly of mini and microparts: Development of anelectrostatic feeder. In Proc. of 6th Al.Te.M. Int. Conf. http://arp.unipi.it/dettaglioar.php?ide=73027 [ Links ]
[6] Hesselbach, J., Buttgenbach, S., Wrege J., Butefisch, S. & Graf, C. 2001. Centering electrostatic microgripper and magazines for microassembly tasks. In Proc. of SPIE Microrobotics and Micromanipulation, 4568, pp 270-277, Newton. doi:10.1117/12.444126 [ Links ]
[7] Peirs, J. 2001. Design of Micromechatronic Systems: Scale Laws,Technologies, and Medical Apllications. PhD thesis, KUL, Belgium. [ Links ]
[8] Lambert, P., Seigneur, F., Koelemeijer, S. & Jacot, J. 2006. A case study of surface tension gripping: The watch bearing. J. Micromech. Microeng , 16 (7), pp 1267-1276. http://dx.doi.org/10.1088/0960-1317/16/7Z021 [ Links ]
[9] Lambert, P. 2007. Capillary Forces in Microassemby: Modelling , Simulation, Experiments, and Case Study. Springer. [ Links ]
[10] Matope, S & Van der Merwe, A. F. 2010. Micro-material Handling Employing Van-der-Waals' forces. Proceedings of the International Conference on Competitive Manufacturing (COMA 10), pp 261-267, Stellenbosch. [ Links ]
[11] Matope, S., Rabinovich, Y. I. & Van der Merwe, A.F. 2012b. Van der Waals Interaction of silica with e-beam created metallic thin films. Colloids and Surfaces A, 411, pp 87-93. DOI: 10.1016.j.colsurfa. 2012.07.006 [ Links ]
[12] Fukuda, T. & Arai, F. 1999. Microrobotics. In Handbook of Industrial Robotics: Ed. Nof, pp. 187198. New York: John Wiley & Sons, Inc. [ Links ]
[13] Parsegian, V.A. 2006. Van der Waals' forces. A handbook for biologists, chemists, engineers, and physicists. Cambridge University Press, [ Links ]
[14] Israelachvili, J. N. 2011. Intermolecular and surface forces, Third Edition. Academic Press, Oxford. [ Links ]
[15] Rabinovich, Y. I. & Churaev, N.V. 1990. Results of numerical calculation of dispersion forces for solids, liquid interlayers and films. Colloid Journal of the USSR 52, pp 256- 262. [ Links ]
[16] Van der Merwe, A. F. & Matope, S. 2010. Manipulation of Van-der-Waals' Forces by Geometrical Parameters in Micro-material Handling. Journal for New Generation Sciences, 8(3), pp 152-166. http://www.sabinet.co.za/abstracts/newgen/newgen_v8_n3_a10.html [ Links ]
[17] Rabinovich, Y. I, Adler, J. J., Ata, A., Singh, R.K. & Moudgil, B. M. 2000. Adhesion between nanoscale rough surfaces. I. Role of asperity geometry. J. Colloid Interface Surf. 232, pp 10-16. http://dx.doi.org/10.1006/jcis.2000.7167 [ Links ]
[18] Rabinovich, Y. I, Adler, J. J., Ata, A., Singh, K. J.& Moudgil, M.B. 2000. Adhesion between Nanoscale Rough Surfaces II. Measurement and Comparison with Theory. Journal of Colloid and Interface Science , 232, pp 10-24. http://dx.doi.org/10.1006/jcis.2000.7168 [ Links ]
[19] Rabinovich, Y. I., Adler, J. J., Esayanur, M. S., Ali, A., Singh, R. K. & Moudgil, B. M. 2002. Capillary forces between surfaces with nanoscale roughness. Advances in Colloid and Interface Sci, 97, pp 213-230. [ Links ]
[20] Drelich, J., Tormoen, G. W. & Beach, E. R. 2004. "Determination of solid surface tension from particle- substrateetermination of solid surface tension from particle-substrate pull-off forces measured with the atomic force microscope". J. Colloid Interface Sci. 280 (2), pp 484-497. [ Links ]
[21] Drelich, J. 2006. "Adhesion forces measured between particles and substrates with nanoroughnesss." Minerals and Metallurgical Processing 23, pp 226-232. [ Links ]
[22] Tormoen G. W. & Drelich, J. 2005. "Deformation of soft colloidal probes during AFM pull-off force measurements: elimination of nano-roughness effects" J. Adhesion Sci and Tech. 19 (3-5), pp 181-198. [ Links ]
[23] Beach, E. R., Tormoen, G. W., Drelich, J. & Han, R. 2002. "Pull-off force measurements between rough surfaces by atomic force microscopy." J. Colloid Interface Sci. 247, pp 84-99 [ Links ]
[24] Butt, H.-J. 2008. Capillary forces: Influence of roughness and heterogeneity. Langmuir 24, pp 4715-4721. [ Links ]
[25] Butt, H. J., Farshchi-Tabrizi, M.& Kappl, M. 2006. Using capillary force to determine the geometry of nanocontacts. J Appl. Physics 100 (2). 024312. http://link.aip.org/link/doi/10.1063/1.2210188 [ Links ]
[26] Matope, S., van der Merwe A. F.& Rabinovich Y. I. (2012a). Micro-material handling employing e-beam coatings of copper and silver. South Africa Journal of Industrial Engineering, 23 (1), pp 114-121. http://sajie.journals.ac.za/pub/article/view/223 [ Links ]
[27] Matope S., Van der Merwem A. F., Nkosi, M., Maaza, M. & Nemutudi, R. (2011). Micro-material Handling Employing E-beam Generated Topographies of Copper and Aluminium. South Africa Journal of Industrial Engineering, 22 (2), pp 175-188. http://sajie.journals.ac.za/pub/article/view/24 [ Links ]
[28] Ducker, W. A., Senden, T. J.& Pashley, R. M. (1992). Measurement of forces in liquids using a force microscope. Langmuir 8, pp 1831- 1836. DOI: 10.1021/la00043a024. [ Links ]
[29] Rabinovich, Y. I., Sing, A., Hahn, M., Brown, S. & Moudgil, B. M. (2011). Kinetics of Liquid Annulus Formation and Capillary Forces. Langmuir 27, pp 13514- 13523. DOI: 10.1021/la202191c. [ Links ]
[30] Groover, M.P. (2011). Principles of Modern Manufacturing. John Wiley & Sons, Asia. [ Links ]
* Corresponding author














