Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Industrial Engineering
versão On-line ISSN 2224-7890
versão impressa ISSN 1012-277X
S. Afr. J. Ind. Eng. vol.23 no.3 Pretoria Jan. 2012
CASE STUDIES
The application of a computerised decision support system for generator maintenance scheduling: a South African case study
E.B. SchlünzI; J.H. van VuurenII, *
IDepartment of Logistics Stellenbosch University, South Africa. schlunzeb@gmail.com
IIDepartment of Logistics Stellenbosch University, South Africa. vuuren@sun.ac.za
ABSTRACT
In the generator maintenance scheduling (GMS) problem, a schedule is sought for the planned maintenance outages of generating units in a power system. The GMS model considered in this paper is formulated as a mixed-integer quadratic program assuming a reliability objective, subject to certain constraints. A generic GMS solution methodology is derived, capable of solving general GMS problem instances that conform to this model structure, and implemented in a computerised decision support system. The decision support system is then used to solve a real-life case study in the South African national power system.
OPSOMMING
In die generator-instandhoudingskeduleringsprobleem (GISP) word daar gesoek na 'n skedule vir die beplande instandhouding van kragopwekkingseenhede binne 'n kragstelsel. Die GISP-model wat in hierdie artikel beskou word, is 'n gemengde, heeltallige, kwadratiese program, en bevat 'n betroubaarheidsdoel, onderhewig aan sekere beperkings. 'n Generiese GISP-oplossingsmetodiek is ontwikkel om enige GISP van die vorm soos in hierdie model te kan oplos. Die oplossingsmetodiek word in 'n gerekenariseerde besluitsteunstelsel geïmplementeer, waarna 'n realistiese gevallestudie, binne die konteks van die Suid-Afrikaanse nasionale kragstelsel, daarmee opgelos word.
1. INTRODUCTION
The problem considered in this paper is known as the generator maintenance scheduling (GMS) problem, and involves finding a schedule for the planned preventative maintenance outages of generating units in a power system. Preventative maintenance of a generating unit is necessary to ensure that its life-expectency is prolonged and its power generating efficiency is maintained. Regular maintenance also ensures that the risk of an unplanned outage (i.e. failure) is kept to a minimum. However, finding good maintenance schedules for large modern power systems, especially when they are burdened by increasing electricity demands, is a very difficult task. Electricity utilities face growing challenges to ensure reliable electricity supply at cost-effective rates.
A number of different models and solutions for the GMS problem have been considered in the literature. Typically, some form of economic or reliability objective is chosen as the optimality criterion for the GMS problem. The most commonly chosen economic objective is the minimisation of operating cost, examples of which may be found in Edwin & Curtius [1] and in Kuzle et al. [2]. With some countries having deregulated their electricity market, competetive market environments have started to emerge, shifting the economic objective to maximise profit, as seen in Kim et al. [3]. Sueyoshi & Tadiparthi [4] developed a decision support system that may be used to analyse the effectiveness of different trading strategies in such a competitive market. The most commonly chosen objective for reliability is the levelling of the reserve load over the planning horizon. This objective may be achieved in a number of ways - most often by minimising the sum of the squares of the reserve loads, as done by Dahal & Chakpitak [5]. The above-mentioned objective functions were all formulated in a single objective environment. However, the GMS problem has also been formulated in a multi-objective environment by Huang et al. [6] and by Moro & Ramos [7].
The constraints of the GMS problem depend on the power system under consideration, but all GMS models require at least two sets of constraints. The first set is the so-called maintenance window constraint set, which ensures that each generating unit is scheduled for maintenance between a pre-specified earliest and latest time period. The second set is the so-called load constraint set, which ensures that the power system load demand is met during each time period over the planning horizon. Additional constraints, such as those considered by Kralj & Petrovic [8], may also be added to a GMS model.
There has been much research into solution techniques for the GMS problem, since the problem is typically a large combinatorial optimisation problem that is difficult to solve, suffering from the 'curse of dimensionality'. Suitable techniques should be able to obtain good or optimal solutions for such large problem instances within reasonable computational times. A review of the many solution techniques employed to solve the GMS problem may be found in Ahmad & Kothari [9]. In an exact solution approach, solution techniques include methods such as branch-and-bound algorithms, dynamic programming, and Benders' decomposition method [10]. Approximate solution approaches include solution techniques such as basic search heuristics, metaheuristics (including genetic algorithm [5], tabu search, simulated annealing [11], ant colony optimisation, particle swarm optimisation [12]), fuzzy logic modelling, and expert system approaches [13]. General purpose decision support systems such as the spreadsheet-based optimisation tool developed by Savic et al. [14] may also be used to solve the GMS problem.
The solution techniques employed in the GMS literature are typically optimised (in respect of parameter value specification) for a specific case study or theoretical benchmark test system. This optimisation process is usually very time-consuming, problem-instance specific, and user-dependent. In this paper we present a generic GMS solution methodology that is capable of solving general GMS problem instances conforming to a GMS model in the form of a mixed-integer quadratic program (MIQP). This methodology employs a hybridised simulated annealing (SA) algorithm for solving the GMS problem approximately, and is implemented in a computerised decision support system (DSS). The DSS is used to solve a large real-life case study in the South African national power system. The results that are obtained prove very promising.
2. MATHEMATICAL PROBLEM FORMULATION
The GMS model considered in this paper is formulated as a mixed-integer quadratic program (MIQP). Levelling the reserve load over the planning horizon is chosen as reliability objective, and is achieved practically by minimising the sum of the squares of the reserve loads. The constraints in the GMS model consist of adherence to maintenance windows, the system meeting the load demand together with a safety margin, adherence to maintenance crew (manpower) availability, and respecting general exclusion constraints.
2.1 Notation
The following notation is used to facilitate the GMS problem formulation: Indices
i index for generating units
j index for time periods
k index for generating unit subsets.
Sets
J set of indices for generating units
J set of indices for time periods
K set of indices for generating unit subsets
Jk subset of indices for generating unit subset fe.
Parameters
n number of generating units in the power system
m number of time periods in the planning horizon
e¡ earliest time period during which maintenance of generating unit i may begin
li latest time period during which maintenance of generating unit i may begin
d¡ maintenance duration of generating unit i
gi,j power generating capacity of generating unit i during time period j
Di system load demand during time period j
S safety margin as a proportion of the system load demand m? manpower required by generating unit i during its q-th period of maintenance
mqi manpower required by generating unit i when undergoing
m'p, i, j maintenance during time period j, if maintenance is started during time period ρ
Mj maximum available manpower during time period j
K number of generating unit subsets
Kk maximum number of generating units within generating unit subset k that are allowed to be in simultaneous maintenance during any time period.
Variables
Xi,j a binary decision variable of value 1, if maintenance of generating unit i starts during time period j, or zero otherwise
Yi,j a binary auxiliary variable of value 1, if generating unit i is in maintenance during time period j, or zero otherwise
rj the unused power during time period j, excluding the safety margin capacity.
Therefore, 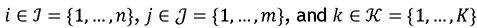 .
.
2.2 Mixed-integer quadratic program
The GMS problem formulation is the MIQP in which the objective is to minimise

subject to the constraints

The objective function in (1) is simply the sum of the squares of the actual reserve loads. Constraint set (2) is the maintenance window constraint set, while constraint sets (3) and (4) are added to set the variables outside the maintenance windows to zero, to reduce the number of dependent and independent variables. Constraint set (5) specifies that the maintenance of each unit should occur for a given duration, while constraint sets (6) and (7) ensure that the maintenance occurs contiguously. The load demand and safety margin constraints are specified in constraint set (8). Constraint set (9) ensures adherence to the maintenance crew constraints. The parameters m'p,i, j are calculated as
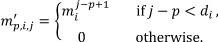
The general exclusion constraints are specified in constraint set (10). Finally, constraint sets (11) and (12) specify the nature of the variables.
3. SOLUTION APPROACH
As stated in the introductory section, we adopt a hybrid simulated annealing approach towards solving GMS problem instances approximately. A brief description of the general SA method is given below, before details of the hybridisation and our specific implementation are presented. Descriptions of the generic GMS solution methodology and the resulting computerised DSS then follow.
3.1 Simulated annealing
The SA method was first proposed by Kirkpatrick et al. [15]. It solves a combinatorial optimisation problem approximately, in a manner analogous to the physical process of annealing. Annealing may be used to strengthen metals by ensuring that their final physical state corresponds to the lowest energy state in which the metal particles lie in an ordered, crystal-like packing. This is achieved by heating the metal to a high temperature, and then slowly cooling it in stages, with sufficient time being spent at each temperature stage so that the particles settle in a low energy state, reaching thermodynamic equilibrium. If this controlled cooling strategy is performed correctly, the metal solidifies in a stable and strong state, corresponding to its lowest energy state. The metal is then said to be frozen.
The SA method is initialised with an initial solution of the problem under consideration, as well as a sufficiently high initial temperature T. A small modification is made to the solution (i.e., a neighbouring solution is generated) and the energy difference ΔE (i.e., the difference in objective function values between the original and modified solution) is calculated. For a minimisation problem, if the objective function value improves (ΔE < 0), the modified solution is accepted as the new solution. However, if ΔE > 0, the Metropolis acceptance rule is followed, where the solution is only accepted with probability exp(-ΔE/ T). Repeated iterations of this modification process lead to the system approaching equilibrium for a given temperature. If the system has reached equilibrium, a test is performed to determine whether the system has reached its final, frozen state. If it has not, the temperature is decreased according to a specific cooling schedule, and the process repeats. Otherwise the method terminates, and the current solution is the final solution provided by the method. A number of different approaches exist for choosing an initial temperature, cooling schedule, neighbourhood move operator (how the modifications are performed), and termination criteria (how to test for equilibrium and a frozen state). The flow diagram in Figure 1 illustrates the basic working of the SA method.
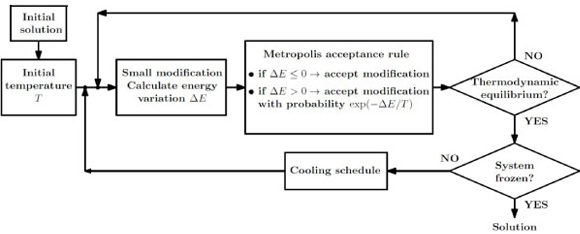
Figure 1: The general simulated annealing method
3.2 Solution methodology
In order to explore the solution space more effectively, and to make provision for highly constrained problems that do not necessarily have feasible solutions, our implementation of the SA algorithm allows a candidate solution of the GMS problem to violate any of the constraints. For such constraint violations, corresponding penalty values are incurred, and the total penalty value P, calculated as the weighted sum

is added to the objective function value associated with the candidate solution. The values Pw,Pℓ,Pc, and Pe are the constraint violations associated with the maintenance window, load demand, maintenance crew, and exclusion constraint sets, respectively; the values ww, wℓ, wc, and we denote the corresponding weights, respectively.
A solution to the GMS problem is denoted by a vector χ = (x1,xn) of length η where the element x¡ is an integer value representing the time period during which the maintenance of generating unit t starts. If a unit requires more than one maintenance outage, dummy units are added to the system for each additional outage of that unit, and their capacities are subtracted from the total system capacity.
3.2.1 The neighbourhood move operators
We implement two neighbourhood move operators within the SA algorithm, used for different purposes. The first move operator (found in the GMS literature [16,11]), hereafter referred to as the 'classical' operator, generates a neighbouring solution by randomly selecting one unit and randomly changing its maintenance starting time to a new value within its allowed maintenance window.
The second move operator, hereafter referred to as the 'ejection chain' operator, generates a neighbouring solution in the following way: an initial unit is randomly selected and its maintenance starting time is randomly changed to a new value within its allowed maintenance window; next, a unit whose maintenance starts during this newly selected maintenance starting time is randomly chosen, and its maintenance starting time is randomly changed to a new value within its allowed maintenance window. This procedure is repeated until the newly selected maintenance starting time corresponds to the original maintenance starting time of the first unit, or until no unit is found for which the maintenance starts during the newly selected maintenance starting time. The ejection chain operator acts more globally than the classical operator, exploring the solution space more effectively.
Any reference to random selection in the descriptions above is assumed to be according to a uniform distribution.
3.2.2 The local search heuristic
A hybridisation is achieved by introducing a local search heuristic into the SA algorithm. In the heuristic, an initial solution is received as an input and its full classical neighbourhood is explored. The best improving neighbour is then selected as the new solution. The process is repeated until no further improvement is possible.
3.2.3 Implementation of the hybrid SA algorithm
The hybrid SA algorithm is initialised with a randomly generated initial solution. For each unit i, a maintenance starting time period xt is chosen randomly, according to a uniform distribution, between the unit's earliest and latest maintenance starting time periods. Any possible constraint violations are calculated, and the total penalty value is then calculated according to (13). The local search heuristic may be applied to the random initial solution to potentially obtain a 'good' initial solution for the algorithm. The initial temperature is calculated according to a method presented by Dréo et al. [17] as
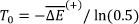
where 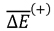 is the average increase in energy, estimated by executing a random walk over the solution space, using the random initial solution as the starting point.
is the average increase in energy, estimated by executing a random walk over the solution space, using the random initial solution as the starting point.
Candidate solutions are modified using the ejection chain neighbourhood move operator, and the Metropolis acceptance rule is followed if the neighbouring solution does not yield an improved objective function value. The modification iteration scheme during each temperature stage (proposed by Dréo et al. [17]) is followed, where the system reaches equilibrium when one of the following two conditions is satisfied: a maximum of 12n solutions are accepted, or a maximum of 100n solutions are attempted (modified).
Two cooling schedules are implemented in the algorithm to add functionality to the DSS. The 'standard' method uses the adaptive cooling schedule proposed by Van Laarhoven & Aarts [18], with a decreasing temperature function of
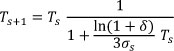
where Ts is the temperature at stage s, as is the standard deviation observed in the changing objective function values when reaching stage s, and δ is a 'small' number. The value is chosen as δ = 0.15/0.25/0.35, depending on which constraint sets are present. The standard method requires more computational time, but obtains a very high solution quality.
The 'quick' method uses the adaptive cooling schedule proposed by Huang et al. [19], with a decreasing temperature function of
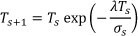
where λ e (0,1] is a constant, chosen here as λ = 0.6. The quick method is about 10 times faster than the standard method, but it results in a lower solution quality.
The incumbent solution is stored during the execution of the SA algorithm. On termination of the SA algorithm, the incumbent solution, and not the current solution, is returned as the final solution. The SA algorithm is hybridised by applying the local search heuristic to each new incumbent solution found during the algorithm's execution. The current solution remains unaffected. This hybrid local search/SA algorithm achieves superior results to those of the standard SA algorithm.
Finally, the hybridised SA algorithm terminates when the system is frozen - in this case when one of the following two conditions is satisfied: (i) the temperature at the current stage reaches a pre-specified minimum temperature Tmin = 1; or (ii) a pre-specified number, such as Ώfrozen = 3, of successive temperature stages occurs without any acceptance.
3.3 The decision support system
There are significant difficulties when attempting to solve different GMS problem instances using a generic methodology. The unknown, unique penalty weight values for the different constraint sets (dictated by different objective functions) have to be determined and, unfortunately, there is no general rule-of-thumb for determining these values. Furthermore, different GMS problem instances may perform differently for certain SA algorithm parameter values, increasing the difficulty of designing a generic solution methodology that performs well across the board.
The only way to determine the penalty weight values is to perform experiments during a penalty weight analysis (which is typically very time-consuming). In the DSS, a trade-off between penalty accuracy and computational time is achieved as follows. The penalty weight of a constraint set is set as 10fc, with k initially equal to zero. The remaining constraint sets have penalty weights set to a significantly large value so that any incumbent solution will not violate one of the remaining constraint sets. Ten problem instances are solved using an unmodified SA algorithm with the classical neighbourhood move operator, using the geometric cooling schedule as Ts+1 = 0.7TS. If seven or more of the problem instances result in feasible incumbent solutions, the penalty weight is chosen at its current value; otherwise the value of k is incremented by one, and the process is repeated. Due to the exponential increase in weight, the nature of the classical neighbourhood structure, and the small parameter value in the geometric cooling schedule, this trade-off attempts to keep the computational time for determining the penalty weights as short as possible.
The choices of initial temperature, neighbourhood move operator, cooling schedules, hybridisation, and parameter settings presented in the section above are all based on extensive experimentation done for three GMS benchmark test systems by Schlünz [20]. The aim was to obtain a representative/most appropriate SA algorithm to use for a general GMS problem instance, taking into account the solution quality and computational time of the results.
The generic solution methodology presented above was used for the development of a computerised decision support system that was capable of solving general GMS problem instances conforming to the MIQP presented in this paper. The DSS was implemented in the MathWorks software suite MATLAB version R2009a. It consists of a collection of MATLAB script files with a corresponding graphical user interface (GUI). The input and output files, containing the power system data and solution results respectively, are Microsoft Excel workbooks (version 2007 or later). The GUI of the DSS is shown in Figure 2. Some of the user options include the selection of the objective function and constraint sets of the problem instance, as well as which solution method to use.

Figure 2: Screenshot of the GUI of the DSS
4. CASE STUDY
The DSS was used to solve a large, real-life case study in the South African national power system, provided by Eskom (the South African electricity utility). The data do not represent the exact Eskom generation system, to maintain confidentiality. However, the case study does represent a realistic GMS scenario. Constraints in the scenario are restricted to the adherence to maintenance windows, the system meeting the load demand together with a safety margin, and respecting exclusion constraints.
The Eskom case study consists of a GMS problem instance containing 157 generating units requiring maintenance over a 365-day planning horizon - dimensions that are considerably larger than test systems in the literature. Within the MIQP formulation, the problem instance has 114 975 variables and 164 258 constraints (or 279 233 if constraint sets (11) and (12) are included). A theoretical lower bound on the objective function value is 10 501 819 298 MW2. The case study system specifications are available on request from the authors.
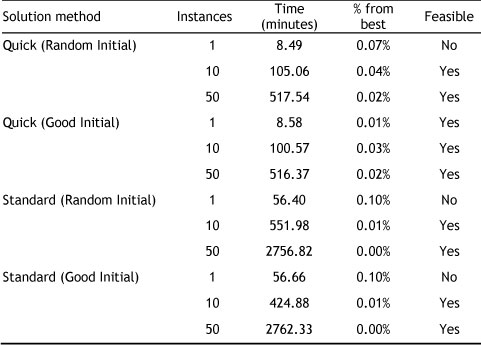
The best solution obtained by the DSS attained an objective function value of 11 101 712 702 MW2 with zero penalty which is only 5.7% from the theoretical lower bound. A summary of the DSS results for the Eskom data set is provided in Table 1. The percentage by which each objective function value differs from the best solution found is listed.
Table 1: Results obtained by the DSS on the Eskom case study
The best schedule obtained by the DSS is shown graphically in Figure 3. Notice that the schedule splits the maintenance into two parts over the year, corresponding to the times that have lower demand.
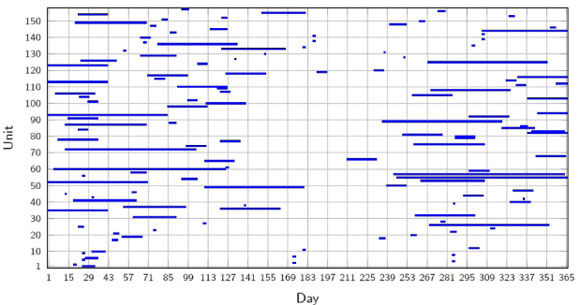
Figure 3: Best schedule obtained by the DSS on the Eskom case study
The load demand, safety margin, and available generating capacities over the planning horizon for the best schedule found are shown in Figure 4. Notice how constrained the problem instance becomes over the second half of the year, indicated by the close proximity of the safety margin and available capacity graphs.
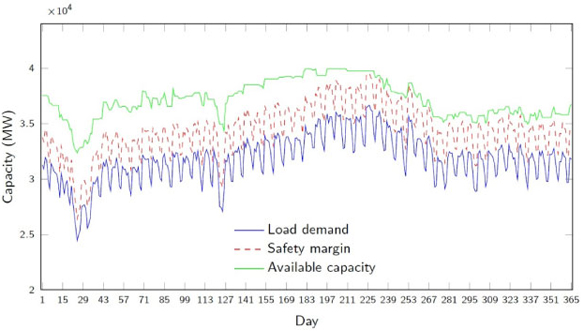
Figure 4: The load demand, safety margin, and available capacities over the planning horizon for the schedule in Figure 3
The actual reserve capacities over the planning horizon are shown in Figure 5 for the best schedule found. The graph indicates how the objective of levelling reserve loads was achieved approximately in two parts: the first part in the beginning of the year at a level close to the average reserve, and the second part in the latter half of the year at a lower level, since the problem was much more constrained during those time periods. The spikes in reserve are simply the result of short-term (weekly) fluctuations in the demand; the same capacity was available, but the demand was lower, creating a spike in reserve.
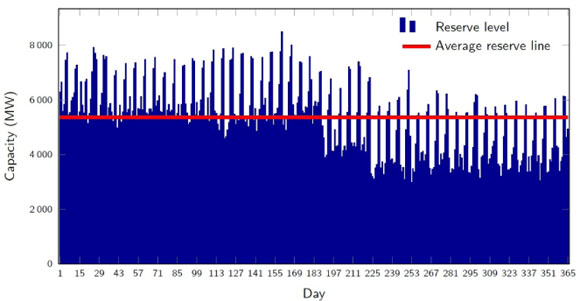
Figure 5: The reserve capacities over the planning horizon for the schedule in Figure 3
5. CONCLUSION
A general GMS model was presented in this paper, formulated as an MIQP. The model assumes a reliability objective that attempts to level the reserve loads over a planning horizon, subject to the constraints of respecting maintenance windows, meeting the load demand together with the safety margin, adhering to manpower limitations, and respecting exclusion constraints. A generic solution methodology was derived that is capable of solving general GMS problem instances conforming to this model, employing a hybridised SA algorithm. The methodology was implemented on a personal computer and presented in the form of a computerised DSS. The DSS was used to solve a large real-life GMS case study in the South African national power system. It proved to be highly effective by obtaining a best maintenance schedule for the problem instance, achieving an objective function value only 5.7% away from a theoretical lower bound.
REFERENCES
[1] Edwin, K.W. & Curtius, F. 1990. New maintenance-scheduling method with production cost minimization via integer linear programming, Electrical Power & Energy Systems, 12(3), pp. 165170. [ Links ]
[2] Kuzle, I., Pandzic, H. & Brezovec, M. 2007. Implementation of the benders decomposition in hydro generating units maintenance scheduling. Paper presented at the Hydro 2007 Conference: New Approaches for a New Era, Cairns. [ Links ]
[3] Kim, J.H., Park, J.B., Park, J.K. & Chun, Y.H. 2005. Generating unit maintenance scheduling under competitive market environments, Electrical Power & Energy Systems, 27, pp, 189-194. [ Links ]
[4] Sueyoshi, T. & Tadiparthi, G.R. 2008. An agent-based decision support system for wholesale electricity market, Decision Support Systems, 44, pp. 425-446. [ Links ]
[5] Dahal, K.P. & Chakpitak, N. 2007. Generator maintenance scheduling in power systems using metaheuristic-based hybrid approaches, Electric Power Systems Research, 77, pp. 771-779. [ Links ]
[6] Huang, C.J., Lin, C.E. & Huang, C.L. 1992. Fuzzy approach for generator maintenance scheduling, Electric Power Systems Research, 24, pp. 31-38. [ Links ]
[7] Moro, L.M. & Ramos, A. 1999. Goal programming approach to maintenance scheduling of generating units in large scale power systems, IEEE Transactions on Power Systems, 14(3), pp. 1021-1028. [ Links ]
[8] Kralj, B.L. & Petrovic, R. 1988. Optimal preventative maintenance scheduling of thermal generating units in power systems - A survey of problem formulations and solution methods, European Journal of Operational Research, 35, pp. 1-15. [ Links ]
[9] Ahmad, A. & Kothari, D.P. 1998. A review of recent advances in generator maintenance scheduling, Electric Power Components and Systems, 26(4), pp. 373-387. [ Links ]
[10] Canto, S.P. 2008. Application of Benders' decomposition to power plant preventive maintenance scheduling, European Journal of Operations Research, 184, pp. 759-777. [ Links ]
[11] Saraiva, J.T., Pereira, M.L., Mendes, V.T. & Sousa, J.C. 2011. A simulated annealing based approach to solve the generator maintenance scheduling problem, Electric Power Systems Research, 81, pp. 1283-1291. [ Links ]
[12] Yare, Y. & Venayagamoorthy, G.K. 2010. Optimal maintenance scheduling of generators using multiple swarms-MDPSO framework, Engineering Applications of Artificial Intelligence, 23, pp. 895-910. [ Links ]
[13] Lin, C.E., Huang, C.J., Huang, C.L., Liang, C.C. & Lee, S.Y. 1992. An expert system for generator maintenance scheduling using operation index, IEEE Transactions on Power Systems, 7(3), pp. 1141-1148. [ Links ]
[14] Savic, D.A., Bicik, J. & Morley, M.S. 2011. A DSS generator for multiobjective optimisation of spreadsheet-based models, Environmental Modelling & Software, 26, pp. 551-561. [ Links ]
[15] Kirkpatrick, S., Gelatt, C.D. & Vecchi, M.P. 1983. Optimization by simulated annealing, Science, 220, pp. 671-680. [ Links ]
[16] Satoh, T. & Nara, K. 1991. Maintenance scheduling by using simulated annealing method, IEEE Transactions on Power Systems, 6, pp. 850-857. [ Links ]
[17] Dréo, J., Pétrowski, A., Siarry, P. & Taillard, E. 2006. Metaheuristics for hard optimization - Methods and case studies, Springer-Verlag, Berlin. [ Links ]
[18] Van Laarhoven, P.J.M. & Aarts, E.H.L. 1987. Simulated annealing: Theory and applications, Reidel, Dordrecht. [ Links ]
[19] Huang, M.D., Romeo, F. & Sangiovanni-Vincentelli, A.L. 1986. An efficient general cooling schedule for simulated annealing, Proceedings of the IEEE International Conference on Computer-Aided Design, IEEE, Santa Clara, pp. 381-384. [ Links ]
[20] Schlünz, E.B. 2011. Decision support for generator maintenance scheduling in the energy sector. Masters thesis, Stellenbosch University. [ Links ]
* Corresponding author














